Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 87)

Đề bài. Cho tứ giác ABCD có AB = AD, CB = CD, $\widehat{C}=60°;\widehat{A}=100°$ .

a) Chứng minh AC là đường trung trực của BD.

b) Tính $\widehat{B},\widehat{D}$ .

Lời giải:

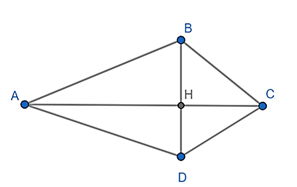
a) Theo giả thiết có AB = AD suy ra tam giác ABD cân tại A

Nên đường thẳng kẻ từ A xuống BD vừa là đường cao vừa là phân giác vừa là đường trung trực, tức A thuộc đường trung trực của BD. (1)

Lại có: CD = CB ⇒ Tam giác CBD cân tại C

⇒ Đường thẳng kẻ từ C xuống đáy BD vừa là đường cao vừa là phân giác vừa là đường trung trực, tức C thuộc đường trung trực của BD (2)

Từ (1) và (2): AC là đường trung trực của BD.

b) Xét ∆ABC và ∆ADC có:

AB = AD

BC = DC

AC chung

⇒ ∆ABC = ∆ADC (c.c.c)

⇒ $\widehat{ABC}=\widehat{ADC}$

Mà CH là phân giác của $\widehat{CBD}$ nên $\widehat{BCA}=\frac{1}{2}\widehat{BCD}=\frac{1}{2}.60°=30°$

AH là phân giác $\widehat{BAD}$ nên $\widehat{BAC}=\frac{1}{2}\widehat{BAD}=\frac{1}{2}.100°=50°$

Lại có trong tam giác ABC có: $\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180°$

⇒$\widehat{ABC}=180°-\left(\widehat{BAC}+\widehat{BCA}\right)=180°-50°-30°=100°$

Vậy $\widehat{ABC}=\widehat{ADC}=100°$ .