Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 25)

Câu 1: Cho a + b + c = 0 và a² + b² + c² = 14. Tính B = a⁴ + b⁴ + c⁴.

Lời giải:

Ta có: a + b + c = 0

(a + b + c)² = 0

a² + b² + c² + 2ab + 2ac + 2bc = 0

14 + 2(ab + ac + bc) = 0

2ab + 2bc + 2ac = -14

(2ab + 2bc + 2ac)² = 196

4a²b² + 4a²c² + 4b²c² + 8ab²c + 8a²bc + 8abc² = 196

4(a²b² + b²c² + c²a²) + 8abc(b + a + c) = 196

4(a²b² + b²c² + c²a²) = 196

2(a²b² + b²c² + c²a²) = 98

Ta có: a² + b² + c² = 14

(a² + b² + c²)² = 196

a⁴ + b⁴ + c⁴ + 2(a²b² + b²c² + a²c²) = 196

Mà 2(a²b² + b²c² + a²c²) = 98

a⁴ + b⁴ + c⁴ = 98

Vậy a⁴ + b⁴ + c⁴ = 98.

Câu 2: Chứng minh rằng với mọi số nguyên x, y thì:

A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y⁴ là số chính phương.

Lời giải:

Ta có: A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y⁴

= [(x + y)(x + 4y)][(x + 2y)(x + 3y)] + y⁴

= (x² + 5xy + 4y²)(x² + 5xy + 6y²) + y⁴

Gọi x² + 5xy + 4y² = a

A = a(a + 2y²) + y⁴

= a² + 2ay² + y⁴

= (a + y²)²

= (x² +  5xy + 4y² + y²)²

= (x² + 5xy + 5y²)²

Suy ra A là một số chính phương.

Câu 3: Theo kế hoạch, năm vừa qua nhà máy phải sản xuất 1250 sản phẩm. Đến hết năm, nhà sản xuất được 1375 sản phẩm. Hỏi năm vừa qua nhà sản xuất vượt mức kế hoạch bao nhiêu phần trăm?

Lời giải:

Năm vừa qua nhà máy sản xuất vượt mức kế hoạch số sản phẩm là :

1 375 – 1 250 = 125 (sản phẩm)

Năm vừa qua nhà máy sản xuất vượt mức kế hoạch :

$\frac{125}{1250}\times 100\%=10\%$

Đáp số: 10%.

Câu 4: Trong ngày đại hội thể dục thể thao, số học sinh của một trường khi xếp thành 12 hàng, 18 hàng và 21 hàng đều thừa 1 học sinh. Hỏi trường đó có bao nhiêu học sinh? (Biết số học sinh trong khoảng từ 500 đến 600).

Lời giải:

Gọi x (học sinh) là số học sinh của trường (x ∈ ℕ*; 500 < x < 600)

Theo bài ra, số học sinh của một trường khi xếp thành 12 hàng, 18 hàng, 21 hàng đều thừa 1 học sinh nên x – 1  chia hết cho 12; 18; 21

Hay x – 1 là ƯC(12, 18, 21).

Ta có: 12 = 2².3; 18 = 2.3²; 21 = 3.7.

BCNN(12, 18, 21) = 2².3².7 = 252

x – 1 = 252k (k ∈ ℕ*)

x = 252k +1

Mà 500 < x < 600

500 < 252k + 1 < 600

1,98 < k < 2,38

k = 2

Do đó x  = 2.252 + 1

x = 505

Vậy số học sinh của trường là 505.

Câu 5: Tìm thương của phép chia, biết rằng nếu thêm 15 vào số bị chia và thêm 5 vào số chia thì thương và số dư không thay đổi.

Lời giải:

Gọi số bị chia, số chia, thương và số dư lần lượt là a, b, c, d. Ta có:
a : b = c (dư d)
Hay a = c.b + d
Mặt khác theo bài cho ta có:

(a + 15) : (b + 5) = c (dư d)

a + 15 = c.(b + 5) + d
a + 15 = c.b + c.5 + d
Mà a = c.b + d nên:
a + 15 = c.b + c.5 + d
c.b + d + 15 = c.b + c.5 + d
15 = c.5
c = 3

Vậy thương của phép chia là 3.

Câu 6: Tính: $\frac{6^{2007}-6^{2006}}{6^{2006}}$.

Lời giải:
Ta có: $\frac{6^{2007}-6^{2006}}{6^{2006}}$

$=\frac{6^{2006}\left(6-1\right)}{6^{2006}}=5$.

Câu 7: Hệ thức lượng trong tam giác vuông.

Lời giải:

 

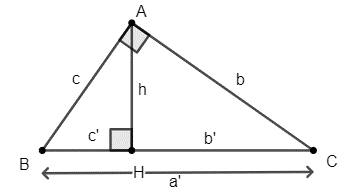
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó, ta có hệ thức sau:

• b² = ab’; c² = ac’

• h² = b’c’

• ah = bc

• b² + c² = a² (định lý Py-ta-go)

•  $\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}$

Câu 8: Thùng thứ nhất có 20 kg kẹo, thùng thứ hai có nhiều hơn thùng thứ nhất là 0,5 kg kẹo. Người ta đem toàn bộ số kẹo này đóng vào các hộp, mỗi hộp chứa 0,75 kg kẹo. Hỏi có bao nhiêu hộp kẹo?

Lời giải:

Thùng thứ hai có số kg kẹo là:

 20 + 0,5 = 20,5 (kg)

Tổng số ki-lô-gam kẹo của thùng thứ 1 và thùng thứ 2 là:

20 + 20,5 = 40,5 (kg)

Vậy số hộp kẹo là:

40,5 : 0,75 = 54 (hộp)

Đáp số: 54 hộp.

Câu 9: Một dãy phố có 100 nhà. Biết các số nhà đều có các số chẵn liên tiếp và tổng các số của các số nhà đó là 2 100. Số nhà đầu tiên của dãy này là bao nhiêu?

Lời giải:

Số nhà cuối cùng hơn số nhà đầu tiên là:

(100 − 1) ´ 2 = 198

Tổng của số nhà đầu tiên và cuối cùng là:

 2100 : (100 : 2) = 42.

Số nhà đầu tiên của dãy nhà là:

(198 − 42) : 2 = 78.

Đáp số: 78

Câu 10: Để lát một căn phòng, người ta dùng hết 200 viên gạch hình vuông có cạnh dài 40cm. Hỏi căn phòng đó có diện tích bao nhiêu mét vuông, biết diện tích phần mạch vữa không đáng kể?

Lời giải:

Diện tích viên gạch là :

40 × 40 = 1600 (cm²)

Vậy diện tích căn phòng là :

1600 × 200 = 320 000 (cm²) = 32 (m²).

Đáp số: 32 m².

Câu 11: 12 người may xong một lô hàng hết 5 ngày. Muốn may hết lô hàng đó sớm một ngày thì cần thêm mấy người (biết năng suất của mỗi người là như nhau)?

Lời giải:

Một người may hết lô hàng hết số ngày là:

5 ´ 12 = 60 (ngày)

Suy ra để may hết lô hàng sớm hơn 1 ngày (may xong trong 4 ngày) cần số người là:

60 : 4 = 15 ( người)

Vậy cần thêm số người là:

15 – 12 =  3 ( người)

 Đáp số: 3 người.

Câu 12: 15 người làm xong một đoạn đường hết 1 tuần. Hỏi 21 người làm xong đoạn đường đó trong bao nhiêu ngày ? (biết sức làm việc của mỗi người như nhau)

Lời giải:

Một người làm xong đoạn đường đó trong số ngày là:

15 ´ 7 = 105 (ngày)

Vậy 21 người làm xong đoạn đường đó trong số ngày là:

105 : 21 = 5 (ngày).

Đáp số: 5 ngày.

Câu 13: 20 người làm xong một công việc trong 7 ngày. Hỏi phải thêm bao nhiêu người để xong công việc đó sớm hơn 2 ngày? (biết năng suất làm việc của mỗi người như nhau)?

Lời giải:

Một người làm xong công việc trong số ngày là:

20 ´ 7 = 140 (ngày)

Số người làm việc để hoàn thành công việc sớm hơn 2 ngày (làm trong 5 ngày) là:

140 : 5 = 28 (người)

Khi đó, cần thêm số người để xong công việc đó sớm hơn 2 ngày là:

28 – 20 = 8 (người)

Đáp số: 8 người.

Câu 14: Đổi 15 kg 9 dag = … dag

Lời giải:

Ta có: 1 kg = 100 dag

Suy ra: 15 kg = 1500 dag

Vậy 15 kg 9 dag = 1509 dag.

Câu 15: Một khu đất hình vuông có chu vi là 1 km. Hỏi diện tích khu đất đó là bao nhiêu hecta?

Lời giải:

Đổi: 1 km = 1 000 m.

Chiều dài cạnh khu đất hình chữ nhật là:

1 000 : 4 = 250 (m)

Diện tích khu đất hình chữ nhật là:

250 ´ 250 = 62 500 (m²)

Đổi: 62 500 m² = 6,25 (ha)

Đáp số: 6,25 ha.

Câu 16: Một người gửi tiết kiệm 15 000 000 đồng với lãi suất 0,6% một tháng thì sau một tháng người đó thu được tất cả bao nhiêu tiền?

A. 15 090 000 đồng;

B. 15 080 000 đồng;

C. 15 085 000 đồng;

D. 15 100 000 đồng.

Lời giải:

Đáp án đúng là: A

Tiền lãi thu được sau 1 tháng là:

15 000 000 . 0,6% = 90 000 (đồng)

Tổng số tiền thu được sau 1 tháng là:

15 000 000 + 90 000 = 15 090 000 (đồng).

Vậy tổng số tiền thu được sau 1 tháng là 15 090 000 đồng.

Câu 17: Một đơn vị bộ đội chuẩn bị đủ gạo cho 70 người ăn trong 30 ngày. Sau khi ăn được 6 ngày thì 10 người chuyển đi nơi khác. Hỏi số gạo còn lại đó đơn vị ăn thêm được bao nhiêu ngày nữa so với dự kiến ban đầu? 

Lời giải:

Số phần ăn đã chuẩn bị là:

70 ´ 30 = 2 100 (phần ăn)

Sau 6 ngày thì số phần ăn đã ăn là:

70 ´ 6 = 420 (phần ăn)

Số phần ăn còn lại:

2100 – 420 = 1 680 (phần ăn)

Số người còn lại là:

70 – 10 = 60 (người)

Sau 6 ngày thì số gạo đó đủ ăn thêm:

1680 : 60 = 28 (ngày)

Tổng số ngày ăn được là:

6 + 28 = 34 (ngày)

Số gạo còn lại đơn vị ăn thêm số ngày là:

34 – 30 = 4 (ngày)

Đáp số: 4 ngày.

Câu 18: Một bếp ăn dự trữ đủ gạo cho 120 người ăn trong 18 ngày. Nay có 80 người chuyển đi nới khác. Hỏi số gạo đó đủ cho những người ăn còn lại trong bao nhiêu ngày? (mức ăn của mỗi người là như nhau)

Lời giải:

Sau khi chuyển đi 80 người thì còn lại số người là:

120 – 80  = 40 (người)

Lúc đầu, một người ăn hết số gạo đó trong số ngày là:

120 ´ 18 = 2160 (ngày)

40 người ăn hết số gạo đó trong số ngày là:

2160 : 40 = 54 (ngày)

Đáp số: 54 ngày.

Câu 19: Một người bán được một lượng gạo tẻ và gạo nếp, trong đó có 20 kg gạo nếp chiếm 25% tổng số gạo đã bán. Hỏi người đó bán được tất cả bao nhiêu ki-lô-gam gạo?

Lời giải:

Tổng số ki-lô-gam gạo đã bán được là:

20 : 25 ´ 100  = 80 (kg)

Đáp số: 80 kg.

Câu 20: Một người bán được một lượng gạo tẻ và gạo nếp, trong đó có 60 kg gạo tẻ chiếm 75% tổng số gạo đã bán. Hỏi người đó bán được tất cả bao nhiêu ki-lô-gam gạo?

A. 125 kg;          

B. 215 kg;           

C. 80 kg;     

D. 100 kg.

Lời giải:

Đáp án đúng là: C

Tổng số ki-lô-gam gạo đã bán được là:

60 : 75 ´ 100 = 80 (kg)

Đáp số: 80 kg.

Câu 21: Hai số có hiệu số là 95. Nếu xóa bỏ chữ số 5 ở tận cùng của số lớn thì ta đc số bé. Tìm tổng 2 số đó.

Lời giải:

Nếu số lớn xóa bỏ chữ số 5 ở tận cùng

Suy ra số lớn gấp 10 lần số bé và hơn 5 đơn vị.

Số bé là: (95 – 5) : (10 – 1) = 10

Số lớn là: 10 × 10 + 5 = 105 

Tổng của hai số đó là:

10 + 105 = 115.

Đáp số: 115.

Câu 22: Một đơn vị bộ đội chuẩn bị một số gạo đủ cho 50 người ăn trong 10 ngày, 3 ngày sau được tăng thêm 20 người. Hỏi đơn vị cần chuẩn bị thêm bao nhiêu suất gạo nữa để cả đơn vị đủ ăn trong những ngày sau đó? (Biết số gạo mỗi người ăn trong một ngày là một suất gạo).

Lời giải:

Sau khi ăn được 3 ngày, số gạo còn lại đủ cho 50 người ăn trong số ngày là:

10 – 3 = 7 (ngày)

Muốn ăn hết số gạo còn lại trong 1 ngày thì cần số người là:

50 × 7 = 350 (người)

Sau khi nhận thêm 20 người thì đơn vị có tổng số người là:

50 + 20 = 70 (người)

Số gạo còn lại đủ cho 70 người ăn trong số ngày là:

350 : 70 = 5 (ngày)

Số gạo còn lại hết sớm hơn dự tính số ngày là:

7 – 5 = 2 (ngày)

Đơn vị đó cần chuẩn bị thêm số suất ăn nữa là:

70 × 2 = 140 (suất)

Đáp số 140 suất.

Câu 23: Dấu hiệu chia hết cho 7.

Lời giải:

• Để nhận biết một số có thể chia hết cho 7, cắt giảm chữ số cuối cùng đi 1 số, nhân đôi chữ số đó và lấy số cắt giảm trừ đi số đã nhân đôi.

Điều này cần được thực hiện lặp đi lặp lại một vài lần, đến khi thu được một số có thể chia hết cho 7 (như 14, 7, 0, -7...) thì số đã cho chia hết cho 7. 

• Lấy chữ số đầu tiên nhân với 3, cộng thêm chữ số tiếp theo, được bao nhiêu lại nhân với 3 rồi cộng thêm chữ số tiếp theo ... cứ như vậy cho đến hết chữ số cuối cùng của số cần nhận biết.

Nếu kết quả cuối cùng này chia hết cho 7 thì số đó chia hết cho 7.

• Lấy chữ số đầu tiên bên phải nhân với 5 rồi cộng với chữ số thứ hai sau đó trừ cho bội của 7, được bao nhiêu nhân với 5 cộng với chữ số thứ 3 rồi trừ cho bội của 7, được bao nhiêu nhân với 5 cộng với chữ số thứ 4 rồi trừ cho bội của 7 ...

Nếu kết quả cuối cùng là một số chia hết cho 7 thì số đã cho chia hết cho 7.

Câu 24: Biết $\frac{7}{10}$ số học sinh của một lớp học là 21 em. Hỏi lớp học đó có bao nhiêu học sinh ?

Lời giải:

Chia số học sinh của lớp thành 10 phần bằng nhau, mỗi phần có:

21 : 7 = 3 (học sinh)

Số học sinh của lớp đó:

3 × 10 = 30 (học sinh)

Đáp số: 30 học sinh.

Câu 25: Phân tích đa thức thành nhân tử:
a) ax – bx – a² + 2ab – b²;

b) x² + 4x – y² + 4.

Lời giải:
a) ax – bx – a² + 2ab – b²

= (a – b)x – (a² – 2ab + b²)

= (a – b)x – (a – b)²

= (a – b)(x – a + b)

b) x² + 4x – y² + 4

= (x² + 4x + 4) – y²

= (x + 2)² – y²

= (x + 2 + y)(x + 2 – y)

Câu 26: Một người mua hai loại hàng và phải trả tổng cộng 2,17 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đố với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?

Lời giải:

Gọi x, y (triệu đồng) lần lượt là giá của loại hàng thứ nhất và thứ hai không tính VAT (x, y > 0, ; x < 2,17; y < 2,17).

Nếu áp dụng mức thuế VAT 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai thì :

+) Giá mặt hàng thứ nhất tính cả thuế VAT là: x + 10%.x = x + 0,1x = 1,1x

+) Giá mặt hàng thứ hai tính cả thuế VAT là: y + 8%.y = y + 0,08y = 1,08y.

Số tiền người đó phải trả là 2,17 triệu đồng nên ta có phương trình:

1,1x + 1,08y = 2,17   (1)

Nếu áp dụng mức thuế VAT 9% đối với cả hai loại hàng thì :

+) Giá mặt hàng thứ nhất tính cả thuế VAT là : x + 9%.x = x + 0,09x = 1,09x

 +) Giá mặt hàng thứ hai tính cả thuế VAT là : y + 9%.y = y + 0,09y = 1,09y.

Số tiền người đó phải trả là 2,18 triệu đồng nên ta có phương trình:

1,09x + 1,09y = 2,18 $\Rightarrow$ x + y = 2   (2)

Từ (1) và (2) ta có hệ phương trình :

$$\begin{gathered} \left\{\begin{array}{l}\mathrm{1,1}x+\mathrm{1,08}y=\mathrm{2,17}\\ x+y=2\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{1,1}x+\mathrm{1,08}y=\mathrm{2,17}\\ \mathrm{1,1}x+\mathrm{1,1}y=\mathrm{2,2}\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{0,02}y=\mathrm{0,03}\\ x+y=2\end{array}\right.\iff \left\{\begin{array}{l}y=\mathrm{1,5}\\ x=\mathrm{0,5}\end{array}\right. \end{gathered}$$

Vậy nếu không tính thuế VAT thì người đó phải trả: 0,5 triệu cho loại hàng thứ nhất và 1,5 triệu cho loại thứ 2.

Câu 27: Trung bình cộng của số thứ nhất và số thứ hai là 39. Trung bình cộng của số thứ hai và số thứ ba là 30. Trung bình cộng của số thứ nhất và số thứ ba là 36. Tìm ba số đó?

Lời giải:

Tổng của số thứ nhất và số thứ hai là: 39 ´ 2 = 78

Tổng của số thứ hai và số thứ ba là: 30 ´ 2 = 60

Tổng của số thứ nhất và số thứ ba là: 36 ´ 2 = 72

2 lần tổng của ba số là: 78 + 60 + 72 = 210

Tổng của ba số là: 210 : 2 = 105

Số thứ nhất là: 105 – 60 = 45

Số thứ hai là: 78 – 45 = 33

Số thứ ba là: 72 – 45 = 27

Đáp số: Số thứ nhất: 45;

Số thứ hai: 33;

Số thứ ba: 27.

Câu 28: Trung bình cộng của số thứ nhất và số thứ hai là 36, trung bình cộng của số thứ hai và số thứ ba là 44, trung bình cộng của số thứ nhất và số thứ ba là 40. Ba số đó là:

A. 36; 40 và 44;

B. 32; 40 và 48;

C. 32; 40 và 44;

D. 35; 40 và 44.

Lời giải:
Đáp án đúng là: B

Tổng của số thứ nhất và số thứ hai là: 36 ´ 2 = 72

Tổng của số thứ hai và số thứ ba là: 44 ´ 2 = 88

Tổng của số thứ nhất và số thứ ba là: 40 ´ 2 = 80

2 lần tổng của ba số là: 72 + 88 + 80 = 240

Tổng của ba số là: 240 : 2 = 120

Số thứ nhất là: 120 – 88 = 32

Số thứ hai là: 72 – 32 = 40

Số thứ ba là: 88 – 40 = 48

Vậy đáp án đúng là B.

Câu 29: Chứng minh rằng: n²(n + 1) + 2n(n + 1) luôn chia hết cho 6 với mọi số nguyên n.

Lời giải:

Ta có: n²(n + 1) + 2n(n + 1)

= (n² + 2n)(n + 1)

= n(n + 2)(n + 1)

Vì n và n + 1 là 2 số nguyên liên tiếp nên có một số chia hết cho 2

Suy ra n(n + 1) ⋮ 2

Vì n; n + 1; n + 2 là ba số nguyên liên tiếp nên trong ba số đó có một số chia hết cho 3.

Suy ra n(n + 1)(n + 2) $⋮$ 3 mà ƯCLN(2, 3) = 1

Vậy n(n + 1)(n + 2) $⋮$ 2.3 hay n(n + 1)(n + 2) $⋮$ 6 $\forall n\in \mathbb{Z}$.

Câu 30: Tìm x biết: (19x + 2.5²) : 14 = (13 – 8)² – 4²

Lời giải:
(19x + 2.5²) : 14 = (13 – 8)² – 4²

(19x + 2.25) : 14 = 5² – 4²

(19x + 50) : 14 = 25 – 16

(19x + 50) : 14 = 9

19x + 50 = 9.14

19x + 50 = 126

19x = 126 – 50 = 76

x = 76 : 19

x = 4

Vậy x = 4.

Câu 31: Một ô tô cứ đi 100 km thì tiêu thụ hết 12,5 lít xăng. Hỏi ô tô đó đi quãng đường dài 60 km thì tiêu thụ hết bao nhiêu lít xăng?

Lời giải:

Đi 1 km tiêu thụ số lít xăng là:

12,5 : 100 = 0,125 (l)

Vậy đi 60 km tiêu thụ số lít xăng là:

0,125 . 60 = 7,5 (l)

Đáp số: 7,5 lít xăng

Câu 32: Tình nhanh: A = 1 + 3 – 5 – 7 + 9 + 11 – 13 – 15 + … – 405 – 407 .

Lời giải:

A = 1 + 3 – 5 – 7 + 9 + 11 – 13 – 15 + … – 405 – 407

= 1 + (3 – 5) + (9 – 7) + (11 – 13) + (17 – 15) + … + (403 – 405) – 407

= 1 – 2 + 2 – 2 + 2 + … – 2 – 407

= 1 – 2 – 407 = –408

Câu 33: Dấu hiệu nhận biết hình vuông.

Lời giải:

Dấu hiệu nhậ biết hình vuông:

Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

Hình thoi có một góc vuông là hình vuông.

Hình thoi có hai đường chéo bằng nhau là hình vuông.

Câu 34: Tích của hai số là 625. Nếu gấp thừa số thứ nhất lên 2 lần và gấp thừa số thứ hai lên 3 lần thì tích mới là bao nhiêu?

Lời giải:

Do gấp thừa số thứ nhất lên 2 lần nên tích mới sẽ gấp lên 2 lần.

Do gấp thừa số thứ hai lên 3 lần nên tích mới sẽ gấp lên 3 lần.

Nếu gấp thừa số thứ nhất lên 2 lần và gấp thừa số thứ hai lên 3 lần thì tích mới gấp lên 2 × 3 = 6 (lần).

Vậy tích mới là 625 × 6 = 3750.

Câu 35: Một mảnh vải 8m giá 180 000 đồng. Người ta cắt ra 1,4 m để may áo với giá tiền công may áo là 20 000 đồng. Hỏi toàn bộ số tiền may chiếc áo đó là bao nhiêu?

Lời giải:

Giá tiền 1 m vải là:

180 000 : 8 = 22 500 (đồng)

Giá tiền 1,4 m vải là:

22 500 × 1,4 = 31 500 (đồng)

Toàn bộ số tiền để may chiếc áo đó là:

31 500 + 20 000 = 51 500 (đồng)

 Đáp án: 51 500 đồng

Câu 36: (−9 + 5²⁰²² : 5²⁰²¹) ´ 3 – 8

Lời giải:

(−9 + 5²⁰²² : 5²⁰²¹) ´ 3 – 8

= (−9 + 5^{2022 – 2021}) ´ 3 – 8

= (−9 + 5) ´ 3 – 8

= −4 ´ 3 – 8

= −12 – 8

= −20.

Câu 37: Hà viết tuổi của mình sau tuổi bố, rồi lấy số có bốn chữ số này trừ đi giá trị tuyệt đối của hiệu giữa tuổi của bố và con thì được số 4289. Tính tổng số tuổi của hai bố con Hà.

Lời giải:

Gọi tuổi của bố là ab, tuổi của con là cd (tuổi của bố không thể là số có 3 chữ số) và ab > cd, ta có tuổi của con viết sau tuổi của bố là abcd. Theo bài ra ta có :

abcd – (ab – cd) = 4289

 ab ´ 100 + cd − ab + cd = 4289

 ab ´ 99 + cd ´ 2 = 4289.

 ab ´ 99 = 4289 – cd ´ 2

Vậy (4289 − cd ´ 2) phải chia hết cho 99.

Vì cd là số có hai chữ số nên cd ´ 2 sẽ là số có hai chữ số hoặc số có ba chữ số nhưng nhỏ hơn 200.

Vậy 4 089 < 4 289 − cd ´ 2 < 4 269.

Trong các số từ 4 089 đến 4 269 thì chỉ có các số 4 158, 4 257 là chia hết cho 99.

• ab ´ 99 = 4 158. Suy ra ab = 42 và cd = (4289 − 4158) = 131 (loại, vì cd là số có hai chữ số)

• ab ´ 99 = 4 257. Suy ra ab = 43; cd = (4 289 − 4257) : 2 = 16 (thỏa mãn)

Đáp số: Bố 43 tuổi, con 16 tuổi.

Câu 38: Bạn An có khung tranh là hình bình hành ABCD với AB = 35 cm, AD = 30 cm. Độ dài viền khung tranh là bao nhiêu?

Lời giải:

Độ dài viền khung tranh chính là chu vi hình bình hành.

Vậy độ dài viền khung tranh là:

(35 + 30) ´ 2 = 65 ´ 2 = 130 (cm)

Đáp số: 130 cm.

Câu 39: Viết số thích hợp vào chỗ chấm:

a) 2,5 . 0,4 = 25 . 4 : … 

b) 2,5 . 0,4 = 25 . 4 . …

c) 0,8 . 0,06 = 8 ´ 6 : …

d) 0,8 . 0,06 = 8 . 6 . …

Lời giải:

a) 2,5 . 0,4 = 25 . 4 : 100 

b) 2,5 . 0,4 = 25 . 4 . 0,01

c) 0,8 . 0,06 = 8 . 6 : 1000

d) 0,8 . 0,06 = 8 . 6 . 0,001

Câu 40: Một hình trụ có bán kính mặt đáy bằng 5 cm. Thiết diện qua trục của hình trụ có diện tích bằng 40 cm² . Tính diện tích xung quanh của hình trụ.

Lời giải:

Ta có: 2r = 10; h.2r = 40

$\Rightarrow h=\frac{40}{2r}=\frac{40}{10}=4$.

Diện tích xung quanh của hình trụ là:

S_xq = 2πrh = 40π (cm²)

Vậy diện tích xung quanh của hình trụ là 40π cm².

Câu 41: Một đơn vị thanh niên xung phong chuẩn bị một số gạo đủ cho đơn vị ăn trong 30 ngày. Sau 10 ngày đơn vị nhận thêm 10 người nữa . Hỏi số gạo còn lại đó đơn vị sẽ đủ ăn trong bao nhiêu ngày, biết lúc đầu đơn vị có 90 người.

Lời giải:

Số suất ăn chuẩn bị cho 90 người trong 30 ngày là :

30 ´ 90 = 2 700 (suất)

Số suất ăn dành cho 90 người trong 10 ngày là :

10 ´ 90 = 900 ( suất)

Số suất ăn còn lại là :

2700 − 900 = 1 800 (suất)

Số người sau khi đến thêm là :

90 + 10 = 100 (người)

Số suất ăn còn lại đủ cho 100 người trong số ngày là :

1800 : 100 = 18 (ngày)

Đáp số: 18 ngày.

Câu 42: Có một cân hai đĩa. Một quả cân 5 kg và một quả cân 2 kg. Hỏi chỉ dùng hai lần cân làm thế nào để lấy được 1kg gạo từ thùng gạo to?

Lời giải:

Lần 1: Đặt quả cân 5 kg lên đĩa cân bên trái và cho quả cân 2 kg cùng với một số gạo lên đĩa cân bên phải sao cho hai đĩa cân bằng nhau.

Khi đó, mỗi đĩa cân nặng 5kg, số gạo cân được lúc này là 5 – 2 = 3 (kg).

Lần 2: lấy quả cân 5 kg ở đĩa cân bên trái xuống và chuyển quả cân 2 kg từ đĩa cân bên phải sang đĩa cân bên trái.

Sau đó ta thực hiện bớt chỗ gạo ở đĩa cân bên phải sao cho hai đĩa cân bằng nhau.

Số gạo đã bớt ra bằng: 3 – 2 = 1 (kg).

Câu 43: Chọn câu đúng trong các câu sau:

A. Tứ giác có 4 góc nhọn;        

B. Tứ giác có ba góc vuông, một góc nhọn;

C. Tứ giác có nhiều nhất hai góc tù, nhiều nhất hai góc nhọn;    

D. Tứ giác có ba góc nhọn, một góc tù.

Lời giải:

Đáp án đúng là C.

Câu 44: Tính: 3⁴ – 3³.

Lời giải:

Ta có 3⁴ – 3³ = 81 – 27 = 54.

Câu 45: Tính giá trị của lũy thừa sau:

a) 5.5.4.4.3.3;

b) 6.6.3.3.2.2;

c) 2.2.2.3.3.3;

Lời giải:

a) 5.5.4.4.3.3 = 5². 4².3²

= (5.4.3)² = 60².

b) 6.6.3.3.2.2 = 6².3².2²

= (6.3.2)² = 36².

c) 2.2.2.3.3.3 = 2³.3³

= (2.3)³ = 6³.

Câu 46: Mua 0,5 kg nho và 1 kg táo phải trả 60 000 đồng. Mua 1 kg nho và 0,5 kg táo phải trả 72 000 đồng. Tính giá tiền mua 1 kg nho, giá tiền mua 1 kg táo.

Lời giải:

Mua 0,5 kg nho và 1 kg táo phải trả 60 000 đồng.

Mua 1 kg nho và 0,5 kg táo phải trả 72 000 đồng.

Mua 1,5 kg nho và 1,5 kg táo phải trả số tiền là:

60 000 + 72 000 = 132 000 (đồng)

Giá của 1 kg nho và 1 kg táo là:

132 000 : 1,5 = 88 000 (đồng)

Giá trị của 1 kg nho là:
(88 000  – 60 000) . 2 = 56 000 (đồng)

Giá trị của 1 kg táo là:

(88 000 – 72 000) . 2 = 32 000 (đồng)

Đáp số: 1 kg nho: 56 000 đồng

1 kg táo: 32 000 đồng.

Câu 47: Hợp số là gì?

Lời giải:

Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn 2 ước.

Ví dụ: số 12 là hợp số do 12 = 3 . 4.

Câu 48: Tính tổng các góc ngoài của tứ giác, ngũ giác, thập giác.

Lời giải:

+) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của tứ giác (lồi) là 180°

 Tổng số đo các góc trong và góc ngoài của tứ giác là 4.180° = 720°

Mặt khác, tổng các góc trong của tứ giác là: (4 − 2).180° = 360°

 Tổng số đo các góc ngoài của tứ giác là: 720° − 360° = 360°.

+) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của ngũ giác (lồi) là 180°

 Tổng số đo các góc trong và góc ngoài của ngũ giác là 5.180° = 900°

Mặt khác, tổng các góc trong của ngũ giác là: (5 − 2).180° = 540°

 Tổng số đo các góc ngoài của ngũ giác là: 900° − 540° = 360°.

+) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của thập giác (lồi) là 180°

 Tổng số đo các góc trong và góc ngoài của thập giác là 10.180° = 1800°

Mặt khác, tổng các góc trong của thập giác là: (10 − 2).180° = 1440°

 Tổng số đo các góc ngoài của thập giác là: 1800° − 1440° = 360°.

Câu 49: Tính tổng các số nguyên âm lớn nhất có 1 chữ số, có 2 chữ, 3 chữ số.

Lời giải:

Số nguyên âm lớn nhất có 1 chữ số là: −1.

Số nguyên âm lớn nhất có 2 chữ số là: −10

Số nguyên âm lớn nhất có 3 chữ số là: −100

Vậy tổng của ba số trên là: −1 – 10 – 100 = −111.

Câu 50: Cho a + b + c = 0. Chứng minh a³ + b³ + c³ = 3abc.

Lời giải:

Ta có: a + b + c = 0

(a + b + c)³ = 0

a³ + b³ + c³ + 3a²b + 3ab² + 3b²c  + 3bc² + 3a²c + 3ac² + 6abc = 0

a³ + b³ + c³ + (3a²b + 3ab² + 3abc) + (3b²c + 3bc² + 3abc) + (3a²c + 3ac² + 3abc) – 3abc = 0

 a³ + b³ + c³ + 3ab(a + b + c) + 3bc(a + b + c) + 3ac(a + b + c) = 3abc

a³ + b³ + c³ = 3abc ( do a + b + c = 0) (đpcm)