Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 111)

482. Tính nhanh: 2² + 4² + 6² + ... + 20²

Phương pháp giải: 

Áp dụng công thức tổng các bình phương của n số tự nhiên

Lời giải:

483. 

Phương pháp giải: 

Vẽ hình: Vẽ hai đường thẳng cắt nhau tại một điểm. Đặt tên các điểm và góc rõ ràng.

Định nghĩa góc đối đỉnh: Hai góc đối đỉnh là hai góc có chung đỉnh, cạnh này là phần kéo dài của cạnh kia.

Góc bằng nhau: Theo tính chất, hai góc đối đỉnh luôn bằng nhau.

Lời giải:

484. Dấu hiệu chia hết cho 4; 11 là gì?

Phương pháp giải: 

Xét dấu hiệu chia hết theo đặc điểm của từng số:

Số 4: Dựa vào 2 chữ số cuối.

Số 11: Dựa vào hiệu của tổng các chữ số hàng chẵn và hàng lẻ.

Lời giải:

Dấu hiệu chia hết cho 11 là : Hiệu của tổng các chữ số hàng chẵn với tổng các chữ số hàng lẻ chia hết cho 11

Dấu hiệu chia hết cho 4 là : 2 chữ chữ số tận cùng tạo thành số chia hết cho 4.

486. Vườn rau nhà bạn Jenny có dạng hình chữ nhật, chiều dài 36m, chiều rộng 17m. Xung quanh vườn rau bố của Jenny làm đường đi với kích thước như hình vẽ. Tính diện tích của đường đi xung quanh vườn rau.

Phương pháp giải: 

Tính chiều dài và chiều rộng toàn bộ khu vườn:
Cộng thêm bề rộng đường đi ở cả hai bên (mỗi bên 1m) vào chiều dài và chiều rộng của khu vườn.

Tính diện tích toàn bộ khu vườn (gồm cả đường đi):
Áp dụng công thức tính diện tích hình chữ nhật: $\text{diện tích} = \text{chiều dài} \times \text{chiều rộng}$.

Tính diện tích trồng rau:
Diện tích trồng rau là diện tích của hình chữ nhật bên trong (không tính đường đi).

Tính diện tích đường đi:
Lấy diện tích toàn bộ khu vườn trừ diện tích trồng rau.

Lời giải:

​Chiều rộng khu vườn là: 17 + 2 = 19 (m)

Chiều dài khu vườn là: 36 + 2 = 38 (m)

Diện tích khu vườn là : 19 x 38 = 722 (m²)

Diện tích trồng rau là : 17 x 36 = 612 (m²)

Diện tích đường đi là : 722 – 612 = 110 (m²)

487. Cho phương trình :$\sin (x+\frac{\mathrm{\pi }}{3})-\sin 2x=0$

Giải phương trình trên, tìm nghiệm x€(0;2π)

Phương pháp giải: 

Sử dụng công thức lượng giác:

Áp dụng công thức $\sin A - \sin B = 2\cos\left(\frac{A + B}{2}\right)\sin\left(\frac{A - B}{2}\right)$ để đưa phương trình về tích.

Phân tích và giải phương trình tích:

Xét từng nhân tử bằng 0 để tìm nghiệm tổng quát.

Xác định nghiệm trong đoạn $(0; 2\pi)$:

Sử dụng điều kiện $x \in (0; 2\pi)$ để loại bỏ các nghiệm không thuộc đoạn này.

Lời giải:

488.  So sánh A = $\frac{1}{3} + \frac{1}{3^2} + \frac{1}{3^3} + ... + \frac{1}{3^{99}}$ với $\frac{1}{2}$

Phương pháp giải: 

Để so sánh, bài toán sử dụng tính chất của chuỗi hình học hội tụ. Cụ thể:

Với chuỗi hình học giảm $S = \frac{1}{r} + \frac{1}{r^2} + \dots$ (với $0 < r < 1$), tổng của chuỗi là:
$S = \frac{\frac{1}{r}(1 - r^n)}{1 - r},$
với $n$ là số hạng của chuỗi.

Trong bài toán, $r = 3$, nên $A = \frac{1 - \frac{1}{3^{99}}}{2}$​​ và suy ra $A < \frac{1}{2}$​.

Lời giải:

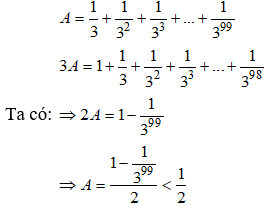
489. Một hình vuông có diện tích là 81cm². Tính chu vi của hình vuông đó

Phương pháp giải: 

Tính cạnh của hình vuông từ diện tích, biết diện tích $A = 81 \, \text{cm}^2$.

Dùng công thức chu vi hình vuông $C = 4 \times \text{cạnh}$ để tính chu vi.

Lời giải:

492. Một mảnh đất hình chữ nhật có chu vi bằng 28m và độ dài đường chéo bằng 10m. Tính chiều dài và chiều rộng của mảnh đất đó theo đơn vị mét.

Phương pháp giải: 

Gọi chiều dài mảnh đất là $x$ và chiều rộng là $y$, áp dụng công thức chu vi $2(x + y) = 28$ để tìm mối quan hệ giữa $x$ và $y$.

Áp dụng định lý Pythagoras $x^2 + y^2 = 100$ để tạo thành hệ phương trình.

Giải hệ phương trình $x + y = 14$ và $x^2 + y^2 = 100$ để tìm giá trị của $x$ và $y$.

Lời giải:

493. Chứng minh các biểu thức sau ko phụ thuộc vào biến:

B = ${(x-1)}^3-{(x+1)}^3+6(x+1)(x-1)$

Phương pháp giải: 

Mở rộng các biểu thức $(x - 1)^3$ và $(x + 1)^3$ bằng cách sử dụng công thức khai triển hằng đẳng thức.

Tính toán biểu thức $6(x + 1)(x - 1)$ và rút gọn.

Kết hợp và rút gọn các biểu thức để chứng minh rằng kết quả không còn phụ thuộc vào $x$.

Lời giải:

494. Cho tam giác ABC.Trên cạnh AB lấy điểm E sao cho AE = $\frac{2}{3}$AB.Trên cạnh AC lấy điểm D sao cho AD = $\frac{1}{3}$AC

Phương pháp giải: 

Tỷ số diện tích của hai tam giác cùng chung một đỉnh tỉ lệ với tỷ số các đoạn tương ứng trên các cạnh của tam giác.

Diện tích tam giác tỉ lệ với tích tỷ lệ các đoạn phân chia trên các cạnh.

Áp dụng công thức $\frac{\text{Diện tích tam giác ABD}}{\text{Diện tích tam giác ABC}} = \frac{AE}{AB} \times \frac{AD}{AC}$​ để tính tỷ số diện tích.

Lời giải:

Tỷ số diện tích của tam giác $ABD$ và tam giác $ABC$ là:

Thay các giá trị vào:

• $\frac{AE}{AB} = \frac{2}{3}$​,
• $\frac{AD}{AC} = \frac{1}{3}$​.

Vậy tỷ số diện tích là:

$\frac{\text{Diện t}\acute{\text{ı}}\text{ch tam gi}\acute{\text{a}}\text{c ABD}}{\text{Diện t}\acute{\text{ı}}\text{ch tam gi}\acute{\text{a}}\text{c ABC}}=\frac{2}{3}\times \frac{1}{3}=\frac{2}{9}\mathrm{.}$