Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 101)

Minh Nguyệt Ngày: 09-11-2024 Tổng hợp kiến thức

387

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 101)

Câu 1: Rút gọn biểu thức $a = 1 - 2 + 2^{2} - 2^{3} + 2^{4} - \dots - 2^{99} + 2^{100}$

Phương pháp giải:

Nhận diện chuỗi cấp số nhân với dấu xen kẽ, số hạng đầu $a_0$ và công bội $r$ .

Áp dụng công thức tổng của cấp số nhân với các giá trị cụ thể của $a_0$ , $r$ , và số lượng số hạng.

Thực hiện phép tính để rút gọn biểu thức.

Lời giải:

Ta xét biểu thức: $a = 1 - 2 + 2^{2} - 2^{3} + 2^{4} - \dots - 2^{99} + 2^{100}$

Biểu thức này là một chuỗi có dạng: $a = \sum_{k = 0}^{100} (- 2)^{k}$

Đây là một cấp số nhân với số hạng đầu $a_0 = 1$ và công bội $r = -2$ . Tổng của cấp số nhân gồm $n + 1$ số hạng (từ $k = 0$ đến $k = 100$ ) được tính theo công thức: $S = a_{0} \frac{1 - r^{n + 1}}{1 - r}$

Áp dụng vào trường hợp này, ta có:

$a_0 = 1$
$r = -2$
$n + 1 = 101$ (vì số mũ cuối là $100$ )

Khi đó: $a = \frac{1 - (- 2)^{101}}{1 - (- 2)}$

Mẫu số có dạng: $1 - (- 2) = 3$

Tử số có dạng: $1 - (- 2)^{101} = 1 + 2^{101}$

Khi đó: $a = \frac{1 + 2^{101}}{3}$

Vậy, biểu thức đã được rút gọn thành: $a = \frac{1 + 2^{101}}{3}$

Câu 2: So sánh A và B biết A = $\frac{2010}{2011} + \frac{2011}{2012} + \frac{2012}{2010}$ và B = $\frac{1}{3} + \frac{1}{4} + \frac{1}{5} + . . . + \frac{1}{17}$

Phương pháp giải:

Biến đổi và nhóm phân số trong $A$ : Sử dụng một đẳng thức để viết lại phân số $\frac{2012}{2010}$ và sau đó nhóm các phân số để đơn giản hóa biểu thức.

Ước lượng giá trị của $B$ : Sử dụng trung bình cộng của số hạng đầu và cuối để tính xấp xỉ tổng của $B$ .

So sánh giá trị xấp xỉ của $A$ và $B$ để suy ra kết luận $A > B$ .

Lời giải:

Ta có: $\frac{2012}{2010} = 1 + \frac{1}{2011} + \frac{1}{2012}$ (1)

Thay (1) vào A, ta có:

$\frac{2010}{2011} + \frac{2011}{2012} + 1 + \frac{1}{2011} + \frac{1}{2012}$

= $(\frac{2010}{2011} + \frac{1}{2011}) + 1 + (\frac{2011}{2012} + \frac{1}{2012})$

= 1+1+1 = 3 = $\frac{51}{17}$

Suy ra A = $\frac{51}{17}$

Ta có B = $\frac{1}{3} + \frac{1}{4} + \frac{1}{5} + . . . + \frac{1}{17}$ (có 15 số hạng)

B = $((\frac{1}{17} + \frac{1}{3}) . 15) \div 2$

B = $\frac{50}{17}$ (2)

Từ (1) và (2) => A > B

Câu 3: Tìm nghiệm nguyên của phương trình: $x^{2} - x y + y^{2} = x - y$

Phương pháp giải:

Chuyển đổi phương trình về dạng chuẩn.

Nhóm các hạng tử liên quan đến $x$ và viết dưới dạng phương trình bậc 2.

Tính delta để xác định điều kiện có nghiệm.

Giải bất phương trình liên quan để tìm giá trị của $y$ .

Thay giá trị của $y$ vào phương trình để tìm giá trị tương ứng của $x$ .

Lời giải:

$x^{2} - x y + y^{2} = x - y \Leftrightarrow x^{2} - x y + y^{2} - x + y = 0 \Leftrightarrow x^{2} - (y + 1) x + (y^{2} + y) = 0$

Trong phương trình bậc 2 theo $x$ , hệ số có dạng:

$a = 1, b = - (y + 1), c = y^{2} + y$

$Δ = b^{2} - 4 a c$

Thay vào ta có:

$Δ = (- (y + 1))^{2} - 4 (1) (y^{2} + y) = (y + 1)^{2} - 4 (y^{2} + y)$

$Δ = (y^{2} + 2 y + 1) - (4 y^{2} + 4 y) = - 3 y^{2} - 2 y + 1$

Để phương trình có nghiệm nguyên, $\Delta$ phải là một số chính phương. $- 3 y^{2} - 2 y + 1 \geq 0$

Ta giải bất phương trình này bằng cách tìm nghiệm của phương trình: $- 3 y^{2} - 2 y + 1 = 0$

$\Rightarrow Δ^{'} = (- 2)^{2} - 4 (- 3) (1) = 4 + 12 = 16$

Nghiệm của phương trình là: $y = \frac{- (- 2) \pm \sqrt{16}}{2 \cdot (- 3)} = \frac{2 \pm 4}{- 6}$

Nghiệm 1: $y = \frac{6}{-6} = -1$
Nghiệm 2: $y = \frac{-2}{-6} = \frac{1}{3}$

Vì $y$ là số nguyên, nên $y = -1$ là nghiệm duy nhất.

Thay $y = -1$ vào phương trình gốc: $x^{2} - (- 1) x + (- 1)^{2} = x - (- 1)$

$\Leftrightarrow x^{2} + x + 1 = x + 1$

$\Leftrightarrow x^{2} = 0 ⟹ x = 0$

Nghiệm nguyên của phương trình $x^2 - xy + y^2 = x - y$ là: $(x, y) = (0, - 1)$

Câu 4: Viết số 64 dưới dạng aⁿ với a thuộc Z . Có bao nhiên cách viết ?

Phương pháp giải:

Biến đổi số trên về dạng số có mũ sao cho số đó bằng số đề bài yêu cầu.

Lời giải:

Có 6 cách viết:

$64^{1} = 64$

$8^{2} = 64$

${(- 8)}^{2} = 64$

$2^{6} = 64$

${(- 2)}^{6} = 64$

$4^{3} = 64$

Câu 5: Tìm 2 số có hiệu bằng 56 biết số thứ 1 gấp 3 lần số thứ 2

Phương pháp giải:

Dựa vào điều kiện bài toán: Theo đề bài, số thứ nhất gấp 3 lần số thứ hai, nên ta có $S T 1 = 3 S T 2$ .

Lập phương trình từ hiệu của hai số: Ta biết hiệu giữa số thứ nhất và số thứ hai là 56..

Thay giá trị của ST1 từ phương trình đầu vào phương trình thứ hai và giải hệ phương trình.

Lời giải:

Vì số thứ nhất gấp 3 lần số thứ 2

=> Tỉ số giữa số thứ nhất và số thứ 2 là $\frac{3}{1}$

Ta có sơ đồ:

ST1: /-----/-----/-----/

ST2: /-----/ ( 56 )

Số thứ nhất là:

56 : (3 - 1) x 3 = 84

Số thứ hai là:

84 - 56 = 28

Đ/s: Vậy 2 số đó là 84 và 28

Phương pháp giải Tìm 2 số khi niết hiệu và tỉ số

Bước 1: Vẽ sơ đồ

Bước 2: Tìm hiệu số phần bằng nhau

Bước 3: Tìm số bé và số lớn

Số bé = Hiệu : hiệu số phần bằng nhau x số phần của số bé

Số lớn = Hiệu : hiệu số phần bằng nhau x số phần của số lớn

Bước 4: Kết luận, đáp số

Câu 6: Tìm x biết: $5^{2 x - 3} - 2 . 5^{2} = 5^{2} . 3$

Phương pháp giải:

Đưa về cùng cơ số: Tìm cách để tất cả các biểu thức đều là lũy thừa của 5.

Đơn giản hóa phương trình: Chuyển các hạng tử có cùng cơ số về một bên của phương trình và giải để tìm giá trị của $x$ .

Lời giải:

$5^{2 x - 3} - 2 . 5^{2} = 5^{2} . 3$

$5^{2 x - 3} = 2. 5^{2} + 5^{2} . 3$

5^{2x - 3} = 5²(2 + 3)

5^{2x - 3} = 5².5

5^{2x - 3} = 5³

$2 x - 3 = 3$

$2 x = 3 + 3$

$2 x = 6$

$x = 6 : 2 = 3$

$\Rightarrow x = 3$

Câu 7: Từ 200 số tự nhiên 1;2;3;...;200, ta lấy ra k số bất kì sao cho trong các số vừa lấy luôn tìm được 2 số mà số này là bội của số kia. Tìm giá trị nhỏ nhất của k.

Phương pháp giải:

Xây dựng tập hợp không có số nào là bội của số khác:

Chọn 100 số lẻ từ 1 đến 199. Trong tập hợp này, không có số nào là bội của số khác.

Sử dụng nguyên lý Dirichlet khi chọn 101 số:

Khi chọn 101 số từ tập $\{1, 2, 3, \dots, 200\}$ , theo nguyên lý Dirichlet, ít nhất một số trong đó sẽ là chẵn.

Biểu diễn các số dưới dạng $2^a \cdot b$ :

Mỗi số có thể viết dưới dạng $2^a \cdot b$ với $b$ là số lẻ.

Với 101 số đã chọn, sẽ có ít nhất hai số có cùng $b$ nhưng khác số mũ $a$ , làm cho một số là bội của số kia.

Kết luận.

Lời giải:

Xét $k = 100$ ta dễ dàng tìm được tập số có n số mà trong đó không có số nào là bội của số kia. ${101; 102; . . .; 200}$

Ta chứng minh với $k = 101$ thì bài toán đúng

Ta lấy ra ngẫu nhiên 101 số từ tập hợp 200 số đã cho ${a_{1}; a_{1}; . . .; a_{101}}$

Ta biểu diễn 101 số này thành dạng

$a_{1} = 2^{x_{1}} . b_{1}; a_{2} = 2^{x_{2}} . b_{2}; . . .; a_{101} = 2^{x_{101}} . b_{101}$

Với $x_{1}; x_{2}; . . .; x_{101}$ là các số tự nhiên, $b_{1}; b_{2}; . . .; b_{101}$ là các số lẻ và $1 \leq b_{1}; b_{2}; . . .; b_{101} \leq 199$

Ta thấy rằng từ 1 đến 199 có tất cả 100 số lẻ vì thế trong 101 số đã chọn ra tồn tại $m > n$ sao cho $b_{m} = b_{n}$ . Hai số này chính là bội của nhau.

Vậy với k nhỏ nhất là 101 thì thỏa mãn yêu cầu bài toán.

Câu 8: Cho các số dương a, b, c, d có tích bằng 1

CMR: $a^{2} + b^{2} + c^{2} + d^{2} + a b + c d \geq 6$

Phương pháp giải:

Áp dụng bất đẳng thức Cauchy-Schwarz: $a^2 + b^2 + c^2 + d^2 + ab + cd \geq 2ab + 2bc + 2ab + cd = 3(ab + cd)$ .

Tiếp tục sử dụng các biến đổi để đưa về dạng bất đẳng thức cần chứng minh với tổng tối thiểu là 6.

Lời giải:

Áp dụng bất đẳng thức: $x^{2} + y^{2} \geq 2 x y$ ta có:

$a^{2} + b^{2} + c^{2} + d^{2} + a b + c d \geq 2 a b + 2 b c + a b + c d = 3 (a b + c d)$

Mặt khác: $3 (a b + c d) = 3 (a b + \frac{a b c d}{a b}) = 3 (a b + \frac{1}{c d}) \geq 3.2 = 6$ $(B Đ T : \frac{a}{b} + \frac{b}{a} \geq 2)$

Vậy $a^{2} + b^{2} + c^{2} + d^{2} + a b + c d \geq 6$ (đpcm)

Câu 9: Tìm x biết: $5^{x} + 5^{x - 3} = 3150$

Phương pháp giải:

Đưa về cùng cơ số: Tìm cách để tất cả các biểu thức đều là lũy thừa của 5.

Đơn giản hóa phương trình: Chuyển các hạng tử có cùng cơ số về một bên của phương trình và giải để tìm giá trị của $x$ .

Lời giải:

$5^{x} + 5^{x} . 5^{- 3} = 3150$

$5^{x} . (1 + 5^{- 3}) = 3150$

$5^{x} . \frac{126}{125} = 3150$

5^x = $3150 : \frac{126}{125}$

$5^{x} = 3125$

$5^{x} = 5^{5}$

=> x = 5

Câu 10: Tính nhanh:

a) 1 + 2 + 3 + 4 + ... + 2001 + 2002

b) 2 + 4 + 6 + 8 + ... + 100

c) 132 + 128 + 124 + ... + 76 + 72 + 68

Phương pháp giải:

Tổng của một cấp số cộng: Nếu dãy số có dạng $a, a+d, a+2d, \ldots, l$ với:

Số hạng đầu là $a$ ,

Công sai là $d$ ,

Số hạng cuối là $l$ ,

thì tổng của $n$ số hạng đầu được tính theo công thức: $S_{n} = \frac{n}{2} (a + l)$ hoặc $S_{n} = \frac{n}{2} \cdot (2 a + (n - 1) d)$ với $n$ là số lượng các số hạng trong dãy.

Lời giải:

a, 1 + 2 + 3 + 4 + .... + 2001 + 2002

= (2002 + 1). 2002 : 2

= 2003.1001

= 2005003

b, $2 + 4 + 6 + 8 + ... . + 100$

$= (2 + 100) + (4 + 98) + (6 + 96) + (8 + 94) + ...$

$= 102 + 102 + 102 + 102 + ...$

$= 102 \times 25$

$= 2550$

c, Số các số hạng là :

(132 - 68) : 4 + 1 = 17 ( số hạng )

Tổng là :

(132 + 68) x 17 : 2 = 1700

Đáp số: 1700

Câu 11: Một thửa đất hình chữ nhật có chu vi là 56m. Nếu giảm chiều rộng 2m và tăng chiều dài 4m thì diện tích tăng thêm 8 m² . Tìm chiều rộng và chiều dài thửa đất.

Phương pháp giải:

Gọi chiều rộng của thửa đất là $x$ (m), suy ra chiều dài là $28 - x$ (m) dựa vào chu vi.

Lập biểu thức diện tích ban đầu là $x \cdot (28 - x)$ .

Sau khi thay đổi chiều rộng và chiều dài, diện tích mới là $(x - 2)(32 - x)$ .

Thiết lập phương trình dựa trên việc diện tích tăng thêm 8 m²: $x (28 - x) + 8 = (x - 2) (32 - x)$

Giải phương trình để tìm $x$ và từ đó suy ra chiều rộng và chiều dài.

Lời giải:

Gọi chiều rộng của thửa đất là x (m) (x > 2)

Nửa chu vi của thửa đất là: 56:2 = 28(m)

Chiều dài của thửa đất là 28 – x (m)

Diện tích của thửa đất là x(28 – x) (m²)

Khi tăng chiều dài lên 4m, giảm chiều rộng đi 2m ta có diện tích là

(x – 2)(28 – x + 4) = (x – 2)(32 – x) ( m² )

Khi đó diện tích tăng thêm 8 m 2 nên ta có phương trình.

x(28 – x) + 8 = (x – 2)(32 – x))

⇔ 28 x – x 2 + 8 = 34 x – x 2 – 64

⇔ 6x = 72 ⇔ x = 12 (tmđk)

Vậy chiều rộng của thửa đất là 12m, chiều dài thửa đất là 28 – 12 = 16m.

Phương pháp giải: Giải bài toán bằng cách lập phương trình

Bước 1. Lập phương trình:

+ Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.

+ Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình.

Bước 3. Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.

Câu 12: Cho hình thoi ABCD cạnh a có góc A = 60◦.Một đường thẳng bất kì đi qua C cắt tia đối của các tia BA và DA theo thứ tự tại M và N.

a) Chứng minh rằng tích BM.DN có giá trị không đổi.

b) Gọi K là giao điểm của BN và DM. Tính góc BKD

Phương pháp giải:

a) Sử dụng các tính chất của hình thoi và tam giác đồng dạng để chứng minh tích $BM \cdot DN$ không đổi.

Tìm mối liên hệ giữa các đoạn thẳng và các góc trong tam giác để chứng minh $\triangle MBC$ đồng dạng với $\triangle CDN$ .

Từ sự đồng dạng, suy ra tỉ số các cạnh tương ứng và chứng minh tích $BM \cdot DN$ không đổi.

b) Sử dụng tính chất của tam giác đều và tam giác đồng dạng để tính góc $\angle BKD$ .

Chứng minh tam giác $\triangle ABD$ là tam giác đều.

Sử dụng tính chất tam giác đồng dạng và các góc trong tam giác để xác định góc $\angle BKD$ .

Lời giải:

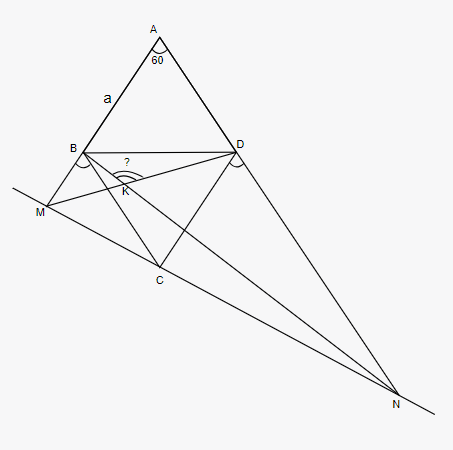
Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 101) (ảnh 1)

a) Ta có : $\hat{A B C} = 12 0^{o} \Rightarrow \hat{M B C} = 18 0^{o} - 12 0^{o} = 6 0^{o}$

Tương tự $\hat{C D N} = 6 0^{o}$ => $\hat{M B C} = \hat{C D N}$ (1)

Mặt khác: $\hat{B M C} = \hat{B C D} = 6 0^{o}$ , Hai góc này ở vị trí so le trong

=> BM//CD

=> $\hat{B M C} = \hat{D C N}$ ( đồng vị ) (2)

Từ (1) , (2)

=> MBC đồng dạng với CDN (g-g)

=> $\frac{B M}{D C} = \frac{B C}{D N} \Rightarrow B M . D N = B C . D C = a^{2}$ Không đổi

b) Xét tam giác ABD có: AB=AD =a => ABD cân và góc A bằng 60 độ

=> Tam giác ABD đều

=> AB=BD=AD=a

và $\hat{M B D} = 18 0^{o} - \hat{A B D} = 18 0^{o} - 6 0^{o} = 12 0^{o}$

Tương tự $\hat{B D N} = 12 0^{o}$

=> $\hat{M B D} = \hat{B D N}$ (3)

Ta lại có: $M B . D N = a^{2} = B D . B D \Rightarrow \frac{M B}{B D} = \frac{B D}{D N}$ (4)

Từ (3), (4) Suy ra ΔBMD=ΔDBN(c.g.c)

=> $\hat{B M D} = \hat{D B N}$

=> $\hat{B K D} = \hat{K B M} + \hat{B M K} = \hat{N B M} + \hat{B M D} = \hat{N B M} + \hat{D B N} = \hat{D B M} = 12 0^{o}$ .

Câu 13: Quãng đường AD dài 9 km, gồm đoạn AB lên dốc, đoạn BC nằm ngang, đoạn CD xuống dóc. 1 người người đi bộ từ A đến D rồi quay trở về A hết tất cả 3h41'. Tính quãng đường BC, biết vận tốc lúc lên dốc của người đó là 4km/h, lúc xuống dốc là 6km/h và lúc đi nằm ngang là 5km/h.

Phương pháp giải:

Gọi độ dài đoạn $BC$ (đoạn nằm ngang) là $x$ km.

Tính tổng độ dài quãng đường cả đi lẫn về cho từng đoạn lên dốc, xuống dốc và nằm ngang.

Thiết lập phương trình thời gian dựa trên tổng thời gian cả đi lẫn về là 3 giờ 41 phút (hay 3,6833 giờ).

Giải phương trình để tìm giá trị của $x$ (quãng đường $BC$ ).

Lời giải:

Gọi độ dài đoạn nằm ngang $B C$ là $x (k m) (0 < x < 9)$

Độ dài đoạn nằm ngang $B C$ cả đi lẫn về là $2 x (k m)$

Tổng độ dài 2 đoạn $A B + C D$ cả đi lẫn về là $18 - 2 x (k m)$ .

Độ dài đoạn lên dốc cả đi lẫn về là $9 - x (k m)$

Độ dài đoạn xuống dốc cả đi lẫn về là $9 - x (k m)$

Thời gian lên dốc cả đi lẫn về là $\frac{9 - x}{4} (h)$

Thời gian xuống dốc cả đi lẫn về là $\frac{9 - x}{6} (h)$

Thời gian đi hết đoạn nằm ngang cả đi lẫn về là $\frac{2 x}{5} (h)$

Vì thời gian đi hết quãng đường $A D$ cả đi lẫn về là 3 giờ 41 phút $= \frac{221}{60} (h)$

nên ta có pt: $\frac{9 - x}{4} + \frac{2 x}{5} + \frac{9 - x}{6} = \frac{221}{60}$

$\Leftrightarrow 15 (9 - x) + 24 x + 10 (9 - x) = 221 \Leftrightarrow 135 - 15 x + 24 x + 90 - 10 x = 221 \Leftrightarrow 225 - x = 221 \Leftrightarrow x = 4 (T / m)$

Vậy độ dài đoạn nằm ngang $B C$ là $4 (k m)$ .

Phương pháp giải: Giải bài toán bằng cách lập phương trình

Bước 1. Lập phương trình:

+ Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.

+ Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình.

Bước 3. Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.

Câu 14: Cho $\frac{a}{b} = \frac{c}{d}$ . Chứng minh: $\frac{a - c}{a + c} = \frac{b - d}{b + d}$

Phương pháp giải:

Áp dụng tính chất của dãy tỉ số bằng nhau để giải bài toán trên:

Toán lớp 7 | Lý thuyết - Bài tập Toán 7 có đáp án

Lời giải:

Áp dụng tính chất của dãy tỉ số bằng nhau,ta có :

$\frac{a}{b} = \frac{c}{d} = \frac{a - c}{b - d} = \frac{a + c}{b + d}$

$\Rightarrow \frac{a - c}{a + c} = \frac{b - d}{b + d}$

Câu 15: Tính nhanh : 998 x 2 + 2 x 2 = ?

Phương pháp giải:

Nhóm các số hạng để tính nhanh bằng cách đặt làm thừa số chung.

Lời giải:

998 x 2 + 2 x 2

= 2 x (998 + 2)

= 2 x 1000

= 2000

Mở rộng:

Tính nhanh : 5 x 10 + 7 x 10 - 10 x 2

= 10x(5 + 7 - 2)

= 10 x 10

= 100

Câu 16: Tìm số nguyên tố p nhỏ nhất sao cho p + 2 và p + 4 cũng là số nguyên tố.

Phương pháp giải:

Xét các trường hợp của và kiểm tra tính nguyên tố của và để tìm số nguyên tố nhỏ nhất thỏa mãn điều kiện.

Lời giải:

Nếu p = 2 thì p + 2 = 2 + 2 = 4 không là số nguyên tố

2 + 4 = 6 không là số nguyên tố

Vậy p = 2 không thỏa mãn

Nếu p = 3 thì p + 2 = 3 + 2 = 5 là số nguyên tố

3 + 4 = 7 là số nguyên tố

Vậy p = 3 thỏa mãn

Nếu p > 3 thì p = 3k + 1 hoặc p = 3k + 2

Khi p = 3k + 1 thì p + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1) không là số nguyên tố

Vậy p = 3k + 1 không thỏa mãn

Khi p = 3k + 2 thì p + 4 = 3k + 2 + 4 = 3k + 6 = 3(k + 2) không là số nguyên tố

Vậy p = 3k + 2 không thỏa mãn

Vậy p = 3 thỏa mãn duy nhất.

Câu 17: Tính: $\frac{45}{9} - \frac{45}{10}$

Phương pháp giải:

Quy đồng 2 phân số sao cho về cùng mẫu số và thực hiện phép tính

Lời giải:

$= \frac{450 - 405}{90}$

$= \frac{45}{90} = \frac{1}{2}$

Cách quy đồng mẫu số các phân số:

Khi quy đồng mẫu số hai phân số có thể làm như sau:

- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.

- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

Chú ý: ta thường lấy mẫu số chung là số tự nhiên nhỏ nhất khác 0 và cùng chia hết cho tất cả các mẫu.

Câu 18: Tìm các số nguyên dương x, y sao cho 8x³ + y³ - 6xy + 1 là số nguyên tố

Phương pháp giải:

Phân tích biểu thức 8x³ + y³ - 6xy + 1 thành tích các thừa số để tìm điều kiện cần thiết thỏa mãn cho giá trị này là số nguyên tố.

Lời giải:

$8 x^{3} + y^{3} - 6 x y + 1 = {(2 x + y)}^{3} - 6 x y (2 x + y) - 6 x y + 1$

$\Leftrightarrow (2 x + y + 1)$ $[{(2 x + y)}^{2} - (2 x + y) + 1 - 6 x y]$

$\Leftrightarrow (2 x + y + 1)$ $(4 x^{2} + y^{2} - 2 x - y - 2 x y + 1)$

$\Leftrightarrow {\begin{cases} 2 x + y + 1 = 1 \\ 4 x^{2} + y^{2} - 2 x - y - 2 x y + 1 = 1 \end{cases}$

Trường hợp 1: $2x + y + 1 = 1$

$2x + y + 1 = 1 \Rightarrow 2x + y = 0$

Vì $x$ và $y$ là các số nguyên dương, nên $2x + y = 0$ không thể xảy ra. Do đó, không có giá trị nào của $x$ và $y$ thỏa mãn trong trường hợp này.

Trường hợp 2: $4x^2 + y^2 - 2xy - 2x - y + 1 = 1$

Ta có:

$4x^2 + y^2 - 2xy - 2x - y + 1 = 1$

Rút gọn phương trình:

$4x^2 + y^2 - 2xy - 2x - y = 0$

Để giải phương trình này, ta sẽ thử các giá trị nhỏ của $x$ và $y$ để tìm các nghiệm nguyên dương.

Với $x = 1$ :

Khi $x = 1$ , ta thay vào phương trình:

$4 (1)^{2} + y^{2} - 2 \cdot 1 \cdot y - 2 \cdot 1 - y = 0 4 + y^{2} - 2 y - 2 - y = 0 y^{2} - 3 y + 2 = 0$

Phương trình này có nghiệm:

$y = 1 hoặc y = 2$

Vậy ta có các cặp nghiệm $(x, y) = (1, 1)$ và $(x, y) = (1, 2)$ .

Với $x = 2$ :

Khi $x = 2$ , ta thay vào phương trình:

$4 (2)^{2} + y^{2} - 2 \cdot 2 \cdot y - 2 \cdot 2 - y = 0 16 + y^{2} - 4 y - 4 - y = 0 y^{2} - 5 y + 12 = 0$

Phương trình này không có nghiệm nguyên dương.

Từ các trường hợp trên, các cặp số nguyên dương $(x, y)$ thỏa mãn bài toán là:

$(x, y) = (1, 1)$

$(x, y) = (1, 2)$

Kết luận

Các cặp số nguyên dương $(x, y)$ thỏa mãn để $8x^3 + y^3 - 6xy + 1$ là số nguyên tố là: $(x, y) = (1, 1) v \overset{ˋ}{a} (x, y) = (1, 2)$

Câu 19: Cho hình thang ABCD (AB//CD) có $\hat{A} = 120 °$ .

a, Tính $\hat{D}$ .

b, Biết $\frac{\hat{D}}{\hat{B}} = \frac{1}{2}$ , Tính $\hat{B}, \hat{C}$

Phương pháp giải:

Sử dụng tính chất của hình thang cân để tính góc.

- Trong hình thang cân hai cạnh bên bằng nhau.

- Trong hình thang cân hai đường chéo bằng nhau.

Sử dụng mối quan hệ giữa các góc trong tam giác và tính chất góc trong hình thang để tìm các góc còn lại.

Lời giải:

AB song song CD trong hình thang cân

$\Leftrightarrow \hat{A} + \hat{D} = 18 0^{o}$

$\Leftrightarrow \hat{D} = 18 0^{o} - 12 0^{o}$

$\Leftrightarrow \hat{D} = 6 0^{o}$

$\frac{\hat{D}}{\hat{B}} = \frac{1}{2}$

$\Leftrightarrow \hat{B} = 12 0^{o}$

$\hat{C} = 18 0^{o} - \hat{D} = 6 0^{o}$

Câu 20: Giá bán một máy thu thanh là 425000 đồng. Sau 2 lần giảm giá liên tiếp, mỗi lần giảm 10% giá trước đó thì giá bán của máy thu thanh còn bao nhiêu đồng?

Phương pháp giải:

Tính số tiền giảm giá ở mỗi lần giảm (10% của giá trước đó).

Trừ số tiền giảm được từ giá hiện tại để tìm giá sau mỗi lần giảm.

Thực hiện các bước trên hai lần để tìm giá bán cuối cùng.

Lời giải:

Lần thứ nhất giá bán máy đó được giảm:

425 000 : 100 x 10 = 42 500 (đồng)

Giá bán chiếc máy sau khi giảm lần thứ nhất là:

425 000 - 42 500 = 382 500 (đồng)

Lần thứ hai giá bán máy đó được giảm:

382 500 : 100 x 10 = 38 250 (đồng)

Sau hai lần giảm giá thì giá bán chiếc máy đó là:

382 000 - 38 250 = 344 250 (đồng)

Đ/S: 344 250 đồng.

Câu 21: Hai người đi xe máy cùng khởi hành từ A và B cách nhau 106,25km và đi ngược chiều nhau. Sau 1 giờ 15 phút họ gặp nhau tại một điểm trên quãng đường AB. Tìm vận tốc của mỗi xe biết rằng xe máy đi từ A với vận tốc bằng 8/9 vận tốc xe máy đi từ B.

Phương pháp giải:

Đổi thời gian gặp nhau từ 1 giờ 15 phút sang đơn vị giờ.

Tính tổng vận tốc của hai xe bằng cách chia quãng đường cho thời gian gặp nhau.

Sử dụng tỉ lệ vận tốc giữa hai xe để phân chia tổng vận tốc theo tỉ lệ $8 : 9$ .

Tính vận tốc của từng xe dựa vào tổng vận tốc và tỉ lệ đã cho.

Lời giải:

Đổi: 1 giờ 15 phút = 1,25 giờ

Tổng vận tốc hai xe là:

106,25 : 1,25 = 85 (km/giờ)

Ta có sơ đồ:

Vận tốc xe thứ nhất /.../.../.../.../.../.../.../.../

Vận tốc xe thứ hai /.../.../.../.../.../.../.../.../.../ 85 km/giờ

Vận tốc xe thứ nhất là: 85 : (9 + 8) x 8 = 40 (km/giờ)

Vận tốc xe thứ hai là: 85 - 40 = 45 (km/giờ)

Đáp số: Vận tốc xe thứ nhất: 40 km/giờ

Vận tốc xe thứ hai: 45 km/giờ

Câu 22: Tổng của 2 số là 43,75. Nếu thêm vào số lớn 3,6 và bớt số bé đi 2,5 thì hiệu mới của hai số là 20,15. Tìm hai số đó.

Phương pháp giải:

Khi thêm vào số lớn 3,6 và bớt số bé 2,5, ta tính tổng mới của hai số.

Dùng tổng mới và hiệu mới để tính giá trị của hai số.

Từ đó, suy ra giá trị ban đầu của hai số.

Lời giải:

Khi thêm vào số lớn 3,6 đơn vị và bớt ở số bé 2,5 đơn vị thì tổng mới của 2 số là:

43,75 + 3,6 - 2,5= 44,85

Số bé là:

(44,85 - 20,15):2= 12,35

Số lớn là:

(44,85 + 20,15):2 = 32,5

Số lớn ban đầu là:

32,5 - 3,6 = 28,9

Số bé ban đầu là:

12,35 + 2,5= 14,85

Câu 23: Cho x - y = 2. Tính giá trị biểu thức A = $2 . (x^{3} - y^{3}) - 3 . {(x + y)}^{2}$

Phương pháp giải:

Phân tích biểu thức $A = 2(x - y)(x^2 + xy + y^2) - 3(x^2 + 2xy + y^2)$ .

Thực hiện phép nhân và rút gọn các hạng tử.

Sử dụng giá trị $x - y = 2$ để tính kết quả cuối cùng.

Lời giải:

Ta có: A = 2.(x - y)(x² + xy +y²) - 3(x² + 2xy + y²)

= 4 (x² + xy + y²) - 3x² - 6xy - 3y²

= 4x² + 4xy + 4y²- 3x² - 6xy - 3y²

= x² - 2xy + y²

= (x - y)² = 2² = 4.

Câu 24: Tính bằng cách thuận tiện nhất: $8, 12 x 6 + 16, 24 x 4 - 4, 06 x 8$

Phương pháp giải:

Nhóm các hạng tử để dễ dàng thực hiện phép nhân bằng cách nhận thấy rằng các số 8,12, 16,24, và 4,06 đều có thể được biểu diễn qua 8,12 và các hệ số.

Lời giải:

$8, 12 x 6 + 16, 24 x 4 - 4, 06 x 8 = 8, 12 x 6 + 8, 12 x 2 x 4 - 8, 12 x 0, 5 x 8 = 8, 12 x [6 + 8 - 4] = 8, 12 x 10 = 81, 2$

Mở rộng:

Các cách tính bằng cách thuận tiện nhất bao gồm :

Cách 1: Nhóm hoặc tách các số trong biểu thức thành từng nhóm có tổng hoặc hiệu là các số tròn chục, trong trăm, tròn nghìn,...

Cách 2: Vận dụng các tính chất của các phép toán cộng, trừ, nhân, chia

Cách 3 : Vận dụng các tính chất của các số đặc biệt

Cách 4 : Tính thuận tiện với biểu thức có phân số

Câu 25: Với a , b , c là các số thực dương . Chứng minh rằng :

$\frac{a^{5}}{a^{2} + a b + b^{2}} + \frac{b^{5}}{b^{2} + b c + c^{2}} + \frac{c^{5}}{c^{2} + a c + a^{2}}$ > $\frac{a^{3} + b^{3} + c^{3}}{3}$

Phương pháp giải:

Sử dụng Bất đẳng thức Cauchy-Schwarz và Bất đẳng thức AM-GM (Bất đẳng thức trung bình cộng - trung bình nhân).

Lời giải:

Ta có :

$\frac{a^{6}}{a^{3} + a^{2} b + a b^{2}} + \frac{b^{6}}{b^{3} + b^{2} c + b c^{2}} + \frac{c^{6}}{c^{3} + a c^{2} + a^{2} c} \geq \frac{{(a^{3} + b^{3} + c^{3})}^{2}}{a^{3} + a^{2} b + a b^{2} + b^{3} + b^{2} c + b c^{2} + c^{3} + c a^{2} + c^{2} a}$

( BĐT ..... )

TA đi cm : $a^{3} + a b^{2} + a^{2} b + b^{3} + b^{2} c + b c^{2} + c^{3} + a c^{2} + a^{2} c$ $\leq 3 (a^{3} + b^{3} + c^{3})$

(*) CM : $a^{2} b + a b^{2} = a b (a + b) \leq a^{3} + b^{3}$ ( cái này tự cm )

Tương tự bc² ; b²c ; ca² ; c²a ...

=> $a^{3} + a b (a + b) + b^{3} + b c (b + c) + c^{3} + a c (a + c) \leq a^{3} + a^{3} + b^{3} + b^{3} + b^{3} + c^{3} + c^{3} + a^{3} + c^{3}$ = 3 (a³ + b³ + c³ )

BĐT được CM.

Dấu "=" xảy ra khi a = b = c.

Câu 26: Phân tích các đa thức sau thành nhân tử:

a) $a^2 + 2b^2 - 2c^2 + 3ab + ac$

b) $a^2 - 2b^2 - 2c^2 - ab + 5bc - ac$

c) $a^4 + 2a^3 + 1$

d) $x^5 + x + 1$

e) $x^{8} + x^{4} + 1$

Phương pháp giải:

Phương pháp đặt nhân tử chung

+ Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.

+ Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.

Chú ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử.

( lưu ý tính chất: A = -(-A)).

Lời giải:

a) $a^{2} + 2 b^{2} - 2 c^{2} + 3 a b + a c$

= (a²+ 2ab + b²) + (b²- c²) + (ab + ac) - c²

= (a + b)² - c² + (b + c)(b - c) + a(b + c)

= (a + b - c)(a + b + c) + (b + c)(a + b - c)

=(a + b - c)(a + 2b + 2c)

b) $a^{2} - 2 b^{2} - 2 c^{2} - a b + 5 b c - a c$

$= a^{2} - {(b - 2 c)}^{2} - (b + c) (b - 2 c) - a (b + c)$

$= (a - b + 2 c) (a + b - 2 c) - (b + c) (a + b - 2 c)$

$= (a + b - 2 c) (a - 2 b + c)$

c) a⁴+ 2a³+ 1

= a⁴+a³+a³+a²-a²-a+a+1

= a³(a+1)+a²(a+1)-a(a+1)+(a+1)

= (a+1)(a³+a²-a+1)

d) x⁵+x+1

= (x⁵+x⁴+x³)-x⁴-x³-x²+x²+x+1

= x³(x²+x+1) -x²(x²+x+1) +(x²+x+1)

= (x²+x+1)((x³-x²+1)

e) $x^{8} + x^{4} + 1$

$= x^{8} + 2 x^{4} + 1 - x^{4}$

$= {(x^{4} + 1)}^{2} - x^{4}$

$= (x^{4} + x^{2} + 1) (x^{4} - x^{2} + 1)$

$= (x^{2} - x + 1) (x^{2} + x + 1) (x^{4} - x^{2} + 1)$

Câu 27: 2^x = 16. Tìm x.

Phương pháp giải:

Nhận diện giá trị của hằng số trong phương trình (ở đây là $16$ ).

Biểu diễn hằng số dưới dạng lũy thừa của cơ số giống như trong phương trình.

So sánh số mũ để tìm giá trị của $x$ .

Lời giải:

$2^{x} = 2^{4}$

$\Rightarrow x = 4$

Vậy x = 4

Câu 28: Giáo viên chủ nhiệm muốn chia 240 bút bi, 210 bút chì và 180 quyển vở thành một số phần thưởng như nhau để phát thưởng cho học sinh. Hỏi có thể chia được nhiều nhất là bao nhiêu phần thưởng. Mỗi phần thưởng có bao nhiêu bút bi, bút chì và tập vở?

Phương pháp giải:

Để tìm số phần thưởng tối đa có thể chia cho học sinh, ta cần tính Ước chung lớn nhất (ƯCLN) của ba số: 240, 210 và 180.

Lời giải:

Số phần thưởng chia được nhiều nhất là ƯCLN(240, 210, 180)

240 = 2⁴ . 3 . 5

210 = 2 . 3 . 5 . 7

180 = 2² . 3² . 5

=> ƯCLN(240, 210, 180) = 2 . 3 . 5 = 30

Vậy số phần thưởng chia được nhiều nhất là 30

Khi đó : Mỗi phần thưởng có số bút bi là : 240 : 30 = 8

có số bút chì là : 210 : 30 = 7

có số quyển vở là : 180 : 30 = 6

Tìm ước chung lớn nhất của hai hay nhiều số lớn hơn 1:

- Bước 1: Phân tích mỗi số ra thừa số nguyên tố;

- Bước 2: Chọn ra các thừa số nguyên tố chung;

- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.

* Chú ý:

- Nếu $a ⋮ b$ thì ƯCLN (a, b) = b.

- ƯCLN (a, 1) = 1; ƯCLN (a, b, 1) = 1.

Câu 29: Hôm nay là chủ nhật. Hỏi 616 ngày sau là thứ mấy?

Phương pháp giải:

Đổi: 1 tuần = 7 ngày

Lời giải:

Đổi: 616 ngày = 80 tuần

Vậy 616 ngày sau là chủ nhật

Câu 30: Chứng minh rằng: n⁵+ 10n⁴- 5n³- 10n²+ 4n chia hết cho 120

Phương pháp giải:

Thực hiện chia trường hợp và tính toán cho từng trường hợp

Sau đó kết luận

Lời giải:

$n^{5} + 10 n^{4} - 5 n^{3} - 10 n^{2} + 4 n = n (n + 1) (n - 1) (n^{2} + 10 n - 4)$

✱A chia hết cho 5 vì:

n luôn có dạng 5k; 5k+1; 5k+2; 5k+3; 5k+4 (k ∈ N)

*Với n=5k thì A⋮5

*Với n=5k+1 thì $(n - 1)$ ⋮5 suy ra A⋮5

*Với n=5k+4 thì $(n + 1)$ ⋮5 suy ra A⋮5

*Với n=5k+2 hoặc n=5k+3 thì $(n^{2} + 10 n - 4)$ ⋮5 suy ra A⋮5

✱A chia hết cho 3 vì trong 3 số liên tiếp luôn có một số chia hết cho 3

✱A chia hết cho 8 vì:

*Với n=2m (m ∈ N) thì n⋮2 ; $(n^{2} + 10 n - 4)$ ⋮4 suy ra A⋮8

*Với n=2m+1 (m ∈ N) thì $(n + 1); (n - 1)$ là 2 số chẵn liên tiếp suy ra A⋮8

✽Vì 8,3,5 là 3 số nguyên tố cùng nhau nên A⋮120

Câu 31: Rút gọn rồi tính giá trị của biểu thức

a) A = (x + 3)²+ (x - 3)(x + 3) - 2(x + 2)(x - 4); với x= $\frac{- 1}{2}$

b) B = (3x + 4)²- (x - 4)(x + 4) -10x; với x = $\frac{- 1}{10}$

c) C = (x + 1)²- (2x - 1)²+ 3(x - 2)(x + 2); với x = 1

d) D = (x - 3)(x + 3) + (x - 2)²- 2x(x - 4); với x = -1

Phương pháp giải:

Rút gọn biểu thức:

Sử dụng các quy tắc đại số để rút gọn từng phần của biểu thức.

Áp dụng hằng đẳng thức, như hằng đẳng thức hiệu hai bình phương, bình phương của một tổng, hoặc bình phương của một hiệu.

Kết hợp các hạng tử tương tự lại với nhau để đơn giản hóa biểu thức.

Thay giá trị cụ thể vào biểu thức đã rút gọn:

Sau khi đã rút gọn biểu thức, thay giá trị cụ thể của $x$ vào biểu thức đó.

Tính toán kết quả để tìm giá trị của biểu thức.

Lời giải:

a) A = (x+3)² + (x-3)(x+3) - 2(x+2)(x - 4)

= (x + 3)(x + 3) + (x - 3)(x + 3) - 2[x(x - 4) + 2(x - 4)]

= x(x + 3) + 3(x + 3) + x(x + 3) - 3(x + 3) - 2[x² - 4x + 2x - 8]

= x² + 3x + 3x + 9 + x² + 3x - 3x - 9 - 2(x² - 2x - 8)

= x² + 3x + 3x + 9 +x² + 3x - 3x - 9 - 2x² + 4x + 16

= (x² + x² - 2x²⁾ + (3x + 3x + 3x - 3x + 4x) + (9 - 9 + 16) = 10x + 16

Thay x = -1/2 vào biểu thức trên ta có : $10 \cdot (- \frac{1}{2}) + 16 = - 5 + 16 = 11$

b) $B = {(3 x + 4)}^{2} - (x - 4) (x + 4) - 10 x$

$B = 9 x^{2} + 24 x + 16 - x^{2} + 16 - 10 x$

$B = (9 x^{2} - x^{2}) + (24 x - 10 x) + (16 + 16)$

$B = 8 x^{2} + 14 x + 32$

Thay x = -1/10 vào biểu thức trên ta có : $B = 8 \cdot {(- \frac{1}{10})}^{2} + 14 \cdot (- \frac{1}{10}) + 32 = \frac{767}{25}$

c) $C = {(x + 1)}^{2} - {(2 x - 1)}^{2} + 3 (x - 2) (x + 2)$

$C = x^{2} + 2 x + 1 - (2 x - 1) (2 x - 1) + 3 (x^{2} - 4)$

$C = x^{2} + 2 x + 1 - 2 x (2 x - 1) + 1 (2 x - 1) + 3 x^{2} - 12$

$C = x^{2} + 2 x + 1 - 4 x^{2} + 2 x + 2 x - 1 + 3 x^{2} - 12$

$C = (x^{2} - 4 x^{2} + 3 x^{2}) + (2 x + 2 x + 2 x) + (1 - 1 - 12)$

$C = 6 x - 12$

Thay x = 1 vào biểu thức ta có : C = 6.1 - 12 = 6 -12 = - 6

d) $D = (x - 3) (x + 3) + {(x - 2)}^{2} - 2 x (x - 4)$

$= x^{2} - 9 + x^{2} - 4 x + 4 - 2 x^{2} + 8 x$

$= 4 x - 5$

Thay x = -1 vào biểu thức ta có : D = 4.(-1) - 5 = - 9

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

164

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

139

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm