Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 80)

Câu 1: Tính giá trị biểu thức: –3752 – (29 – 3652) – 51.

Lời giải:

–3752 – (29 – 3652) – 51

= –3752 – 29 + 3652 – 51

= (3652 – 3752) – (51 + 29)

= –100 – 80

= –180.

Câu 2: Bạn An cho biết tổng abc và mnp là 579. Em có thể nói ngay kết quả của anp +mbc; mbp + anc là bao nhiêu không? Giải thích tại sao?

Lời giải:

Ta có: abc + mnp = 579 (1)

Suy ra: anp + mbc =579 (2)

mbp + anc = 579 (3)

Vì: Ta thay đổi các chữ số trong các số hạng của biểu thức (1) thì sẽ có các phép cộng của biểu thức (2) và (3).

Ví dụ: ở biểu thức (1) b đứng ở vị trí hàng chục của số hạng thứ nhất, chuyển sang biểu thức (2) thì b vẫn đứng ở vị trí hàng chục nhưng ở số hạng thứ hai.... Các chữ số còn lại đều thay đổi như vậy. Nên tổng không thay đổi.

Câu 3: Cho hình thang cân EFGH, biết chu vi hình thang là 68 cm, chiều dài 2 cạnh đáy lần lượt là 20 cm và 26 cm. Tính chiều dài cạnh bên của hình thang.

Lời giải:

Gọi chiều dài cạnh bên của hình thang EFGH là x

Theo đề bài, ta có :

Chu vi của EFGH = (2 . x) + 20 + 26 = 68

⇒ x = 11

Vậy chiều dài cạnh bên của hình thang là 11cm.

Câu 4: Một cửa hàng gạo nhập vào kho 480 tấn, biết rằng trước dó, trong kho không còn gạo. Mỗi ngày, cửa hàng bán đi 20 tấn. Gọi y (tấn) là số gạo còn lại sau x (ngày) bán.

a) Viết công thức biểu diễn y theo x.

b) Tỉnh số gạo còn lại trong kho sau khi bán một tuần?

Lời giải:

a) y = 480 – 20x

b) Ta có: 1 tuần = 7 ngày

Thay x = 7 vào ta được:

Số gạo còn lại trong kho sau khi bán 1 tuần là:

y = 480 – 20.7 = 340 (tấn).

Câu 5: Một người nuôi ong thu hoạch được 40 lít mật ong. Người đó muốn đổ vào các chai, mỗi chai chứa 0,72 lít cần ít nhất bao nhiêu chai để chứa hết số dầu đó?

Lời giải:

Để đựng hết 40 lít mật ong thì người đó cần số chai là:

40 : 0,72 = 55 (chai) và dư 0,4 lít

Do thừa 0,4 lít mật ong nên cần thêm 1 chai nữa.

Vậy tổng số chai người đó cần là:

55 + 1 = 56 (chai)

Đáp số: 56 chai.

Câu 6: Số các số tự nhiên có 4 chữ số là?

Lời giải:

Số tự nhiên nhỏ nhất có 4 chữ số là: 1000

Số tự nhiên lớn nhất có 4 chữ số là: 9999

Vậy số các số tự nhiên có 4 chữ số là:

(9999 – 1000) : 1 + 1 = 9000 (số).

Câu 7: Trong kì thi học sinh giỏi cấp trường, lớp 10A có 17 bạn được công nhận học sinh giỏi Văn, có 25 bạn được công nhận học sinh giỏi Toán. Biết cả lớp 10A có 45 học sinh và có 13 học sinh không đạt học sinh giỏi. Số học sinh giỏi cả Văn lẫn Toán là?

Lời giải:

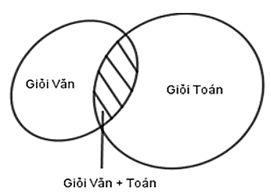
Tổng số học sinh giỏi là: 45 – 13 = 32

Số học sinh chỉ giỏi Văn là: 32 – 25 = 7

Số học sinh chỉ giỏi Toán là: 32 – 17 =15

Số học sinh giỏi cả hai môn là: 32 – 7 – 15 = 10.

Câu 8: Trong một khu vườn hình chữ nhật, người ta làm một lối đi lát sỏi với các kích thước như hình vẽ sau. Chi phí cho mỗi mét vuông làm lối đi hết 120 nghìn đồng. Hỏi chi phí để làm lối đi là bao nhiêu?

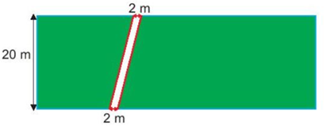
Lời giải:

Diện tích lối đi là:

2 . 20 = 40 (m²)

Chi phí làm lối đi là:

40 . 120000 = 4800000 (đồng).

Câu 9: Với a = 15 thì biểu thức: 256 – 3a có giá trị bằng bao nhiêu?

Lời giải:

256 – 3a = 256 – 3.15 = 256 – 45 = 211.

Câu 10: Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4 m còn kích thước cửa ở giữa là 3 m × 4 m. Hãy tính khoảng cách giữa hai điểm A và B.

Lời giải:

Đỉnh G có tọa độ (0; 4) nên a . 0² + b . 0 + c = 4

Do đó c = 4.

Điểm D có tọa độ (2; 3) nên a . 2² + b . 2 + 4 = 3

⇔ 4a + 2b = −14 (1)

Điểm C có tọa độ (–2; 3) nên a . (−2)² + b . (−2) + 4 = 3

⇔ 4a – 2b = −14 (2)

Từ (1) và (2) suy ra a = – 0,25; b = 0.

Khi đó parabol có dạng y = −0,25 . x² + 4

Điểm A và B có tung độ y = 0

⇔ −0,25 . x² + 4 = 0

⇔ x = 4 hoặc x = – 4

Suy ra điểm B có tọa độ (4; 0) và điểm A có tọa độ (– 4; 0).

Vậy khoảng cách giữa hai điểm A và B là 8.

Câu 11: Tính bằng cách thuận tiện: 25 . 343 + 343 . 75.

Lời giải:

25 . 343 + 343 . 75

= 343(25 + 75)

= 343 . 100

= 34300.

Câu 12: Trong hình sau có mấy cặp cạnh song song?

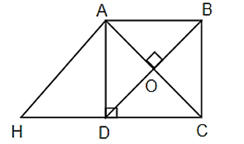
Lời giải:

Trong hình trên có:

AB song song với HD, AB song song với DC

AB song song với HC, AD song song với BC

Vậy ta chọn đáp án: 4 cặp cạnh.

Câu 13: Tìm x, biết: x + 28,4 = 264,75 : 5.

Lời giải:

x + 28,4 = 264,75 : 5

⇔ x + 28,4 = 52,95

⇔ x = 52,95 – 28,4

⇔ x = 24,44

Vậy x = 24,44.

Câu 14: 900 cm² bằng bao nhiêu m².

Lời giải:

1m² = 10000cm²

Suy ra: 900cm² = 0,09 m²

Câu 15: Hiệu của hai số bằng 0,14 . Tìm hai số đó biết rằng 5 lần số lớn trừ đi số bé thì được 18,1.

Lời giải:

Hiệu sau hơn hiệu trước số đơn vị là

18,1 − 0,14 = 17,96

Nếu ta coi số bé là 1 phần thì số lớn sẽ là 1 phần như thế và 0,14 đơn vị. Và 5 lần số lớn là 5 phần như thế.

Vậy 4 lần số lớn sẽ bằng số đơn vị mà hiệu sau hơn hiệu trước.

Vậy số lớn là

17,96 : 4 = 4,49.

Số bé là

4,49 − 0,14 = 4,35.

Câu 16: Một mảnh đất hình vuông có chu vi là 820m. Tính diện tích mảnh đất đó?

Lời giải:

Độ dài một cạnh mảnh đất là:

820 : 4 = 205 (m)

Diện tích mảnh đất là:

205 . 205 = 42025 (m²).

Câu 17: Số đối của –(–5) là gì?

Lời giải:

Số đối của –(–5) là –5

Vì –(–5) + –5 = 5 – 5 = 0.

Câu 18: Tìm 3 số nguyên liên tiếp có tổng bằng 0.

Lời giải:

Gọi 3 số cần tìm là n – 1; n; n + 1

Theo đề bài ta có

(n – 1) + n + (n + 1) = 0

⇔ n – 1 + n + n + 1 = 0

⇔ 3n + 1 – 1 = 0

⇔ 3n + 0 = 0

⇔ 3n = 0 – 0

⇔ 3n = 0

⇔ n = 0

Suy ra: n – 1 = 0 – 1 = –1

Suy ra: n + 1 = 0 + 1 = 1

Vậy số cần tìm là –1; 0; 1.

Câu 19: Phân tích đa thức thành nhân tử: (xy + 1)² – x² – y(2x + y).

Lời giải:

(xy + 1)² – x² – y(2x + y)

= x²y² + 2xy + 1 – x² – y² – 2xy

= x²y² – x² – y² + 1

= x²(y² – 1) – (y² – 1)

= (y² – 1)(x² – 1)

= (y + 1)(y – 1)(x – 1)(x + 1).

Câu 20: Tính 372,95 : 3.

Lời giải:

372,95 : 3 = 124,316666667.

Câu 21: Trung bình cộng của số gạo 2 bao là 45,6kg. Nếu chuyển từ bao thứ nhất sang bao thứ hai 2,7kg gạo thì số gạo có trong hai bao bằng nhau. Hỏi lúc đầu mỗi bao có bao nhiêu ki–lô–gam gạo?

Lời giải:

Tổng số gạo của 2 bao là:

45,6 . 2 = 91,2 (kg)

Nếu chuyển từ bao thứ 1 sang bao thứ hai 2,7 kg gạo thì số gạo ở 2 bao bằng nhau

Hiệu số gạo của 2 bao là:

2,7 . 2 = 5,4 (kg gạo)

Lúc đầu bao thứ 1 có:

(91,2 + 5,4) : 2 = 48,3 (kg gạo)

Lúc đầu bao thứ 2 có:

91,2 – 48,3 = 42,9 (kg gạo).

Câu 22: May một bộ quần áo hết 2,8 m vải hỏi có 371,5 m vải thì may được nhiều nhất bai nhiêu bộ quần áo như thế và còn thừa mấy m vải?

Lời giải:

Có 371,5 mét vải thì may được số mét vải như thế là:

371,5 : 2,8 = 132 (bộ) dư 1,9 m vải

Đáp số: 132 bộ quần áo và dư 1,9 m vải.

Câu 23: Tại hai điểm A và B trên cùng một đường thẳng cách nhau 120 km 2 ô tô cùng khởi hành một lúc chạy ngược chiều nhau, xe đi từ A có vận tốc V₁ = 30 km/h, Xe đi từ B có vận tốc V₂ = 50 km h

a) Xác định thời điểm và vị trí hai xe gặp nhau.

b) Xác định thời điểm và vị trí hai xe cách nhau 40 km.

Lời giải:

a) Gọi thời gian hai xe gặp nhau là t(h), t > 0

Vì hai xe xuất phát cùng một lúc, ngược chiều nhau nên ta lập được phương trình :

v₁t + v₂t = s

⇔ 30t + 50t = 120

⇔ 80t = 120

⇔ t = 1,5(h)

Với thời điểm hai xe xuất phát là t₀(h) , thì thời điểm hai xe gặp nhau là:

t₀ + t = t₀ + 1,5(h)

Vị trí hai xe gặp nhau cách A:

s_A = v₁t = 30.1,5 = 45(km)

b) Gọi t₁(h) là thời gian hai xe gặp nhau (t₁ > 0)

Trường hợp 1 : Cách nhau 40(km) khi hai xe chưa gặp nhau

Vì xuất phát cùng lúc, đi ngược chiều nên tổng quãng đường hai xe đi được là :

s₁ = s – 40 = 120 – 40 = 80 (km)

Ta có phương trình :

v₁t₁ + v₂t₂ = 80

⇔ 30t₁ + 50t₁ = 80

⇔ 80t₁ = 80

⇔ t₁ = 1(h)

Khi ấy xe 1 cách A :

s_A’ = t₁v₁ = 30.1 = 30 (km)

Khi ấy xe 2 cách B :

s_B' = s₁ − s_A' = 80 − 30 = 50 (km)

Trường hợp 2 : Kể từ khi hai xe đã gặp nhau

Với cách lập luận như Trường hợp 1, tổng quãng đường hai xe đi được là :

s₁ = s + 40 = 120 + 40 = 160 (km)

Ta có phương trình :

v₁t₁ + v₂t₂ = 80

⇔ 30t₁ + 50t₁ = 160

⇔ 80t₁=160

⇔ t₁ = 2(h) (TM)

Khi ấy xe 1 cách A :

s_A' = t₁v₁ = 30.2 = 60 (km)

Khi ấy xe 2 cách B :

s_B' = s₁ − s_A' = 160 – 60 =100 (km)

Câu 24: Tính giá trị biểu thức: (10² + 11² + 12²) : (13² + 14²).

Lời giải:

(10² + 11² + 12²) : (13² + 14²)

= (100 + 121 + 144) : (169 + 196)

= 365 : 365

= 1.

Câu 25: Cho đa giác đều 36 đỉnh. Có bao nhiêu hình chữ nhật có 4 đỉnh đều là đỉnh của đa giác đều trên?

Lời giải:

Chia đa giác đều thành 4 phần sao cho mỗi phần chứa 9 đỉnh

Ta nhận thấy, ở phần thứ 1 nếu chọn ra 1 đỉnh A₁ bất kỳ, phần thứ 2 chọn ra 1 đỉnh B₁ bất kỳ

⇒ Ở 2 phần còn lại sẽ chỉ chọn ra được 2 đỉnh cố định để tạo thành được hình chữ nhật

⇒ 9 đỉnh A₁, A₂, A₃, A₄, A₅,...A₉ với đỉnh B₁ tạo được 9 hình chữ nhật

Tương tự, A₁ với B₁, B₂, B₃,....B₉ tạo được 9 hình chữ nhật

⇒ Tổng thu được: 9.9 = 81 hình chữ nhật

(Ta ko xét phần thứ 3, thứ 4 vì các đỉnh ở phần này đã được tính khi xếp với A₁,...B₉)

Vậy có 81 hình chữ nhật.

Câu 26: Tính tổng các số tự nhiên liên tiếp từ 1200 đến 1360.

Lời giải:

Từ 1200 đến 1360 có số số hạng là:

(1360 − 1200) : 1 + 1 = 161 (số hạng)

Tổng các số tự nhiên liên tiếp từ 1200 đến 1360 là:

(1360 + 1200) . 161 : 2 = 206080.

Câu 27: Cho hàm số y = f(x) = (5 – 3a)x + a + 6 biết f(–2) = 10. Tính f(2).

Lời giải:

Ta có: f(–2) = 10

⇒ (5 – 3a).(–2) + a + 6 = 10

⇔ a = 2

Ta có hàm số f(x) = –x + 8

f(2) = –2 + 8 = 6.

Câu 28: Tính nhanh: 1.4 + 2.5 + 3.6 + ... + 100.103.

Lời giải:

Đặt A = 1.4 + 2.5 + 3.6 + ... + 100.103

= 1(2.2) + 2(3 + 2) + 3(4+ 2) + ...+ 100(101+ 2)

= 1.2 + 2.3 + 3.4 + ...+ 100.101 + (1.2 + 2.2 + 3.2 + ... + 100.2)

= 1.2 + 2.3 + 3.4 + ... + 100.101 + 2(1 + 2 + 3 + ... + 100)

= 1.2 + 2.3 + 3.4 + ... + 100.101 + 10100

Đặt B = 1.2 + 2.3 + 3.4 + ... + 100.101

⇒ 3B = 1.2.3 + 2.3.3 + 3.4.3 + 100.101.3

⇒ 3B = 1.2.3 + 2.3(4 – 1) + 3.4(5 – 2) + ... + 100.101(102 − 99)

⇒ 3B = 1.2.3 + 2.3.4 − 1.2.3 + 3.4.5 − 2.3.4 + ... + 100.101.102 − 99.100.101

⇒ 3B = 100.101.102

⇒ B = 343400

Khi đó A = B + 10100 = 343400 + 10100 = 353500.

Câu 29: Tính (532.7 – 266.14) . ( 532.7 + 266).

Lời giải:

(532 . 7 – 266 . 14) . ( 532 . 7 + 266)

= [7.(532 – 266 × 2)].(532.7 + 266)

= 7.(532 – 532).(532.7 + 266)

= 7.0.(532.7 + 266)

= 0.

Câu 30: Tứ giác có hai góc đối bằng 90 độ có phải là hình chữ nhật không?

Lời giải:

Tứ giác có 2 góc đối bằng 90° không có nghĩa tứ giác đấy là hình chữ nhật, vì tứ giác có 3 góc bằng 90° mới là hình chữ nhật.

Câu 31: Một quyển sách có 1234 trang. Hỏi người ta phải dùng bao nhiêu chữ số để đánh hết số trang sách đó.

Lời giải:

Từ trang 1 đến 9 cần số chữ số là:

(9 − 1) : 1 + 1 = 9 (chữ số)

Từ 10 đến 99 cần số chữ số là:

(99 − 10) : 1 + 1 = 180 (chữ số)

Từ 100 đến 1234 cần số chữ số là:

(1234 − 100) : 1 + 1 = 1135 (số)

Vậy người ta cần phải dùng :

9 + 180 + 1135 = 1324 (chữ số).

Câu 32: Xe thứ 1 chở 54 tạ thóc, xe 2 chở 66 tạ, xe 3 chở 72 tạ, xe thứ 4 chở được ít hơn trung bình cộng số thóc cả 4 xe đã cho là 9 tạ thóc. Hỏi xe thứ 4 chở được bao nhiêu tạ thóc?

Lời giải:

3 lần trung bình cộng số tạ thóc cả 4 xe chở được là:

54 + 66 + 72 – 9 = 183 (tạ thóc).

Trung bình cộng số tạ thóc cả 4 xe chở được là:

183 : 3 = 61 (tạ thóc).

Số tạ thóc xe thứ 4 chở được là:

61 – 9 = 52 (tạ thóc).

Đáp số: 52 tạ thóc.

Câu 33: Xét tính chẵn lẻ: y = x.cotx + cosx.

Lời giải:

y = f(x) = xcotx + cosx

D = ℝ\{kπ; k ∈ ℤ}

x ∈ D ⇒ –x ∈ D

⇒ Miền D là miền đối xứng

f(−x) = −xcot(−x) + cos(−x) = xcotx + cosx = f(x)

⇒ Hàm số là hàm chẵn.

Câu 34: Lớp 10A có 45 học sinh trong đó có 15 bạn được xếp lực học giỏi, 20 bạn được xếp hạnh kiểm tốt, có 10 bạn vừa được xếp lực học giỏi vừa được hạnh kiểm tốt. Số học sinh của lớp 10A được nhận khen thưởng là:

Lời giải:

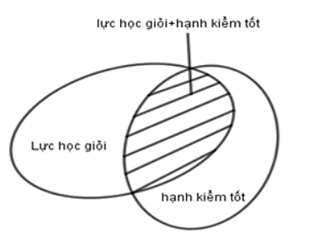
Số học sinh chỉ đạt học lực giỏi là: 15 – 10 = 5

Số học sinh chỉ đạt hạnh kiểm tốt là: 20 – 10 = 10

Số học sinh được nhận thưởng là: 5 + 10 + 10 = 25.

Câu 35: Hai người đi xe từ A đến C. Người thứ nhất đi theo đường từ A đến B rồi từ B đến C. Người thứ hai đi thẳng từ A đến C. Cả hai đều về đích cùng lúc. Tính quãng đường và độ dịch chuyển của người thứ nhất và người thứ hai, so sánh và nhận xét kết quả biết ABC tạo thành tam giác vuông 1 tam giác vuông.

Lời giải:

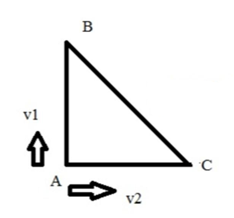
Theo bất đẳng thức tam giác ta có tổng độ dài hai cạnh bất kỳ lớn hơn độ dài cạnh còn lại. Ta có: AB + BC > AC

Mà s₁ = AB + BC

s₂ = AC

⇒ s₁ > s₂

Lại có cả hai đến đích cùng lúc, do đó v₁ > v₂ (do thời gian bằng nhau).

Câu 36: Tìm 1 số tự nhiên có 4 chữ số biết rằng khi viết thêm chữ số 7 vào bên phải số đó thì được số lớn hơn số phải tìm 11212 đơn vị.

Lời giải:

Số tự nhiên có 4 chữ số khi viết thêm chữ số 7 vào bên phải số đó, thì số đó gấp lên 10 lần và tăng thêm 7 đơn vị

Ta có sơ đồ như hình vẽ

Từ sơ đồ ta thấy 9 phần số cần tìm là:

11212 – 7 = 11205 (đơn vị)

Số phải tìm là:

11205 : 9 = 1245

Đáp số: 1245.

Câu 37: Khi nào ta làm tròn độ khi tính số đo góc?

Lời giải:

Khi các số đo góc tính ra quá lẻ, chúng ta sẽ làm tròn độ, phút, giây tùy từng trường hợp.

Khi số phút vượt 30 độ thì ta +1 độ vào.

Ví dụ: 30 độ 32′ 4′′ thì làm tròn thành 31 độ.

Câu 38: Phân tích đa thức thành nhân tử: 5x² – 5xy – 10x + 10y.

Lời giải:

5x² – 5xy – 10x + 10y

= 5(x² –xy – 2x + 2y)

= 5[(x² – xy) – (2x – 2y)]

= 5[x(x – y) – 2(x – y)]

= 5(x – y)(x – 2).

Câu 39: Cho một số tự nhiên có 3 chữ số. Biết rằng thêm chữ số 3 vào bên phải số đó thì số đó tăng thêm 2892 đơn vị. Tổng các chữ số của số đó là?

Lời giải:

Khi viết thêm chữ số 3 vào bên phải một số thu được số mới gấp 10 lần số ban đầu và cộng thêm 3 đơn vị.

Nếu số ban đầu là 1 phần thì số mới là 10 phần cộng thêm 3 đơn vị.

Hiệu số phần bằng nhau là:

10 – 1 = 9 (phần)

Số đã cho là:

(2892 − 3) : 9 . 1 = 321

Tổng các chữ số của số đã cho là: 3 + 2 + 1 = 6.

Câu 40: Cho số A = 1.2.3.4…100

số B = 1000....00000.

Hỏi số B có nhiều nhất là bao nhiêu chữ số 0 biết A chia hết cho B.

Lời giải:

A = 1.2.3.4…100 = 100!

Từ 1 đến 100 có :

(100 – 10) : 10 + 1 = 10 (số hạng chia hết cho 10)

(100 – 2) : 2 + 1 = 50 (số hạng chia hết cho 2)

(100 – 5) : 5 + 1 = 20 (số chia hết cho 5)

⇒ Các số chia hết cho 2 không chia hết cho 10 là : 50 – 10 = 40 (số hạng)

⇒ Số chia hết cho 5 chia hết cho 10 là : 20 – 10 = 10 (số hạng)

Vì 10 < 40 ⇒ Tích giữa các số chỉ chia hết cho 2 với số chỉ chia hết cho 5 có 10 chữ số 0

mà có 10 số chia hết cho 10

⇒ A có 20 số 0 tận cùng

mà A chia hết cho B

⇒ B có 20 chữ số 0.

Câu 41: Một đơn vị bộ đội chuẩn bị 768kg lương thực đủ cho 80 người ăn trong 12 ngày luyện tập trước ngày tập trung quân ban chỉ huy báo về là số người sẽ tăng gấp 3 số dự kiến vậy để đủ ăn trong số ngày luyện tập như dự kiến đơn vị đó phải mua thêm số lương thực là bao nhiêu?

Lời giải:

Mỗi người ăn hết số kg lương thực trong 12 ngày là:

768 : 12 = 64 (kg)

Số người sau khi tăng lên gấp 3 của đơn vị là:

12 . 3 = 36 (người)

Số lương thực cần cho 36 người là:

36 . 64 = 2304 (kg)

Số lương thực cần mua thêm là:

2304 – 768 = 1536 (kg)

Đáp số: 1536 kg lương thực.

Câu 42: Cho dãy gồm 6 số nguyên tố phân biệt và tăng dần. Hiệu giữa hai số liên tiếp của dãy số đã cho đều bằng nhau. Chứng minh rằng hiệu giữa số lớn nhất và số bé nhất không nhỏ hơn 150.

Lời giải:

Gọi 6 số đó là p, p + d, p + 2d, p + 3d, p + 4d, p + 5d.

p + d, p + 2d là 2 số lẻ ⇒ hiệu ⋮ 2 (p + d ≥ 4)

p + d, p + 2d, p + 3d > 3 các số này ⋮̸ 3 nên có 2 số có cùng số dư khi chia 3.

Hiệu của chúng là d hoặc 2d ⋮ 3

⇒ d ⋮ 3

⇒ d ⋮ 6 nên d ≥ 6

p + d, p + 2d, p + 3d, p + 4d, p + 5d là 5 số, các số này không chia hết 5 nên có 2 số có cùng số dư khi chia 5.

Hiệu của chúng là d, 2d, 3d hoặc 4d ⋮ 5

⇒ d ⋮ 5

⇒ d ⋮ 30

Ta có : d ≥ 30

⇒ 5d ≥ 150 (đpcm)

Vậy hiệu giữa số lớn nhất và số bé nhất không nhỏ hơn 150.

Câu 43: Tính giá trị biểu thức: 80 – (4.5² – 3.2³).

Lời giải:

80 – (4.5² – 3.2³)

= 80 – (4.25 – 3.8)

= 80 – (100 – 24)

= 80 – 76

= 4.

Câu 44: Đồ thị hàm số y = x – 3 cắt trục hoành Ox tại điểm có tọa độ là?

Lời giải:

Đồ thị hàm số y = x − 3 cắt trục hoành Ox

⇒ y = 0

Thay y = 0 vào y = x – 3 ta có:

x – 3 = 0

⇔ x = 3

Vậy đồ thị hàm số y = x − 3 cắt trục hoành Ox tại điểm có tọa độ là (3;0).

Câu 45: Một đội công nhân có 77 người nhận sửa xong một quãng đường trong 9 ngày. Hỏi muốn làm xong quãng đường đó trong 7 ngày thì cần thêm bao nhiêu người ? (mức làm của mỗi người như nhau)

Lời giải:

Nếu muốn sửa xong quãng đường trong 1 ngày thì cần số người là:

77 . 9 = 693 (người)

Muốn làm xong quảng đường đó trong 7 ngày thì số người là:

693 : 7 = 99 (người)

Cần thêm số người là:

99 – 77 = 22 (người)

Đáp số: 22 người.

Câu 46: Đổi 1dam² = …cm².

Lời giải:

1dam² = 1000000 cm².

Câu 47: Cho định lí: "Nếu m,n là hai số nguyên dương và mỗi số đều chia hết cho 3 thì m² + n² cũng chia hết cho 3". Hãy phát biểu và chứng định lí đảo của định lí trên (nếu có).

Lời giải:

Định lí đảo : “Nếu m, n là hai nguyên dương và m² + n² chia hết cho 3 thì cả m và n đều chia hết cho 3”.

Nếu một số không chia hết cho 3 và số kia chia hết cho 3 thì rõ ràng tổng bình phương hai số đó không chia hết cho 3. Giả sử m và n đều không chia hết cho 3. Nếu m = 3k + 1 hoặc 3k + 2 ta đều có m² chia 3 dư 1 thành thử m² + n² chia 3 dư 2.

Vậy nếu m² + n² chia hết cho 3 thì chỉ có thể xảy ra khả năng cả m và n đều chia hết cho 3.
Vậy: Điều kiện cần và đủ để m² + n² chia hết cho 3 (m, n ∈ ℕ) là cả m và n đều chia hết cho 3.

Câu 48: Có 5 người thợ dệt trong 8 giờ được 240 sản phẩm. Hỏi muốn làm được 192 sản phẩm như thế thì 4 người phải làm trong bao lâu? (Mức lao động của mỗi người là như nhau)

Lời giải:

5 người thợ làm trong 1 giờ được số sản phẩm là:

240 : 8 = 30 (sản phẩm)

1 người thợ làm trong 1 giờ được số sản phẩm là:

30 : 5 = 6 (sản phẩm)

4 người thợ làm trong 1 giờ được số sản phẩm là:

6 . 4 = 24 (sản phẩm)

Để làm được 192 sản phẩm như thế, 4 người cần làm số giờ là:

192 : 24 = 8 (giờ).

Câu 49: Có bao nhiêu số nguyên là tổng của ba phần tử phân biệt của tập hợp {1; 4; 7; 10; 13; 16; 19}.

Lời giải:

Có 13 số nguyên: {12; 15; 18; 21; 24; 27; 30; 33; 36; 39; 42; 45; 48}.

Câu 50: Hiện nay em 4 tuổi, anh 10 tuổi. Hỏi mấy năm nữa tuổi anh gấp đôi tuổi em?

Lời giải:

Anh hơn em số tuổi là:

10 – 4 = 6 (tuổi)

Vì mỗi năm anh tăng 1 tuổi thì em cũng tăng 1 tuổi, nên hiệu số tuổi của hai anh em luôn không đổi. Vậy khi tuổi anh gấp đôi số tuổi của em thì anh vẫn hơn em 6 tuổi.

Số tuổi của em khi tuổi anh bằng hai lần tuổi em là:

6 : (2 – 1) = 6 (tuổi)

Sau số năm nữa tuổi anh gấp 2 lần tuổi em là:

6 – 4 = 2 (năm)

Đáp số: 2 năm.