Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 11)
Câu 1: Tìm x để (x + 17) chia hết cho (x + 3).
Lời giải:
Ta có x + 17 ⋮ x + 3
(x + 3) + 14 ⋮ x + 3
14 ⋮ x + 3
Do đó x + 3 Ư(14) = {−14; −7; −2; −1; 1; 2; 7; 14}.
Vậy x {−17; −10; −5; −4; −2; −1; 4; 11}.
Câu 2: Tìm tập hợp X sao cho {a; b} ⊂ X ⊂ {a; b; c; d}.
Lời giải:
X = {a; b}
X = {a; b; c}; X = {a; b; d}
X = {a; b; c; d}.
Câu 3: Tìm tập hợp X sao cho X ⊂ A và X ⊂ B, trong đó
A = {a; b; c; d; e} và B = {a; c; e; f}.
Lời giải:
X ⊂ A và X ⊂ B Þ X ⊂ (A ⋂ B) = {a; c; e}.
Vậy:
X = {a}; X = {c}; X = {e}
X = {a; c}; X = {a; e}; X = {c; e}
X = {a; c; e}
Lời giải:
Mỗi tầng hơn nhau 1 khối lập phương.
Vậy để xếp được cái tháp cao 8 tầng thì cần số khối lập phương là:
Áp dụng công thức .
Vậy số khối lập phương cần tìm là: (khối).
Lời giải:
Do độ dài của tập F bằng 5: (2m + 2) − (2m − 3) = 5.
Nên C = E ∪ F có độ dài bằng 5 khi và chỉ khi C = F
E F
Lời giải:
Vì A có đọ dài bằng 3 nên A giao B không thể là một tập có độ dài bằng 5.
Vậy không có giá trị nào của m thỏa mãn.
Lời giải:
Ta có:
Vậy .
Lời giải:
Ta có:
Mặt khác: .
Nên .
Hay .
Câu 9: Chứng minh S = 2R2.sin A.sin B.sin C với S là diện tích tam giác ABC.
Lời giải:
Ta có: .
Áp dụng định lí sin, ta có:
.
Lời giải:
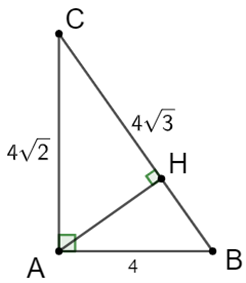
Theo hệ thức lượng trong tam giác ABC vuông tại A có AH là đường cao nên ta có:
• AH.BC = AB.AC
Suy ra .
• AB2 = HB.BC
Suy ra .
Vậy .
Lời giải:
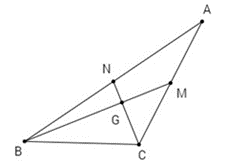
Gọi G là giao điểm của hai trung tuyến BM, CN.
Áp dụng công thức tính trung tuyến, ta có:
• ;
• .
BM và CN vuông góc với nhau khi BG2 + CG2 = BC2.
4a2 + b2 + c2 = 9a2
b2 + c2 = 5a2.
Câu 12: Cho tam giác ABC. Chứng minh c.mc = b.mb khi b2 + c2 = 2a2.
Lời giải:
Ta có c.mc = b.mb
2c2(a2 + b2) − c4 = 2b2(a2 + c2) − b4
2c2a2 + 2c2b2 − c4 = 2b2a2 + 2b2c2 − b4
b4 − c4 = 2b2a2 − 2c2a2
(b2 + c2)(b2 − c2) = 2a2(b2 − c2)
b2 + c2 = 2a2 (với b ≠ c).
Lời giải:
Ta có
Lời giải:
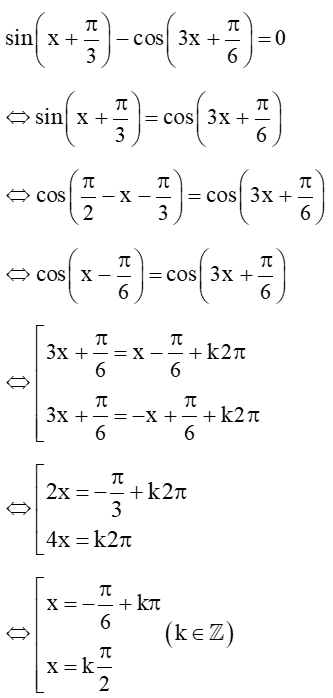
Lời giải:
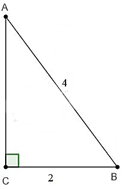
Gọi thang là AB (A là điểm dựa vào tường, B là điểm trên mặt đất), chân tường là C
Xét tam giác ABC vuông tại C có:
Vậy góc tạo bởi thang với mặt đất là 60° và góc tạo bởi thang với mặt tường là 30°.
Lời giải:
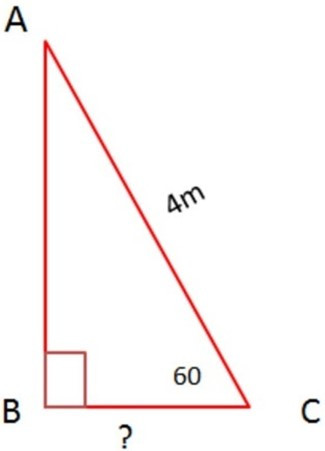
Xét ∆ABC vuông tại A có:
(m)
Vậy khoảng cách giữa chân thang và tường bằng 2 m.
A. A(3; 2);
B. C(3; −2);
C. B(2; −3);
D. D(−2; 3).
Lời giải:
Biểu thức tọa độ của phép đối xứng qua đường thẳng x − y = 0 là: .
Vậy ảnh của M qua phép đối xứng qua đường thẳng x − y = 0 là A(3; 2).
Đáp án cần chọn là A.
A. A(−2; −3);
B. A(2; −3);
C. A(3; 2);
D. A(3; −2).
Lời giải:
Biểu thức tọa độ của phép đối xứng qua đường thẳng x − y = 0 là:
Vậy ảnh của M qua phép đối xứng qua đường thẳng x − y = 0 là A(3; −2).
Đáp án cần chọn là D.
Câu 19: Tính giá trị biểu thức A = 3x3y + 6x2y2 + 3xy3 tại .
Lời giải:
Với thì:
Câu 20: Rút gọn biểu thức A = 1 + 2 + 21 + 22 + … + 225.
Lời giải:
Ta có: A = 1 + 2 + 21 + 22 + … + 225.
Suy ra 2A = 2 . (1 + 2 + 21 + 22 + … + 225) = 2 + 21 + 22 + … + 226.
Do đó 2A – A = (2 + 21 + 22 + … + 226) – (1 + 2 + 21 + 22 + … + 225)
= 2 + 21 + 22 + … + 226 – 1 – 2 – 21 – 22 – … – 225
= (2 – 2) + (21 – 21) + (22 – 22) + … (225 – 225) + 226 – 1.
= 226 – 1.
Câu 21: Tìm giá trị nhỏ nhất của A = x2 − 6x + 17.
Lời giải:
A = x2 − 6x + 17
= (x2 − 6x + 9) + 8 = (x − 3)2 + 8
Có (x − 3)2 ≥ 0 với mọi x
(x − 3)2 + 8 ≥ 8 Þ A ≥ 8.
Dấu ''='' xảy ra x − 3 = 0 x = 3.
Câu 22: Tìm giá trị nhỏ nhất hoặc lớn nhất của biểu thức sau:
A = x2 + 6x + 10.
Lời giải:
Ta có A = x2 + 6x + 10
= (x2 + 6x + 9) + 1 = (x + 3)2 + 1
Có (x + 3)2 ≥ 0 với mọi x
Þ (x + 3)2 + 1 ≥ 1 Þ A ≥ 1
Dấu ''='' xảy ra x + 3 = 0 x = −3.
Câu 23: Tìm giá trị lớn nhất nhỏ nhất của hàm số: .
Lời giải:
Ta có
.
Vậy GTNN của hàm số là khi
Vậy GTLN của hàm số là khi
Câu 24: Hàm số đạt giá trị lớn nhất tại giá trị bao nhiêu?
Lời giải:
Ta có
Do đó GTLN của hàm số là khi
.
Vậy GTLN của hàm số là khi .
Câu 25: Cho các số nguyên tố p, q thỏa mãn p2 − 2q2 = 17. Tính p + q.
Lời giải:
Vì p, q là các số nguyên tố nên p.q > 1
Lại có p2 − 2q2 = 17 Þ p2 > 17 Þ p ≥ 5
* Xét p = 5, thay vào ta có q = 2.
Khi đó, p + q = 7.
* Xét p > 5, vì p là số nguyên tố nên p có dạng 6k + 1 hoặc 6k + 5 (k Î ℤ+).
• Với p = 6k + 1, ta có:
(6k + 1)2 − 2q2 = 17
36k2 + 12k + 1 − 2q2 = 17
36k2 + 12k − 2q2 = 16
18k2 + 6k − q2 = 8
Ta thấy VP ⋮ 2 nên VT ⋮ 2
Mà 18k2 + 6k ⋮ 2 q2 ⋮ 2 q = 2
Thay vào ta được p = 5
• Với p = 6k + 5, ta có:
(6k + 5)2 − 2q2 = 17
36k2 + 60k + 25 − 2q2 = 17
36k2 + 60k − 2q2 = −8
18k2 + 30k − q2 = −4
Ta thấy VP ⋮ 2 VT ⋮ 2
Mà 18k2 + 30k ⋮ 2 q2 ⋮ 2 q = 2.
Thay vào ta được p = 5.
Vậy p + q = 7.
Câu 26: Tìm tất cả các cặp số nguyên (p; q) sao cho p2 − 2q2 = 41.
Lời giải:
Ta có: p2 − 2q2 = 41 (1)
p2 = 2q2 + 41 là số lẻ, suy ra p là số lẻ
Đặt p = 2k + 1 (k ℤ+), khi đó ta có:
2q2 + 41 = (2k + 1)2
2q2 + 41 = 4k2 + 4k + 1
q2 = 2k2 + 2k − 20
q2 ⋮ 2 q = 2.
Khi đó thay vào (1) ta có p = 7 (TM).
Vậy (p; q) = (7; 2).
Lời giải:
Ta có:
Lời giải:
Vì .
Nên
Do đó .
Vậy A > 5.
Lời giải:
Ta có
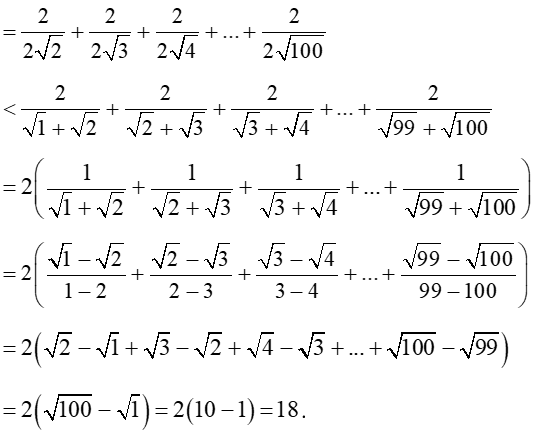
Vậy .
Câu 30: Chứng minh rằng 2x2 − x + 1 > 0 với mọi giá trị của x.
Lời giải:
Ta có: 2x2 − x + 1
Do
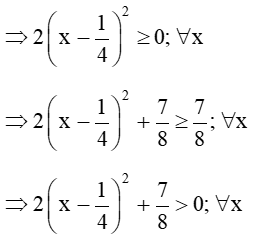
Vậy 2x2 − x + 1 > 0 với mọi số thực x.
Câu 31: Chứng minh: 2x − 2x2 − 1 < 0 với mọi số thực x.
Lời giải:
Ta có: 2x − 2x2 – 1 = − (2x2 − 2x + 1)
Do
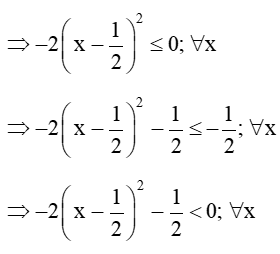
Vậy 2x − 2x2 − 1 < 0 với mọi số thực x.
Câu 32: Cho tam giác ABC. Chứng minh nếu b + c = 2a thì .
Lời giải:
Ta có .
Khi đó, với b + c = 2a thì .
Lời giải:
Ta có .
Do đó
Lời giải:
ĐK: .
Khi đó
(TMĐK)
Câu 35: Phương trình cot 3x = cot x có mấy nghiệm thuộc (0, 10π].
Lời giải:
ĐK:
Ta có cot 3x = cot x
3x = x + kp
Với
k {1; 3; 5; 7; 9; 11; 13; 15; 17; 19}.
Suy ra phương trình đã cho có 10 nghiệm thỏa mãn.
Câu 36: Khảo sát sự biên sự biến thiên của hàm số: trên khoảng (1; +∞).
Lời giải:
Với mọi x1, x2 (1; +∞) và x1 ≠ x2, ta có:
Do x1, x2 (1; +∞) x1 − 1 > 0; x2 − 1 > 0
(x1 − 1)(x2 − 1) > 0
Vậy hàm số nghịch biến trên (1; +∞)
Câu 37: Giải tam giác ABC vuông tại A biết: a = 12 cm, .
Lời giải:
Ta có: .
Suy ra ∆ABC vuông cân tại A nên b = c.
Khi đó
Câu 38: Giải tam giác ABC vuông tại A, biết rằng c = 10 cm, .
Lời giải:
Ta có: .
Suy ra ∆ABC vuông cân tại A nên b = c = 10 cm.
Khi đó .
Vậy a ≈ 14,14 cm; b = 10 cm; .
Lời giải:
Tổng số học sinh thích cả Toán và Tiếng Việt là:
45 − 3 = 42 (học sinh)
Có số học sinh thích cả 2 môn là:
(28 + 20) − 42 = 6 (học sinh)
Đáp số: 6 học sinh thích cả Toán và Tiếng Việt.
Lời giải:
Số học sinh giỏi là:
45 : 100 . 20 = 9 (học sinh)
Số học sinh tiên tiến là:
9 : = 21 (học sinh)
Tổng số học sinh giỏi và học sinh tiên tiến của lớp đó là:
21 + 9 = 30 (học sinh)
Số học sinh trung bình là:
45 − 30 = 15 (học sinh)
Tỉ số phần trăm số học sinh trung bình so với số học sinh cả lớp là:
(số học sinh trong lớp).
Vậy số học sinh trung bình chiếm số học sinh trong lớp.
Lời giải:
Ta có
cos 2x(cos x + 2) + sin x(2cos2 x − 1) = 0
cos 2x(cos x + 2) + sin x. cos 2x = 0
cos 2x(cos x + sin x + 2) = 0
Vì cos x + sin x + 2 > 0 nên cos 2x = 0
.
Lời giải:
Ta có
sin 2x + cos 2x = sin x − cos x
Câu 43: Giải phương trình lượng giác: .
Lời giải:
Phương trình đã cho tương đương với:
• TH1: .
• TH2:
Vậy nghiệm của phương trình đã cho là: ; ; với .
Câu 44: Giải phương trình: sin3 x + cos3 x − sin x − cos x = cos 2x.
Lời giải:
Ta có sin3 x + cos3 x − sin x − cos x = cos 2x
(sin x + cos x)(sin2 x − sin x.cos x + cos2 x) − (sin x + cos x) − (cos2 x − sin2 x) = 0
(sin x + cos x)(1 − sin x.cos x) − (sin x + cos x) − (sin x + cos x)(cos x − sin x) = 0
(sin x + cos x)(1 − sin x.cos x − 1 − cos x + sin x) = 0
(sin x + cos x)(− sin x.cos x − cos x + sin x) = 0
• TH1: sin x + cos x = 0
• TH2: − sin x.cos x − cos x + sin x = 0 (1)
Đặt t = sin x − cos x; t Î (−2; 2)
Phương trình (1) Û
Câu 45: Giải phương trình: sin x.sin 7x = sin 3x.sin 5x.
Lời giải:
Ta có sin x.sin 7x = sin 3x.sin 5x
cos 8x − cos 6x = cos 8x − cos 2x
cos 6x = cos 2x
Câu 46: Tìm giá trị của x, biết: .
Lời giải:
Ta có .
Câu 47: Tìm giá trị nhỏ nhất của .
Lời giải:
ĐK: x ≥ 0
Ta có
.
Áp dụng BĐT AM-GM cho hai số dương, ta có:
Do đó A ≥ 2.5 − 6 = 4.
Dấu “=” xảy ra khi .
Vì nên .
Câu 48: Cho . Tìm giá trị nhỏ nhất của Q.
Lời giải:
ĐK: x ≥ 0.
Ta có
.
Áp dụng BĐT AM-GM cho hai số dương, ta có:
Do đó Q ≥ 2.5 − 6 = 4.
Dấu “=” xảy ra khi .
Vì nên .
Câu 49: Cho biểu thức . Tìm x để |A| > A.
Lời giải:
ĐK: x ≥ 0; x ≠ 4
Để |A| > A Þ A < 0
Mà
Kết hợp ĐK nên suy ra 0 £ x < 4.
a) Tính số học sinh mỗi loại.
b) Số học sinh giỏi bằng bao nhiêu phần trăm số học sinh cả lớp?
Lời giải:
a) Số học sinh khá là:
35 : 125% = 28 (hoc sinh)
Số học sinh giỏi là:
28 . = 20 (học sinh)
Số học sinh trung bình là:
20 . 10% = 2 (học sinh)
b) Tỉ số phần trăm của số học sinh giỏi so với số học sinh cả lớp là:
(số học sinh cả lớp).
Vậy số học sinh giỏi bằng 40% số học sinh cả lớp.
a) Hỏi lớp có bao nhiêu học sinh?
b) Tính tỉ số phần trăm của số học sinh mỗi loại so với số học sinh cả lớp?
Lời giải:
a) Số học sinh khá bằng 50% số học sinh cả lớp, tức bằng số học sinh cả lớp.
Số học sinh trung bình bằng số học sinh cả lớp.
Số học sinh giỏi bằng:
(số học sinh cả lớp)
Vậy số học sinh cả lớp là:
(học sinh)
b) Tỉ số phần trăm của số học sinh trung bình so với số học sinh cả lớp là:
.
Tỉ số phần trăm của số học sinh giỏi so với số học sinh cả lớp là:
100% − 50% − 40% = 10%.