Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 9)

Câu 1: Giải phương trình: $\sqrt{x^3+1}=x^2-3x-1$

Lời giải:

Điều kiện xác định: $\left\{\begin{array}{l}{x}^3+1\ge 0\\ x^2-3x-1\ge 0\end{array}\right.\iff \left\{\begin{array}{l}x\ge -1\\ \left[\begin{array}{l}x\ge \frac{3+\sqrt{13}}{2}\\ x\ge \frac{3-\sqrt{13}}{2}\end{array}\right.\end{array}\right.\iff \left[\begin{array}{l}x\ge \frac{3+\sqrt{13}}{2}\\ -1\le x\le \frac{3-\sqrt{13}}{2}\end{array}\right.$

$\sqrt{x^3+1}=x^2-3x-1\iff \sqrt{(x+1)(x^2-x+1)}=x^2-x+1-2\left(x+1\right)$

Đặt $a=\sqrt{x+1}$; $b=\sqrt{x^2-x+1}$ (a ≥ 0, b > 0)

Khi đó, ta có phương trình:

⇔ b² – 2a² = ab

⇔ 2a² + ab – b² = 0

⇔ (a + b)(2a – b) = 0

$\iff \left[\begin{array}{l}a+b=0\left(KTM\right)\\ 2a-b=0\left(TM\right)\end{array}\right.$

⇔ 2a = b

$\iff 2\sqrt{x+1}=\sqrt{x^2-x+1}$

⇔ 4x + 4 = x² – x + 1

⇔ x² – 5x – 3 = 0

Có ∆ = 5² + 3.4 = 37 > 0 ⇒ Phương trình có hai nghiệm phân biệt.

$x_1=\frac{5+\sqrt{37}}{2};x_2=\frac{5-\sqrt{37}}{2}$

Vậy phương trình có 2 nghiệm $x_1=\frac{5+\sqrt{37}}{2};x_2=\frac{5-\sqrt{37}}{2}$

Câu 2: Cho tam giác ABC có trung tuyến AM. Gọi I la trung điểm AM va K là điểm thuộc AC sao cho $AK=\frac{1}{3}AC$. Chứng minh B, I, K thẳng hàng.

Lời giải:

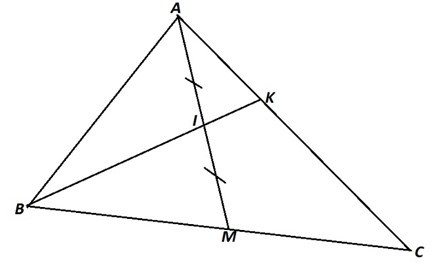
Ta có:

$$\begin{gathered} \left\{\begin{array}{l}\overrightarrow{BI}=\overrightarrow{BA}+\overrightarrow{AI}\\ \overrightarrow{BI}=\overrightarrow{BM}+\overrightarrow{MI}\end{array}\right.\Rightarrow 2\overrightarrow{BI}=\overrightarrow{BA}+\overrightarrow{BM}+\left(\overrightarrow{AI}+\overrightarrow{MI}\right)=\overrightarrow{BA}+\overrightarrow{BM} \\ =\overrightarrow{BA}+\frac{\overrightarrow{BC}}{2}\Rightarrow 4\overrightarrow{BI}=2\overrightarrow{BA}+\overrightarrow{BC} \end{gathered}$$

Lại có:

$$\begin{gathered} \overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}=\overrightarrow{BA}+\frac{\overrightarrow{AC}}{3} \\ \Rightarrow 3\overrightarrow{BK}=3\overrightarrow{BA}+\overrightarrow{AC}=2\overrightarrow{BA}+\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=2\overrightarrow{BA}+\overrightarrow{BC} \end{gathered}$$

Do đó: $4\overrightarrow{BI}=3\overrightarrow{BK}$

Vậy B, I, K thẳng hàng.

Câu 3: Chữ số tận cùng của kết quả $2^{64}$.

Lời giải:

Theo công thức:

4²ⁿ⁺¹ có chữ số tận cùng là 4; 4²ⁿ có chữ số tận cùng là 6

Ta có: 2⁶⁴ = 4³²

Vì 32 = 2.16 (Dạng 2n) nên 2⁶⁴ = 4³² có chữ số tận cùng là 6.

Câu 4: Cho phương trình x² – 4x – m² – 1 = 0. Tìm m để phương trình có 2 nghiệm x₁, x₂  sao cho biểu thức x₂ = –5x₁.

Lời giải:

Xét phương trình x² – 4x – m² – 1 = 0

∆’ = (–2)² – 1.(–m² – 1) = 4 + m² + 1 = 5 + m² > 0 với mọi m

Áp dụng hệ thức Vi–ét ta có:

$\left\{\begin{array}{l}{x}_1+x_2=\frac{-(-4)}{1}=4\\ x_1.x_2=-m^2-1\end{array}\right.$

Theo đề bài có: x₂ = –5x₁ ⇒ 5x₁ + x₂ = 0

Ta có hệ phương trình: $\left\{\begin{array}{l}{x}_1+x_2=4\\ 5x_1+x_2=0\end{array}\right.\iff \left\{\begin{array}{l}{x}_1=-1\\ x_2=5\end{array}\right.$

$\Rightarrow -m^2-1=(-1).4\Rightarrow -m^2-1=-4\Rightarrow m^2=3\Rightarrow m=\pm \sqrt{3}$

Câu 5: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; –1) và B(3; 2). Tìm M thuộc trục tung sao cho $M{A}^2+M{B}^2$ nhỏ nhất.

Lời giải:

M thuộc trục tung nên ta có: M(0; y)

$\begin{array}{l}\Rightarrow M{A}^2+M{B}^2=1+{\left(y+1\right)}^2+3^2+{\left(y-2\right)}^2\\ =2y^2-2y+15\\ =2\left(y^2-y+\frac{1}{4}\right)+\frac{29}{2}\\ =2{\left(y-\frac{1}{2}\right)}^2+\frac{29}{2}\ge \frac{29}{2}\end{array}$

Hay $M{A}^2+M{B}^2\ge \frac{29}{2}$

Dấu bằng xảy ra hay $M{A}^2+M{B}^2$ nhỏ nhất  khi và chỉ khi  $y=\frac{1}{2}$

Vậy $M\left(0;\frac{1}{2}\right)$

Câu 6: Giải phương trình: $\frac{4x}{x^2+x+3}+\frac{5x}{x^2-5x+3}=-\frac{3}{2}$

Lời giải:

$\begin{array}{l}\frac{4x}{x^2+x+3}+\frac{5x}{x^2-5x+3}=-\frac{3}{2}\\ \Rightarrow \frac{4x\left(x^2-5x+3\right)+5x\left(x^2+x+3\right)}{\left(x^2-5x+3\right)\left(x^2+x+3\right)}+\frac{3}{2}=0\\ \Rightarrow \frac{8x\left(x^2-5x+3\right)+10x\left(x^2+x+3\right)+3\left(x^2+x+3\right)\left(x^2-5x+3\right)}{2\left(x^2+x+3\right)\left(x^2-5x+3\right)}=0\\ \Rightarrow 8x\left(x^2-5x+3\right)+10x\left(x^2+x+3\right)+3\left(x^2+x+3\right)\left(x^2-5x+3\right)=0\\ \Rightarrow 3\left(x^2-3x+3\right)\left(x^2+5x+3\right)=0\\ \Rightarrow \left[\begin{array}{l}{x}^2-3x+3=0\\ x^2+5x+3=0\end{array}\right.\Rightarrow x=\frac{-5}{2}\pm \frac{\sqrt{13}}{2}\left(TM\right)\end{array}$

Câu 7: Cho các chữ số 1, 2, 5, 7, 8. Có bao nhiêu cách lập ra một số gồm ba chữ số khác nhau từ 5 số trên sao cho:

a) Số tạo ra là số chẵn.

b) Số tạo thành là 1 số ko có chữ số 7.

c) Số tạo thành nhỏ hơn 278.

Lời giải:

Gọi số cần tìm là $\overline{abc}$

a)

Số cách chọn chữ số c là: 2

Số cách chọn chữ số b là: 4

Số cách chọn chữ số a là: 3

Vậy số số chẵn có thể tạo ra là: 2.4.3 = 24 (số)

b)

Số cách chọn chữ số a là: 4

Số cách chọn chữ số b là: 3

Số cách chọn chữ số c là: 2

Vậy số cách lập số thỏa mãn yêu cầu là: 4.3.2 = 24 (số)

c)

Nếu hàng trăm là 2 thì có 8 số: 251; 257; 271; 275; 215; 217; 258; 218.

Nếu hàng trăm là 1 thì số cách là: $A_4^2=12$

Vậy có 8 + 12 = 20 (cách)

Câu 8: Cho tam giác ABC, G là trọng tâm. Chứng minh $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

Lời giải:

Gọi I là trung điểm của BC

Trọng tâm G của tam giác ABC nằm trên trung tuyến AI.

Do đó, A, G, I thẳng hàng.

Ta có: $\overrightarrow{AG}=2\overrightarrow{GI}$ (1)

Ta có: $\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}$

$\Rightarrow \left(\overrightarrow{GB}-\overrightarrow{GI}\right)+\left(\overrightarrow{GC}-\overrightarrow{GI}\right)=\overrightarrow{0}$

$\begin{array}{l}\Rightarrow \overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GI}+\overrightarrow{GI}\\ \Rightarrow \overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GI}\left(2\right)\end{array}$

Từ (1) và (2) ta có:

$\begin{array}{l}\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{AG}\Rightarrow \overrightarrow{GB}+\overrightarrow{GC}-\overrightarrow{AG}=\overrightarrow{0}\\ \Rightarrow \overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GA}=\overrightarrow{0}\end{array}$

Câu 9: Giải phương trình sinx = cos3x.

Lời giải:

$\begin{array}{l}\sin x=cos3x\\ \iff cos3x=cos\left(\frac{\pi }{2}-x\right)\\ \iff \left[\begin{array}{l}3x=\frac{\pi }{2}-x+k2\pi \\ 3x=x-\frac{\pi }{2}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)\\ \iff \left[\begin{array}{l}4x=\frac{\pi }{2}+k2\pi \\ 2x=-\frac{\pi }{2}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)\\ \iff \left[\begin{array}{l}x=\frac{\pi }{8}+k\frac{\pi }{2}\\ x=-\frac{\pi }{4}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)\end{array}$

Câu 10: Số cách chia 12 phần quà cho 3 bạn sao cho ai cũng có ít nhất 2 phần quà ?

Lời giải:

Chia trước cho mỗi học sinh một phần quà thì số phần quà còn lại là 9 phần quà.

Chia 9 phần quà cho 3 học sinh sao cho học sinh nào cũng có ít nhất một phần quà.

Đặt 9 phần quà theo một hàng ngang, giữa các phần quà sẽ có 8 khoảng trống, chọn 2 khoảng trống trong 8 khoảng trống đó để chia 9 phần quà còn lại thành 3 phần quà mà mỗi phần có ít nhất một phần quà, có $C_8^2$​. Vậy tất cả có $C_8^2$​ = 28 cách chia.

Câu 11: Một trang trại cần thuê xe vận chuyển 450 con lợn và 35 tấn cám. Nơi cho thuê xe chỉ có 12 xe lớn và 10 xe nhỏ. Một chiếc xe lớn có thể chở 50 con lợn và 5 tấn cám. Tiền thuê một xe lớn là 4 triệu đồng, một xe nhỏ là 2 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thuê xe là thấp nhất ?

Lời giải:

Gọi số xe loại lớn, nhỏ cần thuê lần lượt là x, y xe (x, y ≥ 0, x, y ∈ ℤ)

⟶ T = 4x + 2y (triệu đồng) là số tiền thuê xe. Suy ra để số tiền thuê xe nhỏ nhất thì T = 4x + 2y nhỏ nhất.

Theo bài ta có:

$\left\{\begin{array}{l}0\le x\le 12\\ 0\le y\le 10\\ 40x+30y\ge 450\\ 5x+y\ge 35\end{array}\right.$

Vẽ miền nghiệm của hệ trên, thấy các điểm giao nhau là:

A(12; 10), B(12; 0), C(11; 250), D(5; 10), $E\left(\frac{60}{11};\frac{85}{11}\right)$

Suy ra: T_A = 68; T_B = 48; T_C = 45; T_D = 40.

⟶ T_D nhỏ nhất vì x,y ∈ ℤ

⟶ Cần thuê 5 xe lớn và 10 xe nhỏ.

Câu 12: Hãy rút gọn phân thức: $\frac{8x-4}{8x^3-1}$.

Lời giải:

$\frac{8x-4}{8x^3-1}=\frac{4\left(2x-1\right)}{{\left(2x\right)}^3-1}=\frac{4\left(2x-1\right)}{\left(2x-1\right)\left(4x^2+2x+1\right)}=\frac{4}{4x^2+2x+1}$

Câu 13: Giải phương trình sau: $\frac{cos4x-6{\sin }^{2}x+2}{2\sin x-1}$

Lời giải:

$\frac{cos4x-6{\sin }^{2}x+2}{2\sin x-1}=0$

Điều kiện xác định:

2sinx – 1 ≠ 0

$\begin{array}{l}\iff \sin x\ne \frac{1}{2}\\ \iff \sin x\ne \sin \frac{\pi }{6}\\ \iff \left\{\begin{array}{l}x\ne \frac{\pi }{6}+k2\pi \\ x\ne \frac{5\pi }{6}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)\end{array}$

$\begin{array}{l}\frac{cos4x-6{\sin }^{2}x+2}{2\sin x-1}=0\\ \Rightarrow \cos 4x-6{\sin }^{2}x+2=0\\ \Rightarrow 2{\cos }^{2}2x-1+3-6{\sin }^{2}x+2=0\\ \iff 2{\cos }^{2}2x-1+3\left(1-2{\sin }^{2}x\right)-1=0\\ \iff 2\cos 2x\left(cos2x+2\right)-\left(cos2x+2\right)=0\\ \iff \left(2\cos 2x-1\right)\left(\cos 2x+2\right)=0\end{array}$

$\begin{array}{l}\iff 2\cos 2x-1=0\left(cos2x+2\ge 1\right)\\ \iff cos2x=\frac{1}{2}\\ \iff 2x=\pm \frac{\pi }{3}+k2\pi \left(k\in \mathbb{Z}\right)\\ \iff x=\pm \frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)\left(1\right)\end{array}$

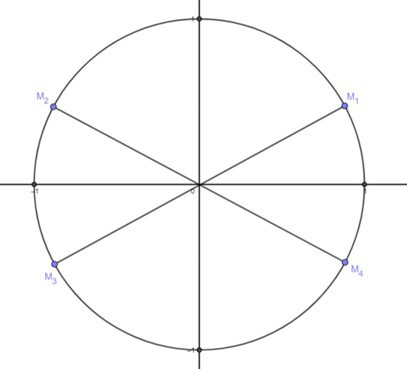
Họ nghiệm (1) biểu diễn bởi các điểm M₁, M₂, M₃, M₄ trên đường tròn lượng giác.

Họ nghiệm làm cho phương trình không xác định biểu diễn bởi các điểm M₁, M₂ trên đường tròn lượng giác.

Tổng hợp lại ta có nghiệm phương trình biểu diễn bởi các điểm M₃, M₄ trên đường tròn lượng giác.

Hay $x=\frac{-5\pi }{6}+k2\pi ;x=\frac{-\pi }{6}+k2\pi \left(k\in \mathbb{Z}\right)$

Câu 14: Tính nhanh: (317 + 49) – 117

Lời giải:

(317 + 49) – 117

= 317 + 49 – 117

= (317 – 117) + 49

= 200 + 49

= 249

Câu 15: Phân tích đa thức thành nhân tử: x⁴ + 2x³ – 4x – 4.

Lời giải:

x⁴ + 2x³ – 4x – 4

= x⁴ – 2x² + 2x³ – 4x + 2x² – 4

= x²(x² – 2) + 2x(x² – 2) + 2(x² – 2)

= (x² – 2)(x² + 2x + 2)

Câu 16: Cho hàm số bậc nhất y = (m – 1)x + m + 1 (1)

1) Vẽ đồ thị hàm số (1) với m = 2

2) Tìm m để đồ thị hàm số song song với đường thẳng y = 2x + 1

3) Tìm khoảng cách từ gốc tọa độ đến đường thẳng y = 2x + 4

Lời giải:

a)

Với m = 2 ta có hàm số: y = x + 3

Đồ thị hàm số đi qua hai điểm (0; 3) và (–3; 0)

Ta có đồ thị hàm số trong hình vẽ dưới đây:

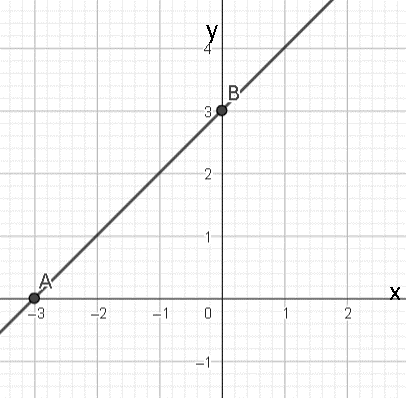
b)

Để  y = (m – 1)x + m + 1 song song với y = 2x + 1

Thì: $\left\{\begin{array}{l}m-1=2\\ m+1\ne 1\end{array}\right.\Rightarrow \left\{\begin{array}{l}m=3\\ m\ne 0\end{array}\right.$

Vậy m = 3 thỏa mãn yêu cầu đề bài

c)

Đồ thị hàm số y = 2x + 4 đi qua điểm (0; 4) và (–2; 0) như hình vẽ:

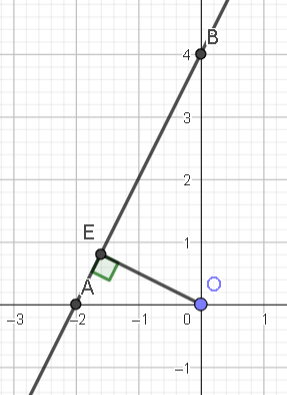
Kẻ OE vuông góc với AB tại E .

Xét tam giác OAB vuông tại O có:

OA = 2; OB = 4

OE là đường cao ứng với cạnh huyền.

Áp dụng hệ thức lượng trong tam giác vuông  ta có:

$\frac{1}{O{E}^2}=\frac{1}{O{A}^2}+\frac{1}{O{B}^2}\Rightarrow \frac{1}{O{E}^2}=\frac{1}{2^2}+\frac{1}{4^2}=\frac{5}{16}\Rightarrow OE=\frac{4\sqrt{5}}{5}$

Vậy khoảng cách từ gốc tọa độ đến đường thẳng y = 2x + 4 là $OE=\frac{4\sqrt{5}}{5}$

Câu 17: Giải phương trình lượng giác: cos2x – cosx + 1 = 0

Lời giải:

cos2x – cosx + 1 = 0

$\begin{array}{l}\iff 2{\cos }^{2}x-1-\cos x+1=0\\ \iff 2{\cos }^{2}x-\cos x=0\\ \iff \cos x\left(2\cos x-1\right)=0\\ \iff \left[\begin{array}{l}cosx=0\\ cosx=\frac{1}{2}\end{array}\right.\iff \left[\begin{array}{l}x=\pm \frac{\pi }{3}+k2\pi \\ x=\frac{\pi }{2}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)\end{array}$

Câu 18: Giải phương trình: cos2x + cosx + 1 = 0

Lời giải:

cos2x + cosx + 1 = 0

$\begin{array}{l}\iff 2{\cos }^{2}x-1+\cos x+1=0\\ \iff 2{\cos }^{2}x+\cos x=0\end{array}$

$\begin{array}{l}\iff \cos x\left(2\cos x+1\right)=0\\ \iff \left[\begin{array}{l}cosx=-\frac{1}{2}\\ cosx=\end{array}\right.\iff \left[\begin{array}{l}x=\pm \frac{2\pi }{3}+k2\pi \\ x=\frac{\pi }{2}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)\end{array}$

Câu 19: Cho x, y ∈ ℕ*. Tìm giá trị nhỏ nhất của A = |36^x – 5^y|

Lời giải:

Vì x, y ∈ ℕ* nên nếu:

36^x ≡ a (mod 100) và 5^y ≡ b (mod 100)

Thì a ∈ {36; 96; 56; 16; 76} và b ∈ {25}

Gọi m là giá trị nhỏ nhất của A

Dễ thấy: m ≤ 36 – 5² = 11

Bây giờ, xét m có thể bằng 25 – 16 = 9 hay không ?

Giả sử m = 25 – 16 = 9 thì 5^y – 36^x =  9 nên suy ra 5^y ≡ 9 (mod 36)

Nhưng điều đó là vô lý vì 5^y chia cho 36 chỉ cho các số dư là 5; 25; 17; 13; 29; 1.

Vậy GTNN của A là 11.

Câu 20: Tìm x, biết 35 chia hết cho x.

Lời giải:

Vì 35 ⋮ x ⇒ x ∈ Ư(35)  ⇒ x ∈ {±1; ±5; ±7; ±35}

Câu 21: Tìm x, biết: ${\left(\frac{4}{5}\right)}^{2x+5}=\frac{256}{625}$

Lời giải:

$\begin{array}{l}{\left(\frac{4}{5}\right)}^{2x+5}=\frac{256}{625}\\ \iff {\left(\frac{4}{5}\right)}^{2x+5}={\left(\frac{4}{5}\right)}^4\\ \iff 2x+5=4\\ \iff x=-\frac{1}{2}\end{array}$

Câu 22: Giải phương trình: ${\sin }^{2}x-3\sin x.\cos x+1=0$

Lời giải:

$\begin{array}{l}{\sin }^{2}x-3\sin x.\cos x+1=0\\ \iff {\sin }^{2}x-3\sin x.\cos x+{\sin }^{2}x+{\cos }^{2}x=0\\ \iff 2{\sin }^{2}x-2\sin x.\cos x+co{s}^{2}x-\sin x.\cos x=0\\ \iff 2\sin x\left(\mathrm{s}\text{inx}-\cos x\right)+\cos x\left(\cos x-\sin x\right)=0\\ \iff \left(\sin x-\cos x\right)\left(2\sin x-\cos x\right)=0\\ \iff \left[\begin{array}{l}\sin x-\cos x=0\\ 2\sin x-\cos x=0\end{array}\right.\iff \left[\begin{array}{l}\sqrt{2}.cos\left(x+\frac{\pi }{4}\right)=0\\ \frac{2}{\sqrt{5}}\sin x-\frac{1}{\sqrt{5}}\cos x=0\end{array}\right.\end{array}$

$\begin{array}{l}\iff \left[\begin{array}{l}\cos \left(x+\frac{\pi }{4}\right)=0\\ sin\left(x+\alpha \right)=0\left(\alpha =\arcsin \frac{1}{\sqrt{5}}\right)\end{array}\right.\\ \iff \left[\begin{array}{l}x=\frac{\pi }{4}+k\pi \\ x=\alpha +k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)\end{array}$

Câu 23: Cho A = (5; 7] và B = [m; m+3). Tìm m để:

a) A ⊂ B

b) B ⊂ A

Lời giải:

a)

$A\subset B\iff \left\{\begin{array}{l}m\le 5\\ m+3>7\end{array}\right.\iff 4<m\le 5$

b)

$B\subset A\iff \left\{\begin{array}{l}m>5\\ m+3\le 7\end{array}\right.\iff \left\{\begin{array}{l}m>5\\ m\le 4\end{array}\right.\iff m\in \varnothing$

Câu 24: Cho hai tập hợp A = [1; 3] và B = [m; m + 1]. Tìm m để B là tập con của A.

Lời giải:

$B\subset A\iff \left\{\begin{array}{l}m\ge 1\\ \text{M}+1\le 3\end{array}\right.\iff \left\{\begin{array}{l}m\ge 1\\ m\le 2\end{array}\right.\iff 1\le m\le 2$

Câu 25: Biết rằng parabol (P): y = ax² + bx + c (a ≠ 0) đi qua hai điểm A(0; –3), B(2; 1) và cắt trục hoành tại hai điểm phân biệt M, N thỏa mãn MN = 2. Tính giá trị biểu thức a² – b².

Lời giải:

A, B ∈ (P) nên tọa độ A, B là nghiệm của phương trình:

$\left\{\begin{array}{l}-3=a{.0}^2+b.0+c\\ 1=a{.2}^2+b.2+c\end{array}\right.\Rightarrow \left\{\begin{array}{l}c=-3\\ 4a+2b=4\end{array}\right.\Rightarrow \left\{\begin{array}{l}c=-3\\ b=2-2a\end{array}\right.$

Vì (P) giao Ox tại M và N nên gọi tọa độ của M(x­­­_M; 0) , N(x_N; 0)

MN = 2 $\iff \sqrt{{\left(x_N-x_M\right)}^2+{\left(y_N-y_M\right)}^2}=2$

⇔ x_N – x_M = 2 (*)

$x_N=\frac{-b+\sqrt{\Delta }}{2a};x_M=\frac{-b-\sqrt{\Delta }}{2a}$

$x_N-x_M=\frac{\sqrt{\Delta }}{a}=\frac{\sqrt{{\left(-b\right)}^2-4ac}}{a}=2$

⇔ b² – 4ac = 4a²

⇔ b² – 4a.(–3) = 4a²

⇔ (2 – 2a)² + 12a – 4a² = 0

⇔ 4a² – 8a + 4 + 12a – 4a² = 0

⇔ 4a + 4 = 0

Do đó, nếu a = –1 thì b = 4

Vậy a² – b² = (–1)² – 4² = –15

Câu 26: Chứng minh rằng $1+{\tan }^{2}x=\frac{1}{co{s}^{2}x}$

Lời giải:

Xét VT = $1+\frac{{\sin }^{2}x}{co{s}^{2}x}=\frac{{\sin }^{2}x+{\cos }^{2}x}{co{s}^{2}x}=\frac{1}{co{s}^{2}x}=VP$(đcpcm)

Câu 27: Giải phương trình lượng giác: tanx + cotx = 2

Lời giải:

tanx + cotx = 2  $\left(x\ne k\pi ;x\ne \frac{\pi }{2}+k\pi \right)$

$\iff \frac{\mathrm{s}\text{inx}}{\cos x}+\frac{\cos x}{\sin x}=2$

$\begin{array}{l}\iff \frac{{\sin }^{2}x+co{s}^{2}x}{\sin x.\cos x}=2\\ \iff \frac{1}{\sin x.\cos x}=2\\ \iff 2\sin x.\cos x=1\\ \iff \sin 2x=1\\ \iff 2x=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)\\ \iff x=\frac{\pi }{4}+k\pi \left(k\in \mathbb{Z}\right)\end{array}$

Câu 28: Nghiệm của phương trình tanx + cotx  = – 2 là ?

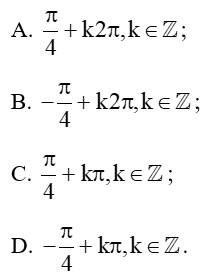
Lời giải:

tanx + cotx = –2  $\left(x\ne k\pi ;x\ne \frac{\pi }{2}+k\pi \right)$

 

 

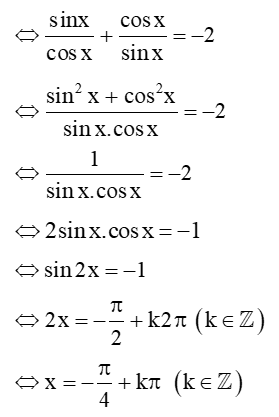
Đáp án đúng là D.

Câu 29: Rút gọn phân thức:

a) $\frac{5x^2+10xy+5y^2}{3x^2+3y^2}$

b) $\frac{-15x\left(x-y\right)}{3\left(y-x\right)}$

Lời giải:

a)

$\frac{5x^2+10xy+5y^2}{3x^2+3y^2}=\frac{5x^2+5xy+5xy+5y^2}{3x^2+3y^2}=\frac{5x\left(x+y\right)+5y\left(x+y\right)}{3\left(x^2+y^2\right)}=\frac{5{\left(x+y\right)}^2}{3\left(x^2+y^2\right)}$

b)

$\frac{-15x\left(x-y\right)}{3\left(y-x\right)}=\frac{15x\left(y-x\right)}{3\left(y-x\right)}=5x$.

Câu 30: Cho biểu thức $P=\frac{x^2+x}{x^2-2x+1}:\left(\frac{x+1}{x}-\frac{1}{1-x}+\frac{2-x^2}{x^2-x}\right)$ .

a) Rút gọn P.

b) Tìm x để P < 1.

c) Tìm giá trị nhỏ nhất của P khi x > 2.

Lời giải:

a) $P=\frac{x^2+x}{x^2-2x+1}:\left(\frac{x+1}{x}-\frac{1}{1-x}+\frac{2-x^2}{x^2-x}\right)$

$$\begin{gathered} =\frac{x\left(x+1\right)}{{\left(x-1\right)}^2}:\left[\frac{x+1}{x}+\frac{1}{x-1}+\frac{2-x^2}{x\left(x-1\right)}\right] \\ =\frac{x\left(x+1\right)}{{\left(x-1\right)}^2}:\left[\frac{\left(x+1\right)\left(x-1\right)+x+2-x^2}{x\left(x-1\right)}\right] \\ =\frac{x\left(x+1\right)}{{\left(x-1\right)}^2}:\frac{x+1}{x\left(x-1\right)}=\frac{x\left(x+1\right)}{{\left(x-1\right)}^2}.\frac{x\left(x-1\right)}{x+1}=\frac{x^2}{x-1} \end{gathered}$$

b) Ta có $P<1\iff \frac{x^2}{x-1}<1$

$\iff \frac{x^2}{x-1}-1<0\iff \frac{x^2-x+1}{x-1}<0$

$\iff \frac{{\left(x-\frac{1}{2}\right)}^2+\frac{3}{4}}{x-1}<0\iff x-1<0$ (vì ${\left(x-\frac{1}{2}\right)}^2+\frac{3}{4}\ge \frac{3}{4}>\mathrm{0,}\forall x\in ℝ$ ).

⇔ x < 1.

Vậy x < 1 thì P < 1.

c) Vì x > 2 nên x – 2 > 0.

Do đó x – 1 > x – 2 > 0.

Ta có $P=\frac{x^2}{x-1}=\frac{x^2-1+1}{x-1}=x+1+\frac{1}{x-1}=x-1+\frac{1}{x-1}+2$ .

Áp dụng bất đẳng thức Cauchy, ta có:

$x-1+\frac{1}{x-1}\ge 2\sqrt{\frac{x-1}{x-1}}=2\sqrt{1}=\mathrm{2,}\forall x>2$ .

$\iff x-1+\frac{1}{x-1}+2\ge 2+2=4$.

⇔ P ≥ 4.

Dấu “=” xảy ra ⇔ (x – 1)² = 1 ⇔ x – 1 = 1 hoặc x – 1 = –1.

⇔ x = 2 (loại vì x > 2) hoặc x = 0 (loại vì x > 2).

Vậy P không có giá trị nhỏ nhất khi x > 2.

Câu 31: Cho biểu thức $A=\frac{\sqrt{x}-1}{\sqrt{x}+1}$  và $B=\frac{\sqrt{x}+6}{\sqrt{x}-1}$ .

Đặt P = A.B. Tìm x hữu tỉ để P có giá trị nguyên nhỏ nhất.

Lời giải:

Ta có $P=A.B=\frac{\sqrt{x}-1}{\sqrt{x}+1}.\frac{\sqrt{x}+6}{\sqrt{x}-1}=\frac{\sqrt{x}+1+5}{\sqrt{x}+1}=1+\frac{5}{\sqrt{x}+1}$ .

Để P có giá trị nguyên thì $5⋮\left(\sqrt{x}+1\right)$ .

$\Rightarrow \sqrt{x}+1\in$ Ư(5).

Ta có bảng sau:

$\sqrt{x}+1$	–5	–1	1	5
x	Vô nghiệm	Vô nghiệm	0	16

Với x = 0, ta có $P=1+\frac{5}{\sqrt{0}+1}=6$ .

Với x = 16, ta có $P=1+\frac{5}{\sqrt{16}+1}=2$ .

Vậy P có giá trị nguyên nhỏ nhất khi và chỉ khi x = 16.

Câu 32: Từ các chữ số 0; 1; 2; 3; 4; 5; 6; 8; 9, có thể lập được bao nhiêu số tự nhiên có 5 chữ số và lớn hơn 65000?

Lời giải:

Gọi $\overline{abcde}$  là số tự nhiên cần tìm (0 ≤ a, b, c, d, e ≤ 9; a ≠ 0; a, b, c, d, e ∈ ℕ \ {7}).

Trường hợp 1: a = 6, b = 5.

Chọn tùy ý các chữ số c, d, e từ 9 chữ số đã cho, ta luôn được số thỏa mãn trừ trường hợp c = d = e = 0.

Số các số lập được là: 1.1.9³ – 1 = 728 (số).

Trường hợp 2: a = 6, b ∈ {6; 8; 9}.

Chọn tùy ý các chữ số c, d, e trong 9 chữ số đã cho, ta luôn được số thỏa mãn.

Số các số lập được là: 1.3.9³ = 2187 (số).

Trường hợp 3: a ∈ {8; 9}.

Chọn tùy ý các chữ số b, c, d, e trong 9 chữ số đã cho, ta luôn được số thỏa mãn.

Số các số lập được là: 2.9⁴ = 13122 (số).

Vậy số các số thỏa mãn yêu cầu bài toán là: 728 + 2187 + 13122 = 16037 số.

Câu 33: Xét tính bị chặn của dãy số (u_n) với $u_n=\frac{2n+1}{n+1}$ .

Lời giải:

Ta có $u_n=\frac{2n+1}{n+1}=\frac{2\left(n+1\right)-1}{n+1}=2-\frac{1}{n+1}$ .

Do n ∈ ℕ^* nên $\frac{1}{n+1}\le \frac{1}{2}$ .

Suy ra $2-\frac{1}{n+1}\ge 2-\frac{1}{2}=\frac{3}{2}$ .

Vậy dãy (u_n) đã cho bị chặn dưới bởi $\frac{3}{2}$ .

Câu 34: Xét tính tăng hay giảm và bị chặn của dãy số: $u_n=\frac{2n-1}{n+3},n\in {\mathbb{N}}^{*}$ .

A. Dãy số giảm, bị chặn trên;

B. Dãy số tăng, bị chặn dưới;

C. Dãy số tăng, bị chặn;

D. Dãy số giảm, bị chặn dưới.

Lời giải:

Đáp án đúng là: C

⦁ Ta có $u_{n+1}-u_n=\frac{2\left(n+1\right)-1}{n+1+3}-\frac{2n-1}{n+3}=\frac{2n+1}{n+4}-\frac{2n-1}{n+3}$

 

$$\begin{gathered} =\frac{\left(2n+1\right)\left(n+3\right)-\left(2n-1\right)\left(n+4\right)}{\left(n+4\right)\left(n+3\right)}=\frac{7}{n^2+7n+12} \\ =\frac{7}{{\left(n+\frac{7}{2}\right)}^2-\frac{1}{4}}>\mathrm{0,}\forall n\in {\mathbb{N}}^{*} \end{gathered}$$

Vậy dãy (u_n) là dãy số tăng.

⦁ Ta có $u_n=\frac{2n-1}{n+3}=\frac{2\left(n+3\right)-7}{n+3}=2-\frac{7}{n+3}$ .

Do n ∈ ℕ^* nên $\frac{1}{n+3}\le \frac{1}{4}$ .

Suy ra $2-\frac{7}{n+3}\ge 2-\frac{1}{4}=\frac{7}{4}$ .

Vì vậy dãy số (u_n) bị chặn dưới bởi $\frac{7}{4}$ .

Lại có u_n bị chặn trên (do u_n < 2, ∀n ∈ ℕ^*).

Vậy (u_n) bị chặn.

Do đó ta chọn phương án C.

Câu 35: Chứng minh sin2a = 2sina.cosa.

Lời giải:

Ta có sin2a = sin(a + a) = sina.cosa + cosa.sina = 2sina.cosa.

Vậy ta có điều phải chứng minh.

Câu 36: Chứng minh hệ thức sau: $\frac{{\left(\sin a+\cos a\right)}^2-{\left(\sin a-\cos a\right)}^2}{\sin a.\cos a}=4$ .

Lời giải:

Ta có $VT=\frac{{\left(\sin a+\cos a\right)}^2-{\left(\sin a-\cos a\right)}^2}{\sin a.\cos a}$

$$\begin{gathered} =\frac{\left(\sin a+\cos a+\sin a-\cos a\right)\left(\sin a+\cos a-\sin a+\cos a\right)}{\sin a.\cos a} \\ =\frac{2\sin a.2\cos a}{\sin a.\cos a}=4=VP \end{gathered}$$

Vậy ta có điều phải chứng minh.

Câu 37: Một tổ chuyên môn tiếng Anh của trường đại học X gồm 7 thầy giáo và 5 cô giáo, trong đó thầy Xuân và cô Hạ là vợ chồng. Tổ chọn ngẫu nhiên 5 người để lập hội đồng chấm thi vấn đáp tiếng Anh B1 khung châu Âu. Xác suất sao cho hội đồng có 3 thầy, 2 cô và nhất thiết phải có thầy Xuân hoặc cô Hạ nhưng không có cả hai là

A. $\frac{5}{44}$ ;

B. $\frac{5}{88}$ ;

C. $\frac{85}{792}$ ;

D. $\frac{85}{396}$ .

Lời giải:

Đáp án đúng là: D

Số cách chọn ngẫu nhiên 5 người trong 12 người là: $n\left(\Omega \right)=C_{12}^5$ .

Trường hợp 1: Trong hội đồng gồm thầy Xuân, 2 thầy giáo trong số 6 thầy còn lại và 2 cô giáo trong số 4 cô còn lại (cô Hạ không được chọn).

Khi đó ta có $C_6^2.C_4^2$  (cách chọn).

Trường hợp 2: Trong hội đồng gồm cô Hạ, 1 cô giáo trong số 4 cô còn lại, và 3 thầy giáo trong số 6 thầy giáo (thầy Xuân không được chọn).

Khi đó ta có $C_4^1.C_6^3$  (cách chọn).

Vậy xác suất cần tìm là: $P=\frac{C_6^2.C_4^2+C_4^1.C_6^3}{C_{12}^5}=\frac{85}{396}$ .

Do đó ta chọn phương án D.

Câu 38: Một tổ chuyên môn gồm 7 thầy giáo và 5 cô giáo, trong đó thầy An và cô Bình là vợ chồng. Chọn ngẫu nhiên 5 người để lập hội đồng chấm thi vấn đáp. Có bao nhiêu cách lập sao cho hội đồng có 3 thầy, 2 cô và nhất thiết phải có thầy An hoặc cô Bình nhưng không có cả hai.

A. 170;

B. 250;

C. 200;

D. 120.

Lời giải:

Đáp án đúng là: A

Trường hợp 1: Trong hội đồng gồm thầy An, 2 thầy giáo trong số 6 thầy còn lại và 2 cô giáo trong số 4 cô còn lại (cô Bình không được chọn).

Khi đó ta có $C_6^2.C_4^2$  (cách chọn).

Trường hợp 2: Trong hội đồng gồm cô Bình, 1 cô giáo trong số 4 cô còn lại, và 3 thầy giáo trong số 6 thầy giáo (thầy An không được chọn).

Khi đó ta có $C_4^1.C_6^3$  (cách chọn).

Vậy ta có tất cả $C_6^2.C_4^2+C_4^1.C_6^3=170$  cách chọn.

Câu 39: Cho A, B, C thẳng hàng và điểm M không thuộc đường thẳng đó. Gọi A’, B’, C’ lần lượt là điểm đối xứng của A, B, C qua M. Chứng minh A’, B’, C’ thẳng hàng.

Lời giải:

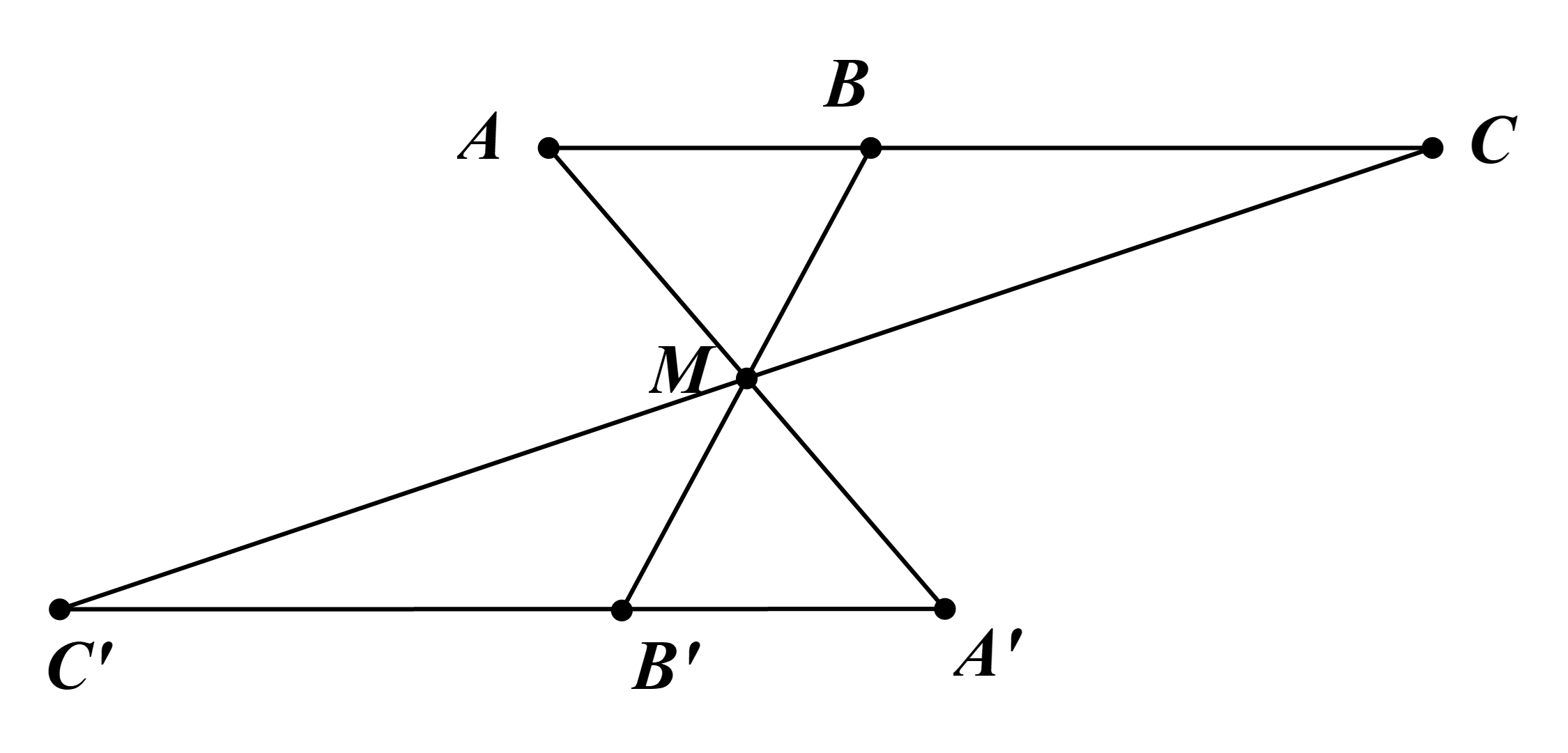
Các đoạn thẳng A’B’, B’C’, C’A’ lần lượt đối xứng với các đoạn thẳng AB, BC, CA qua điểm M nên ta có A’B’ = AB, B’C’ = BC, C’A’ = CA.

Giả sử A, B, C thẳng hàng theo thứ tự đó, ta có AB + BC = AC.

Suy ra A’B’ + B’C’ = A’C’.

Vậy ba điểm A’, B’, C’ thẳng hàng.

Câu 40: Cho $A=\frac{7}{\sqrt{x}+8}$  và $B=\frac{\sqrt{x}+8}{\sqrt{x}+3}$ . Tìm x để P = A.B có giá trị là số nguyên.

Lời giải:

Điều kiện x ≥ 0.

$P=A.B=\frac{7}{\sqrt{x}+8}.\frac{\sqrt{x}+8}{\sqrt{x}+3}=\frac{7}{\sqrt{x}+3}$.

P có giá trị là số nguyên ⇔ 7 chia hết cho $\sqrt{x}+3$ .

Ư(7) ∈ {–7; –1; 1; 7}.

Ta có bảng sau:

$\sqrt{x}+3$	–7	–1	1	7
x	Vô nghiệm	Vô nghiệm	Vô nghiệm	16

So với điều kiện x ≥ 0, ta nhận x = 16.

Vậy x = 16 thỏa mãn yêu cầu bài toán.

Câu 41: Cho $A=\frac{x^2-9}{3\left(x+5\right)}$  và $B=\frac{3}{x+3}$ . Cho P = A.B. Tìm giá trị nguyên của x để P có giá trị nguyên.

A. x ∈ {–6; –7; –9; –3; –4; 1};

B. x ∈ {–13; –9; –7; –6; 4; –1; 3};

C. x ∈ {–8; –7; –9; –13; –4; 1};

D. x ∈ {–8; –7; –9; –3; –4; –1}.

Lời giải:

Điều kiện: x ≠ –5; x ≠ –3  (*)

Ta có 

$P=\frac{x^2-9}{3\left(x+5\right)}.\frac{3}{x+3}=\frac{\left(x-3\right)\left(x+3\right)}{3\left(x+5\right)}.\frac{3}{x+3}=\frac{x-3}{x+5}=\frac{x+5-8}{x+5}=1-\frac{8}{x+5}$

P nhận giá trị nguyên ⇔ 8 chia hết cho (x + 5).

Ta có Ư(8) ∈ {–8; –4; –2; –1; 1; 2; 4; 8}.

Ta có bảng sau:

x + 5	–8	–4	–2	–1	1	2	4	8
x	–13	–9	–7	–6	4	–3	–1	3

So với điều kiện (*), ta nhận x ∈ {–13; –9; –7; –6; 4; –1; 3}.

Vậy ta chọn phương án B.

Câu 42: Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho $\frac{MA}{AD}=\frac{NC}{CB}=\frac{1}{3}$ . Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là

A. Một hình bình hành;

B. Một hình thang với đáy lớn gấp 2 lần đáy nhỏ;

C. Một hình thang với đáy lớn gấp 3 lần đáy nhỏ;

D. Một tam giác.

Lời giải:

Đáp án đúng là: B

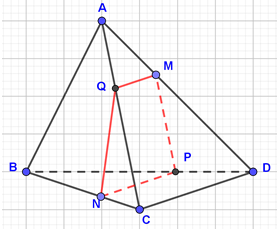
Trong (BCD): kẻ NP // CD.

Suy ra  $\frac{NP}{CD}=\frac{BN}{BC}=\frac{2}{3}$ (1)

Trong (ACD): kẻ MQ // CD.

Suy ra  $\frac{MQ}{CD}=\frac{AM}{AD}=\frac{1}{3}$  (2)

Từ (1), (2), suy ra NP = 2MQ.

Vậy thiết diện cần tìm là hình thang MQNP với NP = 2MQ.

Do đó ta chọn phương án B.

Câu 43: Cô Hoàn mua 5 kg gạo tẻ và 5 kg gạo nếp. Giá 1 kg gạo tẻ là 9300 đồng, 1 kg gạo nếp là 11200 đồng. Hỏi cô Hoàn phải trả hết bao nhiêu tiền?

Lời giải:

Cô Hoàn mua 5 kg gạo tẻ hết: 5.9300 = 46500 (đồng).

Cô Hoàn mua 5 kg gạo nếp hết: 5.11200 = 56000 (đồng).

Cô Hoàn phải trả: 46500 + 56000 = 102500 (đồng).

Đáp số: 102500 đồng.

Câu 44: Với những giá trị nào của m thì đồ thị của các hàm số y = 12x + (5 – m) và y = 3x + (3 + m) cắt nhau tại một điểm trên trục tung?

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị đã cho là 12x + (5 – m) = 3x + (3 + m)

Û 9x = 2m – 2

$\iff x=\frac{2m-2}{9}$

Ta có hai đường thẳng đã cho cắt nhau tại một điểm trên trục tung tức hoành độ của giao điểm bằng 0 

Suy ra $0=\frac{2m-2}{9}$

=> 2m = 2.

=> m = 1.

Vậy m = 1 thỏa mãn yêu cầu bài toán.

Câu 45: Cho hàm số y = (m + 2)x + 2m² + 1. Tìm m để 2 đường thẳng (d): y = (m + 2)x + 2m² + 1 và (d’): y = 3x + 3 cắt nhau tại 1 điểm trên trục tung.

Lời giải:

Để (d) cắt (d’) thì m + 2 ≠ 3 Û m ≠ 1.

Phương trình hoành độ giao điểm của (d) và (d’) là:

(m + 2)x + 2m² + 1 = 3x + 3

Û (m – 1)x = 2 – 2m²

$\iff x=\frac{2-2m^2}{m-1}$

Ta có hai đường thẳng đã cho cắt nhau tại một điểm trên trục tung, tức hoành độ của giao điểm bằng 0

Suy ra $0=\frac{2-2m^2}{m-1}$

=> 2m² – 2 = 0.

=> m = ±1.

Kết hợp điều kiện m ≠ 1 ta có m = –1.

Vậy m = –1 thỏa mãn yêu cầu bài toán.

Câu 46: Một trang trại cần thuê xe vận chuyển 450 con lợn và 35 tấn cám. Nơi cho thuê xe chỉ có 12 xe lớn và 10 xe nhỏ. Một chiếc xe lớn có thể chở 50 con lợn và 5 tấn cám. Một chiếc xe nhỏ có thể chở 30 con lợn và 1 tấn cám. Tiền thuê một xe lớn là 4 triệu đồng, một xe nhỏ là 2 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thuê xe là thấp nhất?

Lời giải:

Gọi x, y (xe) lần lượt là số xe loại lớn, số xe loại nhỏ cần thuê (x, y ≥ 0, x, y ∈ ℤ).

Suy ra T = 4x + 2y (triệu đồng) là số tiền thuê xe.

Do đó yêu cầu bài toán ⇔ T nhỏ nhất.

Theo đề, ta có hệ: $\left\{\begin{array}{l}0\le x\le 12\\ 0\le y\le 10\\ 50x+30y\ge 450\\ 5x+y\ge 35\end{array}\right.$ (*)

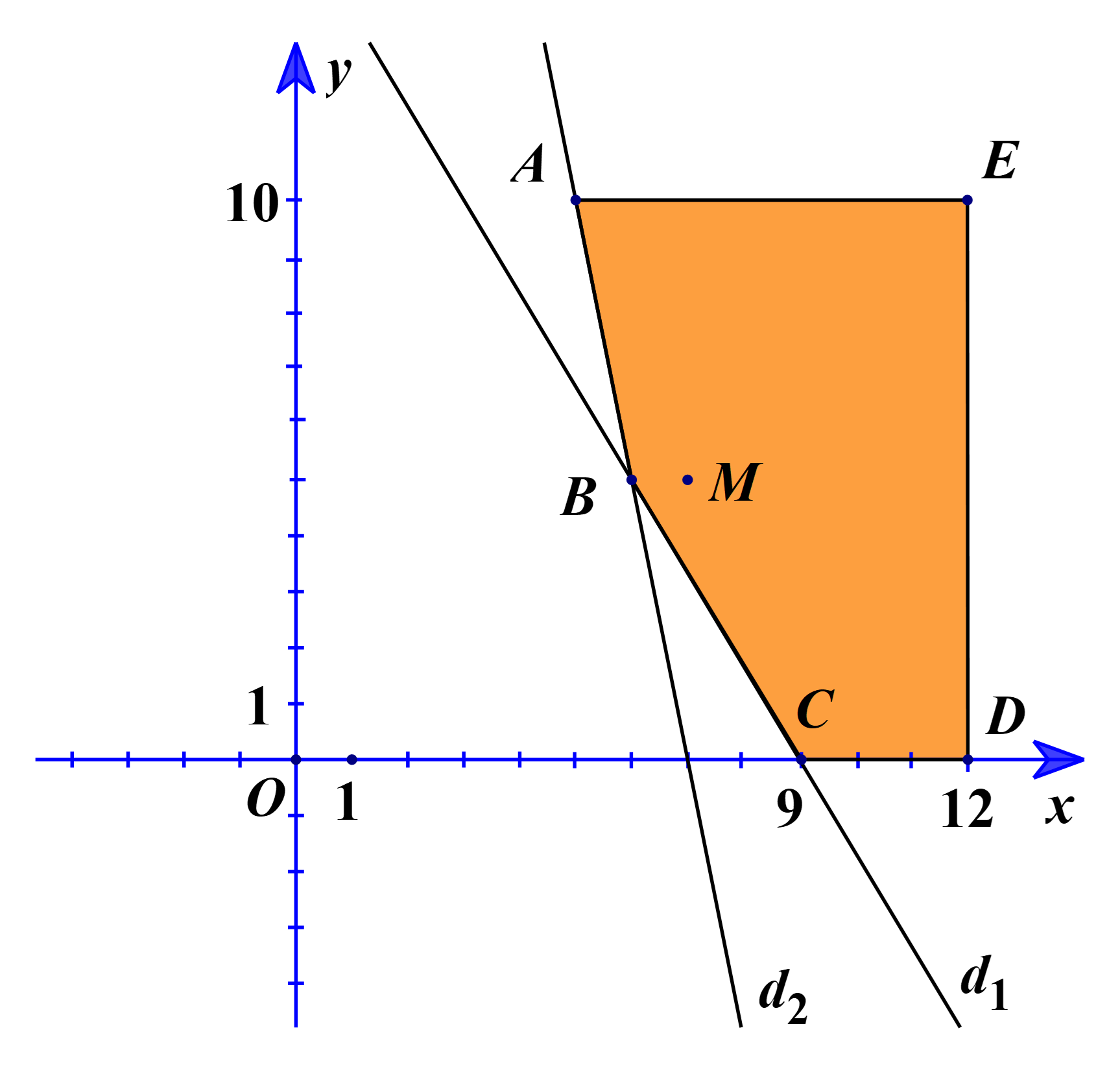
Vẽ các đường thẳng d₁: 50x + 30y = 450 và d₂: 5x + y = 35 trên cùng một hệ trục tọa độ.

Tiếp theo, ta lấy điểm M(7; 5). Khi đó ta có: $\left\{\begin{array}{l}0\le 7\le 12\\ 0\le 5\le 10\\ 50.7+30.5\ge 450\\ 5.7+5\ge 35\end{array}\right.$  (đúng).

Suy ra miền nghiệm của hệ (*) là phần ngũ giác ABCDE, kể cả các đoạn thẳng AB, BC, CD, DE, EA, với A(5; 10), B(6; 5), C(9; 0), D(12; 0), E(12; 10).

Ta có T_A = 40, T_B = 34, T_C = 36, T_D = 48, T_E = 68.

Do đó T nhỏ nhất ⇔ x = 6, y = 5.

Vậy trang trại phải thuê 6 xe lớn, 5 xe nhỏ để chi phí thuê xe là thấp nhất.

Câu 47: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; –1) và B(3; 2). Tìm M thuộc trục tung sao cho MA² + MB² nhỏ nhất.

Lời giải:

Ta có M ∈ Oy. Suy ra tọa độ M(0; y).

Ta có MA² + MB² = 1² + (–1 – y)² + 3² + (2 – y)²

= 1 + 1 + 2y + y² + 9 + 4 – 4y + y²

= 2y² – 2y + 15

$=2{\left(y-\frac{1}{2}\right)}^2+\frac{29}{2}\ge \frac{29}{2},\forall y\in ℝ$.

Dấu “=” xảy ra $\iff y=\frac{1}{2}$ .

Vậy tọa độ $M\left(0;\frac{1}{2}\right)$  thỏa mãn yêu cầu bài toán.

Câu 48: Cho hình chóp S.ABCD, ABCD là hình bình hành, M là trung điểm của SA.

a) Xác định giao điểm của SB và (MCD).

b) Tìm thiết diện của hình chóp S.ABCD khi cắt bởi (MCD).

Lời giải:

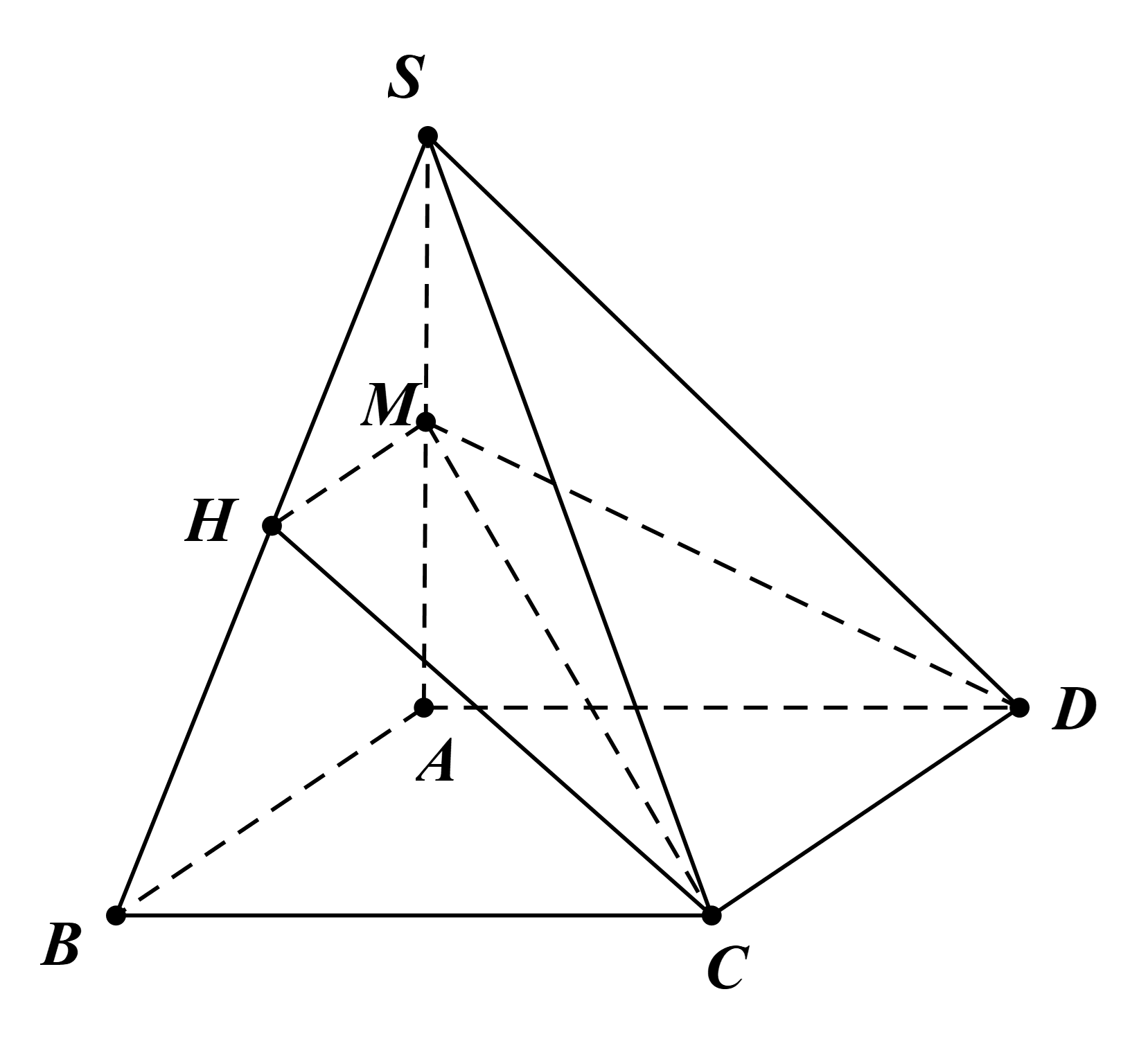
a) Ta có: AB // CD (do ABCD là hình bình hành) và M ∈ (SAB) ∩ (MCD).

Suy ra MH = (SAB) ∩ (MCD), với MH // AB, H ∈ SB.

Vậy giao điểm của SB và (MCD) là H.

b) Ta có:

+ MH = (SAB) ∩ (MCD).

+ HC = (SBC) ∩ (MCD).

+ CD = (SCD) ∩ (MCD).

+ DM = (SAD) ∩ (MCD).

+ MH // CD (do MH // AB, AB //CD).

Vậy thiết diện cần tìm là hình thang MHCD.

Câu 49: Tìm tất cả các giá trị thực của tham số m để phương trình x² – 5x + 7 + 2m = 0 có nghiệm thuộc đoạn [1; 5].

A. $\frac{3}{4}\le m\le 7$ ;

B. $\frac{-7}{2}\le m\le \frac{-3}{8}$ ;

C. 3 ≤ m ≤ 7;

D. $\frac{3}{8}\le m\le \frac{7}{2}$ .

Lời giải:

Ta có x² – 5x + 7 + 2m = 0 ⇔ x² – 5x + 7 = –2m  (*)

Phương trình (*) là phương trình hoành độ giao điểm của (P): y = x² – 5x + 7 và đường thẳng d: y = –2m (song song hoặc trùng với trục hoành).

Ta có y’ = 2x – 5.

Bảng biến thiên của hàm số y = x² – 5x + 7:

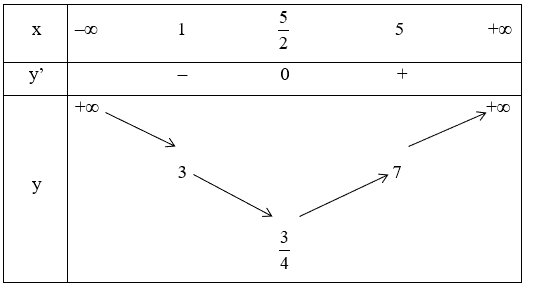
Dựa vào bảng biến thiên, ta thấy khi x ∈ [1; 5] thì $y\in \left[\frac{3}{4};7\right]$ .

Khi đó phương trình (*) có nghiệm ⇔ $\frac{3}{4}\le -2m\le 7\iff \frac{-3}{8}\ge m\ge \frac{-7}{2}$ .

Vậy ta chọn phương án B.

Câu 50: Tập xác định của hàm số $y=\frac{\cot x}{\sin x-1}$  là

A. $D=ℝ\backslash \left\{\frac{\pi }{3}+k2\pi |k\in \mathbb{Z}\right\}$ ;

B. $D=ℝ\backslash \left\{\frac{k\pi }{2}|k\in \mathbb{Z}\right\}$ ;

C. $D=ℝ\backslash \left\{\frac{\pi }{2}+k2\pi ;k\pi |k\in \mathbb{Z}\right\}$ ;

D. $D=ℝ\backslash \left\{\frac{\pi }{2}+k2\pi |k\in \mathbb{Z}\right\}$ .

Lời giải:

Đáp án đúng là: C

ĐKXĐ: $\left\{\begin{array}{l}\sin x\ne 0\\ \sin x\ne 1\end{array}\right.\iff \left\{\begin{array}{l}x\ne k\pi \\ x\ne \frac{\pi }{2}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$ .

TXĐ: $D=ℝ\backslash \left\{\frac{\pi }{2}+k2\pi ;k\pi |k\in \mathbb{Z}\right\}$ .

Vậy ta chọn phương án C.