Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 98)
Câu 1: Tìm GTNN hoặc GTLN của biểu thức sau:
A = -4 - x2 + 6x
B = 3x2 - 5x + 7
Phương pháp giải:
+ Với mọi x:
+ Với mọi a; b ta có:
. Dấu = xảy ra khi a+ b = 0 Và 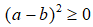
• Cho biểu thức A(x):
+ Nếu 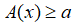
+ Nếu 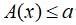
+ Nếu
+ Nếu
+ Với mọi A; B ta có:
Lời giải:
A = - 4 - x2 + 6x
= - (x2 - 6x + 9) + 5
= - (x - 3)2 + 5
Ta có (x - 3)2 0 => - (x - 3)2 0
=>
Dấu "=" xảy ra khi x = 3
Vậy giá trị lớn nhất của A là 5, khi x = 3
B = 3x2 - 5x + 7
Ta có
Dấu "=" xảy ra khi
Vậy giá trị nhỏ nhất của B là
a)
b)
Phương pháp giải:
* Các tính chất của phép cộng như sau:
+ Tính giao hoán: a + b = b + a.
+ Tính kết hợp: (a + b) + c = a + (b + c).
+ Cộng với số 0: a + 0 = 0 + a = a
+ Cộng với số đối: a + (-a) = 0
* Để tính nhanh, tính hợp lí giá trị một biểu thức ta có thể làm theo các cách sau:
- Áp dụng các tính chất của phép cộng để nhóm các số lại với nhau sao cho tổng của mỗi nhóm là một số tròn trục, tròn trăm…
- Nhóm các số lại với nhau sao cho mỗi nhóm có cùng kết quả, sau đóthực hiện cộng các số đã nhóm.
Lời giải:
a)
b)
Câu 3: Tính giá trị của biểu thức: 100 - (2,6 + 23,4 : 6 ) x 10,8
Phương pháp giải:
Khi thực hiện tính giá trị của biểu thức ta thực hiên nhân chia trước, cộng trừ sau, nếu có ngoặc thì ta ưu tiên thực hiện trong ngoặc trước
Lời giải:
100 - (2,6 + 23,4 : 6 ) x 10,8
= 100 - ( 2,6 + 3,9) x 10,8
= 100 - 6,5 x 10,8
= 100 - 70,2
= 29,8
Mở rộng:
Kết quả của biểu thức: 2000 + (32,4 : 3 – 10,8) x 0,25 là:
A. 2000
B. 502,7
C. 500
D. 0,500
Đáp án: A
Câu 4: Tính bằng cách thuận tiện nhất: 1 + 2 + 3 + ... + 8 + 9
Phương pháp giải:
Ta nhóm hoặc tách các hạng tử thành từng nhóm có tổng hoặc hiệu là các số tròn chục, trong trăm, tròn nghìn,..., sau đó tính tổng của phép tính sẽ nhanh hơn.
Lời giải:
1 + 2 + 3 + ... + 8 + 9
= (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 5
= 10 + 10 + 10 + 10 + 5
= 45
Mở rộng:
9 - 8 + 7 - 6 + 5 - 4 + 3 - 2 + 1 - 0
= (9 - 8) + (7 - 6) + (5 - 4) + (3 - 2) + (1 - 0)
= 1 + 1 + 1 + 1 + 1
= 5
Câu 5: Tìm số tự nhiên n để 3n + 6 là số nguyên tố.
Phương pháp giải:
Số nguyên tố là số tự nhiên khác 0, 1, chỉ có ước là 1 và chính nó.
Hợp số là số tự nhiên khác 0, 1, có nhiều hơn 2 ước.
Nếu a⋮m; b⋮m thì (a + b)⋮m
Lời giải:
n = 0 ta có: 3n + 6 = 30 + 6 = 7 là số nguyên tố
n ≠ 0 ta có 3n ⋮ 3 ; 6 ⋮ 3 nên 3n + 6 ⋮ 3 ; 3n + 6 > 3
Số 3n + 6 là hợp số vì ngoài ước 1 và chính nó còn có ước là 3.
Vậy với n = 0 thì 3n + 6 là số nguyên tố.
Mở rộng:
Tìm số tự nhiên x sao cho 41 . x là số nguyên tố.
Phương pháp
Xét các trường hợp của x để 41.x chỉ có 2 ước là 1 và chính nó.
Lời giải
+) Nếu x = 0 thì 41 . x = 0 không là số nguyên tố (Loại)
+) Nếu x = 1 thì 41 . x = 41 . 1 = 41 là số nguyên tố ( Thỏa mãn)
+) Nếu x 2 thì 41 . x nhận 1; 41; x; 41.x làm ước của nó nên là hợp số ( Loại)
Vậy với x = 1 thì 41 . x là số nguyên tố.
Phương pháp giải:
Công thức tính diện tích xung quanh của hình lập phương:
Sxq = S1m x 4
Thể tích hình lập phương là: V = a x a x a
Lời giải:
Diện tích một mặt của hình lập phương là :
16 : 4 = 4 (cm)
Vì 4 = 2 x 2 nên suy ra cạch hình lập phương là 2 cm
Thể tích hình lập phương đó là :
2 x 2 x 2 = 8 (cm)
Đáp số : 8 cm.
Mở rộng:
Vì 125 = 5 x 5 x 5 nên độ dài cạnh của hình lập phương đó là 5 m.
Diện tích xung quanh hình lập phương đó là:
(5 x 5) x 4 = 100 (cm2)
Đáp số: 100 cm2.
Câu 7: Không thực hiện phép tính hãy so sánh: A = 20022; B = 2001 x 2023
Phương pháp giải:
Với a, b, c tùy ý ta có:
Nếu thì
Nếu thì
Nếu thì
Nếu thì
Lời giải:
A = 20022
= 2002 x 2002
= (2001 + 1) x (2003 - 1)
= 2001 x 2003 + 1 x 2003 - 2001 x 1 - 1 x 1
= 2001 x 2003 +1 > B
Vậy A > B
Mở rộng:
Không tính ra kết quả hãy so sánh A và B, biết :
A = 2007 × 2007; B = 2004 × 2008
Lời giải:
Câu 8: Tìm x biết 5x + 5x+2 = 650
Lời giải:
=>
=>
=>
=>
=>
=> = 25
=>
=> x = 2
Mở rộng:
Giải phương trình
Ta có:
Lời giải:
Cách 1:
h = 5,5 m
A = 7500 J
D = 1000 kg/m3
Đổi :
Công máy bơm sinh ra trong là :
Trọng lượng nước bơm lên trong là :
Thể tích nước được bơm lên :
Cách 1:

Câu 10: Cho hình bình hành ABCD có góc A = 45o ; AB = BD = 18cm
a) Tính AD
b) Tính diện tích ABCD
Phương pháp giải:
Định lý Pythagore: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Công thức tính diện tích tam giác vuông = tích 2 cạnh góc vuông
Lời giải:
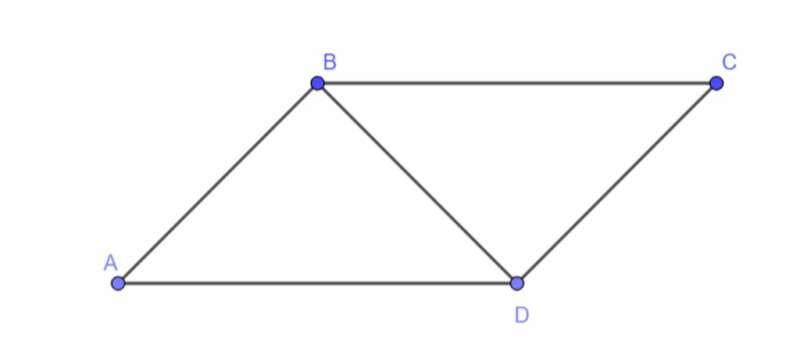
vuông cân tại
là hình bình hành
vuông cân tại D
Câu 11: Có bao nhiêu số nhỏ hơn 1000 chia cho 5 dư 1. Tính tổng các số đó.
Phương pháp giải:
B1: Tính số các số thỏa mãn yêu cầu đề bài dựa vào công thức tính số số hạng của dãy số cách đều (cách 5)
Số số hạng = (số hạng cuối – số hạng đầu) : khoảng cách + 1
B2 : Tính tổng các số đó theo công thức tính tổng dãy số cách đều (cách 5)
Tổng dãy số cách đều = (số hạng đầu + số hạng cuối) × số số hạng : 2
Lời giải: Số chia cho 5 dư 1 sẽ có dạng 5k + 1
Vậy:
Số lớn nhất là: 996
Số bé nhất là: 1
Khoảng cách giữa các số là 5
Số các số nhỏ hơn 1000 chia 5 dư 1 là:
(số)
Tổng các số nhỏ hơn 1000 chia 5 dư 1 là:
(1 + 996)x 200 : 2 = 99 700
Vậy có 200 số nhỏ hơn 1000 chia 5 dư 1. Tổng các số đó là 99 700
Câu 12: Hãy điền thêm dấu phép tính vào dãy số sau: 6 6 6 6 6
để được biểu thức có giá trị lần lượt bằng : 0, 1, 2, 3, 4, 5, 6
Phương pháp giải:
Các dấu có thể thêm vào + (cộng) - (trừ) x (nhân) : (chia); và có thể thêm dấu ( ) kết hợp thử các trường hợp có thể xảy ra để ra được phép tính có giá trị đề bài yêu cầu
Lời giải:
a, Bằng 0:
(6 – 6 ) x (6 + 6 +6)
(6 – 6 ) : (6 + 6 + 6)
b, Bằng 1 :
6 + 6 – 66 : 6
6 – ( 66 : 6 – 6 )
c, Bằng 2:
(6 + 6) : 6 x 6 : 6
(6 x 6 : 6 + 6) : 6
6 : (6 x 6 : (6 + 6))
d, Bằng 3:
6 : 6 + (6 + 6) : 6
6 : (6 : 6 + 6 : 6)
e, Bằng 4:
6 – (6 : 6 + 6 : 6)
(6 + 6 + 6 + 6) : 6
g, Bằng 5:
6 – 6 : 6 x 6 : 6
6 – 6 x 6 : 6: 6
h, Bằng 6:
66 – 66 + 6
6 : 6 – 6 : 6 + 6
6 x 6 – 6 x 6 + 6
a/ khi xe lửa chở hàng từ B bắt đầu đi thì xe lửa tốc hành đã đi được bao nhiêu km?
b/ hai xe lửa gặp nhau lúc mấy giờ?
Phương pháp giải:
Các công thức cần nhớ
- Thời gian đi = quãng đường : vận tốc = giờ đến – giờ khởi hành – giờ nghỉ (nếu có).
- Giờ khởi hành = giờ đến nơi – thời gian đi – giờ nghỉ (nếu có).
- Giờ đến nơi = giờ khởi hành + thời gian đi + thời gian nghỉ (nếu có).
- Vận tốc = quãng đường : thời gian (v = s:t)
- Quãng đường = vận tốc × thời gian (s = v.t)
- Vận tốc vật thứ nhất kí hiệu là v1.
- Vận tốc vật thứ hai kí hiệu là v2.
- Quãng đường hai vật cách nhau trong cùng thời điểm xuất phát là s.
- Thời gian để hai vật gặp nhau là t, thì :
t = s : (v1 + v2)
Chú ý: s là quãng đường hai vật cách nhau trong cùng thời điểm xuất phát. Nếu vật nào xuất phát trước thì phải trừ quãng đường xuất phát trước đó.
Lời giải:
Khi xe chở hàng xuất phát, thời gian xe lửa đã đi được:
giờ phút giờ phút phút giờ
Khi xe chở hàng xuất phát, xe lửa đã đi được quãng đường:
Khi xe chở hàng xuất phát, khoảng cách giữa hai xe là:
Tổng vận tốc của hai xe là:
Thời gian cần để hai xe lửa gặp nhau là:
(giờ)
Hai xe lửa gặp nhau lúc:
giờ phút giờ giờ phút
Đáp số: giờ phút
Câu 14: Cho tìm giá trị của n để
A là phân số
A là số nguyên
Phương pháp giải:
Để chứng minh A là số nguyên tức là tử số sẽ chia hết cho mẫu số, ta tìm các giá chị của n để mẫu số là ước của tử số
Sử dụng kiến thức về ước và bội, dấu hiệu chia hết để biện luận giá trị biểu thức là số nguyên
Lời giải:
Để A là phân số
Để A là số nguyên
=> n - 2 chia hết cho n + 3
Mà n - 2 = n + 3 - 5 => (n - 2) + 5 = n + 3
=> 5 chia hết cho n + 3
=> n + 3Ư(5)
=> n + 3{1;-1;5;-5}
=> n{-2;-4;2;-8}
Vậy với n{-2;-4;2;-8} thì A là số nguyên
Câu 15: Điền số thích hợp vào chỗ trống
19,76 cm3 = .... dm3,
5m2 6dm2 = ..... dm2
2 năm 6 tháng = ..... tháng
12 phút = ..... giây
Phương pháp giải:
1 cm3 = 0,001 dm3
1 dm2 = 0,01 m2 => 1 m2 = 100 dm2
1 năm = 12 tháng
1 phút = 60 giây
Lời giải:
19,76 cm3 = 0,01976 dm3 (lấy 19,76 x 0,001 = 0,01976)
5m2 6dm2 = 506 dm2 (Lấy 5 x 100 + 6 = 506)
2 năm 6 tháng = 30 tháng (lấy 2 x 12 + 6 = 30)
12 phút = 720 giây (lấy 12 x 60 = 720)
Câu 16: Tìm y biết (y + 3)3 - (y + 1)3 = 56
Phương pháp giải:
Hiệu hai lập phương: Với A, B là hai biểu thức bất kì, ta có:
A3 – B3 = (A – B)(A2 + AB + B2)
Lập phương của một tổng: Với A, B là hai biểu thức bất kì, ta có:
(A + B)3 = A3 + 3A2B + 3AB2 + B3
Lời giải:
Cách 1:
Áp dụng công thức hiệu của 2 lập phương thì ta có A = y + 3; B = y + 1
<=> [(y + 3) - (y + 1)][(y + 3)2 + (y + 3)(y + 1) + (y + 1)2] = 56
<=> (y + 3 - y - 1)(y2 + 6y + 9 + y2 + 4y + 3 + y2 + 2y + 1) = 56
<=> 2.(3y2 + 12y + 13) = 56
<=> 6y2 + 24y - 30 = 0
<=> y2 + 4y - 5 = 0
<=> y2 - y + 5y - 5 = 0
<=> y(y - 1) + 5(y - 1) = 0
Vậy y = -5 hoặc y = 1
Cách 2:
Áp dụng công thức lập phương của một tổng, ta có:
<=> (y3 + 9y2 + 27y + 27) - (y3 + 3y2 + 3y + 1) = 56
<=> y3 + 9y2 + 27y + 27 - y3 - 3y2 - 3y - 1 = 56
<=> 6y2 + 24y - 30 = 0
<=> y2 + 4y - 5 = 0
<=> y2 - y + 5y - 5 = 0
<=> y(y - 1) + 5(y - 1) = 0
Vậy y = -5 hoặc y = 1
a) Sau 1 giờ khoảng cách giữa hai ô tô là bao nhiêu?
b) Sau 2,5 giờ khoảng cách giữa hai ô tô là bao nhiêu?
Phương pháp giải:
- Vận tốc = quãng đường : thời gian (v = s:t)
- Quãng đường = vận tốc × thời gian (s = v.t)
- Vận tốc vật thứ nhất kí hiệu là v1.
- Vận tốc vật thứ hai kí hiệu là v2.
- Quãng đường hai vật cách nhau trong cùng thời điểm xuất phát là s.
s = (v1 + v2) . t
Lời giải:
a)
Cách 1:
Sau 1 giờ ô tô thứ nhất đi được là: 58.1 = 58 (km)
Sau 1 giờ ô tô thứ hai đi được là: 62.1 = 62 (km)
Vậy sau 1 giờ khoảng cách giữa 2 ô tô là: 58 + 62 = 120 km
Cách 2:
Tổng vận tốc của 2 xe là: 58 + 62 = 120 (km/h)
Sau 1 giờ khoảng cách giữa 2 ô tô là: 120.1 = 120 km
b) Tương tự:
Cách 1:
Sau 2,5 giờ khoảng cách giữa 2 ô tô là: 58.2,5 + 62.2,5 = 300 km
Cách 2:
Sau 2,5 giờ khoảng cách giữa 2 ô tô là: (58 + 62).2,5 = 300 km
Câu 18: Tính hợp lí 11 - 12 + 13 - 14 + 15 - 16 + 17 - 18 + 19 - 20
Phương pháp giải:
* Để tính nhanh, tính hợp lí giá trị một biểu thức ta có thể làm theo các cách sau:
- Áp dụng các tính chất của phép cộng để nhóm các số lại với nhau sao cho tổng của mỗi nhóm là một số tròn trục, tròn trăm…
- Nhóm các số lại với nhau sao cho mỗi nhóm có cùng kết quả, sau đó thực hiện cộng các số đã nhóm.
Lời giải:
11 - 12 + 13 - 14 + 15 - 16 + 17 - 18 + 19 - 20
= (11 - 12) + (13 - 14) + (15 - 16) + (17 - 18) + (19 - 20)
= (-1) + (-1) + (-1) + (-1) + (-1)
= (-1).5
= -5
Mở rộng:
Tính hợp lí: 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + …. + 99 – 100
Lời giải:
1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + …. + 99 – 100
= (1 – 2) + (3 – 4) + (5 – 6) + (7 – 8) + …. + (99 – 100)
Từ 1 đến 100 có 100 số nên sẽ có 50 cặp.
= (-1) + (-1) + (-1) + (-1) +… + (-1) (50 số (-1))
= -50.
Câu 19: Viết các biểu thức sau dưới dạng tích:
a, 27x3 - 27x2 + 3x + 1
b, x3 - 3x2 + 3x - 1
c, + x3
d, 0,001 - 1000x3
Phương pháp giải:
Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.
Một số phương pháp phân tích đa thức thành nhân tử:
+ Phương pháp đặt nhân tử chung
+ Phương pháp dùng hằng đẳng thức
+ Phương pháp nhóm hạng tử
+ Phối hợp nhiều phương pháp
Lời giải:
a)
b)
c)
d)
Câu 20: So sánh 2019 x 2021 và 2020 x 2020
Phương pháp giải:
Đây là bài toán biểu diễn biểu thức A theo biểu thức B hoặc ngược lại, hoặc biểu diễn hai biểu thức theo một biểu thức chung để từ đó so sánh giá trị hai biểu thức mà không cần tính toán
Lời giải:
Cách 1:
Ta có:
2019 x 2021 = (2020 - 1)x(2020 + 1)
= 2020 x 2020 + 2020x1 - 1x2020 - 1
= 2020 x 2020 + 2020 - 2020 - 1
= 2020 x 2020 - 1
=> 2019 x 2021 = 2020 x 2020 - 1
Vậy 2019 x 2021 < 2020 x 2020
Cách 2:
Ta có:
2019 x 2021 = 2019 x (2020 + 1)
= 2019 x 2020 + 2019
2020 x 2020 = (2019 + 1) x 2020
= 2019 x 2020 + 2020
mà 2019 < 2020 nên 2019 x 2020 + 2019 < 2019 x 2020 + 2020
Vậy 2019 x 2021 < 2020 x 2020
Câu 21: Cho hình 19 biết AB//CD, CD//EF. Tính và .
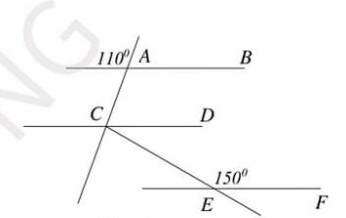
Phương pháp giải:
Góc đồng vị là hai góc ở cùng phía của đường cắt, và cả hai đều nằm cùng phía với hai đường thẳng song song.
Góc so le trong là hai góc nằm ở hai phía đối diện của đường cắt và ở bên trong hai đường thẳng song song.
Các góc so le trong và góc đồng vị luôn bằng nhau.
Hai góc bù nhau là hai góc có tổng số đo bằng 180°
Lời giải:
Vì AB // CD nên (2 góc ở vị trí đồng vị)
Suy ra:
Lại có:
Mà (2 góc so le trong vì DC // EF)
Nên:
Suy ra: .
Câu 22: Điền vào ô trống: 15 giờ 6 phút 4 = ?
Phương pháp giải:
1 giờ = 60 phút
1 phút = 60 giây
Lời giải:
Bước 1: Đổi giờ ra phút
Bước 2: Chia cho 4
Bước 3: Đổi lại từ phút ra giờ và phút
Kết quả:
15 giờ 6 phút : 4 = 3 giờ 46 phút 30 giây.
Phương pháp giải:
* Để tính nhanh, tính hợp lí giá trị một biểu thức ta có thể làm theo các cách sau:
- Áp dụng các tính chất của phép cộng để nhóm các số lại với nhau sao cho tổng của mỗi nhóm là một số tròn trục, tròn trăm…
- Nhóm các số lại với nhau sao cho mỗi nhóm có cùng kết quả, sau đó thực hiện cộng các số đã nhóm.
Áp dụng hằng đẳng thức:
Lời giải:
53.47 = (50 + 3)(50 - 3) = = 2500 - 9 = 2491
Câu 24: Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho phần tử của tập hợp đó
a) A = {1; 2; 3; 4; 5}
b) B = {0; 1; 2; 3; 4}
c) C = {1; 2; 3; 4}
d) D = {0; 2; 4; 6; 8}
e) E = {1; 3; 5; 7; 9; ...; 49}
f) F = {11; 22; 33; 44; ...; 99}
Phương pháp giải:
Để viết mỗi tập hợp bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó, ta cần xác định quy luật hoặc tính chất chung mà các phần tử trong tập hợp thỏa mãn.
Lời giải:
a)
b)
c)
d)
e)
f)
Phương pháp giải:
Để đổi một số thập phân ra phân số, ta làm theo các bước sau:
Viết số thập phân thành phân số với mẫu số là 10, 100, 1000,... tùy theo số chữ số sau dấu phẩy.
Rút gọn phân số nếu cần.
Lời giải:
Số 12,5 có 1 chữ số sau dấu phẩy. Ta viết 12,5 thành phân số với mẫu là 10:
12,5 =
Rút gọn phân số: Tử số và mẫu số đều chia hết cho 5, ta chia cả tử và mẫu cho 5:
Vậy, đổi ra phân số là .