Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 99)

Admin Vietjack Ngày: 06-11-2024 Tổng hợp kiến thức

455

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 99)

Câu 1: Cho a, b là các số thực không âm. Chứng minh rằng $a^{3} + b^{3} \geq a^{2} b + a b^{2}$

Phương pháp giải: Sử dụng hằng đẳng thức trong toán học, để chứng minh bài toán trên.

$A^{3} - B^{3} = (A - B) (A^{2} + A B + B^{2})$

Lời giải:

Ta có

$a^{3} + b^{3} \geq a^{2} b + a b^{2}$

$\Leftrightarrow (a + b) (a^{2} - a b + b^{2}) \geq a b (a + b)$

$\Leftrightarrow (a + b) {(a - b)}^{2} \geq 0$ luôn đúng do a,b không âm

Đẳng thức xảy ra <=> a = b

Sử dụng biến đổi tương đương

Một số kĩ thuật cơ bản:

+ Kỹ thuật xét hiệu hai biểu thức

+ Kỹ thuật sử dụng các hằng đẳng thức

+ Kỹ thuật thêm bớt một hằng số, một biểu thức

+ Kỹ thuật đặt biến phụ

+ Kỹ thuật sắp thứ tự các biến.

+ Kỹ thuật khai thác tính bị chặn của các biến

Câu 2: Cho 2 số nguyên dương x; y thỏa mãn $x^{2} + y^{2} - x ⋮ x y$ . Chứng minh: x là số chính phương.

Phương pháp giải:

Sử dụng tính chất ước chung lớn nhất (UCLN) và các phép biến đổi đại số để chứng minh rằng $x$ là số chính phương khi thỏa mãn phương trình ban đầu.

Dựa vào tính chất đặc biệt.

Ta có thể chứng minh một tính chất rất đặc biệt : “Nếu a, b là hai số tự nhiên nguyên tố cùng nhau và a.b là một số chính phương thì a và b đều là các số chính phương”.

Lời giải:

Ta có:

$x^{2} + y^{2} - x ⋮ x y \Rightarrow x^{2} + y^{2} - x ⋮ x \Rightarrow y^{2} ⋮ x$

Đặt $y^{2} = x k$ với $k \in ℤ^{+}$ .

Thay vào điều kiện ban đầu:

$x^{2} + {(x k)}^{2} - x ⋮ x y \Rightarrow x + x k^{2} - 1 ⋮ y$

Gọi $d = UCLN (x, k)$ . Vì $y^{2} = x k \Rightarrow y^{2} ⋮ d^{2} \Rightarrow y ⋮ d$

Suy ra $x + x k^{2} - 1 ⋮ y ⋮ d$ . Mà $x ⋮ d \Rightarrow 1 ⋮ d \Rightarrow d = 1$

Có nghĩa là $x, k$ nguyên tố cùng nhau. Mà $x k = y^{2}$ là 1 số chính phương, do đó bản thân $x$ cũng là số chính phương.

Ta có đpcm.

Câu 3: Tìm x:

$\frac{2}{3} - \frac{1}{3} . (x - \frac{3}{2}) - \frac{1}{2} . (2 x + 1) = 5$

Phương pháp giải:

Phân phối và khai triển biểu thức: Khai triển các hằng số ngoài ngoặc vào trong ngoặc.

Quy đồng mẫu số: Cộng/trừ các phân số bằng cách quy đồng mẫu.

Rút gọn biểu thức: Gộp các hạng tử chứa biến và hằng số.

Chuyển vế: Chuyển các hạng tử giữa hai vế của phương trình.

Nhân cả hai vế của phương trình: Loại bỏ hệ số của $x$ bằng cách nhân với nghịch đảo.

Giải phương trình bậc nhất: Tìm giá trị của $x$ sau khi rút gọn.

Lời giải:

Ta có:

$\frac{2}{3} - \frac{1}{3} . (x - \frac{3}{2}) - \frac{1}{2} . (2 x + 1) = 5$

$\Rightarrow \frac{2}{3} - \frac{1}{3} x + \frac{1}{3} . \frac{3}{2} - x - \frac{1}{2} = 5$

$\Rightarrow \frac{2}{3} - (\frac{1}{3} x + x) + \frac{1}{2} - \frac{1}{2} = 5$

$\Rightarrow \frac{4}{3} x = \frac{2}{3} - 5 = - \frac{13}{3}$

$\Rightarrow x = - \frac{13}{3} : \frac{4}{3} = - \frac{13}{3} . \frac{3}{4} = - \frac{13}{4}$

Vậy $x = - \frac{13}{4}$

Câu 4: Tìm x biết $x \div 2 = 5 \times 10$

Phương pháp giải:

Chuyển tất cả các hạng tử chứa $x$ về một vế và các hạng tử tự do về vế còn lại.

Rút gọn và tìm $x$ bằng cách chia cả hai vế cho hệ số của $x$ .

Lời giải:

$x \div 2 = 5 \times 10 \Leftrightarrow x \div 2 = 50 \Leftrightarrow x = 50 \times 2 \Leftrightarrow x = 100$

Vậy x = 100.

Câu 5: Rút gọn biểu thức sau: $\frac{36^{10} . 14.126}{35^{5} . 6}$

Phương pháp giải:

Bước 1: Phân tích các số thành thừa số nguyên tố

Bước 2: Thay vào biểu thức

Bước 3: Rút gọn biểu thức

Lời giải:

$\frac{36^{10} . 14.126}{35^{5} . 6} = \frac{{(6^{2})}^{10} . (2.7) . (2 . 3^{2} . 7)}{{(5.7)}^{5} . (2.3)} = \frac{6^{20} . 2^{2} . 7^{2} . 3^{2}}{5^{5} . 7^{5} . 2.3} = \frac{6^{20} . 6}{5^{5} . 7^{3}} = \frac{6^{21}}{1071875}$

Câu 6: Có ba con đường a1, a2, a3 đi từ A đến B ,có hai con đường b1, b2 đi từ B đến C.Và có ba con đường c1, c2, c3 đi từ C đến D .Viết tập hợp các con đường đi từ A đến D lần lượt qua B và C.

Phương pháp giải:

Sử dụng quy tắc nhân để tính tổng số con đường, kết hợp với việc liệt kê từng tổ hợp để thể hiện rõ ràng tập hợp các con đường từ $A$ đến $D$ qua $B$ và $C$ .

Lời giải:

Để tìm tập hợp các con đường đi từ $A$ đến $D$ , lần lượt qua $B$ và $C$ , chúng ta sẽ liệt kê các con đường theo từng chặng.

Các chặng đường:

Từ $A$ đến $B$ : Có 3 con đường $a_1, a_2, a_3$ .

Từ $B$ đến $C$ : Có 2 con đường $b_1, b_2$ .

Từ $C$ đến $D$ : Có 3 con đường $c_1, c_2, c_3$ .

Tập hợp các con đường:

Tổng số con đường từ $A$ đến $D$ được tạo thành từ việc chọn một con đường từ $A$ đến $B$ , một con đường từ $B$ đến $C$ , và một con đường từ $C$ đến $D$ . Ta liệt kê tất cả các tổ hợp này như sau:

Các đường bắt đầu từ $A$ , qua $B$ , rồi qua $C$ , và cuối cùng đến $D$ sẽ có dạng: $(a_{i}, b_{j}, c_{k})$

với $i = 1, 2, 3$ , $j = 1, 2$ , và $k = 1, 2, 3$ .

Vậy tập hợp các con đường từ $A$ đến $D$ là:

${(a_{1}, b_{1}, c_{1}), (a_{1}, b_{1}, c_{2}), (a_{1}, b_{1}, c_{3}), (a_{1}, b_{2}, c_{1}), (a_{1}, b_{2}, c_{2}), (a_{1}, b_{2}, c_{3}), (a_{2}, b_{1}, c_{1}), (a_{2}, b_{1}, c_{2}), (a_{2}, b_{1}, c_{3}), (a_{2}, b_{2}, c_{1}), (a_{2}, b_{2}, c_{2}), (a_{2}, b_{2}, c_{3}), (a_{3}, b_{1}, c_{1}), (a_{3}, b_{1}, c_{2}), (a_{3}, b_{1}, c_{3}), (a_{3}, b_{2}, c_{1}), (a_{3}, b_{2}, c_{2}), (a_{3}, b_{2}, c_{3})}$

Câu 7: Tìm x biết

${(x - 3)}^{3} - (x - 3) (x^{2} + 3 x + 9) + 6 {(x + 1)}^{2} + 3 x^{2} = - 33$

Phương pháp giải:

Khai triển và rút gọn từng phần của phương trình

Áp dụng hằng đẳng thức đáng nhớ

Bình phương của một tổng:

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Lập phương của một hiệu:

${(A - B)}^{3} = A^{3} - 3 A^{2} B + 3 A B^{2} - B^{3}$

Lời giải:

${(x - 3)}^{3} - (x - 3) (x^{2} + 3 x + 9) + 6 {(x + 1)}^{2} + 3 x^{2} = - 33 \Leftrightarrow (x - 3) [{(x - 3)}^{2} - (x^{2} + 3 x + 9)] + 6 (x^{2} + 2 x + 1) + 3 x^{2} + 33 = 0 \Leftrightarrow (x - 3) (x^{2} - 6 x + 9 - x^{2} - 3 x - 9) + 6 x^{2} + 12 x + 6 + 3 x^{2} + 33 = 0 \Leftrightarrow x^{3} - 6 x^{2} + 9 x - x^{3} - 3 x^{2} - 9 x - 3 x^{2} + 18 x + 27 + 3 x^{2} + 9 x - 27 + 6 x^{2} + 12 x + 6 + 3 x^{2} + 33 = 0 \Leftrightarrow 39 x = - 39 \Leftrightarrow x = - 1$

Câu 8: Có bao nhiêu số nguyên x thỏa mãn: $- \frac{2}{5} < \frac{x}{10} < - \frac{1}{4}$

Phương pháp giải:

Biến đổi phân số trên về dạng cùng mẫu số.

Triệt tiêu phần mẫu số và thực hiện các phép tính tìm x.

Lời giải:

$- \frac{2}{5} < \frac{x}{10} < - \frac{1}{4} \Leftrightarrow - \frac{8}{20} < \frac{2 x}{20} < - \frac{5}{20} (n h â n c ả t ử v à m ẫ u c h o m ộ t s ố đ ể c ù n g m ẫ u s ố) \Leftrightarrow - 8 < 2 x < - 5 \Leftrightarrow - 4 < x < - \frac{5}{2}$

Câu 9: Tìm:

a. Ước của 60

b. Bội của 60, mà số đó bé hơn 80

Phương pháp giải:

Sử dụng phân tích thừa số nguyên tố để tìm các ước.

Cách phân tích một số ra thừa số nguyên tố

Ta có thể phân tích theo chiều dọc như sau:

Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.

Sử dụng định nghĩa bội và tính toán các bội bé hơn giới hạn cho trước.

+ Muốn tìm bội của một số tự nhiên khác 0, ta nhân số đó với các số tự nhiên 0, 1, 2, 3,..

Lời giải:

a. Tìm các ước của 60

Phương pháp tìm ước của một số bao gồm các bước sau:

Phân tích số thành thừa số nguyên tố:

Phân tích 60 thành tích của các thừa số nguyên tố.

$60 = 2^2 \times 3 \times 5$

Liệt kê tất cả các tích của thừa số nguyên tố:

Các ước của 60 sẽ là tích của các thừa số nguyên tố với các số mũ từ 0 đến số mũ tối đa của từng thừa số.

Ví dụ: $2^2$ có thể lấy các giá trị $2^0, 2^1, 2^2$ tương tự cho các thừa số khác.

Liệt kê tất cả các ước:

Từ các tích này, chúng ta liệt kê được tất cả các ước của 60: $\{1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60\}$ .

b. Tìm bội của 60 bé hơn 80

Phương pháp tìm bội của một số bao gồm các bước:

Bội của một số:

Bội của một số $a$ là các số có dạng $a \times k$ với $k$ là số nguyên dương.

Xác định giới hạn (80):

Tìm các bội của 60 bắt đầu từ 60x0; $60 \times 1$ và tăng dần cho đến khi kết quả vượt quá 80.

Liệt kê các bội:

60 x 0 = 0

$60 \times 1 = 60$

$60 \times 2 = 120$ (không thỏa mãn vì lớn hơn 80).

Kết luận: Bội của 60 nhỏ hơn 80 có 0 và 60.

Câu 10: Cho n là số nguyên không chia hết cho 3. Chứng minh rằng:

P = $3^{2 n} + 3^{n} + 1$ chia hết cho 13.

Phương pháp giải:

Để giải bài toán trên, ta áp dụng:

Phép đồng dư (Modulo):

Phép đồng dư giúp ta xác định phần dư khi chia một số cho một số nguyên khác. Ở đây, ta sử dụng modulo 13, tức là ta quan tâm đến phần dư khi chia cho 13.

Ký hiệu: $a \equiv b \ (\text{mod}\ m)$ , nghĩa là $a$ và $b$ có cùng phần dư khi chia cho $m$ (hoặc $a - b$ chia hết cho $m$ ).

Định lý Fermat nhỏ:

Định lý Fermat nhỏ nói rằng nếu $p$ là số nguyên tố và $a$ là số nguyên không chia hết cho $p$ , thì $a^{p-1} \equiv 1 \ (\text{mod}\ p)$ .

Ở đây, $p = 13$ và $a = 3$ , nên $3^{12} \equiv 1 \ (\text{mod}\ 13)$ . Điều này giúp ta tính các lũy thừa lớn của 3 theo modulo 13 một cách dễ dàng.

Phân tích dạng của $n$ :

Vì $n$ không chia hết cho 3, nên $n$ có thể được biểu diễn dưới hai dạng: $n = 3k + 1$ hoặc $n = 3k + 2$ , giúp ta phân trường hợp để giải bài toán.

Tính lũy thừa theo modulo:

Sử dụng $3^{12} \equiv 1 \ (\text{mod}\ 13)$ , ta có thể đơn giản hóa các lũy thừa lớn của 3 về các lũy thừa nhỏ hơn trong phép tính modulo 13, giúp ta tính toán nhanh hơn.

Lời giải:

Ta có: $3^{2 n} + 3^{n} + 1$

Vì n không chia hết cho 3 nên: n có dạng là $3 k + 1$ và $3 k + 2$

Trường hợp 1: $n = 3 k + 1$

Thế vào: Ta có: $3^{6 k + 2} + 3^{3 k + 1} + 1$

$= 72 9^{k} \cdot 9 + 2 7^{k} \cdot 3 + 1$

Mặt khác: $729 \equiv 27 \equiv 1$ (mod 13)

Do đó: $72 9^{k} \cdot 9 + 2 7^{k} \cdot 3 + 1 \equiv 1 \cdot 9 + 1 \cdot 3 + 1 = 13$ (mod 13)

Vậy .............

Trường hợp 2: $n = 3k + 2$

Thế vào: Ta có: $3^{2 (3 k + 2)} + 3^{3 k + 2} + 1 = 3^{6 k + 4} + 3^{3 k + 2} + 1$

$= 729^{k} . 81 + 27^{k} . 9 + 1$

$729 \equiv 27 \equiv 1$

Do đó: $72 9^{k} \cdot 81 + 2 7^{k} \cdot 9 + 1 \equiv 1 \cdot 81 + 1 \cdot 9 + 1 = 91$ (mod 13)

Vậy .............

Câu 11: Cho biểu thức M = $\frac{3 x + 3}{x^{3} + x^{2} + x + 1}$

a) Rút gọn

b) Tìm giá trị nguyên của x để M nhận giá trị nguyên

c) Tìm giá trị lớn nhất của M

Phương pháp giải:

a) Rút gọn biểu thức $M$ :

Ta phân tích tử số và mẫu số của biểu thức:

Tử số: $3x + 3 = 3(x + 1)$
Mẫu số: $x^3 + x^2 + x + 1$

Biểu thức trở thành:

$M = \frac{3(x + 1)}{x^3 + x^2 + x + 1}$

b) Tìm giá trị nguyên của $x$ để $M$ là số nguyên:

Để $M$ nhận giá trị nguyên, thì mẫu số $x^3 + x^2 + x + 1$ phải chia hết cho tử số $3(x + 1)$ , tức là:

$x^3 + x^2 + x + 1 \div (x + 1)$

Ta thực hiện phép chia đa thức $x^3 + x^2 + x + 1$ cho $x + 1$ :

Sử dụng phương pháp chia đa thức hoặc phân tích nhân tử để thực hiện phép chia.

Sau khi thực hiện phép chia, ta có thể xác định các giá trị nguyên của $x$ sao cho $M$ là số nguyên.

c) Tìm giá trị lớn nhất của $M$ :

Sau khi rút gọn và tính toán, ta có thể khảo sát giá trị của $M$ với các giá trị nguyên của $x$ tìm được ở câu b) và so sánh để tìm giá trị lớn nhất của $M$ .

Lời giải:

ĐK: $x^{3} + x^{2} + x + 1 \neq 0 \Leftrightarrow x \neq - 1$

a) $M = \frac{3 (x + 1)}{x^{2} (x + 1) + (x + 1)} = \frac{3 (x + 1)}{(x^{2} + 1) (x + 1)} = \frac{3}{x^{2} + 1}$

b) Để M nhận giá trị nguyên thì $x^{2} + 1 \in Ư (3) = {- 3; - 1; 1; 3}$

Mà $x^{2} + 1 \geq 1 \forall x$ do đó $x^{2} + 1 \in {1; 3} \Leftrightarrow x^{2} \in {0; 2} \Leftrightarrow x \in {0; \sqrt{2}}$

Mà x nguyên nên x = 0

c) Do $x^{2} + 1 \geq 0 + 1 = 1 \Rightarrow M = \frac{3}{x^{2} + 1} \leq \frac{3}{1} = 3$

Đẳng thức xảy ra khi x = 0

Vậy Max M = 3

Câu 12: Tính nhanh $126^{2} - 152.126 + 5776$

Phương pháp giải:

Nhóm các số hạng trong biểu thức thành từng nhóm có tổng (hoặc hiệu) là các số tròn chục, tròn trăm, tròn nghìn... rồi cộng (hoặc trừ) các kết quả lại.

Trong các phép tính tổng (hoặc hiệu), tích ( hoặc thương), cần chú ý các tính chất giao hoán, tính chất kết hợp của các số để có thể tính một cách thuận tiện nhất.

Công thức tổng quát:

Một số nhân với một tổng: a x (b + c) = a x b + a x c

a x b + a x c = a x (b + c)

Áp dụng hằng đẳng thức bình phương của 1 hiệu: (a - b)² = a² - 2ab + b²

Lời giải:

$126^{2} - 152.126 + 5776$

= 126² - 2.76.126 + 76²

= (126 - 76)²

= 50²

$= 2500$

Câu 13 : $\sqrt{x} . \sqrt{x} = ?$

Phương pháp giải:

Ta sử dụng tính chất của căn bậc hai:

$\sqrt{a} \cdot \sqrt{a} = a$

Lời giải:

$\sqrt{x} . \sqrt{x} = \sqrt{x^{2}} = x$ (x > 0)

Mở rộng:

$2 \sqrt{x} . \sqrt{x} = 2 \sqrt{x^{2}} = 2 x$

Câu 14: Tìm giá trị lớn nhất, nhỏ nhất của hàm số: y = $2 \sin x - \frac{4}{3} \sin^{3} x$ trên [0;π]

Phương pháp giải:

Xác định miền giá trị của hàm số:

Đầu tiên, nếu hàm số có liên quan đến $\sin x$ (vì miền giá trị của $\sin x$ trên $[0; \pi]$ là từ 0 đến 1), ta đặt $t = \sin x$ , khi đó $t \in [0, 1]$ .

Thay biến đổi đó vào hàm số, ta tìm được biểu thức của hàm theo $t$ .

Tính đạo hàm của hàm số:

Tính đạo hàm $y'$ của hàm số theo $t$ .

Giải phương trình $y' = 0$ để tìm các giá trị $t$ tại đó hàm số đạt cực trị.

Tính giá trị của hàm số tại các điểm đặc biệt:

Tính giá trị của hàm tại các giá trị biên của khoảng, cụ thể là tại $t = 0$ và $t = 1$ (tương ứng với $x = 0$ và $x = \pi$ ).

Tính giá trị của hàm số tại các điểm tìm được từ bước giải phương trình $y' = 0$ .

So sánh các giá trị để tìm giá trị lớn nhất và nhỏ nhất:

So sánh các giá trị của hàm số tại các điểm biên và các điểm cực trị để xác định giá trị lớn nhất và nhỏ nhất.

Lời giải:

y = $2 \sin x - \frac{4}{3} \sin^{3} x$ trên [0;π]

Đặt t = sinx => t ∈ [0; 1] (vì x ∈ [0;π])

=> y = $2 t - \frac{4}{3} t^{3}$ .

y' = $2 - 4 t^{2}$

=> y' = 0 <=> $- 4 t^{2}$ + 2 = 0 <=> $t^{2}$ = $\frac{1}{2}$ <=> $[\begin{matrix} t = \frac{- \sqrt{2}}{2} \\ t = \frac{\sqrt{2}}{2} \end{matrix}] (l o ạ i t = \frac{- \sqrt{2}}{2})$

Có $y = (\frac{\sqrt{2}}{2})$ = $\frac{2 \sqrt{2}}{3}$

y(0) = 0

y(1) = $\frac{2}{3}$

=> Min y = 0 khi t = 0 <=> sinx = 0 <=> $[\begin{matrix} x = 0 \\ x = π \end{matrix}]$

Max y = $\frac{2 \sqrt{2}}{2}$ khi t = $\frac{\sqrt{2}}{2}$ <=> sinx = $\frac{\sqrt{2}}{2}$ <=> $\sin x = \sin (\frac{π}{4})$

<=> $[\begin{matrix} x = \frac{π}{4} \\ x = \frac{3 π}{4} \end{matrix}]$

Câu 15: Giải phương trình: $\frac{x - 3}{13} + \frac{x - 3}{14} = \frac{x - 3}{15} + \frac{x - 3}{16}$

Phương pháp giải:

Sử dụng phương pháp phân tích đa thức thành nhân tử. Trong bài này sử dụng phương pháp đặt nhân tử chung.

Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.

Lời giải:

$\frac{x - 3}{13} + \frac{x - 3}{14} = \frac{x - 3}{15} + \frac{x - 3}{16}$

$\Leftrightarrow \frac{x - 3}{13} + \frac{x - 3}{14} - \frac{x - 3}{15} - \frac{x - 3}{16} = 0$

$\Leftrightarrow (x - 3) . (\frac{1}{13} + \frac{1}{14} - \frac{1}{15} - \frac{1}{16}) = 0$

$(V ì \frac{1}{13} + \frac{1}{14} - \frac{1}{15} - \frac{1}{16} > 0)$

$\Leftrightarrow x - 3 = 0 \Rightarrow x = 3$

Câu 16: Tính Nhanh:

(98 x 7676 - 9898 x 76) x (2001 x 2002 x 2003 x......x 2017)

Phương pháp giải:

Nhận biết các hạng tử chung:

Ta có thể nhận thấy rằng $98 \times 76$ là một nhân tử chung trong hai hạng tử đầu tiên của biểu thức.

Rút gọn biểu thức:

Sử dụng tính chất phân phối của phép nhân, ta đưa $98 \times 76$ ra ngoài và rút gọn biểu thức.

Sử dụng tính chất của tích:

Nhận xét rằng dãy tích từ $2001$ đến $2017$ nhân với 0 thì sẽ bằng 0

Lời giải:

(98 x 7676 - 9898 x 76) x (2001 x 2002 x 2003 x......x 2017)

= (98 x 76 x 101 - 98 x 101 x 76) x (2001 x 2002 x 2003 x......x 2017)

= 0 x (2001 x 2002 x 2003 x......x 2017)

= 0

Mở rộng:

(98 x 7676 - 9898 x 76) : (2001 x 2002 x 2003 x ... x 2010)

= (98 x 76 x 101 - 98 x 101 x 76) : (2001 x 2002 x 2003 x ... x 2010)

= 0 : (2001 x 2002 x 2003 x ... x 2010)

= 0

Câu 17: Tính chiều cao của cây trong hình bên, biết rằng người đo đứng cách cây 2,25 m và khoảng cách từ mắt người đo đến mặt đất là 1,5 m.

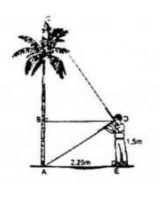
Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 99) (ảnh 1)

Phương pháp giải:

Công thức tính đường cao trong tam giác vuông

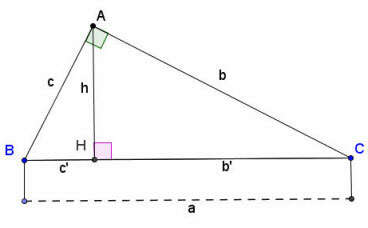
Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 99) (ảnh 3)

Giả sử có tam giác vuông ABC vuông tại A như hình vẽ trên:

Công thức tính cạnh và đường cao trong tam giác vuông:

1. a²= b²+ c²

2. b²= a.b′ và c²= a.c′

3. a.h = b.c

4. h²= b′.c'

5. $\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}$

Trong đó:

a, b, c lần lượt là các cạnh của tam giác vuông như hình trên;
b’ là đường chiếu của cạnh b trên cạnh huyền;
c’ là đường chiếu của cạnh c trên cạnh huyền;
h là chiều cao của tam giác vuông được kẻ từ đỉnh góc vuông A xuống cạnh huyền BC.

Lời giải:

Áp dụng công thức tính cạnh và đường cao cho tam giác vuông DAC ta có:

$B C = \frac{B D^{2}}{B A} \Leftrightarrow B C = \frac{2, 25^{2}}{1, 5} \Leftrightarrow B C = 3, 375 m$

Chiều cao cây là:

$C A = A B + B C = 1, 5 + 3, 375 = 4, 875 m$

Vậy chiều cao cây là 4,875 m.

Câu 18: Tính nhanh: $\frac{1}{2} - \frac{43}{101} + (- \frac{1}{3}) - \frac{1}{6}$

Phương pháp giải:

Nhóm các số hạng trong biểu thức thành từng nhóm có tổng (hoặc hiệu) là các số tròn chục, tròn trăm, tròn nghìn... rồi cộng (hoặc trừ) các kết quả lại.

Trong các phép tính tổng (hoặc hiệu), tích (hoặc thương), cần chú ý các tính chất giao hoán, tính chất kết hợp của các số để có thể tính một cách thuận tiện nhất.

Công thức tổng quát:

Một số nhân với một tổng: a x (b + c) = a x b + a x c

a x b + a x c = a x (b + c)

Lời giải:

$= (\frac{1}{2} - \frac{1}{3} - \frac{1}{6}) + (- \frac{43}{101})$

$= \frac{3 - 2 - 1}{6} + \frac{- 43}{101}$

$= 0 + \frac{- 43}{101}$

$= - \frac{43}{101}$

+TH1: x ⋮ 3 và y ⋮ 3 thì $x^{2}$ ⋮ 3 và $y^{2}$ ⋮ 3 => $x^{2} + y^{2}$ ⋮ 3.

+TH2: x ⋮ 3 và y $⋮$ 3 (hoặc x $⋮$ 3 và y⋮3)

+TH3: x mod 3 = 1 và y mod 3 = 1

+TH4: x mod 3 = 2 và y mod 3 = 2

+TH5: x mod 3 = 1 và y mod 3 = 2 (hoặc x mod 2 = 1 và y mod 3 = 1)

+ TH1: x ⋮ 3 và y ⋮ 3 thì $x^{2}$ ⋮ 3 và $y^{2}$ ⋮ 3 => $x^{2} + y^{2}$ ⋮ 3.

+ TH2: x ⋮ 3 và y $⋮$ 3 (hoặc x $⋮$ 3 và y ⋮ 3)

=> $x^{2}$ ⋮ 3 và $y^{2} ⋮$ 3 => $x^{2} + y^{2} ⋮$ 3 -> Loại

+TH3: x mod 3 = 1 và y mod 3 = 1

Giả sử x = 3a + 1; y = 3b + 1

$x^{2} + y^{2} = {(3 a + 1)}^{2} + {(3 b + 1)}^{2} = 9 a^{2} + 6 a + 1 + 9 b^{2} + 6 b + 1 = 3 (3 a^{2} + 2 a + 3 b^{2} + 2 b) + 2$

=> $x^{2} + y^{2}$ chia 3 dư 2 -> Loại.

+TH4: x mod 3 = 2 và y mod 3 = 2

Giả sử x = 3a - 1; y = 3b - 1

$x^{2} + y^{2} = {(3 a - 1)}^{2} + {(3 b - 1)}^{2} = 9 a^{2} - 6 a + 1 + 9 b^{2} - 6 b + 1 = 3 (3 a^{2} - 2 a + 3 b^{2} - 2 b) + 2$

=> $x^{2} + y^{2}$ mod 3 = 2 -> Loại

+TH5: x mod 3 = 1 và y mod 3 = 2 (hoặc x mod 2 = 1 và y mod 3 = 1)

Giả sử x = 3a + 1; y = 3b - 1

$x^{2} + y^{2} = {(3 a + 1)}^{2} + {(3 b - 1)}^{2} = 9 a^{2} + 6 a + 1 + 9 b^{2} - 6 b + 1 = 3 (3 a^{2} + 2 a + 3 b^{2} - 2 b) + 2$

=> $x^{2} + y^{2}$ mod 3 = 2 -> Loại

Vậy: $x^{2} + y^{2}$ chia hết cho 3 khi và chỉ khi x và y chia hết cho 3.

Câu 20: Một hình tam giác có diện tích 48 $c m^{2}$ , độ dài đáy 12 cm thì chiều cao của tam giác là

Diện tích của một hình tam giác được tính theo công thức:

$S = \frac{1}{2} x đ á y x c h i ề u c a o$

Trong đó:

$S$ là diện tích của tam giác,
Đáy là 12 cm,
Chiều cao là $h$ (cần tìm).

Theo đề bài, diện tích của tam giác là 48 cm² và đáy là 12 cm. Ta thay các giá trị vào công thức:

$48 = \frac{1}{2} \times 12 \times h$

$\Rightarrow 48 = 6 \times h$

$\Rightarrow h = \frac{48}{6} = 8$

Vậy chiều cao của tam giác là 8 cm.

Mở rộng:

1 hình tam giác có diện tích là 27,5 cm2 và chiều cao là 11 cm. Độ dài đáy của hình tam giác đó là

a 16,5 cm b 2,5 cm c 38,5 cm d 5 cm

Câu 21: Một tam giác có diện tích là 15 $c m^{2}$ , cạnh đáy là 0,8 dm thì chiều cao là bao nhiêu?

Diện tích của một hình tam giác được tính theo công thức:

$S = \frac{1}{2} x đ á y x c h i ề u c a o$

=> chiều cao = 2.S : độ dài đáy

Đổi 0,8 dm = 8 cm

Chiều cao hình tam giác là :

15 x 2 : 8 = 3,75 (cm)

Đáp số : 3,75 cm

Mở rộng:

Một tam giác có diện tích 12,6 $d m^{2}$ và chiều cao tương ứng là 45 dm thì cạnh đáy tam giác là bao nhiêu?

Cạnh đáy của tam giác là :

$= 12, 6 : \frac{45}{2} = 0, 56$

Câu 22: Giải phương trình nghiệm nguyên: $x^{2} - 6 x + y^{2} + 10 y = 24$

Áp dụng quy tắc phương trình bậc hai: $a x^{2} + 2 a c x + c = {(a + c)}^{2}$

$\Leftrightarrow x^{2} - 6 x + 9 + y^{2} + 10 x + 25 = 58 \Leftrightarrow {(x - 3)}^{2} + {(y + 5)}^{2} = 58$

$\Leftrightarrow {(x - 3)}^{2} \leq 58 \Leftrightarrow {(x - 3)}^{2} \in {0; 1; 4; 9; 16; 25; 36; 49}$

Dễ nhận thấy chỉ có tổng của 49 và 9; 9 và 49 thỏa mãn (vì các số trên là số chính phương)

$\Rightarrow \begin{array}{ll} {\begin{cases} {(x - 3)}^{2} = 49 \Leftrightarrow x - 3 = 7 \Leftrightarrow x = 10 \\ {(y + 5)}^{2} = 9 \Leftrightarrow y + 5 = 3 \Leftrightarrow y = - 2 \end{cases} \end{array}$

+) ${(x - 3)}^{2} + {(y + 5)}^{2} = 9 + 49 \Rightarrow \{\begin{array}{l} x - 3 = 3 \Leftrightarrow x = 6 \\ y + 5 = 7 \Leftrightarrow y = 2 \end{array}$

Vậy có 2 cặp (x,y)={(6;2);(10;-2)} thỏa mãn điều kiện.

Câu 23: Cho một hình chữ nhật có diện tích bằng 456 $c m^{2}$ . Biết nếu giảm chiều dài đi 5cm thì ta được hình vuông có diện tích bằng 361 $c m^{2}$ . Tìm chiều dài của hình chữ nhật đã cho.

Áp dụng diện tích hình vuông: S = a x a

Diện tích hình chữ nhật là a x b

Câu 24: 2,5 giờ = ... giờ ... phút

1 giờ = 60 phút

1 phút = 60 giây

0,5 giờ = 0,5 × 60 phút = 30 phút.

Vậy 2,5 giờ = 2 giờ 30 phút.

Mở rộng:

2,5 giờ = 2 giờ 30 phút

1 giờ 24 phút = 1,6 giờ

45 phút = 0,75 giờ

Câu 25: Tìm x biết: $(3 x + 2) (3 x - 2) - {(3 x - 1)}^{2} = 5$

Sử dụng hằng đẳng thức:

Bình phương của một hiệu

Công thức: ${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

Hiệu hai bình phương

Công thức: $A^{2} - B^{2} = (A - B) (A + B)$

Phân tích và khai triển biểu thức ở cả hai vế của phương trình.

Sau đó, đơn giản hóa phương trình để tìm nghiệm.

$\Leftrightarrow (9 x^{2} - 2^{2}) - (9 x^{2} - 6 x + 1) = 5$

$\Leftrightarrow 9 x^{2} - 4 - 9 x^{2} + 6 x - 1 - 5 = 0$

$\Leftrightarrow 6 x = 10$

$\Leftrightarrow x = \frac{5}{3}$

Vậy $S = {\frac{5}{3}}$

Câu 26: Cho A = $\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + . . . + \frac{1}{16} + \frac{1}{17}$ . Chứng minh rằng A không phải là số tự nhiên.

Tính tổng dãy số đã cho bằng cách tính tổng các phân số từng cặp.

Đưa tổng về một phân số dưới dạng tối giản.

Kiểm tra xem kết quả có phải là số tự nhiên hay không.

Ta có:
A = (1/2 + 1/3 + 1/4 + 1/5) + (1/6 + 1/7 + 1/8) + (1/9 + 1/10 + 1/11) + (1/12 + 1/13 + 1/14) + (1/15 + 1/16 + 1/17)   <
(1/2 + 1/3 + 1/4 + 1/5) + 3(1/6) + 3(1/9) + 3(1/12) + 3(1/15) = 2(1/2 + 1/3 + 1/4 + 1/5) < 2(1/2 + 1/2 + 1/4 + 1/4) = 3
Mặt khác
A = (1/2 + 1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) + (1/9 + 1/10 + 1/11 + 1/12) + (1/13 + 1/14 + 1/15 + 1/16) + 1/17    >
(1/2 + 1/3 + 1/4) + 4(1/8) + 4(1/12) + 4(1/16) = 2(1/2 + 1/3 + 1/4)   >    2(1/2 + 1/4 + 1/4) = 2

=> 2 < A < 3

Vậy A không là số tự nhiên

Câu 27: Một trường tiểu học được xây trên một khu đất, trong đó diện tích khu phòng học được xây dựng là 1500 m², chiếm 60% diện tích khu đất, diện tích đường đi chiếm 10% diện tích khu đất, phàn còn lại là sân chơi, bãi tập. Tính diện tích sân chơi, bãi tập.

Phương pháp giải:

Tính diện tích khu đất dựa trên diện tích và tỉ lệ phần trăm của khu phòng học.

Tính phần trăm diện tích còn lại dành cho sân chơi và bãi tập.

Tính diện tích sân chơi và bãi tập dựa trên tỉ lệ phần trăm này.

Lời giải:

Diện tích khu đất là :

1500 : 60 x 100 = 2500 m²

Tỉ số phần trăm giữa sân chơi bãi tập so với diện tích khu đất là :

100% - 60% - 10% = 30%

Diện tích sân chơi bãi tập là :

2500 : 100 x 30 = 750 m²

Đáp số : 750 m²

Câu 28: Một tổ công nhân làm theo kế hoạch phải trồng một số cây chia làm 3 đợt. Đợt 1 trồng $\frac{1}{3}$ số cây, đợt 2 trồng $\frac{3}{7}$ số cây, đợt 3 trồng nốt 160 cây. Tính số cây mà tổ đó phải trồng theo kế hoạch.

Phương pháp giải:

Tính tổng số cây đợt 3 trồng được.

Dùng số liệu về các đợt trồng để tìm ra số cây cần trồng trong kế hoạch.

Lời giải:

Đợt 3 trồng số cây là :

$1 - \frac{1}{3} - \frac{3}{7} = \frac{5}{21}$ ( tổng số cây)

Số cây mà tổ đó phải trồng theo kế hoạch là :

$160 : \frac{5}{21} = 672$ (cây)

Đ/s : $672$ cây

Câu 29: Tính tổng S = 1 + 2 + 3 + 4 + ... + 1998 + 1999

Phương pháp giải:

Tính số lượng số hạng của S

Tính tổng của S

Tổng của dãy số cách đều = (số hạng đầu + số hạng cuối) x số số hạng : 2

Lời giải:

Số lượng số hạng là:

$(1999 - 1) : 1 + 1 = 1999$ (số hạng)

Tổng của S là:

$(1999 + 1) \times 1999 : 2 = 1999000$

Đáp số: 1999000

Câu 30: Cho a, b, c > 0. Chứng minh: S = $\frac{a}{b + 2 c} + \frac{b}{c + 2 a} + \frac{c}{a + 2 b} \geq 1$

Phương pháp giải:

Sử dụng bất đẳng thức Cauchy-Schwarz trong dạng mở rộng để chứng minh bất đẳng thức trên.

Ta luôn có $(a^{2} + b^{2} + c^{2}) (x^{2} + y^{2} + z^{2}) \geq {(a x + b y + c z)}^{2} .$ Dấu bằng xảy ra khi và chỉ khi $\frac{a}{x} = \frac{b}{y} = \frac{c}{z} .$

Ta luôn có $(a_{1}^{2} + a_{2}^{2} + . . . + a_{n}^{2}) (x_{1}^{2} + x_{2}^{2} + . . . + x_{n}^{2}) \geq {(a_{1} x_{1} + a_{2} x_{2} + . . . + a_{n} x_{n})}^{2} .$ Dấu bằng xảy ra khi và chỉ khi $\frac{a_{1}}{x_{1}} = \frac{a_{2}}{x_{2}} = . . . = \frac{a_{n}}{x_{n}} .$

Lời giải:

$\Rightarrow S \geq \frac{{(a + b + c)}^{2}}{3 (a b + b c + c a)} \geq \frac{3 (a b + b c + c a)}{3 (a b + b c + c a)} = 1$

Dấu "=" xảy ra khi $a = b = c$ .

Câu 31: Tính giá trị của P = 2y⁴ + 7x - 2z⁴ biết x,y,z nguyên và thỏa mãn ( x² + 1 )² + ( y - z )² = 100

Phương pháp giải:

Bước 1: Phân tích điều kiện $(x^2 + 1)^2 + (y - z)^2 = 100$

Bước 2: Thử các giá trị của và tính ( x² + 1 )²

Bước 3: Tìm $y$ và $z$ khi $x = 3$ hoặc $x = -3$

Bước 4: Tính $P$ với các giá trị tìm được

Bước 5: Thay các giá trị của $x$

Kết luận

Lời giải:

Vì $(x^2 + 1)^2$ là một số nguyên không âm và nhỏ hơn hoặc bằng 100, nên ta có thể xem xét các giá trị có thể của $x$ sao cho $(x^2 + 1)^2 \leq 100$ .

$\Rightarrow x^{2} + 1 \leq \sqrt{100} = 10$

Suy ra $x^2 \leq 9$ , tức là $x$ có thể nhận các giá trị $x = -3, -2, -1, 0, 1, 2, 3$ .

Ta có bảng sau:

$x$	$x^2 + 1$	$(x^2 + 1)^2$
-3	10	100
-2	5	25
-1	2	4
0	1	1
1	2	4
2	5	25
3	10	100

Ta thấy chỉ có hai giá trị của $(x^{2} + 1)^{2} = 100$ khi $x = 3$ hoặc $x = -3$ .

Khi $(x^2 + 1)^2 = 100$ , điều kiện còn lại là:

$(y - z)^{2} = 100 - 100 = 0$

Suy ra $y = z$ .

Vì $y = z$ , ta có:

$P = 2 y^{4} + 7 x - 2 z^{4} = 2 y^{4} + 7 x - 2 y^{4} = 7 x$

Ta có: $P = 7x$ .

Với $x = 3$ :

$P = 7 \times 3 = 21$

Với $x = -3$ :

$P = 7 \times (- 3) = - 21$

Vậy, giá trị của $P$ có thể là $21$ hoặc $-21$ .

Câu 32: Cho tam giác ABC có góc B = 45 độ và góc C = 15 độ. Trên tia đối của tia AB lấy điểm D sao cho AD = 2AB. Tính góc DCB.

Phương pháp giải:

Sử dụng các tính chất của tam giác vuông và tam giác cân để tìm mối quan hệ giữa các góc và độ dài các đoạn thẳng.

Sử dụng trung điểm và tính chất của tam giác đều trong tam giác vuông.

Áp dụng các tính chất đối xứng trong các tam giác vuông cân để suy ra các góc cần tìm.

Lời giải:

Gọi F là trung điểm của CD

Có FE là đường trung tuyến ứng với cạnh huyền của tam giác vuông CDE

$\Rightarrow F E = C F = F D = B C = \frac{C D}{2}$

⇒ ΔCFE cân

Mà $180 ° - \hat{B C A} = \hat{F C E}$

$\Rightarrow \hat{F C E} = 60 °$

$\Rightarrow ∆ C F E đ ề u$

$\Rightarrow C F = F E = C E$

Xét tam giác BFE và DCE có:

CE = FE

$\hat{F C E} = \hat{C F E} = 60 °$

BF = CD(BC = CF = FD)

$\Rightarrow ∆ B F E = ∆ D C E (c - g - c)$

$\hat{F B E} = \hat{C D E} = 90 ° - 60 ° = 30 °$

$\Rightarrow ∆ B E D c â n t ạ i E$

⇒BE=ED (1)

Xét Δ ABC có:

$\hat{A B C} + \hat{A C B} + \hat{B A C} = 180 ° \Rightarrow \hat{C A B} = 180 ° - (\hat{A B C} + \hat{A C B}) = 180 ° - 165 ° = 15 °$

$Mà \hat{E B A} + \hat{F B E} = \hat{C B A} = 45 ° \Rightarrow \hat{E B A} = 45 ° - 30 ° = 15 ° = \hat{C A B} \Rightarrow ∆ B E A c â n t ạ i E$

=> BE = AE (2)

Từ (1) và (2) => ED = AE.

=> Δ ADE cân tại E

Đồng thời tam giác ADE có $\hat{D E A} = 90 °$

⇒ ΔADE là tam giác cân vuông

$\Rightarrow \hat{E D A} = \hat{D A E} = \frac{90 °}{2} = 45 ° Mà \hat{BDA} = \hat{CDE} - \hat{EDA} = 30 ° + 45 ° = 75 °$

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

Tìm kiếm