Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 91)
b) Tứ giác OKME là hình chữ nhật.
c) P, O, N thẳng hàng và KE // PN.
Lời giải:
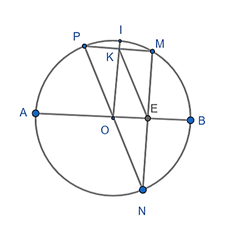
a) Xét (O) có PM // AB
⇒ 2 cung và bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN (∆BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến)
⇒
⇒
b) Xét (O) có OI đi qua điểm chính giữa của PM (giả thiết)
⇒ OI vuông góc với dây PM tại K
⇒
Xét tứ giác OKME có 3 góc vuông: (cmt),
( MN vuông góc với OB tại E)
(vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M)
⇒ OKME là hình chữ nhật
c) Ta có: ( vì 2 góc đồng vị, MP//AB)
mà (∆POK vuông tại K)
⇒
⇒
⇒ P, O, N thẳng hàng
- Xét ∆PMN có KE đường trung bình (K là trung điểm PM, E là trung điểm MN)
⇒ KE//PN.
Đề bài. Cho đa thức R(x) = x2 – 2x. Tính giá trị biểu thức
Lời giải:
R(x) = x2 – 2x = x(x – 2)
R(3) = 32 – 2.3 = 3(3 – 2) = 1.3
R(4) = 2.4
R(5) = 3.5
….
R(2023) = 2021.2023
Đề bài. Rút gọn biểu thức: (4x – 1)3 - (4x − 3)(16x2 + 3).
Lời giải:
(4x – 1)3 - (4x − 3)(16x2 + 3)
= 64x3 – 48x2 + 12x – 1 – (64x3 + 12x – 48x2 – 9)
= 64x3 – 48x2 + 12x – 1 – 64x3 – 12x + 48x2 + 9
= 8.
Lời giải:
Với cách lấy điểm I như trên, ta có điểm I cố định. Khi đó MN đi qua I, thật vậy:
Theo giả thiết có:
⇒
Suy ra I là trung điểm MN hay MN đi qua I cố định.
Đề bài. Tìm m để A giao B bằng rỗng biết A = [m; m + 1] và B = (-1; 3).
Lời giải:
Để A ∩ B = ∅ thì: .
Lời giải:
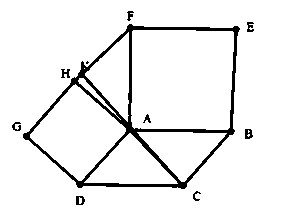
Gọi K là giao điểm của AC và HF
a) Do ABEF và ADGH đều là hình vuông nên
AH = BA, AH = DA
Do ABCD là hình bình hành nên BA=DC.
Suy ra AF = DC
Ta chứng minh được và
Suy ra
Xét hai tam giác HAF và ADC, ta có:
AH = DA
AF = DA
Suy ra ΔHAF = ΔADC (c.g.c)
b) Ta có: và nên
Mà (vì ΔHAF = ΔADC), suy ra
Trong tam giác AHK, ta có:
Suy ra
Vậy AK ⊥ HK hay AC ⊥ HF.
Đề bài. Cho tứ giác ABCD. M, N là trung điểm của AC và BD.
Chứng minh: AB2 + BC2 + CD2 + DA2 = AC2 + BD2 + 4MN2.
Lời giải:
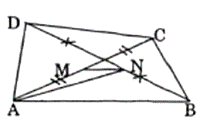
Trong tam giác ABD ta có AN là đường trung tuyến:
⇒ AB2 + AD2 = 2AN2 + (1)
Trong tam giác CBD có CN là đường trung tuyến:
⇒ CB2 + CD2 = 2CN2 + (2)
Cộng (1) với (2) ta được: AB2 + AD2 + CB2 + CD2 = 2AN2 + 2CN2 + BD2 (3)
Xét tam giác CAN có NM là trung tuyến:
⇒ AN2 + CN2 = 2MN2 + (4)
Thay (4) vào (3) ta được:
AB2 + AD2 + CB2 + CD2 = 2.(2MN2 + ) + BD2 = 4MN2 + AC2 + BD2
Vậy B2 + BC2 + CD2 + DA2 = AC2 + BD2 + 4MN2.
Lời giải:
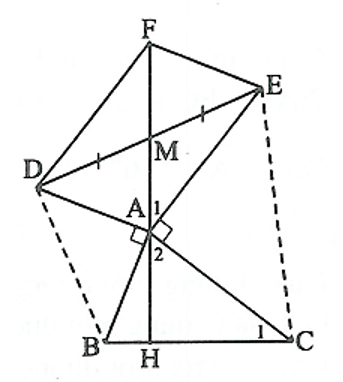
Vẽ hình bình hành DAEF. Khi đó AF đi qua M.
Gọi H là giao điểm của MA với BC.
Ta có: EF = AD = AB.
mà nên
Xét tam giác AEF và CAB có:
AC = AE
AB = AF
⇒ ΔAEF = ΔCAB (g.c.g)
⇒
Lại có:
Suy ra:
Do đó: AM vuông góc BC.
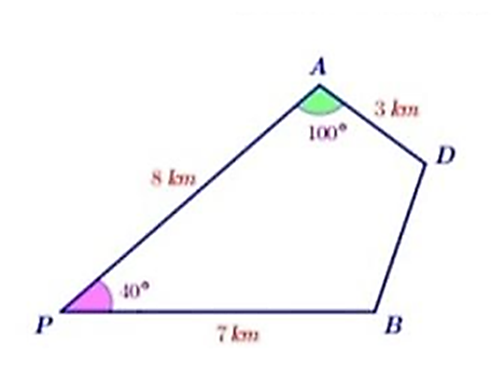
Lời giải:
Xét △PAB:
AB2 = AP2 + BP2 − 2.AP.BP.cos = 82 + 72 − 2.8.7.cos40° ≈ 27,2
Suy ra: AB ≈ 5,22 (km)
cos
⇒
Suy ra:
Xét △ABD:
DB2 = AD2 + BA2 − 2.DA.BA.cos = 32 + 5,222 − 2.3.5,22.cos40° ≈ 12,26
⇒ DB ≈ 3,5 (km)
Vậy Hưng phải đi khoảng 3,5km nữa để đến được đích.
Đề bài. Chứng minh B = 3 + 32 + … + 399 không phải là số chính phương.
Lời giải:
B = 3 + 32 + … + 399
3B = 32 + 33 + … + 3100
3B - B = (32 + 33 + … + 3100) – (3 + 32 + … + 399)
2B = 3100 – 3
Mà không thể viết được dưới dạng n2
Nên B không phải số chính phương.
Đề bài. Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 1,8cm, HC = 3,2cm
b) Tính góc B, C (làm tròn đến độ).
c) Tia phân giác góc B cắt AC tại D. Tính BD.
Lời giải:
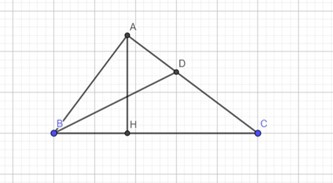
a) Ta có: ΔABC vuông tại A, AH ⊥ BC
⇒ AH2 = HB.HC (Hệ thức lượng trong tam giác vuông)
⇒ AH2 = 5.76
⇒ AH = 2,4
Suy ra:
BC = HB + HC = 5.
b) Ta có:
Suy ra: .
c) Vì BD là phân giác
Nên:
⇒
⇒
⇒
.
d) .
Đề bài. Tìm các cặp số nguyên (x; y) thỏa mãn x2 – xy + y + 2 = 0.
Lời giải:
x2 – xy + y + 2 = 0
⇔ x2 – 1 – xy + y = -3
⇔ (x – 1)(x + 1) – y(x – 1) = -3
⇔ (x – 1)(x + 1 – y) = -3
Vì x, y là số nguyên nên x – 1 và x – y + 1 là số nguyên
Nên x – 1 và x – y + 1 đều là ước của -3
Suy ra: x – 1; x – y + 1 ∈ {-3; -1; 1; 3}
Ta có bảng:
|
x – 1 |
-3 |
-1 |
1 |
3 |
|
x – y + 1 |
1 |
3 |
-3 |
-1 |
|
x |
-2 |
0 |
2 |
4 |
|
y |
-2 |
-2 |
6 |
6 |
Vậy (x;y) ∈ {(-2;-2), (0;-2), (2;6), (4;6)}.
Lời giải:
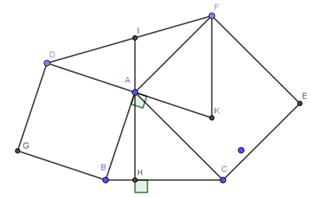
Qua F kẻ đường thẳng song song với AI cắt AD tại K
Xét tam giác ABC và AKF có:
(cùng phụ với )
(góc đồng vị)
⇒ △ABC ∽ △AKF (g.g)
⇒ (Vì ACEF là hình vuông nên AC = AF)
Suy ra: AB = AK
Mà AB = AD nên AD = AK
AI // FK nên theo định lý Ta-lét:
Vậy DI = IF.
Đề bài. Tìm x biết 12x.(3 - 4x) + 7(4x - 3) = 0.
Lời giải:
12x.(3 - 4x) + 7(4x - 3) = 0
⇔ (3 – 4x)(12x – 7) = 0
⇔
⇔ .
Đề bài. Tìm GTNN của A = x2 – 6x + 6.
Lời giải:
A = x2 – 6x + 6
A = x2 – 6x + 9 – 3
A = (x – 3)2 – 3
Vì (x – 3)2 ≥ 0 với mọi x nên (x – 3)2 – 3 ≥ – 3 với mọi x
Vậy GTNN của A là – 3 khi x – 3 = 0 hay x = 3.
a) Tứ giác BEDC là hình thang cân.
c) Bốn điểm A, I, O, J thẳng hàng.
Lời giải:
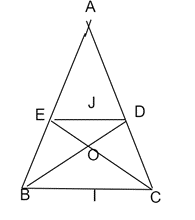
a) Ta có: (vì tam giác ABC cân tại A)
⇒
Xét tam giác DBC và tam giác ECB có:
(vì )
BC là cạnh chung
⇒ ∆DBC = ∆ECB (g.c.g)
⇒ BE = CD mà AB = AC
Nên ta có:
⇒ ED // BC
b) Từ phần a trên đã có BE = CD
Có: (so le trong)
mà (BD là phân giác)
⇒
⇒ Tam giác BED cân tại E
⇒ BE = ED
⇒ BE = ED = CD.
c) AI cắt ED tại J', ta chứng minh J' ≡ J
Từ tính chất tam giác đồng dạng ta có:
⇒ EJ' = ⇒ J' là trung điểm ED ⇒ J' ≡ J
Vậy A, I, J thẳng hàng
*OI cắt ED tại J" ta chứng minh J" ≡ J
Xét tam giác ODE và tam giác OBC có:
(đối đỉnh)
(so le trong, DE // BC)
∆ODE ∽ ∆OBC (g.g)
⇒
Mặt khác: (so le trong), (đối đỉnh)
⇒ ∆J"DO ∽ ∆IBO (g.g)
⇒
⇒
⇒ J" là trung điểm ED ⇒ J" ≡ J
Tóm lại A, I, O, J thẳng hàng.
b, Chứng minh 4 điểm A, B, M, O cùng thuộc một đường tròn.
c, Gọi E là giao điểm của OM với HB. Chứng minh ED là tiếp tuyến của đường tròn (O;R).
Lời giải:
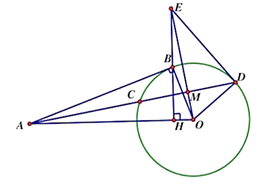
a) Xét tam giác AMO vuông tại A có AH vuông góc MO
Áp dụng hệ thức lượng: OH.OM = OA2 = R2
b) Xét (O) có M là trung điểm CD nên OM vuông góc CD (bán kính vuông góc dây cung)
⇒
Lại có: BA là tiếp tuyến nên
Suy ra: M, B thuộc đường tròn đường kính OA
Hay A, B, M, O cùng thuộc một đường tròn.
c) Xét tam giác OHE và tam giác OMA có:
Chung
⇒ ∆OHE ∽ ∆OMA (g.g)
⇒
Suy ra:
Xét tam giác ODE và tam giác OMD có:
Chung
⇒ ∆ODE ∽ ∆OMD (c.g.c)
⇒
Suy ra: OD ⊥ ED mà D thuộc (O) nên ED là tiếp tuyến của (O).
Đề bài. Chứng minh đẳng thức: .
Lời giải:
⇔
⇔
⇔
⇔
⇔ cotx + tanx = cotx + tanx (vì tanx.cotx = 1 luôn đúng)
Vậy .
Đề bài. Tìm số tròn trăm biết: 18650 < X . 3 < 18920.
Lời giải:
18650 < X . 3 < 18920
⇔
⇔ 6216,67 < X < 6306,67
Vì X là số tròn trăm nên X = 6300.
Vậy X = 6300.
Lời giải:
Gọi số học sinh khối 6 là a (a ∈ ℕ*, 400 < a < 500).
Theo đề bài ta có a ∈ BC(6, 8, 10)
Ta có
6 = 2 . 3
8 = 23
10 = 2 . 5
Suy ra BCNN(6, 8, 10) = 23 . 3 . 5 = 120
Suy ra BC(6, 8, 10) ={0; 120; 240; 360; 480; 600; ...}
Mà 400 < a < 500
Suy ra a = 480
Vậy số học sinh là 480 em.
Đề bài. Cho tống S = 30 + 42 - 6 + x với x thuộc ℕ. Tìm x để S chia hết cho 6.
Lời giải:
Ta có: S = 30 + 42 – 6 + c = 66 + x
Để S chia hết cho 6 thì (66 + x) chia hết cho 6
Mà 66 luôn chia hết cho 6.
Suy ra: x ⋮ 6
Hay x = 6k (k ∈ ℕ).
Đề bài. Cho A = 2 + 22 +....... + 260.
b) Chứng tỏ rằng: A chia hết cho 3, 5, 7.
Lời giải:
a) A = 2 + 22 +....... + 260
2A = 22 + 23 +....... + 261
2A – A = (22 + 23 +....... + 261) – (2 + 22 +....... + 260)
A = 261 – 2.
b) A = 2 + 22 +....... + 260
A = (2 + 22) + (23 + 24) +....... + (259 + 260)
A = 2(1 + 2) + 23(1 + 2) + … + 259(1 + 2)
A = (1 + 2)(2 + 23 + … + 259)
A = 3.(2 + 23 + … + 259) ⋮ 3
Lại có: A = 2 + 22 +....... + 260
A = (2 + 22 + 23) + (24 + 25 + 26) + ....... + (258 + 259 + 260)
A = 2(1 + 2 + 22) + 24(1 + 2 + 22) + … + 258(1 + 2 + 22)
A = (1 + 2 + 22)(2 + 24 + … + 258)
A = 7.(2 + 24 + … + 258) ⋮ 7
Lại xét: A = 2 + 22 +....... + 260
A = (2 + 22 + 23 + 24)+ ....... + (257 + 258 + 259 + 260)
A = 2(1 + 2 + 22 + 23) + … + 257(1 + 2 + 22 + 23)
A = (1 + 2 + 22 + 23)(2 + … + 257)
A = 15.(1 + 2 + 22 + 23)
A = 3.5.(1 + 2 + 22 + 23) ⋮ 5
Vậy A ⋮ 3, 5, 7.
Lời giải:
Ta thấy: , lại có 99 ⋮ 11 nên
Suy ra:
Vậy
Đề bài. Tìm 2 số tự nhiên a và b biết a - b = 84 , ƯCLN(a, b) = 12 .
Lời giải:
Do ƯCLN(a, b) = 12
⇒ a = 12m; b = 12n (với m, n là 2 số nguyên tố cùng nhau)
Ta có: a – b = 12(m − n) = 84
⇒ m – n = 7; mà m, n là hai số nguyên tố cùng nhau và ƯCLN(12m, 12n) = 1
⇒ m = 8; n = 1
⇒ a = 96; b = 12
Vậy 2 số cần tìm là 96 và 12.
Đề bài. Chứng minh tồn tại vô hạn các số nguyên tố.
Lời giải:
Giả sử chỉ có hữu hạn các số nguyên tố là p1; p2; p3; …; pn và giả sử p1 < p2 < p3 < …< pn.
Xét tích A = p1. p2. p3. …pn + 1. Rõ ràng A > pn nên A là hợp số, do đó A có ít nhất một ước nguyên tố p.
Khi đó p1; p2; p3; …; pn là tất cả các số nguyên tố nên tồn tại I thuộc {1, 2, …, n} sao cho p = pi.
Như vậy A chia hết cho p; p1; p2; p3; …; pn chia hết cho p nên 1 chia hết cho p, mâu thuẫn.
Do đó, giả sử chỉ có hữu hạn số nguyên tố là sai.
Vậy có vô hạn các số nguyên tố.
Đề bài. Đội văn nghệ có 36 bạn, được xếp thành các hàng có số người bằng nhau. Hỏi có thể có những cách xếp hàng nào, biết mỗi hàng có từ 4 đến 12 bạn.
Lời giải:
36 chia hết cho 4; 6; 9; 12
Suy ra có 4 hàng
Hàng 4 người thì có số nhóm là:
36 : 4 = 9 (nhóm)
Hàng 6 người thì có số nhóm là:
36 : 6 = 6 (nhóm)
Hàng 9 người thì có số nhóm là:
36 : 9 = 4 (nhóm)
Hàng 12 người thì có số nhóm là:
36 : 12 = 3(nhóm)
Đáp số: 4 nhóm
Nhóm 4 người: 9 nhóm
Nhóm 6 người: 6 nhóm
Nhóm 9 người: 4 nhóm
Nhóm 12 người: 3 nhóm
Đề bài. Tính nhanh: A = 1 - 3 + 5 - 7 + 9 - 11 + ... + 91 - 93 + 95 - 97 + 99.
Lời giải:
A = 1 - 3 + 5 - 7 + 9 - 11 + ... + 91 - 93 + 95 - 97 + 99
= 99 - 97 + 95 - 93 + 91 -...+11 - 9 +7 - 5 +3 - 1
= (99 - 97) + (95 - 93) + ... + (7 - 5) + (3 - 1)
= 2 + 2+ ... + 2 + 2 (có 25 số 2 vì có (99 – 1) : 2 + 1 = 50 số hạng, mỗi nhóm 2 số hạng)
= 2.25
= 50.
Đề bài. Tìm n sao cho 25 < 3n < 250.
Lời giải:
25 < 3n < 250
Ta có: 33 = 27 > 25; 32 = 9
Theo đề: 25 < 3n; 3n > 32 (1)
Lại có: 35 = 243 < 250 < 36
Suy ra: 25 < 33, 34, 35 < 250
Vậy n ∈ {3; 4; 5}.
Đề bài. Tìm miền giá trị của .
Lời giải:
TXĐ: D = ℝ
Ta có:
⇔ ycosx + 2y = sinx + 1
⇔ ycosx – sinx = 1 – 2y
Phương trình có nghiệm khi: y2 + 1 ≥ (1 – 2y)2
⇔ 3y2 – 4y ≤ 0
⇔
Vậy
Đề bài. Cho A = 2 + 22 + … + 2100. Chứng minh rằng A chia hết cho 3.
Lời giải:
A = 2 + 22 + … + 2100
A = (2 + 22) + (23 + 24) + … + (299 + 2100)
A = 2(1 + 2) + 23(1 + 2) + … + 299(1 + 2)
A = (1 + 2)(2 + 23 + … + 299)
A = 3.(2 + 23 + … + 299)
Vì 3 chia hết cho 3 nên 3.(2 + 23 + … + 299) chia hết cho 3
Vậy A chia hết cho 3.
Đề bài. Tìm x biết (x – 1)5 = 32.
Lời giải:
(x – 1)5 = 32
⇔ (x – 1)5 = 25
⇔ x – 1 = 2
⇔ x = 3
Vậy x = 3.
Đề bài. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng song song nhau nếu chúng không có điểm chung.
C. Hai đường thẳng cùng song song với một mặt phẳng thì song song với nhau.
D. Không có mặt phẳng nào chứa cả hai đường thẳng a và b thì ta nói a và b chéo nhau.
Lời giải:
Chọn D.
- Hai đường thẳng cùng song song với một đường thẳng thứ ba thì có thể trùng nhau ⇒ A sai.
- Hai đường thẳng không có điểm chung thì song song hoặc chéo nhau ⇒ B sai.
- Hai đường thẳng cùng song song với một mặt phẳng thì có thể cắt, trùng hoặc chéo nhau ⇒ C sai.
- Hai đường thẳng chéo nhau nếu chúng không đồng phẳng ⇒ D đúng.
Đề bài. Tìm chu kì T của hàm số y = cos3x + cos5x.
Lời giải:
Hàm số y = cos3x tuần hoàn với chu kì .
Hàm số y = cos5x tuần hoàn với chu kì .
Suy ra hàm số y = cos3x + cos5x tuần hoàn với chu kì T = 2π.
Đề bài. Cho hình chóp S.ABCD, đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm SA, CD. Chứng minh MN // (SBC).
Lời giải:
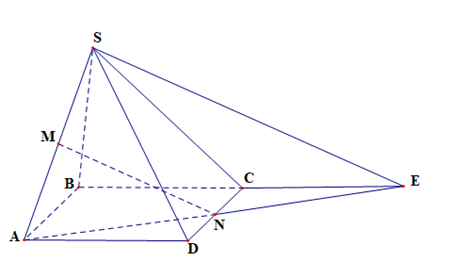
Trong mp(ABCD) nối AN kéo dài cắt BC kéo dài tại E
Suy ra E ∈ (SBC)
Vì N là trung điểm của CD nên NC = ND
Vì AD // BE nên (Định lí Ta – let)
Suy ra AN = EN
Do đó N là trung điểm của AE
Xét tam giác SAE có
N là trung điểm của AE
M là trung điểm của AS
Suy ra MN là đường trung bình
Do đó MN // SE
Vậy MN // (SBC).
Lời giải:
Tuổi mẹ hiện nay là:
(24 + 56) : 2 = 40 tuổi)
Tuổi con hiện nay là:
56 - 40 = 16 (tuổi).
Vậy tuổi con là 16 tuổi, tuổi mẹ là 40 tuổi.
Lời giải:
Số tiền ông A còn nợ ngân hàng sau lần trả thứ nhất:
(100 + 100. 0,01) – m = 100.1,01 – m (triệu đồng)
Số tiền ông A còn nợ ngân hàng sau lần trả thứ hai:
(100 + 1,01 - m) .1,01 – m = 100.1,012 - (1,01 + 1) m (triệu đồng)
Vì ông A đã hoàn cho ngân hàng toàn bộ số tiền nợ, sau lần trả thứ ba, nên
0 = [ 100.1,012 - (1,01 + 1)m] .1,01 - m= 100.1,013 - [ 1,012 + 1,01 + 1]m
Từ đó suy ra:
.
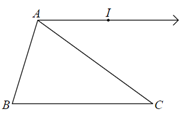
Đề bài. Cho hình vẽ sau. Tính số đo góc x?
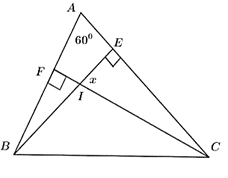
Lời giải:
Xét tam giác ACF có:
⇔
⇔
Xét tam giác IEC có:
⇔
⇔ .
Đề bài. Chứng minh biểu thức không phụ thuộc vào x.
Lời giải:
Lời giải:
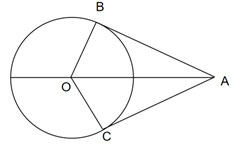
Xét tam giác ABC có AB = AC (tính chất 2 tiếp tuyến cắt nhau)
Do đó: tam giác ABC cân tại A
Xét ∆ABC cân tại A có OA là đường phân giác
Suy ra: OA đồng thời là đường trung trực của tam giác ABC
Hay OA là trung trực của BC.
Đề bài. Giải phương trình x(x − 3) – x + 3 = 0.
Lời giải:
x(x − 3) – x + 3 = 0
⇔ x(x − 3) – (x – 3) = 0
⇔ (x – 3)(x – 1) = 0
⇔
Vậy phương trình có nghiệm x = 3 hoặc x = 1.
Đề bài. Giải phương trình (x – 1)5 = 32.
Lời giải:
(x – 1)5 = 32
⇔ (x – 1)5 = 25
⇔ x – 1 = 2
⇔ x = 3
Vậy x = 3.
Đề bài. Biến đổi thành tích: A= cosx + cos3x + cos5x + cos7x.
Lời giải:
A = cosx + cos3x + cos5x + cos7x
= 2cos4x.cos3x + 2cos4x.cosx
= 2cos4x.(cos3x + cosx)
= 4cos4x.cos2x.cosx
Đề bài. Tìm nghiệm nguyên của phương trình 5(xy + yz + zx) = 4xyz.
Lời giải:
Xét x = y = z = 0 là nghiệm của phương trình do 0 = 0 (thỏa mãn)
Xét x, y, z đều khác 0 ta có:
5(xy + yz + zx) = 4xyz
⇔
⇔
Vì 5 không chia hết cho 4 mà 4 ⋮ 4 nên
Ta có:
Tương tự:
Suy ra:
Mà
Suy ra:
Mà từ 3 đến -3 chỉ có 0 chia hết cho 4 mà x, y, z khác 0 nên vô lí
Vậy phương trình có nghiệm nguyên là x = y = z = 0.
Lời giải:
1km ô tô tiêu thụ là:
12 : 100 = 0,12 (lít)
Cả hai quãng đường ô tô tiêu thụ là:
(169 + 131) . 0,12 = 36 (lít)
Đáp số: 36 lít.
Lời giải:
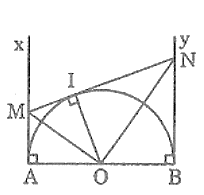
Gọi I là tiếp điểm của tiếp tuyến MN với đường tròn (O). Nối OI
Ta có: (hai góc kề bù)
OM là tia phân giác của góc AOI (tính chất hai tiếp tuyến cắt nhau)
ON là tia phân giác của góc BOI (tính chất hai tiếp tuyến cắt nhau)
Suy ra : OM ⊥ ON (tính chất hai góc kề bù)
Vậy .
Đề bài. Cho tam giác ABC có . Tính .
Lời giải:
Ta có: (tính chất tổng 3 góc trong 1 tam giác)
Suy ra:
.
Đề bài. Tìm giá trị của m để phương trình sin2x – m = 1 có nghiệm.
Lời giải:
Phương trình tương đương: sin2x = m + 1
Vì sin2x ∈ [-1;1] nên để phương trình có nghiệm thì: -1 ≤ m + 1 ≤ 1
Suy ra: -2 ≤ m ≤ 0.
Vậy -2 ≤ m ≤ 0.
Đề bài. Giải phương trình sin3x – cos2x = 0.
Lời giải:
sin3x – cos2x = 0
⇔ sin3x = cos2x
⇔
⇔
⇔ .
Đề bài 1. Cho ∆ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Hỏi bằng vecto nào?
Lời giải:
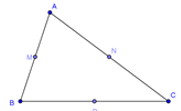
Từ M, N, P lần lượt là trung điểm các cạnh AB, AC, BC, ta suy ra MN, NP, MP là các đường trung bình của tam giác ABC.
Suy ra ANPM là hình bình hành.
Vì ANPM là hình bình hành nên theo quy tắc hình bình hành ta có
Đề bài 2. Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của AB, AC, BC. Xác định hiệu .
Lời giải:
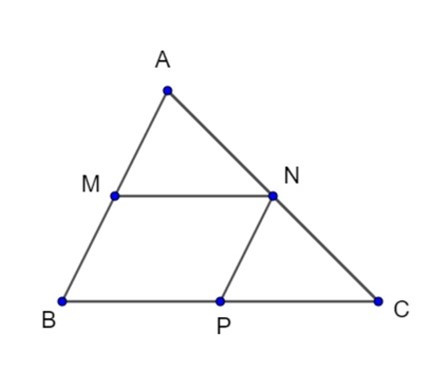
*
N là trung điểm AC nên
*
Xét tam giác ABC có: M, N là trung điểm AB, AC nên MN là đường trung bình
Suy ra: MN // BC;
⇒
*
*
Đề bài. Cho biểu thức . Tìm a ∈ ℤ để E ∈ ℤ.
Lời giải:
Để E ∈ ℤ thì 3 chia hết cho a – 2
Hay a – 2 ∈ Ư(3)
Suy ra: a – 2 ∈ {-1; 1; 3; -3}
⇒ a ∈ {1; 3; 5; -1}
Vậy a ∈ {1; 3; 5; -1}.
Đề bài. Cho tam giác ABC. Chứng minh
Lời giải:
Ta có:
⇔
⇔
⇔
⇔
⇔ .
Đề bài. Cho hình vuông ABCD cạnh a, M bất kì.
Lời giải:
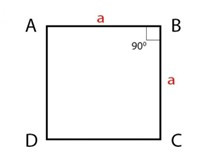
Do
Nên: .
Đề bài. Tìm x để 50 chia hết cho x + 1.
Lời giải:
Ta có: 50 ⋮ (x + 1) nên x + 1 ∈ Ư(50)
Suy ra x + 1 ∈ {±1; ±5; ±10; ±25; ±50}
Hay x ∈ {-2; 0; -6; 4; -11; 9; -26; 24; 49; -51}.
Đề bài. Tìm x, y, z biết: và x – y + z = –4.
Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra:
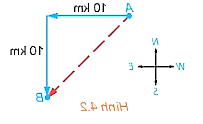
Lời giải:
Ta có hình vẽ sau:
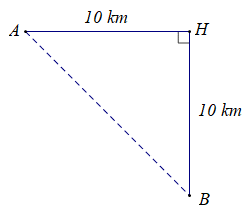
Vì góc giữa hướng đông và hướng nam là bằng 90 độ nên
do đó tam giác AHB vuông tại H.
Xét ΔAHB vuông tại H, áp dụng định lí Py – ta – go ta có: AB2 = AH2 + BH2
Thay số: AB2 = 102 + 10 = 100 + 100 = 200
⇔
ΔAHB vuông tại H, có AH = BH = 10 km nên ΔAHB cân tại H
Suy ra:
Do đó nếu đi từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B thì phải đi theo đường thẳng AB chính là hướng đông nam, tạo với hướng đông một góc 45°.
Vậy nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng đông nam, tạo với hướng đông một góc 45° và đi quãng đường dài
Lời giải:
Gọi số tự nhiên n có dạng là
Nếu xóa c ta được và
Tương tự nếu xóa b ta được và
Nếu xóa a ta được và
Vì
Để thì c = 0
Lại có:
Suy ra: 10b ⋮ (10a + c) mà c = 0 nên 10b ⋮ 10a hay b ⋮ a
Tức a là ước của b (1)
Lại có:
Để thì a ⋮ b
Suy ra: b là ước của a (2)
Từ (1) và (2) ta có: a = b và khác 0.
Suy ra: n = {110; 220; 330; 440; 550; 660; 770; 880; 990}.
Đề bài. Tập giá trị của hàm số y = 2sin2x – sinx – 1 là đoạn [m; M]. Khi đó 8m – 3M bằng?
Lời giải:
Đặt t = sinx (-1 ≤ t ≤ 1)
Khi đó y = 2t2 – t - 1
y' = 4t – 1
Xét y' = 0 ta có: 4t – 1 = 0 ⇔
Ta có bảng biến thiên:
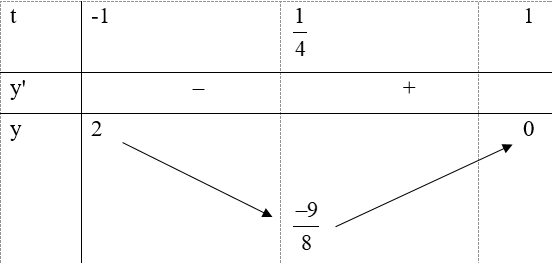
Từ bảng biến thiên ta thấy:
Suy ra:
Khi đó .
Lời giải:
Ta có: y' = 3x2 + 4x + m – 3
Để hàm số có 2 điểm cực trị thì phương trình y' = 0 có 2 nghiệm phân biệt
⇔ ∆' > 0 ⇔
Ta có: nên phương trình đường thẳng đi qua hai điểm cực trị là:
Thay M(9;-5) vào ta có:
⇔ m = 3.
Vậy m = 3.
Lời giải:
Gọi điểm mà đồ thị hàm số luôn đi qua là M(x0; y0)
Ta có: (2m + 10)x0 - 4m - 1 = y0
⇔ 2mx0 + 10x0 – 4m – 1 – y0 = 0
⇔ 2m(x0 – 2) + (10x0 – y0 – 1) = 0
⇔
Vậy đồ thị hàm số luôn đi qua M(2; 19)
Gọi khoảng cách từ A đến d là AH
Xét trong tam giác vuông AHM luôn có: AH ≤ AM
Vậy AHmax khi AH = AM tức AM ⊥ d
Gọi phương trình đường thẳng AM có dạng y = ax + b
Ta có:
Vậy AM có phương trình: y = 4x + 11.
Để AM ⊥ d thì 4.(2m + 10) = -1
Suy ra:
Vậy thì khoảng cách từ A đến đường thẳng d lớn nhất.
Đề bài. Tìm tập hợp các số tự nhiên n sao cho (3n + 7) chia hết cho (n - 2).
Lời giải:
Ta có: 3n + 7 = 3(n – 2) + 16.
Vì 3(n – 2) chia hết cho (n – 2) nên để (3n + 7) chia hết cho (n - 2) thì 16 chia hết cho n – 2
Hay n – 2 ∈ Ư(16)
Mà n là số tự nhiên
Suy ra: n – 2 ∈ {1; 2; 4; 8; 16}
Vậy n ∈ {3; 4; 6; 10; 18}
Đề bài. Tìm tập hợp các số tự nhiên n sao cho (6n + 9) chia hết cho (2n + 1).
Lời giải:
Ta có: 6n + 9 = 3(2n + 1) + 6
Vì 3(2n + 1) chia hết cho 2n + 1
Để 6n + 9 chia hết cho 2n + 1 thì 6 chia hết cho 2n + 1
⇒ 2n + 1 ∈ Ư(6)
Do n ∈ ℕ mà 2n + 1 là số lẻ
⇒ 2n + 1 ∈{1; 3}
⇒ n ∈ {0; 1}
Vậy n ∈ {0; 1}.
Lời giải:
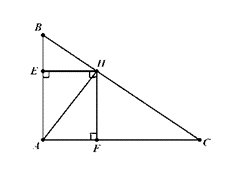
Áp dụng hệ thức lượng trong các tam giác vuông ABC, AHB, AHC ta có:
Lại có: BH2 = AB.BE ⇒ BE =
CH2 = AC.CF ⇒ CF =
Khi đó: (Vì AH2 = BH.CH)
Vậy BC.BE.CF = .
c) OE là tia phân giác của góc xOy.
Lời giải:
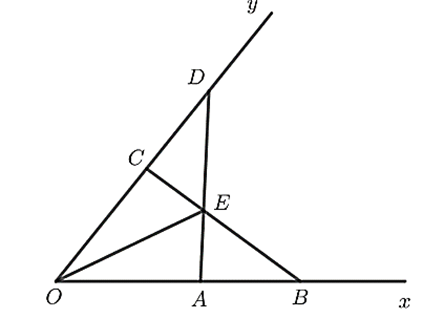
a) Xét tam giác OAD và tam giác OCB có:
OA = OC (giả thiết)
chung
OD = OB
Do đó: ∆OAD = ∆OCB (c.g.c)
Suy ra: AD = BC
b) Do OA = PC, OB = OD nên OB – OA = OD – OC hay AB = CD
Do ∆OAD = ∆OCB (c.g.c) nên
là góc ngoài tại định C của tam giác OBC nên
là góc ngoài tại định C của tam giác OAD nên
Từ (1) và (2) suy ra:
Xét tam giác EAB và ECD có:
AB = CD
Do đó: ∆EAB = ∆ECD (g.c.g)
c) Do ∆EAB = ∆ECD (g.c.g) nên BE = DE
Xét tam giác ODE và OBE có:
OD = OB
OE chung
BE = DE
Do đó: ∆ODE = ∆OBE (c.c.c)
Suy ra:
Vậy OE là tia phân giác của .
a, Chứng minh tam giác BCK đồng dạng tam giác DCH.
b, Chứng minh tam giác CKH đồng dạng tam giác BCA.
d, Tính diện tích của tứ giác AKCH nếu , AB = 4cm, AC = 5cm.
Lời giải:
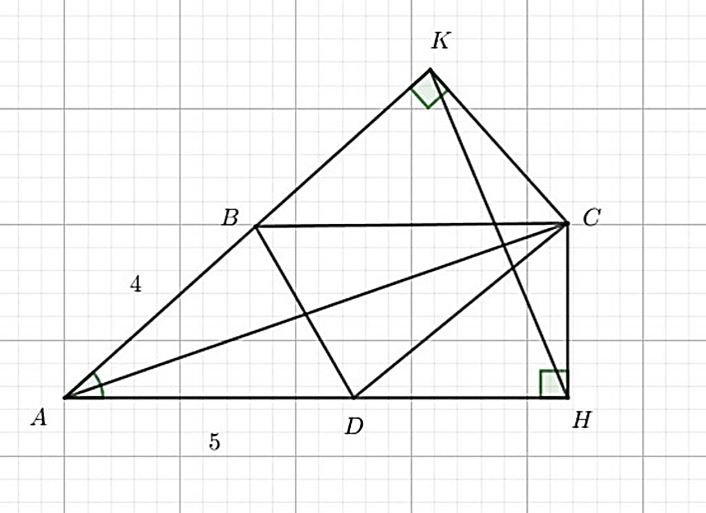
a) Ta có: (2 góc ở vị trí so le trong)
Mà (2 góc đồng vị)
Suy ra:
Xét tam giác BCK và DCH có
⇒ ∆BCK ~ ∆DCH (g.g)
b) Tứ giác AKCH có:
Suy ra: AKCH nội tiếp đường tròn đường kính AC
Suy ra: (góc nội tiếp cùng chắn cung KC) (1)
Và (góc nội tiếp cùng chắn cung HC)
Mà (2 góc so le trong)
⇒ (2)
Từ (1) và (2) suy ra: tam giác CKH đồng dạng tam giác BCA (g.g)
c) Do ∆BCK ∽ ∆DCH (g.g) nên
∆CKH ∽ ∆BCA (g.g) nên
Từ (3):
Từ (4) và (5);
Mà (đồng vị)
Nên: hay HK = AC.sin
d)
DC = AB = 4
Tam giác DHC vuông có:
AH = AD + DH = 5 + 2 = 7
BC = AD = 5
AK = AB + BK =
Vậy SAKCH = SACH + SACK = .
Lời giải:
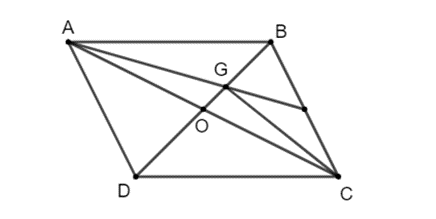
Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD.
Khi đó O là trung điểm của AC và BD.
Do đó BO là đường trung tuyến của tam giác ABC.
Vì G là trọng tâm của tam giác ABC nên G thuộc trung tuyến BO của tam giác ABC.
Theo tính chất trọng tâm ta có:
Mà nên
Hai vectơ cùng hướng và nên
Ta có:
Do ABCD là hình bình hành nên
Lời giải:
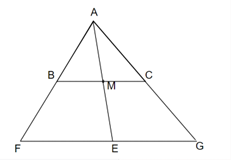
xét ΔBME và ΔCMA có:
BM = MC (giả thiết)
(đối đỉnh)
ME = MA
⇒ ΔBME = ΔCMA (c.g.c)
Suy ra: BE = AC và
Mà 2 góc ở vị trí so le trong nên BE // AC
Suy ra: (2 góc đồng vị)
Xét ΔFBE và ΔBAC có:
FB = BA
BE = AC
⇒ ΔFBE = ΔBAC (c.g.c)
⇒
Mà 2 góc này ở vị trí đồng vị nên BC // EF (1)
chứng minh tương tự ta có ΔEMC = ΔAMB(c.g.c)
⇒ AB = EC (2 cạnh tương ứng) và
chứng minh tương tự ta có ΔACB = ΔCGE (c.g.c)
Suy ra: mà 2 góc này ở vị trí đồng vị nên BC // EG (2)
Từ (1) và (2) ta có FE // BC; EG // BC mà theo tiên đề Ơ-clit thì qua điểm E nằm ngoài đường thẳng BC chỉ có 1 đường thẳng song song vói đường thẳng đó
nên FE trùng EG hay F; E; G thẳng hàng.
Lời giải:
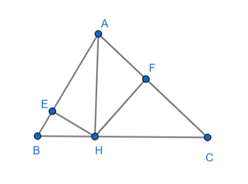
2SAHE = AE.EH
2SBHE = BE.EH
Ta có: 2SAHE + 2SBHE = AE.EH + BE.EH = EH(AE + BE) = EH.AB
⇔ 2.4 + 2.1 = EH.AB
Hay EH.AB = 10
Mà EH = 2cm nên AB = 10 : 2 = 5(cm)
Đề bài. Cho ∆ ABC nhọn, đường cao AH. Kẻ HE ⊥ AB (E ∈ AB), HF ⊥ AC (F ∈ AC).
a) Chứng minh: ∆AEH ∽ ∆AHB. Từ đó suy ra AH2 = AE.AB.
Lời giải:
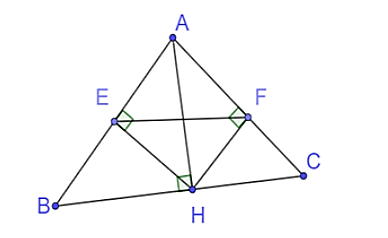
a) Vì AH là đường cao (giả thiết)
AH ⊥ BC
∆AHB vuông tại H
Lại có HE ⊥ AB (giả thiết)
∆AEH vuông tại E
Do đó
Xét ∆AEH và ∆AHB có:
(chứng minh trên)
chung
Do đó ∆AEH ∽ ∆ AHB (g.g)
⇒ (tỉ số đồng dạng)
Suy ra: AH2 = AE.AB. (1)
b) Vì AH ⊥ BC (chứng minh câu a) nên
Vì HF ⊥ AC (giả thiết) nên
Xét ∆AFH và ∆AHC có
chung
Do đó ∆AFH ᔕ ∆AHC (g.g)
⇒ (tỉ số đồng dạng)
Suy ra: AH2 = AF.AC. (2)
Từ (1) và (2) suy ra: AE. AB = AF.AC
c) Theo b có: AE. AB = AF.AC nên:
Xét ∆AEF và ∆ACB có
chung
Do đó ∆AEF ᔕ ∆ACB (c.g.c)
⇒
Theo tính chất dãy tỉ số bằng nhau ta có:
(vì chu vi ∆AEF và ∆ACB lần lượt là 20 cm và 30 cm)
(Do SABC – SAEF = 25 cm2)
Vậy SAEF = 5.4 = 20 (cm2)
SABC = 20 + 25 = 45 (cm2).
Đề bài. Cho tam giác ABC vuông tại A, đường cao AH kẻ HE, HF lần lượt vuông góc với AB, AC
Lời giải:
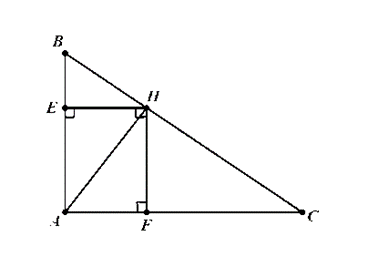
Áp dụng hệ thức lượng trong các tam giác vuông ABC, AHB, AHC ta có:
AB.AC = BC.AH ⇒
AB2 = BH.BC
AC2 = CH.BC
Xét: (đpcm)
b) Từ AB2 = BH.BC ⇒ AB4 = BH2 . BC2 = AB.BE.BC2 (vì BH2 = AB.BE)
Từ AC2 = CH.BC ⇒ AC4 = CH2 . BC2 = AC.CF.BC2 ( vì CH2 = AC.CF)
Xét:
Suy ra: .
Lời giải:
Một cung lượng giác trên đường tròn định hướng có độ dài bằng bán kính thì có số đo 1 rad hoặc -1 rad.
Do đó, một cung lượng giác trên đường tròn định hướng có độ dài bằng nửa bán kính thì số đo theo rađian của cung đó là hoặc .
Lời giải:
Ta có sơ đồ:
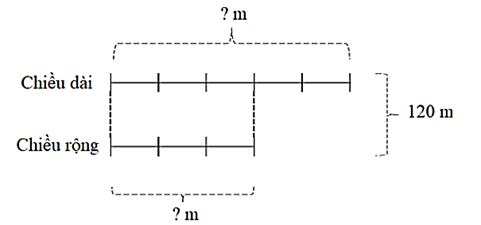
Theo sơ đồ, tổng số phần bằng nhau là:
3 + 5 = 8 (phần)
Chiều rộng sân trường đó là:
120 : (8 . 3) = 45 (m)
Chiều dài sân trường đó là:
120 - 45 = 75 (m)
Diện tích sân trường đó là:
75 . 45 = 3375 (m2)
Đổi 3375 m2 = 0,3375 ha
Đáp số: 3375 m2; 0,3375 ha.
Đề bài. Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:
Lời giải:
Vậy .
Đề bài. Cho A = 2 + 22 + 23 + … + 248. Chứng minh rằng A chia hết cho 2, 3, 7.
Lời giải:
* Xét A = 2 + 22 + 23 + … + 248
Ta thấy: 2 ⋮ 2; 22 ⋮ 2, … , 248 ⋮ 2
Nên: 2 + 22 + 23 + … + 248 ⋮ 2 hay A chia hết cho 2.
* Xét A = 2 + 22 + 23 + … + 248
A = (2 + 22) + (23 + 24) + … + (247 + 248)
A = 2(1 + 2) + 23(1 + 2) + … + 247(1 + 2)
A = 2.3+ 23.3 + … + 247.3
A = 3(2 + 23 + … + 247)
Vì 3 ⋮ 3 nên 3(2 + 23 + … + 247) ⋮ 3
Vậy A chia hết cho 3.
* Xét A = 2 + 22 + 23 + … + 248
A = (2 + 22 + 23) + (24 + 25 + 26) + … + (246 + 247 + 248)
A = 2(1 + 2 + 22) + 24(1 + 2 + 22) + … + 246(1 + 2 + 22)
A = (1 + 2 + 22)(2 + 24 + … + 246)
A = 7.(2 + 24 + … + 246)
Vì 7 ⋮ 7 nên 7.(2 + 24 + … + 246)⋮ 7
Vậy A chia hết cho 7.
Đề bài. Cho A = 33.22.19. Hỏi các số 27; 4; 16; 19; 24 có là ước của A không?
Lời giải:
A = 33.22.19 = 27.4.19
Vì 27 ⋮ 27 nên 27.4.19 ⋮ 27
4 ⋮ 4 nên 27.4.19 ⋮ 4
19 ⋮ 19 nên 27.4.19 ⋮ 19
Vậy các số là ước của A là 27;4;19.
Đề bài. Cho A = 5 + 52 + … + 52022. Tìm x để 4A + 5 = 5x.
Lời giải:
A = 5 + 52 + … + 52022
⇒ 5A = 52 + … + 52023
⇒ 5A – A = (52 + … + 52023) – (5 + 52 + … + 52022)
4A = 52023 – 5
Khi đó: 4A + 5 = 52023 = 5x
Vậy x = 202.
Đề bài. Tính biết a là nghiệm dương của phương trình x2 + x – 1 = 0.
Lời giải:
Xét phương trình: x2 + x – 1 = 0
⇔
⇔
⇔
⇔
Vì a dương nên
Khi đó:
Vậy C = 5.
Lời giải:
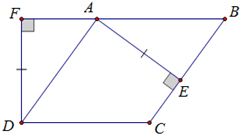
Ta có: (vì AD // BC)
Xét tam giác AFD và tam giác BEA có:
DF = AE (giả thiết)
Suy ra: ∆AFD = ∆BEA (g.c.g)
⇒ AD = AB (2 cạnh tương ứng)
Xét hình bình hành ABCD có AD = AB nên ABCD là hình thoi.
Đề bài. Cho a + b + c = 0 và a2 + b2 + c2 = 1. Tính a4 + b4 + c4.
Lời giải:
Ta có a + b + c = 0.
⇔ (a + b + c)2 = 0.
⇔ a2 + b2 + c2 + 2(ab + bc + ca) = 0.
⇔ 2 + 2(ab + bc + ca) = 0.
⇔ 2(ab + bc + ca) = –2.
⇔ ab + bc + ca = –1.
Ta có ab + bc + ca = –1.
Suy ra (ab + bc + ca)2 = 1.
⇔ a2b2 + b2c2 + c2a2 + 2(ab2c + bc2a + a2bc) = 1.
⇔ a2b2 + b2c2 + c2a2 + 2abc(b + c + a) = 1.
⇔ a2b2 + b2c2 + c2a2 + 2abc.0 = 1.
⇔ a2b2 + b2c2 + c2a2 = 1.
Đặt P = a4 + b4 + c4
= (a2 + b2 + c2)2 – 2(a2b2 + b2c2 + c2a2)
= 22 – 2.1 = 2.
Vậy a4 + b4 + c4 = 2.
Đề bài. Tìm GTLN của a2 + b2 + c2 biết a, b, c thỏa mãn 1 ≤ a, b, c ≤ 2 và a + b + c = 6.
Lời giải:
Ta có: (a – 1)(a – 2) ≤ 0 ⇒ a2 ≤ 3a – 2
Tương tự: (b – 1)(b – 2) ≤ 0 ⇒ b2 ≤ 3b – 2
(c – 1)(c – 2) ≤ 0 ⇒ c2 ≤ 3c – 2
Cộng 3 vế ta có:
a2 + b2 + c2 ≤ 3(a + b + c) – 6 = 3.6 – 6 = 12
Vậy GTLN của a2 + b2 + c2 là 12 khi a = b = c = 2.
Đề bài. Cho a,b là các số thực dương thoả mãn điều kiện . Tìm min của .
Lời giải:
Ta có:
Do đó:
Vậy P min = 2 khi a = b = 1.
Lời giải:
Vì a chia 5 dư 1 nên đặt a = 5x + 1 (x ∈ ℕ); b chia 5 dư 4 nên đặt b = 5y + 4(y ∈ ℕ).
Ta có a.b + 1 = (5x + 1)(5y + 4) + 1 = 25xy + 20x + 5y + 5.
ab + 1 = 5(5xy + 4x + y + 1) ⋮ 5 (đpcm).
Lời giải:
AB =
AC =
BC =
Chu vi tam giác ABC = AB + AC + BC =
Phương trình đường thẳng BC là: 5(x + 1) + 1(y + 3) = 0 hay 5x + y + 8 = 0
d(A;BC) =
SABC = .
Lời giải:
Ta có: 160 + a2 = 5 + b2
⇔ b2 – a2 = 155
⇔ (b – a)(b + a) = 155 (1)
Lại có: b - a, b + a là các số nguyên, b – a < b + a (2).
Từ (1), (2) ta có bảng:
|
b - a |
1 |
5 |
|
b + a |
155 |
31 |
|
a |
77 |
13 |
Với a = 77 thì 320 + a2 = 5 + c2, suy ra c không phải số nguyên
Với a = 13 thì 320 + a2 = 5 + c2 = 320 + 132 = 489
⇒ c2 = 484 ⇒ c = 22.
Vậy a = 13.
Đề bài. Cho 2 số thực dương a, b thỏa mãn a2 + 2ab + 2b2 – 2b = 8.
Chứng minh rằng 0 < a + b ≤ 3.
Lời giải:
Ta có: a, b > 0 nên a + b > 0
a2 + 2ab + 2b2 – 2b = 8
⇔ (a + b)2 = 8 – (b2 – 2b)
⇔ (a + b)2 = 9 – (b – 1)2
Vì (b – 1)2 ≥ 0 với mọi b nên 9 – (b – 1)2 ≤ 9
Suy ra: (a + b)2 ≤ 9
⇒ -3 ≤ a + b ≤ 3
Mà a + b > 0 nên 0 < a + b ≤ 3
Vậy 0 < a + b ≤ 3.
Đề bài. Cho a, b, c, d thỏa mãn a2 + b2 = 25; c2 + d2 = 16; ac + bd ≥ 20. Tìm max a + d.
Lời giải:
Đặt
Từ ac + bd ≥ 20 ta có: 20cosα.cosβ + 20sinα.sinβ ≥ 20
⇔ 20cos(α – β) ≥ 20
Vậy cos(α – β) = 1 ⇔ α – β = k2π (k ∈ ℤ) ⇔ α = β + k2π
Suy ra:
Ta có: a + d = 5cosα + 4sinβ = 5cosα + 4sinα ≤
Dấu “=” khi:
Vậy max a + d = khi .
Lời giải:
Xét: ab + bc + ca =
Suy ra: a2b2 + b2c2 + c2a2 = (ab + bc + ca)2 – 2abc(a + b + c) = (-10)2 – 2.11.3 = 34
a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca) = 3.(29 + 10) = 117
Suy ra: a3 + b3 + c3 = 150
Xét a5 + b5 + c5 = (a3 + b3 + c3)(a2 + b2 + c2) – [( a2b2 + b2c2 + c2a2)(a + b + c) – abc(ab + ac + bc) = 150.29 – [(34.3 – 11.(-10)] = 4138.
Vậy a5 + b5 + c5 = 4138.
Đề bài. Cho a, b >0 thỏa mãn a + b ≤ 1. Tìm GTNN của .
Lời giải:
Áp dụng bất đẳng thức Cosi ta có:
Mặt khác:
Suy ra:
Suy ra:
Vậy
Dấu “=” xảy ra khi: .
Đề bài. Cho . Chứng minh rằng .
Lời giải:
Nhân hai vế của với a + b + c ta được:
⇔
⇔ .
Lời giải:
Ta có:
a2 + 3a = b2 + 3b
⇔ (a2 – b2) + (3a – 3b) = 0
⇔ (a – b)(a +b + 3) = 0
Vì a và b phân biệt nên a – b ≠ 0
Suy ra: a + b + 3 = 0 hay a + b = -3
Suy ra: (a + b)2 = 9
⇔ a2 + 2ab + b2 = 9 (1)
Mà a2 + 3a = b2 + 3b = 2
Suy ra: a2 + b2 + 3a + 3b = 2 + 2 = 4
a2 + b2 = 4 – 3(a + b) = 4 – 3.(-3) = 13 (2)
Từ (1) và (2) suy ra: 2ab = -4 hay ab = -2 (2)
Lấy (2) + (3): a2 - ab + b2 = 15
Do đó: a3 + b3 = (a + b)(a2 – ab + b2) = 15.(-3) = -45.
Đề bài. Cho hai tập hợp A = (-1;2] và B = {x ∈ R| mx ≥ 1} (với m là tham số thực). Xác định tất cả giá trị của tham số m để A ∩ B = ∅.
Lời giải:
* Xét m = 0 thì B = ∅ ⇒ A ∩ B = ∅ nên m = 0 thỏa mãn (1)
* Xét m < 0 ⇒ ⇒ A ∩ B = ∅ khi và chỉ khi:
Hay:
Kết hợp với điều kiện m < 0 suy ra: -1 ≤ m < 0 (2)
* Xét m > 0 ⇒ ⇒ A ∩ B = ∅ khi và chỉ khi:
Hay: (3)
Từ (1), (2) và (3): Kết luận: A ∩ B = ∅ khi .
Đề bài. Cho A = 3 + 32 + 33 + … + 399 + 3100. Hỏi 2A + 3 có phải là số chính phương không?
Lời giải:
A = 3 + 32 + 33 + … + 399 + 3100
3A = 32 + 33 + … + 3100 + 3101
3A – A = (32 + 33 + … + 3100 + 3101) – (3 + 32 + 33 + … + 399 + 3100)
2A = 3101 – 3
2A + 3 = 3101
Mà 3101 không phải là số chính phương
Vậy 2A + 3 không phải là số chính phương.
Đề bài. Cho A = [1;2], B = [m; m + 2]. Tìm m để B là tập con của của A.
Lời giải:
Ta có: B ⊂ A thì: 1 ≤ m ≤ m+ 2 ≤ 2
⇔ ⇔ (vô lí).
Vậy không có giá trị nào của m thỏa mãn yêu cầu bài toán.
Đề bài. Cho A = (2m - 1; 2m + 3) và B = (-1; 1).
Xác định m để B là tập con A và A ∩ B = ∅.
Lời giải:
Để A ∩ B = ∅ thì:
Vậy m ≥ 1 hoặc m ≤-2 thì thỏa mãn yêu cầu bài toán.