Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 61)

Câu 1: Hình trụ có bán kính đáy bằng a, chu vi của thiết diện qua trục bằng 10a. Tính thể tích của khối trụ đã cho.

Lời giải:

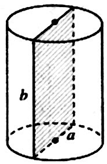
Thiết diện qua trục là 1 hình chữ nhật.

Giả sử chiều cao của hình trụ là b.

Theo đề ta có:

2(2a + b) =10a

⇒ b = 3a

Thể tích khối trụ là:

$V=S.h=\pi .a^2.3a=3\pi a^3$

Vậy thể tích của khối trụ đã cho là $3\pi a^3$.

Câu 2: Giải phương trình: sin²x + 2sinx – 3 = 0.

Lời giải:

sin²x + 2sinx – 3 = 0

⇔ sin²x – sinx + 3sinx – 3 = 0

⇔ (sinx – 1)(sinx + 3) = 0

Vì –1 ≤ sinx ≤ 1 nên sinx + 3 ≠ 0

Do đó sinx – 1 = 0

⇔ sinx = 1

$\iff x=\frac{\pi }{2}+k2\pi (k\in \mathbb{Z})$

Vậy $x=\frac{\pi }{2}+k2\pi (k\in \mathbb{Z})$.

Câu 3: Có 6 quả cầu xanh đánh số từ 1 đến 6, 5 quả cầu đỏ đánh số từ 1 đến 5 và 7 quả màu vàng đánh số từ 1 đến 7. Hỏi có bao nhiêu cách lấy ra 3 quả cầu vừa khác màu vừa khác số?

Lời giải:

Để lấy ra ba quả cầu vừa khác màu vừa khác số ta phải thực hiện qua ba giai đoạn:

• Chọn một quả cầu đỏ.

• Chọn một quả cầu xanh.

• Chọn một quả cầu vàng.

• Chọn quả cầu đỏ có 5 cách chọn.

• Chọn quả cầu xanh có 5 cách chọn (trừ quả cầu được đánh số trùng với quả cầu đỏ).

• Chọn quả cầu vàng có 5 cách chọn (trừ hai quả cầu được đánh số trùng với quả cầu đỏ và quả cầu xanh).

Theo quy tắc nhân ta được 5. 5. 5 = 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số.

Vậy có 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số.

Câu 4: Gọi S là tập hợp tất cả các số tự nhiên gồm 5 chữ số đôi một khác nhau được lập từ các chữ số 5, 6, 7, 8, 9. Tính tổng tất cả các số thuộc tập S.

Lời giải:

Số phần tử của tập S là 5! = 120 (số).

Mỗi số 5, 6, 7, 8, 9 có vai trò như nhau và xuất hiện ở hàng đơn vị số lần là:

4! = 24 (lần)

Tổng các chữ số xuất hiện ở hàng đơn vị là:

4! . (5 + 6 + 7 + 8 + 9) = 840 (chữ số)

Tương tự với các chữ số hàng chục, hàng tram, hàng nghìn và hàng chục nghìn.

Tổng tất cả các số thuộc tập S là:

840 . (10⁴ + 10³ + 10² + 10 + 1) = 9 333 240 (số)

Vậy tổng tất cả các số thuộc tập S là 9 333 240 số.

Câu 5: Tìm giá trị lớn nhất của hàm số: y = 2sinx – 3cos2x + 1.

Lời giải:

y = 2sinx – 3cos2x + 1 = 2sinx – 3(1 – 2sin²x) + 1 = 6sin²x + 2sinx – 2

$$\begin{gathered} y=6\left({\sin }^{2}x+2\cdot \frac{1}{6}\sin x+\frac{1}{36}-\frac{1}{36}-\frac{2}{6}\right) \\ y=6{\left(\sin x+\frac{1}{6}\right)}^2-\frac{13}{6} \end{gathered}$$

Hàm số y đạt giá trị lớn nhất khi sinx = 1 khi và chỉ khi y = 6.

Vậy giá trị lớn nhất của y = 6.

Câu 6: Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng toạ độ thoả mãn điều kiện |z − i| = 1.

Lời giải:

Giả sử ta có số phức z = a + bi.

Thay vào |z − i| = 1 ta có:

|a + bi − i| = 1 ⇔ |a + (b − 1)i| = 1

⇔ a² + (b − 1)² = 1.

Vậy tập hợp các điểm biểu diễn số phức z trên mặt phẳng toạ độ thoả mãn điều kiện |z − i| = 1 là đường tròn tâm I(0;1) và bán kính R = 1.

Câu 7: Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng toạ độ thoả mãn điều kiện z² là một số ảo.

Lời giải:

Giả sử M(z) = (a;b) $(a;b\in ℝ)$

⇒ z = a + bi

⇒ z² = a² – b² + 2abi.

Khi đó z² là một số ảo ⇔ a² – b² = 0 ⇔ a = ± b

⇒ M(z) = (± b; b).

Vậy tập hợp các điểm biểu diễn số phức z trên mặt phẳng toạ độ thoả mãn điều kiện z² là số ảo là đường thẳng y = x và y = − x (trừ gốc tọa độ O).

Câu 8: Hàm số y = x³ − 3x + 2 đồng biến trên khoảng nào?

Lời giải:

TXĐ: $D=ℝ$ 

Ta có: y′ = 3x² – 3

Cho y′ ≥ 0

⇔ 3x² − 3 ≥ 0

⇔ x ∈ (−∞; −1] ∪ [1; +∞).

Vậy hàm số đồng biến trên (−∞; −1) và (1; +∞).

Câu 9: Hàm số y = x³ – 3x² + 2 nghịch biến trên khoảng nào?

Lời giải:

Ta có y’ =3x² – 6x = 0

Bảng biến thiên:

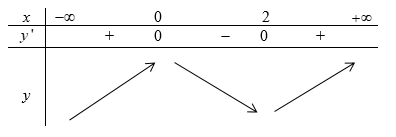
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên khoảng {0; 2}.

Câu 10: Khi cộng hai số thập phân, Minh đã viết nhầm dấu phẩy của số hạnh thứ nhất sang bên phải một chữ số nên được tổng là 159,8. Tìm hai số đó biết tổng đúng là 47,3.

Lời giải:

Khi viết dấu phẩy sang bên phải mổ hàng nghĩa là số đó đã gấp lên 10 lần . 

9 lần số hạng thứ nhất là:

159,8 − 47,3 = 112,5

Số hạng thứ nhất là:

112,5 : 9 = 12,5

Số hạng thứ hai là:

47,3 − 13,5 = 33,8

Vậy số hạng cần tìm là 33,8.

Câu 11: Khi cộng hai số thập phân, một học sinh viết nhầm dấu phẩy của một số hạng bên phải một hàng, do đó được tổng là 49,1. Em hãy tìm hai số đã cho, biết rằng tổng đúng là 27,95.

Lời giải:

Khi viết nhầm như vậy thì số hạng đó tăng thêm 10 lần.

Vậy tổng sẽ tăng lên một lượng bằng 9 lần số hạng đó.

 Lượng tăng là:

49,1 − 27,95 = 21,15

Vậy số hạng đó là:

21,15 : 9 = 2,35

Còn số hạng kia là:

27,95 − 2,35 = 25,6

Đáp số : 2,35 và 25,6

Câu 12: Một đề trắc nghiệm có 50 câu hỏi gồm 20 câu mức độ nhận biết, 20 câu mức độ vận dụng và 10 câu mức độ vận dụng cao. Xác suất để bạn An làm hết 20 câu mức độ nhận biết là 0,9; 20 câu mức độ vận dụng là 0,8 và 10 câu mức độ vận dụng cao là 0,6. Xác suất để bạn An làm trọn vẹn 50 câu là?

Lời giải:

Gọi A là biến cố “bạn An làm trọn vẹn 50 câu”

• A₁ là biến cố “bạn An làm hết 20 câu nhận biết”

• A₂ là biến cố“ bạn An làm hết 20 câu vận dụng”

• A₃ là biến cố “bạn An làm hết 10 câu vận dụng cao”

Khi đó: A = A₁A₂A₃. Vì các biến cố A₁; A₂; A₃ là độc lập nhau nên theo quy tắc nhân xác suất ta có:

P(A) = P(A₁) . P(A₂) . P(A₃) = 0,9 . 0,8 . 0,6 = 0,432.

Vậy xác suất để bạn An làm trọn vẹn 50 câu là 0,432.

Câu 13: Cho đường thẳng (d): y = x – 1. Tính khoảng cách từ gốc tọa độ đến đường thẳng d.

Lời giải:

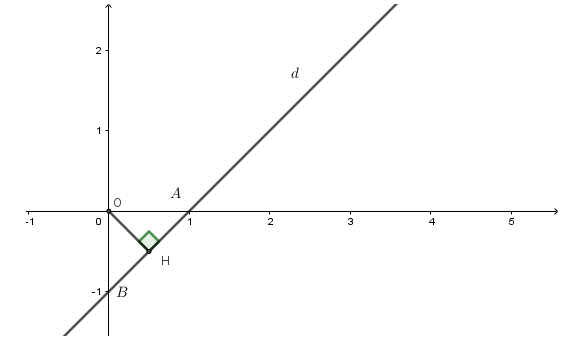
Ta có:

• d ∩ Ox tại A(1; 0) nên OA = 1

• d ∩ Oy tại B(0; −1) nên OB =1

Ta có: OA ⊥ OB

Gọi H là hình chiếu của O trên đường thẳng AB

Áp dụng hệ thức lượng trong tam giác vuông ta có:

$$\begin{gathered} \frac{1}{O{H}^2}=\frac{1}{O{A}^2}+\frac{1}{O{B}^2}=2 \\ \Rightarrow OH=\frac{\sqrt{2}}{2} \end{gathered}$$

Vậy khoảng cách từ gốc tọa độ đến đường thẳng d là $\frac{\sqrt{2}}{2}$.

Câu 14: Cho hàm số y = sinx – 3cosx. Tính vi phân của hàm số.

Lời giải:

Ta có: dy = y’dx = (sinx – 3cosx)’dx = (cosx + 3sinx)dx

Vậy vi phân của hàm số đã cho là (cosx + 3sinx)dx.

Câu 15: Chú Nam gửi vào ngân hàng 10 triệu đồng với lãi đơn 5%/năm thì sau 5 năm số tiền chú Nam nhận được cả vốn lẫn lãi là bao nhiêu?

Lời giải:

Số tiền cả gốc lẫn lãi chú Nam nhận được sau 5 năm là:

S₅ = 10.(1 + 5.0,05) = 12,5 (triệu đồng).

Đáp số: 12,5 triệu đồng.

Câu 16: Chị Hằng gửi ngân hàng 3 350 000 đồng, theo phương thức lãi đơn, với lãi suất 0,4% trên nửa năm. Hỏi ít nhất bao lâu chị rút được cả vốn lẫn lãi là 4 020 000 đồng?

Lời giải:

Gọi n là số chu kỳ gửi ngân hàng, áp dụng công thức lãi đơn ta có:

4 020 000 = 3 350 000(1 + n.0,04)

4 020 000 = 3 350 000 + 134 000.n

670 000 = 134 000.n

Suy ra, n = 5 (chu kỳ)

Mà nửa năm = 6 tháng

Thời gian ít nhất chị rút được cả vốn lẫn lãi là 4 020 000 đồng là:

 5.6 = 30 (tháng)

Đáp số: 30 tháng

Câu 17: Chứng minh đồ thị hàm số y = 2x² đi qua điểm A(–1; 2)

Lời giải:

Thay x = −1 vào y = 2x², ta được:

y = 2.(−1)² = 2

⇒ Đồ thị hàm số y = 2x² đi qua điểm (−1;2).

Vậy đồ thị hàm số y = 2x² đi qua điểm (−1;2).

Câu 18: Điểm N(1; 4) có thuộc đồ thị hàm số y = –2x không?

Lời giải:

Thay toạ độ điểm N(1; 4) vào đồ thị hàm số y = –2x ta có:

y = –2x = –2.1 = –2 ≠ 4

Vậy điểm N(1; 4) không thuộc đồ thị hàm số y = –2x.

Câu 19: Với sự phát triển của khoa học kỹ thuật hiện nay, người ta tạo ra nhiều mẫu xe lăn đẹp và tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn cho người khuyết tật với số vốn ban đầu là 500 triệu đồng. Chi phí sản để sản xuất ra một chiếc xe lăn là 2 500 000 đồng. Gía bán ra mỗi chiếc là 3 000 000 đồng. Viết hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn (gồm vốn ban đầu và chi phí sản xuất) và hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn.

Lời giải:

Tổng chi phí vốn cố định và vốn sản xuất ra x chiếc xe lăn (đơn vị triệu đồng): y = 500 + 2,5x.

Hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn là: y = 3x.

Vậy hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn (gồm vốn ban đầu và chi phí sản xuất) là y = 500 + 2,5x và hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn là y = 3x.

Câu 20: Bác Kim gửi một số tiền vào ngân hàng với lãi suất là 7% và kì hạn là một năm. Sau một năm bác Kim tới ngân hàng rút cả vốn lẫn lãi được 128 400 000 đồng. Hỏi lúc đầu bác Kim gửi vào ngân hàng bao nhiêu tiền?

Lời giải:

Gọi số tiền bác Kim gửi vào ngân hàng là x (đồng) ($x\in {\mathbb{N}}^{*}$)

Số tiền lãi sau một năm là:

x.7% = 0,07x (đồng)

Sau một năm bác tới ngân hàng rút là 128 400 000 nên ta có phương trình là:

x + 0,07x = 128 400 000

⇔1,07x = 128 400 000

⇔ x = 120 000 000 (TM)

Đáp số: 120 000 000 đồng.

Câu 21: Bà Mai vay ngân hàng 200 triệu trong thời gian 2 năm để mở một cửa hàng chuyên sản xuất và bán quà lưu niệm. Theo hợp đồng vay vốn, lãi suất vay trong một năm là 10%. Sau 1 năm, tiền lãi của năm đầu sẽ được cộng vào vốn của năm sau. Hỏi sau 2 năm, Bà Mai phải trả ngân hàng bao nhiêu tiền?

Lời giải:

Số tiền lãi bà Mai phải trả năm đầu là:

200. 10 : 100 = 20 (triệu đồng)

Số tiền bà phải trả cả gốc lẫn lãi năm đầu là:

200 + 20 = 220 (triệu đồng)

Số tiền lãi năm 2 bà Mai phải trả là:

220. 10 : 100 = 22 (triệu đồng)

Số tiền bà Mai phải trả trong 2 năm là:

220 + 22 = 242 (triệu đồng)

Đáp số: 242 triệu đồng.

Câu 22: Số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang là?

Lời giải:

Vì có 10 ghế nên bạn thứ nhất có 10 cách xếp.

• Bạn thứ hai có 9 cách xếp.

• Bạn thứ ba có 8 cách xếp.

• Bạn thứ tư có 7 cách xếp.

• Bạn thứ năm có 6 cách xếp.

• Bạn thứ sáu có 5 cách xếp.

Như vậy có: 10 . 9 . 8 . 7 . 6 . 5 = ${{\rm A}}_{10}^6$ (cách xếp).

Vậy có ${{\rm A}}_{10}^6$ cách xếp.

Câu 23: Khai triển đa thức P(x) = (2x – 1)¹⁰⁰⁰ ta được P(x) = a₁₀₀₀ x¹⁰⁰⁰ + a₉₉₉ x⁹⁹⁹ + … + a₁x + a_0.

Lời giải:

Ta có

P(x) = a₁₀₀₀ x¹⁰⁰⁰ + a₉₉₉ x⁹⁹⁹ + … + a₁x + a₀

Cho x = 1 ta được

P(1) = a₁₀₀₀ + a₉₉₉ + … + a₁ + a₀

Mặt khác

P(x) = (2x – 1)¹⁰⁰⁰

Do đó P(1) = (2 . 1 – 1)¹⁰⁰⁰ = 1

Từ đó suy ra P(1) = a₁₀₀₀ + a₉₉₉ + … + a₁ + a₀ = 1

Do đó a₁₀₀₀ + a₉₉₉ + … + a₁ = 1 – a₀

Mà là số hàng không chứa x trong khai triển P(x) = (2x – 1)¹⁰⁰⁰

Nên $a_0=C_{1000}^{1000}{\left(2x\right)}^0{(-1)}^{1000}=1$.

Vậy a₁₀₀₀ + a₉₉₉ + … + a₁ = 0.

Câu 24: Tìm m để đường thẳng y = 2m – 1x + 3 song song với đường thẳng y = 5x – 1.

Lời giải:

Vì đường thẳng y = 2m – 1x + 3 song song với đường thẳng y = 5x – 1 nên ta có:

$\left\{\begin{array}{l}2m-1\ne 0\\ 2m-1=5\end{array}\right.\iff \left\{\begin{array}{l}m\ne \frac{1}{2}\\ m=3\left(TM\right)\end{array}\right.$

Vậy với m = 3 thì đường thẳng y = 2m – 1x + 3 song song với đường thẳng y = 5x – 1.

Câu 25: Cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số cắt đường thẳng (d’): y = 2x + 1 tại điểm có hoành độ bằng –2.

Lời giải:

Để đường thẳng (d) cắt đường thẳng (d’) thì 2k – 1 ≠ 2 hay $k\ne \frac{3}{2}$

Thay x = –2 vào hàm số y = 2x + 1

⇔ y = 2. (–2) + 1 = –3

Gọi A(–2; –3)

Do đường thẳng (d) và (d’) cắt nhau tại A nên:

–3 = (2k – 1)( –2) + 3 – k

⇔ –4k + 2 + 3 – k + 3 = 0

⇔ –5k + 8 = 0

$\iff k=\frac{-8}{5}$ (TMĐK)

Vậy giá trị k thỏa mãn là $k=\frac{-8}{5}$.

Câu 26: Cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số song song với đường thẳng (m):  y = 0,5x – 3.

Lời giải:

Để đường thẳng (d) // (m) thì:

$\left\{\begin{array}{c}2k-1=\mathrm{0,5}\\ 3-k\ne -3\end{array}\right.\iff \left\{\begin{array}{c}k=\frac{3}{4}\left(TM\right)\\ k\ne 6\end{array}\right.$

Vậy giá trị k thỏa mãn là $k=\frac{3}{4}$.

Câu 27: Sau khi giảm giá 20% thì giá của một quyển sách là 9 600 đồng. Hỏi lúc đầu gái của quyển sách là bao nhiêu tiền?

Lời giải:

Coi giá ban đầu là 100% thì giá sách sau khi giảm đi 20% là:

100% – 20% = 80%

Vậy lúc đầu giá của cuốn sách đó là:

9600 : 80 × 100 = 12 000 (đồng)

Đáp số: 12000 đồng

Câu 28: Tìm tập xác định D của hàm số: y = log₂ (x² + 5x − 6).

Lời giải:

Điều kiện xác định x² + 5x – 6 > 0

$\iff \left\{\begin{array}{l}x<-6\\ x>1\end{array}\right.$

⇒ (–∞; –6) È (1; +∞)

Câu 29: Tìm tập xác định D của hàm số y = log₂(x³ − 8)¹⁰⁰⁰.

Lời giải:

Điều kiện (x³ − 8)¹⁰⁰⁰ > 0 ⇔ x ≠ 2

Tập xác định D = R∖{2}

Câu 30: Xếp 4 bạn nam và 2 bạn nữ thành một hàng ngang. Xác xuất để 2 bạn nữ không ngồi cạnh nhau là?

Lời giải:

Xếp 4 bạn nam và 2 bạn nữ thành 1 hàng ngang

⇒ n(W) = 6! = 720.

Gọi A là biến cố: “ 2 bạn nữ không ngồi cạnh nhau”.

Xếp 4 bạn nam có 4! cách, khi đó sẽ tạo ra 5khaongr trống giữa 4 bạn nam, xếp 2 bạn nữ vào 2 trong 5 khoảng trống nay có $A_5^2$ cách.

$\Rightarrow n\left(A\right)=4!.A_5^2=480$.

Vậy $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{480}{720}=\frac{2}{3}$.

Câu 31: Xếp 5 nam và 2 nữ vào một bàn dài gồm 7 chỗ ngồi. Tính xác suất để 2 nữ không ngồi cạnh nhau.

Lời giải:

Xếp 7 bạn vào 7 vị trí có n(Ω) = 7! = 5 040 (cách)

Gọi A là biến cố 2 bạn nữ ngồi cạnh nhau.

Chọn 2 bạn từ 2 bạn nữ có 1 cách

Coi 2 bạn nữ đó là một ẩn, xếp 6 vào 6 vị trí có 6! cách

Xếp 2 bạn nữ đảo chỗ cho nhau có 2 cách

Do đó số cách xếp 2 bạn ngồi cạnh nhau là:

n(A) = 1.6!.2 = 1440 (cách)

Xác suất xếp 2 bạn nữ ngồi cạnh nhau là:

$P\left(A\right)=\frac{1440}{5040}=\frac{2}{7}$.

Xác suất xếp 2 bạn nữ không ngồi cạnh nhau là: $1-\frac{2}{7}=\frac{5}{7}$.

Câu 32: Trong mặt phẳng Oxy, cho điểm B (−3; 6). Tìm tọa độ điểm E sao cho B là ảnh của E qua phép quay tâm O góc quay (−90º).

Lời giải:

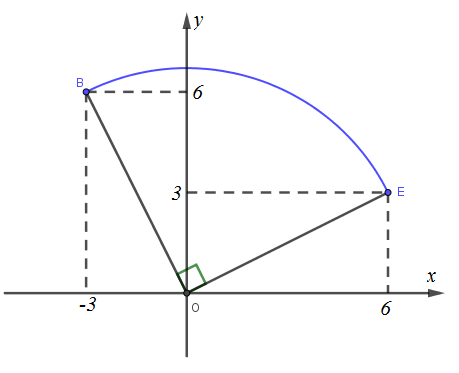
Tọa độ điểm E sao cho B là ảnh của E qua phép quay tâm O góc quay (−90º).

Khi đó, tọa độ cần tìm là E(3; 6).

Câu 33: Tìm x, biết: (x + 2)² – 9 = 0.

Lời giải:

(x + 2)² – 9 = 0

(x + 2)² = 9

x + 2 = 3 hoặc x + 2 = −3

x = 1 hoặc x = –5.

Vậy x ∈ {1; –5}.

Câu 34: Tìm x, biết: (x + 2)² – x² + 4 = 0.

Lời giải:

x + 2)² – x² + 4 = 0

⇔ 4x + 8 = 0

⇔ 4x = –8

⇔ x = –2

Vậy x = –2.

Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao điểm K của đường thẳng AM với (SBD).

Lời giải:

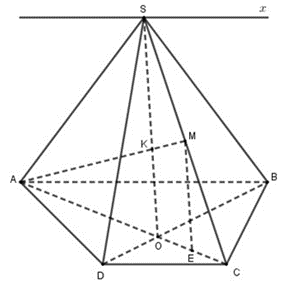
Ta có: AM ⊂ (SAC)

Dễ thấy S ∈ (SAC) ∩ (SBD)

Gọi O là giao điểm của AC và BD

Khi đó O ∈ AC⊂ (SAC),

O ∈ BD ⊂ (SBD)

Do đó O ∈ (SAC) ∩ (SBD)

⇒ SO = (SAC) ∩ (SBD)

Trong (SAC) gọi AM ∩ SO = {K} 

Ta có: K ∈ AM, K ∈ SO ⊂ (SBD) 

⇒ AM ∩ (SBD) = {K}.

Vậy giao điểm K của đường thẳng AM với (SBD) là giao điểm của AM và SO.

Câu 36: Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh giỏi Toán và Lý, 5 học sinh giỏi Hoá và Lý, 4 học sinh giỏi Toán và Hoá, 3 học sinh giỏi cà 3 môn. Hỏi số học sinh giỏi ít nhất 1 môn trong 3 môn là bao nhiêu em?

Lời giải:

Theo giả thiết đề bài cho, ta có biểu đồ Ven:

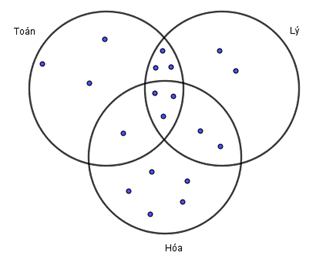
Dựa vào biểu đồ Ven, ta thấy:

Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: 

6 – 3 = 3 (em)

Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: 

4 – 3 = 1 (em)

Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là: 

5 – 3 = 2 (em)

Số học sinh chỉ giỏi một môn Toán là: 

10 – 3 – 3 – 1 = 3 (em)

Số học sinh chỉ giỏi một môn Lý là: 

10 – 3 – 3 – 2 = 2 (em)

Số học sinh chỉ giỏi một môn Hóa là: 

11 – 1 – 3 – 2 = 5 (em)

Số học sinh giỏi ít nhất một trong ba môn là:

3 + 2 + 5 + 1 + 2 + 3 + 3 =19 (em)

Đáp số: 19 em.

Câu 37: Có 40 học sinh giỏi, mỗi em giỏi ít nhất 1 môn. Có 22 em giỏi Văn, 25 em giỏi Toán, 20 em giỏi Anh. Có 8 em giỏi đúng hai môn Văn, Toán. Có 7 em giỏi đúng hai môn Toán, Anh. Có 6 em giỏi đúng hai môn Anh, Văn. Hỏi có bao nhiêu em giỏi cả ba môn Văn, Toán, Anh?

Lời giải:

Ta có sơ đồ Ven, ta có:

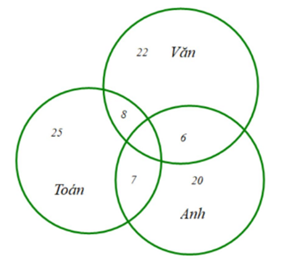
Số học sinh giỏi ít nhất hai môn là:

7 + 6 + 8 = 21 (em)

Số học sinh giỏi cả ba môn Toán, Văn, Anh là:

22 + 25 + 20 – 40 – 21 = 6 (em)

Đáp số: 6 em.

Câu 38: Trong mặt phẳng với hệ tọa độ Oxy, phép quay tâm I góc quay I(4; –3) biến đường thẳng d: x + y – 5 = 0 thành đường thẳng d' có phương trình là bao nhiêu?

Lời giải:

Lấy A(5; 0) thuộc d và B(0; 5) thuộc d

Phép quay Q_{(I; −180°)} là phép đối xứng tâm I

• Q_{(I; −180°)} (A) ® A’ nên A’(3; 6).

• Q_{(I; −180°)} (B) ® B’ nên B’(8; –11).

Khi đó $\frac{x-3}{8-3}=\frac{y+6}{-11+6}$

⇔ –5x – 5y – 15 = 0 ⇔ x + y + 3 = 0.

Vậy phương trình đường thẳng d’ là: x + y + 3 = 0.

Câu 39: Việt và Nam chơi cờ. Trong một ván cờ, xác suất Việt thắng Nam là 0,3 và Nam thắng Việt là 0,4. Hai bạn dừng chơi khi có người thắng, người thua. Tính xác suất để hai bạn dừng chơi sau 2 ván cờ.

Lời giải:

Xác suất 2 bạn hòa nhau là: 1 – 0,3 – 0,4 = 0,3.

Để hai bạn dừng chơi sau 2 ván cờ  thì ván 1 hòa, ván 2 không hòa.

Vậy xác suất để hai bạn dừng chơi sau 2 ván cờ là: 0,3 . 0,7 = 0,21.

Câu 40: Có bao nhiêu số tự nhiên có 5 chữ số trong đó các chữ số cách đều chữ số đứng giữa thì giống nhau?

Lời giải:

Gọi số cần tìm là $\overline{abcba}(a,b\in \mathbb{N},0<a\le \mathrm{9,}0\le b\le 9)$

• Có 9  cách chọn a (vì a khác 0)

• Có 10 cách chọn b.

• Có 10 cách chọn c.

Vậy có 9.10.10 = 900 (số).