Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 55)

Câu 1: Chứng minh nếu p và 8p² + 1 là hai số nguyên tố lẻ thì 8p² + 2p + 1 là số nguyên tố.

Lời giải:

Số tự nhiên p có một trong các dạng:

$3k\mathrm{,3}k+\mathrm{1,3}k+\mathrm{2,}$ với $k\in \mathbb{N}.$

• Nếu p = 3k mà p là số nguyên tố lẻ nên p = 3

Khi đó:

8p² + 1 = 8 . 3² + 1 = 73 là số nguyên tố lẻ;

8p² + 2p + 1= 8 . 3² + 2 . 3 + 1 = 79 là số nguyên tố.

• Nếu p = 3k + 1 thì 8p² + 1 = 8(3k + 1)² + 1 = 72k² + 48k + 9 ⋮ 3 là hợp số nên loại.

• Nếu p = 3k + 2 thì 8p² + 1 = 8(3k + 2)² + 1 = 72k² + 96k + 33 ⋮ 3 là hợp số nên loại.

Vậy minh nếu p và 8p² + 1 là hai số nguyên tố lẻ thì 8p² + 2p + 1 là số nguyên tố.

Câu 2: Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.

Lời giải:

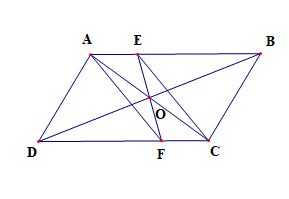
Vì ABCD là hình bình hành nên AB // CD, hay AE // CF

Mà AE = CF (giả thiết)

Suy ra AECF là hình bình hành

Do đó hai đường chéo AC và EF cắt nhau tại trung điểm của mỗi đường

Gọi O là giao điểm của AC và AF                           (1)

Vì ABCD là hình bình hành

Nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường

Mà O là trung điểm AC

Suy ra O là trung điểm của BD và AC                     (2)

Từ (1) và (2) suy ra ba đường thẳng AC, BD, EF đồng quy

Vậy ba đường thẳng AC, BD, EF đồng quy.

Câu 3: Phát biểu định lí về hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba.

Lời giải:

Định lí: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.

Câu 4: Cho đường thẳng d: y = 2x + 6. Giao điểm của d với trục tung là:

A. $P\left(0;\frac{1}{6}\right)$;

B. N(6; 0);

C. M(0; 6);

D. D(0; –6).

Lời giải:

Đáp án đúng là: C

Giao điểm của đường thẳng d và trục tung có hoành độ x = 0

Thay x = 0 vào y = 2x + 6 ta được

y = 2 . 0 + 6 = 6

Khi đó tọa độ giao điểm là M(0; 6)

Vậy ta chọn đáp án C.

Câu 5: Cho hàm số y = x³ – 3x² – 3x – 2 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục tung.

Lời giải:

Gọi A là giao điểm của đồ thị (C) và trục tung

Suy ra x_A = 0, y_A = 0³ – 3 . 0² – 3 . 0 – 2 = – 2

Do đó A(0; – 2)

Ta có: y’ = 3x² – 6x – 3

y’ (0) = – 3

Phương trình tiếp tuyến của (C) tại điểm A(0; – 2) là

y = y’(0)(x – 0) – 3 = – 3x – 2

Vậy phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục tung là y = – 3x – 2.

Câu 6: Một hình thang có đáy nhỏ là 4 cm , chiều cao là 5 cm, diện tích là 40 cm². Tính chiều dài đáy lớn.

Lời giải:

Diện tích hình thang là: $\text{S}=\frac{\left(a+b\right).h}{2}$

Suy ra $b=\frac{2\text{S}}{4}-a$

Đáy lớn hình thang là

40 . 2 : 5 – 4 = 12 (cm)

Vậy chiều dài đáy lớn là 12 cm.

Câu 7: Tổng của tất cả các số nguyên a mà –7 < a ≤ 7 là:

A. 7;

B. –7;

C. –1;

D. 0.

Lời giải:

Đáp án đúng là: A

Các số a thỏa mãn –7 < a ≤ 7 là –6, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, 7

Tổng là: (–6) + (–5) + (–4) + ... + 7

= (6 – 6) + (5 – 5) + (4 – 4) + (3 – 3) + (2 – 2) + (1 – 1) + 0 + 7

= 7

Vậy ta chọn đáp án A.

Câu 8: Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. $y=\frac{\sin x}{x}$;

B. y = tanx + x;

C. y = 10x² + 19;

D. y = – 9cotx.

Lời giải:

Đáp án đúng là: D

Xét hàm số y = – 9cotx

Tập xác định D = ℝ \ {kπ, k ∈ ℤ}

Với mọi x ∈ D, k ∈ ℤ ta có:

x – kπ ∈ D và x + kπ ∈ D

cot(x + kπ) = cotx

Suy ra y = – 9cotx là hàm số tuần hoàn

Vậy ta chọn đáp án D.

Câu 9: Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.

Lời giải:

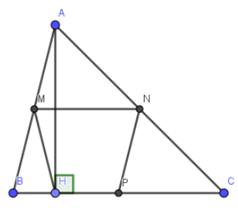
Xét tam giác ABC có M, N lần lượt là trung điểm của AB, AC.

Suy ra MN là đường trung bình.

Do đó MN // BC, hay MN // PH.

Suy ra tứ giác MNPH là hình thang

Xét tam giác ABH vuông tại H có HM là trung tuyến

Suy ra $HM=\frac{1}{2}AB$                              (1)

Xét tam giác ABC có P, N lần lượt là trung điểm của CB, AC

Suy ra PN là đường trung bình

Do đó $PN=\frac{1}{2}AB$                               (2)

Từ (1) và (2) suy ra HM = PN

Xét hình thang MNPH có PN = HM (chứng minh trên)

Suy ra MNPH là hình thang cân (dấu hiệu)

Vậy tứ giác MNPH là hình thang cân.

Câu 10: Một cấp số cộng gồm 5 số hạng. Hiệu số hạng đầu và số hạng cuối bằng 20. Tìm công sai d của cấp số cộng đã cho

A. d = –5;

B. d = 4;

C. d = –4;

D. d = 5.

Lời giải:

Đáp án đúng là: A

Gọi năm số hạng của cấp số cộng đã cho là: u₁; u₂; u₃; u₄; u₅

Theo đề bài ta có: 

u₁ – u₅ = 20

⇔ u₁ − (u₁ + 4d) = 20

⇔ d = −5

Vậy ta chọn đáp án A.

Câu 11: Phân tích đa thức thành nhân tử: x³ – 7x – 6.

Lời giải:

Ta có:

x³ – 7x – 6 = x³ + x² – x² – x – 6x – 6 

= (x³ + x²) – (x² + x) – (6x + 6)

= x²(x + 1) – x(x + 1) – 6(x + 1)

= (x + 1)(x² – x – 6)

= (x + 1)(x² + 2x – 3x – 6)

= (x + 1)[(x² + 2x) – (3x + 6)]

= (x + 1)[x(x + 2) – 3(x + 2)]

= (x + 1)(x + 2)(x – 3).

Câu 12: Cho A = [m; m + 1] và B = (–1; 3). Điều kiện để (A ∩ B) = ∅ là gì?

Lời giải:

Để (A ∩ B) = ∅ thì có thể xảy ra 2 trường hợp sau:

+) TH1: m + 1 ≤ – 1 ⇔ m ≤ – 2

Khi đó khoảng biểu diễn của A nằm bên trái B và không trùng điểm nào với đoạn biểu diễn B

+) TH2: m ≥ 3

Khi đó khoảng biểu diễn của A nằm bên phải B và không trùng điểm nào với đoạn biểu diễn B.

Câu 13: Một hộp đựng có 4 bi đỏ, 5 bi xanh và 7 bi vàng. Hỏi có bao nhiêu cách lấy được 3 viên bi trong đó chỉ có hai màu.

Lời giải:

Gọi A là biến cố “ ba viên bi lấy được chỉ có hai màu”

Ta có số phần tử của không gian mẫu là $C_{16}^3=560$

Số cách chọn được 3 viên bi chỉ có 1 màu là $C_4^3+C_5^3+C_7^3=49$

Số cách chọn được 3 viên bi có đủ 3 màu là $C_4^1+C_5^1+C_7^1=140$

Vậy xác xuất cần tìm là $P\left(A\right)=1-\frac{49+140}{560}=\frac{53}{80}$.

Câu 14: Tìm x, y, z thỏa mãn: x² + y² + 2z² + xy + 2yz + 2zx + x + y + 1 = 0.

Lời giải:

Ta có:

x² + y² + 2z² + xy + 2yz + 2zx + x + y + 1 = 0

⇔ 2(x² + y² + 2z² + xy + 2yz + 2zx + x + y + 1) = 0

⇔ 2x² + 2y² + 4z² + 2xy + 4yz + 4zx + 2x + 2y + 2 = 0

⇔ (x² + 2xy + y²) + 4z(x + y) + 4z² + (x² + 2x + 1) + (y² + 2y + 1) = 0

⇔ (x + y)² + 4z(x + y) + 4z² + (x + 1)² + (y + 1)² = 0

⇔ (x + y + 2z)² + (x + 1)² + (y + 1)² = 0

Vì (x + y + 2z)² ≥ 0 với mọi x, y, z

(x + 1)² ≥ 0 với mọi x

(y + 1)² ≥ 0 với mọi y

Nên (x + y + 2z)² + (x + 1)² + (y + 1)²  ≥ 0 với mọi x, y, z

Suy ra $\left\{\begin{array}{l}x+y+2\text{z}=0\\ x+1=0\\ y+1=0\end{array}\right.\iff \left\{\begin{array}{l}2\text{z}=-x-4\\ x=-1\\ y=-1\end{array}\right.\iff \left\{\begin{array}{l}\text{z}=1\\ x=-1\\ y=-1\end{array}\right.$

Vậy x = –1, y = –1, z = 1.

Câu 15: Tìm x: 4x² – 25 = 0.

Lời giải:

Ta có: 4x² – 25 = 0

⇔ (2x – 5)(2x + 5) = 0

$$\begin{gathered} \iff \left[\begin{array}{l}2\text{x}-5=0\\ 2\text{x}+5=0\end{array}\right. \\ \iff \left[\begin{array}{l}\text{x}=\frac{5}{2}\\ \text{x}=\frac{-5}{2}\end{array}\right. \end{gathered}$$

Vậy $\text{x}\in \left\{\frac{5}{2};-\frac{5}{2}\right\}$.

Câu 16: Chứng minh rằng 7 . 5²ⁿ + 12 . 6ⁿ chia hết cho 19.

Lời giải:

Ta có:

7 . 5²ⁿ + 12 . 6ⁿ

= 7 . 5²ⁿ + (19 – 7) . 6ⁿ

= 7 . 5²ⁿ + 19 . 6ⁿ – 7 . 6ⁿ

= 7 . (5²ⁿ –  6ⁿ) + 19 . 6ⁿ

= 7 . (25ⁿ –  6ⁿ) + 19 . 6ⁿ

Vì 7 . (25ⁿ –  6ⁿ) ⋮ 19 và 19 . 6ⁿ ⋮ 19

Nên 7 . (25ⁿ –  6ⁿ) + 19 . 6ⁿ ⋮ 19

Vậy 7 . 52n + 12 . 6n chia hết cho 19.

Câu 17: Tính nhanh: 50² – 49² + 48² – 47² + ... + 2² – 1².

Lời giải:

Đặt A = 50² – 49² + 48² – 47² + ... + 2² – 1²

A = (50² – 49²) + (48² – 47²) + ... + (2² – 1²)

A = (50 – 49)(50 + 49) + (48 – 47)(48 + 47) + ... + (2 – 1)(2 + 1)

A = 50 + 49 + 48 + 47 + ... + 2 + 1

A = (50 + 1) + (49 + 2) + ... + (25 + 26)

A = 51 + 51 + ... + 51

$A=\frac{51\times 50}{2}=1275$

Vậy A = 1275.

Câu 18: Cho hàm số y = ax⁴ + bx² + c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

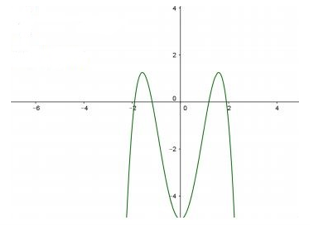
A. a > 0, b < 0, c > 0;

B. a < 0, b > 0, c < 0;

C. a < 0, b < 0, c < 0;

D. a > 0, b < 0, c < 0.

Lời giải:

Đáp án đúng là: B

Nhánh ngoài cùng bên phải của hàm số bậc bốn trùng phương đi xuống nên a < 0.

Đồ thị hàm số bậc bốn trùng phương có ba cực trị nên a.b < 0 ⇒ b > 0

Do đồ thị cắt trục Oy tại điểm có tung độ âm nên c < 0

Vậy đáp án đúng là đáp án B.

Câu 19: Chứng minh a² + b² + c² + 3 ≥ 2(a + b + c).

Lời giải:

Ta có: a² + b² + c² + 3 ≥ 2(a + b + c)

⇔ a² + b² + c² + 3 – 2(a + b + c) ≥ 0

⇔ a² – 2a + 1 + b² – 2b + 1 + c² – 2c + 1 ≥ 0

⇔ (a – 1)² + (b – 1)² + (c – 1)² ≥ 0 (luôn đúng)

Vậy ta có điều phải chứng minh.

Câu 20: Chứng minh rằng:

a) (a + b + c)² ≤ 3(a² + b² + c²)

b) (a + b)² ≤ 2(a² + b²)

Lời giải:

a) Ta có: (a + b + c)² ≤ 3(a² + b² + c²)

⇔ a² + b² + c² + 2ab + 2ac + 2bc ≤ 3a² + 3b² + 3c²

⇔ -2a² – 2b² – 2c² + 2ab + 2ac + 2bc ≤ 0

⇔ -(a – b)² – (b – c)² –  (c – a)² ≤ 0 (đúng với mọi a, b, c)

Dấu “=” xảy ra khi a = b = c.

b) (a + b)² ≤ 2(a² + b²)

⇔ a² – 2ab + b² ≤ 2a² + 2b²

⇔ –a² – 2ab – b² ≤ 0

⇔ –(a + b)² ≤ 0 (đúng với mọi a, b)

Dấu “=” xảy ra khi a = –b

Câu 21: Giải phương trình: log₂x.log₂(2x) – 2 = 0

Lời giải:                         

ĐKXĐ: x > 0

log₂x.log₂(2x) – 2 = 0

⇔ log₂x . (log₂2 + log₂x) – 2 = 0

⇔ log₂x + log₂x. log₂x – 2 = 0

Đặt log₂x = t, ta có: t + t² – 2 = 0 ⇔ (t + 1)(t – 2) = 0

$$\begin{gathered} \iff \left[\begin{array}{l}t+1=0\\ t-2=0\end{array}\right. \\ \iff \left[\begin{array}{l}t=-1\\ t=2\end{array}\right. \\ \iff \left[\begin{array}{l}{\log }_{2}x=-1\\ {\log }_{2}x=2\end{array}\right. \\ \iff \left[\begin{array}{l}x=2^{-1}=\frac{1}{2}\left(TM\right)\\ x=2^2=4\left(TM\right)\end{array}\right. \end{gathered}$$

Câu 22: Trong hệ trục tọa độ Oxy cho hình bình hành OABC, điểm C thuộc trục hoành. Khẳng định nào sau đây đúng?

A. $\overrightarrow{AB}$ có tung độ khác 0;

B. Hai điểm A, B có tung độ khác nhau;

C. C có hoành độ bằng 0;

D. x_A + x_C – x_B = 0

Lời giải:

Đáp án đúng là: D

Vì OABC là hình bình hành nên: $\overrightarrow{AB}=\overrightarrow{OC}$

x_B – x_A = x_C ⇔ x_A + x_C – x_B = 0

Vậy đáp án đúng là đáp án D.

Câu 23: Trong mặt phẳng với hệ tọa độ Oxy cho hình bình hành OABC có tọa độ điểm A(3;1), C(–1;2) (tham khảo hình vẽ bên). Số phức nào sau đây có điểm biểu diễn là điểm B?

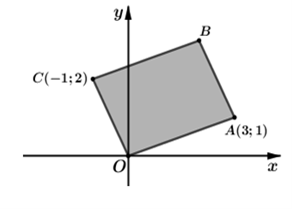A. z₁ = –2 + 3i;

B. z₂ = 2 + 3i;

C. z₃ = 4 – i;

D. z₄ = –4 + i.

Lời giải:

Đáp án đúng là: B

Vì OABC là hình bình hành nên:

$\overrightarrow{OA}=\overrightarrow{BC}\Rightarrow \left\{\begin{array}{l}{x}_A-0=x_B-x_C\\ y_A-0=y_B-y_C\end{array}\right.\Rightarrow \left\{\begin{array}{l}{x}_B=2\\ y_B=3\end{array}\right.$

Suy ra số phức z₂ = 2 + 3i có điểm biểu diễn là B.

Đáp án đúng là B.

Câu 24: Trong hệ tọa độ Oxy, cho ba điểm A(1; 3); B(–1; 2); C(–2; 1).Tìm tọa độ của vectơ $\overrightarrow{AB}-\overrightarrow{AC}$

A. (–5; –3);

B. (1; 1);

C. (–1; 2);

D. (–1; 1).

Lời giải:

$\left\{\begin{array}{l}\overrightarrow{AB}=\left(-2;-1\right)\\ \overrightarrow{AC}=\left(-3;-2\right)\end{array}\right.\Rightarrow \overrightarrow{AB}-\overrightarrow{AC}=\left(-2-\left(-3\right);-1-\left(-2\right)\right)=\left(1;1\right)$

Vậy đáp án đúng là B.

Câu 25: Tìm x biết: x³ + 27 + (x + 3)(x – 9) = 0.

Lời giải:

x³ + 27 + (x + 3)(x - 9) = 0

⇔ x³ + 3³ + (x + 3)(x - 9) = 0

⇔ (x + 3)(x² – 3x + 9) + (x + 3)(x - 9) = 0

⇔ (x + 3)(x² – 3x + 9 + x - 9) = 0

⇔ (x + 3)( x² – 2x) = 0

⇔ x.(x + 3).(x – 2) = 0

$\iff \left[\begin{array}{l}x=0\\ x+3=0\\ x-2=0\end{array}\right.\iff \left[\begin{array}{l}x=0\\ x=-3\\ x=2\end{array}\right.$

Vậy $x\in \left\{0;-3;2\right\}$.

Câu 26: a) Tìm các ước của mỗi số sau: 2, 3, 4, 5, 6, 7, 17, 34.

b) Trong các số trên, những số nào có hai ước, những số nào có nhiều hơn hai ước?

 Lời giải:

a) Các ước của 2 là: 1; 2

Các ước của 3 là: 1; 3

Các ước của 4 là: 1; 2; 4

Các ước của 5 là: 1; 5

Các ước của 6 là: 1; 2; 3; 6

Các ước của 7 là: 1; 7

Các ước của 34 là: 1; 2; 17; 34.

b) Các số 2, 3, 5, 7, 17 chỉ có hai ước là 1 và chính nó. Các số đó được gọi là số nguyên tố.

Các số 4, 6, 34 có nhiều hơn hai ước. Các số đó được gọi là hợp số.

Câu 27: Phân tích đa thức thành nhân tử: (x – y)² + 4(x – y) – 12.

Lời giải:

(x – y)² + 4(x – y) – 12

= (x – y)² + 4(x – y) + 4 – 16

= (x – y)² + 2(x – y).2 + 2² – 16

= (x – y + 2)² – 4²

= (x – y + 2 − 4)(x – y + 2 + 4)

= (x – y – 2)(x – y + 6)

Câu 28: Giải phương trình: (x + 1)(x² – x + 1) – 2x = x(x – 1)(x + 1).

Lời giải:

(x + 1)(x² – x + 1) – 2x = x(x – 1)(x + 1)

⇔ x³ + 1 – 2x = x(x² – 1)

⇔ x³ + 1 – 2x = x³ – x

⇔ x³ – x³ – 2x + x = –1

⇔ –x = –1

⇔ x = 1

Vậy nghiệm của phương trình là x = 1

Câu 29: Thực hiện phép tính: (4x – 1)(2x² – x – 1).

Lời giải:

(4x – 1)(2x² – x – 1)

= 8x³ – 4x² – 4x – 2x² + x + 1

= 8x³ – 6x² – 3x + 1.

Câu 30: Đồ thị hàm số nào dưới đây nhận trục tung làm trục đối xứng?

A. y = sin x – cos x;

B. y = 2sin x;

C. y = 2sin (–x);

D. y = –2cos x.

Lời giải:

Đáp án đúng là: D

Hàm số đó phải là hàm chẵn.

Xét y = –2cos x, có y(–x) = y(x) nên hàm D là hàm chẵn

Vậy đáp án đúng là đáp án D

Câu 31: Nếu lấy 3,14 làm giá trị gần đúng của π thì sai số tuyệt đối là:

A. 0,001;

B. 0,002;

C. 0,003;

D. 0,01.

Lời giải:

Đáp án đúng là: A

Ta có số đúng π = 3,141… nên sai số tuyệt đối của số gần đúng 3,14 là:

∆ = |3,14 – π| < |3,141 – 3,14| = 0,001.

Vậy sai số tuyệt đối của số gần đúng 3,14 là 0,001.

Đáp án đúng là A.

Câu 32: Trong không gian cho ba điểm phân biệt không thẳng hàng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt?

A. 1;

B. 2;

C. 3;

D. 4.

Lời giải:

Đáp án đúng là: A

Qua 3 điểm phân biệt không thẳng hàng có một và chỉ một mặt phẳng đi qua ba điểm đó

Vậy đáp án đúng là đáp án A

Câu 33: Vật thể nào dưới đây không phải là khối đa diện?

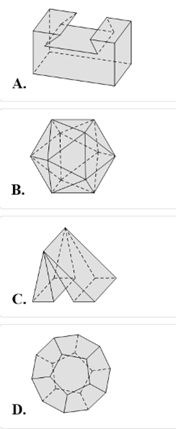
Lời giải:

Đáp án đúng là: C

Vật thể cho bởi hình A, B, D là các khối đa diện.

Vật thể cho bởi hình C không phải khối đa diện vì vi phạm điều kiện mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.

Câu 34: Phân tích các đa thức sau thành nhân tử

a) x² + 4xy – 21y²

b) 5x² + 6xy + y²

c) x² + 2xy – 15y²

d) (x – y)² + 4(x – y) – 12

e) x² – 7xy + 10y²

f) x²yz + 5xyz – 14yz

g) x⁴ + 4x² – 5

h) x³ – 19x – 30

i) x³ – 5x² – 14x

j) x³ – 7x – 6

k) x³ – 5x² – 14

Lời giải:

a) x² + 4xy – 21y²

= x² + 7xy – 3xy – 21y²

= x(x + 7y) – 3y(x + 7y)

= (x + 7y)(x – 3y)

b) 5x² + 6xy + y²

= 5x² + 5xy + xy + y²

= 5x(x + y) + y(x + y)

= (x + y)(5x + y)

c) x² + 2xy – 15y²

= x² + 5xy – 3xy – 15y²

= x(x + 5y) – 3y(x + 5y)

= (x + 5y)(x – 3y)

d) (x – y)² + 4(x – y) – 12

= (x – y)² + 6 (x – y) –  2(x – y) – 12

= (x – y) (x – y + 6) –  2 (x – y + 6)

= (x – y + 6)(x – y – 2)

e) x² – 7xy + 10y²

= x² – 2xy – 5xy + 10y²

= x(x – 2y) – 5y(x – 2y)

= (x – 2y)(x – 5y)

 f) x²yz + 5xyz – 14yz

= x²yz + 7xyz – 2xyz – 14yz

= xyz (x + 7) – 2yz(x + 7)

= yz(x + 7)(x – 2)

g) x⁴ + 4x² – 5

= x⁴ – x² + 5x² – 5

= x² (x² – 1) + 5 (x² – 1)

= (x² – 1) (x² + 5)

= (x – 1)(x + 1)(x² + 5)

h) x³ – 19x – 30

= x³ + 5x² + 6x – 5x² – 25x – 30

= x (x² + 5x + 6) – 5 (x² + 5x + 6)

= (x² + 5x + 6) (x – 5)

= (x – 5)(x² + 2x + 3x + 6)

= (x – 5)[x(x + 2) + 3(x + 2)]

= (x – 5)(x + 2)(x + 3).

i) x³ – 5x² – 14x

= x(x² – 5x – 14)

= x(x² – 7x + 2x – 14)

= x[x(x – 7) + 2 (x – 7)]

= x(x – 7)(x + 2)

j) x³ – 7x – 6

= x³ + 3x² + 2x – 3x² – 9x – 6

= x(x² + 3x + 2) – 3(x² + 3x + 2)

= (x – 3)(x² + 3x + 2)

= (x – 3)(x² + x + 2x + 2)

= (x – 3)[x(x + 1) + 2(x + 1)]

= (x – 3)(x + 1)(x + 2).

Câu 35: Liệt kê các số nguyên tố có 2 chữ số nhỏ hơn 25

Lời giải:

Các số nguyên tố có 2 chữ số nhỏ hơn 25 là: 11; 13; 17; 19; 23.

Câu 36: Khi phương trình bậc hai ax² + bx + x = 0 có biệt thức D = b² – 4ac < 0 thì có bao nhiêu nghiệm?

Lời giải:

Khi phương trình bậc hai ax² + bx + x = 0 có biệt thức D = b² – 4ac < 0 thì phương trình vô nghiệm.

Câu 37: Trong mặt phẳng tọa độ Oxy cho đường thẳng d: x – 2y + 3 = 0 và I(1; –2). Viết phương trình đường thẳng d' sao cho d’ là ảnh của đường thẳng d qua phép đối xứng tâm I.

Lời giải:

Lấy M(–3; 0) thuộc d, khi đó M’ = Đ_I(M) là điểm thuộc d’.

Ta có M’ = Đ_I(M) nên I(1; –2) là trung điểm của MM’

$\Rightarrow \left\{\begin{array}{l}{x}_{M^{\text{'}}}=2.1-\left(-3\right)=5\\ y_{M^{\text{'}}}=2.\left(-2\right)-0=-4\end{array}\right.\Rightarrow M^{\text{'}}\left(5;-4\right)$

d’ là ảnh của d qua phép đối xứng tâm I nên d’ // d và d’ đi qua M’(5; –4)

⇒ (d’): x – 2y – 13 = 0.

Câu 38: Tính chu vi hình thang biết đáy lớn bằng 14cm, đáy bé bằng 10cm, 2 cạnh bên lần lượt bằng 6cm, và 8cm.

A. 36 cm;

B. 38 cm;

C. 32 cm;

D. 34 cm.

Lời giải:

Đáp án đúng là: B

Áp dụng theo công thức tính chu vi hình thang ta có

P = a + b + c + d

= 14 + 10 + 6 + 8

= 38cm

Đáp số: 38cm

Câu 39: Giải phương trình sau (12x + 7)² (3x + 2) (2x + 1) = 3

Lời giải:

(12x + 7)² (3x + 2) (2x + 1) = 3

⇔ (12x + 7)² . 4 . (3x + 2) . 6 . (2x + 1) = 3.4.6

⇔ (12x + 7)² (12x + 8) (12x + 6) = 72

Đặt 12x + 7 = t.

Ta có phương trình ẩn t:

t² (t + 1)(t – 1) = 72

⇔ t² (t² – 1) = 72

⇔ t⁴ – t² – 72 = 0

⇔ t⁴ – 9t² + 8t² – 72 = 0

⇔ t²(t² – 9) + 8(t² – 9) = 0

⇔ (t² – 9)(t² + 8) = 0

mà t² + 8 > 0 với mọi t ⇒ t² – 9 = 0 ⇔ (t - 3)(t + 3) = 0

$\iff \left\{\begin{array}{l}t=3\\ t=-3\end{array}\right.\iff \left\{\begin{array}{l}12x+7=3\\ 12x+7=-3\end{array}\right.\iff \left\{\begin{array}{l}x=-\frac{1}{3}\\ x=-\frac{5}{6}\end{array}\right.$

Vậy phương trình đã cho có tập nghiệm là S = $\left\{-\frac{1}{3};-\frac{5}{6}\right\}$.

Câu 40: Thực hiện phép tính:

a) 483 + (-56) + 263 + (-64)

b) 371 + (-531) + (-271) + 731

c) 3251 – 243 - 3250

d) 279 – (145 + 279)

Lời giải:

a) 483 + (-56) + 263 + (-64)

= 483 + 263 + (-56) + (-64)

= 746 + (-120)

= 626

b) 371 + (-531) + (-271) + 731

= 371+ (-271) + (-531) + 731

= 100 + 200

= 300

c) 3251 – 243 – 3250

= 3251 – 3250 – 243

= 1 – 243

= -242

d) 279 – (145 + 279)

= 279 – 279 – 145

= 0 – 145 = -145

Câu 41: Tính hợp lí:

a) 942 – 2567 + 2563 – 1942

b) 42.53 + 47.156 – 47.114

Lời giải:

a) 942 – 2567 + 2563 – 1942

= (942 – 1942) + (2563 – 2567)

= (-1000) + (-4)

= -1004

b) 42.53 + 47.156 – 47.114

= 42.53 + 47.(156 – 114)

= 42.53 + 47.42

= 42.(53 + 47)

= 42.100

= 4200

Câu 42: Chứng minh rằng: x² + y² +z² ≥ xy + yz + xz với mọi x, y, z.

Lời giải:

x² + y² + z² ≥ xy + yz + xz (1)

⇔ 2x² + 2y² + 2z² ≥ 2xy + 2yz + 2xz

⇔ 2x² + 2y² + 2z² – 2xy – 2yz – 2xz  ≥ 0

⇔ (x² – 2xy + y²) + (y² – 2yz + z²) + (z² – 2xz + x²) ≥ 0

⇔ (x – y)² + (y – z)² + (z – x)² ≥ 0 (đpcm)

Dấu “ = ” xảy ra khi x = y = z

Câu 43: Cho x² + y² +z² = xy + yz + xz. Chứng minh z = x = y.

Lời giải:

x² + y² +z² = xy + yz + xz

⇔ x² + y² +z² – xy – yz – xz = 0

⇔ 2x² + 2y² + 2z² – 2xy – 2yz – 2xz = 0

⇔ (x² – 2xy + y²) + (y² – 2yz + z²) + (z² – 2xz + x²) = 0

⇔ (x – y)² + (y – z)² + (z – x)² = 0

⇔ $\left[\begin{array}{l}x-y=0\\ y-z=0\\ z-x=0\end{array}\right.\iff \left[\begin{array}{l}x=y\\ y=z\\ z=x\end{array}\right.\iff x=y=z$(đpcm)

Câu 44: Tìm tập xác định của hàm số y = (7^x)² + x – 2.

Lời giải:

Tập xác định của hàm số y = (7^x)² + x – 2 là ℝ

Câu 45: Phân tích đa thức sau thành nhân tử x² –xy + x – y

Lời giải:

Cách 1: Nhóm hai hạng tử thứ 1 và thứ 2, hạng tử thứ 3 và thứ 4

x² – xy + x – y

= (x² – xy) + (x – y)

(Nhóm thứ nhất có nhân tử chung là x)

= x(x – y) + (x – y)

(Xuất hiện nhân tử chung x – y)

= (x + 1)(x – y)

Cách 2: Nhóm hạng tử thứ 1 và thứ 3 ; hạng tử thứ 2 và thứ 4

x² – xy + x – y

= (x² + x) – (xy + y)

(nhóm thứ nhất có nhân tử chung là x ; nhóm thứ hai có nhân tử chung là y)

= x.(x + 1) – y.(x + 1)

(Xuất hiện nhân tử chung x + 1)

= (x – y)(x + 1)

Câu 46: Giải phương trình (x² − 1)(x² + 4x + 3) = 192

Lời giải:

Biến đổi phương trình thành:

(x² – 1)(x + 1)(x + 3) = 192 ⇔ (x – 1)(x + 1)² (x + 3) = 192

Đặt x + 1 = y, phương trình trở thành:

(y – 2)y² (y + 2) = 192 ⇔ y²(y² – 4) = 192

Đặt y² – 2 = z thì z + 2 ≥ 0, phương trình trở thành:

(z + 2)(z – 2) = 192 ⇔ z² = 196 ⇔ z = ±14

Loại z = -14 vì trái với điều kiện z + 2 ≥ 0

Với z = 14 thì y² = 16, do đó y = ±4

Với y = 4 thì x + 1 = 4 nên x = 3

Với y = -4 thì x + 1 = -4 nên x = -5

Vậy phương trình có nghiệm là {3; -5}.

Câu 47: Thực hiện phép tính:

a) 17 – 25 + 55 – 17

b) 25 – (-75) + 32 – (32 + 75)

c) (-5).8.(-2).3

d) (-15) + (-122)

e) (7 – 10) + 3

f) |-127| – 18.(5 – 6)

Lời giải:

a) 17 – 25 + 55 – 17

= (17 – 17) + (-25 + 55)

= 0 + 30

= 30

b) 25 – (-75) + 32 – (32 + 75)

= 25 + 75 + 32 – 32 – 75

= 25 + (75 – 75) + (32 – 32)

= 25 + 0 + 0

= 25

c) (-5).8.(-2).3

= (-5).(-2).8.3

= 10.8.3

= 80.3

= 240

d) (-15) + (-122)

= -15 – 122

= -137

e) (7 – 10) + 3

= 7 – 10 + 3

= (7 + 3) – 10

= 10 – 10

= 0

f) |-127| – 18.(5 – 6)

= 127 – 18.(-1)

= 127 + 18

= 145

Câu 48: Cho hàm số y=f(x) có đồ thị trên một khoảng K như hình vẽ bên. Trên K, hàm số có bao nhiêu cực trị?

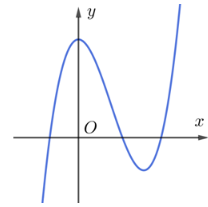
A. 3;

B. 2;

C. 0;

D. 1.

Lời giải:

Đáp án đúng là: B

Trên K, hàm số có 2 cực trị

Vậy đáp án đúng là B.