Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 35)

Câu 1: Tìm hai số tự nhiên, biết:

a) Có tích bằng 720 và ƯCLN bằng 6.

b) Có tích bằng 4050 và ƯCLN bằng 3.

Lời giải:

a) Gọi hai số tự nhiên cần tìm là a, b.

Ta có ƯCLN(a, b) = 6.

Suy ra a = 6m; b = 6n và ƯCLN(m, n) = 1.

Lại có a.b = 720.

Suy ra 6m.6n = 720.

Do đó 36m.n = 720.

Vì vậy m.n = 20.

Chọn các cặp m, n nguyên tố cùng nhau và có tích bằng 20, ta được bảng sau:

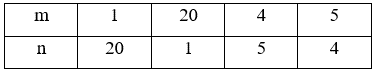
Khi đó ta có:

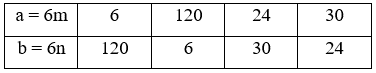
Vậy hai số tự nhiên cần tìm là 6; 120 hoặc 24; 30.

b) Gọi hai số tự nhiên cần tìm là a, b.

Ta có ƯCLN(a, b) = 3.

Suy ra a = 6m; b = 3n và ƯCLN(m, n) = 1.

Lại có a.b = 4050.

Suy ra 3m.3n = 4050.

Do đó 9m.n = 4050.

Vì vậy m.n = 450.

Chọn các cặp m, n nguyên tố cùng nhau và có tích bằng 450, ta được bảng sau:

Khi đó ta có:

Vậy hai số tự nhiên cần tìm là 3; 1350 hoặc 6; 675 hoặc 27; 150 hoặc 54; 75.

Câu 2: Cho tam giác ABC vuông tại A, điểm M bất kì trên cạnh BC. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ M đến AB và AC. Tứ giác ADME là hình gì?

Lời giải:

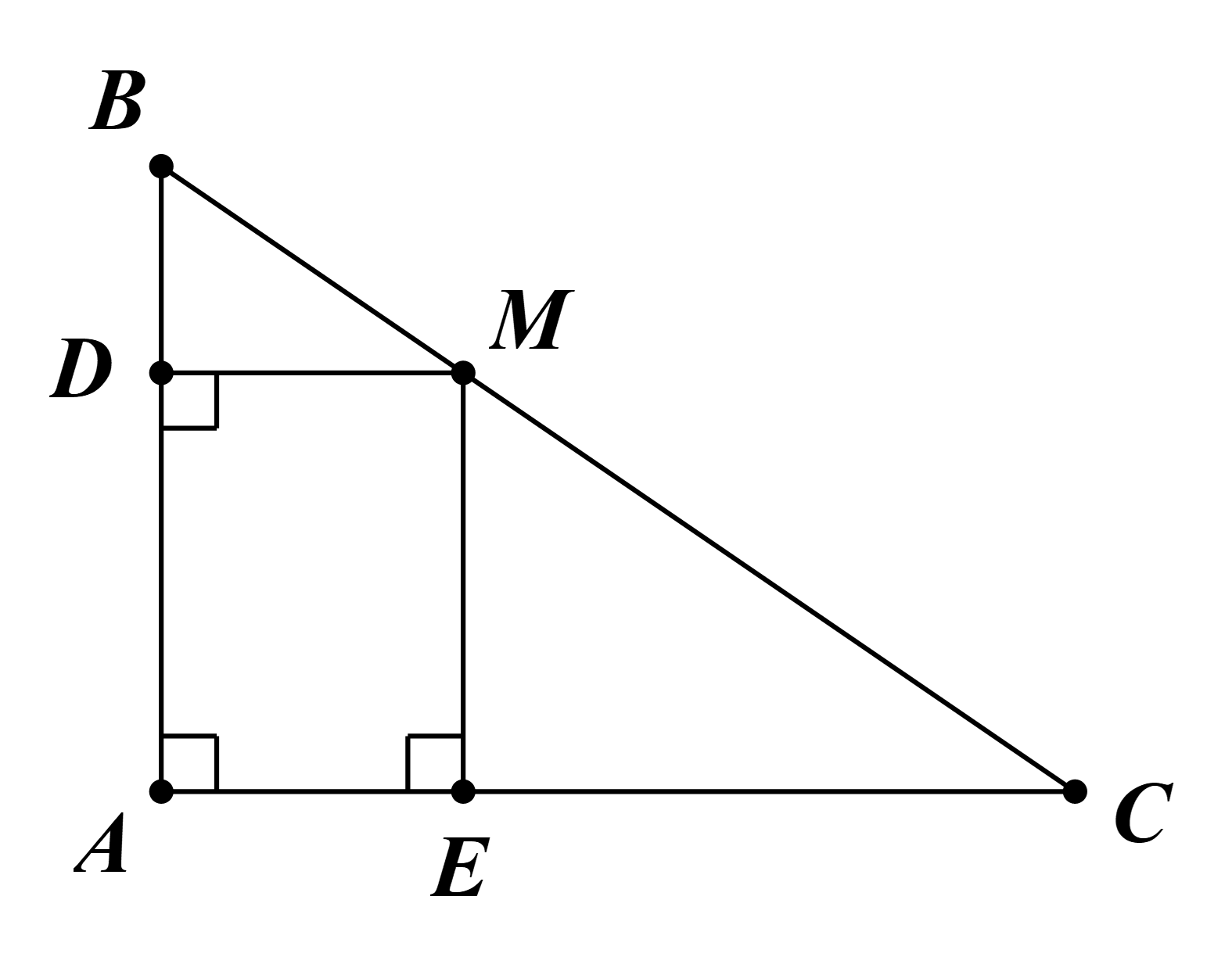
Ta có tam giác ABC vuông tại A.

Suy ra $\widehat{DAE}=90°$ .

Mà $\widehat{MDA}=90°$  (D là chân đường vuông góc kẻ từ M đến AB) và $\widehat{MEA}=90°$  (E là chân đường vuông góc kẻ từ M đến AC).

Do đó $\widehat{DAE}=\widehat{MDA}=\widehat{MEA}=90°$ .

Vậy tứ giác ADME là hình chữ nhật.

Câu 3: Tìm x, y ∈ ℕ, biết: (2x + 1)(y – 3) = 10.

Lời giải:

(2x + 1)(y – 3) = 10 = 1.10 = 10.1 = 2.5 = 5.2.

Ta có:

⦁ $\left\{\begin{array}{l}2x+1=10\\ y-3=1\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{9}{2}\\ y=4\end{array}\right.$  (loại vì x ∉ ℕ).

⦁ $\left\{\begin{array}{l}2x+1=1\\ y-3=10\end{array}\right.\iff \left\{\begin{array}{l}x=0\\ y=13\end{array}\right.$  (nhận).

⦁ $\left\{\begin{array}{l}2x+1=2\\ y-3=5\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{1}{2}\\ y=8\end{array}\right.$  (loại vì x ∉ ℕ).

⦁ $\left\{\begin{array}{l}2x+1=5\\ y-3=2\end{array}\right.\iff \left\{\begin{array}{l}x=2\\ y=5\end{array}\right.$  (nhận).

Vậy (x; y) ∈ {(0; 13), (2; 5)}.

Câu 4: Khi cộng hai số thập phân, một học sinh đã bỏ quên dấu phẩy của một số thập phân có hai chữ số ở phần thập phân nên được kết quả là 158,6. Tìm hai số thập phân đó biết tổng đúng là 36,83.

Lời giải:

Tổng sai hơn tổng đúng là: 158,6 – 36,83 = 121,77.

Vì bạn học sinh đã bỏ quên dấu phẩy của một số thập phân có hai chữ số ở phần thập phân nên số thập phân đó gấp lên 100 lần.

Do đó tổng tăng lên 99 lần số thập phân đó.

Vì vậy 99 lần số thập phân đó là 121,77.

Số thập phân đó là: 121,77 : 99 = 1,23.

Số thập phân còn lại là: 36,83 – 1,23 = 35,6.

Đáp số: 1,23 và 35,6.

Câu 5: Khi cộng hai số thập phân, một học sinh đã bỏ quên dấu phẩy của một số thập phân có hai chữ số ở phần thập phân nên được kết quả là 498,843. Tìm hai số thập phân đó biết tổng đúng là 107,793.

Lời giải:

Tổng sai hơn tổng đúng là: 498,843 – 107,793 = 391,05.

Vì bạn học sinh đã bỏ quên dấu phẩy của một số thập phân có hai chữ số ở phần thập phân nên số thập phân đó gấp lên 100 lần.

Do đó tổng tăng lên 99 lần số thập phân đó.

Vì vậy 99 lần số thập phân đó là 391,05.

Số thập phân đó là: 391,05 : 99 = 3,95.

Số thập phân còn lại là: 107,793 – 3,95 = 103,843.

Đáp số: 3,95 và 103,843.

Câu 6: Một tấm vải dài 36 m. Lần đầu người ta cắt ra 16 mảnh vải, mỗi mảnh vải dài $1\frac{1}{5}$  m. Lần thứ hai người ta cắt được 6 mảnh vải dài như nhau thì vừa hết tấm vải. Hỏi mỗi mảnh vải cắt ra ở lần thứ hai dài bao nhiêu mét?

Lời giải:

Đổi: $1\frac{1}{5}m=\frac{6}{5}m=\mathrm{1,2}m$ .

Số mét vải cắt ra lần đầu là: 1,2 . 16 = 19,2 (m)

Số mét vải cắt ra lần thứ hai là: 36 – 19,2 = 16,8 (m)

Mỗi mảnh vải cắt ra ở lần thứ hai dài số mét là: 16,8 : 6 = 2,8 (m)

Đáp số: 2,8 m.

Câu 7: Chứng minh 43⁴³ – 17¹⁷ chia hết cho 10.

Lời giải:

Ta có:

⦁ 43¹ = 43 có chữ số tận cùng là số 3;

⦁ 43² = 1849 có chữ số tận cùng là số 9;

⦁ 43³ = 79507 có chữ số tận cùng là số 7;

⦁ 43⁴ = 3418801 có chữ số tận cùng là số 1;

⦁ 43⁵ = 147008443 có chữ số tận cùng là số 3.

Suy ra quy luật của nó cứ lặp đi lặp lại theo dãy bốn số 3; 9; 7; 1.

Ta thấy 43 chia 4 dư 3 nên chữ số tận cùng của 43⁴³ là 7.

Tương tự như vậy, ta có chữ số tận cùng của 17¹⁷ là 7.

Vì vậy 43⁴³ – 17¹⁷ ra số có chữ số tận cùng là số 0, mà số có chữ số tận cùng là số 0 thì luôn chia hết cho 10.

Vậy ta có điều phải chứng minh.

Câu 8: Đổi đơn vị: 8 dam = … mm.

Lời giải:

8 dam = 8.10 000 mm = 80 000 mm.

Câu 9: Ở một nhà trẻ có một số cháu được chia thành các nhóm. Mỗi nhóm có một cô giáo phụ trách. Nếu chia mỗi nhóm 6 cháu thì có 4 cháu chưa có ai phụ trách. Nếu chia mỗi nhóm 8 cháu thì thừa một cô. Hỏi có bao nhiêu cháu và bao nhiêu cô giáo?

Lời giải:

Chia 1 nhóm 6 cháu thì có 4 cháu chưa có ai phụ trách.

Chia 1 nhóm 8 cháu thì thừa một cô, tức là thiếu 8 cháu để đủ cho tất cả các cô phụ trách.

Do đó ta có sơ đồ sau:

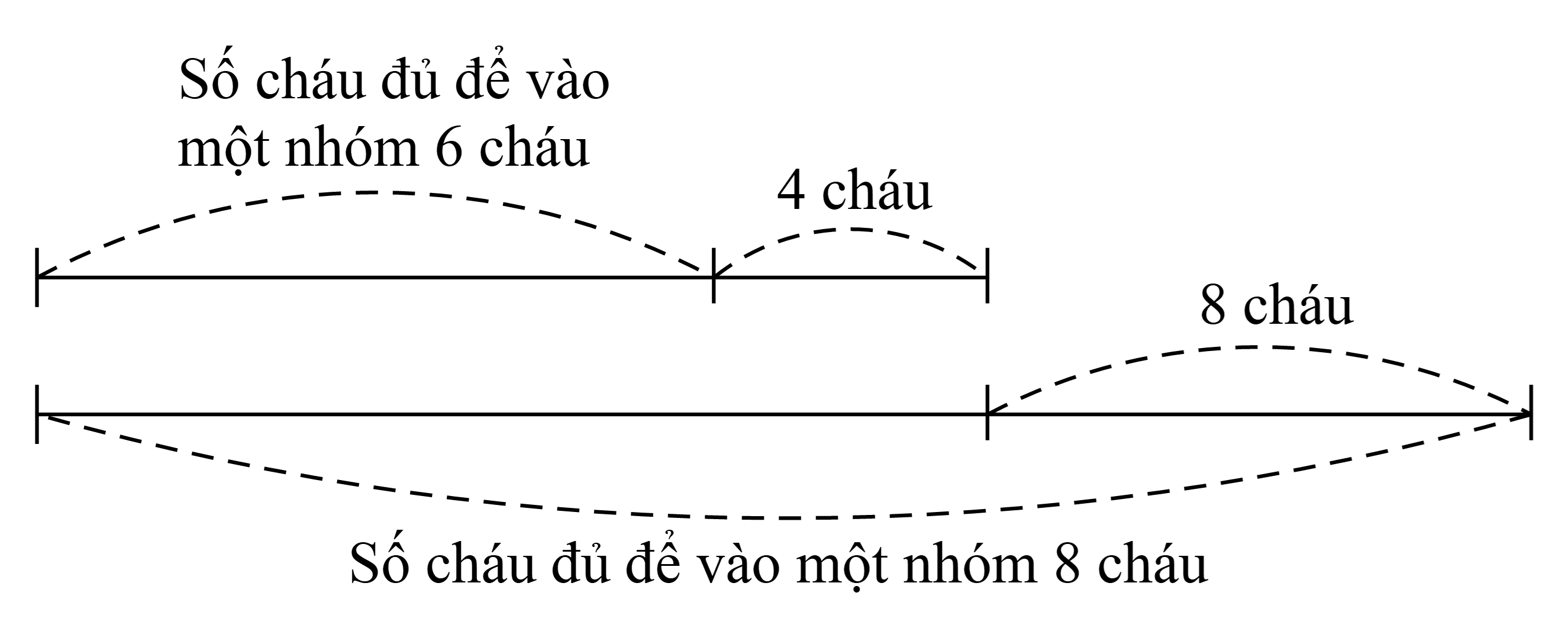
Nếu tất cả các nhóm đều có 8 cháu thì sẽ nhiều hơn nếu tất cả các nhóm đều có 6 cháu là: 4 + 8 = 12 (cháu).

Một nhóm 8 cháu nhiều hơn một nhóm 6 cháu là: 8 – 6 = 2 (cháu).

Số nhóm (hay số cô phụ trách) là: 12 : 2 = 6 (nhóm) hoặc 6 (cô).

Số cháu là: 6 ⨯ 6 + 4 = 40 (cháu) hoặc 8 ⨯ 6 – 8 = 40 (cháu).

Đáp số: 40 cháu và 6 cô.

Câu 10: Một kho chứa 1000 bao gạo, trong đó có 350 bao gạo nếp, còn lại là các bao gạo tẻ. Hỏi:

a) Số bao gạo nếp chiếm bao nhiêu phần trăm số bao gạo trong kho?

b) Tỉ số phần trăm của số bao gạo tẻ và số bao gạo trong kho là bao nhiêu?

Lời giải:

a) Tỉ số phần trăm số bao gạo nếp và số bao gạo trong kho là:

350 : 1000 = 0,35 = 35%.

b) Tỉ số phần trăm của số bao gạo tẻ và số bao gạo trong kho là:

100% – 35% = 65%.

Đáp số: a) 35%; b) 65%.

Câu 11: Một kho chứa 1000 bao gạo, trong đó có 450 bao gạo nếp, còn lại là các bao gạo tẻ. Hỏi:

a) Số bao gạo nếp chiếm bao nhiêu phần trăm số bao gạo trong kho?

b) Tỉ số phần trăm của số bao gạo tẻ và số bao gạo trong kho là bao nhiêu?

Lời giải:

a) Tỉ số phần trăm số bao gạo nếp và số bao gạo trong kho là:

450 : 1000 = 0,45 = 45%.

b) Tỉ số phần trăm của số bao gạo tẻ và số bao gạo trong kho là:

100% – 45% = 55%.

Đáp số: a) 45%; b) 55%.

Câu 12: Tìm một số thập phân có chữ số ở phần thập phân là 3. Biết rằng nếu viết thêm chữ số 2 vào trước dấu phẩy của số đó ta được một số mới gấp 9 lần số phải tìm.

Lời giải:

Gọi số thập phân ban đầu là: a,3 (a ∈ ℕ*)

Số thập phân mới sau khi thêm chữ số 2 vào trước dấu phẩy là a2,3.

Ta có: a,3 = a + 0,3.

           a2,3 = a × 10 + 2,3 = 10 × a + 2,3.

Do số mới gấp 9 lần số phải tìm nên ta có:

10 × a + 2,3 = 9 × (a + 0,3)

10 × a + 2,3 = 9 × a + 9 × 0,3

10 × a – 9 × a = 2,7 – 2,3

a × (10 – 9) = 0,4

a = 0,4 (không thỏa mãn).

Vậy không có số nào thỏa mãn yêu cầu đề bài

Câu 13: Tính nhanh: (–25) . (75 – 45) – 75 . (45 – 25).

Lời giải:

Ta có

(–25) . (75 – 45) – 75 . (45 – 25)

= –25 . 75 – (–25) . 45 – 75 . 45 – (–75) . 25

= –25 . 75 + 25 . 45 – 75 . 45 + 75 . 25

= 75 . (–25 + 25) + 45 . (25 – 75)

= 75 . 0 + 45 . (–50)

= 0 + (–2250 )

= –2250.

Câu 14: Với mỗi số nguyên dương n, kí hiệu S_n là tổng của n số nguyên tố đầu tiên (S₁ = 2; S₂ = 2 + 3 = 5; S₃ = 2 + 3 + 5 = 10; ...).

Chứng minh rằng trong dãy số S₁, S₂, S₃ ... không tồn tại hai số hạng liên tiếp đều là số chính phương.

Lời giải:

Gọi p_n là số nguyên tố thứ n

Giả sử tồn tại m mà S_m-1 = k²; S_m = l²; k, l ∈ ℕ*

Vì S₂ = 5, S₃ = 10, S₄ = 17

Suy ra m > 4

Ta có: P_m = S_m – S_m-1 = l² – k² = (l – k)(l + k)

Vì p_m là số nguyên tố và k + l > 1 nên $\left\{\begin{array}{l}l-k=1\\ l+k=p_m\end{array}\right.$

Suy ra $p_m=2l-1=2\sqrt{S_m}-1$

Suy ra ${\text{S}}_m={\left(\frac{p_m+1}{2}\right)}^2$                          (1)

Do m > 4 nên

S_m ≤ (1 + 3 + 5 + 7 + ... + p_m) + 2 – 1 – 9

$\iff S_m\le 1^2-0^2+2^2-1^2+3^2-2^2+\mathrm{...}+\left[{\left(\frac{p_m+1}{2}\right)}^2-{\left(\frac{p_m-1}{2}\right)}^2\right]-8$

$\iff S_m\le {\left(\frac{p_m+1}{2}\right)}^2-8<{\left(\frac{p_m+1}{2}\right)}^2$ (mâu thuẫn với (1))

Vậy trong dãy số S₁, S₂, S₃ ... không tồn tại hai số hạng liên tiếp đều là số chính phương.

Câu 15: Thắng có 25 viên bi xanh và 15 viên bi đỏ. Hỏi tỉ số phần trăm của số bi đỏ và số bi xanh.

Lời giải:

Tỉ số phần trăm của số bi đỏ và viên bi xanh là:

 $\frac{15}{25}.100=60\%$

Vậy tỉ số phần trăm của số bi đỏ và số bi xanh là 60%.

Câu 16: Tính hợp lí: 19 . 25 + 9 . 95 + 19 . 30.

Lời giải:

19 . 25 + 9 . 95 + 19 . 30

= 19 . 25 + 9 . 5 . 19 + 19 . 30

= 19 . (25 + 45 + 30)

= 19 . 100

= 1 900.

Câu 17: Một thế kỉ rưỡi bằng bao nhiêu năm?

Lời giải:

1 thế kỉ = 100 năm 

Suy ra một thế kỉ rưỡi bằng

100 + (100 : 2) = 150 (năm)

Vậy một thế kỉ rưỡi bằng 150 năm.

Câu 18: Tìm nghiệm nguyên dương của phương trình: x³ – (x + y + z)² = (y + z)³ + 34.

Lời giải:

Đặt y + z = a với a ∈ ℤ, a ≥ 2 ta có:

x³ – (x + a)² = a³ + 34

⇔ x³ – a³ = (x + a)² + 34          (1)

⇔ (x – a)(x² + xa + a²) = x² + 2xa + a² + 34    (2)

⇔ (x² + xa + a²)(x – a – 1) = xa + 34

Vì x, a nguyên dương nên x² + xa + a² > 0 và xa + 34 > 0

Suy ra x – a – 1 > 0 hay x – a ≥ 2

Kết hợp với (2) suy ra x² + 2xa + a² + 34 ≥ 2(x² + xa + a²)

⇔ x² + a² ≤ 34

⇔ x² ≤ 34 ⇔ x < 6

Mà x ≥ a + 2 ≥ 4 nên x ∈ {4; 5}

– Xét x = 5, từ x² + a² ≤ 34 suy ra a ≤ 3, kết hợp a ∈ ℤ, a ≥ 2 (theo cách đặt) ta được a ∈ {2; 3}.

• Với x = 5, a = 2 thay vào (1) không thỏa mãn.

• Với x = 5, a = 3 thỏa mãn (1) và được y = 1; z = 2 hoặc y = 2; z = 1.

– Xét x = 4, từ x – a ≥ 2 suy ra a ≤ 2 (mà a = 2 loại vì không thỏa mãn (1))

Vậy phương trình có nghiệm nguyên dương là (x; y; z) ∈ {(5; 1; 2); (5; 2; 1)}.

Câu 19: Tìm n để (n² – 8)² + 36 là số nguyên tố.

Lời giải:

Ta có: (n² – 8)² + 36

= n⁴ – 16n² + 64 + 36

= n⁴ – 16n² + 100

= n⁴ + 20n² + 100 – 36n²

= (n² + 10)² – (6n)²

= (n² + 6n + 10)(n² – 6n + 10)

Để (n² – 8)² + 36 là số nguyên tố thì n² + 6n + 10 = 1 hoặc n² – 6n + 10 = 1

TH1: n² + 6n + 10 = 1

⇔ n² + 6n + 9 = 0

⇔ (n + 3)² = 0

⇔ n + 3 = 0

⇔ n = –3 (loại)

TH2: n² – 6n + 10 = 1

⇔ n² – 6n + 9 = 0

⇔ (n – 3)² = 0

⇔ n – 3 = 0

⇔ n = 3 (thỏa mãn)

Vậy n = 3 thì (n² – 8)² + 36 là số nguyên tố.

Câu 20: Số chẵn bé nhất có 3 chữ số là bao nhiêu?

Lời giải:

Số chẵn bé nhất có 3 chữ số là: 100.

Câu 21: Giải phương trình (x – 5)⁴ + (x – 3)⁴ = 16.

Lời giải:

Đặt x – 4 = t

Ta có phương trình:

(t – 1)⁴ + (t + 1)⁴ = 16

⇔ (t² – 2t + 1)² + (t² + 2t + 1)² = 16

⇔ t⁴ + 4t² + 1 + 2t² – 4t³ – 4t + t⁴ + 4t² + 1 + 2t² + 4t³ + 4t – 16 = 0

⇔ 2t⁴ + 12t² – 14 = 0

⇔ t⁴ + 6t² – 7 = 0

⇔ t⁴ + 7t² – t² – 7 = 0

⇔ t²(t² + 7) – (t² + 7) = 0

⇔ (t² + 7)(t² – 1) = 0

⇔ t² – 1 = 0 (vì t² + 7 > 0 với mọi t)

⇔ (t – 1)(t + 1) = 0

$$\begin{gathered} \iff \left[\begin{array}{l}t-1=0\\ t+1=0\end{array}\right. \\ \iff \left[\begin{array}{l}t=1\\ t=-1\end{array}\right. \\ \iff \left[\begin{array}{l}x-4=1\\ x-4=-1\end{array}\right. \\ \iff \left[\begin{array}{l}x=5\\ x=3\end{array}\right. \end{gathered}$$

Vậy phương trình có tập nghiệm S = {3; 5}.

Câu 22: Tìm số tự nhiên lớn nhất thỏa mãn điều kiện: Số đó cộng với tổng các chữ số của nó bằng 2013. Số đó là bao nhiêu?

Lời giải:

Số cần tìm nhỏ hơn 2013.

Vì là số lớn nhất nên số đó có 4 chữ số

Gọi số đó là abcd

Theo đề bài abcd + a + b + c + d = 2013

Suy ra abcd < 2013

Do đó a = 1 hoặc a = 2

• Nếu a = 2

Khi đó 2bcd + 2 + b + c +d = 2013 

⇔ 2000 +  bcd + 2 + b + c + d = 2013

⇔ bcd + b + c + d = 11

⇔ bcd < 11

Suy ra b = 0 khi đó cd + c + d = 11

Do đó cd < 11

Không có chữ số c, d thỏa mãn để cd + c + d = 11 nên a = 2 không tìm được số nào thỏa mãn đề bài

• Nếu a = 1

⇔ 1bcd + 1 + b + c + d = 2013

⇔ 1000 + bcd + 1 + b + c + d = 2013

⇔  bcd + b + c + d = 1012

Vì b + c + d lớn nhất bằng 9 + 9 + 9 = 27 nên bcd nhỏ nhất là 1012 – 27 = 985

⇔ b = 9 

⇔ 9cd + 9 + c + d = 1012

⇔ cd + c + d = 103

c + d lớn nhất bằng 9 + 9 = 18 nên cd nhỏ nhất là: 103 – 18 = 85

Suy ra c = 8 hoặc c = 9

c = 8 thì 8d + 8 + d = 103 ⇔ d + d = 15 (loại)

c = 9 thì 9d + 9 + d = 103 ⇔ d + d = 4 ⇔ d = 2

Vậy số cần tìm đó là 1992.

Câu 23: Cho 1 số tự nhiên gồm các số tự nhiên liên tiếp nhau từ 1 đến 2021 được viết theo thứ tự 1 2 3 4 5 6 7 8 9 10 11 12 13 ... 2019 2020 2021 tính tổng các chữ số đó.

Lời giải:

Bước 1: Tính tổng các chữ số từ 0 đến 999:

Thêm các chữ số 0 vào trước các số có 1 và 2 chữ số để ta được dãy số gồm toàn các số có 3 chữ số: 000; 001; 002; 003; 004; ...; 999 (Tổng các chữ số vẫn không thay đổi)

Khi này, dãy số trên có 1000 số

Số các chữ số là: 1000 × 3 = 3 000 (chữ số)

Mỗi chữ số 0; 1; 2; ...; 9 xuất hiện số lần là: 3000 : 10 = 300 (lần)

Vậy, tổng các chữ số từ 0 đến 999 là:

(0 + 1 + 2 + ... + 9) × 300 = 45 × 300 = 13 500

Bước 2: Tính tổng các chữ số từ 1000 đến 1999:

So với dãy số 000 đến 999 thì mỗi số tăng thêm 1 ở hàng nghìn

Vậy tổng các chữ số từ 1000 đến 1999 là:

13 500 + 1 × 1000 = 13 500 + 1000 = 14 500

Bước 3: Tính tổng các chữ số từ 2000 đến 2021:

Ta có tổng các chữ số từ 2000 đến 2021 là:

(2 × 21 + 1 × 10 + 2 + 2 × 45) + (2 + 0 + 2 + 1)

= (42 + 10 + 2 + 90) + 5

= 144 + 5

= 149

Vậy, tổng tất cả các chữ số từ 1 đến 2021 là 13 500 + 14 500 + 149 = 28 149.

Câu 24: Có bao nhiêu phân số thập phân lớn hơn 1 và nhỏ hơn 5 có mẫu số là số có hai chữ số.

Lời giải:

Phân số thập phân có mẫu số là số có hai chữ số

Suy ra mẫu số là 10

Gọi phân số cần tìm là $\frac{x}{10}$

Ta có: $1<\frac{x}{10}<5$

$\iff \frac{10}{10}<\frac{x}{10}<\frac{50}{10}$

⇔ 10 < x < 50

⇔ x ∈ {11; 12; 13; ...; 48; 49} có 49 – 11 + 1 = 39 số

Vậy có 39 phân số thỏa mãn.

Câu 25: Một buổi sáng cửa hàng bán được 45,8kg gạo, buổi chiều cửa hàng bán được ít hơn buổi sáng 5,35kg. Hỏi buổi chiều cửa hàng bán được bao nhiêu kg gạo?

Lời giải:

Buồi chiều cửa hàng bán được số kg gạo là:

45,8 – 5,35 = 40,45 (kg)

Đáp số: 40,45 kg.

Câu 26: Khi chia hai số tự nhiên a và b cho 3 thì cùng có số dư là r. Chứng minh rằng (a –  b) chia hết cho 3.

Lời giải:

Vì a chia 3 dư r nên a = 3p + r

Vì b chia 3 dư r nên b = 3q + r

Xét a – b = (3p + r) – (3q + r)

     = 3p + r – 3q – r

     = 3p + 3q = 3(p + q)

Vì 3(p + q) ⋮ 3 nên (a – b) ⋮ 3

Vậy (a –  b) chia hết cho 3.

Câu 27: Cho a, b là hai số nguyên tố cùng nhau. Chứng tỏ rằng 5a + 2b và 7a + 3b cũng là hai số nguyên tố cùng nhau.

Lời giải:

Gọi d = ƯCLN(5a + 2b, 7a + 3b).

Suy ra 5a + 2b, 7a + 3b chia hết cho d.

Do đó 7(5a + 2b), 5(7a + 3b) cũng chia hết cho d.

Khi đó, ta có: 5(7a + 3b) – 7(5a + 2b) = 35a + 15b – (35a + 14b) = b chia hết cho d.

Ta lại có 3(5a + 2b), 2(7a + 3b) cũng chia hết cho d.

Khi đó, ta có: 3(5a + 2b) – 2(7a + 3b) = 15a + 6b – (14a + 6b) = a cũng chia hết cho d.

Mà a và b nguyên tố cùng nhau nên d = 1.

Vậy 5a + 2b và 7a + 3b là hai số nguyên tố cùng nhau. 

Câu 28: Điền số thích hợp vào chỗ trống theo quy luật 24, 48, 80, 120, ...

Lời giải:

Ta có

48 – 24 = 24;

80 – 48 = 32 = 24 + 8;

120 – 80 = 40 = 32 + 8

Suy ra số tiếp theo là: 40 + 8 + 120 = 168

Vậy số cần tìm là 168.

Câu 29: Số a chia cho 5 dư 2, số b chia cho 5 dư 3. Hỏi a + b chia 5 dư mấy?

Lời giải:

Vì a chia 5 dư 2 nên a = 5x + 2

Vì b chia 5 dưa 3 nên b = 5y + 3

Ta có a + b = 5x + 2 + 5y + 3 = 5x + 5y + 5

Vì 5x ⋮ 5, 5y ⋮ 5, 5 ⋮ 5

Suy ra a + b ⋮ 5

Vậy a + b chia 5 dư 0.

Câu 30: Đổi 2 giờ 45 phút = ... giờ (là số thập phân).

Lời giải:

Ta có 1 giờ = 60 phút nên 2 giờ 45 phút = 2,75 giờ.

Câu 31: Một số nếu giảm đi 6 lần rồi thêm 25,71 thì được 88,5. Tìm số đó.

Lời giải:

Số cần tìm là:

(88,5 – 25,71 ) × 6 = 376,74

Vậy số cần tìm là 376,74.

Câu 32: Ba công nhân có năng suất lao động tương ứng tỉ lệ với 3, 5, 7. Tính tổng số tiền ba người được thưởng nếu biết tổng số tiền thưởng của người thứ nhất và thứ hai là 5,6 triệu.

A. 11 triệu;

B. 15 triệu;

C. 10,5 triệu;

D. 10 triệu.

Lời giải:

Đáp án đúng là: C

Gọi x, y, z lần lượt là số tiền thưởng của ba công nhân (x, y, z > 0) (triệu đồng)

Giả sử x, y, z tỉ lệ thuận với 3; 5; 7 

Ta có $\frac{x}{3}=\frac{y}{5}=\frac{z}{7}$  và x + y = 5,6

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

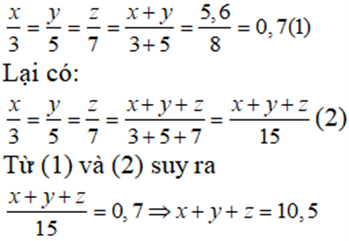
Do đó tổng số tiền thưởng của ba người là 10,5 triệu

Vậy ta chọn đáp án C.

Câu 33: Một người đi ô tô trong 2 giờ đầu, mỗi giờ đi được 42,5 km; trong 4 giờ sau, mỗi giờ đi được 46,25 km. Hỏi trên cả quãng đường, trung bình mỗi giờ người đó đi được bao nhiêu ki – lô – mét?

Lời giải:

Hai giờ đầu người đó đi được:

42,5 × 2 = 85 (km)

Bốn giờ sau người đó đi được:

46,25 × 4 = 185 (km)

Trên cả quãng đường người đó đã đi được:

85 + 185 = 270 (km)

Thời gian ô tô đi trên cả quãng đường là:

2 + 4 = 6 (giờ)

Trung bình mỗi giờ người đó đi được:

270 : 6 = 45 (km)

Vậy trên cả quãng đường, trung bình mỗi giờ người đó đi được 45 km.

Câu 34: Trong một tháng có hai ngày đầu tháng và cuối tháng đều là chủ nhật. Hỏi đó là tháng mấy?

Lời giải:

Một tháng có hai ngày đầu tháng và cuối tháng đều là chủ nhật thì số ngày của tháng đó chia cho 7 dư 1.

Mà trong các tháng từ 1 đến 12 thì chỉ có tháng 2 của năm nhuận (29 ngày) có :

29 : 7 = 4 dư 1

Vậy tháng đó là tháng 2 của năm nhuận.

Câu 35: Tính chu vi và diện tích hình tròn có bán kính 4 cm.

Lời giải:

Chu vi hình tròn đó là:

4 × 2 × 3,14 = 25,12 (cm)

Diện tích hình tròn đó là:

4 × 4 × 3,14 = 50,24 (cm²)

Vậy chu vi hình tròn bằng 25,12 cm và diện tích hình tròn là 50,24 cm².

Câu 36: Hỏi có bao nhiêu phân số thập phân khác 0 mà tổng của mẫu số và tử số là số lẻ nhỏ nhất có tám chữ số?

Lời giải:

Số lẻ nhỏ nhất có 8 chữ số là 10 000 001

Gọi phân số cần tìm là $\frac{a}{b}$  (0 < a, b < 10 000 001)

Vì $\frac{a}{b}$  là phân số thập phân

Nên b ∈ {10; 100; 1 000; 10 000; 100 000; 1 000 000; 10 000 000}

Do đó có 7 cách chọn b

Vì 0 < a < 10 000 001 nên có 10 000 000 cách chọn a

Suy ra có 7 × 10 000 000 = 70 000 000 phân số thỏa mãn

Vậy có 70 000 000 phân số thỏa mãn đề bài.

Câu 37: Số nguyên tố là gì? Ví dụ minh họa.

Lời giải:

Số nguyên tố là tập hợp các số tự nhiên lớn hơn 1, chia hết cho 1 và chính nó. Hoặc hiểu một cách đơn giản, những số tự nhiên nào lớn hơn 1, không chia được cho số nào khác ngoài số 1 và chính số đó thì đó là số nguyên tố.

Ví dụ số nguyên tố là 3, 5, 7, 13, 17, 23, 29, 97, 101, 997….

Câu 38: Có một cái ao ở giữa một khu đất, diện tích cái ao là 30,6 m² và nhỏ hơn diện tích của cả khu đất 45,57 m². Hỏi diện tích khu đất là bao nhiêu m²?

Lời giải:

Diện tích khu đất là:

30,6 + 45,57 = 76,17 (m²)

Vậy diện tích khu đất là 76,17 m².

Câu 39: Có tất cả bao nhiêu cặp số tự nhiên có trung bình cộng là 50?

Lời giải:

Tổng của hai số là: 50 × 2 = 100

Ta có: 100 = 0 + 100 = 1 + 99 = 2 + 98 = 3 + 97 = ... = 49 + 51

Từ 0 đến 100 có: (100 – 0) + 1 = 101 số hạng nên có 50 cặp

Vậy có 50 cặp số tự nhiên có trung bình cộng là 50.

Câu 40: Hai căn phòng hình chữ nhật. Căn phòng thứ nhất có chiều dài là 5,2 m và chiều rộng 3,4 m. Căn phòng thứ hai có chiều dài là 4,8 m chiều rộng là 3,7 m. Hỏi căn phòng nào có diện tích lớn hơn và lớn hơn bao nhiêu mét vuông?

Lời giải:

Diện tích căn phòng thứ nhất là:

5,2 × 3,4 = 17,68 (m²)

Diện tích cân phòng thứ hai là:

4,8 × 3,7 = 17,76 (m²)

Suy ra diện tích căn phòng thứ hai lớn hơn phòng thứ nhất là:

17,76 – 17,68 = 0,08 (m²)

Vậy diện tích căn phòng thứ hai lớn hơn và hơn 0,08 m².

Câu 41: Hiệu của 2 số là 33, lấy số lớn chia cho số nhỏ được thương là 3 và số dư là 3. Tìm 2 số đó.

Lời giải:

Theo bài ra ta có:

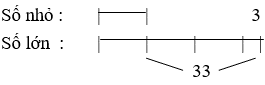
Số nhỏ là: (33 – 3) : 2 = 15

Số lớn là: 33 + 15 = 48

Vậy hai số cần tìm là 15 và 48.

Câu 42: Lãi suất tiết kiệm là 0,65% / tháng. Để sau một tháng nhận được tiền lãi là 832 000 đồng thì khách hàng phải gửi số tiền gốc là bao nhiêu?

Lời giải:

Khách hàng phải gửi số tiền vốn là:

832 000 : 0,65 . 100 = 128 000 000 (đồng)

Vậy khách hàng phải gửi 128 000 000 đồng để sau một tháng nhận 832 000 đồng tiền lãi.

Câu 43: Một người bỏ ra 450 000 đồng tiền vốn để mua một cây quạt. Người đó đã bán cây quạt với giá 486 000 đồng. Hỏi người đó lãi bao nhiêu phần trăm tiền vốn?

Lời giải:

Số tiền lãi là:

486 000 – 450 000 = 36 000 (đồng)

Người đó lãi số phần trăm là:

36 000 : 450 000 . 100 = 8%

Vậy người đó lãi 8% tiền vốn.

Câu 44: Một người mua hai hộp kẹo, mỗi hộp chứa 4 túi kẹo, mỗi túi có 125 g kẹo. Hỏi người đó mua mấy kg kẹo? [giải bằng hai cách].

Lời giải:

Cách 1:

4 túi kẹo nặng số g là:

125 × 4 = 500 (g)

2 hộp kẹo nặng số g là:

500 × 2 = 1000 (g)

Đổi 1000 g = 1 kg

Vậy người đó mua 1 kg kẹo.

Cách 2:

2 hộp kẹo có số túi kẹo là:

4 × 2 = 8 (túi)

2 hộp kẹo nặng số g là:

8 × 125 = 1000 (g)

Đổi 1000g = 1 kg

Vậy người đó mua 1 kg kẹo.

Câu 45: Một đoàn tàu gồm 15 toa, mỗi toa dài 14 m chạy với vận tốc 43,2 km/giờ  vượt qua một người đi bộ ngược chiều. Tính thời gian đoàn tàu vượt qua người đi bộ, biết vận tốc của người đi bộ là 4 km/giờ.

Lời giải:

Đoàn tàu đó dài là:

14 × 15 = 210 (m)

Đổi 210 m = 0,21 km

Tổng vận tốc của tàu và người đi bộ là:

43,2 + 4 = 47,2 (km/giờ)

Thời gian đoàn tàu vượt qua người đi bộ là: 

$\mathrm{0,21}:\mathrm{47,2}=\frac{21}{4720}$ (giờ)

Vậy sau $\frac{21}{4720}$  giờ thì tàu vượt qua người đi bộ.

Câu 46: Một cửa hàng đã bán được 240 kg gạo và số gạo đó bằng 12,5% tổng số gạo trước khi bán. Hỏi trước khi bán cửa hàng có mấy tấn gạo?

Lời giải:

Trước khi bán gạo, cửa hàng có số gạo là:

240 : 12,5 × 100 = 1920 (kg)

Đổi 1920 kg = 1,92 tấn

Vậy trước khi bán cửa hàng có 1,92 tấn gạo.

Câu 47: Tìm các ước của 10.

Lời giải:

Ta thấy 10 chia hết cho 1; 2; 5; 10 và các số đối của các số trên là –1; –2; –5; –10.

Suy ra Ư(10) = {1; 2; 5; 10; –1; –2; –5; –10}.

Câu 48: Nêu dấu hiệu chia hết cho cả 3 và 5.

Lời giải:

Số chia hết cho cả 3 và 5 là số có tổng các chữ số chia hết cho 3 và có tận cùng bằng 0 hoặc 5.

Ví dụ: 120; 135 ; ....

Câu 49:

a) Viết số tự nhiên nhỏ nhất có 3 chữ số.

b) Viết số tự nhiên nhỏ nhất có 3 chữ số khác nhau.

Lời giải:

a) Số tự nhiên nhỏ nhất có 3 chữ số là 100.

b) Số tự nhiên nhỏ nhất có 3 chữ số khác nhau là 102.

Câu 50: Theo kế hoạch, đội sản xuất phải trồng 15 ha rừng trong một năm.

a) Nửa năm đầu đội đã trồng được 7,8 ha rừng. Hỏi trong nửa năm đầu đội đã thực hiện được bao nhiêu phần trăm kế hoạch cả năm?

b) Đến hết năm đội đã trồng được tất cả 16,8 ha rừng. Hỏi đội đó đã thực hiện được bao nhiêu phần trăm và vượt mức kế hoạch bao nhiêu phần trăm?

Lời giải:

a) Nửa năm đầu đội đã thực hiện được số phần trăm kế hoạch là:

7,8 : 15 × 100 = 52%

b) Đội đó thực hiện được số phần trăm kế hoạch là:

16,8 : 15 × 100 = 112%

Như vậy đội đó đã vượt mức kể hoạch:

112 – 100 = 12%.