Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 65)

Câu 1: Tính:

a) 1 - 2 - 3 + 4 + 5 - 6 - 7 + 8 + ... + 2001 - 2002 - 2003 + 2004

b) 1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + 9 + ... + 2002 - 2003 - 2004 + 2005 + 2006

Lời giải:

a) 1 - 2 - 3 + 4 + 5 - 6 - 7 + 8 + ... + 2001 - 2002 - 2003 + 2004

S = (1 + 2 - 3 + 4) + (5 + 6 - 7 - 8) + ... + (2001 + 2002 - 2003 - 2004) + (2005 + 2006)

S = (-4) + (-4) + ... + (-4) + (2005 + 2006)

Dãy S có (2004 - 1) : 1 + 1 = 2004 (số hạng)

Dãy S có 2004 : 4 = 501 chữ số (-4)

Do đó S = (-4) . 501 = -2004

= -2004 + (2005 + 2006)

= -2004 + 4011 = 2007

b) 1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + 9 + ... + 2002 - 2003 - 2004 + 2005 + 2006

S = 1 + (2 - 3 - 4 + 5) + (6 - 7 - 8 + 9) + ... + (2002 - 2003 - 2004 + 2005) + 2006

S = 1 + 0 + 0 + ... + 0 + 2006 = 2007

Câu 2: Điền số thích hợp vào chỗ chấm: 2, 3, 5, 6, 4, 7, 9, 12, 10, 12, 16, 18, 15, 19, 20...

Lời giải:

Trong mỗi dãy gồm bốn số, tổng của hai số ở giữa bằng tổng của số đầu với số cuối: 3 + 5 = 2 + 6, 4 + 12 = 7 + 9, 10 + 18 = 12 + 16.

Vậy số cần điền là: 19 + 20 - 15 = 24

Câu 3: Tìm số dư của phép chia 22,4 : 18

Lời giải:

22,4 : 18 = 1 dư 4,4

Câu 4: Tính: 367 + (-30) + 1672 + (-337).

Lời giải:

367 + (-30) + 1672 + (-337)

= (367 - 337) - 30 + 1672

= 330 - 30 + 1672

= 300 + 1672 = 1972

Câu 5: Tính: 367 + (-30) + 2009 + (-337) + (-2010).

Lời giải:

367 + (-30) + 2009 + (-337) + (-2010)

= (367 - 337) - 30 + (2009 - 2010)

= 330 - 30 - 1

= 300 - 1 = 299

Câu 6: Tính tổng: S = 1 - 3 + 5 - 7 + ... + 2001 - 2003

Lời giải:

S = 1 - 3 + 5 - 7 + ... + 2001 - 2003

S = (1 - 3) + (5 - 7) + ... + (2001 - 2003)

S = (-2) + (-2) + ... + (-2)  (501 số hạng)

S = (-2) . 501

S = -1002

Vậy S = -1002

Câu 7: Tính nhanh: 37 . 444 - 144 . 111 + 15

Lời giải:

37 . 444 - 144 . 111 + 15

= 37 . 4 . 111 - 144 . 111 + 15

= 148 . 111 - 144 . 111 + 15

= 111 . (148 - 144) + 15 = 459

Câu 8: Cho dãy số 1; 2; 3; 4; 5; ...; x. Tìm x để số của dãy gấp 4,5 lần x.

Lời giải:

Số chữ số trong các dãy có một chữ số là:

(9 - 1) .1 .1 = 9 (chữ số)

Số chữ số trong các dãy có hai chữ số là:

(90 - 10 + 1) . 2 = 180 (chữ số)

Số chữ số trong các dãy có ba chữ số là:

(999 - 100 + 1) . 3 = 2700 (chữ số)

Số chữ số trong các dãy có bốn chữ số là:

(9999 - 1000 + 1) . 4 = 36 000 (chữ số)

Ta có thể coi số chữ số có trong dãy số có 5 chữ số là: (x - 10 000 + 1) . 5

Theo đề bài, ta có:

(x - 10 000 + 1) . 5 + 9 + 180 + 2700 + 36 000 = x . 4,5

⇒ x . 5 - 50 000 + 5 + 2889 + 36 000 = x . 4,5

⇒ x . 0,5 = 6111

⇒ x = 12 222

Vậy x = 12 222

Câu 9: Chứng minh 5x + 47y là bội của 17 khi và chỉ khi x + 6y là bội của 17.

Lời giải:

Với x + 6y chia hết cho 17

Ta có: 3(5x + 47y) + 2(x + 6y)

= 15x + 141y + 2x + 12y

= 17x + 153y chia hết cho 17

Mặt khác 2(x + 6y) chia hết cho 17

⇒ 3(5x + 47y) chia hết cho 17

Mà ƯCLN(5, 47) = 1.

Do đó 5x + 47y chia hết cho 17 (đpcm)

Câu 10: Một tấm bìa quảng cáo hình chữ nhật có chiều dài gấp 4 lần chiều rộng và diện tích bằng 1 m². Phải dùng bao nhiêu mét nhôm để viền xung quanh tấm biển đó?

Lời giải:

Vì chiều dài gấp 4 lần chiều rộng nên chiều dài ứng với một phần thì chiều rộng ứng với 4 phần.

Theo bài ra, ta có hình chữ nhật gồm 4 ô vuông, chiều rộng một phần (ứng với cạnh của hình vuông), chiều dài ứng với 4 phần (4 lần cạnh hình vuông)

Diện tích 1 ô vuông là: 1 : 4 = 0,25 (cm²)

Vì 0,25 = 0,5 × 0,5 nên suy ra độ dài cạnh hình vuông (chiều rộng hình chữ nhật) là 0,5 m

Khi đó, chiều dài hình chữ nhật là: 0,5 × 4 = 2 (m)

Số mét nhôm cần dùng là: (2 + 0,5) × 2 = 5 (m)

Đáp số: 5 mét.

Câu 11: Một hình chữ nhật có chiều rộng 8 cm, chiều dài gấp 3 lần chiều rộng. Tính diện tích và chu vi hình đó.

Lời giải:

Chiều dài hình chữ nhật là:

8 × 3 = 24 (cm)

Diện tích hình chữ nhật là:

8 × 24 = 192 (cm²)

Chu vi hình chữ nhật là:
(24 + 8) × 2 = 64 (cm)

Đáp số: Diện tích là 192 cm²

Chu vi là 64 cm

Câu 12: Một mảnh đất hình chữ nhật có chiều dài 36 m, chiều rộng bằng $\frac{1}{4}$chiều dài. Hãy tính diện tích mảnh đất đó ?

Lời giải:

Chiều rộng của mảnh đất hình chữ nhật đó là:

36 : 4 = 9 (m)

Diện tích của mảnh đất hình chữ nhật đó là:

36 × 9 = 324 (m²)

Đáp số: 324 m².

Câu 13: Người ta xếp 187 250 cái áo vào các hộp, mỗi hộp 8 áo. Hỏi có thể xếp được vào nhiều nhất bao nhiêu hộp và còn thừa mấy cái áo?

Lời giải:

Ta có: 187 250 : 8 = 23 406 (dư 2)

Vậy ta có thể xếp được vào nhiều nhất 23 406 hộp và còn thừa 2 cái áo         

Đáp số: 23 406 hộp và còn thừa 2 cái áo

Câu 14: Người ta đổ đều 128 610 lít xăng vào 6 bể. Hỏi mỗi bể đó có bao nhiêu lít xăng?

Lời giải:

Số lít xăng ở mỗi bể là:

128 610 : 6 = 21 435 (l)

Đáp số: 21 435 lít.

Câu 15: Bố hơn con 30 tuổi, biết 5 năm nữa tổng số tuổi của hai bố con là 62 tuổi. Tính tuổi 2 bố con hiện nay.

Lời giải:

Tuổi bố 5 năm trước là:

(62 + 30) : 2 = 46 (tuổi)

Tuổi con 5 năm trước là:

62 - 46 = 16 (tuổi)

Tuổi bố hiện nay là:

46 + 5 = 51 (tuổi)

Tuổi con hiện nay là:

16 + 5 = 21 (tuổi)

Đáp số: Tuổi bố: 51 tuổi;

   Tuổi con: 21 tuổi.

Câu 16: Bố năm nay 30 tuổi sau 5 năm nữa tuổi bố gấp 5 lần tuổi con. Hỏi năm nay con bao nhiêu tuổi?

Lời giải:

Tuổi bố sau 5 năm nữa là:

30 + 5 = 35 (tuổi)

Tuổi con sau 5 năm nữa là:

35 : 5 = 7 (tuổi)

Tuổi con bây giờ là:

7 - 5 = 2 (tuổi)

Đáp số: 2 tuổi.

Câu 17: Thùng to có 21 l dầu, thùng bé có 15 l dầu. Số dầu đó được chứa vào các chai như nhau, mỗi chai có 0,75 l. Hỏi tất cả bao nhiêu chai dầu ?

Lời giải:

Tổng số lít dầu của cả hai thùng là:

21 + 15 = 36 (l)

Có tất cả số chai dầu là:

36 : 0,75 = 48 (chai)

Đáp số : 48 chai dầu

Câu 18: Tích của hai số là 34,6. Nếu gấp thừa số thứ nhất lên 2 lần và gấp thừa số thứ hai lên 4 lần thì tích của hai số mới là bao nhiêu?

Lời giải:

Ta có: Gấp thừa số thứ nhất lên 2 lần, thừa số thứ hai lên 4 lần đồng nghĩa với việc thừa số sẽ được gấp lên 2 lần và 4 lần.

Vậy, tích mới của 2 số là:

34,6 × 2 × 4 = 276,8

Đáp số: 276,8

Câu 19: Tính nhanh: 20,14 × 6,8 + 20,14 × 3,2.

Lời giải:

20,14 × 6,8 + 20,14 × 3,2

= 20,14 × (6,8 + 3,2)

= 20,14 × 10 = 201,4.

Câu 20: Đơn giản biểu thức sau khi bỏ ngoặc:

a) (a + b - c) - (b - c + d);

b) -(a - b + c) + (a - b + d);

c) (a + b) - (-a + b - c);

d) -(a + b) + (a + b + c);

e) (a - b + c) - (a - b + c);

f) -(a - b - c) + (a - b - c).

Lời giải:

a) (a + b - c) - (b - c + d)

= a + b - c - b + c - d

= a + (b - b) + (-c + c) - d

= a - d

b) -(a - b + c) + (a - b + d)

= -a + b - c + a - b + d

= (a - a) + (b - b) - c + d

= d - c.

c) (a + b) - (-a + b - c)

 = a + b + a - b + c

= (a + a) + (b - b) + c

= 2a + c.

d) -(a + b) + (a + b + c)

= -a - b + a + b + c

= (-a + a) + (-b + b) + c = c.

e) (a - b + c) - (a - b + c)

= a - b + c - a + b - c

= (a - a) + (-b + b) + (c - c) = 0.

f) -(a - b - c) + (a - b - c)

= -a + b + c + a - b - c

= (-a + a) + (b - b) + (c - c) = 0.

Câu 21: Tính hợp lý : (-2020) - 2018 - 2016 - ... - 2008.

Lời giải:

(-2020) - 2018 - 2016 - ... - 2008

= -(2008 + ... + 2016 + 2018 + 2020)

= {(2020 . 2008) . [(2020 - 2018) : 2 + 1] : 2}

= -(4028 . 7 : 2)

= -(2014 . 7)

= -14098

Câu 22: Tìm số tự nhiên nhỏ nhất chia cho 5 dư 1, chia cho 7 dư 5.

Lời giải:

Gọi số đó là A (A ∈ ℕ*)

Vì A chia cho 5 dư 1, chia cho 7 dư 5 nên ta có:

A = 5k + 1 = 7h + 5 (∀k, h ∈ ℕ*)

⇒ A + 9 = 5k + 1 + 9 = 5k + 10 = 5.(k + 2)

A + 9 = 7h + 5 + 9 = 7h + 14 = 7.(h + 2)

⇒ A + 9 chia hết cho 5 và 7

⇒ A + 9 là BCNN(5, 7)

Mà ƯCLN(5, 7) = 1 nên BCNN(5, 7) = 5 . 7 = 35

⇒ A + 9 = 35

⇒ A = 35 - 9 = 26

Vậy số cần tìm là 26

Câu 23: Tìm số tự nhiên có hai chữ số, biết rằng nếu viết thêm chữ số 0 vào giữa chữ số hàng chục và hàng đơn vị của nó ta được 1 số gấp 7 lần số đó

Lời giải:

Ta có số cũ dạng $\overline{ab}$, số mới $\overline{a0b}$

Ta có: a . 100 + b = (a . 10 + b) . 7

a . 100 + b = a . 70 + b . 7

a . 30 = b . 6 ⇒ a . 5 = b . 1

Vậy số đó là 15

Câu 24: Một thửa ruộng hình chữ nhật có chu vi 96 m, chiều rộng ngắn hơn chiều dài 30 m. Tính diện tích của thửa ruộng ?

Lời giải:

Nửa chu vi thửa ruộng đó là:

96 : 2 = 48 (m)

Chiều dài thửa ruộng đó là:

(48 + 30) : 2 = 39 (m)

Chiều rộng thửa ruộng đó là:

48 - 39 = 9 (m)

Diện tích thửa ruộng đó là:

39 × 9 = 351 (m²)

Đáp số: 351 m².

Câu 25: Cho dãy số tự nhiên liên tiếp từ 1 đến n. Tìm n biết rằng tổng các số hạng đó bằng 190.

Lời giải:

Số số hạng của dãy số tự nhiên liên tiếp từ 1 đến n là n.

Tổng của các dãy số đó là: (n + 1) × n : 2

Có: (n + 1) × n : 2 = 190

(n + 1) × n = 190 × 2 = 380 = 19 × 20

Suy ra n = 19.

Câu 26: Đâu là cạnh kề cạnh đối cạnh huyền trên tam giác vuông

Lời giải:

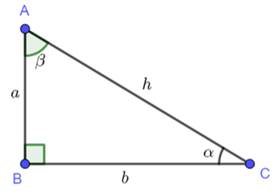
Giả sử ta có tam giác vuông như hình vẽ

Với góc a < 90^° ta có b là cạnh kề, a là cạnh đối, h là cạnh huyền.

Với góc b < 90^° ta có a là cạnh kề, b là cạnh đối, h là cạnh huyền.

Tóm lại :

Cạnh huyền là cạnh đối diện góc vuông,

Cạnh kề là cạnh góc vuông kề với góc đó,

Cạnh đối là cạnh góc vuông đối diện với góc đó

Câu 27: Cho tam giác ABC, trọng tâm G.

a) Vẽ đường thẳng d qua G, cắt các đoạn thẳng AB, AC. Gọi A', B', C' là hình chiếu của A, B, C trên d. Tìm liên hệ giữa các độ dài AA', BB', CC'

b) Nếu đường thẳng d nằm ngoài tam giác ABC và G' là hình chiếu của G trên d thì các độ dài AA', BB', CC', GG' có liên hệ gì ?

Lời giải:

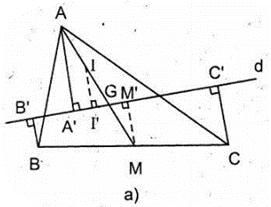
a) (Hình a) Lấy điểm I trên đường trung tuyến AM sao cho I là trung điểm của AG. Kẻ AA', BB', CC', II', MM' vuông góc với d.

Đáp số: AA' = BB' + CC'

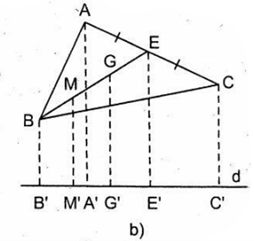
b) (Hình b) Gọi BE là đường trung tuyến của AC, M là trung điểm của BG. Vẽ AA', BB', CC', II', MM' vuông góc với d.

Ta có: MM' + EE' = 2GG'

⇒ 2MM' + 2EE' = 4GG'

⇒ BB' + GG' + AA' + CC' = 4GG'

⇒ AA' + BB' + CC' = 3GG'

Câu 28: Hai bạn Tùng và Hải thường đến thư viện đọc sách. Tùng cứ 8 ngày đến thư viện 1 lần, Hải cứ 10 ngày 1 lần. Lần đầu cả hai bạn cùng đến thư viện vào một ngày. Hỏi sau ít nhất bao nhiêu ngày thì hai bạn cùng đến thư viện?

Lời giải:

Gọi sau ít nhất m ngày thì hai bạn cùng đến thư viện (m ∈ ℕ*)

Vì số ngày ít nhất nên m là BCNN(8, 10)

Ta có: 8 = 2³; 10 = 2 . 5.

BCNN(8, 10) = 2³ . 5 = 40.

Vậy sau 40 ngày thì hai bạn cùng nhau đến thư viện.

Câu 29: Một cửa hàng trong một ngày bán được 3 tạ rưỡi gạo. Buổi sáng bán được 1 tạ rưỡi gạo, buổi chiều bán kém buổi tối là 60 kg. Hỏi buổi chiều và buổi tối, mỗi buổi bán được bao nhiêu tạ gạo ?

Lời giải:

Đổi 3 tạ rưỡi = 350 kg

1 tạ rưỡi  = 150 kg

Buổi chiều và buổi tối bán được số gạo là:

350 - 150 = 200 (kg)

Buổi chiều bán được số gạo là:

(200 - 60) : 2 = 70 (kg)

Buổi tối bán được số gạo là:

200 - 70 = 130 (kg)

Đổi 70 kg = 0,7 tạ

130 kg = 1,3 tạ

Câu 30: Giải phương trình: 2cos²(2x) + 3sin²(x) = 2.

Lời giải:

2cos²(x) + 3sin²(x) = 2

⇔ 2cos²(x) + 2sin²(x) + sin²(x) = 2 (do sin²(x) + cos²(x) = 1)

⇔ 2 + sin²(x) = 2

⇔ sin²(x) = 0

⇔ sin(x) = 0

⇔ x = kp (k ∈ ℤ)

Vậy phương trình đã cho có nghiệm x = kp (k ∈ ℤ)

Câu 31: Cho 10^k - 1 chia hết cho 19 với k > 1. Chứng minh rằng:

a) 10^2k - 1 chia hết cho 19.

b) 10^3k - 1 chia hết cho 19.

Lời giải:

a) 10^2k - 1 = (10^k)² - 1² ⋮ (10^k - 1)

Mà 10^k - 1 ⋮ 19

⇒ 10^2k - 1 ⋮ 19

b) 10^3k - 1 = (10^k)³ - 1³ ⋮ (10^k - 1)

mà 10^k - 1 ⋮ 19

⇒ 10^3k - 1 ⋮ 19

Câu 32: Cách đây 4 năm tuổi bố gấp 5 lần tuổi con. Tính tuổi của mỗi người hiện nay biết rằng bố hơn có 28 tuổi.

Lời giải:

Ta có sơ đồ:

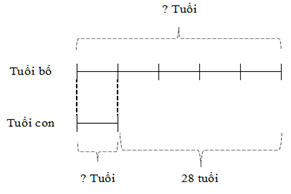
Theo sơ đồ, hiệu số phần bằng nhau là:

5 - 1 = 4 (phần)

Tuổi của bố là:
(28 : 4) . 5 + 4 = 39 (tuổi)

Tuổi của con là:

39 - 28 = 11 (tuổi)

Đáp số: Tuổi bố: 39 tuổi;

   Tuổi con: 11 tuổi.

Câu 33: Phân tích đa thức x³ + 2x - 3 thành nhân tử.

Lời giải:

x³ + 2x - 3 = x³ - x² + x² - x + 3x - 3

= x²(x - 1) + x(x - 1) + 3(x - 1)

= (x - 1)(x² + x + 3)

Câu 34: Phân tích đa thức thành nhân tử: x³ - 10x² + 25x.

Lời giải:

x³ - 10x² + 25x

= x(x² - 10x + 25)

= x(x² - 2 . x . 5 + 5²)

= x(x - 5)²

Câu 35: Một khu đất hình chữ nhật có chiều dài hơn chiều rộng 35 m. Nếu mỗi chiều tăng thêm 5 m thì diện tích tăng thêm 1450 m². Hỏi khu đất đó có diện tích là bao nhiêu héc-ta?

Lời giải:

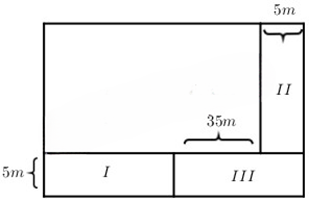
Theo đề bài ta có hình vẽ:

Chia phần tăng thêm thành ba hình chữ nhật như hình vẽ

Hình III có chiều rộng là 5 m, chiều dài là: 35 + 5 = 40 (m)

Diện tích hình III là:

40 × 5 = 200 (m²)

Hình I và hình II vì đều có chiều rộng bằng 5 m và chiều dài bằng chiều rộng cũ của khu đất

Tổng diện tích khu đất hình I và hình II là:

1450 - 200 = 1250 (m²)

Diện tích hình I hay hình II là:

1250 : 2 = 625 (m²)

Chiều rộng của khu đất là:

625 : 5 = 125 (m)

Chiều dài của khu đất là:

125 + 35 = 160 (m)

Diện tích của khu đất là:

160 × 125 = 20 000 (m²)

Đổi: 20 000 m² = 2 ha

Đáp số: 2 ha

Câu 36: Giải phương trình: 18 + 3(x - 2) = 63

Lời giải:

18 + 3(x - 2) = 63

⇔ 3(x - 2) = 63 - 18

⇔ 3(x - 2) = 45

⇔ x - 2 = 45 : 3

⇔ x - 2 = 15

⇔ x = 15 + 2

⇔ x = 17

Vậy nghiệm của phương trình đã cho là x = 17.

Câu 37: An, Bình, Chi mỗi bạn có một số nhãn vở, An có 27 nhãn vở. Nếu An chuyển cho Bình 3 nhãn vở, Bình chuyển cho Chi 1 nhãn vở thì 3 bạn có số nhãn vở bằng nhau. Hỏi:

a) Bình, Chi mỗi bạn có bao nhiêu nhãn vở?

b) Cả ba bạn có bao nhiêu nhãn vở?

Lời giải:

a) Sau khi An cho Bình 3 nhãn vở, Bình cho Chi 1 nhãn vở thì mỗi bạn có số nhãn vở là:

27 - 3 = 24 (nhãn vở)

Lúc đầu Bình có số nhãn vở là:

24 + 1 = 25 (nhãn vở)

Lúc đầu Chi có số nhãn vở là:

24 - 1 = 23 (nhãn vở)

b) Cả ba bạn có số nhãn vở là:

24 + 27 + 23 = 74 (nhãn vở)

Đáp số: a) Bình: 25 nhãn vở; Chi: 23 nhãn vở;

    b) 74 nhãn vở.

Câu 38: Cô giáo đem chia một số kẹo cho các em. Cô nhẩm tính, nếu chia cho mỗi em 5 chiếc thì thừa 3 chiếc, nếu chia cho mỗi em 6 chiếc thì thiếu 5 chiếc. Hỏi cô giáo có bao nhiêu cái kẹo?

Lời giải:

Số kẹo đủ để chia cho mỗi bạn 6 chiếc nhiều hơn số kẹo đủ để chia cho mỗi bạn 5 chiếc là:

3 + 5 = 8 (chiếc)

Số kẹo mỗi bạn được chia 6 chiếc nhiều hơn số kẹo mỗi bạn được chia 5 chiếc là:

6 - 5 = 1 (chiếc)

Số bạn có tất cả là:
8 : 1 = 8 (bạn)

Số kẹo có tất cả là:

8 × 5 + 3 = 43 (chiếc)

Đáp số: 43 chiếc kẹo

Câu 39: Chứng minh rằng không có số tự nhiên nào chia cho 15 dư 6 và chia 9 dư 1

Lời giải:

Giả sử số tự nhiên chia hết cho 15 dư 6 và chia 9 dư 1 là A

Do A chia hết cho 15 dư 6 suy ra A = 15m + 6 (m là số tự nhiên bất kì)

A chia hết cho 9 dư 1 suy ra A = 9n + 1 (n là số tự nhiên bất kì)

⇒ 15m + 6 = 9n + 1

⇒ 9n - 15m = 6 - 1 (Quy tắc chuyển vế)

⇒ 9n - 15m = 5

Ta lại có: $\left\{\begin{array}{l}9n⋮3\\ 15m⋮3\end{array}\right.\Rightarrow \left(9n-15m\right)⋮3$ (theo tính chất chia hết của một hiệu)

Khi đó 5 phải chia hết cho 3 (Vô lí)

Vậy không tồn tại số tự nhiên nào thoả mãn điều kiện chia hết cho 15 dư 6 và chia 9 dư 1

Câu 40: Hiện nay anh 13 tuổi và em 3 tuổi. Hỏi sau bao nhiêu năm nữa thì tuổi anh sẽ gấp 3 lần tuổi em?

Lời giải:

Anh hơn em số tuổi là:

13 - 3 = 10 (tuổi)

Vì mỗi năm mỗi người tăng thêm một tuổi nên anh luôn luôn hơn em 10 tuổi.

Số tuổi của anh gấp 3 lần số tuổi của em nên ta có sơ đồ hiệu tỉ 

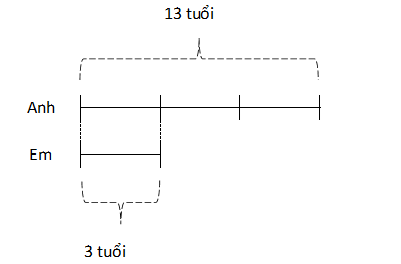
Theo sơ đồ, hiệu số phần bằng nhau là:

3 - 1 = 2 (phần)

Khi tuổi anh gấp 3 lần tuổi em thì khi đó tuổi em là:

10 : 2 = 5 (tuổi)

Vậy sau số năm tuổi anh gấp 3 lần tuổi em là:

5 - 3 = 2 (năm)

Đáp án: 2 năm

Câu 41: Lớp 5A có số học sinh nam nhiều hơn số học sinh nữ là 4 học sinh. Biết số học sinh nữ bằng $\frac{4}{5}$ số học sinh nam. Hỏi lớp 5A có bao nhiêu học sinh nam, bao nhiêu học sinh nữ ?

A. 18 học sinh nữ; 22 học sinh nam.

B. 22 học sinh nữ; 18 học sinh nam.

C. 16 học sinh nữ; 20 học sinh nam.

D. 20 học sinh nữ; 16 học sinh nam.

Lời giải:

Đáp án đúng là: C

Ta có sơ đồ:

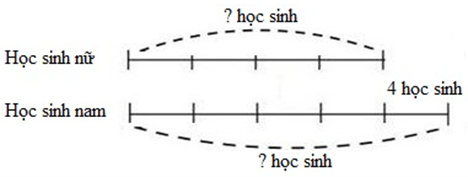
Theo sơ đồ, hiệu số phần bằng nhau là:

5 - 4 = 1 (phần)

Lớp 5A có số học sinh nữ là:

4 : 1 × 4 = 16 (học sinh)

Lớp 5A có số học sinh nam là:

16 + 4 = 20 (học sinh)

Đáp số: 16 học sinh nữ; 20 học sinh nam

Câu 42: Một vườn trẻ dự trữ gạo cho 120 em bé ăn trong 20 ngày. Sau đó có thêm một số em bé mới đến nên số ngày ăn giảm đi 4 ngày. Hỏi có bao nhiêu em bé mới đến thêm?

Lời giải:

Để ăn hết số gạo đó trong 1 ngày cần số em là:

120 × 20 = 2400 (em)

Số gạo còn ăn được trong số ngày nữa là:

20 - 4 = 16 (ngày)

Số em đến thêm là:

(2400 : 16) - 120 = 30 (em)

Đáp số: 30 em.

Câu 43: Tìm số tự nhiên nhỏ nhất chia cho 5, 7, 9 có số dư lần lượt là 3, 4, 5.

Lời giải:

Gọi số cần tìm là a

Giả sử a : 5 được b dư 3

⇒ a = 5b + 3

⇒ 2a = 10b + 6 = 10b + 5 + 1

⇔ 2a - 1 = 10b + 5 hay (2a - 1) ⋮ 5    (1)

Giả sử a : 7 được c dư 4

⇒ a = 7c + 4

⇒ 2a = 14c + 8 = 14c + 7 + 1

⇒ 2a - 1 = 14c + 7 hay (2a - 1) ⋮ 7     (2)

Giả sử a : 9 được d dư 5

⇒ a = 9d + 5

⇒ 2a = 18d + 10 = 18d + 9 + 1

⇒ 2a - 1 = 18d + 9 hay (2a - 1) ⋮ 9     (3)

Từ (1), (2), (3) suy ra (2a - 1) chia hết cho 5, 7 và 9.

Vì đề yêu cầu tìm số tự nhiên nhỏ nhất nên ta tìm bội chung nhỏ nhất của 5, 7, 9.

BCNN(5, 7, 9) = 5 . 7 . 9 = 315

⇒ 2a - 1 = 315

⇒ 2a = 316

⇒ a = 158

Vậy số cần tìm là 158.

Câu 44: Trước đây mua 5m vải phải trả 60 000 đồng. Hiện nay giá bán mỗi mét vải đã giảm 2000 đồng. Hỏi với 60 000 đồng, hiện nay có thể mua được bao nhiêu mét vải như thế?

Lời giải:

Trước đây giá 1 m vải là:

60 000 : 5 = 12 000 (đồng)

Hiện nay, giá 1 m vải là:

12 000 - 2000 = 10 000 (đồng)

Hiện nay, với 60 000 đồng có thể mua được:

60 000 : 10 000 = 6 (m)

Đáp số: 6 m vải.

Câu 45: Tìm 3 số, biết tổng số thứ nhất và số thứ hai là 182, tổng số thứ nhất và số thứ ba là 188, tổng số thứ hai và số thứ ba là 176.

Lời giải:

Tổng của ba số là:

(182 + 188 + 176) : 2 = 273

Số thứ nhất là:

273 - 176 = 97

Số thứ hai là:

273 - 188 = 85

Số thứ ba là:

273 - 182 = 91

Đáp số: Số thứ nhất: 97;

  Số thứ hai: 85;

  Số thứ ba: 91.

Câu 46: Tìm số tự nhiên A khác 0, biết rằng:

a) A lớn nhất; 360 chia hết cho A và 560 chia hết cho A.

b) A khác 0; A nhỏ nhất; A chia hết cho 15 và chia hết cho 25.

Lời giải:

a) Ta có: 360 và 560 chia hết cho A ⇒ A ∈ ƯC(360, 560)

Mặt khác: A lớn nhất nên A = ƯCLN(360, 560)

Ta có: 360 = 2³ . 3² . 5; 560 = 2⁴ . 5 . 7.

Do đó A = ƯCLN(360, 560) = 2³ . 5 = 40

Vậy A = 40.

b) Ta có: A chia hết cho 15 và 25 ⇒ A ∈ BC(15, 25)

Mặt khác A ≠ 0 và nhỏ nhất ⇒ A = BCNN(15, 25)

Ta có: 15 = 3 . 5; 25 = 5².

Do đó A = BCNN(15, 25) = 3 . 5² = 75.

Câu 47: Nếu chiều dài của một hình chữ nhật tăng lên gấp 3 lần, chiều rộng tăng lên gấp 2 lần thì diện tích hình chữ nhật đó tăng lên gấp mấy lần ?

Lời giải:

Nếu tăng chiều dài bao nhiêu lần thì diện tích tăng bấy nhiêu lần

Nếu tăng chiều rộng bao nhiêu lần thì diện tích tăng bấy nhiêu lần

Vậy diện tích tăng số lần là: 3 . 2 = 6 (lần)

Đáp số: 6 lần

Câu 48: Trong hộp có ba loại bi là bi trắng, bi xanh và bi đỏ. Biết tổng số viên bi trong hộp nhiều hơn tổng số bi trắng và viên bi đỏ là 48 viên bi, số viên bi xanh nhiều hơn bi viên bi trắng 5 viên và ít hơn viên bi đỏ 12 viên. Tính tổng số viên bi trong hộp ?

Lời giải:

Ta có số bi xanh là 48 viên

Số bi trắng là:

48 - 5 = 43 (viên)

Số bi đỏ là:

48 + 12 = 60 (viên)

Tổng số viên bi trong hộp là:

48 + 43 + 60 = 151 (viên)

Đáp số: 151 viên

Câu 49: Tính M = 1² + 2² + 3² + ... + 99² + 100²

Lời giải:

Ta có: M = 1² + 2² + 3² + ... + 99² + 100²

= 1 + 2(1 + 1) + ... + 99(98 + 1) + 100(99 + 1)

= 1 + 1.2 + 2 + ... + 98.99 + 99 + 99.100 + 100

= (1.2 + 2.3 + ... + 99.100) + (1 + 2 + ... + 99 + 100)

= 333 300 + 5050 = 338 050

Câu 50: Cho 4 số tự nhiên không chia hết cho 5 khi chia hết cho 5 được những số dư khác nhau. Chứng minh rằng tổng của chúng chia hết cho 5

Lời giải:

Gọi 4 số đó là a + 1; a + 2; a + 3; a + 4

4 số đó chia cho 5 được những số dư khác nhau ⇒ Các số dư là 1; 2; 3 và 4

Giả sử (a + 1) : 5 dư 1; ....

⇒ [(a + 1) - 1] = a ⋮ 5; ...

Tổng của chúng là:

(a + 1) + (a + 2) + (a + 3) + (a + 4) = a + 1 + a + 2 + a + 3 + a + 4

= 5a + 1 + 2 + 3 + 4 = 5a + 10

Vì 5a ⋮ 5 và 10 ⋮ 5

⇒ Tổng của 4 số chia hết cho 5