Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 64)

Câu 1: Trung bình cộng của 4 số bằng 25 .Trung bình cộng của 3 số đầu bằng 22. Trung bình cộng của 3 số cuối bằng 20. Tìm trung bình cộng của số thứ 2 và số thứ 3?

Lời giải:

Tổng của 4 số là: 25 × 4 = 100 

Tổng của 3 số đầu là: 22 × 3 = 66 

Tổng của 3 số cuối là: 20 × 3 = 60 

Số thứ nhất là: 100 − 60 = 40 

Số thứ tư là: 100 − 66 = 34 

Tổng của số thứ hai và số thứ ba là: 100 − (40 + 34) = 26 

Trung bình cộng của số thứ 2 và số thứ ba là: 26 : 2 = 13 

Đáp số: 13.

Câu 2: Trung bình cộng của 4 số là 20, biết trung bình cộng của 3 số đầu là 25. Số thứ tư là bao nhiêu?

Lời giải:

Tổng bốn số là: 20 × 4 = 80

Tổng ba số đầu là: 25 × 3 = 75

Số thứ tư là: 80 − 75 = 5

Đáp số: 5.

Câu 3: Trung bình cộng của ba số là 120, biết rằng số thứ ba bằng $\frac{1}{2}$ trung bình cộng của hai số còn lại. Tìm số thứ ba?

Lời giải:

Tổng của ba số là: 120 × 3 = 360

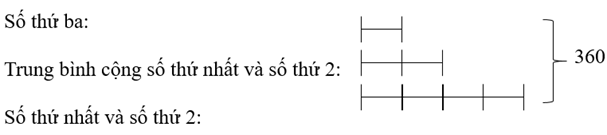
Tổng số phần là: 1 + 4 = 5 (phần)

Số thứ ba là: 360 : 5 = 72

Đáp số: 72.

Câu 4: Trung bình cộng của ba số là 21. Tìm ba số đó biết số thứ ba gấp 3 lần số thứ 2, số thứ hai gấp 2 lần số thứ nhất?

Lời giải:

Tổng của ba số là: 21 × 3 = 63

Vì số thứ ba gấp 3 lần số thứ hai và số thứ hai gấp 2 lần số thứ nhất nên số thứ ba gấp 6 lần số thứ nhất.

Ta có sơ đồ:

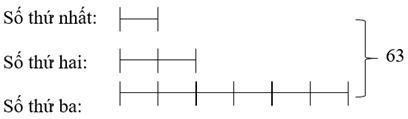
Theo sơ đồ, tổng số phần bằng nhau là: 1 + 2 + 6 = 9 (phần)

Số thứ nhất là: 63 : 9 = 7

Số thứ hai là: 7 × 2 = 14

Số thứ ba là: 7 × 6 = 42

Đáp số: Số thứ nhất: 7;

   Số thứ hai là 14;

   Số thứ ba là 42.

Câu 5: Tìm trung bình cộng của các số tự nhiên nhỏ hơn 1025.

Lời giải:

Dãy các số tự nhiên nhỏ hơn 1 025 là: 0; 1; 2; ….; 1 024.

Số số hạng của dãy là: (1 024 – 0) : 1 + 1 = 1 025 (số hạng)

Tổng các số của dãy là: (1 024 + 0) × 1025 : 2 = 524 800

Trung bình cộng của các số tự nhiên nhỏ hơn 1025 là: 524 800 : 1 025 = 512.

Đáp số: 512.

Câu 6: Trung bình cộng của hai số bằng 2016. Nếu tăng số thứ nhất lên 3 lần thì trung bình cộng của chúng bằng 4125. Tìm số thứ nhất.

Lời giải:

Tổng của hai số ban đầu là: 2 016 × 2 = 4 032

Tổng của hai số sau khi tăng số thứ nhất lên 3 lần là: 4 125 × 2 = 8 250

Phần tăng thêm chính là hai lần số thứ nhất.

Hai lần số thứ nhất là: 8 250 – 4 032 = 4 218

Số thứ nhất là: 4 218 : 2 = 2 019.

Đáp số: 2 019.

Câu 7: Trung bình cộng của ba số bằng 34. Nếu tăng số thứ nhất gấp hai lần thì trung bình cộng của chúng bằng 38. Nếu tăng số thứ hai gấp 3 lần thì trung bình cộng của chúng bằng 46. Tìm số thứ nhất và số thứ hai.

Lời giải:

Tổng của ba số là: 34 × 3 = 102

Tổng của ba số khi số thứ nhất gấp hai lần là: 38 × 3 = 114

Phần tăng thêm chính là số thứ nhất: 114 – 102 = 12

Tổng của ba số khi số thứ hai gấp 3 lần là: 46 × 3 = 138

Phần tăng thêm chính là hai lần số thứ hai

Hai lần số thứ hai là: 138 – 102 = 36

Số thứ hai là: 36 : 2 = 18

Đáp số: Số thứ nhất: 12;

   Số thứ hai là 18.

Câu 8: Tổng của hai số là 80. Số thứ nhất bằng $\frac{7}{9}$ số thứ hai. Tìm hai số đó?

Lời giải:

Ta có sơ đồ

Theo sơ đồ, tổng số phần bằng nhau là: 7 + 9 = 16 (phần)

Số thứ nhất là: 80 : 16 × 7 = 35

Số thứ hai là: 80 – 35 = 45

Đáp số: Số thứ nhất: 35;

   Số thứ hai:  45.

Câu 9: Cho M = 1 + 3 + 3² + 3³ + 3⁴ + …+ 3⁹⁹ + 3¹⁰⁰.

a) Tìm số dư khi chia M cho 13.

b) Tìm số dư khi chia M cho 40.

Lời giải:

a) Ta có: M = 1 + 3 + 3² + 3³ + 3⁴ + …+ 3⁹⁹ + 3¹⁰⁰

= (1 + 3) + (3² + 3³ + 3⁴) + …+ (3⁹⁸ + 3⁹⁹ + 3¹⁰⁰)

= 4 + 3² . (1 + 3 + 3²) + …+ 3⁹⁸ . ( 1 + 3 + 3²)

 4 + (3² + …+ 3⁹⁸) . 13

Do đó M chia cho 13 ta được số dư là 4.

b) Ta có: M = 1 + 3 + 3² + 3³ + 3⁴ + …+ 3⁹⁹ + 3¹⁰⁰

= 1 + (3 + 3² + 3³ + 3⁴) + …+ (3⁹⁷ + 3⁹⁸ + 3⁹⁹ + 3¹⁰⁰)

= 1 + 3.(1 + 3 + 3² + 3³) + …+ 3⁹⁷ . ( 1 + 3 + 3² + 3³)

= 1 + (3 + …+ 3⁹⁷) . 40

Do đó M chia cho 40 ta được số dư là 1.

Câu 10: Tính: M = 1 + 3 + 3² + 3³ + …+ 3¹¹ + 3¹².

Lời giải:

Ta có M = 1 + 3 + 3² + 3³ + …+ 3¹¹ + 3¹²

Suy ra 3M = 3 + 3² + 3³ + …+ 3¹² + 3¹³

Do đó 3M – M = 3¹³ – 1

Hay 2M = 3¹³ – 1

Do đó $M=\frac{3^{13}-1}{2}$.

Câu 11: Một hình chữ nhật có chu vi là bằng 88 m. Nếu tăng chiều rộng lên 8m thì hình chữ nhật trở thành hình vuông. Tính diện tích hình chữ nhật?

Lời giải:

Nửa chu vi của hình chữ nhật là:

88 : 2 = 44 (m)

Vì nếu tăng chiều rộng thêm 8 m thì hình chữ nhật trở thành hình vuông nên chiều dài hơn chiều rộng 8 m.

Chiều rộng của hình chữ nhật là:

(44 − 8) : 2 = 18 (m)

Chiều dài của hình chữ nhật là:

44 − 18 = 26  (m)

Diện tích của hình chữ nhật là:

18 × 26 = 468 (m²)

Đáp số : 468 m².

Câu 12: Tìm số tự nhiên, biết rằng khi chia 147 và 193 cho n thì số dư lần lượt là 17 và 11.

Lời giải:

Vì 147 chia cho n dư 17 và 193 chia cho n dư 11 nên ta có:

$$\begin{gathered} \left\{\begin{array}{l}\left(147-17\right)⋮n\\ \left(193-11\right)⋮n\end{array}\right. \\ \Rightarrow \left\{\begin{array}{l}130⋮n\\ 182⋮n\end{array}\right. \end{gathered}$$

⇒ n ∈ ƯC(130, 182)

Ta có 130 = 2 . 5 . 13; 182 = 2 . 7 . 13

⇒ ƯCLN(130, 182) = 2 . 13 = 26

⇒ ƯC(130, 182) = Ư(26) = {1; 2; 13; 26}

⇒ n ∈ {1; 2; 13; 26}.

Vậy n ∈ {1; 2; 13; 26}.

Câu 13: Tìm một số, biết 15% của số đó là 75.

A. 11,925;

B. 50;

C. 500;

D. 5.

Lời giải:

Đáp án đúng là: C

Số cần tìm là:

75 : 15% = 500.

Đáp số: 500.

Câu 14: An chia một số cho 40 được thương là 80 và có dư. Biết số dư là số lớn nhất có thể. Hỏi An chia số nào cho 40?

Lời giải:

Số dư lớn nhất có thể là 39 vì số chia là 40.

Số mà An cần tìm là: 40 × 80 + 39 = 3239.

Đáp số: 3239.

Câu 15: Đội tuyển thi đá cầu và đấu cờ vua của Trường Tiểu học Võ Thị Sáu có 22 em, trong đó có 15 em thi đá cầu và 12 em thi đấu cờ vua. Hỏi có bao nhiêu em trong đội tuyển thi đấu cả hai môn ?

Lời giải:

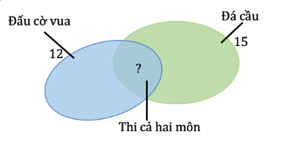
Dựa vào hình vẽ, ta thấy số em chỉ thi đá cầu là: 

22 – 12 = 10 (em)

Số em trong đội tuyển thi đấu cả hai môn là:

15 – 10 = 5 (em)

Đáp số: 5 em.

Câu 16: Mỗi hộp kẹo cân nặng 0,25kg; mỗi hộp bánh cân nặng 0,125 kg. Hỏi 15 hộp kẹo và 18 hộp bánh cân nặng bao nhiêu ki - lô - gam?

Lời giải:

15 hộp kẹo cân nặng là:

0,25 × 15 = 3,75 (kg)

18 hộp bánh cân nặng là:

0,125 × 18 = 2,25 (kg)

15 hộp kẹo và 18 hộp bánh cân nặng là:

3,75 + 2,25 = 6 (kg)

Đáp số: 6 kg.

Câu 17: Cho S = 1 + 3 + 3² + … + 3³⁰. Tìm chữ số tận cùng của S. Từ đó, suy ra S không phải là số chính phương.

Lời giải:

Ta có S = 1 + 3 + 3² + … + 3³⁰

= (1 + 3 + 3² + 3³) + (3⁴ + 3⁵ + 3⁶ + 3⁷) +…+ (3²⁴ + 3²⁵ + 3²⁶ + 3²⁷) + 3²⁸ + 3²⁹+ 3³⁰

= (1 + 3 + 3² + 3³) + 3⁴.(1 + 3 + 3² + 3³) +…+ 3²⁴.(1 + 3 + 3² + 3³) + 3²⁸ + 3²⁹ + 3³⁰

= 40 + 3⁴ . 40+…+ 3²⁴ . 40 + 3²⁸ + 3²⁹ + 3³⁰

= 40 . (1 + 3⁴ + … + 3²⁴) + 3²⁸ + 3²⁹ + 3³⁰

= 4 . 10 . (1 + 3⁴ + … + 3²⁴) + 3²⁸ + 3²⁹ + 3³⁰

Nhận thấy 4 . 10 . (1 + 3⁴ + … + 3²⁴) có chữ số tận cùng là 0.

• 3²⁸ = 3^4.7 = …1

• 3²⁹ = 3²⁸.3 = …1 × 3 = …3

• 3³⁰ = 3²⁸.3² = …1 × 9 = …9

Tổng S có tận cùng là: 0 + 1 + 3 + 9 = …3.

Vì số chính phương không có tận cùng là 3 nên S không là số chính phương.

Câu 18: Người ta trồng lúa trên một thửa ruộng hình chữ nhật có chiều rộng là 35m, chiều dài bằng $\frac{7}{5}$ chiều rộng. Cứ trung bình 1m² thửa ruộng đó thu hoạch được 20kg thóc. Hỏi cả thửa ruộng trên thu hoạch được bao nhiêu tấn thóc?

Lời giải:

Chiều dài của thửa ruộng hình chữ nhật đó là:

$35\times \frac{7}{5}=49$ (m)

Diện tích của thửa ruộng hình chữ nhật đó là:

49 × 35 = 1 715 (m²)   

Số tấn thóc thu hoạch được trên thửa ruộng đó là:

1 715 × 20 = 34 300 (kg) 

Đổi: 343 00 kg =  34,3 tấn thóc.

Đáp số: 34,3 tấn thóc.

Câu 19: Cho n ∈ ℤ, chứng minh A = n⁴ – 4n³ – 4n² + 16n chia hết cho 384 với mọi n chẵn.

Lời giải:

A = n⁴ – 4n³ – 4n² + 16n

A = n(n³ – 4n² – 4n + 16)

A = n(n – 4)(n² – 4)         (1)

Vì n là số chẵn nên n = 2k (k là số nguyên dương) thay vào (1), ta được:

A = 2k(2k – 4)(4k² – 4) 

A = 16k(k – 2)(k – 1)(k + 1) 

A = 16(k – 2)(k – 1)k(k + 1)      (2)

Do (k – 2)(k – 1)k(k + 1)  là tích của 4 số nguyên liên tiếp nên tích này luôn chia hết cho 3 và 8, mà ƯC(3, 8) = 1 nên (k – 2)(k – 1)k(k + 1) chia hết cho 24                (3)

Từ (2) và (3), suy ra  A = n⁴ – 4n³ – 4n² + 16n chia hết cho 384.

Câu 20: Lúc 8 giờ sáng, một người đi xe máy từ A với vận tốc 45 km/giờ về phía B. Cùng thời điểm đó, tại điểm C (trên đường từ A đến B) cách A 20 km, một người đi xe đạp với vận tốc 15 km/giờ cũng đi về phía B. Hỏi lúc mấy giờ thì hai xe gặp nhau?

Lời giải:

Hiệu vận tốc hai xe là: 45 – 15 = 30 (km/giờ)

Thời gian để hai xe gặp nhau là:

20 : 30 = $\frac{2}{3}$(giờ) = 40 (phút)

Hai xe gặp nhau lúc:

8 giờ + 40 phút = 8 giờ 40 phút.

Đáp số: 8 giờ 40 phút.

Câu 21: Một người đi xe đạp, trong 3 giờ đầu mỗi giờ đi được 10,8 km, trong 4 giờ tiếp theo mỗi giờ đi được 9,52 km. Hỏi người đó đi được bao nhiêu ki-lô-mét?

Lời giải:

Trong 3 giờ đầu người đó đi được:

10,8 × 3 = 32,4 (km)

Trong 4 giờ tiếp người đó đi được:

9,52 x 4 = 38,08 (km)

Người đó đã đi được tất cả:

32,4 + 38,08 = 70,48 (km)

Đáp số: 70,48 (km).

Câu 22: Tổng của hai số là 780. Biết số bé là số có hai chữ số và khi viết thêm chữ số 6 vào bên trái số bé thì ta được số lớn. Tìm hai số đó.

Lời giải:

Vì viêt số 6 vào bên trái số bé thì ta được số lớn nên số lớn hơn số bé 600 đơn vị.

Do đó, số lớn là: (780 + 600) : 2 = 690.

Số bé là: 690 – 600= 90

Đáp số: Số lớn: 690;

   Số bé : 90.

Câu 23: Trung bình cộng của ba số là 120. Hỏi cần thêm vào số nào để trung bình cộng của các số nhận được là 110?

Lời giải:

Tổng của ba số là: 120 × 3 = 360

Tổng của bốn số là: 110 × 4 = 440

Số cần thêm là: 440 – 360 = 80.

Đáp số: 80.

Câu 24: Tìm ba số có trung bình cộng bằng 120, biết rằng nếu viết thêm chữ số 0 vào bên phải số thứ nhất thì được số thứ hai và số thứ ba gấp 4 lần số thứ nhất?

Lời giải:

Tổng của ba số là: 120 × 3 = 360

Nếu viết thêm chữ số 0 vào bên phải số thứ nhất thì được số thứ hai, vậy số thứ hai gấp 10 lần số thứ nhất

ta có sơ đồ:

 

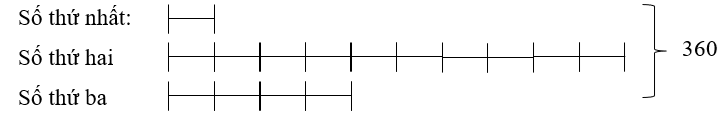
Tổng số phần bằng nhau là:

1 + 10 + 4 = 15 (phần)

Số thứ nhất là:

360 : 15 × 1 = 24

Số thứ hai là:

24 × 10 = 240

Số thứ ba là:

360 − (24 + 240) = 96

     Đáp số: Số thứ nhất: 24

                    Số thứ hai: 240

                    Số thứ ba: 96.

Câu 25: Tìm 7 số tự nhiên liên tiếp biết trung bình cộng của chúng bằng số lẻ bé nhất có 2 chữ số?

Lời giải:

Số lẻ bé nhất có hai chữ số là 11.

Vì trung bình cộng của chúng là số hạng ở giữa. Do đó số hạng thứ 4 là 11.

Vậy 7 số liên tiếp đó là 8; 9; 10; 11; 12; 13; 14.

Câu 26: Tìm hai số chẵn biết rằng tổng của chúng là 40 đơn vị và giữa hai số đó có đúng một số chẵn?

Lời giải:

Vì giữa hai số đó có đúng một số chẵn nên hiệu của hai số chẵn đó là 2 đơn vị.

Số chẵn lớn là: (40 + 2) : 2 = 22

Số chẵn bé là: 40 – 22 = 18

Đáp số: 18 và 22.

Câu 27: Hiện nay ông hơn cháu 59 tuổi. Ba năm nữa, tổng số tuổi hai ông cháu là 81 tuổi. Tính tuổi mỗi người hiện nay?

Lời giải:

Mỗi năm mỗi người tăng thêm 1 tuổi

Tổng số tuổi của hai ông cháu hiện nay là:

81 – 3 – 3 = 75 (tuổi)

Tuổi của cháu hiện nay là: (75 – 59) : 2 = 8 (tuổi)

Tuổi của ông hiện nay là: 8 + 59 = 67 (tuổi)

Đáp số: Tuổi cháu: 8 tuổi

              Tuổi ông: 67 tuổi.

Câu 28: Để lát nền một căn phòng hình chữ nhật, người ta dùng loại gạch men hình vuông có cạnh 30 cm. Hỏi cần bao nhiêu viên gạch để lát kín nền căn phòng đó, biết rằng căn phòng có chiểu rộng 6 m, chiều dài 9 m? (Diện tích phần mạch vữa không đáng kể)

Lời giải:

Diện tích nền căn phòng là:

9 × 6 = 54 (m²)

Đổi: 54 m² = 5 400 dm²;  30 cm = 3 dm

Diện tích một viên gạch là:

3 × 3 = 9 (dm²)

Số viên gạch cần dùng là:

5 400 : 9 = 600 (viên)

Đáp số: 600 viên gạch.

Câu 29: Phân tích đa thức 4a² – 4b² – 4a + 1 thành nhân tử.

Lời giải:

4a² – 4b² – 4a + 1

= (4a² – 4a + 1) – 4b²

= (2a − 1)² – 4b²

= (2a – 2b −1)(2a + 2b −1)

Câu 30: Điền vào chỗ chấm

a) 5 tấn 8 tạ = …. kg

b) 8 tấn 5 tạ = …. kg

Lời giải:

a) 5 tấn 8 tạ = 5 800 kg.

b) 8 tấn 5 tạ = 8 500 kg.

Câu 31: Tìm số tự nhiên x lớn nhất biết: x < 3,005.

Lời giải:

Vì x < 3,005 ⇒ x ∈ {0; 1; 2; 3}

Mà x là số tự nhiên lớn nhất nên x = 3.

Câu 32: Tìm số x tự nhiên lớn nhất biết 75 ⋮ x và 105 ⋮ x.

Lời giải:

Vì 75 ⋮ x và 105 ⋮ x nên x ∈ ƯC(75, 105)

Mà x là số tự nhiên lớn nhất nên x là ƯCLN(75, 105)

Có 75 = 3 . 5²; 105 = 3 . 5 . 7

⇒ x = ƯCLN(75, 105) = 3.5 = 15.

Vậy x = 15.

Câu 33: Giá gạo tháng 3 cao hơn tháng 2 là 20%. Giá gạo tháng 4 thấp hơn tháng 3 là 10%. Hỏi giá gạo tháng 4 so với tháng 2 cao hơn hay thấp hơn bao nhiêu %?

Lời giải:

Coi giá gạo tháng 2 là 100% thì giá gạo tháng 3 so với tháng 2 là:

100% + 20%  = 120%

Coi giá gạo tháng 3 là 100% thì giá gạo tháng 4 so với giá gạo tháng 3 là:

100% − 10% = 90%

Giá tháng 4 so với giá gạo tháng 2 là:

120% × 90% = 108%

Vậy giá gạo tháng 4 đắt hơn giá gạo tháng 2 là:

108% − 100% = 8%.

Đáp số: giá gạo tháng 4 cao hơn 8% so với giá gạo tháng 2.

Câu 34: Có 9 can nước mắm như nhau đựng tất cả 6,75 lít nước mắm. Hỏi 6 can nước mắm như thế đựng bao nhiêu lít nước mắm?

Lời giải:

Một can nước mắm đựng được số lít là:

6,75 : 9 = 0,75 (lít)

6 can nước mắm có số lít là:

0,75 × 6 = 4,5 (lít)

Đáp số: 4,5 lít.

Câu 35: Hình chữ nhật có nửa chu vi là 99 m. Nếu tăng chiều rộng thêm 5 m và giảm chiều dài đi 5 m thì diện tích không thay đổi. Tính chiều dài và chiều rộng.

Lời giải:

Chiều dài hình chữ nhật là:

(99 + 5) : 2 = 52 (m)

Chiều rộng hình chữ nhật là:

52 - 5 = 47 (m)

Đáp số: Chiều dài: 52 m;

   Chiều rộng: 47 m.

Câu 36: Tìm số dư của phép chia 158 : 2,8 nếu chỉ lấy đến hai chữ số ở phần thập phân của thương.

Lời giải:

Ta có: 158 : 2,8 = 56,42 (dư 0,24)

Vậy số dư của phép chia 158 : 2,8 là 0,24.

Câu 37: Tính tổng: 1 + 3 + 5 + 7 + ... + (2n - 1).

Lời giải:

Khoảng cách giữa các dãy số bằng 2

Số hạng đầu dãy là 1

Số hạng cuối dãy là 2n - 1

⇒ Số các số hạng là:

(2n - 1 - 1) : 2 + 1 = n

⇒ Tổng các dãy số là:

[(1 + 2n - 1) . n] : 2

= 2n . n : 2 = n².

Câu 38: Tổng của hai số là 10,2. Nếu gấp số thứ nhất lên 3 lần và gấp số thứ hai lên 5 lần thì tổng của hai số là 41,4. Tìm hai số đó.

Lời giải:

Nếu cả hai số gấp lên 3 lần thì tổng của chúng là:

10,2 × 3 = 30,6

Số thứ hai là:

(41,4 - 30,6) : (5 - 3) = 5,4

Số thứ nhất là:

10,2 - 5,4 = 4.8

Câu 39: Tìm x, biết:

a) x - 4 là bội của x - 1;

b) 2x - 1 là ước của 3x + 2.

Lời giải:

a) Ta có x - 4 chia hết cho x - 1

⇒ (x - 1) - 3 chia hết cho x - 1

⇒ 3 chia hết cho x - 1 (vì x - 1 chia hết cho x - 1)

⇒ x - 1 ∈ Ư(3) = {-1; -3; 1; 3}

Ta có bảng giá trị

x - 1	-1	-3	1	3
x	0	-2	2	4

Vậy x ∈ {0; -2; 2; 4}.

b) 2x - 1 là ước của 3x + 2

⇔ 3x + 2 là bội của 2x - 1

⇒ 2(3x + 2) là bội của 2x - 1

⇒ 6x + 4 là bội của 2x - 1

⇒ 6x - 3 + 7 là bội của 2x - 1

⇒ 3(2x - 1) + 7 chia hết cho 2x - 1

Mà 3(2x + 1) chia hết cho 2x - 1

⇒ 7 chia hết cho (2x - 1) 

⇒ 2x - 1 ∈ Ư(7) = {-1; -7; 1; 7}

Ta có bảng giá trị:

2x - 1	-1	-7	1	7
2x	0	-6	2	8
x	0	-3	1	4

Vậy x ∈ {0; -3; 1; 4}.

Câu 40: Tính bằng cách thuận tiện nhất: 1 - 4 + 7 - 10 + 13 - 16 + ... + 103 - 106 + 109.

Lời giải:

1 - 4 + 7 - 10 + 13 - 16 + ... + 103 - 106 + 109

= (1 + 7 + 13 + ... + 103 + 109) - (4 + 10 + 16 + ... + 106)

= [(1 + 109) × 19 : 2] - [(106 + 4) × 18 : 2]

= 1045 - 990 = 55.