Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 6)

Bài 1: Tính tổng: A = 1 + 2 + 3 + ... + 100.

Lời giải:

Số số hạng của A là:

(100 – 1) + 1 = 100 (số)

Tổng A là:

(100 + 1) × 100 : 2 = 5 050

Đáp số: 5 050.

Bài 2: Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ ở hai bên như hình vẽ. Biết chiều cao cổng parabol là 4 m, còn kích thước cửa ở giữa là 3 m × 4 m. Hãy tính khoảng cách giữa 2 điểm A và B.

Lời giải:

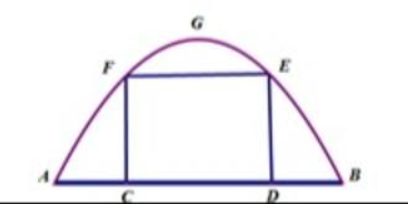
Đỉnh G có tọa độ (0; 4) ⇒ a² . 0 + b . 0 + c = 4 ⇒ c = 4

Điểm E có tọa độ (2; 3) ⇒ a² . 2 + b . 2 + 4 = 3 ⇔ 4a + 2b = – 1 (1)

Điểm F có tọa độ (– 2; 3) ⇒ a² . (– 2) + b . (– 2) + 4 = 3 ⇔ 4a – 2b = – 1 (2)

Từ (1) và (2) suy ra: a = – 0,25; b = 0. 

Do đó, parabol có dạng y = – 0,25x² + 4. 

Điểm A và B có tung độ y = 0 ⇔ – 0,25 . x² + 4 = 0 ⇔ x = 4 hoặc x = – 4.

Suy ra điểm B có tọa độ (4; 0) và điểm A có tọa độ (– 4; 0).

Vậy khoảng cách giữa hai điểm A và B là 8.

Bài 3: Cho hai tập hợp A = [– 1; 3], B = [m; m + 5]. Tìm m để A giao B khác rỗng.

Lời giải:

Để A ∩ B = ∅ thì $\left[\begin{array}{l}m+5<-1\\ m>3\end{array}\right.\iff \left[\begin{array}{l}m<-6\\ m>3\end{array}\right.$.

Do đó, để A ∩ B ≠ ∅ thì – 6 ≤ m ≤ 3.

Bài 4: Cho a + b + c = 0. Chứng minh rằng a³ + b³ + c³ = 3abc.

Lời giải:

Ta có: a³ + b³ + c³ – 3abc = (a³ + b³) + c³ – 3abc

= (a + b)³ – 3ab(a + b) + c³ – 3abc

= [(a + b)³ + c³] – [3ab(a + b) – 3abc]

= (a + b + c)[(a + b)² – (a + b)c + c²] – 3ab(a + b + c)

= (a + b + c)(a² + b² + c² – ab – ac – bc)

Mà a + b + c = 0 nên suy ra a³ + b³ + c³ – 3abc = 0.

Suy ra a³ + b³ + c³ = 3abc (đpcm).

Bài 5: Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt cạnh AC, AB lần lượt tại D và E. Gọi H là giao điểm của BD và CE, K là giao điểm của DE và AH, F là giao điểm của AH và BC, M là trung điểm của AH. Chứng minh MD² = MK.MF.

Lời giải:

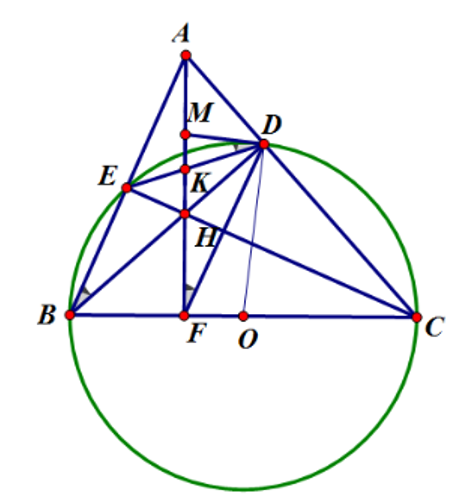
Vì B; E; D; C cùng thuộc đường tròn đường kính BC.

Suy ra \(\widehat {BEC} = \widehat {BDC}\) = 90° (góc nội tiếp chắn nửa đường tròn).

BD và CE là đường cao của tam giác ABC nên H là trực tâm của tam giác.

Suy ra AH vuông góc BC tại F.

\( \Rightarrow \widehat {AFB} = \widehat {ADB}\) = 90° hay đỉnh D, F cùng nhìn AB dưới một góc 90°

Do đó, tứ giác ABED nội tiếp.

\( \Rightarrow \widehat {ABD} = \widehat {AFD}\) (góc nội tiếp cùng chắn cung AD) (1).

Lại có tam giác ADH vuông tại D, M là trung điểm của AH nên DM là đường trung tuyến ứng với cạnh huyền AH, suy ra DM = AM nên tam giác ADM cân tại M.

\( \Rightarrow \widehat {MAD} = \widehat {MDA}\) (2).

Mà OD = OC (bán kính đường tròn (O)), suy ra tam giác ODC cân tại O.

\( \Rightarrow \widehat {ODC} = \widehat {OCD}\) (3).

Cộng vế theo vế (2) với (3) ta được: \(\widehat {MAD} + \widehat {OCD} = \widehat {MDA} + \widehat {ODC}\).

Do AF vuông góc với BC nên \(\widehat {MAD} + \widehat {OCD} = 90^\circ \).

Suy ra \(\widehat {MDA} + \widehat {ODC} = 90^\circ \)\( \Rightarrow \widehat {MDO} = 90^\circ \).

Khi đó MD là tiếp tuyến của đường tròn (O).

Suy ra \(\widehat {ABD} = \widehat {MDE}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây chắn cung ED) (4).

Từ (1) và (4) suy ra \(\widehat {MDE} = \widehat {AFD}\).

Xét tam giác MDK và tam giác MFD có:

\(\widehat {DMF}\): góc chung

\(\widehat {MDK} = \widehat {MFD}\,\,\,\,\,\left( {\widehat {MDE} = \widehat {AFD}} \right)\)

Do đó, tam giác MDK đồng dạng với tam giác MFD (g.g).

Suy ra \(\frac{{MD}}{{MF}} = \frac{{MK}}{{MD}}\)\( \Rightarrow M{D^2} = MK.MF\) (đpcm).

Bài 6: Phân tích đa thức thành nhân tử: x³ + 10x² + 25x – xy².

Lời giải:

Ta có: x³ + 10x² + 25x – xy²

= x(x² + 10x + 25 – y²)

= x[(x + 5)² – y²]

= x(x + 5 – y)(x + 5 + y).

Bài 7: Tính (a – b – c)³.

Lời giải:

(a – b – c)³ = [(a – b) – c]³ = (a – b)³ – 3(a – b)² + 3(a–b).c² – c³

= a³ – 3a²b + 3ab² – b³ – 3(a² – 2ab + b²) + 3ac² – 3bc² – c³

= a³ – b³ – c³ – 3a²b + 3ab² + 3ac² – 3bc² – 3a²– 3b² + 6ab

Bài 8: Tìm các giá trị x; y nguyên dương sao cho x² = y² + 2y + 13

Lời giải

Có:x² = y² + 2y + 13

⇒ x² =(y² + 2y + 1) + 12

⇒ x² = (y+1)² + 12

⇒ x² – (y+1) ² = 12

⇒ (x – y – 1)(x + y + 1) = 12

vì x, y là các số nguyên dương

⇒ x – y – 1 < x + y + 1

Xét các trường hợp

TH1: x – y – 1 = 1 và x + y + 1 = 12

⇒  x – y = 2 và x + y = 11

⇒  x = 6,5 và y = 4,5 (Loại vì x,y là các số nguyên dương)

TH2: x – y – 1 = 2 và x + y + 1 = 6

⇒ x – y = 3 và x + y = 5

⇒  x = 4 và y = 1 (Thỏa mãn)

TH3: x – y – 1 = 3 và x + y + 1 = 4

⇒ x – y = 4 và x + y = 3(Loại vì x – y < x + y)

Vậy x = 4,  y = 1

Bài 9: Cho tam giác ABC. Chứng minh: $\cot A+\cot B+\cot C=\frac{a^2+b^2+c^2}{4S}$.

Lời giải

Ta có:

\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)

Mà:

\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)

\(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)

\(\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)

\(S = \frac{{abc}}{{4R}}\)

Từ đó, ta có:

\(\begin{array}{l}\cot A + \cot B + \cot C\\ = \frac{{\cos A}}{{\sin A}} + \frac{{\cos B}}{{\sin B}} + \frac{{\cos C}}{{\sin C}}\\ = \frac{{\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}}}{{\frac{a}{{2R}}}} + \frac{{\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}}}{{\frac{a}{{2R}}}} + \frac{{\frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}}}{{\frac{a}{{2R}}}}\\ = \frac{R}{{abc}}\left( {{b^2} + {c^2} - {a^2} + {c^2} + {a^2} - {b^2} + {a^2} + {b^2} - {c^2}} \right)\\ = \frac{{{a^2} + {b^2} + {c^2}}}{{4S}}\end{array}\)

Bài 10: Có bao nhiêu số tự nhiên có hai chữ số mà hai chữ số đều chẵn ?

Lời giải

Ta gọi số tự nhiên có hai chữ số cần tìm là \(\overline {ab} \) với

a ∈ {1; 2; 3; 4; 5; 6; 7; 8; 9} và b ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}

Tập hợp chữ số tự nhiên chẵn:

A = {0; 2; 4; 6; 8} có 5 phần tử.

Chữ số a có 4 cách chọn. (a ≠ 0; a ϵ A)

Chữ số b có 5 cách chọn. (b ϵ A)

Vậy số tự nhiên có hai chữ số mà hai chữ số đều chẵn có:

4.5 = 20 (số)

Bài 11: Cho đường tròn (O; R) có đường kính BC. Lấy A thuộc (O) sao cho AB < AC, vẽ đường cao AH của tam giác ABC.

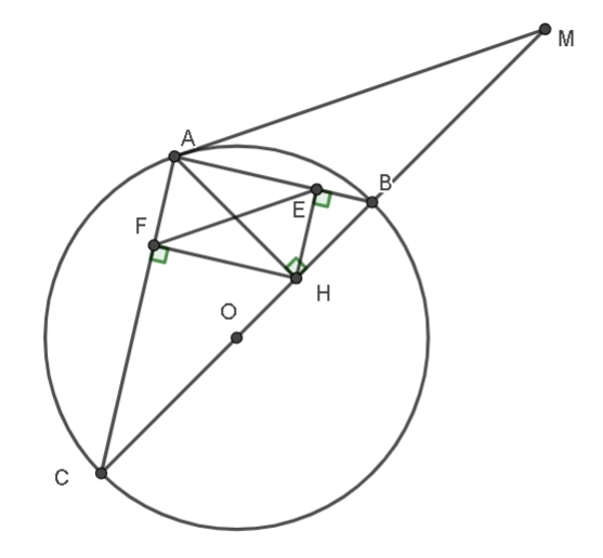
a) Chứng minh: AH.BC = AB.AC.

b) Tiếp tuyến tại A của (O) cắt đường thẳng BC tại M. Chứng minh rằng:

MA² = MB.MC.

c) Kẻ HE vuông góc với AB (E thuộc AB) và HF vuông góc với AC (F thuộc AC). Chứng minh AM \({\rm{//}}\) EF.

Lời giải

a)

Xét tam giác ABC có: \(\widehat {BAC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Do đó, tam giác ABC vuông tại A

\({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}AB.AC\)

⇒ AH.BC = AB.AC

b)

Xét tam giác MAB và tam giác MCA có:

\(\widehat M\) chung

\(\widehat {MAB} = \widehat {MCA}\) (cùng chắn cung AB)

Do đó, tam giác MAB đồng dạng với tam giác MCA  (g.g)

\( \Rightarrow \frac{{MA}}{{MC}} = \frac{{MB}}{{MA}}\)

⇒ MA² = MB.MC

c)

AM vuông góc với AO (do AM là tiếp tuyến của (O))

Xét tam giác AOC có:

AO = OC

Do đó, tam giác AOC cân tại O

\( \Rightarrow \widehat {OAC} = \widehat {OCA}\)

Mà \(\widehat {AFE} = \widehat {ABC}\)

\(\widehat {OCA} + \widehat {ABC} = 90^\circ \)

\( \Rightarrow \widehat {OAC} + \widehat {AFE} = 90^\circ \)

Do đó, AO vuông góc với EF

Do đó, EF \({\rm{//}}\) AM

Bài 12: Tìm nghiệm của phương trình: sinx + $\sqrt{3}$cosx = 1

Lời giải

Ta có:

$\begin{array}{l}\sin x+\sqrt{3}\cos x=1\\ \iff \frac{1}{2}\sin x+\frac{\sqrt{3}}{2}\cos x=\frac{1}{2}\\ \iff cos\frac{\pi }{3}\sin x+\sin \frac{\pi }{3}\cos x=\frac{1}{2}\\ \iff \sin \left(x+\frac{\pi }{3}\right)=\frac{1}{2}\\ \iff \sin \left(x+\frac{\pi }{3}\right)=\sin \frac{\pi }{6}\\ \iff \left[\begin{array}{l}x+\frac{\pi }{3}=\frac{\pi }{6}+k2\pi \\ x+\frac{\pi }{3}=\pi -\frac{\pi }{6}+k2\pi \end{array}\right.k\in \mathbb{Z}\\ \iff \left[\begin{array}{l}x+\frac{\pi }{3}=\frac{\pi }{6}+k2\pi \\ x+\frac{\pi }{3}=\frac{5\pi }{6}+k2\pi \end{array}\right.k\in \mathbb{Z}\\ \iff \left[\begin{array}{l}x=-\frac{\pi }{6}+k2\pi \\ x=\frac{\pi }{2}+k2\pi \end{array}\right.k\in \mathbb{Z}\end{array}$

Vậy tập nghiệm của phương trình là \(D = \left\{ { - \frac{\pi }{6} + k2\pi |k \in \mathbb{Z}} \right\} \cup \left\{ {\frac{\pi }{2} + k2\pi |k \in \mathbb{Z}} \right\}\)

Bài 13: Chứng minh rằng với mọi góc α $\left(0^{\circ }\le \alpha \le {180}^{\circ }\right)$ ta đều có cos²a + sin²a = 1.

Lời giải

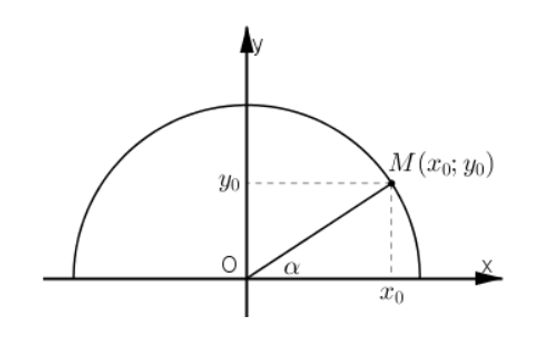
Vẽ đường tròn lượng giác (O; 1)

Với mọi α $\left(0°\le \alpha \le 180°\right)$ ta đều có điểm M(x₀; y₀) thuộc nửa đường tròn sao cho $\widehat{MOx}=\alpha$

Khi đó ta có: sin α = y₀ ; cos α = x₀

Áp dụng định lý Py–ta–go ta có: x₀² + y₀² = OM² = 1 hay cos²a + sin²a = 1.

Bài 14: Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng ?

Lời giải

Làm vòng tay mỗi giờ được 10 ngàn đồng

Làm vòng đeo cổ mỗi giờ được \(\frac{{40}}{3} \approx \)13 ngàn đồng

Vậy làm vòng đeo cổ có lợi hơn nên ưu tiên làm tối đa số vòng cổ trước.

Làm 4 vòng đeo cổ hết 4.6 = 24 giờ, bán được 4.80 = 320 ngàn đồng.

Để làm được ít nhất 400 ngàn đồng cần làm thêm vòng tay để thu về 80 ngàn đồng hay cần làm thêm 2 cái vòng tay ⇒ cần thêm 2.4 = 8 giờ

Vậy cần tối thiểu: 24 + 8 = 32 giờ một tuần để An bán được ít nhất 400 ngàn đồng.

Bài 15: Gọi x₁, x₂ là các nghiệm của phương trình: 12x² – 6mx + m² – 4 + $\frac{12}{m^2}$ = 0 (1). Tìm m sao cho x₁³ + x₂³  đạt giá trị lớn nhất.

Lời giải

Phương trình (1) có nghiệm khi và chỉ khi ∆’ ≥ 0

⇔ \(9{m^2} - 12\left( {{m^2} - 4 + \frac{{12}}{{{m^2}}}} \right) \ge 0\)

⇔ 4 ≤ m² ≤ 12 ⇔ \(m \in \left[ { - 2\sqrt 3 ; - 2} \right] \cup \left[ {2;2\sqrt 3 } \right]\)

Theo định lý Vi–ét, phương trình (1) có hai nghiệm x₁, x₂ thỏa mãn: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{m}{2}\\{x_1}{x_2} = \frac{1}{{12}}\left( {{m^2} - 4 + \frac{{12}}{{{m^2}}}} \right)\end{array} \right.\)

⇒ x₁³ + x₂³ = (x₁ + x₂)³ – 3x₁x₂(x₁ + x₂) = \(\frac{m}{2} - \frac{3}{{2m}}\)

Xét hàm số \(y = \frac{m}{2} - \frac{3}{{2m}}\) có:

TXD: D = \(\left[ { - 2\sqrt 3 ; - 2} \right] \cup \left[ {2;2\sqrt 3 } \right]\)

\(y' = \frac{1}{2} + \frac{3}{{2{m^2}}}\)  > 0 với mọi m

Do đó, hàm số y luôn đồng biến với mọi m thuộc D.

Ta có: \(y(2) = \frac{2}{2} - \frac{3}{{2.2}} = \frac{1}{4};\,\,y(2\sqrt 3 ) = \frac{{2\sqrt 3 }}{2} - \frac{3}{{2.2\sqrt 3 }} = \frac{{3\sqrt 3 }}{4}\)

Vì \(y(2\sqrt 3 ) > y(2)\) nên giá trị lớn nhất của x₁³ + x₂³ là \(\frac{{3\sqrt 3 }}{4}\) khi m = \(2\sqrt 3 \)

Bài 16: Tìm x ∈ ℤ để A ∈ ℤ

a) $A=\frac{x+3}{x-2}$

b) $A=\frac{1-2x}{x+3}$

c) $A=\frac{\sqrt{x}+1}{\sqrt{x}-3}$

Lời giải

a)

\(A = \frac{{x + 3}}{{x - 2}} = \frac{{x - 2 + 5}}{{x - 2}} = 1 + \frac{5}{{x - 2}}\)

Để A ∈ ℤ thì x – 2 ∈ {±1; ±5} hay x ∈ {3; 1; 7; –3} (thỏa mãn x ∈ ℤ)

b)

\(A = \frac{{1 - 2x}}{{x + 3}} = \frac{{1 - \left( {2x + 6} \right) + 6}}{{x + 3}} = \frac{{7 - 2(x + 3)}}{{x + 3}} = \frac{7}{{x + 3}} - 2\)

Để Để A ∈ ℤ thì x + 2 ∈ {±1; ±7} hay x ∈ {–1; –3; 5; –9} (thỏa mãn x ∈ ℤ)

c)

$A=\frac{\sqrt{x}+1}{\sqrt{x}-3}=\frac{\sqrt{x}-3+4}{\sqrt{x}-3}=1+\frac{4}{\sqrt{x}-3}$

 

Để Để A ∈ ℤ thì \(\sqrt x  - 3\) ∈ {±1; ±2; ±4}

Mà x ∈ ℤ nên x ∈ {4; 16; 25; 1; 49}

Bài 17: Cho $A=\frac{3x+\sqrt{9}x-3}{x+\sqrt{x}-2}-\frac{\sqrt{x}+1}{\sqrt{x}+2}+\frac{\sqrt{x}+2}{1-\sqrt{x}}$ (x ≥ 0; x ≠ A)

a) Rút gọn A

b) Tìm x ∈ ℤ để A ∈ ℤ

Lời giải

a)

$\begin{array}{l}A=\frac{3x+\sqrt{9}x-3}{x+\sqrt{x}-2}-\frac{\sqrt{x}+1}{\sqrt{x}+2}+\frac{\sqrt{x}+2}{1-\sqrt{x}}\left(x\ge 0;x\ne A\right)\\ =\frac{3x+3\sqrt{x}-3}{x+\sqrt{x}-2}-\frac{\sqrt{x}+1}{\sqrt{x}+2}+\frac{\sqrt{x}+2}{1-\sqrt{x}}\\ =\frac{3x+3\sqrt{x}-3}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}-\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}-\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\end{array}$

$\begin{array}{l}=\frac{3x+3\sqrt{x}-3-\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\\ =\frac{3x+3\sqrt{x}-3-\left(x-1\right)-{\left(\sqrt{x}+2\right)}^2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\\ =\frac{3x+3\sqrt{x}-3-x+1-x-2\sqrt{x}-4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\\ =\frac{x+\sqrt{x}-6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\frac{\sqrt{x}-3}{\sqrt{x}-1}\end{array}$

b)

$A=\frac{\sqrt{x}-3}{\sqrt{x}-1}=\frac{\sqrt{x}-1-2}{\sqrt{x}-1}=1-\frac{2}{\sqrt{x}-1}$

Để A ∈ ℤ thì $\left\{\begin{array}{l}\sqrt{x}-1\in \left\{\pm 1;\pm 2\right\}\\ x\in \mathbb{Z}\end{array}\right.\iff x\in \left\{4;0;9\right\}$

Bài 18: Cho tam giác ABC thỏa mãn: $\frac{a.\cos A+b.\cos B+c.\cos C}{a+b+c}=\frac{1}{2}$ (A, B, C là các góc của tam giác a = BC, b = CA, c = AB). Chứng minh tam giác ABC là tam giác đều.

Lời giải

\(\begin{array}{l}\frac{{a.\cos A + b.\cos B + c.\cos C}}{{a + b + c}} = \frac{1}{2} \Leftrightarrow \sin 2A + \sin 2B + \sin 2C = \sin A + \sin B + \sin C\\ \Leftrightarrow \sin A.\sin B.\sin C = cos\frac{A}{2}.cos\frac{B}{2}.cos\frac{C}{2}\\ \Leftrightarrow 8\sin \frac{A}{2}.\sin \frac{B}{2}.\sin \frac{C}{2} = 1\\ \Leftrightarrow 4\sin \frac{A}{2}\left( {cos\frac{{B - C}}{2} - cos\frac{{B + C}}{2}} \right) = 1 \Leftrightarrow 4{\sin ^2}\frac{A}{2} - 4cos\frac{{B - C}}{2}.\sin \frac{A}{2} + 1 = 0\\ \Leftrightarrow {\left( {2\sin \frac{A}{2} - cos\frac{{B - C}}{2}} \right)^2} + 1 - co{s^2}\frac{{B - C}}{2} = 0\\ \Leftrightarrow \left\{ \begin{array}{l}cos\frac{{B - C}}{2} = 1\\\sin \frac{A}{2} = \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}B = C\\A = \frac{\pi }{3}\end{array} \right.\end{array}\)

Do đó, tam giác ABC là tam giác đều (có hai góc ở đáy bằng nhau và 1 góc bằng 60^o)

Bài 19: Chúng tỏ rằng với a, b ∈ ℕ thì ƯCLN (a, b) = ƯCLN (5a + 2b, 7a + 3b)

Lời giải

Gọi d = ƯCLN (a; b)

Đặt:

a = d.m  ; b = d.n ⇒ (m; n) = 1

5a + 2b = d(5m + 2n)

7a + 3b = d(7m + 3n)

Gọi d’ = ƯCLN (5m + 2n; 7m + 3n)

\(\left\{ \begin{array}{l}5m + 2n \vdots d'\\7m + 3n \vdots d'\end{array} \right. \Rightarrow \left\{ \begin{array}{l}5m + 2n \vdots d'\\2m + n \vdots d'\end{array} \right. \Rightarrow \left\{ \begin{array}{l}5m + 2n \vdots d'\\4m + 2n \vdots d'\end{array} \right. \Rightarrow m \vdots d'\)

Từ đó suy ra: 2n ⋮ d’ và 3n ⋮ d’ do đó, n⋮ d’

Do đó, d’ thuộc tập ƯC (m;n)

Mà ƯCLN (m; n) = 1 nên d’ = 1

Do đó, ƯCLN (5m + 2n; 7m + 3n) = 1 ⇒ ƯCLN (5a + 2b; 7a + 3b) = d = ƯCLN (a; b)

Bài 20: Cho P = $\frac{\sqrt{x}}{\sqrt{x}+2}$ (x ≥ 0), hãy so sánh P và $\sqrt{P}$.

Lời giải:

Ta có: P = $\frac{\sqrt{x}}{\sqrt{x}+2}$ = $\frac{\sqrt{x}+2-2}{\sqrt{x}+2}=1-\frac{2}{\sqrt{x}+2}$.

Ta thấy: $\sqrt{x}$≥ 0 $\Rightarrow \sqrt{x}+2\ge 2\Rightarrow \frac{2}{\sqrt{x}+2}\le \frac{2}{2}=1$

$\Rightarrow 1-\frac{2}{\sqrt{x}+2}\ge 0$ ⇒ P ≥ 0.

Mặt khác: \(\sqrt x \)≥ 0

$\Rightarrow \sqrt{x}+2>0\Rightarrow \frac{2}{\sqrt{x}+2}>0$

$\Rightarrow 1-\frac{2}{\sqrt{x}+2}<1$ ⇒ P < 1.

Do đó, 0 ≤ P < 1, suy ra P < \(\sqrt P \).

Bài 21: Cho P = $\frac{\sqrt{x}}{\sqrt{x}-1}$ với x > 1. So sánh P và \(\sqrt P \).

Lời giải:

Ta có: P = $\frac{\sqrt{x}}{\sqrt{x}-1}$

Vì x > 1 $\Rightarrow \sqrt{x}>1\Rightarrow \sqrt{x}-1>0\Rightarrow \frac{\sqrt{x}}{\sqrt{x}-1}>0$ ⇒ P > 0.

Mà $\sqrt{x}>\sqrt{x}-1$ $\Rightarrow \frac{\sqrt{x}}{\sqrt{x}-1}>1\Rightarrow P>1$ ⇒ P² > P ⇒ P > \(\sqrt P \).

Bài 22: Tìm tập tất cả các nghiệm của phương trình sin 2x + 2sin² x – 6sin x – 2cos x + 4 = 0.

Lời giải:

Ta có: sin 2x + 2sin² x – 6sin x – 2cos x + 4 = 0

⇔ (2sin x cos x – 2cos x) + (2sin² x – 6sin x + 4) = 0

⇔ 2cos x(sin x – 1) + 2(sin x – 2)(sin x – 1) = 0

⇔ (sin x – 1)(sin x + cos x – 2) = 0

\( \Leftrightarrow \left[ \begin{array}{l}\sin \,x = 1\\\sin \,x + \cos \,x = 2\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \,\,\,\,\left( {k \in \mathbb{Z}} \right)\\\sin \left( {x + \frac{\pi }{4}} \right) = \sqrt 2 \,\left( {VN} \right)\end{array} \right.\)\( \Leftrightarrow x = \frac{\pi }{2} + k2\pi \,\,\,\,\left( {k \in \mathbb{Z}} \right)\).

Bài 23: Khoảng cách BC trong hình vẽ dưới đây bằng bao nhiêu mét, biết M và N lần lượt là trung điểm của AB và AC, MN = 5x – 18 (mét); BC = 4x + 198 (mét).

Lời giải:

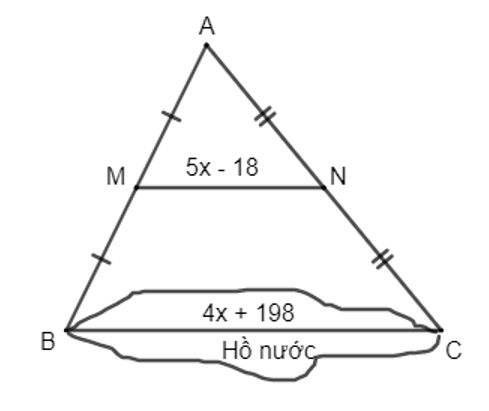
Xét tam giác ABC có M, N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.

Suy ra MN = \(\frac{1}{2}\)BC.

Mà MN = 5x – 18 và BC = 4x + 198 nên ta có: 5x – 18 = \(\frac{1}{2}\)(4x + 198)

⇔ 5x – 18 = 2x + 99

⇔ 3x = 117

⇔ x = 39 (mét).

Vậy khoảng cách BC trong hình vẽ đã cho là BC = 4 . 39 + 198 = 354 (mét).

Bài 24: Từ một điểm A nằm ngoài đường tròn (O; R), kẻ hai tiếp tuyến AB, AC với (O; R) (B và C là 2 tiếp điểm).

a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn và AO ⊥ BC tại H.

b) Vẽ đường kính BD. Đường thẳng qua O và vuông góc với AD cắt tia BC tại E. Chứng minh: DC // OA và CD . CO = BA . CE.

Lời giải:

 

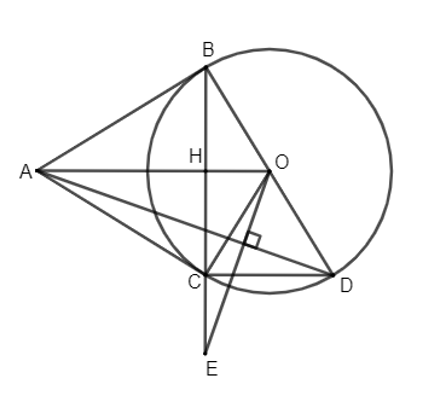
a) Vì AB, AC là hai tiếp tuyến cắt nhau tại A của đường tròn (O; R) nên \(\widehat {ABO} = \widehat {ACO} = 90^\circ \).

Xét tứ giác ABOC có $\widehat{ABO}+\widehat{ACO}=90°+90°=180°$.

Suy ra tứ giác ABOC là tứ giác nội tiếp.

Vậy bốn điểm A, B, O, C cùng thuộc một đường tròn.

Lại có theo tính chất của hai tiếp tuyến cắt nhau AC và AB, suy ra AO là đường trung trực của BC nên AO ⊥ BC tại H.

b) Vì AO ⊥ BC tại H và AO là đường trung trực của BC nên H là trung điểm của BC.

Mà O là trung điểm của BD (đường kính BD trong đường tròn tâm O).

Do đó, OH là đường trung bình của tam giác BCD.

Suy ra OH // CD nên OA // CD.

Bài 25: Số các số tự nhiên có 5 chữ số khác nhau và chia hết cho 10 là bao nhiêu?

Lời giải:

Để lập số tự nhiên có 5 chữ số khác nhau và chia hết cho 10 ta thực hiện liên tiếp các công đoạn sau:

- Chọn chữ số hàng đơn vị là chữ số 0, có 1 cách chọn;

- Chọn chữ số hàng chục nghìn, có 9 cách chọn;

- Chọn chữ số hàng nghìn, có 8 cách chọn;

- Chọn chữ số hàng trăm, có 7 cách chọn;

- Chọn chữ số hàng chục, có 6 cách chọn.

Do vậy, theo quy tắc nhân có 1 . 9 . 8. 7 . 6 = 3 024 số tự nhiên có 5 chữ số khác nhau và chia hết cho 10.

Bài 26: Góc chung là gì?

Lời giải:

Góc chung là khái niệm dùng để chỉ một góc mà nằm ở 2 đa giác khác nhau.

Chẳng hạn tam giác ABC và tam giác ADE có góc chung là góc A.

Bài 27: Cho hình vẽ dưới đây:

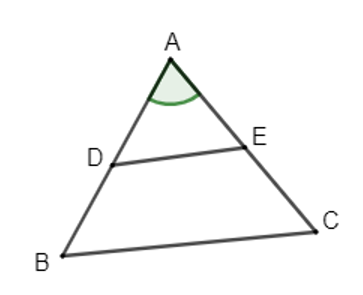
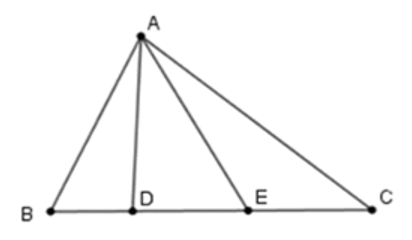
Góc AEB là góc chung của những tam giác nào:

A. ∆AEB; ∆ABD.

B. ∆AEB; ∆AED.

C. ∆AEB; ∆ABC.

D. ∆AEB; ∆AEC.

Lời giải:

Đáp án đúng là: B

Từ hình vẽ ta thấy góc AEB là góc chung của tam giác AEB và tam giác AED.

Bài 28: Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:

$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}=\overrightarrow{AF}+\overrightarrow{BD}+\overrightarrow{CE}$.

Lời giải:

Ta có: $\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\left(\overrightarrow{AE}+\overrightarrow{ED}\right)+\left(\overrightarrow{BF}+\overrightarrow{FE}\right)+\left(\overrightarrow{CD}+\overrightarrow{DF}\right)$ (quy tắc ba điểm)

$=\left(\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\right)+\left(\overrightarrow{ED}+\overrightarrow{DF}+\overrightarrow{FE}\right)$

$=\left(\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\right)+\left(\overrightarrow{EF}+\overrightarrow{FE}\right)$

$=\left(\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\right)+\overrightarrow{0}$ $=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}$

Vậy $\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}$ (1).

Lại có: $\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}=\left(\overrightarrow{AF}+\overrightarrow{FE}\right)+\left(\overrightarrow{BD}+\overrightarrow{DF}\right)+\left(\overrightarrow{CE}+\overrightarrow{ED}\right)$

$=\left(\overrightarrow{AF}+\overrightarrow{BD}+\overrightarrow{CE}\right)+\left(\overrightarrow{FE}+\overrightarrow{ED}+\overrightarrow{DF}\right)$

$=\left(\overrightarrow{AF}+\overrightarrow{BD}+\overrightarrow{CE}\right)+\left(\overrightarrow{FD}+\overrightarrow{DF}\right)$

$=\left(\overrightarrow{AF}+\overrightarrow{BD}+\overrightarrow{CE}\right)+\overrightarrow{0}$

$=\overrightarrow{AF}+\overrightarrow{BD}+\overrightarrow{CE}$.

Vậy $\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}=\overrightarrow{AF}+\overrightarrow{BD}+\overrightarrow{CE}$ (2).

Từ (1) và (2) suy ra $\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}=\overrightarrow{AF}+\overrightarrow{BD}+\overrightarrow{CE}$.

Bài 29: Cho đường tròn (O). Một điểm M nằm ngoài đường tròn (O), kẻ tiếp tuyến MA (A là tiếp điểm). Kẻ đường kính AOC và dây AB vuông góc với OM tại H.

1. Chứng minh BC // OM và tứ giác AOBM nội tiếp đường tròn.

2. Kẻ dây CN của đường tròn (O) đi qua H. Tia MN cắt (O) tại điểm thứ hai D. Chứng minh MA² = MN.MD.

3. Chứng minh: B, O, D thẳng hàng.

Lời giải:

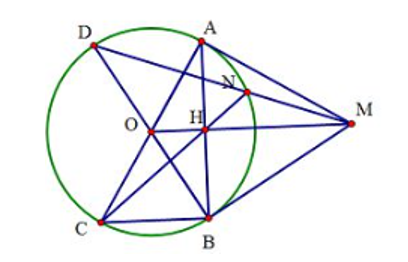
1. Ta có \(\widehat {ABC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Suy ra AB ⊥ BC, mà AB ⊥ OM, do đó BC // OM.

Vì đường tròn (O) có AB ⊥ OM tại H nên H là trung điểm của AB.

Khi đó, tam giác MAB có MH vừa là đường cao vừa là đường trung tuyến nên tam giác MAB cân tại M.

Suy ra \(\widehat {MAH} = \widehat {MBH}\).

Lại có tam giác OAB cân tại O (OA = OB) nên \(\widehat {OBH} = \widehat {OAH}\).

Mà \(\widehat {OAH} + \widehat {MAH} = \widehat {OAM} = 90^\circ \) (do MA là tiếp tuyến của đường tròn (O)).

Do đó, \(\widehat {MBH} + \widehat {OBH} = 90^\circ \) hay \(\widehat {OBM} = 90^\circ \).

Xét tứ giác AOBM có \(\widehat {OAM} = \widehat {OBM} = 90^\circ \).

Suy ra tứ giác AOBM là tứ giác nội tiếp.

2. Xét tam giác MAN và tam giác MDA có:

\(\widehat {AMD}\): góc chung

\(\widehat {MAN} = \widehat {ADM}\)(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung)

Do đó, tam giác MAN đồng dạng với tam giác MDA (g.g).

Suy ra \(\frac{{MN}}{{MA}} = \frac{{MA}}{{MD}}\)\( \Rightarrow \) MA² = MN . MD (đpcm).

3. Xét tam giác OAD có OA = OD nên tam giác OAD cân tại O.

Suy ra \(\widehat {ODA} = \widehat {OAD}\) (1).

Xét đường tròn (O), có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung AB).

Suy ra \(\widehat {ACB} = \widehat {ODA}\) (2).

Từ (1) và (2) suy ra \(\widehat {ACB} = \widehat {OAD}\).

Lại có \(\widehat {ACB} + \widehat {CAB} = 90^\circ \) (do tam giác ABC vuông tại B).

Do đó, \(\widehat {OAD} + \widehat {CAB} = 90^\circ \) hay \(\widehat {BAD} = 90^\circ \) nên góc BAD chắn nửa đường tròn.

Suy ra BD là đường kính của đường tròn (O).

Vậy B, O, D thẳng hàng.

Bài 30: Tìm các ước của 240.

Lời giải

Ta có: 240 = 2⁴ . 3 . 5.

Số các ước nguyên dương của 240 là: (4 + 1) . (1 + 1) . (1 + 1) = 20.

Các ước nguyên dương của 240 là: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240.

Bài 31: Cho tam giác ABC nhọn. Vẽ AH vuông góc với BC tại H. Chứng minh rằng:

AC² + BH² = AB² + CH².

Lời giải:

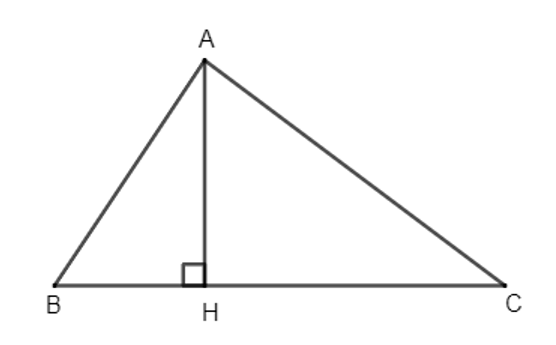
Vì tam giác ABH vuông tại H nên AB² = AH² + BH² (định lí Pythagore).

Suy ra BH² = AB² – AH².

Vì tam giác ACH vuông tại H nên AC² = AH² + HC² (định lí Pythagore).

Do đó ta có: AC² + BH² = (AH² + HC²) + (AB² – AH²) = AB² + HC² (đpcm).2^{2222222======}

Bài 32: Cho đường thẳng y = 2x + 2.

a) Vẽ y = 2x + 2.

b) Tính góc tạo bởi đường thẳng y = 2x + 2 với trục hoành Ox.

Lời giải:

a) Với x = 0 thì y = 2, với y = 0 thì x = – 1. Do đó đường thẳng y = 2x + 2 đi qua hai điểm A(0; 2) và B(– 1; 0).

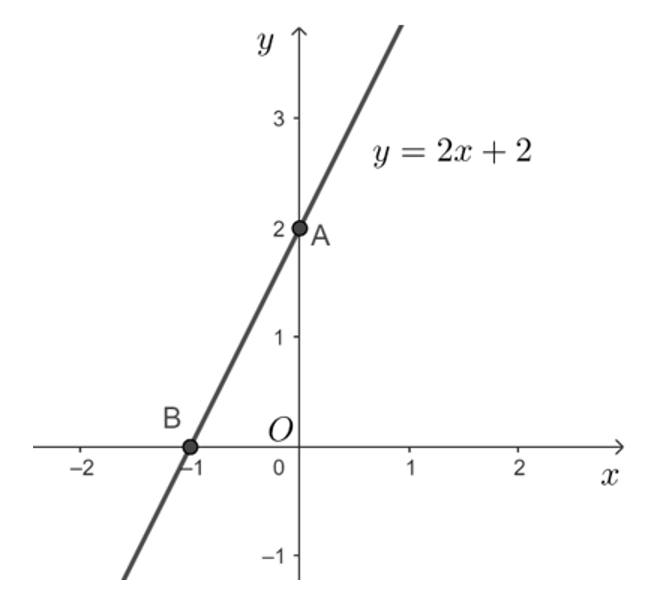
b) Ta có: OA = 2, OB = 1.

Góc tạo bởi đường thẳng y = 2x + 2 với trục hoành Ox là góc ABO.

Xét tam giác ABO vuông tại O, ta có: tanABO = \(\frac{{AO}}{{BO}} = \frac{2}{1} = 2\).

Suy ra \(\widehat {ABO} \approx 63^\circ 26'\).

Bài 33: Cho tam giác ABC có M và N lần lượt là trung điểm của các cạnh BC và AC. Lấy D đối xứng với M qua N.

a) Chứng minh tứ giác ABMN là hình thang.

b) Tứ giác ADCM là hình gì? Vì sao?

c) Gọi I là trung điểm của đoạn thẳng AM. Chứng minh rằng: B, I, D thắng hàng.

d) Qua điểm D kẻ đường thẳng song song với AC, cắt đường thẳng BC tại E. Đường

thắng IN cắt DE tại F. Tìm điều kiện của tam giác ABC để tứ giác MNFE là hình thang cân.

Lời giải:

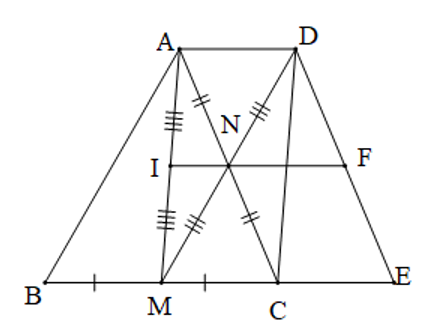
a) Vì M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác ABC, suy ra MN // AB.

Do đó, tứ giác ABMN là hình thang.

b) Vì D đối xứng với M qua N nên N là trung điểm của MD, mà N là trung điểm của AC và AC, MD là hai đường chéo của tứ giác ADCM. Do đó ADCM là hình bình hành.

c) Vì ADCM là hình bình hành nên AD // MC và AD = MC.

Mà MB = MC (M là trung điểm của BC).

Do đó, AD = BM và AD // BM.

Suy ra tứ giác ABMD là hình bình hành.

Suy ra hai đường chéo AM và BD cắt nhau tại trung điểm của mỗi đường, mà I là trung điểm của AM nên I cũng là trung điểm của BD.

Vậy, B, I, D thẳng hàng.

d) MNFE là hình thang cân, suy ra \(\widehat {NME} = \widehat {FEM}\).

Mà \(\widehat {FEM} = \widehat {ACB}\) (AC // DE), \(\widehat {NME} = \widehat {ABC}\) (MD // AB).

Suy ra \(\widehat {ABC} = \widehat {ACB}\), do đó tam giác ABC cân tại A.

Vậy để tứ giác MNFE là hình thang cân thì tam giác ABC là tam giác cân tại A.

Bài 34: Tìm m để hai đường thẳng (d₁): y = 3mx – m² và (d₂): y = 3x + m – 2 cắt nhau tại một điểm nằm trên trục tung.

Lời giải:

Ta có: (d₁) cắt (d₂) tại 1 điểm trên trục tung ⇔ a ≠ a′; b = b′.

Ta có: a ≠ a′ ⇔ 3m ≠ 3 ⇔ m ≠ 1.

b = b′ ⇔ − m² = m – 2 ⇔ m² +m - 2 = 0 ⇔ m = 1 (loại) hoặc m = – 2 (t/m).

Vậy m = – 2 thì (d₁) cắt (d₂) tại 1 điểm trên trục tung.

Bài 35: Chứng minh rằng n³ – n chia hết cho 6 với mọi số nguyên n.

Lời giải:

Ta có: n³ – n = n(n² – 1) = n(n – 1)(n + 1).

Với n ∈ ℤ thì (n – 1), n, (n + 1) là ba số nguyên liên tiếp.

+) Trong 3 số nguyên liên tiếp sẽ có ít nhất 1 số chẵn nên n(n – 1)(n + 1) chia hết cho 2.

+) Trong 3 số nguyên liên tiếp sẽ có 1 số chia hết cho 3 nên n(n – 1)(n + 1) chia hết cho 3.

Do đó tích n(n – 1)(n + 1) chia hết cho cả 2 và 3.

Mà 2 và 3 là hai số nguyên tố cùng nhau nên tích đó chia hết cho 6 hay n³ – n chia hết cho 6 với mọi số nguyên n.

Bài 36: Cho hình vẽ. Biết CD = 3 cm, giá trị của x là:

A. 4 cm.

B. \(3\sqrt 3 \) cm.

C. \(2\sqrt 3 \) cm.

D. \(3\sqrt 2 \) cm.

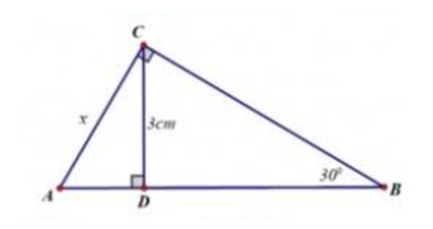
Lời giải:

Đáp án đúng là: C

Vì tam giác CBD vuông tại D, nên ta có: BC = \(\frac{{CD}}{{\sin B}} = \frac{3}{{\sin 30^\circ }} = 6\) (cm).

Vì tam giác ACB vuông tại C, nên ta có: x = AC = BC tanB = 6 . tan30° = \(2\sqrt 3 \) (cm).

Bài 37: Tìm x, biết: x : 0,25 + x × 11 = 24.

Lời giải:

x : 0,25 + x × 11 = 24

x : \(\frac{1}{4}\) + x × 11 = 24

x × 4 + x × 11 = 24

x × (4 + 11) = 24

x × 15 = 24

x = \(\frac{{24}}{{15}}\).

Vậy x = \(\frac{{24}}{{15}}\).

Bài 38: Mọi số thực đều có căn bậc 3, đúng hay sai?

Lời giải:

+ Căn bậc ba của một số a là số x sao cho x³ = a.

+ Căn bậc ba của số a được kí hiệu là \(\sqrt[3]{a}\).

Như vậy \({\left( {\sqrt[3]{a}} \right)^3} = a\).

Mọi số thực đều có căn bậc ba.

Bài 39: Cho đường tròn (O; R), và điểm A nằm ngoài đường tròn (O) sao cho OA = 2R. Vẽ tiếp tuyến AB với đường tròn (O). Gọi BH là đường cao của Δ ABO, BH cắt đường tròn (O) tại C

a) Chứng minh: AC là tiếp tuyến của đường tròn (O).

b) Từ O vẽ đường thẳng vuông góc với OB cắt AC tại K. Chứng minh: KA = KO.

c) Đoạn thẳng OA cắt đường tròn (O) tại I. Chứng minh: KI là tiếp tuyến của đường tròn (O).

d) AI cắt đường tròn (O) tại điểm thứ hai D. Chứng minh: ΔAIC ∽ Δ ACD.

Lời giải:

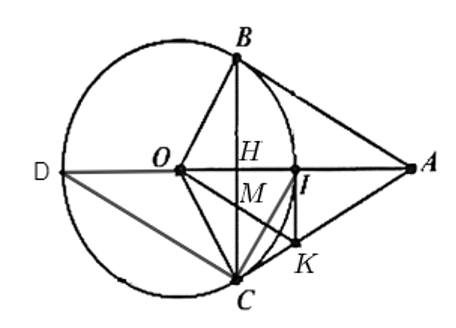
a) Xét tam giác OBC có OB = OC = R nên tam giác OBC cân tại O, có OH là đường cao nên OH là đường phân giác của góc BOC \( \Rightarrow \widehat {AOB} = \widehat {AOC}\).

Xét tam giác ABO và tam giác ACO có:

AO: cạnh chung

OB = OC = R

\(\widehat {AOB} = \widehat {AOC}\) (chứng minh trên).

Do đó, ∆ABO = ∆ACO (cgc).

Suy ra \(\widehat {ACO} = \widehat {ABO} = 90^\circ \) (do AB là tiếp tuyến của (O; R)).

Do đó, AC vuông góc với CO tại C.

Vậy AC là tiếp tuyến của đường tròn (O).

b) Gọi M là giao điểm của OK và BC.

Xét tam giác BMO vuông tại O có OH vuông góc với BM, ta suy ra \(\widehat {MOH} = \widehat {HBO}\) (cùng phụ với góc BOH).

Xét tam giác ABO vuông tại B có BH vuông góc với AO, ta suy ra \(\widehat {HBO} = \widehat {BAH}\) (cùng phụ với góc HBA).

Do đó, \(\widehat {MOH} = \widehat {BAH}\).

Mặt khác, \(\widehat {BAH} = \widehat {HAK}\) (tính chất hai tiếp tuyến AB, AC cắt nhau).

Suy ra \(\widehat {MOH} = \widehat {HAK}\,\,\,hay\,\,\widehat {KOA} = \widehat {KAO}\). Khi đó, tam giác KAO cân tại K.

Vậy KO = KA.

c) Ta có: OA = OI + AI

⇒ AI = OA – OI = 2R – R = R

⇒ AI = OI = R ⇒ I là trung điểm của OA.

Xét tam giác KAO cân tại K có KI là đường trung tuyến nên KI cũng là đường cao.

Suy ra KI vuông góc OA tại I hay KI vuông góc với OI.

Vậy KI là tiếp tuyến của đường tròn (O).

d)  Xét tam giác AIC và tam giác ACD có:

\(\widehat {DAC}\): góc chung

\(\widehat {ACI} = \widehat {ADC}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung IC)

Do đó, ΔAIC ∽ Δ ACD (g – g).

Bài 40: Giải phương trình: cos3x – sin3x = 1.

Lời giải:

Ta có: cos3x – sin3x = 1

\( \Leftrightarrow \frac{{\sqrt 2 }}{2}\left( {\cos 3x - \sin 3x} \right) = \frac{{\sqrt 2 }}{2}\)

\( \Leftrightarrow \frac{{\sqrt 2 }}{2}\cos 3x - \frac{{\sqrt 2 }}{2}\sin 3x = \frac{{\sqrt 2 }}{2}\)

\( \Leftrightarrow \sin \frac{\pi }{4}\cos 3x - \cos \frac{\pi }{4}\sin 3x = \frac{{\sqrt 2 }}{2}\)

\( \Leftrightarrow \sin \left( {\frac{\pi }{4} - 3x} \right) = \sin \frac{\pi }{4}\)

 

$\iff \left[\begin{array}{l}\frac{\pi }{4}-3x=\frac{\pi }{4}+k2\pi \\ \frac{\pi }{4}-3x=\pi -\frac{\pi }{4}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=k\frac{2\pi }{3}\\ x=-\frac{\pi }{6}+k\frac{2\pi }{3}\end{array}\right.\left(k\in \mathbb{Z}\right)$.

Vậy các nghiệm của phương trình đã cho là \(x = k\frac{{2\pi }}{3}\), $x=-\frac{\pi }{6}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right)$.

Bài 41: Cho hai biểu thức $A=\frac{2\sqrt{x}+1}{\sqrt{x}}$ và $B=\frac{x-3\sqrt{x}+4}{x-2\sqrt{x}}-\frac{1}{\sqrt{x}-2}$  (với x > 0 và x ≠ 4).

a) Tính giá trị của A khi x = 9.

b) Rút gọn biểu thức B.

c) Cho $P=\frac{B}{A}$. Tìm x để |P| > P.

Lời giải:

a) Ta có: $A=\frac{2\sqrt{x}+1}{\sqrt{x}}$  với x > 0.

Thay x = 9 vào A ta được: $A=\frac{2\sqrt{9}+1}{\sqrt{9}}=\frac{2.3+1}{3}=\frac{7}{3}$.

Vậy với x = 9 thì \(A = \frac{7}{3}\).

b) Ta có: $B=\frac{x-3\sqrt{x}+4}{x-2\sqrt{x}}-\frac{1}{\sqrt{x}-2}$ (với x > 0 và x ≠ 4).

$=\frac{x-3\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}-\frac{1}{\sqrt{x}-2}=\frac{x-3\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}-\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}$

$=\frac{x-3\sqrt{x}+4-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}=\frac{x-4\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}$

$=\frac{{\left(\sqrt{x}-2\right)}^2}{\sqrt{x}\left(\sqrt{x}-2\right)}=\frac{\sqrt{x}-2}{\sqrt{x}}$.

c) Ta có: \(P = \frac{B}{A}\)$=\frac{\sqrt{x}-2}{\sqrt{x}}:\frac{2\sqrt{x}+1}{\sqrt{x}}=\frac{\sqrt{x}-2}{\sqrt{x}}.\frac{\sqrt{x}}{2\sqrt{x}+1}=\frac{\sqrt{x}-2}{2\sqrt{x}+1}$ (với x > 0 và x ≠ 4).

|P| > P \( \Leftrightarrow \left[ \begin{array}{l} - P > P\\P > P\,\,\left( {ktm} \right)\end{array} \right.\)

Ta có – P > P khi

$-\frac{\sqrt{x}-2}{2\sqrt{x}+1}>\frac{\sqrt{x}-2}{2\sqrt{x}+1}\iff \frac{\sqrt{x}-2}{2\sqrt{x}+1}+\frac{\sqrt{x}-2}{2\sqrt{x}+1}<0$

$\iff \frac{2\sqrt{x}-4}{2\sqrt{x}+1}<0$.

Do x > 0 nên $2\sqrt{x}+1>0$ với mọi x. Do đó $\frac{2\sqrt{x}-4}{2\sqrt{x}+1}<0\iff 2\sqrt{x}-4<0$ $\iff \sqrt{x}<2$

\( \Rightarrow x < 4\).

Kết hợp điều kiện, vậy 0 < x < 4 thì |P| > P.

Bài 42: Cho tam giác ABC thỏa $\frac{a^3+b^3+c^3}{abc}+\frac{2r}{R}=4$. Chứng minh tam giác ABC là tam giác đều.

Lời giải:

Ta có: \(S = \frac{{abc}}{{4R}} = pr = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)

\( \Rightarrow {S^2} = \frac{{abc.pr}}{{4R}} = p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)\)

\( \Rightarrow \frac{{2r}}{R} = \frac{{8p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}}{{abcp}}\)

\( \Rightarrow \frac{{2r}}{R} = \frac{{\left( {a + b - c} \right)\left( {b + c - a} \right)\left( {c + a - b} \right)}}{{abc}}\).

Theo giả thiết ta có: \(\frac{{{a^3} + {b^3} + {c^3}}}{{abc}} + \frac{{2r}}{R} = 4\)

\( \Leftrightarrow \frac{{{a^3} + {b^3} + {c^3}}}{{abc}} + \frac{{\left( {a + b - c} \right)\left( {b + c - a} \right)\left( {a + c - b} \right)}}{{abc}} = 4\)

⇔ a³ + b³ + c³ + (a + b – c)(b + c – a)(a + c – b) = 4abc

⇔ a²b + ab² + b² c + bc² + c²a + ca² = 6abc (1)

Áp dụng bất đẳng thức AM-GM:

a²b + ab² + b² c + bc² + c²a + ca² ≥ 6abc

Do đó (1) đúng khi a = b = c.

Vậy tam giác ABC là tam giác đều.

Bài 43: Bác Năm dự định trồng khoai lang và khoai mì trên mảnh đất có diện tích 8 ha. Nếu trồng 1 ha khoai lang thì cần 10 ngày công và thu được 20 triệu đồng. Nếu trồng 1 ha khoai mì thì cần 15 ngày công và thu được 25 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng được không quá 90 ngày công cho việc trồng khoai lang và khoai mì.

Lời giải:

Gọi x, y (ha) lần lượt là diện tích trồng khoai lang và khoai mì (x, y ≥ 0).

Theo bài ra ta có hệ bất phương trình: \(\left\{ \begin{array}{l}10x + 15y \le 90\\x + y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\).

Số tiền thu được khi trồng x ha khoai lang và y ha khoai mì là F(x; y) = 20x + 25y (triệu đồng).

Bài toán trở thành: Tìm x, y thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}10x + 15y \le 90\\x + y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\) để F(x; y) = 20x + 25y lớn nhất.

Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}10x + 15y \le 90\\x + y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\) lên mặt phẳng tọa độ.

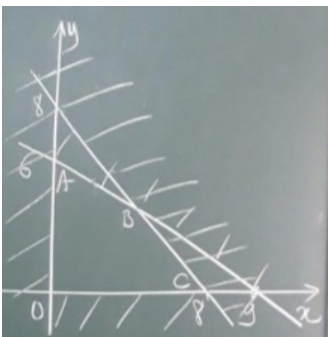
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}10x + 15y \le 90\\x + y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\)là miền tứ giác OABC với O là gốc tọa độ, A(0; 6), B(6; 2), C(8; 0).

Ta có: F(0; 0) = 0

F(0; 6) = 20 . 0 + 25 . 6 = 150

F(6; 2) = 20 . 6 + 25 . 2 = 170

F(8; 0) = 20. 8 + 25 . 0 = 160

Do đó, F(x; y) lớn nhất tại (x; y) = (6; 2).

Vậy bác Năm cần trồng 6 ha khoai lang và 2 ha khoai mì để thu được nhiều tiền nhất.

Bài 44: Cho biểu thức $P=\frac{2\sqrt{x}+5}{2\sqrt{x}+2}$ với x ≥ 0, x ≠ 1, x ≠ 9. So sánh P và P².

Lời giải:

Ta có: $P=\frac{2\sqrt{x}+5}{2\sqrt{x}+2}$$=\frac{2\sqrt{x}+2+3}{2\sqrt{x}+2}=1+\frac{3}{2\sqrt{x}+2}$

Với x ≥ 0, x ≠ 1, x ≠ 9 ta có: $2\sqrt{x}+2>0\forall x\in ℝ$ $\Rightarrow \frac{3}{2\sqrt{x}+2}>0\forall x\in ℝ$

$\Rightarrow 1+\frac{3}{2\sqrt{x}+2}>1\forall x\in ℝ$ hay P > 1 với mọi số thực x nên P < P².

Bài 45: Một bàn tròn 6 chỗ ngồi được đánh số thứ tự. Hỏi có mấy cách xếp 6 người: A, B, C, D, E, F sao cho A và B ngồi cạnh nhau.

Lời giải:

Ta coi 2 người A và B như 1 thì bàn trên còn 5 người.

Người thứ nhất có 5 cách chọn vị trí.

Người thứ hai do người thứ nhất đã ngồi rồi nên còn 4 cách chọn vị trí.

Tương tự người thứ 3 có 3 cách chọn vị trí.

Người thứ 4 có 2 cách chọn.

Người thứ 5 có 1.

Do đó, số cách xếp 5 người này ngồi vào bàn là 5.4.3.2.1 = 5! (cách).

Nhưng do 2 người ngồi cạnh nhau mà ta coi như là 1 này có thể đổi vị trí cho nhau (tức là ngồi bên phải hoặc bên trái của nhau) nên mỗi sự lựa chọn trên lại có 2 cách xắp xếp
Do đó đáp án của bài toán trên là: 2 . 5! = 240 (cách xếp).

Bài 46: Rút gọn: $A=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{2012}}$.

Lời giải:

Ta có: \(A = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{2012}}}}\)

Suy ra \(2A = 2 + 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{2011}}}}\).

Ta có: \(2A - A = \left( {2 + 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{2011}}}}} \right) - \left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{2012}}}}} \right)\)

\( \Leftrightarrow A = 2 - \frac{1}{{{2^{2012}}}}\).

Vậy \(A = 2 - \frac{1}{{{2^{2012}}}} = \frac{{{2^{2013}}}}{{{2^{2012}}}} - \frac{1}{{{2^{2012}}}} = \frac{{{2^{2013}} - 1}}{{{2^{2012}}}}\).

Bài 47: Cho đường tròn (O; R), đường kính AB, dây cung DE. Tia DE cắt AB ở C. Biết $\widehat{DOE}$ = 90° và OC = 3R.

a) Tính độ dài CD và CE theo R;

b) Chứng minh CD . CE = CA . CB.

Lời giải:

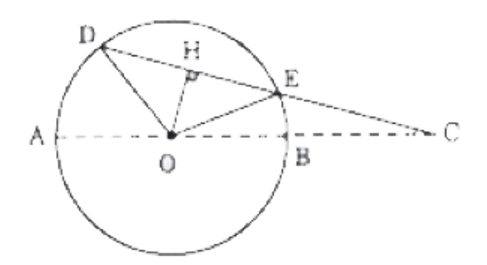
a) Tam giác DOE vuông tại đỉnh O có OD = OE = R, do đó \(DE = \sqrt {{R^2} + {R^2}}  = R\sqrt 2 \).

Từ O, hạ OH vuông góc với DE tại H, ta tính được \(OH = DH = HE = \frac{{DE}}{2} = \frac{{R\sqrt 2 }}{2}\).

Tam giác vuông HOC có OC² = OH² + HC² (định lí Pythagore)

Suy ra HC² = OC² – OH² = (3R)² – \({\left( {\frac{{R\sqrt 2 }}{2}} \right)^2}\) = \(\frac{{17{R^2}}}{2}\), do đó \(HC = \frac{{R\sqrt {34} }}{2}\).

Suy ra CE = HC – HE = $\frac{R\sqrt{34}}{2}-\frac{R\sqrt{2}}{2}=\frac{R\sqrt{34}-R\sqrt{2}}{2}$.

và CD = HC + HD = $\frac{R\sqrt{34}}{2}+\frac{R\sqrt{2}}{2}=\frac{R\sqrt{34}+R\sqrt{2}}{2}$.

b) Ta có: CD . CE = $\frac{R\sqrt{34}-R\sqrt{2}}{2}.\frac{R\sqrt{34}+R\sqrt{2}}{2}=\frac{34R^2-2R^2}{4}=8R^2$.

Lại có: CB = OC – OB = 3R – R = 2R và CA = OC + OA = 3R + R = 4R.

Do đó, CA . CB = 4R . 2R = 8R².

Vậy CD . CE = CA . CB = 8R².

Bài 48: Cho hàm số y = (2 – m)x + m + 1 (với m là tham số và m ≠ 2) có đồ thị là đường thẳng d.

a) Khi m = 0, hãy vẽ d trên hệ trục tọa độ Oxy.

b) Tìm m để d cắt đường thẳng y = 2x – 5 tại điểm có hoành độ bằng 2.

c) Tìm m để d cùng với các trục tọa độ Ox, Oy tạo thành một tam giác có diện tích bằng 2.

Lời giải:

a) Khi m = 0, ta có hàm số: y = 2x + 1.

Với x = 0 thì y = 1, với x = 1 thì y = 3. Do đó đường thẳng d đi qua hai điểm có tọa độ (0; 1) và (1; 3).

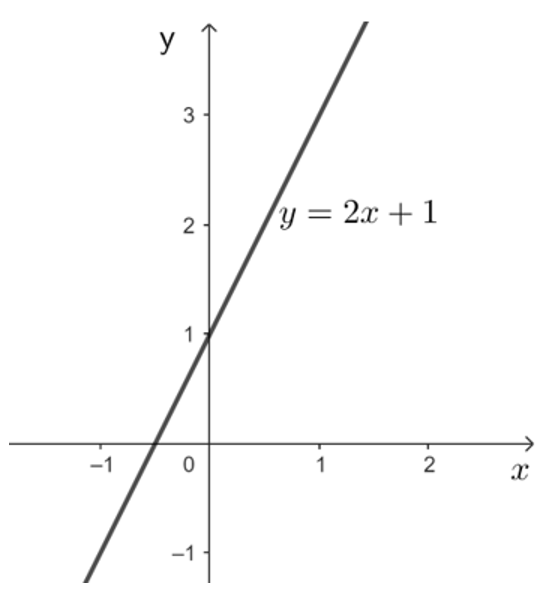
b) Ta có d: y = (2 – m)x + m + 1.

Đường thẳng d cắt đường thẳng y = 2x – 5 tại điểm có hoành độ bằng 2, suy ra x = 2.

Suy ra y = 2 . 2 – 5 = – 1.

Do đó, đường thẳng d đi qua điểm có tọa độ (2; – 1). Thay x = 2, y = – 1 vào d ta được:

– 1 = (2 – m) . 2 + m + 1 ⇔ 4 – 2m + m + 1 = – 1 ⇔ m = 6.

c) Ta có d: y = (2 – m)x + m + 1.

+ Cho y = 0, suy ra \(x = \frac{{ - m - 1}}{{2 - m}} = \frac{{m + 1}}{{m - 2}}\)  (do m ≠ 2).

Đường thẳng d cắt trục Ox tại A\(\left( {\frac{{m + 1}}{{m - 2}};\,0} \right)\). Ta có: OA = \(\left| {\frac{{m + 1}}{{m - 2}}} \right|\).

+ Cho x = 0, suy ra y = m + 1.

Đường thẳng d cắt trục Oy tại điểm B(0; m + 1). Ta có: OB = |m + 1|.

S_OAB = 2 \( \Leftrightarrow \frac{1}{2}OA.OB = 2 \Leftrightarrow OA.OB = 4\)

\( \Leftrightarrow \left| {\frac{{m + 1}}{{m - 2}}} \right|.\left| {m + 1} \right| = 4\)

\( \Leftrightarrow {\left( {m + 1} \right)^2} = 4\left| {m - 2} \right|\)

TH1: m > 2, ta có: (m + 1)² = 4(m – 2)

⇔ m² + 2m + 1 = 4m – 8

⇔ m² – 2m + 9 = 0

\( \Leftrightarrow \left[ \begin{array}{l}m = 1 + \sqrt {10} \,\left( {t.m} \right)\\m = 1 - \sqrt {10} \,\,\,\left( {loai} \right)\end{array} \right.\).

TH2: m < 2, ta có: (m + 1)² = – 4(m – 2)

⇔ m² + 2m + 1 = – 4m + 8

⇔ m² + 6m – 7 = 0

$\iff \left[\begin{array}{l}m=1\left(t.m\right)\\ m=-7\left(t.m\right)\end{array}\right.$.

Vậy \(m \in \left\{ { - 7;\,1;\,1 + \sqrt {10} } \right\}\) thì thỏa mãn yêu cầu bài toán.

Bài 49: Cho hàm số: y = (m + 3)x + 2 có đồ thị là đường thẳng d.

a) Với m = 0 thì hàm số trên là hàm bậc nhất đồng biến hay nghịch biến? Tại sao?

b) Tìm m để đồ thị hàm số trên đi qua điểm M(– 1; 3).

c) Tìm m để đường thẳng d cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 4 (đơn vị diện tích).

Lời giải:

a) Với m = 0, ta có hàm số: y = 3x + 2 là hàm số bậc nhất.

Vì a = 3 > 0 nên hàm số y = 3x + 2 đồng biến trên ℝ.

b) Đồ thị hàm số y = (m + 3)x + 2 đi qua điểm M(– 1; 3) khi và chỉ khi

(m + 3) . (– 1) + 2 = 3 ⇔ – m – 3 + 2 = 3 ⇔ m = – 4.

Vậy m = – 4.

c) Ta có: y = (m + 3)x + 2

Cho y = 0 thì x = \(\frac{{ - 2}}{{m + 3}}\) (với m ≠ – 3), d cắt trục Ox tại A\(\left( { - \frac{2}{{m + 3}};\,0} \right)\). Ta có: \(OA = \left| {\frac{{ - 2}}{{m + 3}}} \right|\).

Cho x = 0 thì y = 2, d cắt trục Oy tại B(0; 2). Ta có: OB = 2.

Ta có: S = \(\frac{1}{2}.\left| {\frac{{ - 2}}{{m + 3}}} \right|.2 = 4\)

⇔ |m + 3| = \(\frac{1}{2}\)

$\iff \left[\begin{array}{l}m+3=\frac{1}{2}\\ m+3=-\frac{1}{2}\end{array}\right.\iff \left[\begin{array}{l}m=-\frac{5}{2}\\ m=-\frac{7}{2}\end{array}\right.$ (tm).

Vậy \(m \in \left\{ { - \frac{7}{2};\, - \frac{5}{2}} \right\}\) thì thỏa mãn yêu cầu bài toán.

Bài 50: Cho hàm số bậc nhất y = (2m – 1)x + m – 1 (d).

a) Tìm m để hàm số đồng biến.

b) Tìm m để đường thẳng (d) cắt đường thẳng y = 2x + 1 tại một điểm trên trục tung.

c) Cho m = 2 vẽ đường thẳng (d) và tính khoảng cách từ gốc tọa độ đến đường thẳng (d).

Lời giải:

a) Hàm số đã cho đồng biến khi 2m – 1 > 0 ⇔ m > \(\frac{1}{2}\).

b) Đường thẳng (d) cắt đường thẳng y = 2x + 1 tại một điểm trên trục tung, suy ra x = 0. Khi đó: y = 2 . 0 + 1 = 1.

Do đó, đường thẳng (d) đi qua điểm có tọa độ (0; 1).

Suy ra (2m – 1) . 0 + m – 1 = 1 ⇔ m = 2.

Vậy m = 2.

c) Với m = 2, ta có (d): y = (2 . 2 – 1)x + 2 – 1 hay y = 3x + 1.

Với x = 0 thì y = 1, với x = 1 thì y = 4. Do đó đường thẳng (d) đi qua hai điểm có tọa độ là (0; 1) và (1; 4).

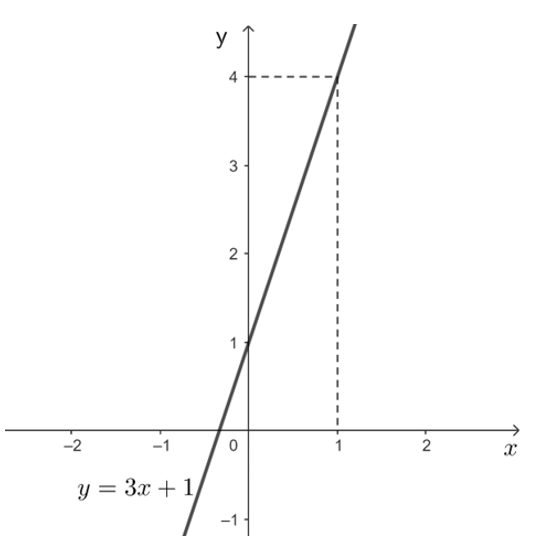
(d) cắt trục hoành tại điểm có tọa độ \(\left( { - \frac{1}{3};\,0} \right)\).

Gọi h là khoảng cách từ gốc tọa độ đến đường thẳng (d).

Ta có: \(\frac{1}{{{h^2}}} = \frac{1}{{{1^2}}} + \frac{1}{{{{\left( {\frac{1}{3}} \right)}^2}}} \Rightarrow h = \frac{{\sqrt {10} }}{{10}}\).

Bài 51: Cho tam giác ABC có M, D lần lượt là trung điểm của AB, BC và N là điểm trên cạnh AC sao cho $\overrightarrow{AN}=\frac{1}{2}\overrightarrow{NC}$. Gọi K là trung điểm của MN.

a) Chứng minh rằng: $\overrightarrow{AK}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$;

b) Chứng minh rằng: $\overrightarrow{KD}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$.

Lời giải:

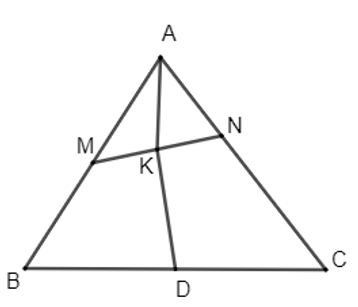
a) Vì M là trung điểm của AB nên $\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}$.

Vì$\overrightarrow{AN}=\frac{1}{2}\overrightarrow{NC}$ nên $\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}$.

Vì K là trung điểm của MN nên $\overrightarrow{AK}=\frac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)$.

Do đó, $\overrightarrow{AK}=\frac{1}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\right)=\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$.

b) Vì D là trung điểm của BC nên $\overrightarrow{AD}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)$.

$\begin{array}{l}\overrightarrow{KD}=\overrightarrow{KA}+\overrightarrow{AD}\\ =-\overrightarrow{AK}+\overrightarrow{AD}\\ =-\left(\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}\right)+\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\end{array}$

$=\frac{1}{4}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$

Bài 52: Có 3 người khách vào 4 quầy hàng 1 cách ngẫu nhiên. Xác suất 3 người này vào cùng 1 quầy hàng là bao nhiêu?

Lời giải:

Xác suất để một người vào một quầy hàng là \(\frac{1}{4}\).

Suy ra xác suất để 3 người cùng vào 1 quầy hàng là \({\left( {\frac{1}{4}} \right)^3} = \frac{1}{{64}}\).

Bài 53: Trong một kì thi tốt nghiệp phổ thông ở một trường kết quả thí sinh đạt danh hiệu xuất sắc như sau:

Toán: 48 thí sinh

Lý: 37 thí sinh

Văn: 42 thí sinh

Toán hoặc Lý: 75 thí sinh

Toán hoặc Văn: 76 thí sinh

Lý hoặc Văn: 66 thí sinh

Cả 3 môn: 4 thí sinh

Hỏi có bao nhiêu học sinh xuất sắc về:

a) 1 môn;

b) 2 môn;

c) ít nhất 1 môn.

Lời giải:

Ta có:

Số học sinh được danh hiệu xuất sắc cả hai môn Toán và Lí là

48 + 37 – 75 = 10 (học sinh).

Số học sinh được danh hiệu xuất sắc cả hai môn Toán và Văn là

48 + 42 – 76 = 14 (học sinh).

Số học sinh được danh hiệu xuất sắc cả hai môn Văn và Lí là

42 + 37 – 66 = 13 (học sinh).

Ta có số học sinh được danh hiệu xuất sắc cả 3 môn là 4 thí sinh.

Suy ra học sinh được danh hiệu xuất sắc chỉ môn Toán là

48 – 10 – 14 – 4 = 20 (học sinh).

Số học sinh được danh hiệu xuất sắc chỉ môn Lí là

37 – 10 – 13 – 4 = 10 (học sinh).

Số học sinh được danh hiệu xuất sắc chỉ môn Văn là

42 – 13 – 14 – 4 = 11 (học sinh).

a) Số học sinh được danh hiệu xuất sắc về 1 môn là

20 + 10 + 11 = 41 (học sinh).

b) Số học sinh được danh hiệu xuất sắc về 2 môn là

10 + 14 + 13 – 4 . 2 = 29 (học sinh).

c) Số học sinh được danh hiệu xuất sắc ít nhất 1 môn là

20 + 10 + 11 + 10 + 13 + 14 – 4 . 2 = 70 (học sinh).

Bài 54: Cho tam giác ABC vuông góc tại A có AC = 12 cm, BC = 16 cm. Lấy H thuộc BC sao cho CH = 9 cm. Kẻ phân giác của góc ACH cắt AH tại M. Kẻ phân giác của góc BAH cắt BH tại N.

a) Chứng minh: tam giác CAB đồng dạng với tam giác CHA và AH vuông góc BC.

b) Tính NB, NH.

c) Chứng minh MN // AB.

d) MB cắt AN tại O, cắt đường thẳng qua N và song song với AH tại I. Chứng minh \(\frac{1}{{MO}} = \frac{1}{{MI}} + \frac{1}{{MB}}\).

Lời giải:

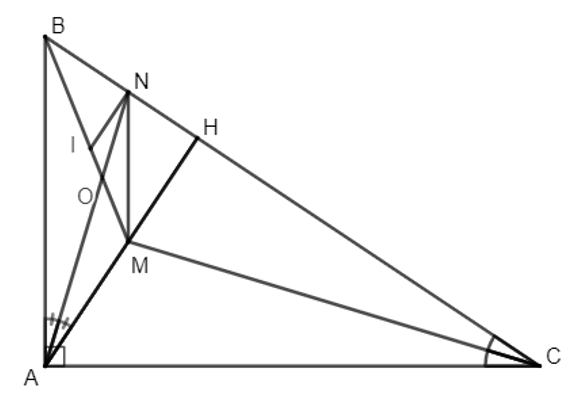
a) Ta có: \(\frac{{CA}}{{CH}} = \frac{{12}}{9} = \frac{4}{3}\) và \(\frac{{CB}}{{CA}} = \frac{{16}}{{12}} = \frac{4}{3}\). Do đó, \(\frac{{CA}}{{CH}} = \frac{{CB}}{{CA}}\) hay \(\frac{{CA}}{{CB}} = \frac{{CH}}{{CA}}\).

Xét tam giác ACB và tam giác HCA có:

\(\widehat {ACB}\): góc chung

\(\frac{{CA}}{{CB}} = \frac{{CH}}{{CA}}\) (cmt)

Do đó, hai tam giác ACB và HCA đồng dạng (c – g – c).

Suy ra \(\widehat {AHC} = \widehat {BAC} = 90^\circ \) nên AH vuông góc với BC tại H.

b) Tam giác ABC vuông tại A, theo định lí Pythagore ta có:

BC² = AB² + AC², suy ra AB² = BC² – AC² = 16² – 12² = 112, suy ra AB = \(4\sqrt 7 \) (cm).

Tam giác AHC vuông tại H, theo định lí Pythagore ta có:

AC² = AH² + HC², suy ra AH² = AC² – CH² = 12² – 9² = 63 ⇒ AH = \(3\sqrt 7 \) (cm).

Ta có: BH + HC = BC, suy ra BH = BC – HC = 16 – 9 = 7 (cm).

Vì AN là tia phân giác của góc BAH nên \(\frac{{NB}}{{NH}} = \frac{{AB}}{{AH}} = \frac{{4\sqrt 7 }}{{3\sqrt 7 }} = \frac{4}{3}\).

\( \Rightarrow \frac{{NB}}{{NB + NH}} = \frac{4}{{4 + 3}} \Rightarrow \frac{{NB}}{{BH}} = \frac{4}{7} \Rightarrow NB = \frac{4}{7}BH = \frac{4}{7}.7 = 4\) (cm).

Suy ra NH = BH – NB = 7 – 4 = 3 (cm).

c) Vì CM là tia phân giác của góc ACH nên \(\frac{{MH}}{{MA}} = \frac{{CH}}{{AC}} = \frac{9}{{12}} = \frac{3}{4}\).

Suy ra \(\frac{{MH}}{{HA}} = \frac{3}{7}\).

Ta có: \(\frac{{NH}}{{HB}} = \frac{3}{7}\). Do đó, \(\frac{{MH}}{{HA}} = \frac{{NH}}{{HB}}\).

Theo định lí Talet trong tam giác HAB, ta suy ra MN // AB.

d)

Theo giả thiết ta có: NI // AH nên \(\frac{{MO}}{{OI}} = \frac{{AO}}{{ON}} \Rightarrow \frac{{MO}}{{MO + OI}} = \frac{{AO}}{{AO + ON}} \Rightarrow \frac{{MO}}{{MI}} = \frac{{AO}}{{AN}}\).

Theo câu c ta có: MN // AB nên \(\frac{{MO}}{{BO}} = \frac{{NO}}{{AO}} \Rightarrow \frac{{MO}}{{MO + BO}} = \frac{{NO}}{{NO + AO}} \Rightarrow \frac{{MO}}{{MB}} = \frac{{NO}}{{AN}}\).

Từ đó suy ra: \(\frac{{MO}}{{MI}} + \frac{{MO}}{{MB}} = \frac{{AO}}{{AN}} + \frac{{NO}}{{AN}} = \frac{{AO + NO}}{{AN}} = \frac{{AN}}{{AN}} = 1\).

Suy ra \(\frac{{MO}}{{MI}} + \frac{{MO}}{{MB}} = 1 \Leftrightarrow MO\left( {\frac{1}{{MI}} + \frac{1}{{MB}}} \right) = 1 \Leftrightarrow \frac{1}{{MI}} + \frac{1}{{MB}} = \frac{1}{{MO}}\).

Vậy \(\frac{1}{{MO}} = \frac{1}{{MI}} + \frac{1}{{MB}}\) (đpcm).