Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 29)

Câu 1: Tính nhanh: 0,8 × 96 + 1,6 × 2.

Lời giải:

0,8 × 96 + 1,6 × 2

= 0,8 × 96 + 0,8 × 2 × 2

= 0,8 × 96 + 0,8 × (2 × 2)

= 0,8 × 96 + 0,8 × 4

= 0,8 × (96 + 4)

= 0,8 × 100

= 80.

Câu 2: Tính nhanh: 3,6 : 0,5 + 1,8 × 8 + 3,6 : 0,25.

Lời giải:

3,6 : 0,5 + 1,8 × 8 + 3,6 : 0,25

= 1,8 × 2 × 2 + 1,8 × 8 + 1,8 × 2 × 4

= 1,8 × (2 × 2) + 1,8 × 8 + 1,8 × (2 × 4)

= 1,8 × 4 + 1,8 × 8 + 1,8 × 8

= 1,8 × (4 + 8 + 8)

= 1,8 × 20

= 36.

Câu 3: Tìm x biết: 2x – (–17) = 15.

Lời giải:

2x – (–17) = 15

2x + 17 = 15

2x = 15 – 17 

2x = –2

x =  $\frac{-2}{2}$

x = –1.

Câu 4: Số dư của phép chia 37,99 : 16 nếu lấy đến 2 chữ số ở phần thập phân của thương là bao nhiêu?

Lời giải:

Ta có:

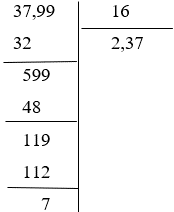
Như vậy, số dư của phép chia 37,99 : 16 nếu lấy đến 2 chữ số ở phần thập phân của thương là 7.

Cây 5: Cho a và b là hai số tự nhiên. Biết a chia cho 3 dư 1; b chia cho 3 dư 2. Chứng minh rằng ab chia cho 3 dư 2.

Lời giải:

Ta có: a chia cho 3 dư 1 ⇒ a = 3q + 1 (q ∈ ℕ)

b chia cho 3 dư 2 ⇒ b = 3k + 2 (k ∈ ℕ)

a.b = (3q + 1)(3k + 2) = 9qk + 6q + 3k + 2

Vì 9 ⋮ 3 nên 9qk ⋮ 3

Vì 6 ⋮ 3 nên 6q ⋮ 3

Vì 3 ⋮ 3 nên 3k ⋮ 3

Vậy a.b = 9qk + 6q + 3k + 2 = 3(3qk + 2q + k) + 2 chia cho 3 dư 2 (đpcm).

Câu 6: Tính: (131,4 – 80,8) : 2,3 + 21,84 × 2.

Lời giải:

(131,4 – 80,8) : 2,3 + 21,84 × 2

= 50,6 : 2,3 + 43,68

= 22 + 43,68

= 65,68.

Câu 7: Hai số thập phân có tổng là 55,22. Nếu dời dấu phẩy của số bé sang trái một hàng, rồi lấy hiệu giữa số lớn và số bé ta được 37,07. Tìm 2 số đó?

Lời giải:

Khi dời dấu phẩy của số bé sang trái một hàng tức là ta đã giảm số đó đi 10 lần. Nếu số bé mới bằng 1 phần thì số bé cần tìm bằng 10 phần như thế. 

Ta nhận thấy : 55,22 – 37,07 chính là 11 phần.

Số bé là : (55,22 – 37,07) : 11 × 10 = 16,5 

Số lớn là : 55,22 – 16,5 = 38,72. 

Đáp số: Số lớn: 38,72. Số bé: 16,5.

Câu 8: Hai số thập phân có hiệu là 5,37. Nếu dời dấu phẩy của số lớn sang trái 1 hàng rồi cộng với số bé ta được 11,955. Tìm 2 số đó?

Lời giải:

Khi dời dấu phẩy của số lớn sang trái 1 hàng tức là ta đã giảm số đó đi 10 lần.

Ta có sơ đồ:

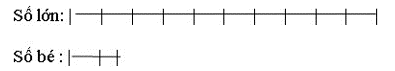
Ta có: $\frac{1}{10}$  số lớn + số bé = 11,955

Mà số lớn – số bé = 5,37.

Do đó 11 lần của $\frac{1}{10}$  số lớn là: 11,955 + 5,37 = 17,325

Số lớn là: 17,325 : 11 × 10 = 15,75.

Số bé là : 15,75 – 5,37 = 10, 38.

Đáp số: Số lớn: 15,75; Số bé: 10,38.

Câu 9: Tìm một số có hai chữ số biết nếu viết số 0 vào giữa hai chữ số của số đó ta được số mới gấp 7 lần số phải tìm?

Lời giải:

Gọi số cần tìm là $\overline{ab}$

Nếu viết số 0 vào giữa hai chữ số của số đó ta được số mới là $\overline{a0b}$

Ta có $\overline{a0b}=\overline{ab}.7$

a × 100 + b = (a × 10 + b) × 7              (phân tích cấu tạo số)

a × 100 + b = a × 70 + b × 7                (Bỏ ngoặc ở vế phải)

a × 30 = b × 6                                      (trừ cả hai vế cho a × 70 + b)

a × 5 = b                                              (Chia cả 2 vế cho 6)

Vậy a = 1 và b = 5.

Đáp số: 15.

Câu 10: Một can nước (tính cả vỏ can) nặng 12 kg. Sau đó người ta đổ bớt $\frac{1}{3}$ số nước ra ngoài. Biết rằng can rỗng nặng 600 g. Hỏi sau khi đổ bớt nước ra ngoài, can nước cân nặng bao nhiêu?

Lời giải:

Đổi 12 kg = 12000 g.

Không tính vỏ thì can nặng số kg là: 12 000 – 600 = 11 400 (g)

Số nước người ta đổ bớt đi là: 11400 × $\frac{1}{3}$ = 3800 (g)

Sau khi đổ bớt nước ra ngoài, can nước nặng là: 12000 – 3800 = 8200 (g)

Đáp số: 8200 gam.

Câu 11: Một hình chữ nhật có chiều dài 25,4 m, chiều rộng bằng 4,6 m. Tính chu vi và diện tích hình chữ nhật đó.

Lời giải:

Chu vi hình chữ nhật là: (25,4 + 4,6) × 2 = 60 (m)

Diện tích hình chữ nhật là: 25,4 × 4,6 = 116,84 (m²).

Câu 12: Mua 12 quyển vở hết 24 000 đồng. Mua 30 quyển vở như thế hết bao nhiêu tiền?

Lời giải:

Mua 1 quyển vở hết số tiền là: 24 000 : 12 = 2 000 (đồng)

Mua 30 quyển vở hết số tiền là: 30 × 2000 = 60 000 (đồng).

Đáp số: 60 000 đồng.

Câu 13: Các cột điện trước đây cách nhau 60 m, hiện nay trồng lại cách nhau 45 m. Hỏi sau cột đầu tiên không phải trồng lại thì cột gần nhất không phải trồng lại là cột thứ mấy?

Lời giải:

Gọi khoảng cách từ cột đầu tiên đến cột gần nhất không phải trồng lại là a (m). (a > 0).

Vì a chia hết cho 60 và a chia hết cho 45.

Nên a là BCNN(60, 45).

Ta có: 60 = 2² . 3 . 5; 45 = 3² . 5.

⇒ a = BCNN(60, 45) = 2² . 3² . 5 = 180.

Mà các cột trồng lại cách nhau 45 m.

Ta có: 180 : 45 = 4.

Vậy cột gần nhất không phải trồng lại cột thứ 4.

Câu 14: Tổng của hai số là 0,6. Thương của hai số cũng bằng 0,6. Tìm hai số đó?

Lời giải:

Vì thương của hai số là 0,6 hay $\frac{6}{10}=\frac{3}{5}$ nên tỉ số của hai số đó là $\frac{3}{5}$ .

Số bé là: 0,6 : (3 + 5) × 3 = 0,225

Số lớn là: 0,6 – 0,225 = 0,375

Đáp số: 0,225 và 0,375.

Câu 15: Tìm ba chữ số tận cùng của tích mười hai số nguyên dương đầu tiên.

Lời giải:

12 số nguyên dương đầu tiên là:

1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12.

Tích của 12 số nguyên dương đầu tiên là :

1 . 2 . 3 . 4 . 5 . 6 . 7 . 8 . 9 . 10 . 11 . 12 = 479 001 600

Ba chữ số tận cùng của tích 12 số nguyên dương đầu tiên là: 600.

Câu 16: Cho x,y × 9,9 = xx,yy. Hãy tìm chữ số thích hợp thay cho x và y để được phép tính đúng với x và y khác nhau và khác 0 .

Lời giải:

x,y × 9,9 = xx,yy

⇔ 10 × x,y × 10 × 9,9 = 100 × xx,yy

⇔ xy × 99 = xxyy

⇔ (10x + y) × 99 = 1000x + 100x + 10y + y

⇔ 990x + 99y = 1100x + 11y

⇔ 88y = 110x

⇔ (88 : 22) × y = (110 : 22) × x

⇔ 4 × y = 5 × x

Vậy nên y = 5; x = 4.

Câu 17: Tìm nghiệm nguyên của phương trình x² + 5y² + 6z² + 2xy – 4xz = 10.

Lời giải:

x² + 5y² + 6z² + 2xy – 4xz = 10

⇔ x² + y² + 4z² + 2xy – 4xz – 4yz + 4y² + 4yz + z² + z² = 10

⇔ (x + y – 2z)² + (2y + z)² + z² = 10   (1)

Vì x, y, z là các số nguyên nên (x + y – 2z)², (2y + z)², z² là các số chính phương.

Ta có 10 = 0 + 1 + 9.

Trường hợp 1: z² = 0 ⇔ z = 0.

Khi đó ta có (2y)² = 1 hoặc (2y²) = 9.

Lúc này không có nghiệm y nguyên vì 2y là số chẵn.

Trường hợp 2: (2y + z)² = 0 ⇔ z = –2y.

Suy ra z² = (–2y)² = 1 hoặc z² = (–2y)² = 9.

Tương tự trường hợp 1, ta cũng không có nghiệm y nguyên vì 2y là số chẵn.

Trường hợp 3: (x + y – 2z)² = 0.

Khi đó phương trình (1) tương đương với: 

 $$\begin{gathered} \left[\begin{array}{c}\left\{\begin{array}{c}{\left(x+y-2z\right)}^2=0\\ {\left(2y+z\right)}^2=1\\ z^2=9\end{array}\right.\\ \left\{\begin{array}{c}{\left(x+y-2z\right)}^2=0\\ {\left(2y+z\right)}^2=9\\ z^2=1\end{array}\right.\end{array}\right. \\ \iff \left[\begin{array}{c}\left\{\begin{array}{c}x+y-2z=0\\ 2y+z=1\\ z=\pm 3\end{array}\right.\\ \left\{\begin{array}{c}x+y-2z=0\\ 2y+z=9\\ z=\pm 1\end{array}\right.\end{array}\right. \\ \iff \left[\begin{array}{c}\left\{\begin{array}{c}x=7\\ y=-1\\ z=3\end{array}\right.\\ \left\{\begin{array}{c}x=-8\\ y=2\\ z=-3\end{array}\right.\\ \left\{\begin{array}{c}x=-2\\ y=4\\ z=1\end{array}\right.\\ \left\{\begin{array}{c}x=-7\\ y=5\\ z=-1\end{array}\right.\end{array}\right. \end{gathered}$$

Vậy (x; y; z) ∈ {(7; –1; 3); (–8; 2; –3); (–2; 4; 1); (–7; 5; –1)}.

Câu 18: Tính bằng cách thuận tiện nhất: 0,125 × 6,94 × 80.

Lời giải:

0,125 × 6,94 × 80

= 6,94 × (80 × 0,125)

= 6,94 × (80 : 8)

= 6,94 × 10

= 69,4.

Câu 19: Tìm x thuộc ℤ biết: 11 ⁝ (2x + 1).

Lời giải:

Ta có: Ư(11) = {±11; ±1}.

11 chia hết cho 2x + 1 khi 2x + 1 là ước của 11.

Ta có các trường hợp sau:

+) 2x + 1 = – 11 ⇒ x = – 6 ∈ ℤ

+) 2x + 1 = 11 ⇒ x = 5 ∈ ℤ

+) 2x + 1 = – 1 ⇒ x = – 1 ∈ ℤ

+) 2x + 1 = 1 ⇒ x = 0 ∈ ℤ

Vậy x ∈ {– 6; – 1; 0; 5}.

Câu 20: Tính nhanh: 245,9 × 0,49 – 245,9 × 0,58 + 24,59 × 10.

Lời giải:

245,9 × 0,49 – 245,9 × 0,58 + 24,59 × 10

= 245,9 × 0,49 – 245,9 × 0,58 + 245,9

= 245,9 × 0,49 – 245,9 × 0,58 + 245,9 × 1

= 245,9 × (0,49 – 0,58 + 1)

= 245,9 × 0,91

= 223,769.

Câu 21: Tính bằng cách thuận tiện nhất: 28 + 62 × a × (a × 1 – a : 1 ) + 28 × 8 + 28.

Lời giải:

28 + 62 × a × (a × 1 – a : 1) + 28 × 8 + 28

= 28 × 1 + 62 × a × 0 + 28 × 8 + 28 × 1

= 28 × 1 + 28 × 8 + 28 × 1

= 28 × (1 + 8 + 1)

= 28 × 10

= 280.

Câu 22: Cho hình tròn tâm O, đường kính AB = 8 cm.

a. Tính chu vi hình tròn tâm O đường kính AB, hình tròn tâm M, đường kính AO và hình tròn tâm N, đường kính OB.

b. So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi hình tròn tâm O.

c. Tính diện tích phần đã tô đậm của hình tròn tâm O.

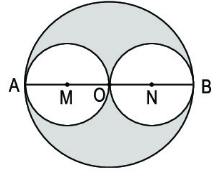
Lời giải:

Hai hình tròn tâm M và N đều có đường kính là: 8 : 2 = 4 (cm)

a. Chu vi hình tròn tâm O là: 8 × 3,14 = 25,12 (cm)

Chu vi hình tròn tâm M (hoặc tâm N) là: 4 × 3,14 = 12,56 (cm)

b. Tổng chu vi của hình tròn tâm M và hình tròn tâm N là: 12,56 × 2 = 25,12 (cm).

Vậy tổng chu vi của hình tròn tâm M và hình tròn tâm N bằng chu vi hình tròn tâm O.

c. Diện tích phần tô đậm của hình tròn tâm O bằng diện tích hình tròn tâm O trừ đi tổng diện tích của hình tròn tâm M và hình tròn tâm N.

Diện tích hình tròn tâm O là: 4 × 4 × 3,14 = 50,24 (cm²)

Diện tích hình tròn tâm M (hoặc tâm N) là: 2 × 2 × 3,14 = 12,56 (cm²)

Diện tích phần đã tô đậm của hình tròn tâm O là: 50,24 – 12,56 × 2 = 25,12 (cm²).

Câu 23: Trong hộp có 40 viên bi, trong đó có 24 viên bi xanh. Tỉ số phần trăm của số bi xanh và số bi trong hộp là bao nhiêu?

Lời giải:

Tỉ số phần trăm của số bi xanh và số bi trong hộp là:

24 : 40 . 100% = 60 %

Vậy tỉ số phần trăm của số bi xanh và số bi trong hộp là 60%.

Câu 24: Một trường tổ chức cho học sinh khối 6 khoảng 350 đến 400 học sinh đi tham quan bằng ô tô. Tính số học sinh đi tham quan biết rằng nếu xếp 30 hay 45 người ngồi vào 1 xe thì không còn dư một ai.

Lời giải:

Gọi số học sinh khối 6 trường đó là x ( x ∈ ℕ*, 350 <  x < 400)

Theo đề bài xếp 30 hay 45 người ngồi vào 1 xe thì không còn dư một ai

Suy ra x chia hết cho cả 30 và 45

Do đó x ∈ BC(30, 45)

Ta có:

30 = 2 . 3 . 5

45 = 3² . 5

Suy ra BCNN(30, 45) = 2 . 3² . 5 = 90

Do đó BC(30, 45) = {0; 90; 180; 270; 360; 450; ...}

Mà 350 <  x < 400

Suy ra x = 360

Vậy trường đó có 360 học sinh khối 6.

Câu 25: Số học sinh khối 6 của một trường trong khoảng từ 400 đến 500 em. Nếu xếp hàng 7 em thì thừa ra 3 em, còn nếu xếp hàng 6 em, 8 em hoặc 10 em thì vừa đủ. Hỏi số học sinh khối 6 của trường là bao nhiêu em?

Lời giải:

Gọi số học sinh khối 6 là a (a ∈ ℕ*, 400 < a < 500)

Theo đề bài ta có a ∈ BC(6; 8; 10)

Ta có

6 = 2 . 3

8 = 2³

10 = 2 . 5

Suy ra BCNN(6, 8, 10) = 2³ . 3 . 5 = 120

Suy ra BC(6, 8, 10) ={0; 120; 240; 360; 480; 600; ...}

Mà 400 < a < 500

Suy ra a = 480

Vậy số học sinh là 480 em.

Câu 26: Tổng của hai số là 0,6. Thương của hai số cũng bằng 0,6. Tìm hai số đó.

Lời giải:

Vì thương của số bé vá số lớn là 0,6 hay $\frac{3}{5}$  nên tỉ số của hai số đó là $\frac{3}{5}$

Ta coi số bé là 3 phần bằng nhau thì số lớn là 5 phần bằng nhau như vậy.

Tổng số phần bằng nhau

3 + 5 = 8 (phần)

Giá trị của một phần

0,6 : 8 = 0,075

Số bé là:

0,075 × 3 = 0,225.

Số lớn là:

0,6 − 0,225 = 0,375.

Vậy hai số cần tìm là 0,225 và 0,375.

Câu 27: Một lớp học có 25 học sinh, trong đó có 13 học sinh nữ. Hỏi số học sinh nữ chiếm bao nhiêu phần trăm số học sinh của lớp đó?

Lời giải:

Tỉ số phần trăm của số học sinh nữ và số học sinh cả trường là:

13 : 25 × 100% = 52%

Vậy số học sinh nữ chiếm 52% số học sinh của lớp đó.

Câu 28: Có bao nhiêu hình tứ giác trong hình sau

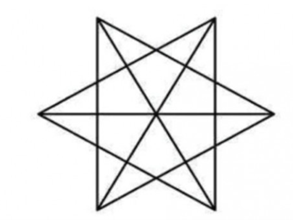
Lời giải:

Từ hình vẽ ta thấy có 42 hình tứ giác.

Câu 29: Cho A = 1 + 3 + 3² + 3² + … + 3¹¹. Chứng minh rằng:

a) A chia hết cho 13.

b) A chia hết cho 40.

Lời giải:

a) Ta có : 

A = 1 + 3 + 3² + 3² + … + 3¹¹

A = (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + (3⁶ + 3⁶ + 3⁸) + (3⁹ + 3¹⁰ + 3¹¹)

A = 1.(1 + 3 + 3²) + 3³.(1 + 3 + 3²) + 3⁶.(1 + 3 + 3²) + 3⁹.(1 + 3 + 3²)

A = (1 + 3 + 3²) . (1 + 3³ + 3⁶ + 3⁹)

A = 13 . (1 + 3³ + 3⁶ + 3⁹)

Vì 13 ⋮ 13 nên 13 . (1 + 3³ + 3⁶ + 3⁹) ⋮ 13

Vậy A ⋮ 13.

b) Ta có : 

A = 1 + 3 + 3² + 3² + … + 3¹¹

A = (1 + 3 + 3² + 3³) + (3⁴ + 3⁵ + 3⁶ + 3⁷) + (3⁸ + 3⁹ + 3¹⁰ + 3¹¹)

A = 1 . (1 + 3 + 3² + 3³) + 3⁴ . (1 + 3 + 3² + 3³) + 3⁸ . (1 + 3 + 3² + 3³)

A = (1 + 3 + 3² + 3³).(1 + 3⁴ + 3⁸)

A = 40 . (1 + 3⁴ + 3⁸)

Vì 40 ⋮ 40 nên 40 . (1 + 3⁴ + 3⁸) ⋮ 40

Vậy A ⋮ 40.

Câu 30: Mua 4 m vải phải trả 80 000 đồng. Hỏi mua 6,8 m vải cùng loại phải trả nhiều hơn bao nhiêu tiền?

Lời giải:

Mua 1 m vải hết số tiền là:

80 000 : 4 = 20 000 (đồng)

Mua 6,8 m vải cùng loại phải trả số tiền là:

20 000 × 6,8 = 136 000 (đồng)

Mua 6,8 m vải cùng loại phải trả nhiều hơn số tiền là:

136 000 – 80 000 = 56 000 (đồng)

Vậy mua 6,8 m vải cùng loại phải trả nhiều hơn 56 000 đồng.

Câu 31: Mua 5 kg đường phải trả 85 000 đồng. Hỏi mua 3,5 kg đường cùng loại phải trả ít hơn bao nhiêu tiền?

Lời giải:

Mua 1 kg đường phải trả:

85 000 : 5 = 17 000 (đồng)

Mua 3,5 kg đường cùng loại phải trả :

17 000 × 3,5 = 59 500 (đồng)

Mua 3,5 kg đường cùng loại thì phải trả ít hơn số tiền là

85 000 – 59 500 = 25 500 (đồng)

Vậy mua 3,5 kg đường cùng loại thì phải trả ít hơn 25 500 đồng.

Câu 32: Một chai dầu có 0,75 l dầu, mỗi lít dầu cân nặng 0,8 kg. Hỏi:

a) 150 chai dầu cân nặng bao nhiêu ki – lô – gam?

b) Một can chứa 20 l dầu, can dầu đó nặng bao nhiêu ki – lô – gam?

Lời giải:

a) Cân nặng của một chai dầu là:

0,8 × 0,75 = 0,6 (kg).

Cân nặng của 150 chai dầu là:

0,6 × 150 = 90 (kg).

b) Cân nặng của một can dầu là:

20 × 0,8 = 16 (kg).

Câu 33: Để đánh số trang của một quyển sách dày 250 trang người ta phải dùng tất cả bao nhiêu chữ số?

Lời giải:

Các trang từ 1 đến 9: có 9 trang, mỗi trang viết 1 chữ số

Các trang từ 10 đến 99: có 90 trang, mỗi trang viết 2 chữ số

Các trang từ 100 đến 250 : có 151 trang, mỗi trang viết 3 chữ số.

Vậy phải viết tất cả là: 

9 × 1 + 90 × 2 + 151 × 3 = 642 (chữ số) 

Vậy cần dùng 642 chữ số.

Câu 34: Một cửa hàng bán trứng có 40 giá để trứng, mỗi giá để trứng có 175 quả. Cửa hàng đã bán hết 10 giá trứng. Hỏi cửa hàng đó còn lại bao nhiêu quả trứng?

Lời giải:

Cửa hàng có tất cả:

175 × 40 = 7 000 (quả trứng)

Cửa hàng đã bán:

175 × 10 = 1 750 (quả trứng)

Cửa hàng còn lại:

7 000 – 1 750 = 5 250 (quả trứng)

Vậy cửa hàng còn lại 5 250 quả trứng.

Câu 35: Một hình chữ nhật có chu vi 124 cm. Biết rằng nếu giảm chiều dài đi 15 cm và giảm chiều rộng đi 5 cm thì hình đó trở thành hình vuông. Tính diện tích hình chữ nhật đó?

Lời giải:

Nếu giảm chiều dài 15 cm và giảm chiều rộng 5 cm thì hình chữ nhật trở thành hình vuông nên hình chữ nhật có chiều dài hơn chiều rộng là: 15 – 5 = 10 (cm).

Nửa chu vi hình chữ nhật là: 124 : 2 = 62 (cm).

Chiều dài hình chữ nhật là: (62 + 10) : 2 = 36 (cm).

Chiều rộng là: 36 – 10 = 26 (cm).

Diện tích hình chữ nhật là: 36.26 = 936 (cm²).

Vậy diện tích hình chữ nhật là 936 cm².

Câu 36: Một hình chữ nhật có chu vi gấp 5 lần chiều rộng, biết chiều dài là 30 m. Hình chữ nhật đó có diện tích là bao nhiêu?

Lời giải:

Gọi chiều rộng là a (a > 0).

Theo bài ra ta có phương trình

(a + 30) . 2 = 5a

⇔ 2a + 60 = 5a

⇔ 60 = 3a

⇔ a = 20

Diện tích hình chữ nhật là 20 . 30 = 600 (m²)

Vậy diện tích hình chữ nhật là 600 m².

Câu 37: Một đàn gà có 200 con gà, trong đó có 106 con gà trống. Tỉ số phần trăm số gà mái và tổng số gà là bao nhiêu?

Lời giải:

Số gà mái là:

200 – 106 = 94 (con)

Tỉ số phần trăm giữa gà mái và tổng số gà là:

(94 : 200) × 100% = 47%.

Vậy tỉ số phần trăm số gà mái và tổng số gà là 47%.

Câu 38: Muốn nhân hai lũy thừa khác cơ số và khác cả số mũ ta phải làm sao?

Lời giải:

Muốn nhân hai lũy thừa khác cơ số và số mũ ta sẽ đổi từ dạng lũy thừa sang dạng số tự nhiên và tính bình thường.

Ta có ví dụ sau:

2⁵ . 3² = 32 . 9 = 288.

Câu 39: Công thức tính chiều cao trung bình của trẻ em Việt Nam được xác định như sau:

Chiều cao trung bình của trẻ = 0,75 + 0,05 × (số tuổi theo năm dương lịch của trẻ – 1).

(Đơn vị: mét).

a) Em hãy tính chiều cao trung bình của trẻ em 6 tuổi.

b) Em hãy tính chiều cao trung bình của trẻ em 11 tuổi.

Lời giải:

a) Chiều cao trung bình của trẻ 6 tuổi là 

0,75 + 0,05 × (6 – 1) = 1 (m).

Vậy chiều cao trung bình của trẻ em 6 tuổi là 1 m.

b) Chiều cao trung bình của trẻ 11 tuổi là

0,75 + 0,05 × (11 – 1) = 1,25 (m)

Vậy chiều cao trung bình của trẻ em 11 tuổi là 1,25 m.

Câu 40: Một nông dân cày ruộng bằng máy, trong 6 giờ 30 phút cày được 7 897,5 m². Hỏi trong 4 giờ 15 phút thì anh nông dân đó cày được bao nhiêu mét vuông đất?

Lời giải:

Đổi: 6 giờ 30 phút = 6,5 giờ

1 giờ anh nông dân cày được là:

7 897,5 : 6,5 = 1 215 (m²)

Đổi: 4 giờ 45 phút = 4,75 giờ

Trong 4 giờ 45 phút anh nông dân cày được là:

4,75 × 1 215 = 5 771,25 (m²)

Vậy trong 4 giờ 15 phút thì anh nông dân đó cày được 5 771,25 m² đất.

Câu 41:  

a) Tính tổng các góc của đa giác 15 cạnh.

b) Đa giác nào có tổng các góc bằng 1 620°.

Lời giải:

Tổng số đo các góc của đa giác n cạnh là (n − 2) . 180°.

a) Tổng số đo của đa giác 15 cạnh là (15 − 2) . 180° = 2 340°.

b) Gọi đa giác cần tìm có n cạnh

Từ giả thiết ta có 

(n − 2) . 180° = 1 620°

⇔ n – 2 = 9

⇔ n = 11

Vậy đa giác 11 cạnh có tổng các góc bằng 1 620°.

Câu 42: Số học sinh khối 6 của trường Kết Đoàn khoảng từ 300 đến 400 học sinh. Mỗi lần xếp hàng 12, hàng 15, hàng 18 đều vừa đủ. Hỏi khối 6 của trường Kết Đoàn có bao nhiêu học sinh?

Lời giải:

Gọi số học sinh khối 6 của trường Kết Đoàn là a (học sinh) (a ∈ ℕ*) (300 < a < 400).

Vì xếp hàng 12, hàng 15, hàng 18 đều vừa đủ nên a chia hết cho cả 12, 15 và 18.

Do đó a = BC(12, 15, 18)

Ta có:

12 = 2² . 3;

15 = 3 . 5;

18 = 2 . 3²

Suy ra BCNN(12, 15, 18) = 2² . 3² . 5 = 180

Nên BC(12, 15, 18) = B(180) = {0; 180; 360; 540; …}

Mà 300 < a < 400 nên a = 360 (học sinh)

Vậy số học sinh khối 6 của trường Kết Đoàn là 360 học sinh.

Câu 43: Tìm số trung bình cộng của các số lẻ từ 11 đến 100.

Lời giải:

Số số lẻ là (99 – 11) : 2 + 1 = 45 (số)

Ta có

11 + 13 + 15 + 17+ ... + 99 (45 số hạng)

= (99 + 11) . 45 : 2

= 110 . 45 : 2

=2 475

Số trung bình cộng của 2 475 là

2 475 : 45 = 55

Vậy số trung bình cộng của các số lẻ từ 11 đến 100 là 45.

Câu 44: Tìm số nghiệm của phương trình 2^x + 3^x + 4^x + ... + 2017^x + 2018^x = 2017 – x.

A. 2017;

B. 1;

C. 0;

D. 2016.

Lời giải:

Đáp án đúng là: B

Xét hàm số f(x) = 2^x + 3^x +  ... + 2017^x + 2018^x

Ta có f’(x) = 2^x ln2 + 3^x ln3 + ... + 2017^x ln2017 + 2018^x ln2018 > 0 với mọi x

Suy ra f(x) đồng biến trên ℝ

Xét hàm số g(x) = 2017 – x

Ta có g’(x) = – 1 < 0 với mọi x

Suy ra g(x) nghịch biến trên ℝ

Do đó phương trình 2^x + 3^x + 4^x + ... + 2017^x + 2018^x = 2017 – x có tối đa 1 nghiệm

Ta thấy x = 0 là nghiệm duy nhất của phương trình.

Vậy ta chọn đáp án B.

Câu 45: Tính bằng cách thuận tiện nhất 0,12 × 400.

Lời giải:

Ta có

0,12 × 400

= 0,12 × (100 × 4)

= (0,12 × 100) × 4

= 12 × 4

= 48

Vậy 0,12 × 400 = 48.

Câu 46: Tích A có tận cùng của phần thập phân là chữ số nào biết A = 1,7 × 2,7 × 3,7 × ... × 9,7 × 10,7.

Lời giải:

Ta có A = 1,7 × 2,7 × 3,7 × ... × 9,7 × 10,7.

Ta chia 10 số hạng của A thành các nhóm, mỗi nhóm có 4 số hạng thì có tất cả 10 : 4 = 2 (nhóm) dư 2 số hạng.

Do đó

A = (1,7 × 2,7 × 3,7 × 4,7) × (5,7 × 6,7 × 7,7 × 8,7) × 9,7 × 10,7 

A = ...1 × ...1 × ...9

A = ...9

Vậy tích A có tận cùng là 9.

Câu 47: Lượng nước trong một loại nấm tươi là 85%, trong nấm khô là 60%. Hỏi nếu người ta phơi 80kg nấm tươi thì thu được bao nhiêu kg nấm khô?

Lời giải:

Lượng nước trong 80kg nấm tươi là:

80.85% = 68 (kg).

Khối lượng nấm nguyên chất trong nấm tươi là: 80 – 68 = 12 (kg).

Lượng nấm trên chiếm 100% – 60% = 40% trong nấm khô nên ta thu được số kg nấm khô là:

12 : 40% = 30 (kg).

Vậy nếu phơi 80 kg nấm tươi thì thu được 30 kg nấm khô.

Câu 48: Tính bằng hai cách: (6,75 + 3,25) × 4,2.

Lời giải:

Cách 1:

(6,75 + 3,25) × 4,2

= 10 × 4,2 = 42

Cách 2:

(6,75 + 3,25) × 4,2

= 6,75 × 4,2 + 3,25 × 4,2

= 28,35 + 13,65

= 42.

Câu 49: Cho hình thang ABCD, M là trung điểm của cạnh BC. Diện tích hình thang ABCD là 18 cm². Tính diện tích tam giác ADM.

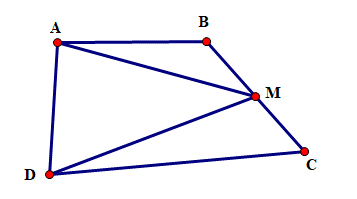
Lời giải:

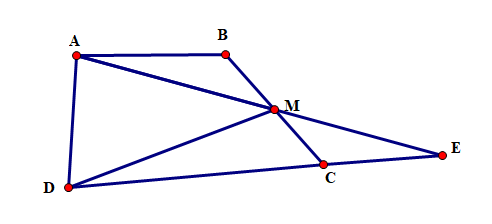
Kéo dài AM cắt DC tại E 

Suy ra S_ABM = S_MCE

Do đó diện tích tam giác ADE bằng diện tích hình thang ABCD nên diện tích tam giác ADE bằng 18cm²

Vì M là trung điểm của AE nên diện tích tam giác ADE gấp đôi diện tích tam giác ADM

Suy ra diện tích tam giác ADM là:

18 : 2 = 9 (cm²)

Vậy diện tích tam giác ADM bằng 9 cm².

Câu 50: Cho đa thức P(x) có tất cả các hệ số đều là số tự nhiên, nhỏ hơn 5, thỏa mãn điều kiện P(5) = 259. Tính P(2049).

Lời giải:

Giả sử P(x)= ax³ + bx² + cx + d (0 ≤ a, b, c, d < 5)

P(5) = 259

⇔ 125a + 25b + 5c + d = 259

Vì 0 ≤ a, b, c, d < 5

Nên a = 2

Suy ra 25 b + 5c + d = 259 – 125 . 2 = 9

Vì 9 < 25 nên b = 0

Khi đó 5c + d = 9

Mà 0 ≤ c, d < 5

Suy ra c = 1, d = 4

Do đó P(x) = 2x³ + x + 4

Suy ra P(2049) = 2 . 2049³ + 2049 + 4 = 17 205 049 351

Vậy P(2049) = 17 205 049 351.

Câu 51: Một hình chữ nhật có chiều dài gấp 5 lần chiều rộng. Nếu bớt ở chiều dài 5 cm và thêm vào chiều rộng 115 cm thì được một hình vuông. Tính chu vi và diện tích của hình chữ nhật.

Lời giải:

Chiều dài hơn chiều rộng số cm là

115 + 5 = 120 (cm).

Do hình chữ nhật có chiều dài gấp 5 lần chiều rộng nên coi chiều rộng là 1 phần thì chiều dài là 5 phần. Hiệu số phần bằng nhau là: 5 – 1 = 4  (phần).

Chiều rộng hình chữ nhật là

120 : 4 = 30 (cm)

Chiều dài hình chữ nhật là

30 . 5 = 150 (cm)

Chu vi hình chữ nhật là

(150 + 30) × 2 = 360 (cm)

Diện tích hình chữ nhật là

150 × 30 = 4 500 (cm²)

Vậy chu vi hình chữ nhật là 360 cm, diện tích hình chữ nhật là  4 500 cm².