Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 17)

Câu 1: Thực hiện phép chia:

a) (x⁴ + 6x² + 8) : (x² + 2);

b) (3x³ – 2x² + 3x – 2) : (x² + 2).

Lời giải:

a) (x⁴ + 6x² + 8) : (x² + 2)

Thực hiện đặt phép chia đa thức như sau:

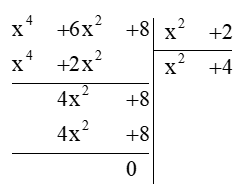
Vậy (x⁴ + 6x² + 8) : (x² + 2) = x² + 4.

b) (3x³ – 2x² + 3x – 2) : (x² + 1)

Thực hiện phép tính chia đa thức sau:

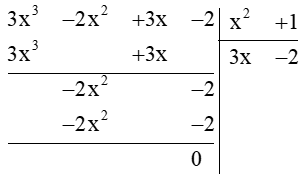
Vậy (3x³ – 2x² + 3x – 2) : (x² + 1) = 3x – 2

Câu 2: Phân tích đa thức thành nhân tử: x⁴ + x² + 1.

Lời giải:

Ta có x⁴ + x² + 1 = x⁴ – x + x² + x + 1

= x(x³ – 1) + (x² + x + 1)

= x(x – 1)(x² + x + 1) + (x² + x + 1)

= (x² + x + 1)[x(x – 1) + 1]

= (x² + x + 1)(x² – x + 1).

Câu 3: Liệt kê tất cả các ước của các số sau: 530; 240; 438.

Lời giải:
Ta có:
• 530 = 2.5.53

Suy ra ta có: Ư(530) = {1; 2; 5; 10; 53; 106; 265; 530}.

• 240 = 2⁴. 3. 5

Suy ra ta có: Ư(240) = {1; 2; 3; 4; 5; 6; 8; 10; 16; 48; 80; 240}.

• 438 = 2. 3. 73

Suy ra ta có:
Ư(438) = {1; 2; 3; 6; 73; 146; 219; 438}.

Câu 4: Phân tích đa thức thành nhân tử: 12x² + 5x – 12y² + 12y – 10xy – 3

Lời giải:

12x² + 5x – 12y² + 12y – 10xy – 3

= 12x² + 9x – 4x – 12y² – 18xy + 8xy  – 3 + 6y – 6y

= (12x² – 18xy + 9x) – (4x – 6y + 3) + (8xy – 12y² + 6y)

= 3x(4x – 6y + 3) – (4x – 6y + 3) + 2y(4x – 6y + 3)

= (4x – 6y + 3)(3x + 2y – 1).

Câu 5: Cho trước hai điểm phân biệt A, B. Tìm tập hợp các điểm M thỏa mãn:

$\left|\overrightarrow{MA}\right|=\left|\overrightarrow{MB}\right|$.

Lời giải:

Ta có: $\left|\overrightarrow{MA}\right|=MA$

$\left|\overrightarrow{MB}\right|=MB$

Nên $\left|\overrightarrow{MA}\right|=\left|\overrightarrow{MB}\right|\iff MA=MB$ .

Hay M là điểm thuộc đường trung trực của đoạn AB.

Vậy tập hợp điểm M là đường trung trực của đoạn thẳng AB.

Câu 6: Cho hai điểm B; C phân biệt. Tập hợp những điểm M thỏa mãn $\overrightarrow{CM}.\overrightarrow{CB}={\overrightarrow{CM}}^2$  là:

A. Đường tròn đường kính BC;

B. Đường tròn (B; BC);

C. Đường tròn (C: BC);

D. Một đường tròn khác.

Lời giải:

Đáp án đúng là: A.

Ta có:

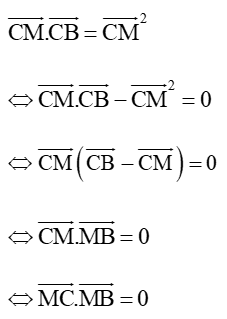
Vậy tập hợp điểm M thuộc đường tròn đường kính BC.

Câu 7: Cô giáo cho một số kẹo. Nếu cô chia số kẹo đó thành 12 phần như nhau thì dư 6 chiếc. Hỏi cô có thể chia đều số kẹo thành 4 phần mà không còn dư hay không?

Lời giải:

Gọi số kẹo mỗi phần là a tổng số kẹo là b

Khi đó ta có:  

12a + 6 = b

b : 4 = (12a + 6 ) : 4

Vì 12a chia hết cho 4 mà 6 : 4 = 1 dư 2 nên b : 4 sẽ dư 2

 Do đó số kẹo của cô chia 4 dư 2

Vậy cô ko thể chia 4 phần mà ko dư.

Câu 8: Mẹ có một số kẹo. Nếu mẹ chia số kẹo thành 6 phần bằng nhau thì dư 3 cái.

a) Hỏi với số kẹo đó, mẹ có thể chia thành 3 phần bằng nhau hay không? Vì sao? b) Với số kẹo đó, mẹ có thể chia thành 2 phần bằng nhau không? Vì sao?

Lời giải:

Mẹ chia số kẹo thành 6 phần bằng nhau thì dư 3 cái 

Tổng số kẹo có dạng: 6k + 3

a) Ta có: $6⋮3\Rightarrow 6k⋮3$

$3⋮3$

Vậy số kẹo đó có thể chia thành 3 phần bằng nhau.

b) Ta có: $6⋮2\Rightarrow 6k⋮2$

$3\cancel{⋮}2$

Vậy số kẹo không thể thành 2 phần bằng nhau.

Câu 9: Chứng minh:
(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac

Lời giải:
Ta có:

(a + b + c)² = (a + b + c)(a + b + c)

= a² + ab + ac + ab + b² + bc + ac + bc + c²

= a² + b² + c² + 2ab + 2bc + 2ac (đpcm)

Vậy (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac.

Câu 10: Tìm x, biết:

a) x(x – 2) + x – 2 = 0;

b) 2(x + 3) – x² – 3x = 0;

Lời giải:
a) Ta có: x(x – 2) + x – 2 = 0

(x – 2)(x + 1) = 0

$\iff \left[\begin{array}{l}x=2\\ x=-1\end{array}\right.$.

Vậy phương trình đã cho có hai nghiệm phân biệt là: x = 2; x = −1.

b) 2(x + 3) – x² – 3x = 0

2x + 6 – x² – 3x = 0

−x² – x + 6 = 0

Ta có: $\Delta$  = 1 – 4.(−1).6 = 25.

Vậy phương trình đã cho có hai nghiệm phân biệt là:

$x=\frac{1+\sqrt{25}}{-2}=-3$; $x=\frac{1-\sqrt{25}}{-2}=2$ .

Câu 11: Tìm x, biết: $\sqrt{3}\cos \left(x-\frac{\pi }{2}\right)+\sin \left(x-\frac{\pi }{2}\right)=2\sin 2x$ .

Lời giải:

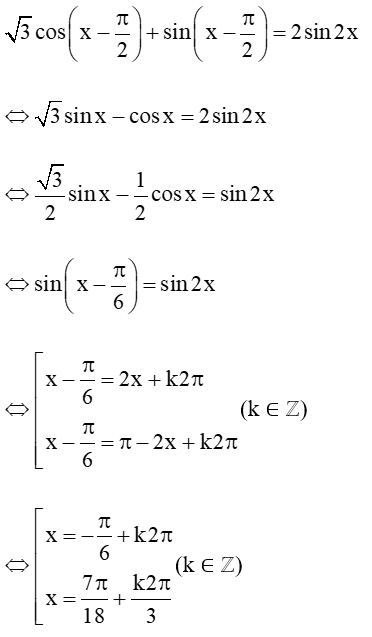
Vậy phương trình đã cho có hai họ nghiệm là: $\left[\begin{array}{l}x=-\frac{\pi }{6}+k2\pi \\ x=\frac{7\pi }{18}+\frac{k2\pi }{3}\end{array}\right.$ .

Câu 12: Giải phương trình tan3x = tanx.

Lời giải:

ĐKXĐ: $x\ne \frac{\pi }{6}+\frac{k\pi }{3}$ , k ∈ ℤ.

Ta có: tan3x = tanx

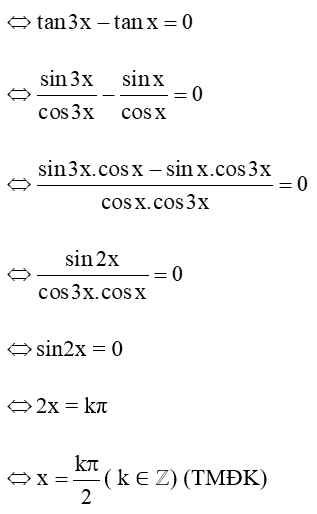
Vậy phương trình đã cho có họ nghiệm là: $x=\frac{k\pi }{2}$ , k ∈ ℤ.

Câu 13: Cho tứ giác ABCD có hai góc đối ở đỉnh B và D cùng bằng 90°. Gọi O là trung điểm của AC. Chứng minh bốn điểm A, B, C, D cùng thuộc đường tròn đường kính AC.

Lời giải:

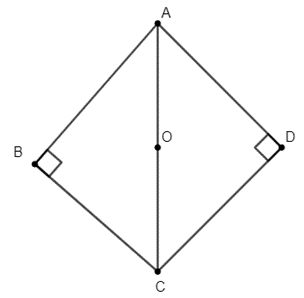
Xét ∆ABC có: $\widehat{ABC}=90°$ (gt)

Suy ra AC là cạnh huyền.

Lại có: AO = OC (gt)

 BO là đường trung tuyến ∆ABC

 BO = AO = OC (đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền) (1)

Tương tự ta chứng minh được: DO = AO = OC (2)

Từ (1) và (2) ta có: BO = AO = OC = DO

Suy ra 4 điểm A, B, C, D cùng thuộc đường trong đường kính AC.

Câu 14: Cho tam giác ABC có $\widehat{A}=90°$ . Chọn câu đúng:

A. a² = b² + c² – 3bc;

B. a² = b² + c² + bc;

C. a² = b² + c² + 3bc;

D. a² = b² + c² – bc.

Lời giải:

Đáp án đúng là: B.

Áp dụng định lí cosin tại đỉnh A, ta có:

A² = b² + c² – 2bc.cosA

 a² = b² + c² – 2bc.cos120° = b² + c² + bc.

Câu 15: Năm nay Lan được 12 tuổi còn mẹ của Lan thì được 32 tuổi. Hỏi sau 8 năm nữa thì số tuổi của mẹ gấp mấy lần số tuổi của Lan?

Lời giải:

Số tuổi của Lan sau 8 năm nữa là: 12 + 8 = 20 (tuổi)

Số tuổi của mẹ Lan sau 8 năm nữa là: 32 + 8 = 40 (tuổi)

Sau 8 năm nữa thì số tuổi của mẹ số lần số tuổi của Lan là:

40 : 20 = 2 (lần)

Vậy sau 8 năm nữa số tuổi của mẹ gấp 2 lần số tuổi của Lan.

Câu 16: Rút gọn biểu thức:

$A=\frac{{\left(\sqrt{x}+\sqrt{y}\right)}^2-4\sqrt{xy}}{\sqrt{x}-\sqrt{y}}-\frac{x\sqrt{y}+y\sqrt{x}}{\sqrt{xy}}$ (với x, y > 0, x ≠ y).

Lời giải:

Câu 17: Tính: $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}$ .

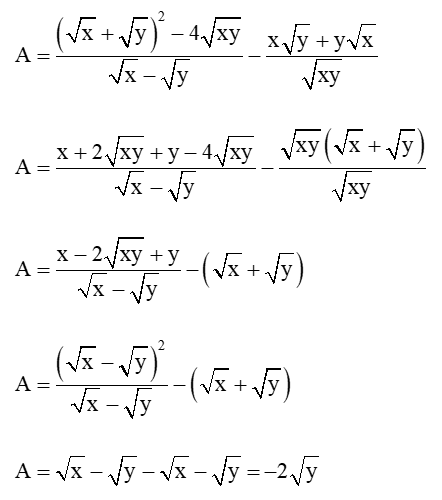
Lời giải:

Ta có $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}$

 

$$\begin{gathered} =\frac{32}{64}+\frac{16}{64}+\frac{8}{64}+\frac{4}{64}+\frac{2}{64}+\frac{1}{64} \\ =\frac{32+16+8+4+2+1}{64} \\ =\frac{63}{64} \end{gathered}$$

Câu 18: Tìm x, biết: cos²x – 3sinx.cosx – 2sin²x – 1 = 0.

Lời giải:

cos²x – 3sinx.cosx – 2sin²x – 1 = 0

$\iff$cos²x – 3sinx.cosx – 2sin²x – sin²x – cos²x = 0

$\iff$−3sinx.cosx – 3sin²x = 0

$\iff$3sinx(cosx – sinx) = 0

$$\begin{gathered} \iff \left[\begin{array}{l}\sin x=0\\ \cos x-\sin x=0\end{array}\right. \\ \iff \left[\begin{array}{l}x=k\pi \\ \sin x=\sin \left(\frac{\pi }{2}-x\right)\end{array}\right. \end{gathered}$$

$\iff \left[\begin{array}{l}x=k\pi \\ \left[\begin{array}{l}x=\frac{\pi }{2}-x+k2\pi \\ x=\pi -\left(\frac{\pi }{2}-x\right)+k2\pi \end{array}\right.\end{array}\right.$ (k ∈ ℤ)

$\iff \left[\begin{array}{l}x=k\pi \\ 2x=\frac{\pi }{2}+k2\pi \end{array}\right.\iff \left[\begin{array}{l}x=k\pi \\ x=\frac{\pi }{4}+k\pi \end{array}\right.$ (k ∈ ℤ).

Vậy phương trình đã cho có hai họ nghiệm là: $x=\frac{\pi }{4}+k\pi$  và x = kπ (k ∈ ℤ).

Câu 19: Cho hàm số y = x³ – 3mx² + 4m³ (m là tham số) có đồ thị C. Xác định m để C có các điểm cực đại và cực tiểu đối xứng với nhau qua đường thẳng y = x.

Lời giải:

Ta có: y’ = 3x² – 6mx = 0

$\iff \left[\begin{array}{l}x=0\\ x=2m\end{array}\right.$

Để hàm số có cực đại và cực tiểu thì m phải khác 0.

Giả sử hàm số có 2 cực trị là:

A(0; 4m³), B(2m; 0) $\Rightarrow \overrightarrow{AB}=\left(2m;-4m^3\right)$

Trung điểm của đoạn AB là: I(m; 2m³)

Điều kiện để AB đối xứng nhau qua đường thẳng y = x là AB vuông góc với đường thẳng y = x và I thuộc đường thẳng y = x

$$\begin{gathered} \Rightarrow \left\{\begin{array}{l}2m-4m^3=0\\ 2m^3=m\end{array}\right. \\ \Rightarrow \left[\begin{array}{l}m=0\\ m^2=\frac{1}{2}\end{array}\right. \\ \iff \left[\begin{array}{l}m=0\\ m=\frac{\pm \sqrt{2}}{2}\end{array}\right. \end{gathered}$$

Kết hợp với điều kiện, ta có: $m=\pm \frac{\sqrt{2}}{2}$ .

Vậy với $m=\pm \frac{\sqrt{2}}{2}$  thì thỏa mãn yêu cầu bài toán.

Câu 20: Cho hàm số y = f(x) = 3x⁴ – 4x² + 3. Trong các mệnh đề sau, mệnh đề đúng?

A. y = f(x) là hàm số chẵn;

B. y = f(x) là hàm số lẻ;

C. y = f(x) là hàm số không có tính chẵn lẻ;

D. y = f(x) là hàm số vừa chẵn vừa lẻ.

Lời giải:

Đáp án đúng là: A.

Tập xác định: D = ℝ.

Ta có: $\forall x\in D\Rightarrow -x\in D$

f(−x) = 3(−x)⁴ – 4(−x)² + 3 = 3x⁴ – 4x² + 3 = f(x), x ∈ D.

Do đó hàm số y = f(x) là hàm số chẵn.

Câu 21: Tìm x, biết: 8x³ – 12x² + 6x – 1 = 0.

Lời giải:

8x³ – 12x² + 6x – 1 = 0

$\iff$ (8x³ – 1) – (12x² – 6x) = 0

$\iff$ [(2x)³ – 1] – 6x(2x – 1) = 0

 $\iff$(2x – 1)(4x² + 2x + 1) – 6x(2x – 1) = 0

 $\iff$(2x – 1)(4x² + 2x + 1 – 6x) = 0

$\iff$ (2x – 1)(4x² – 4x + 1) = 0

$\iff$(2x – 1)(2x – 1)² = 0

$\iff$ 2x – 1 = 0

$\iff x=\frac{1}{2}$.

Vậy phương trình đã cho có nghiệm là: $x=\frac{1}{2}$ .

Câu 22: Cho a + b + c + d = 0. Với a, b, c, d > 0. Chứng minh rằng:

 a³ + b³ + c³ + d³ = 3(b + c)(ad – bc).

Lời giải:

Ta có: a + b + c + d = 0

a + d = −b – c

(a + d)³ = −(b + c)³

a³ + d³ + 3ad² + 3a²d = − b³ – c³ – 3b²c – 3bc²

a³ + b³ + c³ + d³ = −3ad(a + d) – 3bc(b + c)

 a³ + b³ + c³ + d³ =  3ad(b + c) – 3bc(b + c) (do – (a + d) = b + c)

 a³ + b³ + c³ + d³ = 3(b + c)(ad – bc) (đpcm).

Câu 23: Cho hình chữ nhật ABCD, M là điểm bất kì nằm trong hình chữ nhật. Chứng minh rằng: MA² + MC² = MB² + MD².

Lời giải:

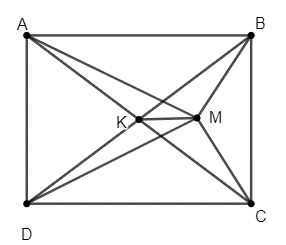
Gọi K là giao điểm của hai đường chéo AC và BD suy ra K là trung điểm của AC và BD.

Trong $\Delta MAC$  có:

$M{A}^2+M{C}^2=2M{K}^2+\frac{1}{2}A{C}^2$ (1) (công thức trung tuyến).

Trong $\Delta MBD$ : $M{B}^2+M{D}^2=2M{K}^2+\frac{1}{2}B{D}^2$  (2) (công thức trung tuyến)

Mặt khác AC = BD (3) (đường chéo hình chữ nhật)

Từ (1) và (2), (3) suy ra MA² + MC² = MB² + MD² (đpcm).

Câu 24: Cho tam giác ABC vuông tại A, đường cao AH, M là trung điểm của BC, có BH = 4 cm, CH = 9 cm. Tính diện tích tam giác AHM?

Lời giải:

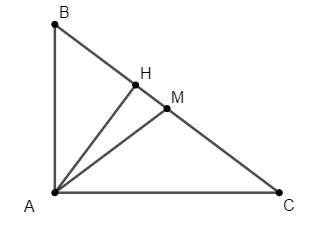
Vì ABC vuông tại A và AH là đường cao nên ta có:

AH² = BH.HC $\iff$ AH² = 4.9 = 36 $\iff$  AH = 6 (cm).

Vì AM là đường trung tuyến của ∆ABC nên ta có:

$$\begin{gathered} AM=\frac{1}{2}BC=\frac{1}{2}\left(4+9\right)=\frac{13}{2} \\ \Rightarrow HM=\sqrt{A{M}^2-A{H}^2}=\sqrt{{\left(\frac{13}{2}\right)}^2-6^2}=\frac{5}{2} \end{gathered}$$

$\Rightarrow S_{AHM}=\frac{1}{2}AH.HM=\frac{1}{2}\mathrm{.6.}\frac{5}{2}=\frac{15}{2}$ (cm²)

Câu 25: Giải phương trình: sin²x – 5sinx.cosx + 6cos²x − 1 = 0.

Lời giải:

sin²x – 5sinx.cosx + 6cos²x − 1 = 0

$\iff$sin²x – 5sinx.cosx + 6cos²x –  sin²x – cos²x = 0

$\iff$−5sinx.cosx + 5cos²x = 0

$\iff$5cosx(sinx – cosx) = 0

$\iff \left[\begin{array}{l}\cos x=0\\ \sin x=\cos x\end{array}\right.$

$\iff \left[\begin{array}{l}x=\frac{\pi }{2}+k\pi \\ x=\frac{\pi }{4}+k\pi \end{array}\right.$  (k ∈ ℤ)

Vậy phương trình đã cho có họ nghiệm là: $x=\frac{\pi }{4}+k\pi$; $x=\frac{\pi }{2}+k\pi$  (k ∈ ℤ).

Câu 26: Tìm x, biết: $\frac{5}{x-3}-\frac{4}{x+3}=\frac{20x^2-5}{x^2-9}$ .

Lời giải:

ĐKXĐ: x ≠ ± 3

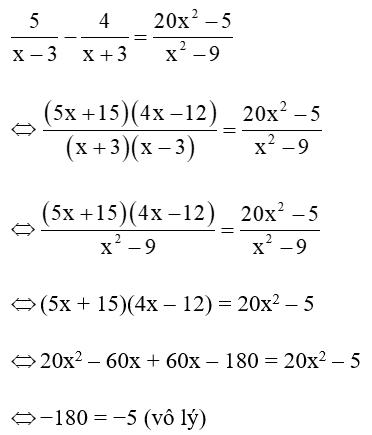
Vậy phương trình đã cho là một phương trình vô nghiệm.

Câu 27: Với x ≠ ± 3. Rút gọn biểu thức sau: $A=\frac{5}{x+3}+\frac{2}{x-3}-\frac{3x^2-2x-9}{x^2-9}$ .

Lời giải:

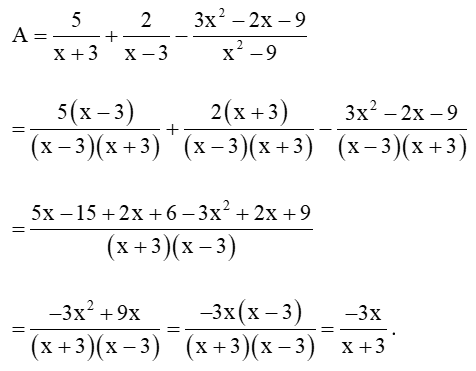
Câu 28: Tìm x, biết: x³ + 27 + (x + 3)(x – 9) = 0.

Lời giải:
x³ + 27 + (x + 3)(x – 9) = 0

$\iff$(x³ + 3³) + (x + 3)(x – 9) = 0

$\iff$(x + 3)(x² – 3x + 9) + (x + 3)(x – 9) = 0

$\iff$(x + 3)(x² – 3x + 9 + x – 9) = 0

$\iff$(x + 3)(x² – 2x) = 0

$\iff$(x + 3).x.(x – 2) = 0

$\iff \left[\begin{array}{l}x+3=0\\ x=0\\ x-2=0\end{array}\right.\iff \left[\begin{array}{l}x=-3\\ x=0\\ x=2\end{array}\right.$

Vậy phương trình đã cho có 3 nghiệm phân biệt là x = −3; x = 0; x = 2.

Câu 29: Với x ≠ −3, rút gọn phân thức $\frac{x^3-27}{9-6x+x^2}$  ta được:

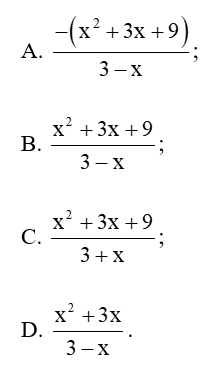
Lời giải:

Đáp án đúng là: A

Ta có

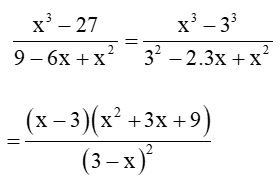
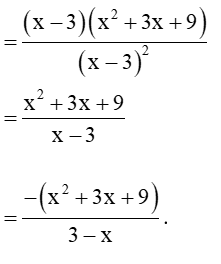
Câu 30: Xét tính chẵn lẻ của hàm số:

F(x) = sin²⁰⁰⁷x + cos nx, với n ∈ ℤ:

A. Hàm số chẵn;

B. Hàm số lẻ;

C. Không chẵn không lẻ;

D. Vừa chẵn vừa lẻ.

Lời giải:

Đáp án đúng là: C

Hàm số có tập xác định: D = ℝ.

Suy ra ta có: x ∈ D thì –x ∈ D.

Ta có: f(-x) = sin²⁰⁰⁷(-x) + cos(−nx) =  −sin²⁰⁰⁷x + cos nx $\ne \pm f\left(x\right)$

Vậy hàm số đã cho là hàm số không chẵn không lẻ.

Câu 31: Hình nào trong các hình sau không có trục đối xứng?

A. Hình tam giác đều;

B. Hình thoi;

C. Hình vuông;

D. Hình bình hành.

Lời giải:

Đáp án đúng là: D

Hình không có trục đối xứng là hình bình hành.

Câu 32: Tìm GTLN của A², biết: $A=\sqrt{x+4}+\sqrt{4-x}$ .

Lời giải:

ĐK: −4 ≤ x ≤ 4.

Ta có:

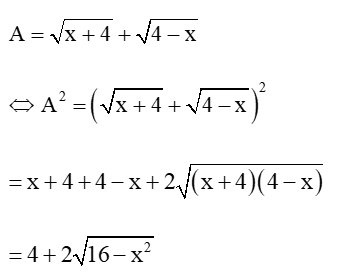
Với −4 ≤ x ≤ 4 $\Rightarrow \sqrt{16-x^2}\le \sqrt{16}=4$  nên suy ra:

A² ≤ 4 + 2.4 = 12

Khi đó: A²_max = 12

Dấu “=” xảy ra khi: x² = 0 $\iff$ x = 0 (TMĐK)

Vậy với x = 0 thì A²_max = 12.

Câu 33: Tìm x, biết: 3x(x – 1) + x – 1 = 0.

Lời giải:

Ta có: 3x(x – 1) + x – 1 = 0

$\iff$3x(x – 1) + (x – 1) = 0

$\iff$(x – 1)(3x + 1) = 0

$$\begin{gathered} \iff \left[\begin{array}{l}x-1=0\\ 3x+1=0\end{array}\right. \\ \iff \left[\begin{array}{l}x=1\\ x=\frac{-1}{3}\end{array}\right. \end{gathered}$$

Câu 34: Cho định lí "Cho số tự nhiên n, nếu n⁵ chia hết cho 5 thì n chia hết cho 5". Định lí này được viết dưới dạng P ⇒ Q.

Phát biểu định lí trên bằng các dùng thuật ngữ "điều kiện đủ".

Lời giải:

Phát biểu định lí trên bằng các dùng thuật ngữ "điều kiện đủ" như sau:

Với n là số tự nhiên, n⁵ chia hết cho 5 là điều kiện đủ để n chia hết cho 5.

Câu 35: Cho tam giác ABC vuông tại A có $\widehat{B}=60°$ .

a) Tính số đo góc C.

b) Trên BC lấy E sao cho BE = BA, tia phân giác của góc B cắt AC tại D. Chứng minh: DE = AD.

Lời giải:

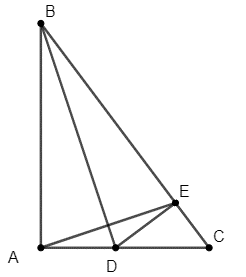
a) Xét ∆BAC có: $\widehat{A}=90°$

$$\begin{gathered} \Rightarrow \widehat{B}+\widehat{C}=90° \\ \iff 60°+\widehat{C}=90°\iff \widehat{C}=30° \end{gathered}$$

b) Xét ∆ABE có

BD là đường phân giác của ∆ABE.

Mặt khác ∆ABE cân tại B nên suy ra BD cũng là đường trung trực của ∆ABE.

Theo tính chất của đường trung trực ta có: DA = DE.

Câu 36: Giá trị nghiệm nguyên của phương trình:

12x² + 6xy + 3y² = 28(x + y).

Lời giải:

12x² + 6xy + 3y² = 28(x + y)

3y² + 2(3x – 14)y + 12x² – 28x = 0 (1)

Xem (1) là phương trình bậc hai ẩn y, ta có:

$\Delta \text{'}$ = (3x – 14)² – 36x² + 84x = k² ≥ 0

= −27x² + 196 = k² ≥ 0

$\Rightarrow$ 27x² ≤ 196 $\Rightarrow$  x² ≤ 7.

$\Rightarrow$ x ∈ {0; ± 1; ± 2}.

• Với x = 0 thì y = 0;

• Với x = 1 thì y = 8;

• Với x = −1 thì y = 10;

• Với x = ± 2 thì y ∉ ℤ.

Vậy các cặp số nguyên cần tìm là (0; 0); (1; 8); (−1; 10).

Câu 37: Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ.

(M ∈ OP), IN // OP (N ∈ OQ). Chứng minh rằng:

1) Tam giác IMN cân tại I.

2) OI là đường trung trực của MN.

Lời giải:

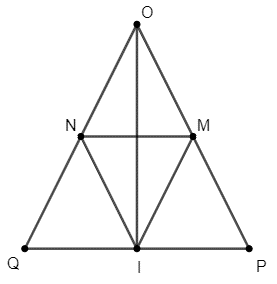
1) Xét ∆OPQ có I là trung điểm của PQ và IN // OP.

Do đó N là trung điểm của OQ (*).

Xét ∆OPQ có I là trung điểm của PQ, IM // OQ.

Do đó M là trung điểm của OP (**).

Từ (*) và (**) suy ra MN là đường trung bình của OPQ suy ra MP = NQ.

Xét ∆MPI và ∆NQI có 

MP = NQ (cmt)

$\widehat{P}=\widehat{Q}$ (gt)

PI = QI (gt)

Do đó ∆MPI = ∆NQI

Suy ra: IM = IN hay ∆IMN cân tại I.

2) Ta có: OM = ON nên O nằm trên đường trung trực của MN (1)

Ta có: IM = IN nên suy I nằm trên đường trung trực của MN (2)

Từ (1) và (2) suy ra OI là đường trung trực của MN.

Câu 38: Giải Phương trình: sin5x + 2cos²x = 1.

Lời giải:
sin5x + 2cos²x = 1

$\iff$ sin5x = 1 – 2cos²x

$\iff$ sin5x = −cos2x = cos(−2x) = $\sin \left(\frac{\pi }{2}-\left(-2x\right)\right)$

$\iff$ sin5x = cos(−2x) = $\sin \left(\frac{\pi }{2}-\left(-2x\right)\right)$

$\iff$ sin5x = $\sin \left(\frac{\pi }{2}-\left(-2x\right)\right)$

$\iff$ sin5x $=\sin \left(2x+\frac{\pi }{2}\right)$

$\iff \left[\begin{array}{l}5x=2x+\frac{\pi }{2}+k2\pi \\ 5x=-2x-\frac{\pi }{2}+k2\pi \end{array}\right.$

$\iff \left[\begin{array}{l}x=\frac{\pi }{6}+2k\frac{\pi }{3}\\ x=-\frac{\pi }{14}+k\frac{2\pi }{7}\end{array}\right.$ (k ∈ ℤ).

Câu 39: Tìm x, biết: 4x² – 25 – (2x – 5)(2x + 7) = 0.

Lời giải:

4x² – 25 – (2x – 5)(2x + 7) = 0

$\iff$[(2x)² – 5²] – (2x – 5)(2x + 7) = 0

$\iff$(2x – 5)(2x + 5) – (2x – 5)(2x + 7) = 0

$\iff$(2x – 5)(2x + 5 – 2x – 7) = 0

$\iff$(2x – 5)(−2) = 0

$\iff$2x – 5 = 0

$\iff x=\frac{5}{2}$.

Vậy $x=\frac{5}{2}$ .

Câu 40: Tìm m để y = x³ – 3x² + m² – m + 1 có 2 điểm cực trị A, B và S_ABC = 7, với C(−2; 4).

Lời giải:

y = x³ – 3x² + m² – m + 1

$\Rightarrow$ y’ = 3x² – 6x = 0

$\iff \left[\begin{array}{l}x=0\\ x=2\end{array}\right.$

Suy ra 2 điểm cực trị là A(0; m² – m + 1) và B(2; m² – m – 3).

Khi đó ta có phương trình đường thẳng AB:

$\frac{x-0}{2-0}=\frac{y-m^2+m-1}{m^2-m-3-m^2+m-1}$

$\iff \frac{x}{2}=\frac{y-m^2+m-1}{-4}$

$\iff$−2x = y – m² + m – 1

$\iff$2x + y – m² + m – 1 = 0

$AB=\sqrt{{\left(0-2\right)}^2+{\left(m^2-m+1-m^2+m+3\right)}^2}=\sqrt{4+16}=2\sqrt{5}$

$d(C;AB)=\frac{\left|-4+4-m^2+m-1\right|}{2\sqrt{5}}$

$\Rightarrow$|−m² + m – 1| = 7

$\iff \left[\begin{array}{l}m=3\\ m=-2\end{array}\right.$

Vậy có hai giá trị của m thỏa mãn yêu cầu bài toán: m = −2; m = 3.

Câu 41: Cho hình chop đều SABC có cạnh bên bằng a hợp với đáy ABC một góc 60°. Tính thể tích hình chop SABC theo a.

Lời giải:

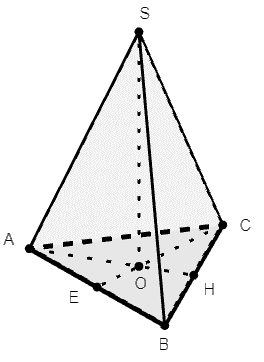
Gọi O là tâm của tam giác ABC

Suy ra $SO\perp SABC$  (do SABC đều)

Khi đó góc hợp giữa SC và (ABC) là góc: $\widehat{SCO}=60°$

Xét ∆SOC vuông tại A.

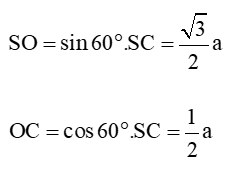
$\Rightarrow CE=\frac{3}{2}OC=\frac{3}{4}a$ (tính chất của đường trung tuyến tam giác đều)

Câu 42: Cho tam giác ABC (AB > AC) có đường cao AH . Gọi M , N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh: NP là đường trung trực của AH.

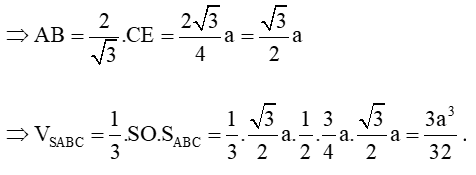
Lời giải:

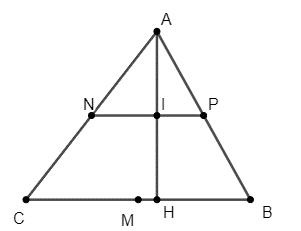
Gọi I là giao điểm của AH và PN.
Xét ∆ABC có: AP = BP và AN = NC.

Do đó PN là đường trung bình của ABC

Suy ra PN // BC mà AH $\perp$BC

Do đó PN $\perp$AH  (1)
Ta có: PN // BC mà PI ∈ PN

Suy ra PI // BC
Xét ∆AHB có: PI // BC và AP = BP

Suy ra AI = IH (2)
Từ (1) và (2) suy ra PN là đường trung trực của AH.

Câu 43: Chứng minh rằng: (2²⁰²² + 2²⁰²⁴) $⋮$  5120.

Lời giải:

Ta có: 2²⁰²² + 2²⁰²⁴

= 2²⁰²²(2² + 1) = 2²⁰²².5

= 2²⁰¹² . 2¹⁰ . 5 = 2²⁰¹² . 1024 . 5

= 2²⁰¹² . 5120.

Suy ra: 2²⁰¹² . 5120 $⋮$  5120

Hay (2²⁰²² + 2²⁰²⁴) $⋮$  5120.