Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 40)

Câu 1: Dũng và Hùng sưu tầm được tất cả 180 con tem. Số tem Dũng sưu tầm được bằng $\frac{5}{7}$  số tem của Hùng. Hỏi Dũng sưu tầm được bao nhiêu con tem?

Lời giải:

Tổng số phần bằng nhau là

5 + 7=12 (phần)

Dũng sưu tầm được số con tem là:

180 : 12 . 7 = 105 (con tem)

Đáp số: 105 con tem.

Câu 2: Giả sử ta có 1 khúc vải, cắt nó ra làm 100 khúc, thời gian để cắt 1 khúc vải là 5 giây. Hỏi nếu cắt liên tục không ngừng nghỉ thì trong bao lâu sẽ cắt xong?

Lời giải:

Cắt được 100 khúc thì sẽ cần cắt 99 lần cắt

Nếu liên tục cắt không ngừng nghỉ thì sau số thời gian sẽ xong là:

5 . 99 = 495 (giây)

Đáp số: 495 giây.

Câu 3: Hiện nay tuổi mẹ gấp 3 lần tuổi Lan. Sau 15 năm nữa tuổi mẹ gấp đôi tuổi Lan. Tính tuổi mẹ hiện nay.

Lời giải:

Gọi tuổi con là x. Tuổi mẹ hiện nay là 3x (x khác 0).

Tuổi con sau 15 năm nữa là x + 15

Tuổi mẹ sau 15 năm là 3x + 15

Ta có:

3x + 15 = 2(x + 15)

3x + 15 = 2x + 30

x = 15

Vậy tuổi con là 15, tuổi mẹ là 45.

Câu 4: Để hút hết nước ở một cái hồ lớn phải dùng 5 máy bơm làm liên tục trong 18 giờ. Hỏi muốn hút hết nước ở hồ đó trong 10 giờ thì phải bổ sung thêm mấy máy bơm như thế?

Lời giải:

Cần số máy bơm là:

(5 . 18) : 10 = 9 (cái)

Phải bổ sung thêm số máy bơm như thế là:

9 – 5 = 4 (máy bơm)

Đáp số : 4 máy bơm.

Câu 5: 1 cửa hàng trong 3 ngày bán được có 2 tấn đường. Ngày đầu bán được 800 kg. Ngày thứ hai bán được bằng $\frac{4}{5}$  số đường bán được ngày ban đầu . Hỏi ngày thứ ba bán được bao nhiêu kg đường?

Lời giải:

Đổi 2 tấn = 2000kg

Ngày thứ hai bán được là:

800 . 4 : 5 = 640 (kg)

Ngày thứ ba bán được là:

2000 – 800 – 640 = 560 (kg)

Đáp số: 560 kg đường.

Câu 6: Cho một miếng đất hình vuông, biết sau khi mở rộng về một phía thêm 8m thì được một hình chữ nhật có chu vi 216m. Hỏi trước khi mở rộng, miếng đất có diện tích là bao nhiêu?

Lời giải:

Chu vi hình vuông ban đầu là: 

216 – 8 . 2 = 200 (m)

Cạnh hình vuông ban đầu là: 

200 : 4 = 50(m)

Diện tích mảnh đất ban đầu là: 

50 . 50 = 2500 (m²).

Đáp số 2 500 m².

Câu 7: Một mảnh đất có kích thước như hình vẽ bên. Diện tích mảnh đất đó là?

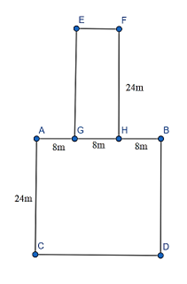
Lời giải:

Diện tích hình EFHG là:

24 . 8 = 192 (m²).

Diện tích hình ABCD là:

24 . (8 + 8 + 8) = 576 (m²).

Diện tích mảnh đất là:

192 + 576 = 768 (m²).

Đáp số: 768 m².

Câu 8: Người ta pha sơn đỏ với sơn trắng theo tỉ lệ 3 : 1. Hỏi đã dùng bao nhiêu lít sơn đỏ để pha, biết rằng sau khi pha, được tất cả 28 lít sơn.

Lời giải:

Số lít sơn đỏ dùng để pha là:

28 : (3 + 1) . 3 = 21 (lít).

Đáp số: 21 lít.

Câu 9: Chứng minh rằng trong 4 số tự nhiên liên tiếp luôn có 2 số chẵn nên tích của nó chia hết cho 4.

Lời giải:

Gọi 4 số tự nhiên liên tiếp là n; n + 1; n + 2; n + 3

+ Nếu n chẵn thì n + 2 chẵn; n + 1 và n + 3 là số lẻ

Suy ra: có 2 số n và n + 2 chẵn hay n ⋮ 2 và  n + 2 ⋮ 2

⇒ n(n + 1)(n + 2)(n + 3) chia hết cho 4

+ Nếu n lẻ thì n + 1 và n + 3 chẵn

Suy ra: có 2 số n + 1 và n + 3 chẵn hay n + 1 ⋮ 2 và  n + 3 ⋮ 2

⇒ n(n + 1)(n + 2)(n + 3) chia hết cho 4.

Câu 10: Tìm giá trị nguyên của x để A = $\frac{1}{7-x}$ có giá trị nguyên lớn nhất.

Lời giải:

ĐKXĐ: x ≠ 7

Để x là số nguyên thì 1 chia hết cho (7 – x)

Hay 7 – x ∈ Ư(1)

Suy ra: 7 – x = 1 hoặc 7 – x = – 1

⇒ x = 6 hoặc x = 8

Với x = 6 thì A = 1

Với x = 8 thì A = –1.

Vậy với x = 6 thì A có giá trị nguyên lớn nhất.

Câu 11: Tăng mỗi cạnh của hình chữ nhật thêm 20% số đo của nó thì diện tích hình chữ nhật tăng thêm bao nhiêu phần trăm?

Lời giải:

Gọi chiều dài là a, chiều rộng là b

Chiều dài lúc sau là:

(100% + 20%) . a = 120% . a =1,2 . a

Chiều rộng lúc sau là:

(100%+20%) . b = 120% . b = 1,2 . b

Diện tích ban đầu của hình chữ nhật là 100% . a . b

Diện tích lúc sau của hình chữ nhật là :

(1,2 . a) . (1,2 . b) =1,44 . a . b =144% . a . b

Diện tích lúc sau tăng số phần trăm là:

144% –100% = 44%.

Câu 12: Tính: 1 + 2 + 3 + … + 99.

Lời giải:

Số các số hạng của dãy là:

99 – 1 + 1 = 99 (số)

Tổng dãy số này là:

(99 + 1) . 99 : 2 = 4950.

Câu 13: Để lát nền một căn phòng, người ta dùng hết 600 viên gạch hình vuông có cạnh là 20 cm.Tính diện tích căn phòng.

Lời giải:

Diện tích mỗi viên gạch là:

20 . 20 = 400 (cm²)

Diện tích căn phòng là:

600 . 400 = 240000 (cm²).

Đáp số: 240 000 cm².

Câu 14: Khai triển đa thức sau: (x – y)⁴ – (a – b⁴).

Lời giải:

(x–y)⁴ – (a – b⁴)

= (x² – 2xy + y²)² – a + b⁴

= x⁴ – 4x³y + 6x²y² – 4xy³ + y⁴ – a + b⁴.

Câu 15: Tìm n biết 3ⁿ + 3ⁿ . 3³ = 252.           

Lời giải:

3ⁿ + 3ⁿ . 3³ = 252

3ⁿ (1 + 3³) = 252

3ⁿ = 9 = 3²

Vậy n = 2.

Câu 16: Chứng minh rằng B = 5⁰ + 5¹ + … + 5²⁰¹¹ chia hết cho 2.

Lời giải:

B = 5⁰ + 5¹ + … + 5²⁰¹¹

B = 1 + 5 + 5² + 5³ + … + 5²⁰¹¹

B = (1 + 5) + (5² + 5³) + … + (5²⁰¹⁰ + 5²⁰¹¹)

B = 6 + 5² (1 + 5) + … + 5²⁰¹⁰ (1 + 5)

B = 6 (1 + 5² + … + 5²⁰¹⁰)

B = 2 . 3 . (1 + 5² + … + 5²⁰¹⁰)

Vì 2 chia hết cho 2 nên 2 . 3 . (1 + 5² + … + 5²⁰¹⁰) chia hết cho 2 hay B chia hết cho 2.

Câu 17: Chứng minh C = 6¹ + 6³ + 6⁵ + … + 6¹⁹ chia hết cho 2 và 3.

Lời giải:

C = 6¹ + 6³ + 6⁵ + … + 6¹⁹

C = 6 (1+ 6² + 6⁴ + … + 6¹⁸)

C = 2 . 3 . (1+ 6² + 6⁴ + … + 6¹⁸)

Từ đây ta thấy C chia hết cho 2 và 3.

Câu 18: Một mảnh đất có kích thước như hình vẽ bên. Diện tích mảnh đất đó là?

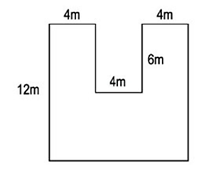
Lời giải:

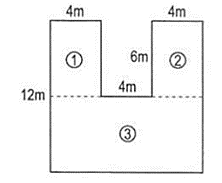
Diện tích hình 1 là:

4 . 6 = 24 (m²)

Diện tích hình 2 là:

4 . 6 = 24 (m²)

Diện tích hình 3 là:

12 . 6 = 72 (m²)

Vậy diện tích mảnh đất là:

24 + 24 + 72 = 120 (m²).

Câu 19: Một mảnh đất có kích thước như hình vẽ bên. Diện tích mảnh đất đó là?

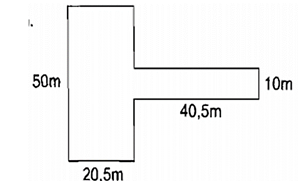
Lời giải:

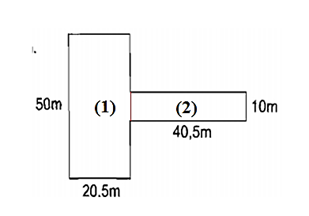
Ta chia mảnh đất thành hai hình hình (1) và hình (2)

Diện tích hình (1) là:

50 . 20,5 = 1025 (m²)

Diện tích hình (2) là:

40,5 . 10 = 405 (m²)

Diện tích mảnh đất là:

1025 + 405 = 1430(m²).

Câu 20: Một đội công nhân có 63 người nhận sửa xong một quãng đường trong 11 ngày. Hỏi muốn làm xong quãng đường đó trong 7 ngày thì cần thêm bao nhiêu người nữa ? (Mức làm của mỗi người như nhau).

Lời giải:

Muốn sửa xong quãng đường trong 1 ngày cần số người là:

63 . 11 = 693 (người)

Muốn sửa xong quãng đưòng trong 7 ngày cần số người là:

693 : 7 = 99 (người)

Số người cần thêm là:

99 – 63 = 36 (người)

Đáp số: 36 người.

Câu 21: Tìm x, y > 0 thỏa mãn x³ + y³ = 3xy – 1.

Lời giải:

x³ + y³ = 3xy – 1

⇔ x³ + y³ – 3xy + 1 = 0

⇔ (x+y)³ – 3xy(x+y) – 3xy + 1 = 0

⇔ (x+y+1)(x² + 2xy + y² – x – y + 1 – 3xy) = 0

Suy ra:

$\left[\begin{array}{l}x+y+1=0\\ x^2+2xy+y^2–x–y+1-3xy=0\end{array}\right.$

Vì x, y > 0 nên x + y + 1 > 0

Xét x² + 2xy + y² – x – y + 1 – 3xy = 0

⇔ 2 (x² + 2xy + y² – x – y + 1 – 3xy) = 0

⇔ (x – y)² + (x² – 2x + 1) + (y² – 2y + 1) = 0

⇔ (x – y)² + (x – 1)² + (y – 1)² = 0

Suy ra:

$\left\{\begin{array}{l}x-y=0\\ x-1=0\\ y-1=0\end{array}\right.$ hay x = y = 1.

Vậy x = y = 1.

Câu 22: Tính giá trị biểu thức B = x¹⁵ – 8x¹⁴ + 8x¹³ – 8x¹² + … – 8x² + 8x – 5 với x = 7.

Lời giải:

Ta có: x = 7 nên x + 1 = 8

B = x¹⁵ – 8x¹⁴ + 8x¹³ – 8x¹² + … – 8x² + 8x – 5

B = x¹⁵ – (x+1)x¹⁴ + (x+1)¹³ – (x+1)x¹² + …. – (x+1)x² + (x+1)x – 5

B = x¹⁵ – x¹⁵ – x¹⁴ + x¹⁴ – x¹³ – …. – x³ – x² + x² + x – 5

B = x – 5

B = 7 – 5

B = 2.

Câu 23: Xã A có 3 cánh đồng cánh đồng thứ nhất có diện tích 28000 mét vuông hơn cánh đồng thứ hai 9750 mét vuông và kém cánh đồng thứ ba 15750 mét vuông. Hỏi cả ba cánh đồng của xã A rộng bao nhiêu hecta?

Lời giải:

Diện tích cánh đồng thứ 2 là:

28000 – 9750 = 18250 (m²)

Diện tích cánh đồng thứ 3 là:

28000 + 15750 = 43750 (m²)

Cả 3 cánh đồng của xã A rộng là:

28000 + 18250 + 43750 = 90000 (m²) = 9(hecta)

Đáp số: 9 ha.

Câu 24: Để lát nền một căn phòng, người ta dùng hết 600 viên gạch hình vuông có cạnh là 30cm. Tính diện tích căn phòng theo m²?

Lời giải:

Đổi 30 cm = 0,3 m 

Diện tích viên gạch hình vuông đó là :

0,3 . 0,3 =  0,09 (m² )

Diện tích căn phòng là :

0,09 . 600 = 54 (m²)

Đáp số: 54m².

Câu 25: Một quyển sách dày 220 trang. Hỏi người ta đã dùng bao nhiêu lượt chữ số để đánh thứ tự các trang của quyển sách đó?

Lời giải:

Để đánh số từ trang 1 đến trang 9 cần số chữ số là:

[(9 – 1) : 1 + 1] . 1 = 9 (chữ số)

Để đánh số từ trang 10 đến trang 99 cần số chữ số là:

[(99 – 10) : 1 + 1] . 2 = 180 (chữ số)

Để đánh số từ trang 100 đến trang 220 cần số chữ số là:

[(220 – 100) : 1 + 1] . 3 = 363 (chữ số)

Để đánh số trang cuốn sách thì cần số chữ số là:

9 + 180 + 363 = 552 (chữ số)

Đáp số: 552 chữ số.

Câu 26: Giải phương trình: (x + 2)(x² – 2x + 4) + x(x – 2)² = 32.

Lời giải:

(x + 2)(x² – 2x + 4) + x(x – 2)² = 32

⇔ x³ + 8 – x(x² – 4x + 4) – 32 = 0

⇔ x³ + 8 – x³ – 4x² + 4x – 32 = 0

⇔ 4x² – 4x – 24 = 0

⇔ x² – x – 6 = 0

⇔ (x + 2)(x – 3)= 0

⇔ $\left[\begin{array}{l}x=-2\\ x=3\end{array}\right.$

Vậy x = –2 hoặc x = 3.

Câu 27: Hiện nay anh hơn em 5 tuổi. Sau 5 năm nữa, tuổi anh và tuổi em cộng lại được 25 tuổi. Tính tuổi của mỗi người hiện nay.

Lời giải:

Anh hơn em 5 tuổi, vậy sau 5 năm nữa anh vẫn hơn em 5 tuổi.

Vậy tuổi anh 5 năm sau là:

(25 + 5) : 2 = 15 (tuổi)

Tuổi anh hiện nay là:

15 – 5 = 10 (tuổi)

Tuổi em hiện nay là:

10 – 5 = 5 (tuổi)

Đáp số: Anh 10 tuổi, Em 5 tuổi.

Câu 28: Tìm hiệu của hai số, biết rằng nếu số bị trừ bớt đi 735 đơn vị và thêm vào số trừ 265 đơn vị được hiệu mới bằng 12000.

Lời giải:

Nếu số bị trừ bớt đi 735 đơn vị và thêm vào số trừ 265 đơn vị thì hiệu sẽ giảm:

735 + 265 = 1000 (đơn vị)

Hiệu hai số ban đầu là:

12000 + 1000 = 13000.

Đáp số: 13 000.

Câu 29: Tìm giá trị nhỏ nhất của A = a² – 4ab + 5b² + 10a – 22b + 28.

Lời giải:

Ta có:

A = a² – 4ab + 5b² + 10a – 22b + 28

A = (a² – 4ab + 4b²) + b² – 2b + 1 + 10a – 22b + 27

A = (a – 2b)² + (b – 1)² + 10(a – 2b) + 27

A = (a – 2b + 5)² + (b – 1)² + 2

Vì (a – 2b + 5)² + (b – 1)² ≥ 0 nên A ≥ 2

Vậy giá trị nhỏ nhất của A là 2 khi:

$\left\{\begin{array}{l}a-2b+5=0\\ b-1=0\end{array}\right.hay\left\{\begin{array}{l}a=-3\\ b=1\end{array}\right.$.

Câu 30: Chứng minh rằng: Với bất kỳ bộ 3 số tự nhiên liên tiếp nào thì tích của số thứ nhất và số thứ 3 cùng bé hơn bình phương của số thứ hai 1 đơn vị.

Lời giải:

Giả sử 3 số tự nhiên liên tiếp là: n – 2; n – 1; n.

Ta có:

n(n – 2) = n² – 2n

(n – 1)² = n² – 2n + 1

Xét: n(n – 2) – (n – 1)²  = n² – 2n – (n² – 2n + 1) = – 1.

Vậy thì tích của số thứ nhất và số thứ 3 cùng bé hơn bình phương của số thứ hai 1 đơn vị.

Câu 31: Một người đi xe máy từ tỉnh A và một người đi xe đạp từ tỉnh B. Hai tỉnh cách nhau 80km. Nếu họ đi gặp nhau thì mất 2 giờ. Nếu họ đi cùng chiều thì xe máy đuổi kịp người đi xe đạp sau 4 giờ. Tính vận tốc của mỗi người. Biết rằng họ cùng khởi hành một lúc.

Lời giải:

Tổng vận tốc của hai xe là:

80 : 2 = 40 (km/giờ)

Hiệu vận tốc của hai xe:

80 : 4 = 20 (km/giờ)

Vận tốc của xe đạp là:

(40 – 20) : 2 = 10 (km/giờ)

Vận tốc của xe máy là:

40 – 10 = 30 (km/giờ)

Đáp số: xe đạp 10 km/giờ, xe máy 30 km/giờ.

Câu 32: Trong đợt phát động ủng hộ sách, vở cho học sinh vùng lũ lụt, lớp 10a thống kê trong lớp có 25 học sinh ủng hộ vở, 27 học sinh ủng hộ sách. Hỏi cả lớp 10a có bao nhiêu học sinh tham gia ủng hộ?

Lời giải:

Số học sinh tham gia ủng hộ là:

25 + 27 = 52 (học sinh)

Đáp số: 52 học sinh.

Câu 33: Tìm số tự nhiên x biết x chia hết cho 5,6,9 và x nằm trong khoảng 300 đến 400.

Lời giải:

Vì x chia hết cho 5, 6, 9 nên x ∈ BCNN (5; 6; 9)

5 = 5¹

6 = 2 . 3

9 = 3²

BCNN (5; 6; 9) = 2 . 3² . 5 = 90

Mà 300 < x < 400 nên x = 360

Vậy x = 360.

Câu 34: Tỷ lệ phế phẩm của một máy là 3%. Tìm xác suất để trong 10 sản phẩm do máy đó sản xuất ra có:

a) 2 phế phẩm.

b) Không quá 1 phế phẩm.

Lời giải:

a) Xác suất để trong 10 sản phẩm có 2 phế phẩm là:

$C_{10}^2.{\left(3\%\right)}^2.{\left(1-3\%\right)}^{10-2}$= 0,032

b) Xác suất để trong 10 sản phẩm có không quá 1 phế phẩm là:

$C_{10}^0.{\left(3\%\right)}^0.{\left(1-3\%\right)}^{10-0}+C_{10}^1.{\left(3\%\right)}^1.{\left(1-3\%\right)}^{10-1}$= 0,965.

Câu 35: Để lát nền một phòng họp nguời ta phải dùng hết 500 viên gạch lát nền hình vuông có cạnh 4 dm. Hỏi diện tích phòng họp đó là bao nhiêu mét vuông? (Biết diện tích phần mạch vữa không đáng kể)

Lời giải:

Diện tích mỗi viên gạch là:

4 . 4 = 16 (dm²).

Diện tích phòng họp đó là:

16 . 500 = 8000 (dm²) = 80 m².

Đáp số: 80 m².

Câu 36: Tìm x biết: (3x + 4)² = 3² + 2³ + 83.

Lời giải:

(3x + 4)² = 3² + 2³ + 83

(3x + 4)² = 100 = 10²

3x + 4 = 10

x = 2

Vậy x = 2.

Câu 37: Tìm giá trị nhỏ nhất của E = (x – 1)(x – 3)(x + 5)(x + 7).

Lời giải:

E = (x – 1)(x – 3)(x + 5)(x + 7)

E = [(x – 1)(x + 5)][(x – 3)(x + 7)]

E = (x² + 4x – 5)(x² + 4x – 21)

Đặt x² + 4x – 5 = t

E = t (t – 16) = t² – 16t = (t–8)² – 64 ≥ –64

Vậy giá trị nhỏ nhất của E là –64 khi: t = 8

Hay x² + 4x – 5 = 8

⇔ x² + 4x – 13 = 0

⇔ (x + 2)² – 17 = 0

⇔(x + 2)² = 17

⇔ $\left[\begin{array}{l}x+2=\sqrt{17}\\ x+2=-\sqrt{17}\end{array}\right.hay\left[\begin{array}{l}x=\sqrt{17}-2\\ x=-\sqrt{17}-2\end{array}\right.$ .

Câu 38: Cho tam giác ABC thỏa mãn a⁴ = b⁴ + c⁴. Chứng minh rằng:

2sin²A = tan B.tan C.

Lời giải:

2 sin²A = tan B. tan C

⇔ 2 sin²A . cos B. cos C = sin B. sin C

⇔  $2{\left(\frac{a}{2R}\right)}^2.\frac{b^2+c^2-a^2}{2bc}.\frac{a^2+b^2-c^2}{2ab}$  = $\frac{b}{2R}.\frac{c}{2R}$

⇔ a⁴ = b⁴ + c⁴ (đúng với giả thiết).

Câu 39: Hiệu hai số bằng 4 lần số bé. Tìm hai số đó biết tổng của chúng bằng 360.

Lời giải:

Gọi số bé là a

Thì hiệu hai số là 4a

Suy ra: số lớn là 5a

Ta có:

5a + a = 360

6a = 360

a = 360 : 6

a = 60

Số lớn là: 5a = 60 . 5 = 300.

Vậy số bé là 60, số lớn là 300.

Câu 40: Tìm x biết: 2x – 18³ = 0.

Lời giải:

2x – 18³ = 0

2x = 5832

x = 2916

Vậy x = 2916.