Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 2)
Bài 1: Cho điểm M có hoành độ là -2 và điểm M thuộc đồ thị hàm số y = −2x2 . Xác định tọa độ điểm M
Lời giải:
Vì M ∈ y = −2x2 và có hành độ là −2
Thay x = −2 vào hàm số y = −2x2 ta có:
y = −2.(−2)2
⇔ y = −8
Vậy tọa độ điểm M là: M (−2; −8)
Bài 2: Cho hàm số y = x - 2 có đồ thị là d.Tìm điểm trên d có hoành độ và tung độ đối nhau
Lời giải:
Vì các điểm trên (d) có hoành độ và tung độ đối nhau nên
y = −x
Thay vào (d) ta được
− x = x – 2
⇔ x = 1
⇒ y = −1
Vậy điểm đó là (1; -1)
Lời giải:
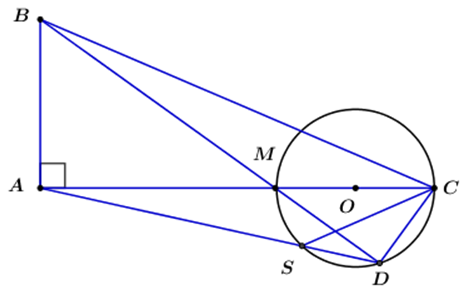
a) Tứ giác ABCD nội tiếp.
Do MC là đường kính của đường tròn (O), D thuộc (O) nên: ∠MDC = 900 = ∠BAC
Suy ra D và A cùng nhìn BC dưới một góc vuông
⇒ Tứ giác ABCD nội tiếp đường tròn đường kính BC.
b) CA là phân giác góc SCB.
Do ABCD là tứ giác nội tiếp nên: (cùng chắn cung AB).
Xét (O) ta có: (hai góc nội tiếp cùng chắn cung MS)
⇒ ∠ACB = ∠ ACS ( = ∠BDA).
Vậy CA là phân giác của ∠SCB (đpcm).
Lời giải:
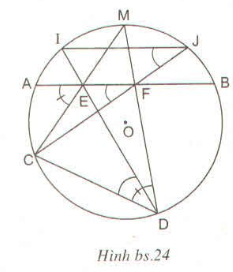
Xem hình vẽ (h.bs.24)
Ta có cung AM và MB bằng nhau nên (cùng bằng nửa số đo của cung nhỏ CM)
Suy ra CDFE là tứ giác nội tiếp.
Từ đó (cùng chắn cung CE)
Lại có (cùng chắn cung CI)
Vậy , suy ra JI song song với AB
Bài 5: Tìm chữ số tận cùng của các số:
a) 799
Lời giải:
Trước hết, ta tìm số dư của phép chia 99 cho 4 :
99 - 1 = (9 - 1)(98 + 97 + … + 9 + 1) chia hết cho 4
99 = 4k + 1 (k thuộc N)
⇒ 799 = 74k + 1 = 74k.7
Do 74k có chữ số tận cùng là 1 (theo tính chất 1c)
⇒ 799 có chữ số tận cùng là 7.
b) Dễ thấy 1414 = 4k (k thuộc N)
⇒ theo tính chất 1d thì 141414 = 144k có chữ số tận cùng là 6.
c) Ta có 567 - 1 chia hết cho 4
⇒ 567 = 4k + 1 (k thuộc N)
⇒ 4567 = 44k + 1 = 44k.4, theo tính chất 1d, 44k có chữ số tận cùng là 6 nên 4567 có chữ số tận cùng là 4.
Lời giải:
Ta có
y′ = 12x3 + 4(m − 2018)x;
Để hàm số có ba điểm cực trị ⇔ 2018 – m > 0 ⇔ m < 2018
Khi đó, tọa độ các điểm cực trị của đồ thị hàm số là:
A (0; 2017)
Do tam giác ABC cân tại A nên ycbt ⇔ 3AB2 = BC2
⇔ (m − 2018)3 = −1 ⇔ m = 2017 (thỏa mãn)
Lời giải:
Ta có:
y′ = 4x3 + 4mx = 4x(x2 + m)
Hàm số (1) có 3 cực trị khi và chỉ khi phương trình y′ = 0 có đúng 3 nghiệm phân biệt. Điều này tương đương với:
m < 0, (2)
Với điều kiện (2), đồ thị hàm số có 3 điểm cực trị là :
Dễ thấy tam giác ABC là tam giác cân tại A. Do đó . Từ đó suy ra . Yêu cầu của bài toán tương đương với:
thỏa mãn (2) nên đó là đáp án của bài toán
Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a) Tính độ dài các đoạn thẳng AB, AC, AH.
Lời giải:
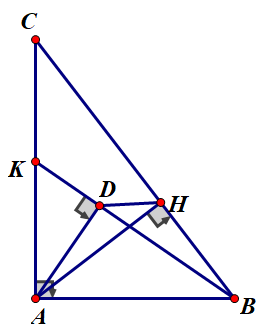
a) Áp dụng HTL tam giác:
b) ADHB nội tiếp
(cùng chắn AD) (1)
c) Áp dụng công thức tính diện tích hình tam giác bằng nửa tích hai cạnh nhân sin góc xen giữa
Mà
(hệ thức lượng)
.
Lời giải:
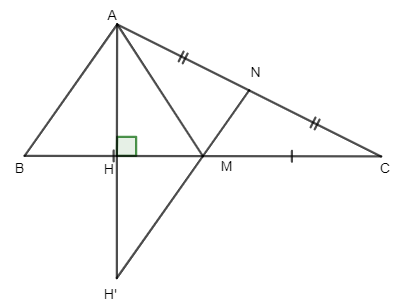
Vẽ cắt MN tại H'
Ta có : (vì MN là trung điểm )
Lại có:
và . Mà
Vậy .
Lời giải:
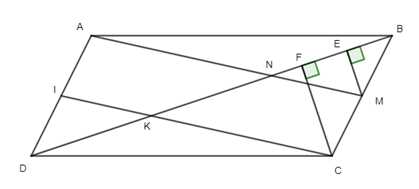
Gọi I là trung điểm của AD, K là giao điểm của CI và BD. Kẻ tại E, tại F.
Ta có
Bài 11: Có bao nhiêu số nguyên âm m để hàm số đồng biến trên khoảng
Lời giải:
Ta có:
- Hàm số đồng biến trến khi và chỉ khi
- Xét hàm số: trên
Có
Bảng biến thiên
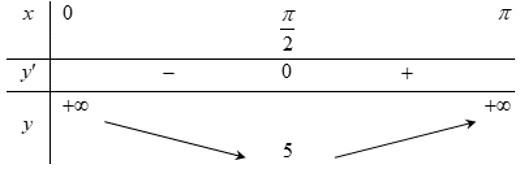
- Do đó :
- Lại do m nguyên âm nên
Vậy có 5 số nguyên âm.
Bài 12: Tìm x ∈ BC(16; 21; 25) và x ≤ 400
Lời giải:
Ta có: 16 = 24; 21 = 3.7; 25 = 52
Suy ra BCNN(16; 21; 25) = 24.3.52.7 = 8 400.
Do đó BC(16; 21; 25) = B(8 400) = {0; 8400; ...}.
Mà x ≤ 400 nên x = 0.
Vậy x = 0.
c, Một đường thẳng qua C và vuông góc với AD cắt đường thẳng AB ở F. Chứng minh BF = CE
Lời giải:
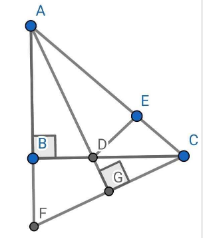
a) Xét và có:
AD chung
(AD là tia phân giác của )
AB = AE (gt)
b) Do
(hai góc tương ứng)
Hay DE vuông góc AC
c) Gọi G là giao điểm của CF và AD
Do (cmt)
Xét hai tam giác vuông: và có:
AG chung
(cmt)
(cạnh góc vuông - góc nhọn kề)
(hai cạnh tương ứng)
Mà
a. Chứng minh tứ giác MECF là hình chữ nhật và EF là tiếp tuyến chung của (I) và (K)
b. Cho AB = 4cm, xác định vị trí điểm C trên AB để diện tích tứ giác IFEK là lớn nhất.
d. Chứng minh 3 điểm: N, E, F thẳng hàng
Lời giải:
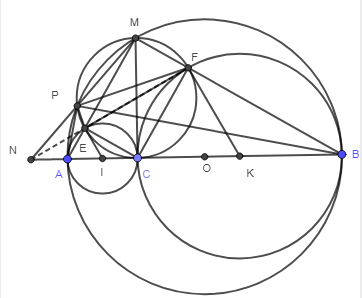
a) Ta thấy MEC và MFC là các tam giác vuông chung cạnh huyền MC nên MECF nội tiếp đường tròn đường kính MC.
Dễ thấy MECF là hình chữ nhật (Tứ giác có 3 góc vuông) nên
Lại có
Hoàn toàn tương tự FE là tiếp tuyến đường tròn (K). Vậy EF là tiếp tuyến chung của hai đường tròn.
b) MECF là hình chữ nhật nên EF = MC.
Do EI và FK cùng vuông góc với EF nên IEFK là hình thang vuông.
với H là điểm chính giữa cung AB.
Vậy để diện tích IEFK lớn nhất thì C nằm chính giữa cung AB. Khi đó
c) Ta thấy (Hai góc nội tiếp cùng chắn cung MF) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn cung CF)
d) Do
Mà hay NPEA là tứ giác nội tiếp.
Tương tự PFBN cũng là tứ giác nội tiếp.
Vậy thì ta có:
Hay N, E, F thẳng hàng.
Lời giải:
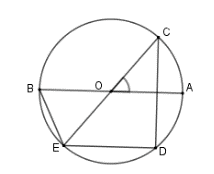
Xét (O) có
hay
Mà E; D; C nên EC là đường kính của (O) hay E; O; C thẳng hàng.
Do đó (đối đỉnh) nên số đo cung nhỏ BE là 55°.
Đáp án cần chọn là: A.
Chứng minh: ME = AD và MD = AE.
Lời giải:
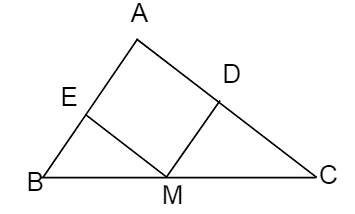
Xét tứ giác AEMD có : MD // AE (vì MD // AB) và ME // AD (vì ME // AC)
⇒ AEMD là hình bình hành. Theo tính chất của hình bình hánh ta suy ra được ME = AD và MD = AE (đpcm).
b) Giả sử AD và 3cm, AE = 4cm. Tính độ dài đoạn thẳng AM và diện tích tam giác DME
Lời giải:
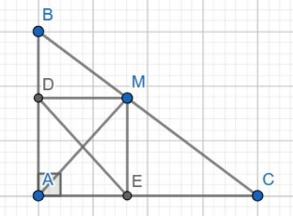
a) Ta có:
Tương tự
Xét tứ giác ADME:
→ Tứ giác ADME là hình chữ nhật (tứ giác có 3 góc vuông)
→ AD = ME, DM = AE
b)
Ta có: AD = ME = 3cm, DM = AE = 4cm
vuông tại D:
(định lý Pytago)
vuông tại M
Bài 18: Cho A, B là hai tập hợp tùy ý. Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm.
Lời giải:
Ta có nên A và B là hai tập hợp rời nhau:

Khi đó mọi phần tử của A và B đều khác nhau.
Vậy và .
Lời giải:
Xác suất để 2 người không bắn trúng bia là: P = 0,3 . 0,2 = 0, 06.
Xác suất để 2 người cùng bắn trúng bia là: P = 0,7 . 0,8 = 0,56.
Xác suất để đúng 1 người cùng bắn trúng bia là: P = 1 – 0,06 – 0,56 = 0,38.
Ta có bảng phân bố xác suất của biến ngẫu nhiên rời rạc X .
|
X |
0 |
1 |
2 |
|
P |
0,06 |
0,38 |
0,56 |
Vậy kỳ vọng của X là E(X) = 0 . 0,06 + 1 . 0,38 + 2 . 0,56 = 1,5.
Lời giải:
Có đúng 1 người bắn trúng bia → (A trúng, B trật) hoặc (A trật, B trúng)
→ xác suất .
Lời giải:
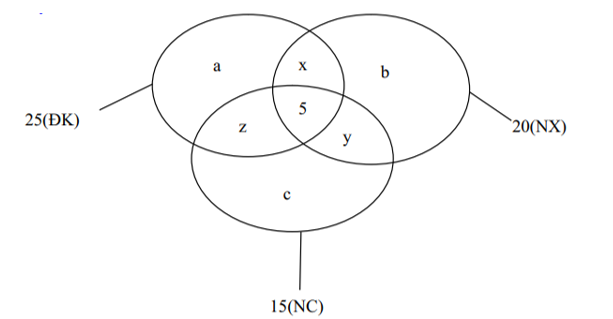
Gọi a, b, c theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao.
x là số học sinh chỉ thi hai môn điền kinh và nhảy xa.
y là số học sinh chỉ thi hai môn nhảy xa và nhảy cao.
z là số học sinh chỉ thi hai môn điền kinh và nhảy cao.
Số em thi ít nhất một môn là: 45 – 7 = 38
Dựa vào biểu đồ ven ta có hệ phương trình sau:
Cộng vế với vế của (1), (2), (3) ta có: a + b + c + 2(x + y + z) + 15 = 60 (5)
Từ (4) và (5) ta có: a + b + c + 2(38 – 5 – a – b – c) + 15 = 60
⟺ a + b + c = 21.
Vậy có 21 học sinh chỉ thi một trong ba nội dung trên.
Lời giải:
Tổng số lượt đi thi là 25 + 20 + 15 = 60 (lượt)
Trong đó có 55 học sinh thi cả 33 môn
→ Có 60 – 5 . 3 = 45 lượt đi thi cho 40 – 7 = 33 học sinh
hay 45 lượt thi sẽ có xx học sinh và yy học sinh thi 2 trong 3 môn
Vậy có 21 học sinh chỉ thi 1 trong 3 môn.
Bài 23: Cho a,b,c là các số không âm thỏa mãn a + b + c = 1. Chứng minh
Lời giải:
Ta có:
Điều phải cm
(luôn đúng)
→đpcm
Dấu “=” xảy ra
Lời giải:
Xét tứ giác AMHN có (1) (2 góc trong tứ giác nội tiếp cùng nhìn xuống cạnh AM)
Mà
(1)(2) ⇒
Xét tam giác ANM và tam giác ABC có:
chung
tam giác ANM đồng dạng tam giác ABC (g – g)
Bài 25: Tìm hệ số của x6 trong khai triển với biết n là số nguyên dương thỏa mãn điều kiện
Lời giải:
Điều kiện: Ta có
Với n = 3, theo khai triển nhị thức Newton, ta có
Hệ số của số hạng chứa x6 ứng với 4k – 10 = 6 k = 4
→ Hệ số cần tìm là
Đáp án cần chọn là: A
Bài 26: Cho n là số nguyên dương thỏa mãn điều kiện Tìm hệ số của x7 trong khai triển
Lời giải:
Đáp án cần chọn là: A
Điều kiện:
Từ giả thiết, ta có:
(vì điều kiện )
Khi đó, ta được khai triển
Theo khai triển nhị thức Newton, ta có:
Suy ra hệ số của x7 ứng với
Hệ số của x7 trong khai triển là
Vậy hệ số cần tìm là .
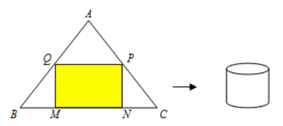
Lời giải:
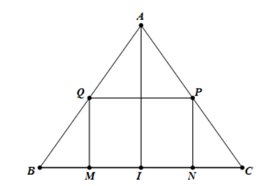
Gọi I là trung điểm của BC. Suy ra I là trung điểm của MN. Đặt
Khi đó ta có: Gọi R là bán kính của hình trụ
Thể tích của khối trụ là:
Xét với Suy ra
Do đó
Lời giải: Sử dụng tổng cấp số nhân, ta có công thức sau:
Trong đó với N là số tiền vay, là lãi suất hàng tháng), a là số tiền trả hàng tháng và n là số tháng.
Khi đó:
Vậy anh A mất 18 tháng thì sẽ trả hết nợ cho ngân hàng.
Lời giải: Ta có hình vẽ sau:
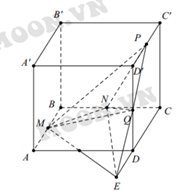
Khi đó ta có:
Do nên ta có:
Vì vậy
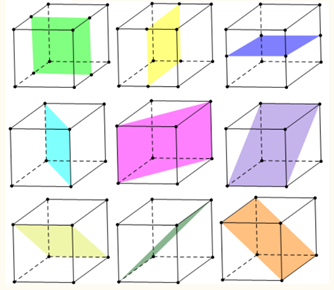
Bài 30: Cho các hình sau thì có bao nhiêu hình là đa diện lồi?
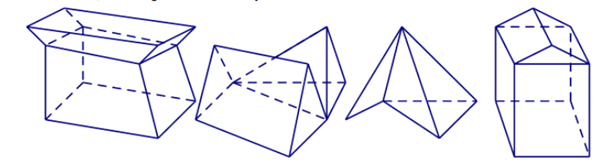
Lời giải: Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kỳ của (H) luôn thuộc (H). Khi đó đa diện giới hạn (H) được gọi là đa diện lồi.
Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó.
Vậy theo định nghĩa trên thì chỉ có 1 hình là đa diện lồi.
Lời giải: Do tam giác ABC vuông cân tại B nên ta có
Đồng thời do
Suy ra Mặt khác: (do J là trung điểm của BC).
Ta có:
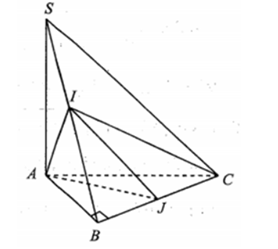
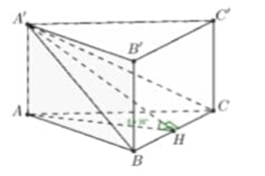
Lời giải: Gọi H là trung điểm của BC. Đặt AB = a ta có:
Xét tam giác A'AH ta tìm được:
Suy ra
Thể tích của khối lăng trụ ABC.
Bài 33: Hình lập phương có bao nhiêu mặt đối xứng?
Lời giải: Hình lập phương có 9 mặt đối xứng
Lời giải:
Xét hàm số f(x) = x3 – 3x2 – 9x + m trên đoạn [– 2; 4].
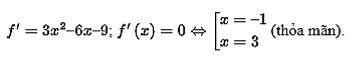
Ta có: f(– 2) = m – 2, f(– 1) = m + 5, f(3) = m – 27, f(4) = m – 20.
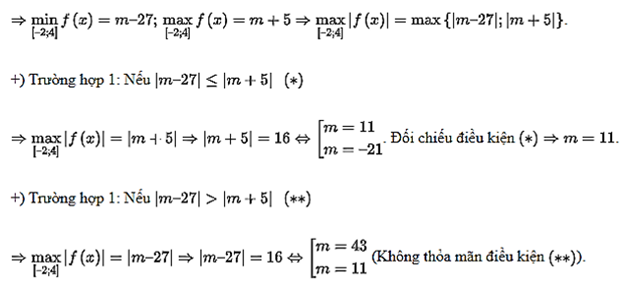
Vậy S = {11}. Do đó S có 1 phần tử.
Lời giải: Ta có:
Để đồ thị hàm số đã cho có 5 điểm cực trị khi và chỉ khi phương trình: y' = 0 có 5 nghiệm phân biệt. Điều này tương đương với Đặt phải có 3 nghiệm phân biệt khác 0 và 2.
Ta có: tức là ta cần đi tìm giá trị của m để đường thẳng y = m cắt đồ thị hàm số tại 3 điểm phân biệt.
Do đó ta khảo sát hàm số thì ta có được:
Vậy S tổng tất cả các giá trị của S là 6.
Câu 36: Đồ thị hàm số có bao nhiêu điểm cực trị?
Lời giải: Xét hàm số Tập xác định D = R
Ta xét đạo hàm bậc nhất: Khi đó ta có BBT sau:
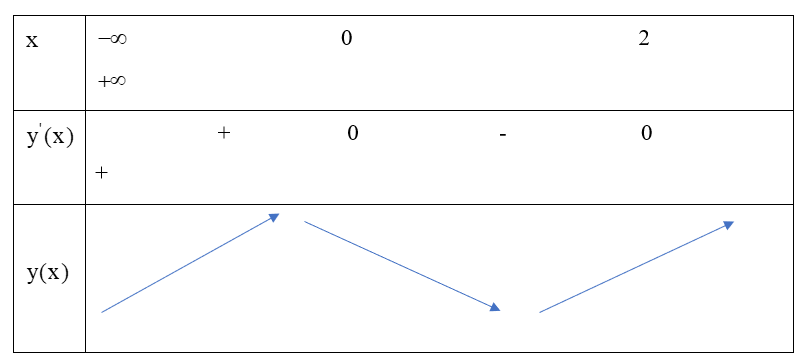
Hàm số là hàm số chẵn và đồ thị của nó được suy ra từ đồ thị hàm số bằng cách bỏ đi phần bên trái trục tung. Giữ nguyên phần bên phải trục tung và lấy đối xứng với phần bên phải Oy qua Oy. Như vậy ta sẽ thu được đồ thị hàm số có dạng sau:
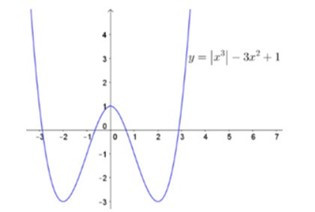
Lời giải:
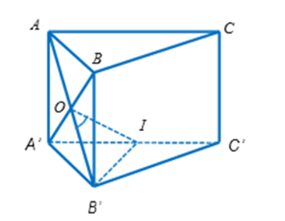
Gọi O là tâm của hình bình hành ABB'A' và I là trung điểm của A'C'. Ta có:
Mặt khác nên là tam giác đều.
Suy ra
Vì là hình lăng trụ tam giác đều nên tam giác AA'B' vuông tại A' và có
Thể tích của khối lăng trụ đã cho là:
Lời giải:
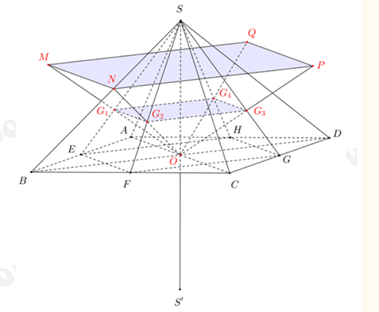
Gọi lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SDA.
Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Ta có:
Mặt khác:
Vậy thể tích của khối chóp S'.MNPQ là:
Lời giải:
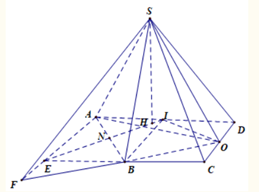
Gọi I, N là trung điểm của AD, AB. Gọi H là tâm đường tròn ngoại tiếp tam giác ABO, vì tam giác ABI đều nên H thuộc NI.
Kẻ HK vuông góc CD, dựng hình bình hành AECD. Gọi F là giao điểm của BO và AE.
Ta có: nên
Vì ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD, nên tam giác BIC và CID là các tam giác đều, do đó ta có:
Suy ra
Diện tích
Thể tích của khối chóp S. AFO là:
Diện tích tam giác SAF:
Vậy
Lời giải:
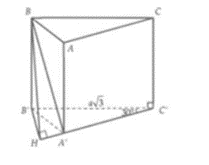
Ta có:
Mà
Vậy suy ra thể tích của khối lăng trụ đứng ABC.A'B'C' là:
Bài 41: Cho G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?
Lời giải: Đáp án C.
Dựa vào đáp án ta có nhận xét: Xác định góc nên
Tương tự ta cũng xác định là góc ngoài của góc C nên
Xác định góc của do đó
Tương tự cho ý đáp án D, ta ra kết quả là
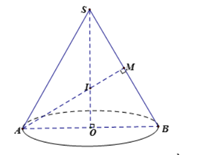
Lời giải: Giả sử cạnh của tam giác đều SAB bằng 1. Gọi thiết diện qua trục hình nón là tam giác đều SAB.
Gọi I là trọng tâm của tam giác đều SAB, khi đó I là tâm mặt cầu nội tiếp hình nón cũng là tâm mặt cầu ngoại tiếp hình nón.
Bán kính mặt cầu ngoại tiếp hình nón là:
Bán kính mặt cầu nội tiếp hình nón là:
Thể tích mặt cầu ngoại tiếp hình nón là:
Thể tích mặt cầu nội tiếp hình nón là:
Vậy
Lời giải: Gọi số tự nhiên có 6 chữ số đôi một khác nhau có dạng:
Sắp xếp cụm số 3, 4, 5 mà số 4 luôn đứng cạnh 3 và 5 thì ta có 2 cách sắp xếp: 345 và 543.
TH1: Nếu các cụm số 3, 4, 5 đứng đầu có các số tạo thành là: (số)
TH2: Nếu các cụm số 3,4,5 không đứng đầu có 3 cách sắp xếp là: x345xx; xx345x; xxx345.
Khi đó 3 chữ số còn lại có: cách chọn và sắp xếp.
Do đó ta có được các số tạo thành là: (số)
Áp dụng quy tắc cộng có: số thỏa mãn yêu cầu bài toán.
Lời giải: Số cách lập số tự nhiên có 6 chữ số đôi một khác nhau từ tập A (không tính chữ số 0 đứng đầu) là: (số).
Số cách lập số tự nhiên có 6 chữ số đôi một khác nhau mà số 3 và số 4 đứng cạnh nhau là: (số).
Xác suất cần tìm thỏa mãn bài toán là:
Lời giải:
Ta có: 0 + 6 = 2 + 4 = 1 + 5
Suy ra a, b, c, d, e, f ∈ {0; 1; 2; 4; 5; 6}
+) a khác 0 nên a có 5 cách, b có 1 cách.
+) c khác a và b nên c có 4 cách, d có 1 cách.
+) e khác a, b, c, d nên e có 2 cách, d có 1 cách.
Do đó có 5.4.2 = 40 cách.
Ta lại có: 0 + 5 = 2 + 3 = 1 + 4
Do đó có 40 cách.
Vậy tổng cộng có 40 + 40 = 80 số.
Bài 46: Cho hình hộp chữ nhật ABCD.A'B'C'D' có Tính diện tích mặt cầu ngoại tiếp hình hộp đã cho.
Lời giải:
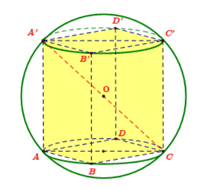
Gọi O là mặt cầu ngoại tiếp của hình hộp chữ nhật ABCD.A'B'C'D' .
Khi đó bán kính của hình hộp sẽ là:
Vậy diện tích của mặt cầu ngoại tiếp hình hộp là:
Lời giải:
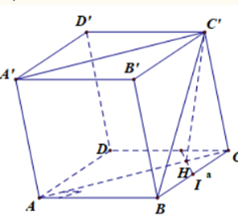
Do nên kẻ Do nên
(với I là trung điểm của BC).
Ta có:
Tam giác vuông tại H nên ta có:
Tam giác vuông ABC có
Vậy thể tích của lăng trụ đã cho là:
Bài 48: Số cách chia 12 phần quà giống nhau cho 3 bạn sao cho ai cũng có ít nhất 2 phần quà.
Lời giải:
+ Chia trước cho mỗi học sinh một phần quà thì số phần quà còn lại là 9 phần quà.
+ Chia 9 phần quà cho 3 học sinh sao cho học sinh nào cũng có ít nhất một phần quà: Đặt 9 phần quà theo một hàng ngang, giữa các phần quà sẽ có 8 khoảng trống, chọn 2 khoảng trống trong 8 khoảng trống đó để chia 9 phần quà còn lại thành 3 phần quà mà mỗi phần có ít nhất một phần quà, có
+ Vậy tất cả có số cách chia là: (cách chia).
Lời giải: Cho 3 học sinh nam cầm tay nhau coi như là một người, cùng với 2 học sinh nữ xếp thành một hàng ngang, có 3! cách.
Ba học sinh nam có thể đổi chỗ cho nhau, có 3! cách.
Vậy theo quy tắc nhân sẽ có: cách xếp.
Lời giải:
B1: Số cách chọn ra 3 bạn nam trong 10 bạn nam là:
B2: Số cách chọn ra 2 bạn nữ trong 8 bạn nữ là:
B3: Áp dụng theo quy tắc nhân ta có số cách chọn ra 5 bạn thỏa mãn đề bài là:
Lời giải: Gọi số cần lập có 3 chữ số đôi một khác nhau có dạng:
Theo giả thiết là các số này sẽ chia hết cho 9, do đó ta có:
Khi đó các số a, b, c thuộc các tập số và
+ TH1: Nếu các số a, b, c thuộc tập A.
Khi đó chữ số a có: 2 cách chọn; chữ số b có 2 cách và c có 1 cách chọn. Vậy ta có: 2.2.1=4 (số).
+ TH2: Nếu các số a, b, c thuộc tập B.
Khi đó a có 3 cách chọn, b có 2 cách và c có 1 cách chọn. Vậy ta có: 3.2.1 = 6 (số).
Áp dụng quy tắc cộng ta có các số tạo thành thỏa mãn bài toán là: 6 + 4 = 10 (số).
Lời giải: Đặt y = 23 xét số trong đó a; b; c; d; e đôi một khác nhau và thuộc tập {0; 1; y; 4; 5}.
Khi đó có 4 cách chọn a; 4 cách chọn b; 3 cách chọn c; 2 cách chọn d và 1 cách chọn e.
Theo quy tắc nhân có 4.4.3.2 = 96 số.
Khi ta hoán vị trong y ta được hai số khác nhau.
Vậy có tất cả: 96.2 = 192 số thỏa mãn yêu cầu bài toán.
Lời giải:
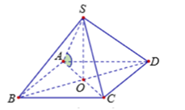
Gọi các cạnh của đáy ABCD đều có độ dài là a.
Vì chóp S. ABCD là chóp tứ giác đều, nên do đó ta có:
Gọi O là tâm của hình vuông ABCD thì ta có:
Suy ra ta có:
Xét tam giác SAO vuông tại O ta có:
Lời giải: Đồ thị hàm số có 2 điểm cực trị nằm về hai phía của Ox
cắt trục Ox tại 3 điểm phân biệt.
có 3 nghiệm phân biệt.
Ta có:
Để (C) cắt trục Ox tại 3 điểm phân biệt khi và chỉ khi (1) có hai nghiệm phân biệt khác 2.
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện trên.
Lời giải:
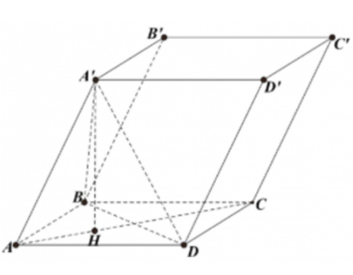
Từ giả thiết ta có các tam giác ABD, A'AD, A'AB là các tam giác đều.
Suy ra ta có: nên H là hình chiếu của A' trên mặt phẳng (ABCD) là tâm đường tròn ngoại tiếp tam giác đều ABD.
Do đó:
Vậy thể tích của khối hộp là:
Lời giải:
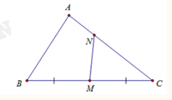
Ta có:
Vậy
Lời giải:
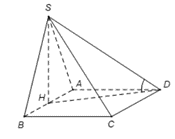
Gọi H là trung điểm của AB. Khi đó ta có nên hình chiếu của SD trên (ABCD) là HD.
Do đó
Mặt khác tam giác SAB đều cạnh a nên
Suy ra
Khi đó xét tam giác vuông SHD, ta có:
Lời giải:
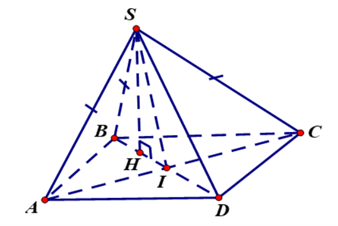
Gọi I là tâm của hình thoi ABCD, H là hình chiếu của S lên mặt (ABCD).
Ta có nên hình chiếu vuông góc của S xuống mặt phẳng (ABCD) trùng với tâm đường tròn ngoại tiếp tam giác ABC hay
Ta có:
Khi đó tam giác SBD vuông tại S. Giả sử Ta có
Ta có:
Ta có:
Suy ra
Vậy
Bài 59: Có bao nhiêu số nguyên dương không lớn hơn 2020 mà chia hết cho 2 hoặc cho 3?
Lời giải:
Số các số chia hết cho 2 là:
Số các số chia hết cho 3 là:
Số các số chia hết cho cả 2 và 3 (đồng nghĩa là chia hết cho 6) là:
Vậy các số thỏa mãn đề bài ra là:
Bài 60: Phương trình có bao nhiêu nghiệm trên đoạn
Lời giải: Ta có:
Vì nên ta có:
Mặt khác k là số nguyên nên k sẽ nhận các giá trị:
Vậy phương trình đã cho có 8 nghiệm trên đoạn