Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Dấu hiệu nhận biết hình bình hành chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết về hình bình hành, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.
Dấu hiệu nhận biết hình bình hành
1. Hình bình hành là gì?
Hình bình hành là tứ giác có các cạnh đối song song.
Ví dụ
Tứ giác ABCD là hình bình hành .
2. Dấu hiệu nhận biết hình bình hành
• Dấu hiệu nhận biết hình bình hành
1. Tứ giác có các cạnh đối song song là hình bình hành.
Tứ giác ABCD có AB//CD và AD//CB thì ABCD là hình bình hành.
2. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
Tứ giác ABCD có AB = CD, AD =BC thì ABCD là hình bình hành.
3. Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Tứ giác ABCD có AB//CD và AB = CD hoặc AD//BC và AD = BC thì ABCD là hình bình hành.
4. Tứ giác có các góc đối bằng nhau là hình bình hành.
Tứ giác ABCD có 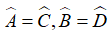
5. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Tứ giác ABCD có AC cắt BD tại O. Nếu OA = OC, OB = OD thì ABCD là hình bình hành.
Ví dụ 1: Trong các tứ giác sau, tứ giác nào là hình bình hành? Vì sao?
Hướng dẫn:
a) Tứ giác ABCD có AB = CD, BC = AD do đó ABCD là hình bình hành.
b) Tứ giác ABCD có 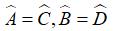
c) Tứ giác ABCD có 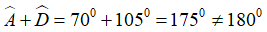
d) Tứ giác ABCD có hai đường chéo là AC vad BD. AC giao BD tại O. Ta có: OA = OC, OB = OD nên ABCD là hình bình hành.
e) Tứ giác ABCD có 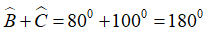
Ví dụ 2: Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
Hướng dẫn:
Xét tam giác ABC có:
E là trung điểm AB
F là trung điểm BC
Suy ra, EF là đường trung bình của tam giác ABC
Xét tam giác ACD có:
H là trung điểm của AD
G là trung điểm củ CD
Suy ra, HG là đường trung bình của tam giác ACD
Từ (1) và (2) suy ra, EF//HG và EF = HG
Xét tứ giác EFGH có: EF//HG và EF = HG
Suy ra, EFGH là hình bình hành.
3. Các dạng toán về hình bình hành
Dạng 1. Vận dụng tính chất của hình bình hành để chứng minh các tính chất hình học
Phương pháp giải: Vận dụng định nghĩa, các tính chất về cạnh, góc và đường chéo của hình bình hành.
Ví dụ: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh:
a) BE = DF; 
b) BE//DF
Lời giải:
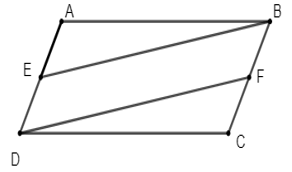
a) Vì E là trung điểm của AD, F là trung điểm của BC
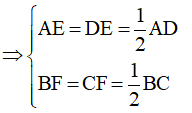
Mà AD = BC do ABCD là hình bình hành.
Do đó:
Lại có do ABCD là hình bình hành:
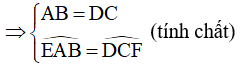
Xét tam giác ABE và tam giác CDF có:
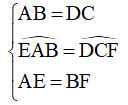
=> ΔABE = ΔCDF (c – g – c)
=> BE = DF (hai cạnh tương ứng) và 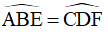 (hai góc tương ứng)
(hai góc tương ứng)
b) Xét tứ giác EBFD có:
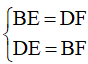 (chứng minh trên)
(chứng minh trên)
Nên tứ giác EBFD là hình bình hành (dấu hiệu nhận biết).
=> BE // DF
Dạng 2. Chứng minh tứ giác là hình bình hành
Phương pháp giải: Áp dụng các dấu hiệu nhận biết của hình bình hành
a) Tứ giác có các cạnh đối song song là hình bình hành;
b) Tứ giác có các cạnh đối bằng nhau là hình bình hành;
c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành;
d) Tứ giác có các góc đối bằng nhau là hình bình hành;
e) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Ví dụ: Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD lần lượt tại H và tại K. Chứng minh tứ giác AHCK là hình bình hành.
Lời giải:
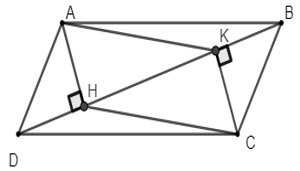
Vì tứ gác ABCD là hình bình hành:
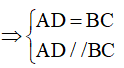
Vì AD // BC nên 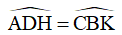 (hai góc so le trong)
(hai góc so le trong)
Ta có:
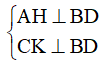
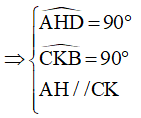
Xét tam giác AHD và tam giác CKB có:
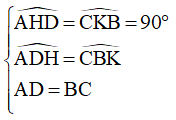
=> ΔAHD = ΔCKB (cạnh huyền - góc nhọn)
=> AH = CK (hai cạnh tương ứng)
Xét tứ giác AHCK có:
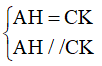
=> tứ giác AHCK là hình bình hành (dấu hiệu nhận biết)
Dạng 3. Chứng minh ba điểm thẳng hàng, các đường thẳng đồng quy
Phương pháp giải: Vận dụng tính chất về đường chéo của hình bình hành: Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Ví dụ 1. Cho tam giác ABC và O là một điểm thuộc miền trong của tam giác. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC, AC và L, M, N lần lượt là trung điểm của các đoạn OA, OB, OC. Chứng minh rằng các đoạn thẳng EL, FM và DN đồng quy.
Lời giải:
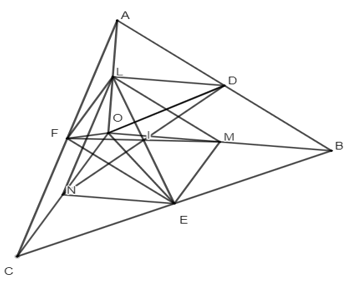
Gọi I là trung điểm của LE.
Vì D là trung điểm của AB, L là trung điểm của AO nên LD là đường trung bình của tam giác AOB.
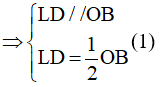
Vì N là trung điểm của OC, E là trung điểm BC nên NE là đường trung bình của tam giác OBC
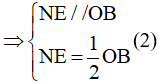
Từ (1) và (2)
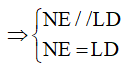
Xét tứ giác DENL có:
NE // LD
NE = LD
Nên tứ giác DENL là hình bình hành
=> Hai đường chéo DN và LE cắt nhau tại trung điểm I của của LE (*)
L là trung điểm của AO, M là trung điểm của OB nên LM là đường trung bình của tam giác OAB
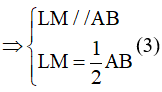
F là trung điểm của AC, E là trung điểm của BC nên FE là đường trung bình của tam giác ABC
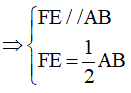
Từ (3) và (4)
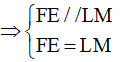
Xét tứ giác LMEF có:
FE // LM
FE = LM
Nên tứ giác LMEF là hình bình hành
=> Hai đường chéo MF là LE cắt nhau tại trung điểm I của LE (**)
Từ (*) và (**) ta có EL, FM, DN đồng quy (do cùng đi qua trung điểm I của EL)
4. Bài tập về hình bình hành
Bài 1. Tính các góc còn lại của hình bình hành ABCD trong hình dưới đây.
Hướng dẫn giải
Vì tứ giác ABCD là hình bình hành nên
Theo định lí tổng các góc trong một tứ giác ta có:
suy ra .
Bài 2. Trong mỗi trường hợp sau, tứ giác nào là hình bình hành, tứ giác nào không phải là hình bình hành? Vì sao?
Hướng dẫn giải
+ Tứ giác EFGH có
Suy ra mà nên theo dấu hiệu nhận biết của hình bình hành ta có tứ giác EFGH là hình bình hành.
+ Tứ giác MNPQ không là hình bình hành vì ta dễ dàng tính được
+ Tứ giác ABCD là hình bình hành vì có các cạnh đối bằng nhau: AB = CD và AD = BC.
Bài 3. Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh Từ đó suy ra tứ giác MBND là hình bình hành.
Hướng dẫn giải
+ Vì O là giao điểm của hai đường chéo của hình bình hành ABCD nên O là trung điểm của BD và AC.
Lại có: AB // CD nên (hai góc so le trong)
+ Xét và có:
(chứng minh trên)
OA = OC (O là trung điểm AC)
(hai góc đối đỉnh)
Do đó (góc - cạnh - góc)
Suy ra OM = ON hay O là trung điểm MN.
+ Xét tứ giác MBND có hai đường chéo MN và BD cắt nhau tại trung điểm O của mỗi đường, suy ra tứ giác MBND là hình bình hành (dấu hiệu nhận biết).
Bài 4. Hình bình hành ABCD có . Tính các góc A, C, D.
Hướng dẫn giải
ABCD là hình bình hành nên ta có: và (tính chất hình bình hành)
Áp dụng định lí tổng các góc của một tứ giác ta có:
Suy ra .
Do đó .
Vậy và .
Bài 5. Cho hình bình hành MNPQ (MQ < MN). Từ M kẻ đường phân giác của cắt QP tại E, từ P kẻ đường phân giác của cắt MN tại F.
a) Chứng minh ∆MQE là tam giác cân.
b) Tứ giác MEPF là hình gì? Tại sao?
Hướng dẫn giải
a) Ta có MNPQ là hình bình hành nên MN // PQ
Do đó (so le trong).
ME là đường phân giác của nên
Suy ra .
Vậy tam giác MQE là tam giác cân tại Q.
b) Do ME là đường phân giác của nên
Do PF là đường phân giác của nên
Mà (hai góc đối của hình bình hành)
Suy ra hay .
Mặt khác, MN // PQ nên (so le trong)
Do đó , mà hai góc này ở vị trí so le trong nên ME // PF
Xét tứ giác MEPF có ME // PF và MF // PE nên là hình bình hành.