Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 16)

Câu 1: Chứng minh hằng đẳng thức:

(a + b + c)³ = a³ + b³ + c³ + 3(a + b)(b + c)(c + a).

Lời giải:

Biến đổi vế trái:

(a + b + c)³ = [(a + b) + c]³

= (a + b)³ + 3(a + b)²c + 3(a +b)c² + c³

= a³ + 3a²b + 3ab² + b³ + 3(a² + 2ab + b²)c + 3ac² + 3bc² + c³

= a³ + 3a²b + 3ab² + b³ + 3a²c + 6abc + 3b²c + 3ac² + 3bc² + c³

= a³ + b³ + c³ + 3a²b + 3ab² + 3a²c + 6abc + 3b²c + 3ac² + 3bc²

= a³ + b³ + c³ + (3a²b + 3ab²) + (3a²c + 3abc) + (3abc + 3bc²) + (3ac² + 3bc²)

= a³ + b³ + c³ + 3ab(a + b) + 3ac(a + b) + 3bc(a + c) + 3c²(a + b)

= a³ + b³ + c³ + (a + b)(3ab + 3ac + 3bc + 3c²)

= a³ + b³ + c³ + (a + b)[(3ab + 3ac) + (3bc + 3c²)]

= a³ + b³ + c³ + (a + b)[3a(b + c) + 3c(b + c)]

= a³ + b³ + c³ + 3(a + b)(b + c)(a + c) (đpcm)

Câu 2: Chứng minh: a³ + b³ + c³ = 3abc biết a + b + c = 0.

Lời giải:

Ta có: A = a³ + b³ + c³ – 3abc

= (a³ + b³) + c³ – 3abc

= (a + b)³ – 3ab(a + b) + c³ – 3abc

= [(a + b)³ + c³] – [3ab(a + b) – 3abc]

= (a + b + c)[(a + b)² – (a + b)c + c²] – 3ab(a + b + c)

= (a + b + c)(a² + b² + c² – ab – bc – ca)

Mà a + b + c = 0 nên suy ra:

A = 0 $\Rightarrow$ a³ + b³ + c³ – 3abc = 0

$\iff$ a³ + b³ + c³ = 3abc (đpcm).

Câu 3: Cho hàm số y = f(x). Hàm số y = f '(x) có đồ thị hàm số như hình bên. Hỏi hàm số y = f(2 – x) đồng biến trên khoảng:

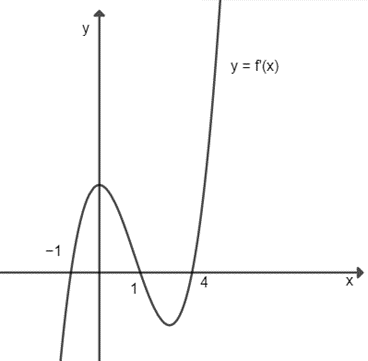
A. (1; 3);

B. x > 3;

C. x < −2;

D. Đáp án khác.

Lời giải:

Đáp án đúng là: D

Ta có ${\left(f\left(2-x\right)\right)}^{\text{'}}={\left(2-x\right)}^{\text{'}}.f^{\text{'}}\left(2-x\right)=-f^{\text{'}}\left(2-x\right)$ .

Hàm số đồng biến khi $\left(f\left(2-x\right)\right)\text{'}>0$

$\iff f^{\text{'}}(2-x)\iff \left[\begin{array}{l}2-x<-1\\ 1<2-x<4\end{array}\right.\iff \left[\begin{array}{l}x>3\\ -2<x<1\end{array}\right.$.

Câu 4: Một nhóm gồm 10 học sinh trong đó có An và Bình, đứng ngẫu nhiên thành một hàng. Xác suất để An và Bình đứng cạnh nhau là:

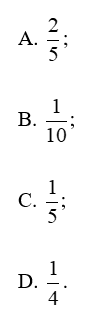
Lời giải:

Đáp án đúng là: C

Xét ngẫu nhiên 10 học sinh thành một hàng có 10! cách ⇒ n(Ω) = 10!

Gọi biến cố “Xếp 10 học sinh thành một hàng sao cho An và Bình đứng cạnh nhau”.

Xem An và Bình là nhóm X.

Xếp X và 8 học sinh còn lại có 9! (cách).

Hoán vị An và Bình trong X có 2! (cách).

Vậy có 9!2! cách ⇒ n(A) = 9!2!

Xác suất của biến cố A là:  $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{9!2!}{10!}=\frac{9!2}{10.9!}=\frac{1}{5}$.

Câu 5: Một nhóm 10 học sinh gồm 5 học sinh nam trong đó có An và 5 học sinh nữ trong đó có Bình được xếp ngồi vào 10 cái ghế trên một hàng ngang. Hỏi có bao nhiêu cách sắp xếp nam và nữ ngồi xen kẽ, đồng thời An không ngồi cạnh Bình?

A. 16.(4!)²;

B. 16.8!;

C. 32.(4!)²;

D. 32.8!.

Lời giải:

Đáp án đúng là: C

Xếp 10 học sinh sao có nam nữ ngồi xen kẽ.

Xếp 5 học sinh nam có 5! cách, xếp 5 học sinh nữ vào 5 vị trí còn lại có 5! cách.

Đổi chỗ nam và nữ có 2 cách.

Suy ra có 2.(5!)² cách xếp 10 học sinh sao có nam nữ ngồi xen kẽ.

* Xếp 8 học sinh không có An và Bình trước:

• TH1:

+ Học sinh nam đứng đầu hàng, có (4!)² cách.

+ Xếp An và Bình vào 1 trong 9 vị trí gồm 7 vị trí giữa 2 học sinh liền kề nhau và 2 vị trí biên. Ứng với mỗi vị trí có 1 cách xếp An và Bình sao cho thỏa mãn yêu cầu, do đó có 9 cách xếp.

 Vậy có 9.(4!)² cách.

• TH2:

+ Học sinh nữ đứng đầu hàng, tương tự TH1 có 9.(4!)² (cách).

Suy ra số cách xếp 10 học sinh xen kẽ mà An luôn cạnh Bình là 2.9.(4!)² (cách).
Vậy số cách sắp xếp nam và nữ ngồi xen kẽ, đồng thời An không ngồi cạnh Bình là:
 2.(5!)² – 2.9.(4!)² = 2.5.5.(4!)² – 18.(4!)² = 32.(4!)² (cách)

Câu 6: Hai bạn An và Khang đi mua 18 gói bánh và 12 gói kẹo để đến lớp ăn liên hoan. An đưa cho cô bán hàng 4 tờ 50 000 đồng và đc trả lại 72 000 đồng. Khang nói "cô tính sai rồi". Em hãy cho biết Khang nói đúng hay sai? Giải thích tại sao?

Lời giải:

Do bạn An và bạn Khang đi mua tất cả là 30 gói bánh kẹo nên số tiền phải trả bắt buộc phải chia hết cho 3.

Số tiền bạn An đưa cho cô bán hàng là: 4. 50 000 = 200 000 (đồng)

Số tiền cô bán hàng nhận là: 200 000 – 72 000 = 128 000 (đồng)

Vì 128 000 $\cancel{⋮}$ 3 nên bạn Khang nói đúng.

Câu 7: Cho tam giác ABC có $\widehat{A}=120°$ , AB = 3 cm, AC = 6 cm. Tính độ dài đường phân giác AD.

Lời giải:           

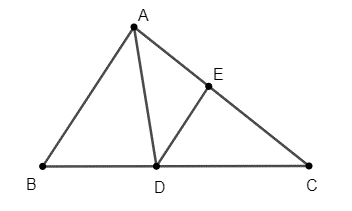
Kẻ DE // AB, ∆ADE đều.

Đặt AD = DE = EA = x.

Ta có: $\frac{DE}{AB}=\frac{CE}{CA}\Rightarrow \frac{x}{3}=\frac{6-x}{6}$

Từ đó x = 2. Vậy AD = 2 cm.

Câu 8: Vào buổi sáng một cửa hàng bán bánh với giá 50 000 đồng/cái. Buổi chiều, chủ cửa hàng quyết định giảm giá 20% so với buổi sáng nhờ đó số lượng bánh bán ra buổi chiều tăng 50% so với  buổi sáng và tổng số tiền thu được cả ngày là 13 200 000 đồng. Hỏi cả ngày cửa hàng bán được bao nhiêu cái bánh?

Lời giải:

Giá bánh buổi chiều : 50000.(1 − 0,2) = 40 000 (đồng/chiếc)

 Gọi lượng bánh bán ra buổi sáng là x chiếc (a > 0)

⇒ Lượng bánh bán ra buổi chiều là : x.(1 + 0,5) = 1,5x (chiếc)

Tổng doanh thu 2 buổi : 50 000x + 40 000.1,5x  = 13 200 000

⇔ 50 000x + 60 000x  = 13 200 000

⇔ 110 000x  = 13 200 000

⇔ x = 120

Vậy cả ngày cửa hàng bán được là:

x + 1,5x = 2,5.x = 2,5.120 = 300 (chiếc)

Câu 9: Trong mặt phẳng tọa độ Oxy cho ba điểm A(0; 3), B(2; −1), C(−1; 5) phép vị tự tâm A tỉ số k biến B thành C khi đó giá trị k bằng bao nhiêu?

Lời giải:

• $\overrightarrow{AB}=(2;-4)=(2;4)$ ;

• $\overrightarrow{AC}=(-1-0;5-3)=(-1;s2)$ .

Ta thấy: $\overrightarrow{AC}=-\mathrm{0,5}\overrightarrow{AB}$

Suy ra có phép tự tâm A, tỉ số $-\frac{1}{2}$  biến B thành C.

Câu 10: Cho hình lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a, A’C hợp với mặt đáy một góc 60^o. Tính thể tích của khối lăng trụ ABC.A’B’C’.

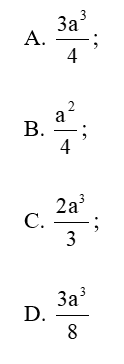
Lời giải:

Đáp án đúng là: A

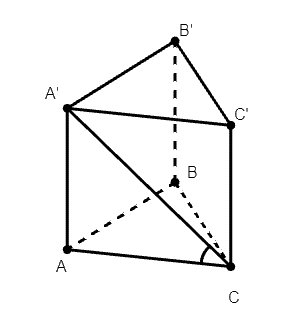
Diện tích đáy $S_{ABC}=\frac{a^2\sqrt{3}}{4}$ .

Độ dài đường cao: AA’ = A’C’.tan60° = $a\sqrt{3}$.

Vậy thể tích của khối lăng tụ là:

$V_{ABC.A\text{'}B\text{'}C\text{'}}=\frac{a^2\sqrt{3}}{4}.a\sqrt{3}=\frac{3a^3}{4}$.

Câu 11: Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB.

Lời giải:

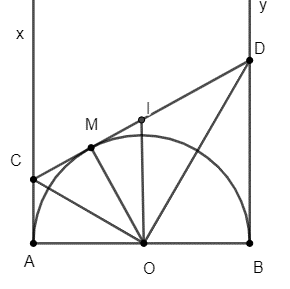
Theo tính chất tiếp tuyến, ta có: Ax ⊥ AB; By ⊥ AB.

Suy ra: Ax // By hay AC // BD.

Suy ra tứ giác ABDC là hình thang.

Gọi I là trung điểm của CD.

Khi đó OI là đường trung bình của hình thang ABDC.

Suy ra: OI // AC ⇒ OI ⊥ AB.

Vì OC và OD lần lượt là phân giác của $\widehat{AOM}$  và $\widehat{BOM}$  nên:

OC $\perp$ OD (tính chất của hai góc kề bù)

$\Rightarrow \widehat{COD}=90°$

 

Suy ra: IC = ID = IO $=\frac{1}{2}CD$  (tính chất tam giác vuông).

Suy ra I là tâm đường tròn đường kính CD.

Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.

Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.

Câu 12: Cho $\Delta ABC$  đều cạnh A và G là trọng tâm. Gọi I là trung điểm của AG. Tính độ dài các vecto $\overrightarrow{AB},\overrightarrow{AG},\overrightarrow{BI}$ .

Lời giải:

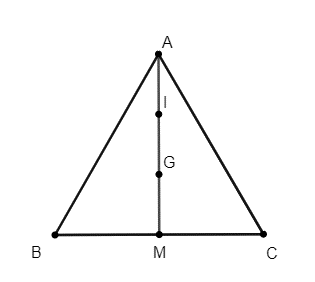
Ta có: $\left|\overrightarrow{AB}\right|=AB=a$ .

Gọi M là trung điểm của BC $\Rightarrow BM=\frac{1}{2}BC=\frac{a}{2}$ .

Tam giác ABM vuông tại M nên $AM=\sqrt{A{B}^2-B{M}^2}=\sqrt{a^2-\frac{a^2}{4}}=\frac{a\sqrt{3}}{2}$ .

Ta có: $\left|\overrightarrow{AG}\right|=AG=\frac{2}{3}AM=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$ .

Mà I là trung điểm của AG nên $MI=AG=\frac{a\sqrt{3}}{3}$ .

$\left|\overrightarrow{BI}\right|=BI=\sqrt{B{M}^2+M{I}^2}=\sqrt{\frac{a^2}{4}+\frac{a^2}{3}}=\frac{a\sqrt{21}}{6}$.

Câu 13: Cho đường tròn (O) bán kính OA = 4 cm. Dây BC vuông góc với OA tại trung điểm của OA. Tính độ dài BC.

Lời giải:

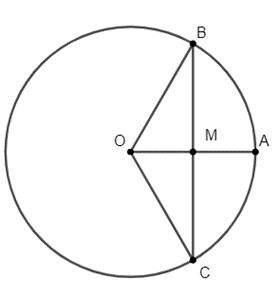
Vì B, C thuộc  đường tròn (O) nên: OB = OA = OC = 4 cm.

M là trung điểm của OA

$\Rightarrow OM=\frac{1}{2}OA=2$ (cm)

Xét $\Delta OBC$  có OB = OC suy ra $\Delta OBC$ cân tại O.

Suy ra OM là đường cao đồng thời là trung tuyến nên ta có:

MB = MC $\Rightarrow MB=\frac{1}{2}BC$

Xét $\Delta OBM$  có $\widehat{M}=90°$

$\Rightarrow$ OB² = OM² + MB²

$\Rightarrow MB=\sqrt{O{B}^2-O{M}^2}=\sqrt{4^2-2^2}=2\sqrt{3}$ (cm)

$\Rightarrow BC=2MB=4\sqrt{3}$ (cm).

Câu 14: Cho tam giác ABC, chứng minh:

$sin\widehat{A}+\sin \widehat{B}+\sin \widehat{C}=4.\cos \frac{\widehat{A}}{2}.\cos \frac{\widehat{B}}{2}.\cos \frac{\widehat{C}}{2}$.

Lời giải:

Ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$

$\Rightarrow \sin \frac{(\widehat{A}+\widehat{B})}{2}=\sin \left(\frac{180°}{2}-\frac{\widehat{C}}{2}\right)=\cos \frac{\widehat{C}}{2}$

Tương tự ta có: $\sin \frac{\widehat{C}}{2}=\cos \frac{\widehat{A}+\widehat{B}}{2}$

$$\begin{gathered} \Rightarrow \sin \widehat{A}+\sin \widehat{B}+\sin \widehat{C}=2\cos \frac{\widehat{C}}{2}.\cos \frac{\widehat{A}-\widehat{B}}{2}+2\cos \frac{\widehat{A}+\widehat{B}}{2}.\cos \frac{\widehat{C}}{2} \\ =2\cos \frac{\widehat{C}}{2}\left(\cos \frac{\widehat{A}-\widehat{B}}{2}+\cos \frac{\widehat{A}+\widehat{B}}{2}\right) \end{gathered}$$

$=4.\cos \frac{\widehat{A}}{2}.\cos \frac{\widehat{B}}{2}.\cos \frac{\widehat{C}}{2}$ (đpcm).

Câu 15: Giải phương trình: sinx + cosx = 1.

Lời giải:

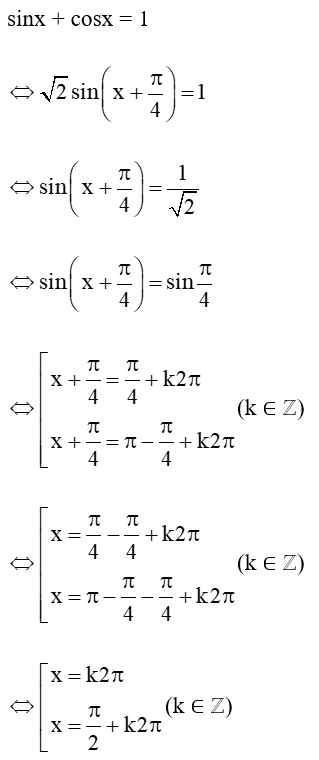
Vậy phương trình lượng giác có hai họ nghiệm là:

x= k2π và $x=\frac{\pi }{2}+k2\pi$  (k ∈ ℤ).

Câu 16: Nếu $\sin x+\cos x=\frac{1}{2}$  thì sinx, cosx bằng?

Lời giải:

Điều kiện −1 ≤ sinx; cosx ≤ 1.

Ta có: $\sin x+\cos x=\frac{1}{2}\iff \cos x=\frac{1}{2}-\sin x$

Mặt khác: sin²x + cos²x = 1 $\iff {\sin }^{2}x+{\left(\frac{1}{2}-\sin x\right)}^2=1$

$$\begin{gathered} \iff {\sin }^{2}x+{\sin }^{2}x-\sin x+\frac{1}{4}=1 \\ \iff 2{\sin }^{2}x-\sin x-\frac{3}{4}=0 \\ \iff \left[\begin{array}{l}\sin x=\frac{1+\sqrt{7}}{4}\\ \sin =\frac{1-\sqrt{7}}{4}\end{array}\right. \end{gathered}$$

Ta có:

• $\sin x=\frac{1+\sqrt{7}}{4}\Rightarrow \cos x=\frac{1-\sqrt{7}}{4}$  (TMĐK)

• $\sin x=\frac{1-\sqrt{7}}{4}\Rightarrow \cos x=\frac{1+\sqrt{7}}{4}$ (TMĐK)

Vậy $\sin x=\frac{1+\sqrt{7}}{4};\cos x=\frac{1-\sqrt{7}}{4}$  hoặc $\sin x=\frac{1-\sqrt{7}}{4};\cos x=\frac{1+\sqrt{7}}{4}$

Câu 17: Giải phương trình $\tan x=-\sqrt{3}$ .

Lời giải:

$\tan x=-\sqrt{3}$, ĐK: $x\ne \frac{\pi }{2}+k\pi$  (k ∈ ℤ)

$\iff \tan x=\tan \frac{-\pi }{3}$ (k ∈ ℤ)

$\iff x=-\frac{\pi }{3}+k\pi$ ( k ∈ ℤ) (Tm)

Vậy phướng trình đã cho có họ nghiệm là: $$$x=-\frac{\pi }{3}+k\pi$  (k ∈ ℤ)

Câu 18: Phương trình $\tan x=\sqrt{3}$  có bao nhiêu nghiệm thuộc khoảng (−2017π; 2017π)?

A. 4033;

B. 2017;

C. 4034;

D. 4035.

Lời giải:

Đáp án đúng là: C
Ta có: $\tan x=\sqrt{3}\iff x=\frac{\pi }{3}+k\pi$ (k ∈ ℤ)

Theo giả thiết ta có: $-2017\pi <\frac{\pi }{3}+k\pi <2017\pi$

$$\begin{gathered} \iff -2017<\frac{1}{3}+k<2017 \\ \iff \frac{-6052}{3}<k<\frac{6050}{3} \end{gathered}$$

Mà (k ∈ ℤ) nên ta có:

k ∈ {−2017; −2016; …; 2015; 2016}.

Vậy có tất cả 2017 + 2016 + 1 = 4034 nghiệm thỏa mãn.

Câu 19: Cho A = 75 + 1205 + 2008 + x, (x ∈ ℕ). Tìm điều kiện của x để $A⋮5$ .

Lời giải:

Cho A = 75 + 1205 + 2008 + x , (x ∈ ℕ).
Ta có 

Để chia hết cho 5 thì chữ số hàng đơn vị phải là 0 hoặc 5
 $\Rightarrow (2008+x)⋮5$
$\Rightarrow$ Số hàng đơn vị của 2008 + số hàng đơn vị của x phải là 0 hoặc 5
$\Rightarrow$ 8 + số hàng đơn vị của x = 0 hoặc 5
$\Rightarrow$ chữ số hàng đơn vị của x = 2 hoặc 7.
Để $A⋮5$  thì chữ số hàng đơn vị của x phải là 2 hoặc 7.

Câu 20: Viết tập hợp A là các số $x⋮5$ , thỏa mãn 124 < x < 145 bằng cách liệt kê các phần tử.

Lời giải:

Ta có các số chia hết cho 5 là các số có hàng đơn vị là 0 hoặc 5.

Tập hợp A là các số $x⋮5$ , thỏa mãn 124 < x < 145 nên ta có:

A = {125; 130; 135; 140}.

Câu 21: Tập giá trị của hàm số $y=2+\sqrt{1-{\sin }^{2}2x}$  là:
A. [1; 2];

B. [0; 2];

C. [1; 3];

D. [2; 3].

Lời giải:
Đáp án đúng là: D.

Do −1 ≤ sin 2x ≤ 1

$\Rightarrow$0 ≤ sin² 2x ≤ 1

$\iff$0 ≤ 1 – sin² 2x ≤ 1

$$\begin{gathered} \iff 0\le \sqrt{1-{\sin }^{2}2x}\le 1 \\ \iff 2\le 2+\sqrt{1-si{n}^{2}2x}\le 3 \end{gathered}$$

Vậy tập giá trị của hàm số đã cho là [2; 3].

Câu 22: Tập giá trị của hàm số $y=2{\sin }^{2}x+8\sin x+\frac{21}{4}$  là:

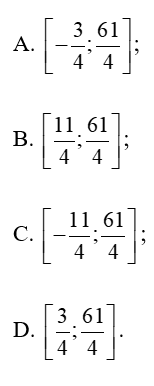
Lời giải:

Đáp án đúng là: A.

Ta có: $y=2({\sin }^{2}x+4\sin x+4)-\frac{11}{4}$

$=2{(\sin x+2)}^2-\frac{11}{4}$

Ta có: −1 ≤ sinx ≤ 1

$\iff$1 ≤ sinx + 2 ≤ 3

$\iff$1 ≤ (sinx + 2)² ≤ 9

$\iff$2 ≤ 2(sinx + 2)² ≤ 18

$\iff -\frac{3}{4}\le 2{(\sin x+2)}^2-\frac{11}{4}\le \frac{61}{4}$.

Vậy tập giá trị của hàm số đã cho là: $\left[-\frac{3}{4};\frac{61}{4}\right]$ .

Câu 23: Biến đổi biểu thức x₁ + 2x₂ = 1 và $\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{2}(x_1+x_2)$  để đưa về biểu thức có chứa tổng nghiệm x₁ + x₂ và tích nghiệm x₁x₂.

Lời giải:

Ta có:

•  $x_1+2x_2=\frac{3}{2}(x_1+x_2)-\frac{1}{2}(x_1-x_2)=1$

$\Rightarrow x_1+2x_2=\frac{3}{2}(x_1+x_2)-\frac{\sqrt{{(x_1+x_2)}^2-4x_1{x}_2}}{2}=1$

• $\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{2}(x_1+x_2)$

$\Rightarrow \frac{x_1+x_2}{x_1{x}_2}=\frac{1}{2}(x_1+x_2)$

Câu 24: Cho hàm số: $y=\frac{m}{3}{x}^3-(m-1)x^2+3(m-2)x+1$ để hàm số đạt cực đại x₁, x₂ thỏa mãn x₁ + 2x₂ = 1 thì giá trị của m bằng?

Lời giải:

Ta có: y' = mx² – 2(m – 1)x + 3(m – 2) (m ≠ 0)

Để hàm số có cực đại tại x₁ và cực tiểu tại x₂ thì phương tình

y' = mx² – 2(m – 1)x + 3(m – 2)  = 0 có 2 nghiệm phân biệt.

 = (m – 1)² – 3m(m – 2) = −2m² + 4m + 1 > 0

$\Rightarrow 1-\frac{\sqrt{6}}{2}<m<1+\frac{\sqrt{6}}{2}$ (1)

Khi đó áp dụng định lý Vi−ét, ta có:

$\left\{\begin{array}{l}{x}_1+x_2=\frac{2(m-1)}{m}\left(2\right)\\ x_1{x}_2=\frac{3(m-2)}{m}\left(3\right)\end{array}\right.$

Mặt khác theo bài cho ta có: x₁ + 2x₂ = 1 (4)

Nếu 2x₁ + x₂ = 0 (5)

Từ (4) và (5) $\Rightarrow x_1=-\frac{1}{3};x_2=\frac{2}{3}$ .

Thay vào (2) ta có: $2\frac{m-1}{m}=\frac{1}{3}\Rightarrow m=\frac{6}{5}$

Thay vào (3) ta có: $3\frac{m-2}{m}=-\frac{2}{9}\Rightarrow m=\frac{54}{9}$

Suy ra 2x₁ + x₂ ≠ 0

Khi đó nhân hai vế của (4) với 2x₁ + x₂ ta có:

(x₁ + 2x₂)(2x₁ + x₂) = 2x₁ + x₂

 2(x₁ + x₂)² + x₁x₂ = 2x₁ + x₂

Thay (2) và (3) vào ta được:

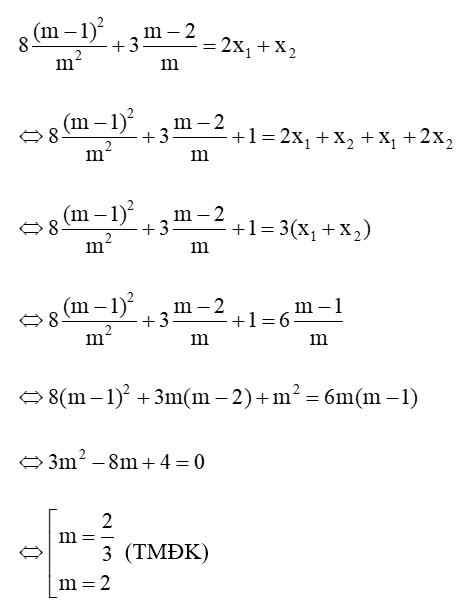
Vậy có hai giá trị m thỏa mãn yêu cầu bài toán là: $m=\frac{2}{3}$ ; m = 2.

Câu 25: Cho phương trình: x² – 2x + m = 0.

a) Tìm m để phương trình có nghiệm.

b) Chứng minh rằng với mọi m phương trình không thể có hai nghiệm cùng là số âm.

Lời giải:

a) Để phương trình có nghiêm thì: $\Delta \text{'}=1^2-m\ge 0$

1 – m ≥ 0

m ≤ 1

Vậy với m ≤ 1 thì phương trình đã cho có nghiệm.

b) Áp dụng định lý Vi−ét, ta có:

$\left\{\begin{array}{l}{x}_1+x_2=2\\ x_1{x}_2=m\end{array}\right.$

Nếu phương trình có hai nghiệm cùng là số âm thì x₁ + x₂ < 0 mà x₁ + x₂ = 2 > 0

Suy ra phương trình không thể có hai nghiệm âm.

Câu 26: Cho phương trình x² – (m + 2)x – 8 = 0 (m là tham số)

a) Giải phương trình khi m = 0.

b) Tính giá trị của m để phương trình luôn có hai nghiệm x₁; x₂ thỏa mãn

x₁(1 – x₂) + x₂(1 – x₁) = 8.

Lời giải:

a) Thay m = 0 vào phương trình ta có:

x² – (0 + 2)x – 8 = 0

x² – 2x – 8 = 0

$\Delta \text{'}=1-1.(-8)=9$

Vậy phương trình có hai nghiệm là: $x_1=1-\sqrt{9}=-2$ ; $x_2=1+\sqrt{9}=4$ .

b) Để phương trình đã cho có hai nghiệm phân biệt thì: $\Delta >0$

$\iff {(m+2)}^2-4.(-8)>0$

$\iff {(m+2)}^2+32>0$ (luôn đúng với $\forall x\in ℝ$ )

Áp dụng hệ thức Vi−ét ta có:

 $\left\{\begin{array}{l}{x}_1+x_2=m+2\\ x_1{x}_2=-8\end{array}\right.$ (*)

Lại có: x₁(1 – x₂) + x₂(1 – x₁) = 8

 x₁ – x₁x₂ + x₂ – x₁x₂ = 8

 (x₁ + x₂) – 2x₁x₂ = 8

Thay (*) vào ta có: m + 2 – 2 . (−8) = 8

⇔ m + 2 + 16 = 8

⇔ m + 18 = 8

m = −10

Vậy với m = −10 thì thỏa mãn yêu cầu bài toán.

Câu 27: Giải phương trình:

a) x² – 11x + 30 = 0.

b) x² – 10x + 21 = 0.

Lời giải:

a) x² – 11x + 30 = 0

Ta có: $\Delta$ = 11² – 4.30 = 121 – 120 = 1 > 0

Vâỵ phương trình đã cho có hai nghiệm phân biệt là:
$x_1=\frac{11-\sqrt{1}}{2}=5$; $x_2=\frac{11+\sqrt{1}}{2}=6$ .

b) x² – 10x + 21 = 0

Ta có: $\Delta \text{'}$  = 5² – 21 = 25 – 21 = 4 > 0

Vậy phương trình đã cho có hai nghiệm phân biệt là:
$x_1=5+\sqrt{4}=7$; $x_2=5-\sqrt{4}=3$ .

Câu 28: Xác định hàm số y = ax + b biết rằng đồ thị của nó đi qua hai điểm A(−1; −3) và B(0; 2).

Lời giải:

Gọi đường thẳng cần tìm là y = ax + b (d)

Vì đồ thị hàm số (d) đi qua A(−1; −3) và B(0; 2) nên tọa độ hai điểm A, B thỏa mãn phương trình đường thẳng (d).

Khi đó ta có hệ phương trình:

$\left\{\begin{array}{l}-a+b=-3\\ a.0+b=2\end{array}\right.\iff \left\{\begin{array}{l}-a+b=-3\\ b=2\end{array}\right.\iff \left\{\begin{array}{l}a=5\\ b=2\end{array}\right.$

Vậy đường thẳng cần tìm là: y = 5x + 2.

Câu 29:  

1) Xác định hàm số y = ax + b, biết rằng đồ thị hàm số đi qua hai điểm

A(2; −4) và B(−1; 5).

2) Trên hệ trục tọa độ Oxy, vẽ đồ thị hàm số y = −2x + 1.

Lời giải:

1) Gọi đường thẳng cần tìm là y = ax + b (d)

Vì đồ thị hàm số (d) đi qua A(2; −4) và B(−1; 5) nên tọa độ hai điểm A, B thỏa mãn phương trình đường thẳng (d).

Khi đó ta có hệ phương trình:

$$\begin{gathered} \left\{\begin{array}{l}2a+b=-4\\ -a+b=5\end{array}\right.\iff \left\{\begin{array}{l}2a+5+a=-4\\ b=5+a\end{array}\right. \\ \iff \left\{\begin{array}{l}3a=-9\\ b=5+a\end{array}\right.\iff \left\{\begin{array}{l}a=-3\\ b=2\end{array}\right. \end{gathered}$$

Vậy đường thẳng cần tìm là: y = −3x + 2.

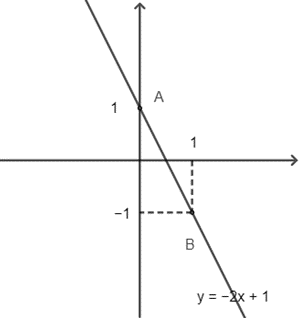
2) y = −2x+1

• Với x = 0  $\Rightarrow$ y = 1 $\Rightarrow$ A(0; 1);

• Với x = 1 $\Rightarrow$  y = −1 $\Rightarrow$ B(1; −1).

Khi đó ta có đồ thị hàm số:

Câu 30: Tính diện tích của tam giác GHK biết diện tích của một ô vuông nhỏ là 10 cm².

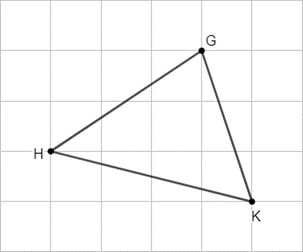
Lời giải:

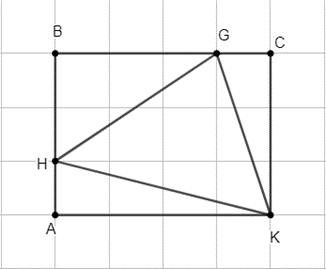
Theo bài cho ta có cạnh của mỗi hình vuông nhỏ là 10 cm.

$S_{ABCD}=S_{BGH}+S_{CGK}+S_{HAK}+S_{HGK}$

Kẻ một hình chữ nhật như hình trên ta có:

Mà: $S_{BGH}=\frac{1}{2}\mathrm{.3.2}=3$  (cm²); $S_{CGK}=\frac{1}{2}\mathrm{.1.3}=\frac{3}{2}$  (cm²);

$S_{HAK}=\frac{1}{2}\mathrm{.1.4}=2$ (cm²); S_ABCD = 4.3 = 12 (cm²).

Suy ra: $S_{HAK}=12-3-\frac{3}{2}-2=\frac{11}{2}$  (cm²).

Câu 31: Cho hình vẽ:

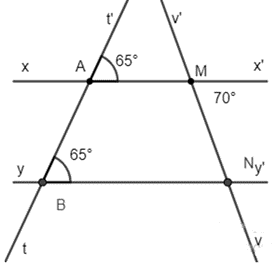
a) Giải thích tại sao xx’ // yy’.

b) Tính số đo $\widehat{MNB}$ .

Lời giải:

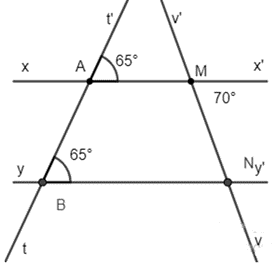
a) Ta có: $\widehat{t\text{'}AM}=\widehat{ABN}=65°$ .

Mà hai góc này ở vị trí so le trong nên suy ra xx’ // yy’.

b) Ta có: xx’ // yy’ nên $\widehat{MNB}=\widehat{x\text{'}MN}=70°$  (hai góc so le trong).

Câu 32: Tìm x, biết:

a) x² + 4 = 4x;

b) 2x² + 7x + 3 = 0.

Lời giải:

a) x² + 4 = 4x

x² + 4 – 4x = 0

x² – 2.x.2 + 2² = 0

(x – 2)² = 0

x – 2 = 0

x = 2.

Vậy x = 2.

b) 2x² + 7x + 3 = 0

2x² + x + 6x + 3 = 0

x(2x + 1) + 3(2x + 1) = 0

(2x + 1)(x + 3) = 0

$$\begin{gathered} \left[\begin{array}{l}2x+1=0\\ x+3=0\end{array}\right. \\ \left[\begin{array}{l}x=\frac{-1}{2}\\ x=-3\end{array}\right. \end{gathered}$$

Vậy $x=\left\{-\frac{1}{2};-3\right\}$ .

Câu 33: Xét dấu của các tam thức bậc hai sau:

a) x² + 8x + 16;

b) −2x² + 7x – 3.

Lời giải:

a) f(x) = x² + 8x + 16

Ta có $\Delta \text{'}$ = 4² – 1.16 = 0; hệ số a = 1 > 0 nên f(x) có nghiệm kép x = −4 và f(x) > 0 với mọi m ≠ −4.

b) f(x) = −2x² +  7x – 3

Ta có $\Delta$ = 7² – 4.(−2).(−3) = 25 > 0, hệ số a = −2 < 0 và có hai nghiệm phân biệt $x_1=\frac{1}{2}$ ; x₂ = 3.

Do đó ta có bảng xét dấu f(x):

x	$-\infty$                          $\frac{1}{2}$                        3                                      $+\infty$
f(x)	−               0             +           0                         −

Suy ra f(x) > 0 $\forall x\in \left(\frac{1}{2};3\right)$  và f(x) < 0 $\forall x\in \left(-\infty ;\frac{1}{2}\right)\cup (3;+\infty )$ .

Câu 34: Rút gọn biểu thức:

S = cos(90° − x).sin(180° − x) – sin(90° − x).cos(180° − x).

Lời giải:

Ta có: S = cos(90° − x).sin(180° − x) – sin(90° − x).cos(180° − x)

= sinx.sinx – cosx.(−cosx)

= sin²x + cos²x = 1.

Câu 35: Cho hình thang ABCD (AB // CD) có BC = 15 cm. Điểm E thuộc cạnh AD sao cho $\frac{AE}{AD}=\frac{1}{3}$ . Qua E kẻ đường thẳng song song với CD cắt BC tại F. Tính độ dài BF.

A. 10 cm;

B. 5 cm;

C. 11 cm;

D. 7 cm.

Lời giải:

Đáp án đúng là: B

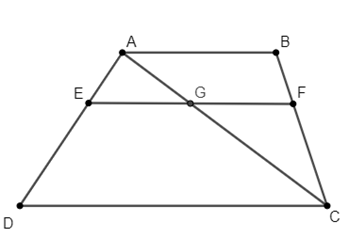
Gọi I là giao điểm của AC và EF.

Xét tam giác ACB có IF // AB nên theo định lý Ta−lét, ta có:

$\frac{BF}{BC}=\frac{AI}{AD}=\frac{1}{3}$ nên $BF=\frac{1}{3}BC=\frac{1}{3}.15=5$  (cm).

Câu 36: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M là trung điểm của SB, G là trọng tâm tam giác SAD. Tìm giao tuyến mp(SGM) với  mp(ABCD). Tìm giao điểm I của GM và mp(ABCD).

Lời giải:

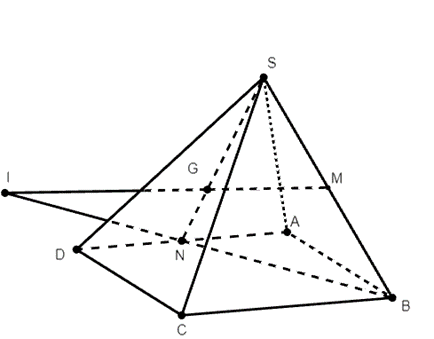
Trong mp(SAD), gọi N là giao điểm của  SG và AD

$\Rightarrow \left\{\begin{array}{l}N\in SG\subset \left(SGM\right)\\ N\in AD\subset \left(ABCD\right)\end{array}\right.$

$\Rightarrow$N ∈ (SMG) ∩ (ABCD) (1)

Mà $\left\{\begin{array}{l}B\in SM\subset \left(SGM\right)\\ B\in \left(ABCD\right)\end{array}\right.\Rightarrow$ B ∈ (SMG) ∩ (ABCD) (2)

Từ (1) và (2) suy ra (SGM) ∩ (ABCD) = BN.

Trong mp(SBN), gọi I là giao điểm của GM và BN.

$\Rightarrow \left\{\begin{array}{l}I\in GM\\ I\in BN\subset \left(ABCD\right)\end{array}\right.$

$\Rightarrow$I = GM ∩ (ABCD).

Câu 37: Cho hình chóp S.ABCD, đáy ABCD là tứ giác có các cạnh đối diện không song song. Lấy điểm M thuộc miền trong tam giác SCD. Tìm giao tuyến của hai mặt phẳng (ABM) và (SCD).

Lời giải:

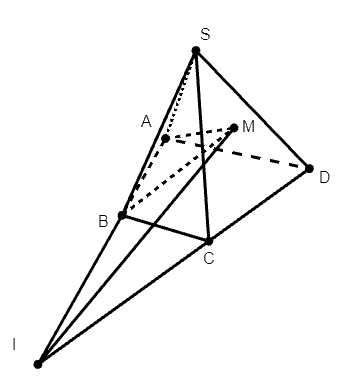
Trong mp(ABCD) gọi I = AB ∩ CD.

Mp(AMB), mp(SCD) có điểm chung là M và I.

Nên suy ra MI là giao tuyến của hai mặt phẳng trên.

Câu 38: Cho tam giác ABC vuông tại A, đường cao AH (H ∈ BC). Biết độ dài đoạn BC = 10 cm và $\sin \widehat{ABC}=\frac{4}{5}$ . Tính độ dài các đoạn AC và BH.

Lời giải:

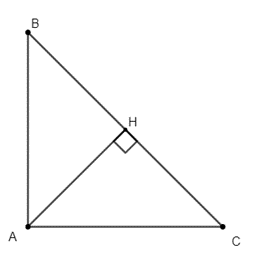
Ta thấy $\Delta ABC$ vuông tại A nên:

$\sin \widehat{ABC}=\frac{AC}{BC}\Rightarrow AC=BC.\sin \widehat{ABC}=10.\frac{4}{5}=8$ (cm)

Áp dụng hệ thức lượng trong tam giác vuông, ta có:

 AC² = CH. BC

$\Rightarrow CH=\frac{A{C}^2}{BC}=\frac{8^2}{10}=\mathrm{6,4}$ (cm)

$\Rightarrow$ BH = 10 – 6,4 = 3,6 (cm).

Câu 39: Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 10 cm và $\sin \widehat{ACB}=\frac{3}{5}$ . Tính độ dài các đoạn AB, AC và AH.

Lời giải:

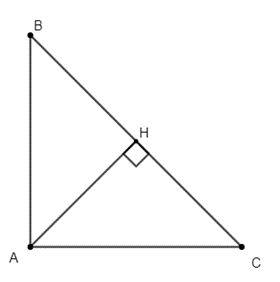
Xét $\Delta ABC$  vuông tại A, ta có:

$\sin \widehat{ACB}=\frac{AB}{BC}\Rightarrow AB=BC.\sin \widehat{ACB}=10.\frac{3}{5}=6$ (cm)

Áp dụng định lý Py−ta−go, ta có:

AB² + AC² = BC²

$\Rightarrow AC=\sqrt{B{C}^2-A{B}^2}=\sqrt{{10}^2-6^2}=8$ (cm).

Áp dụng hệ thức lượng trong tam giác vuông, ta có:

AH.BC = AB.AC

$\Rightarrow AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=\mathrm{4,8}$ (cm)

Vậy AB = 6 cm, AC = 8 cm, AH = 4,8 cm.

Câu 40: Cho tam giác ABC vuông tại A, AB = 3 cm, BC = 5 cm. Độ dài cạnh AC là:

A. 3 cm;

B. 4 cm;

C. 5 cm;

D. 6 cm.

Lời giải:

Đáp án đúng là: B

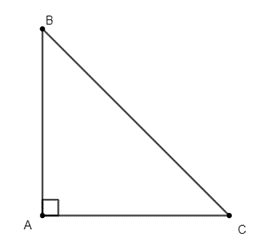
Áp dụng định lý Py−ta−go, ta có:

AB² + AC² = BC²

AC² = BC² – AB² = 5² – 3² = 16

AC = 4 cm.

Vậy AC = 4 cm.

Câu 41: Có bao nhiêu số có 3 chữ số chia hết cho 9 được lập từ các chữ số 1, 3, 5, và 7 biết rằng mỗi chữ số được phép lặp lại?

Lời giải:

Ta có: số chia hết cho 9 là số có tổng các chữ số là một số chia hết cho 9.

Khi đó ta có các số sau chia hết cho 9: 117; 135; 153; 315; 333; 351; 513; 531; 711.

Vậy có 9 số thỏa mãn yêu cầu bài toán.

Câu 42: Cho 5 số 5; 2; 7; 3; 9. Có bao nhiêu số tự nhiên có ba chữ số và chia hết cho 9 được lập từ các số trên mà các chữ số không lặp lại.

A. 6;

B. 4;

C. 5;

D. 2.

Lời giải:

Đáp án đúng là: A

Sử dụng dấu hiệu chia hết cho 9: Các số có tổng chia hết cho 9 thì chia hết cho 9.

Trong 5 số: 5; 2; 7; 3; 9 chỉ có 9 + 2 + 7 = 18 mà 18 ⋮ 9 .

Do đó các số cần tìm được lập bởi ba số 9, 2, 7, chúng là 927; 972; 279; 297; 729; 792.

Vậy ta lập được 6 số thỏa mãn.

Câu 43: Lan lấy một số chia cho 9 dư 5. Hỏi Lan lấy số đó chia 3 dư mấy?

Lời giải:

Vì số cần tìm là một số chia hết cho 9 dư 5 nên ta có:

a = 9k + 5 = 3.3k + 3 + 2 = 3(3k + 1) + 2

Suy ra khi chia số a cho 3 ta sẽ được 3k + 1 và dư 2.

Câu 44: Cho biểu thức $A=1:\left(\frac{x+2\sqrt{x}-2}{x\sqrt{x}+1}-\frac{\sqrt{x}-1}{x-\sqrt{x}+1}+\frac{1}{\sqrt{x}+1}\right)$ .

a) Rút gọn A.

b) Tính giá trị của A nếu $x=7-4\sqrt{3}$ .

Lời giải:

a)

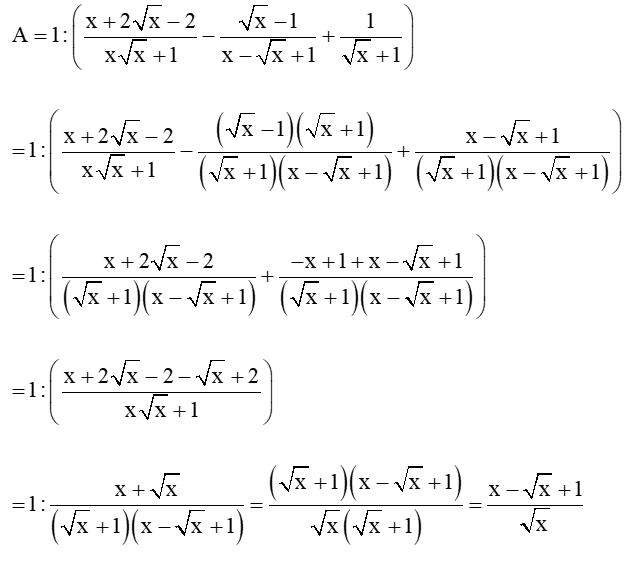
b) $x=7-4\sqrt{3}=4-\mathrm{2.2.}\sqrt{3}+3={\left(2-\sqrt{3}\right)}^2$

Thay vào A ta được:

$$\begin{gathered} A=\frac{7-4\sqrt{3}-\sqrt{{\left(2-\sqrt{3}\right)}^2}+1}{\sqrt{{\left(2-\sqrt{3}\right)}^2}} \\ =\frac{7-4\sqrt{3}-\left(2-\sqrt{3}\right)+1}{2-\sqrt{3}} \\ =\frac{6-3\sqrt{3}}{2-\sqrt{3}}=3 \end{gathered}$$

Câu 45: Tìm tính chất tam giác ABC biết rằng: $BC=2AC.\cos \widehat{C}$ .

Lời giải:

Theo định lý cosin ta có:

$$\begin{gathered} A{B}^2=A{C}^2+B{C}^2-2AC.BC.\cos \widehat{C} \\ =A{C}^2+\left(2AC.\cos \widehat{C}\right)-2AC.2AC.\cos \widehat{C}.\cos \widehat{C} \\ =A{C}^2\left(1+4{\cos }^2\widehat{C}-4{\cos }^2\widehat{C}\right)=A{C}^2 \\ \Rightarrow AB = AC \end{gathered}$$

Suy ra tam giác ABC là tam giác cân.

Câu 46: Cho tập hợp A = [−5; 3). Tập hợp C_RA là:

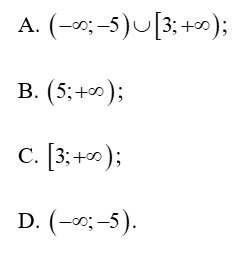
Lời giải:
Đáp án đúng là: A

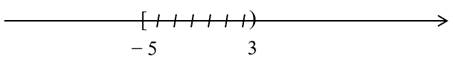
A = [−5; 3) $\Rightarrow C_{R}A=\left(-\infty ;-5\right)\cup \left[3;+\infty \right)$ .

Câu 47: Ước của 240 là:

A. 18;

B. 16;

C. 20;

D. 22.

Lời giải:

Ta có: 240 = 2⁴.3.5

Ta có: A = x^m.yⁿ…z^p

Thì số ước nguyên tính bằng công thức: 2(m + 1)(n + 1)…(p + 1).

Nên 240 có số ước nguyên là: (4 + 1).(1 + 1).(1 + 1) = 20 (ước nguyên dương).