Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 20)

Câu 1: Giải phương trình sinx + cosx = cos2x.

Lời giải:

Ta có

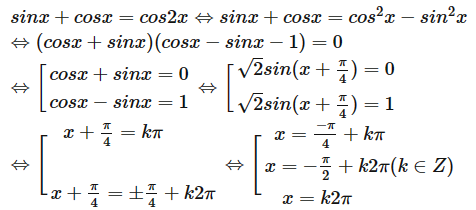
Vậy phương trình có nghiệm $x=\frac{-\pi }{4}+k\pi$ , $x=\frac{-\pi }{2}+k2\pi$ , x = k2π (k ∈ ℤ).

Câu 2: Cách đây vài năm, ngày 20 tháng 3 là Chủ nhật. Hỏi ngày 20 tháng 11 năm đó là ngày thứ mấy? 

Lời giải:

Từ 20/3 đến 20/11 trong 1 năm có số ngày là:

365 – 10 – 31 – 31 – 28 –  20 = 245 (ngày)

Ta có:

245 : 7 = 35

Vậy ngày 20/11 năm đó cũng là ngày Chủ nhật.

Câu 3: Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?

A. M là hình chiếu của A trên BC.

B. M là trung điểm của BC.

C. M trùng B.

D. Đáp án khác.

Lời giải:

Đáp án đúng là: A

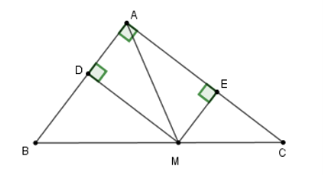
Xét tứ giác ADME có $\widehat{DA\text{E}}=\widehat{A\text{E}M}=\widehat{A\text{D}M}=90°$

Suy ra ADME là hình chữ nhật

Do đó AM = DE

Để DE nhỏ nhất thì AM nhỏ nhất

Khi đó M là hình chiếu của A trên BC

Vậy ta chọn đáp án A.

Câu 4: Một ô tô đi từ Hà Nội lúc 8 giờ sáng, dự kiến đến Hải Phòng vào lúc 10 giờ 30 phút. Nhưng mỗi giờ ô tô đã đi chậm hơn so với dự kiến là 10km nên mãi đến 11 giờ 20 phút xe mới tới Hải Phòng. Tính quãng đường Hà Nội – Hải Phòng.

Lời giải:

Gọi x (km) là quãng đường Hà Nội – Hải Phòng. Điều kiện: x > 0

Thời gian dự định đi:

10 giờ 30 phút – 8 giờ = 2 giờ 30 phút = $\frac{5}{2}$  giờ

Thời gian thực tế đi:

11 giờ 20 phút – 8 giờ = 3 giờ 20 phút = $\frac{10}{3}$  giờ.

Vận tốc dự định đi là $x:\frac{5}{2}=\frac{2x}{5}$  (km/h).

Vận tốc thực tế đi là $x:\frac{10}{3}=\frac{3x}{10}$  (km/h).

Vận tốc thực tế đi chậm hơn vận tộc dự định đi 10 km/h nên ta có phương trình:

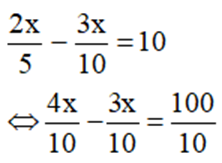
Suy ra x = 100 (thỏa mãn)

Vậy quãng đường Hà Nội – Hải Phòng dài 100 km.

Câu 5: Phép quay tâm I(4; – 3) góc quay 180° biến đường thẳng d: x + y – 5 = 0 thành đường thẳng có phương trình:

A. x – y + 3 = 0;

B. x + y + 5 = 0;

C. x + y + 3 = 0;

D. x + y – 3 = 0.

Lời giải:

Đáp án đúng là: C

Biểu thức tọa độ của phép quay tâm I(x₀; y₀), góc quay φ là

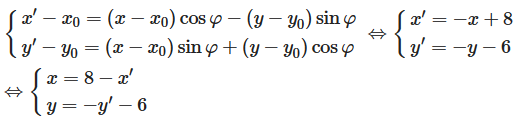
Thay vào phương trình đường thẳng d ta được:

Vậy ta chọn đáp án C.

Câu 6: Một tam giác có độ dài 3 cạnh là 13, 14, 15. Tính diện tích của tam giác đó.

Lời giải:

Nửa chu vi tam giác đó là

p = (13 + 14 + 15) : 2 = 21

Diện tích tam giác đó là

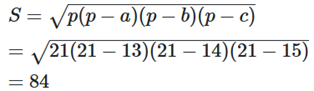
Vậy diện tích tam giác đó bằng 84.

Câu 7: Tìm số lớn nhất có 3 chữ số biết, khi chia cho 75 thì thương và số dư bằng nhau.

Lời giải:

Gọi số cần tìm là abc (a ≠ 0 ; a, b, c là các chữ số)

Gọi k là thương hay số dư với k ∈ ℕ*

Ta có  abc : 75 = k dư k

Hay abc = 75k + k

Suy ra abc = 76k

Vì abc lớn nhất nên 76k lớn nhất có 3 chữ số, 1000 : 75 = 13,333

Suy ra k = 13

Khi đó  abc = 76k = 988

Vậy số cần tìm là 988.

Câu 8: Tìm số tự nhiên x biết: x chia hết cho 14 và 140 < x < 156.

Lời giải:

Vì x ⋮ 14 (x ∈ ℕ)

Nên x ∈ B(14)

Suy ra x ∈ {0; 14; 28; 42; 56; 70; 84; 98; 112; 126; 140; 154; 168; ...}

Mà 140 < x < 156

Suy ra x = 154

Vậy x = 154.

Câu 9: Trong kì thi đánh giá năng lực lần I năm học 2018 – 2019 của trường THPT Triệu Quang Phục, kết quả có 86 thí sinh đạt điểm giỏi môn Toán, 61 thí sinh đạt điểm giỏi môn Vật Lí và 76 thí sinh đạt điểm giỏi môn Hóa Học, 45 thí sinh đạt điểm giỏi cả hai môn Toán và Vật Lí, 21 thí sinh đạt điểm giỏi cả hai môn Vật Lí và Hóa Học, 32 thí sinh đạt điểm giỏi cả hai môn Toán và Hóa Học, 18 thí sinh đạt điểm giỏi cả ba môn Toán, Vật Lí và Hóa Học. Có 782 thí sinh mà cả ba môn đều không điểm giỏi. Hỏi trường THPT Triệu Quang Phục có bao nhiêu thí sinh tham dự kì thi đánh giá năng lực lần I năm học 2018 –2019?

A. 920;

B. 912;

C. 925;

D. 889.

Lời giải:

Đáp án đúng là C

Ta biểu diễn các tập hợp như trong biểu đồ: Thí sinh đạt điểm giỏi môn Toán được biểu diễn màu trắng, Thí sinh đạt điểm giỏi môn Vật Lý được biểu diễn màu xanh. Thí sinh đạt điểm giỏi môn Hóa được biểu diễn màu hồng. Mỗi tập hợp nhỏ bên trong gọi tên như trong hình.

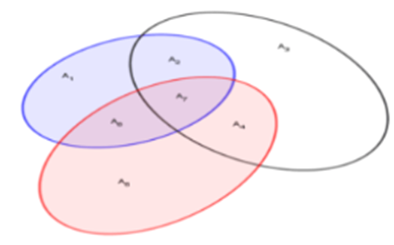
Ta có số thí sinh đạt điểm giỏi cả ba môn Toán, Vật Lí và Hóa Học là

            n(A₇) = 18

45 thí sinh đạt điểm giỏi cả hai môn Toán và Vật Lí ta được 

            n(A₇) + n(A₂) = 45

32 thí sinh đạt điểm giỏi cả hai môn Toán và Hóa Học ta được 

            n(A₇) + n(A₄) = 32

21 thí sinh đạt điểm giỏi cả hai môn Vật Lí và Hóa Học ta được 

            n(A₇) + n(A₆) = 21

Số thí sinh đạt điểm giỏi chỉ hai môn là

n(A₆) + n(A₄) + n(A₂) = n(A₇) + n(A₂) + n(A₇) + n(A₄) + n(A₇) + n(A₆) – 3n(A₇)

= 45 + 32 + 21 – 3 . 18 = 44

86 thí sinh đạt điểm giỏi môn Toán ta được 

            n(A₃) + n(A₄) + n(A₂) + n(A₇) = 86

61 thí sinh đạt điểm giỏi môn Vật Lí ta được 

            n(A₁) + n(A₆) + n(A₂) + n(A₇) = 61

76 thí sinh đạt điểm giỏi môn Hóa Học ta được 

            n(A₄) + n(A₆) + n(A₅) + n(A₇) = 76

Số thí sinh đạt điểm giỏi chỉ một môn là

    n(A₁) + n(A₃) + n(A₅)

= 86 + 61 + 76 – 3n(A₇) – 2[n(A₆) + n(A₄) + n(A₂)]

= 86 + 61 + 76 – 3 . 18 – 2 . 44 = 81

Số thí sinh đạt điểm giỏi gồm

n(A₁) + n(A₂) + n(A₃) + n(A₄) + n(A₅) + n(A₆) + n(A₇)

= [n(A₁) + n(A₃) + n(A₅)] + [n(A₆) + n(A₄) + n(A₂)] + n(A₇)

= 81 + 44 + 18 = 143

Trường THPT Triệu Quang Phục có số thí sinh tham dự kì thi đánh giá năng lực lần I
năm học 2018 – 2019 bao gồm số thí sinh đạt điểm giỏi và số thí sinh không đạt điểm giỏi nên bằng: 782 + 143 = 925 (thí sinh)

Vậy ta chọn đáp án C.

Câu 10: Tìm các số tự nhiên x biết

a) x thuộc B(8) và x ≥ 30.

b) x chia hết cho 9 và x < 40.

c) x chia hết cho 6, x chia hết cho 21 và x < 200.

d) x chia hết cho 5, x chia hết 7, x chia hết cho 8 và ≥ 500.

e) 150 chia hết cho x , 120 chia hết cho x và x lớn nhất.

Lời giải:

a) x thuộc B(8) và x ≥ 30

Ta có: x ∈ B(8) = {0; 8; 16; 24; 32; 40; 48;...}

Mà x ≥ 30

Suy ra x = {32; 40; 48; ...}

b) x chia hết cho 9 và x < 40

Ta có x ⋮ 9

Nên x ∈ B(9) = {0; 9; 18; 27; 36; 45; 54;...}

Mà x < 40

Suy ra x = {0; 9; 18; 27; 36}

c) x chia hết cho 6 , x chia hết cho 21 và x < 200

Do x chia hết cho 6, 21 nên x ∈ BC(6; 21)

Ta có 6 = 2 x 3, 21 = 3 x 7 

Suy ra BCNN(6; 21) = 2 x 3 x 7 = 42

Do đó BC(6; 21) = {0; 42; 84; 126; 168; 210; 252; ...}

Mà x < 200

Suy ra x = {0; 42; 84; 126; 168}

d) x chia hết cho 5, x chia hết 7, x chia hết cho 8 và ≥ 500

Do x chia hết cho 5, 7, 8 nên x ∈ BC(5; 7; 8)

Ta có: 5 = 5; 7 = 7; 8 = 2³ 

Suy ra BCNN(5; 7; 8)= 2³ x 5 x 7 = 280

Do đó BC(5; 7; 8) = {0; 280; 560; 840; 1120;...}

Mà x ≥ 500

Suy ra x={560; 840; 1120;...}

e) 150 chia hết cho x , 120 chia hết cho x và x lớn nhất

Ta có: 150 ⋮ x; 120 ⋮ x nên x ∈ ƯC(150; 120)

Phân tích: 150 = 2 x 3 x 5² ; 120 = 2³ x 3 x 5

Suy ra ƯC(150; 120) = {2; 3; 5; 6; 10; 15; 30}

Mà x lớn nhất suy ra x = 30

Câu 11: Tìm x, biết: x² – 9 = 0.

Lời giải:

Ta có x² – 9 = 0

⇔ (x – 3)(x + 3) = 0

⇔ $\left[\begin{array}{l}x-3=0\\ x+3=0\end{array}\right.\iff \left[\begin{array}{l}x=3\\ x=-3\end{array}\right.$

Vậy x = 3 hoặc x = – 3.

Câu 12: Giải phương trình: 2sin²x – sinx – 1 = 0.

Lời giải:

Ta có 2sin² x – sinx – 1 = 0

⇔ (2sinx + 1)(sinx – 1) = 0

$$\begin{gathered} \iff \left[\begin{array}{l}\mathrm{s}\text{inx}=1\\ \mathrm{s}\text{inx}=\frac{-1}{2}\end{array}\right. \\ \iff \left[\begin{array}{l}\text{x}=\frac{\pi }{2}+k2\pi \\ \text{x}=\frac{-\pi }{6}+k2\pi \\ x=\frac{7\pi }{6}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right) \end{gathered}$$

Vậy phương trình có nghiệm $x=\frac{\pi }{2}+k2\pi$ , $x=\frac{-\pi }{6}+k2\pi$ ,  $x=\frac{7\pi }{6}+k2\pi \left(k\in \mathbb{Z}\right)$ .

Câu 13: Phương trình sin2x = m có nghiệm nếu

A. – 1 ≤ m ≤ 1;

B. – 2 ≤ m ≤ 2;

C. 0 ≤ m ≤ 1;

D. – 1 < m < 1.

Lời giải:

Đáp án đúng là A

Vì – 1 ≤ sin2x ≤ 1 nên phương trình có nghiệm khi – 1 ≤ m ≤ 1

Vậy ta chọn đáp án A.

Câu 14: Chứng minh rằng trong tam giác ABC ta có các hệ thức:

sin A = sinB.cosC + sinC.cosB.

Lời giải:

Theo định lý sin ta có

$\frac{a}{\sin \text{A}}=\frac{b}{\sin B}=\frac{c}{\sin C}=2\text{R}$

Suy ra a = 2R . sinA, b = 2R . sinB, c = 2R . sinC

Ta có a² = a²

$\iff a^2=\frac{a^2+b^2-c^2}{2}+\frac{a^2+c^2-b^2}{2}$

⇔ a² = ab . cosC + ac . cosB

⇔ a = bcosC + ccosB

⇔ 2R . sinA = 2R . sinBcosC + 2R . sinC cosB

⇔ sin A = sinB.cosC + sinC.cosB

Vậy sin A = sinB.cosC + sinC.cosB.

Câu 15: Rút gọn biểu thức $\text{A}=\sqrt{x+\sqrt{2\text{x}-1}}-\sqrt{x-\sqrt{2\text{x}-1}}$ .

Lời giải:

Ta có:

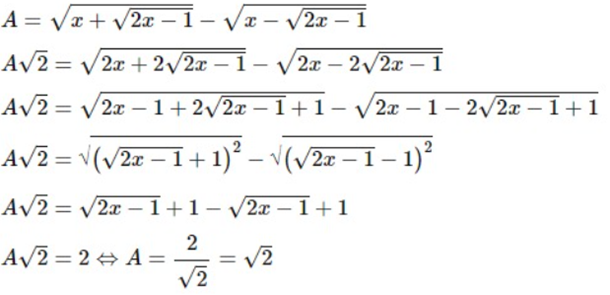
Vậy A = $\sqrt{2}$ .

Câu 16: Cho tứ diện S.ABC. Gọi O là điểm thuộc miền trong của tam giác ABC. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh SA, SC sao cho MN không song song với AC. Tìm thiết diện do (MNO) cắt tứ diện S.ABC.

Lời giải:

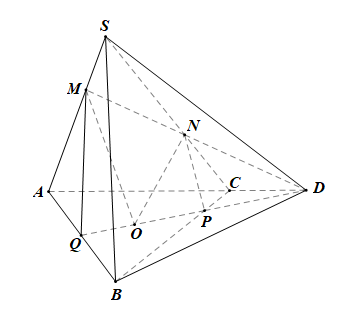
• (OMN) ∩ (SAC) = MN;

• Trong mp(SAC), gọi D = MN ∩ AC.

Trong mp(ABC), gọi P = BC ∩ OD.

Khi đó P ∈ OD ⊂ (OMN) và P ∈ (SBC), suy ra P = (OMN) ∩ (SBC)

Mà N = (OMN) ∩ (SBC), suy ra (OMN) ∩ (SBC) = NP.

• Do P ∈ BC, BC ⊂ (ABC) nên P ∈ (ABC)

Suy ra P = (OMN) ∩ (ABC)

Lại có O = (OMN) ∩ (ABC)

Suy ra (OMN) ∩ (ABC) = OP.

• Trong mp(ABC), gọi Q = OP ∩ AB.

Khi đó Q ∈ (OMN) và Q ∈ (ABC) nên Q = (OMN) ∩ (ABC)

Lại có M ∈ (OMN) và M ∈ (ABC) nên M = (OMN) ∩ (ABC)

Suy ra (OMN) ∩ (ABC) = QM.

Vậy thiết diện do (MNO) cắt tứ diện S.ABC là (MNPQ).

Câu 17: Hãy phân tích các đa thức sau thành nhân tử

a) 6x² – 3xy;

b) x² – y² – 6x + 9.

Lời giải:

a) 6x² – 3xy = 3x(2x – y)

b) x² – y² – 6x + 9 = (x² – 6x + 9) – y²

= (x – 3)² – y²

= (x – 3 – y)(x – 3 + y)

Câu 18: Rút gọn

A = $\sqrt{{\left(\sqrt{5}-2\right)}^2}+\sqrt{{\left(\sqrt{5}-3\right)}^2}$ ;

B = $\sqrt{7-2\sqrt{10}}-\sqrt{6-2\sqrt{5}}$ ;

C = $\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4-\sqrt{15}}$ .

Lời giải:

Ta có

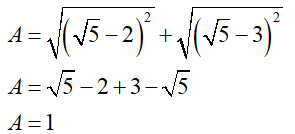
Ta có

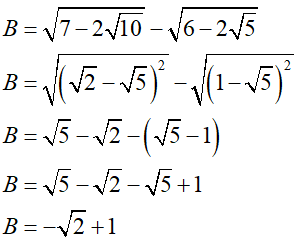
Ta có

Câu 19: Tính nhanh 73² – 27².

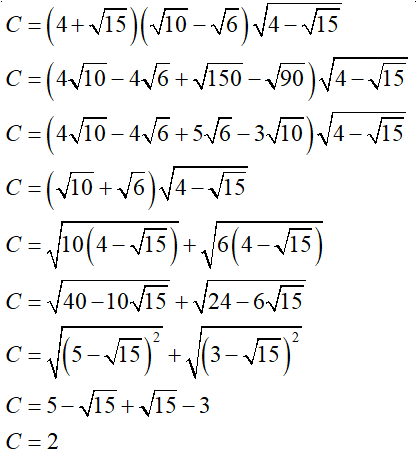
Lời giải:

73² – 27²

= (73 + 27)(73 – 27)

= 100 . 46

= 4 600

Vậy 73² – 27² = 4 600.

Câu 20: Giải phương trình (2x + 1)⁴ = (2x + 1)⁶

Lời giải:

Ta có:

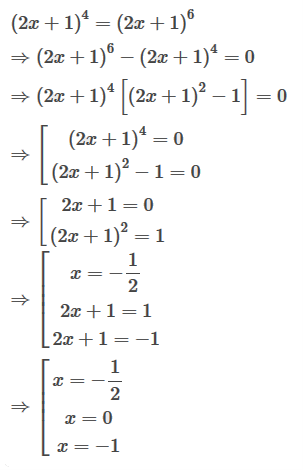
Vậy $\text{x}\in \left\{-1;\frac{-1}{2};0\right\}$ .

Câu 21: Giải phương trình (2x – 1)⁴ = (2x – 1)⁶.

Lời giải:

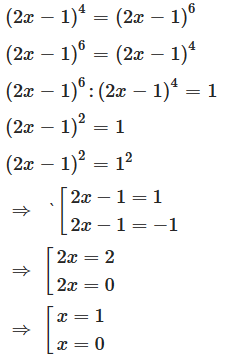
Vậy x ∈ {0; 1}.

Câu 22: Phương trình sin⁶ x + cos⁶ x + 3sinxcosx – m + 2 = 0 có nghiệm khi m thuộc [a; b] thì tích a . b bằng bao nhiêu?

Lời giải:

Ta có

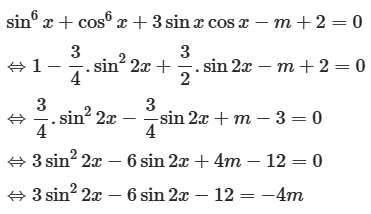
Đặt sin² 2x = t ( t ∈ [– 1; 1])

Suy ta 3t² – 6t – 12 = – 4m                            (*)

Lập bảng biến thiên hàm số f(t) = 3t² – 6t – 12 ta có

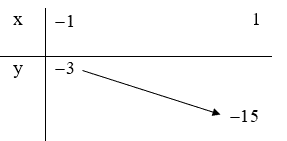
Suy ra phương trình (*) có nghiệm khi

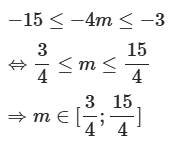
Khi đó $a=\frac{3}{4},b=\frac{15}{4}$

Ta có: $ab=\frac{3}{4}.\frac{15}{4}=\frac{45}{16}$

Vậy $ab=\frac{45}{16}$ .

Câu 23: Có bao nhiêu giá trị nguyên của tham số m để phương trình

 $si{n}^{6}x+co{s}^{6}x+3sinxcosx–\frac{m}{4}+2=0$ có nghiệm thực?

A. 13;

B. 15;

C. 7;

D. 9.

Lời giải:

Đáp án đúng là: A

Ta có

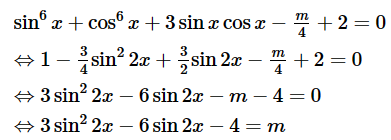
Đặt sin 2x = t (với t ∈ [– 1; 1])

Suy ta 3t² – 6t – 4 = m                        

Xét sự biến thiên hàm số y = f(t) = 3t² – 6t – 4 trong [– 1; 1] có

y’ = 6t – 6

y’ = 0 ⟺ 6t – 6 = 0 ⟺ t = 1

Ta có f(1) = – 7 và f(– 1) = 5

Suy ra phương trình có nghiệm khi – 7 ≤ m ≤ 5

Do đó các giá trị nguyên của m là {– 7; – 6; – 5; – 4; – 3; – 2; – 1; 0; 1; 2; 3; 4; 5}

Vậy ta chọn đáp án A.

Câu 24: Phân tích đa thức thành nhân tử

a) (1 + x²)² – 4x(1 – x²);

b) (x² – 8)² + 36.

Lời giải:

a) (1 + x²)² – 4x(1 – x²)

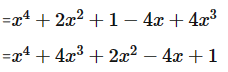
= (x² + 2x – 1)²

b) (x² – 8)² + 36 = x⁴ – 16x² + 64 + 36 = x⁴ – 16x² + 100

= x⁴ + 20x² + 100 – 36x²

= (x² + 10)² – 36x²

= (x² + 10 – 6x)(x² + 10 + 6x).

Câu 25: Phân tích đa thức thành nhân tử: 3x² – 22xy – 4x + 8y + 7y² + 1.

Lời giải:

Ta có:

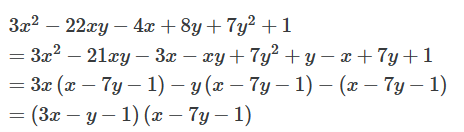
Câu 26: Cho tam giác ABC vuông tại A, biết AC = 10 cm, $\widehat{C}=30°$ . Tính độ dài AB, CB.

Lời giải:

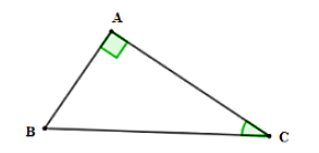
Xét tam giác ABC vuông tại A có

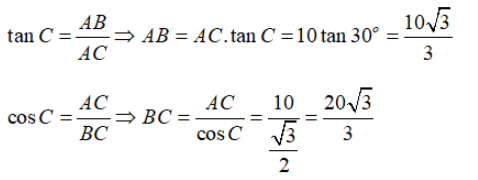
Vậy $AB=\frac{10\sqrt{3}}{3}\left(cm\right),BC=\frac{20\sqrt{3}}{3}\left(cm\right)$ .

Câu 27: Có hàm số nào vừa chẵn, vừa lẻ không? Cho ví dụ.

Lời giải:

Có hàm số vừa chẵn vừa lẻ

Vì dụ hàm số y = f(x) = 0

Giải thích:

f(x) là hàm số chẵn khi f(– x) = f(x)

f(x) là hàm số lẻ khi f(– x) = – f(x)

Mà f(x) là hàm số vừa chẵn vừa lẻ

Suy ra f(x) = – f(x)

Hay f(x) = 0.

Câu 28: Một người mua 5 m vải hết 100 000 đồng. Hỏi người đó mua 7,5 m vải cùng loại thì phải trả bao nhiêu tiền?

Lời giải:

Mua 1 mét vải phải trả số tiền là:

100 000 : 5 = 20 000 ( đồng )

Mua 7,5 mét vải phải trả số tiền là:

20 000 × 7,5 = 150 000 ( đồng )

Vậy người đó mua 7,5 m vải cùng loại thì phải trả 150 000 đồng.

Câu 29: Một hình chữ nhật có chiều dài gấp đôi chiều rộng. Tính chu vi hình chữ nhật đó, biết diện tích của nó là 32 cm².

Lời giải:

Chia đôi nình chữ nhật theo chiều dài, ta được hai hình vuông có diện tích bằng nhau, cạnh hình vuông đúng bằng chiều rộng hình chữ nhật

Diện tích mỗi hình vuông mới là: 32 : 2 = 16 m²

Cạnh hình vuông hay chiều rộng hình chữ nhật là: 4 m.

Chiều dài hình chữ nhật là: 4 × 2 = 8 m.

Chu vi hình chữ nhật là: 24 m.

Vậy chu vi hình chữ nhật đó là 24 m.

Câu 30: Giải phương trình sau: cotx = 0

Lời giải:

Điều kiện xác định: x ≠ kπ, k ∈ ℤ

Ta có cotx = 0

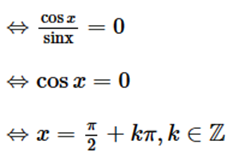
Vậy nghiệm của phương trình là $x=\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ .

Câu 31: Cho hình chữ nhật ABCD. Vẽ điểm E đối xứng với B qua điểm C; vẽ  F đối xứng với điểm D qua C.

a) Chứng minh tứ giác BDEF là hình thoi.

b) Chứng minh AC = DE.

c) Gọi H là trung điểm của CD, K là trung điểm của EF. Chứng minh HK // AF.

d) Biết diện tích tam giác AEF bằng 30 cm². Tính diện tích hình chữ nhật ABCD?

Lời giải:

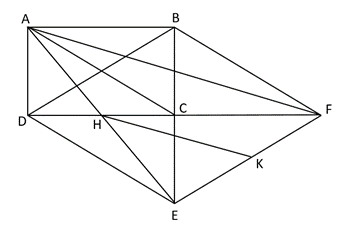
a) Xét tứ giác BDEF có:

C là trung điểm BF (E điểm đối xứng của B qua C)

C là trung điểm DF (F điểm đối xứng của D qua C)

Do đó tứ giác BDEF là hình bình hành

Mặc khác ABCD là hình chữ nhật nên BE ⊥ DF tại C

Vậy tứ giá BDEF là hình thoi.

b) Ta có: ABCD là hình chữ nhật có AC = BD;

BDEF là hình thoi (câu a) có BD = DE

Do đó AC = DE.

c) Ta có: ABCD là hình chữ nhật có AD = BC;

Mà BC = CE (E điểm đối xúng B qua C).

Do đó AD = CE.

Xét tứ giác ADEC có:

AC = DE (câu b)

AD = CE (cmt)

Do đó ADEC là hình hình hành.

Mà H là trung điểm cua CD nên H cũng là trung điểm của AE.

Xét ∆AEF có:

H là trng điểm của AE (cmt);

K là trung điểm của EF

⇒ HK là đường trung bình của ∆AEF nên HK // AF

d)  Ta có: S_∆AEF = S_∆AHF + S_∆HEF

$$\begin{gathered} \iff 30=\frac{1}{2}AD.HF+\frac{1}{2}CE.HF \\ \iff \frac{1}{2}HF\left(AD+CE\right)=30 \\ \iff \frac{1}{2}.\frac{3}{2}CD.\left(AD+AD\right)=30 \\ \iff \frac{3}{2}CD.AD=30 \\ \iff \frac{3}{2}.S_{ABCD}=30 \end{gathered}$$

$\Rightarrow S_{ABCD}=30.\frac{2}{3}=60$ (cm²).

Câu 32: Cho tam giác ABC với A = (2; 3), B = (–1; 4), C = (1; 1). Tìm các tọa độ của đỉnh D của:

a) Hình bình hành ABCD;

b) Hình bình hành ACBD.

Lời giải:

a) Gọi D (a ; b) là đỉnh của hình bình hành ABCD,

Ta có: $\overrightarrow{BC}=\left(1+1;1-4\right)=\left(2;-3\right)$ ; $\overrightarrow{AD}=\left(a-2;b-3\right)$ .

Vì ABCD là hình bình hành nên $\overrightarrow{BC}=\overrightarrow{AD}$

$\Rightarrow \left\{\begin{array}{c}2=a-2\\ -3=b-3\end{array}\right.\iff \left\{\begin{array}{c}a=4\\ b=0\end{array}\right.$

⟹ D(4; 0);

b) Ta có: $\overrightarrow{DA}=\left(2-a;3-b\right)$ .

Vì ACBD là hình bình hành nên $\overrightarrow{BC}=\overrightarrow{DA}$

$\Rightarrow \left\{\begin{array}{c}2=2-a\\ -3=3-b\end{array}\right.\iff \left\{\begin{array}{c}a=0\\ b=6\end{array}\right.$

⇒ D (0; 6).

Câu 33: Tìm A ∪ B ∪ C, A ∩ B ∩ C với:

a) A = [1 ; 4], B = (2; 6), C = (1; 2);

b) A = [ 0; 4], B = (1; 5), C = (–3; 1];

c) A = ( –5; 1], B = [3; +∞), C = ( –∞; – 2).

Lời giải:

a) A ∪ B ∪ C = [1; 6);

A ∩ B ∩ C = ∅;

b) A ∪ B ∪ C = (–3; 5);

A ∩ B ∩ C = ∅;

c) A ∪ B ∪ C = (–∞; 1] ∪ [3; +∞)

A ∩ B ∩ C = ∅.

Câu 34: Rút gọn và tính giá trị của các biểu thức sau:

a) A = (3x + 5)(2x – 1) – (1 – 4x)(3x + 2) tại $\left|x\right|=2$ ;

b) B = (2x + y)(2x – y) + xy(x – y) – xy(x + y) tại x = 0; y = –1.

Lời giải:

a) A = (3x + 5)(2x – 1) – (1 – 4x)(3x + 2)

= 6x² – 3x + 10x – 5 – 3x – 2 + 12x² + 8x

= 18x² + 12x – 7

$\left|x\right|=2\Rightarrow \left[\begin{array}{c}x=2\\ x=-2\end{array}\right.$

 

• Với x = 2, ta có: A = 18.2² + 12.2 – 7 = 89.

• Với x = – 2, ta có: A = 18 (–2)² + 12. (– 2) – 7 = 41.

b) B = (2x + y)(2x – y) + xy(x – y) – xy(x + y)

= 4x² – y² + x²y – xy² – x²y – xy²

= 4x² – 2xy² – y².

Với x = 0; y = –1, ta có:

B =  4.0² – 2.0.( –1)² – (–1)² = –1.

Câu 35: Một thửa ruộng hình chữ nhật có chiều dài 60 m, chiều dài bằng $\frac{3}{2}$  chiều rộng. Trên thửa ruộng đó người ta trồng lúa cứ 100 m² thu hoạch được 50 kg. Hỏi trên cả thửa ruộng thu hoạch được bao nhiêu tạ thóc?

Lời giải:

Chiều rộng của thửa ruộng đó là:

$60:\frac{3}{2}=40$ (m)

Diện tích của thửa ruộng đó là:

60 × 40 = 2400 (m²)

Số thóc thu hoạch được trên thửa ruộng đó là:

$\frac{2400}{100}.50=1200$ (kg)

Đổi: 1200 kg = 12 tạ

Vậy Số thóc thu hoạch được trên thửa ruộng đó là 12 tạ.

Câu 36: Một trường trung học phổ thông có 4 học sinh giỏi khối 12, có 5 học sinh giỏi khối 11, có 6 học sinh giỏi khối 10. Hỏi có bao nhiêu cách sắp xếp 15 học sinh trên thành một hàng ngang để đón đoàn đại biểu, nếu các học sinh ở cùng một khối thì xếp gần nhau.

Lời giải:

Số cách sắp xếp học sinh ba khối 10, 11 và 12 là: 3!;

Số cách sắp xếp các học sinh giỏi khối 12 là: 4!;

Số cách sắp xếp các học sinh giỏi khối 11 là: 5!;

Số cách sắp xếp các học sinh giỏi khối 10 là: 6!;

Vậy số cách sắp xếp 15 học sinh thành hàng ngang để đón đại biểu là: 3!.4!.5!.6!

Câu 37: Số các số tự nhiên có 5 chữ số khác nhau và chia hết cho 10 là:

A. 3260;

B. 3168;

C. 5436;

D. 3024.

Lời giải:

Gọi số tự nhiên có 5 chữ số chia hết cho 10 có dạng: $\overline{abcd0}$ .

Ta có a ≠ 0 nên có 9 cách chọn.

Vì các chữ số khác nhau nên các số b, c, d lần lượt có số cách chọn là: 8; 7; 6

Vậy số các cố tự nhiên có 5 chữ số khác nhau chia hết cho 10 là: 9.8.7.6 = 3024.

Đáp án đúng là D. 

Câu 38: Tìm một số biết rằng gấp số đó lên 2,5 lần rồi trừ đi 1,6 thì được 5,4

Lời giải:

Gọi số cần tìm là x.

Ta có: 2,5x – 1,6 = 5,4

$\Rightarrow x=\frac{\mathrm{5,4}+\mathrm{1,6}}{\mathrm{2,5}}=\mathrm{2,8}$

Vậy số cần tìm là: 2,8.

Câu 39: Tìm giá trị lớn nhất (hoặc nhỏ nhất) của các biểu thức sau: A =  x² − 6x + 11

Lời giải:

Ta có:  A = x² − 6x + 11 = x² – 2.3x + 9 + 2 = (x – 3)² + 2

Vì (x – 3)² ≥ 0 nên (x – 3)² + 2 ≥ 2

Suy ra: A ≥ 2;

⇒ A = 2 khi và chỉ khi x – 3 = 0 ⇒ x = 3

Vậy A = 2 là giá trị nhỏ nhất của biểu thức tại x =3.

Câu 40: Viết biểu thức x³ – 6x² + 12x – 8 dưới dạng lập phương của một hiệu:

A. (x + 4)³;

B. (x – 4)³;

C. (x + 2)³;

D. (x – 2)³.

Lời giải:

Ta có: x³ – 6x² + 12x – 8 = x³ – 3.x².2 + 3.x.2² – 2² = (x – 2)³

Đáp án đúng là D.

Câu 41: Xác định parabol y = ax² + bx + 2, biết rằng parabol đó: Có đỉnh là I(2; – 2)

Lời giải:

Ta có: Parabol y = ax² + bx + 2 với đỉnh I (2; – 2) có:

• $-\frac{b}{2a}=2\Rightarrow b=-4a$

• $\frac{-\Delta }{4a}=-2\Rightarrow \Delta =8a$

+) Với ∆ = b² – 4a.2 = b² – 8a

⇒ b² – 8a = 8a ⇔ b² = 16a

+) Với b = – 4a ⇒ 16a² = 16a

⇒ a = 1 ⇒ b =  – 4.

Vậy parabol cần tìm là: y = x² – 4x + 2.

Câu 42: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B như hình bên. Biết OA = 15 cm, O’A = 13 cm, AB = 24 cm. Tính độ dài OO’.

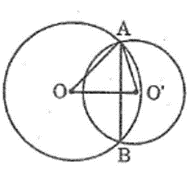
Lời giải:

Gọi H là giao điểm của AB và OO’

Vì OO’ là đường trung trực của AB nên: OO’ ⊥ AB tại H

$\Rightarrow HA=HB=\frac{AB}{2}=\frac{24}{2}=12$ (cm);

Áp dụng định lý Py – ta – go trong ∆AOH có:

AO² = OH² + AH²

⇒ OH² = AO² – AH² = 15² – 12² = 81

⇒ OH = 9 cm

Trong ∆AO’H có: AO’² = O’H² + AH²

⇒ O’H² = AO’² – AH² = 13² – 12² = 25

⇒ O’H = 5 cm

Vậy OO’ = OH + O’H = 9 + 5 = 14 (cm).

Câu 43: Trong không gian hệ tọa độ Oxyz cho mặt phẳng (P):  x – y + 2z – 2 = 0 và 2 điểm A (2; 3; 0); B (2; – 1; 2). Tìm điểm M thuộc mặt phẳng (P) sao cho $\left|MA-MB\right|$  lớn nhất.

Lời giải:

Đặt phương trình dạng: f = x – y + 2z – 2

⇒ f(A) . f(B) = ( –2). 5 = −10 < 0 nên A, B nằm hai phía khác nhau so với mặt phẳng (P).

A’ là điểm đối xứng của A qua (P) có phương trinh đường thẳng AA’: $\frac{x-2}{1}=\frac{y-3}{-1}=\frac{z}{2}$

Gọi I là điểm đường thẳng AA’ và mặt phẳng (P) có: I (2 + t; 3 – t; 2t) ∈ (P)

⇒ t + 2 + t – 3 + 4t – 2 = 0

$\iff t=\frac{1}{2}$

$\Rightarrow I\left(\frac{5}{2};\frac{5}{2};1\right)$

 ⇒ A’ (3; 2; 2).

$\left|MA-MB\right|=\left|MA\text{'}-MB\right|\le A\text{'}B$

$\Rightarrow \left|MA-MB\right|=A\text{'}B$ ⇔ A’; B; M thẳng hàng.

Phương trình đường thẳng A’B: $\left\{\begin{array}{c}x=3+a\\ y=2+3a\\ z=2\end{array}\right.$

Mà M = A’B ∩ (P)

Vậy $M=\left(\frac{9}{2};\frac{13}{2};2\right)$ .

Câu 44: Cho đường tròn (O) và tiếp tuyến AB (B là tiếp điểm). Lấy điểm C thuộc đường tròn (O) sao cho AB = AC. Chứng minh C là tiếp tuyến của đường tròn (O).

Lời giải:

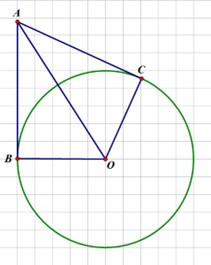
Nối A và O.

Xét ∆ABO và ∆ACO có:

AO: cạnh chung

AB = AC (giả thiết)

BO = CO (bán kính của đường tròn tâm O)

Do đó ∆ABO = ∆ACO (c.c.c)

=> $\widehat{ABO}=\widehat{ACO}=90°$ .

Ta có AC cắt đường tròn tâm O tại C và AC vuông góc với OC tại C nên AC là tiếp tuyến của đường tròn (O).

Câu 45: Trong trường hợp sau, tìm các giá trị của m sao cho 3 đường thẳng sau phân biệt và đồng quy

y = 2x; y = −x + 3; y = mx + 5

Lời giải:

Giao điểm của hai đường thẳng y = 2x và y = −x + 3 là:

2x = −x + 3

<=> 3x = 3

<=> x = 1

=> y = 2

Do đó tọa độ giao điểm của hai đường thẳng đầu là A(1; 2).

Vì 3 đường thẳng đồng quy suy ra y = mx + 5 đi qua điểm A(1; 2)

=> 2 = m + 5 <=> m = −3.

Vậy m = −3.

Câu 46: Cho hình chữ nhật ABCD có AB = 12 cm, BC = 5 cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D.

Lời giải:

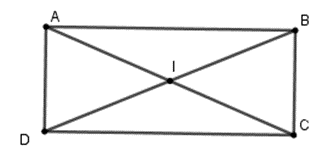
Gọi I là giao hai đường chéo, ta có IA = IB = IC = ID (vì BD = AC và I là trung điểm của mối đường)

Nên bốn điểm A, B, C, D cùng thuộc đường tròn tâm I bán kính $R=\frac{AC}{2}$ .

Theo định lý Py-ta-go trong tam giác vuông ABC, ta có:

$AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{{12}^2+5^2}=13\text{\hspace{0.33em}(cm)}$.

Nên $R=\frac{AC}{2}=\frac{13}{2}=\mathrm{6,5}\left(cm\right)$ .

Vậy bán kính cần tìm là R = 6,5 cm.

Câu 47: Tính bán kính đường tròn ngoại tiếp hình chữ nhật

Lời giải:

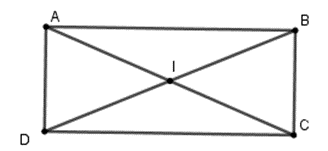
Gọi hình chữ nhật ABCD có AB = a, BC = b và hai đường chéo AC và BD cắt nhau tại I.

Ta có độ dài đường chéo hình chữ nhật là:

$AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{a^2+b^2}$.

Suy ra, bán kính đường tròn ngoại tiếp hình chữ nhật là:

$R=AI=\frac{AC}{2}=\frac{\sqrt{a^2+b^2}}{2}$.

Câu 48: Tìm điều kiện để phép chia là phép chia hết:

a) xⁿyⁿ⁺¹ : x²y⁵;

b) (13x⁴y³ – 5x³y³ + 6x²y²) : 5xⁿyⁿ.

Lời giải:

a) Ta có: xⁿyⁿ⁺¹ ⋮ x²y⁵

$$\begin{gathered} \Rightarrow \left\{\begin{array}{c}n\ge 2\\ n+1\ge 5\end{array}\right. \\ \iff \left\{\begin{array}{c}n\ge 2\\ n\ge 4\end{array}\right. \end{gathered}$$

⇔n ≥ 4

b) Ta có: (13x⁴y³ – 5x³y³ + 6x²y²) ⋮ 5xⁿyⁿ

$$\begin{gathered} \Rightarrow \left\{\begin{array}{c}13x^4{y}^3⋮5x^n{y}^n\\ 5x^3{y}^3⋮5x^n{y}^n\\ 6x^2{y}^2⋮5x^n{y}^n\end{array}\right. \\ \Rightarrow \left\{\begin{array}{c}n\le 4\\ n\le 3\\ n\le 2\end{array}\right. \end{gathered}$$

⇔n ≤ 2

Câu 49: Xác định a, b, c biết parabol y = ax² + bx + c đi qua điểm A (8; 0) và có đỉnh là I (6; −12).

Lời giải:.

Ta có parabol y = ax² + bx + c đi qua điểm A (8; 0)

⇒ 0 = a.8² + b.8 + c ⇒ 64a + 8b + c = 0 (1).

Mà parabol y = ax² + bx + c có đỉnh là I (6 ; –12):

$\frac{-b}{2a}=6\Rightarrow b=-12a$ (2)

$\frac{-\Delta }{4a}=-12$ ⇒ ∆ = 48a ⇒ b² – 4ac = 48a (3)

Từ (1), (2) và (3)

$\left\{\begin{array}{c}64a+8b+c=0\\ b=-12a\\ b^2-4ac=48a\end{array}\right.\Rightarrow \left\{\begin{array}{c}a=3\\ b=-36\\ c=96\end{array}\right.$

Vậy a = 3; b = – 36 ; c = 96 và parabol y = 3x² – 36x + 96.

Câu 50: Cho △ABC cân tại B có đường cao BE. Trên tia đối của tia EB lấy điểm D sao cho ED = EB. Chứng minh: tứ giác ABCD là hình thoi.

Lời giải:

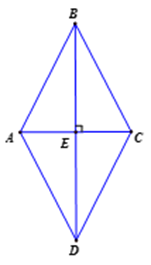
Vì △ABC cân tại B có đường cao BE => BE là đường trung tuyến

=> EA = EC (1)

Ta có: EB = ED (gt) (2)

Từ (1) và (2) suy ra ABCD là hình bình hành.

Vì BE là đường cao của △ABC => BE $\perp$ AC

Hình bình hành ABCD có BE $\perp$ AC => ABCD là hình thoi.