Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 26)
Câu 1: Cho tam giác ABC, biết AB = 21 cm, AC = 28 cm, BC = 35 cm. Chứng minh tam giác ABC vuông.
Lời giải:
Ta có: AB2 = 212 = 441;
AC2 = 282 = 784;
BC2 = 352 = 1 225.
Ta thấy: AB2 + AC2 = BC2 (441 + 784 = 1 225).
Do đó tam giác ABC vuông tại A (theo định lý Py-ta-go đảo)
Câu 2: Các phương pháp chứng minh 3 đường thẳng đồng quy.
Lời giải:
Để chứng minh ba đường thẳng đồng quy (3 đường thẳng giao nhau tại một điểm) chúng ta thường dùng một trong những cách sau:
Cách 1: Chứng minh có một điểm đồng thời thuộc cả ba đường thẳng đó.
Cách 2: Chứng minh giao điểm của 2 đường thẳng này nằm trên đường thẳng thứ ba.
Cách 3: Chứng minh giao điểm của 2 đường thẳng thứ nhất và thứ hai trùng với giao điểm của hai đường thẳng thứ hai và thứ ba.
Cách 4: Sử dụng tính chất đồng quy của ba đường trung tuyến, đường cao, phân giác, trung trực trong tam giác.
Cách 5: Sử dụng tính chất của đường chéo của các tứ giác đặc biệt.
Câu 3: Xếp các số sau theo thứ tự từ bé đến lớn: 892 673; 20 483; 9 876; 89 7125.
Lời giải:
Ta thấy số 20 483 có 5 chữ số, số 9 876 có 4 chữ số, hai số 892 673; 897 125 đều có 6 chữ số. Do đó ta chỉ cần so sánh hai số 892 673; 897 125.
Hai số 892 673; 897 125 có các chữ số ở hàng trăm nghìn cùng là 8, các chữ số ở hàng chục nghìn cùng là 9, ở hàng nghìn có 2 < 7 nên 892 673 < 897 125.
Do đó ta có: 9 876 < 20 483 < 892 673 < 897 125.
Các số sắp xếp theo thứ tự từ bé đến lớn là 9 876; 20 483; 892 673; 897 125.
Câu 4: Cho số hữu tỉ . Tìm a để:
a) y là số dương.
b) y là số âm.
c) y không phải là số âm cũng không phải là số dương.
Lời giải:
a) Để y là số dương thì
b) Để y là số âm thì
c) Để y không phải là số dương cũng không phải là số âm thì: .
Lời giải:
.
Câu 6: Tính giá trị biểu thức 32 × 8 + 48 : 6 – 123 : 3.
Lời giải:
32 × 8 + 48 : 6 – 123 : 3 = 256 + 8 – 41 = 264 – 41 = 223.
Câu 7: Cho A = {–1; 0; 1; 3; 5}; B = {–2; –1; 1; 2; 4}. Tìm .
Lời giải:
.
Lời giải:
.
Câu 9: Phương trình có tập nghiệm là ?
Lời giải:
Vậy tập nghiệm của phương trình đã cho là .
Câu 10: Tìm m để phương trình sinx + cosx = m có nghiệm.
Lời giải:
PT có nghiệm khi và chỉ khi
.
Lời giải:
Số bé nhất có 2 chữ số: 10
Số chia là : 10 – 2 = 8
Thương của hai số đó: 72 : 8 = 9.
Lời giải:
Gọi số bị chia, số chia, thương và số dư lần lượt là a, b, c, d.
Ta có:
a : b = c (dư d) ⟺ a = c.b + d
Ta cũng có: (a + 15) : (b + 5) = c (dư d)
⟺ a + 15 = c.(b + 5) + d
⟺ a + 15 = c.b + c.5 + d
Mà a = c.b + d nên a + 15 = c.b + c.5 + d = (c.b + d) + c.5 = a + c.5
Suy ra 15 = c.5, suy ra c = 3.
Vậy thương của phép chia bằng 3.
Lời giải:
Gọi là số tự nhiên cần tìm (0 ≤ a, b, c, d, e ≤ 9; a ≠ 0; a, b, c, d, e ∈ ℕ \ {7}).
Trường hợp 1: a = 6, b = 5.
Chọn tùy ý các chữ số c, d, e từ 9 chữ số đã cho, ta luôn được số thỏa mãn trừ trường hợp c = d = e = 0.
Số các số lập được là: 1.1.93 – 1 = 728 (số).
Trường hợp 2: a = 6, b ∈ {6; 8; 9}.
Chọn tùy ý các chữ số c, d, e trong 9 chữ số đã cho, ta luôn được số thỏa mãn.
Số các số lập được là: 1.3.93 = 2187 (số).
Trường hợp 3: a ∈ {8; 9}.
Chọn tùy ý các chữ số b, c, d, e trong 9 chữ số đã cho, ta luôn được số thỏa mãn.
Số các số lập được là: 2.94 = 13122 (số).
Vậy số các số thỏa mãn yêu cầu bài toán là: 728 + 2187 + 13122 = 16037 số.
Câu 14: Giải phương trình tanx + 1 = 0.
Lời giải:
ĐK:
tanx + 1 = 0
Vậy .
Câu 15: Trong các phát biểu sau, phát biểu nào là mệnh đề đúng:
A. là một số hữu tỉ.
B. Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.
C. Bạn có chăm học không?
D. Hôm nay trời đep quá!
Lời giải
Đáp án đúng là: B
Đáp án B nằm trong bất đẳng thức tam giác: “ Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại”.
Đáp án A sai vì là một số vô tỉ.
Đáp án C sai vì đây là câu hỏi.
Đáp án D sai vì đây là câu cảm thán.
Câu 16: Cho ∆ABC vuông tại A; đường cao AH;AB = 6 cm; AC = 8 cm. Tính cạnh BC, AH, BH.
Lời giải:
Áp dụng các công thức hệ thức lượng ta có:
⇒ BH = 3,6 (cm); CH = 10 – 3,6 = 6,4 (cm).
Lời giải:
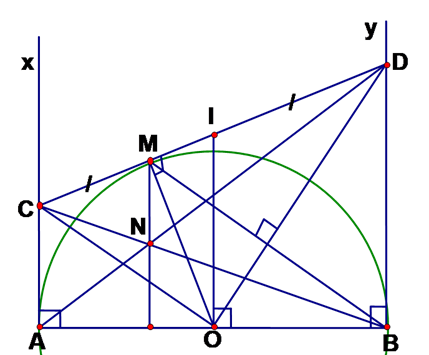
Gọi I là trung điểm của CD, ta có I là tâm đường tròn ngoại tiếp ∆COD, đường kính CD có IO là bán kính.
Theo tính chất tiếp tuyến ta có AC ⊥ AB; BD ⊥ AB ⇒ AC // BD ⇒ tứ giác ACDB là hình thang. Lại có I là trung điểm của CD; O là trung điểm của AB ⇒ IO là đường trung bình của hình thang ACDB.
IO // AC, mà AC ⊥ AB ⇒ IO ⊥ AB tại O ⇒ AB là tiếp tuyến tại O của đường tròn đường kính CD.
Lời giải:
Nếu M ∈ d
Câu 19: Cho góc nhọn a có . Tính cosa, tana, cota.
Lời giải:
Vì a là góc nhọn nên cos a > 0.
Ta có: .
Ta có:
Lại có: tana.cota = 1 .
Lời giải:
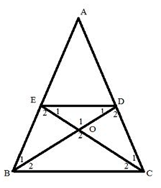
Xét ΔABC có
Do đó: DE // CB
Xét tứ giác BEDC có DE // BC nên BEDC là hình thang
Mà nên BEDC là hình thang cân
Vậy BEDC là hình thang cân.
Lời giải:
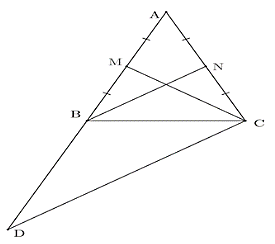
Gọi N là trung điểm cạnh AC.
Suy ra BN là đường trung tuyến của ΔABC.
Vì ΔABC là tam giác cân tại A nên dễ dàng chứng minh được BN = CM. (1)
Xét tam giác ΔACD có B, N lần lượt là trung điểm cạnh AD và AC.
Suy ra BN là đường trung bình của tam giác của ΔACD.
⇒ BN = DC
⇒ DC = 2BN (2)
Từ (1) và (2) suy ra CD = 2CM.
Câu 22: Cho ΔABC nhọn có a = 10 cm, b = 6 cm, S = 24 cm². Tính c.
Lời giải:
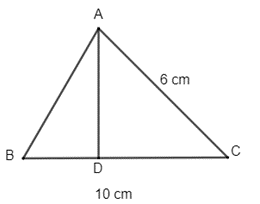
Gọi AD là đường cao của tam giác ABC.
Ta có: (cm2), suy ra AD = 4,8 cm.
Xét tam giác ACD vuông tại D, ta có: .
Vì (do tam giác ABC nhọn) nên cos C > 0.
Do sin2 C + cos2 C = 1 nên ta suy ra cos C = .
Áp dụng định lí côsin trong tam giác ABC ta có:
AB2 = BC2 + AC2 – 2 BC . AC . cos C = 102 + 62 – 2 . 10 . 6 . = 64.
Suy ra AB = 8 cm. Vậy c = AB = 8 cm.
Lời giải:
Nếu cộng 2 số âm: thì cộng phần dương của 2 số được kết quả rồi đặt dấu âm vào trước.
Ví dụ: – 5 + ( –2 ) = – ( 5 + 2) = –7
Nếu trừ 2 số âm: Ta lấy số bị trừ cộng với phần dương của số trừ được kết quả bao nhiêu thì đó là kết quả.
Ví dụ: – 5 – ( –7) = –5 + 7 = 2 hoặc –5 – ( –3) = –5 + 3 = – 2.
Câu 24: Tính tổng các nghiệm trong đoạn [0; 30] của phương trình tanx = tan3x (1)
Lời giải:
Điều kiện để (1) có nghĩa:
Khi đó (1) trở thành
So sánh với điều kiện
Mà nên
Các nghiệm của PT có trong khoảng trên là
Vậy tổng các nghiệm của phương trình là .
Lời giải:
Gọi d: y = ax + b song song với d1.
Có: a = –2; b ≠ 5.
Thay x = –2; y = 1 vào d: 1 = 4 + b ⇒ b = −3
Vậy d: –2x – 3 song song với đường thẳng d1 và đi qua A.
Câu 26: Cho hàm số y = 2x – 3 có đồ thị (d) và điểm A(–1; –5).
a) Viết phương trình đường thẳng d1 qua A và song song với trục Ox .
b) Viết phương trình đường thẳng d2 qua A và song song với đường thẳng d.
c) Viết phương trình đường thẳng d3 qua A và vuông góc với đường thẳng d.
d) Viết phương trình đường thẳng d4 qua A và gốc tọa độ.
Lời giải:
Gọi các đường thẳng có công thức chung là y = ax + b.
a. Đường thẳng d1 qua A và song song với trục Ox
b. Đường thẳng d2 qua A và song song với đường thẳng d
c. Đường thẳng d3 qua A và vuông góc với đường thẳng d
d. Đường thẳng d4 qua A và gốc tọa độ
Câu 27: Giải phương trình 2sinxcos2x – 1 + 2cos2x – sinx = 0.
Lời giải:
2sinxcos2x – 1 + 2cos2x – sinx = 0
⇔ (2sinxcos2x + 2cos2x) – (1 + sin x) = 0
⇔ 2cos2x(sinx + 1) – (1 + sinx) = 0
⇔ (sinx + 1)(2cos2x – 1) = 0
.
Câu 28: Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo. Gọi M, N là trung điểm của OB, OD.
a) Chứng minh AMCN là hình bình hành.
b) AM cắt BC tại E, CN cắt AD tại F. Chứng minh AE = CF và O, E, F thẳng hàng.
Lời giải:
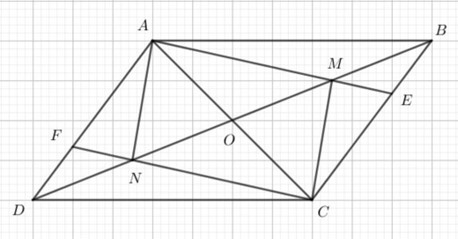
a) Vì O là giao điểm 2 đường chéo của hình bình hành ABCD nên OB = OD.
Mà M, N lần lượt là trung điểm OB, OD nên OM = ON
Mà O là giao điểm 2 đường chéo của hình bình hành ABCD nên OA = OC
Do đó AMCN là hình bình hành (do O là trung điểm AC và MN).
b) Vì AMCN là hình bình hành nên AM // CN hay AE // CF
Mà ABCD là hình bình hành nên AD // BC hay AF // CE
Do đó AECF là hình bình hành nên AE = CF.
Do AECF là hình bình hành mà O là trung điểm của đường chéo AC nên O cũng là trung điểm của đường chéo EF.
Vậy O; E; F thẳng hàng.
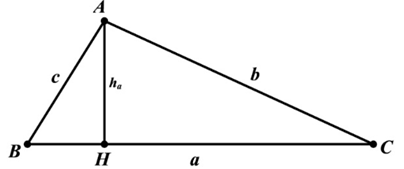
Câu 29: Cho ∆ABC có BC = a, CA = b, AB = c.
Chứng minh rằng .
Lời giải:
Ta có: (định lí côsin trong tam giác ABC)
Hay .
Lời giải:
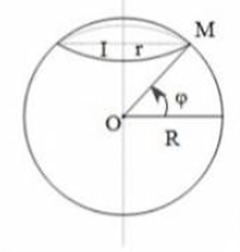
Chu kì quay của trái đất T = 3600.24 = 86400 (s)
Khi trái đất quay quanh trục địa cực thì vị trí M quay trên vĩ tuyến (I, r)
Ta có: r = R.cos với = 30°
Tốc độ dài của M: v = r. =
Gia tốc hướng tâm:
Lời giải:
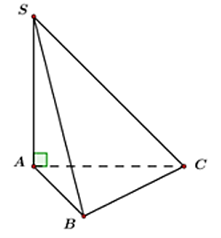
Ta có: (SBC)
Vì
Lại có: AB ⊥ BC (gt)
.
Câu 32: Từ các chữ số 1, 2, 3, 4, 5 lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau đôi một?
Lời giải:
Số các số tự nhiên có 5 chữ số khác nhau đôi một là 5! = 120.
Câu 33: Xét tính chẵn lẻ của hàm số y = sinx + tanx.
Lời giải:
TXĐ: .
Ta có x ∈ D ⇒ – x ∈ D, do đó D là tập đối xứng.
Đặt y = f(x) = sinx + tanx.
Ta có:
⇒ Hàm số đã cho là hàm số lẻ.
Câu 34: Hàm số nào sau đây là hàm số chẵn?
A. y = – cosx.
B. y = –2sinx.
C. y = 2sin(–x).
D y = sinx – cosx.
Lời giải:
Đáp án đúng là: A
Xét phương án A: hàm số y = f(x) = – 2cosx có tập xác định D = ℝ.
Ta có với x ∈ ℝ ⇒ –x ∈ ℝ và f(–x) = – 2cos(–x) = –2cosx.
⇒ f(x) = f( –x)
Vậy hàm số A là hàm số chẵn.
Lời giải:
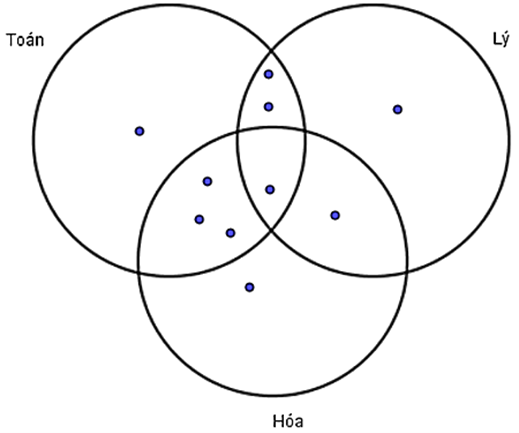
Số học sinh giỏi toán, lý mà không giỏi hóa: 3 – 1 = 2.
Số học sinh giỏi toán, hóa mà không giỏi lý: 4 – 1 = 3.
Số học sinh giỏi hóa, lý mà không giỏi toán: 2 – 1 = 1.
Số học sinh chỉ giỏi môn lý: 5 – 2 – 1 – 1 = 1.
Số học sinh chỉ giỏi môn hóa: 6 – 3 – 1 – 1 = 1.
Số học sinh chỉ giỏi môn toán: 7 – 3 − 2 – 1 = 1.
Số học sinh giỏi ít nhất một (môn toán, lý, hóa) là số học sinh giỏi 1 môn hoặc 2 môn hoặc cả 3 môn: 1 + 1 + 1 + 1 + 2 + 3 + 1 = 10.
Câu 36: Giải phương trình: 3sin2x + 2cos2x = 3.
Lời giải:
3sin2x + 2cos2x = 3
(*)
Nếu cosx = 0 nên cosx = 0 không phải là nghiệm của phương trình
Nếu cosx ≠ 0. Chia cả 2 vế của (*) cho ta được:
Câu 37: Cho hai tập hợp A = (−4; 3) và B = (m – 7; m). Tìm giá trị thực của tham số m để B ⊂ A.
Lời giải:
Để .
Lời giải:
Theo hệ quả của định lí côsin ta có:
.
Diện tích tam giác ABC là .
Vì nên
Lại có: .
Lời giải:
Gọi số cần lập là (0 ≤ a, b, c, d, e ≤ 9; a ≠ 0; a, b, c, d, e ∈ ℕ)
+) Nếu a = 6, b = 5
Chọn tùy ý các chữ số c, d, e trong 9 chữ số đã cho ta luôn được số thỏa mãn trừ trường hợp c = d = e = 0.
Số số lập được là: 93 – 1 = 728 số
+) Nếu a = 6, b ∈ {6; 8; 9}
Chọn tùy ý các chữ số c, d, e trong 9 chữ số đã cho ta luôn được số thỏa mãn
Số số lập được là: 3 . 93 = 2 187 số
+) Nếu a ∈ {8; 9}
Chọn tùy ý các chữ số b, c, d, e trong 9 chữ số đã cho ta luôn được số thỏa mãn
Số số lập được là: 2 . 94 = 13 122 số
Vậy số các số lập được thỏa mãn đề bài là 728 + 2 187 + 13 122 = 16 037 số.
Lời giải:
Vì là số lẻ nên chữ số cuối cùng là số 7
Vì số đứng đầu phải khác 0 nên ta có 4 cách chọn
Có 4 cách chọn cho số thứ 2 và 3 cách chọn chỗ số thứ 3
Vậy có 4 × 4 × 3 = 48 số có thể tạo ra thỏa mãn yêu cầu đề bài
Câu 41: Một khu rừng hình chữ nhật có chu vi 5km 60dam. Chiều dài hơn chiều rộng 800m
a) Hỏi diện tích khu rừng đó bằng bao nhiêu ha ? Bao nhiêu m2?
b) Biết diện tích khu rừng trồng cây mới. Tính tỉ số diện tích trồng cây mới và phần diện tích còn lại của khu rừng.
Lời giải:
Đổi 5km 60dam = 5 600 m
a) Nửa chu vi khu rừng đó là:
5600 : 2 = 2 800 (m)
Chiều rộng khu rừng đó là:
(2800 – 800) : 2 = 1000 (m)
Chiều dài khu rừng đó là: 1000 + 800 = 1 800 (m)
Diện tích khu rừng đó là : 1 800 × 1000 = 1 800 000 (m2) = 180 ha
b) Diện tích phần còn lại của khu rừng chiếm : (diện tích khu rừng)
Tỉ số diện tích trồng cây mới và diện tích còn lại của khu rừng là:
Vậy tỉ số diện tích trồng cây mới và phần diện tích còn lại của khu rừng là .
Câu 42: Trong hình 97, biết diện tích miền gạch sọc là 86 cm2. Tính diện tích hình tròn.
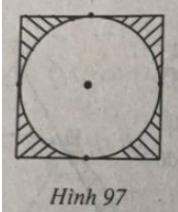
Lời giải:
Gọi R là bán kính hình tròn
Suy ra cạnh hình vuông là 2R
Diện tích hình vuông là: Shv = 4R2
Diện tích hình tròn là: Stròn = πR2
Theo đề, ta có Ssọc = 86
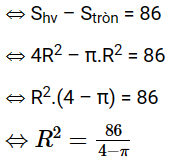
Suy ra
Vậy diện tích hình tròn là cm2.
Câu 43: Cho tứ giác ABCD có E, F là trung điểm AD, BC. Gọi G là trung điểm EF. Chứng minh rằng .
Lời giải:
Áp dụng quy tắc trung điểm ta có
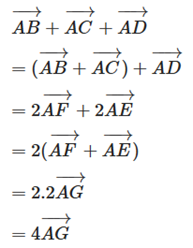
Vậy .
Lời giải:
Hàm số bậc nhất cần tìm có dạng y = ax + b (a ≠ 0)
Vì hàm số có hệ số góc bằng –2 nên ta có: y = –2x + b
Vì đồ thị hàm số đi qua điểm M(1; 3) nên:
3 = –2.1 + b ⇔ b = 5
Vậy hàm số cần tìm là y = –2x + 5.
Câu 45: Tính góc α tạo bởi đường thẳng y = x – 2 và trục Ox.
Lời giải:
Cách 1:
Ta có: hệ số góc của đường thẳng y = x – 2 là a = 1.
Do đó tanα = 1 Þ α = 45°.
Cách 2:
Xét đường thẳng y = x – 2.
Cho y = 0 suy ra x = 2 ta có A(2; 0).
Cho x = 0 suy ra y = – 2 ta có B(0; – 2).
Vẽ đường thẳng đi qua A và B ta được đồ thị hàm số y = x – 2.
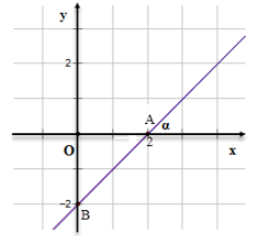
Ta có OA = 2, OB = 2
Xét tam giác OAB vuông tại O có:
Vậy α = 45°.
Câu 46: Cho hàm số bậc nhất y = ax + 3.
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2; 6).
b) Vẽ đồ thị của hàm số với hệ số a tìm được ở câu a.
Lời giải:
a) Đồ thị hàm số đi qua điểm A(2; 6)
Suy ra 6 = 2a + 3
Hay .
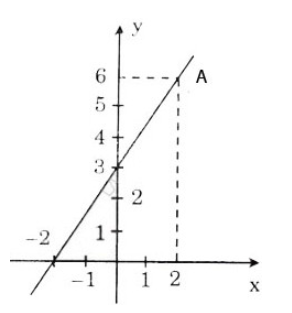
b) Đồ thị hàm số đi qua các điểm A(– 2; 0) và B(0; 3)
Ta có đồ thị
Lời giải:
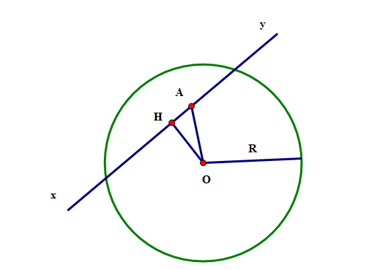
Kẻ OH vuông góc với xy
Vì tam giác OAH vuông tại H, suy ra OH ≤ OA
Mặt khác A nằm trong đường tròn (O;R) nên OA ≤ R.
Vậy đường thẳng xy và đường tròn (O; R) cắt nhau.
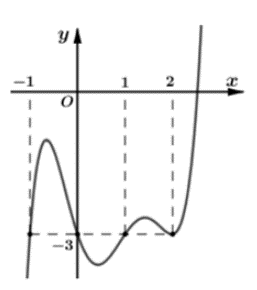
Lời giải:
Đáp án đúng là: B
Xét hàm số h(x) = f(x) + 3x, x ∈ ℝ
h’(x) = f’(x) + 3, x ∈ R
h’(x) = 0 ⇔ f’(x) = – 3
⇔ x ∈ { – 1; 0; 1; 2}
Với x = 2 là nghiệm kép vì qua nghiệm x = 2 thì h’(x) không đổi dấu
Dựa vào đồ thị của f’(x) ta có
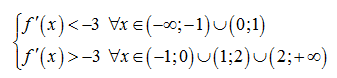
Mà h(0) = f(0) + 3 . 0 = f(0) < 0
Bảng biến thiên của hàm số h(x) = f(x) + 3x
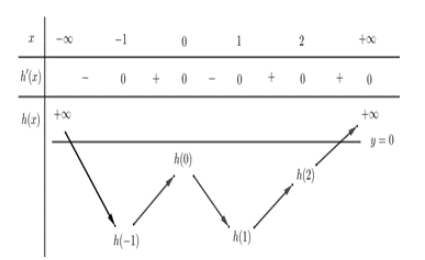
Từ đó suy ra bảng biến thiên của hàm số g(x) = | f(x) + 3x | = | h(x) |
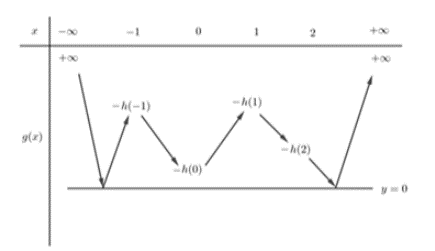
Từ bảng biến thiên ta thấy hàm số có 5 điểm cực trị
Vậy ta chọn đáp án B.
Câu 49: Tìm x biết x4 + 3x3 – x – 3 = 0.
Lời giải:
Ta có x4 + 3x3 – x – 3 = 0
⇔ x3(x + 3) – (x + 3) = 0
⇔ (x + 3)(x3 – 1) = 0
Vậy x = 1 hoặc x = – 3.
Câu 50: Cho tam giác ABC. Gọi M là điểm trên BC sao cho MB = 2MC. Chứng minh
.
Lời giải:
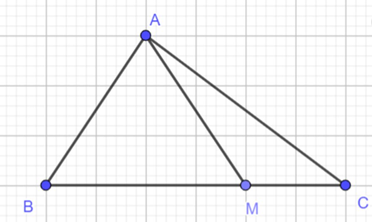
Vì M nằm trên BC sao cho MB = 2MC
Suy ra
Ta có
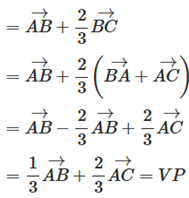
Vậy .