Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 59)

Câu 1: Nhân ngày 20 tháng 10 một cửa hàng thời trang giảm 30% giá niêm yết cho tất cả sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiện của cửa hàng thì được tặng thêm một voucher trị giá bằng 10% số tiền thanh toán tại quầy Thu Ngân:

a) Chị Hoa không có thẻ khách hàng thân thiện của cửa hàng, chị mua một chiếc váy có giá niêm yết là 1 050 000 đồng. Hỏi chị Hoa phải trả bao nhiêu tiền cho chiếc váy đó?

b) Cô Hà có thẻ khách hàng thân thiện, cô mua 1 chiếc túi xách và nhận được một voucher trị giá 91 000 đồng. Hỏi giá niêm yết ban đầu của túi xách là bao nhiêu?

Lời giải:

a) Chị Hoa phải trả số tiền là:

1 050 000 – 1 050 000 × 30% = 735 000 (đồng)

b) Giá chiếc túi đã giảm khi có thẻ khách hàng thân thiết là:

91 000 : 10% = 910 000 (đồng)

Giá chiếc túi ban đầu là:

910 000 : (1 – 30%) = 1 300 000 (đồng)

Vậy giá niêm yết ban đầu của túi xách là 1 300 000 đồng.

Câu 2: Tìm tất cả các số nguyên x, y, z thỏa mãn 3x² + 6y² + 2z² + 3y²z² – 18x = 6.

Lời giải:

Ta có:

3x² + 6y² + 2z² + 3y²z² – 18x = 6

⇔ (3x² – 18x + 27) + 6y² + 2z² + 3y²z² = 6 + 27

⇔ 3(x – 3)² + 6y² + 2z² + 3y²z² = 33                                 (1)

Vì x, y, z nguyên nên z² ⋮ 3 và 2z² ≤ 33

Hay |z| ≤ 3

Mà z nguyên

Suy ra z = 0 hoặc z = 3

+) TH1: z = 0

(1) ⇔  3(x – 3)² + 6y² = 33       

⇔  (x – 3)² + 2y² = 11

Suy ra 2y² ≤ 11

Do đó |y| ≤ 2

$\iff \left[\begin{array}{l}y=0\\ y=1\end{array}\right.$

$\iff \left[\begin{array}{l}{\left(x-3\right)}^2=11\\ {\left(x-3\right)}^2+2=11\end{array}\right.$

⇔  (x – 3)²  + 2 = 11 (vì x nguyên)

⇔  (x – 3)²  = 9 $\iff \left[\begin{array}{l}x-3=3\\ x-3=-3\end{array}\right.\iff \left[\begin{array}{l}x=6\\ x=0\end{array}\right.$

+) TH1: z = 3

(1) ⇔ 3(x – 3)² + 6y² + 2 . 3² + 3y² . 3² = 33                    

⇔  3(x – 3)² + 33y² + 18 = 33

⇔  (x – 3)² + 11y² = 5

Suy ra 11y² ≤ 5

Do đó y = 0

Khi đó  (x – 3)²  = 5 nên không tìm được giá trị x nguyên thỏa mãn phương trình

Vậy phương trình đã cho có nghiệm nguyên (x, y, z) là: (0; 1; 0), (0; –1; 0), (6; 1; 0), (6; –1; 0).

Câu 3: Cho A = (5; 7] và B = [m; m + 3). Tìm m để:

a) A tập hợp con của B.

b) B tập hợp con của A.

Lời giải:

a) Ta có: $\text{A}\subset B\iff \left\{\begin{array}{l}m\le 5\\ m+3>7\end{array}\right.\iff \left\{\begin{array}{l}m\le 5\\ m>4\end{array}\right.\iff 4<m\le 5$.

b) Ta có: $B\subset A\iff \left\{\begin{array}{l}m>5\\ m+3\le 7\end{array}\right.\iff \left\{\begin{array}{l}m>5\\ m\le 4\end{array}\right.\iff m\in \varnothing$.

Câu 4: Chứng minh: (–a – b)² = (a + b)².

Lời giải:

Ta có:

VT = (–a – b)² = [– (a + b)²] = (a + b)² = VP

Vậy (–a – b)² = (a + b)².

Câu 5: Số trung bình cộng của hai số bằng 9. Biết một trong hai số đó bằng 12. Tìm số kia.

Lời giải:

Tổng 2 số là:

9 × 2 = 18 

Số kia là:

18 – 12 = 6

Vậy số còn lại là 6.

Câu 6: Cho 3 tập hợp A = (–∞; 0), B = (1; +∞), C = (0; 1). Tìm (A ∪ B ) ∩ C.

Lời giải:

Ta có:

A ∪ B = (–∞; +∞)

Suy ra (A ∪ B ) ∩ C = (0; 1)

Vậy (A ∪ B ) ∩ C = (0; 1).

Câu 7: Cho a = [m; m + 3] với m là tham số và b = (0; 2). Tìm m để b là con của a.

Lời giải:

Ta có:

$b\subset a\iff \left\{\begin{array}{l}m\le 0\\ m+3\le 2\end{array}\right.\iff \left\{\begin{array}{l}m\le 0\\ m\le -1\end{array}\right.\iff m\le -1$.

Vậy m < –1 thì b ⊂ a.

Câu 8: Cho a, b, c là các số tự nhiên thỏa mãn (a – b) là số nguyên tố và 3c² = c(a + b) + ab. Chứng minh rằng 8c + 1 là số chính phương.

Lời giải:

Ta có:

3c² = c(a + b) + ab

⇔ 2c² = ca + cb + ab + c²

⇔ 2c² = c(a + c) + b(c + a)

⇔ 2c² = (a + c) (b + c)

Gọi d  gcd(a + c, b + c)

Do a – b = p ∈ P nên d = 1 hoặc d = p

+) Nếu d = 1

Thì a + c = x², b + c = y² (xy = 2c)

Suy ra p = (x – y)(x + y).p = 2 (vô lý)

p lẻ thì dễ thấy $\text{x}=\frac{p+1}{2}=\frac{a-b+1}{2}$ và $y=\frac{a-b-1}{2}$

Suy ra $2c=xy=\frac{\left(a-b-1\right)\left(a-b+1\right)}{4}$

Do đó 8c + 1 = (a – b)² là số chính phương

+) Nếu d = p thì a + c = pm², b + c = pn² (2c = pmn)

Suy ra (m – n)(m + n) = 1

Do đó m = 1 và n = 0 (loại)

Vậy 8c + 1 là số chính phương.

Câu 9: Cho 3 chữ số 1; 2; 3. Lập được tất cả bao nhiêu số tự nhiên có 3 chữ số?

Lời giải:

Hàng trăm có 3 lựa chọn

Hàng chục có 3 lựa chọn

Hàng đơn vị có 3 lựa chọn

Ta lập được tất cả số tự nhiên có 3 chữ số là:

3 × 3 × 3  = 27 (số)

Vậy lập được 27 số có 3 chữ số.

Câu 10: Cho biết tổng của sáu số là 42, hãy tính trung bình cộng của sáu số đó.

Lời giải:

Trung bình cộng của 6 số đó là:

42 : 6 = 7 

Vậy trung bình cộng của 6 số đó là 7.

Câu 11: Cho hàm số y = (m – 2)x + 2m + 1 (m là tham số)

a) Với giá trị nào của m thì hàm số đồng biến?

b) Tìm m để đồ thị hàm số song song đường thẳng y = 2x – 1.

c) Tìm điểm cố định mà đồ thị hàm số luôn luôn đi qua với mọi giá trị m.

Lời giải:

a) Để hàm số y = (m – 2)x + 2m + 1 đồng biến

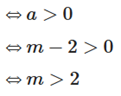
Vậy với m > 2 thì hàm số y = (m – 2)x + 2m + 1 đồng biến.

b) Để đồ thị hàm số y = (m – 2)x + 2m + 1 song song đường thẳng y = 2x – 1 

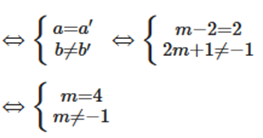
Vậy m = 4 và m ≠ 1.

c) Giả sử đồ thị hàm số y = (m – 2)x + 2m + 1 luôn đi qua một điểm cố định M(x₀; y₀) với mọi m

Khi đó y₀ = (m – 2)x₀ + 2m + 1

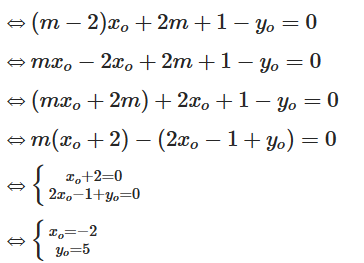
Vậy điểm cố định mà đồ thị hàm số luôn luôn đi qua với mọi giá trị m là M(–2; 5).

Câu 12: Xét tính tuần hoàn và chu kỳ của y = cos²x – 1.

Lời giải:

Tập xác định: D = ℝ

Ta có:  $y=c{\text{os}}^{2}x-1=\frac{1+c\text{os2x}}{2}-1=\frac{1}{2}cos2\text{x}-\frac{1}{2}$

Với mọi x ∈ ℝ thì x + π ∈ ℝ

$f\left(x+\pi \right)=\frac{1}{2}cos\left(2\text{x}+2\pi \right)-\frac{1}{2}=\frac{1}{2}cos2\text{x}-\frac{1}{2}=f\left(\text{x}\right)$

Suy ra hàm số tuần hoàn với chu kì T = π

Vậy hàm số tuần hoàn với chu kì T = π.

Câu 13: Cho mệnh đề: “ ∀ x ∈ ℝ, x² + 3x + 5 > 0”. Mệnh đề phủ định của mệnh đề trên là:

A. ∃ x ∈ ℝ, x² + 3x + 5 ≤ 0

B. ∃ x ∈ ℝ, x² + 3x + 5 > 0

C. ∀ x ∈ ℝ, x² + 3x + 5 < 0

D. ∀ x ∈ ℝ, x² + 3x + 5 ≤ 0.

Lời giải:

Đáp án đúng là: A

Mệnh đề phủ định của ∀ x ∈ R, x² + 3x + 5 > 0 là ∃ x ∈ R, x² + 3x + 5 ≤ 0

Vậy ta chọn đáp án A.

Câu 14: Chứng minh: B = n⁴ + 64 không phải là số nguyên tố với mọi n thuộc ℤ.

Lời giải:

Ta có: B = n⁴ + 64 = n⁴ + 16n² + 64 – 16n²

= (n² + 8)² – (4n)² = (n² – 4n + 8)(n² + 4n + 8)

Suy ra B = n⁴ + 64 không phải là số nguyên tố với mọi n thuộc Z.

Câu 15: Tìm m để các đường thẳng y = (2m – 1)x – 3 và y = mx + m² – 4m cắt nhau tại một điểm nằm trên trục tung.

Lời giải:

Để hai đường thẳng y = (2m – 1)x – 3 và y = mx + m2 – 4m cắt nhau tại một điểm nằm trên trục tung thì

$\left\{\begin{array}{l}2m-1\ne m\\ -3=m^2-4m\end{array}\right.\iff \left\{\begin{array}{l}m\ne 1\\ m^2-4m+3=0\end{array}\right.\iff \left\{\begin{array}{l}m\ne 1\\ \left[\begin{array}{l}m=1\\ m=3\end{array}\right.\end{array}\right.\iff m=3$

Vậy m = 3 thì đường thẳng y = (2m – 1)x – 3 và y = mx + m2 – 4m cắt nhau tại một điểm nằm trên trục tung.

Câu 16: Với 3 chữ số 1, 2, 3 hãy viết tất cả các số có 3 chữ số khác nhau rồi tính tổng của các số đó.

Lời giải:

Các số có 3 chữ số khác nhau là:

123, 132, 231, 213, 321, 312

Tổng của 6 số trên là:

123 + 132 + 213 + 231 + 321 + 312 = 1332.

Câu 17: Có bao nhiêu số tự nhiên nhỏ hơn 100 chia hết cho 2 và 3.

Lời giải:

Số tự nhiên chia hết cho cả 2 và 3 có dạng: 6k, với k là một số tự nhiên.

Theo đề, ta có: 0 ≤ 6k ≤ 100.

$\iff 0\le k\le \frac{50}{3}$.

Mà k ∈ ℕ nên k ∈ {0; 1; 2; 3; ...; 15; 16}.

Vậy có tất cả 17 số tự nhiên thỏa mãn yêu cầu bài toán.

Câu 18: Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có sin²α + cos²α = 1.

Lời giải:

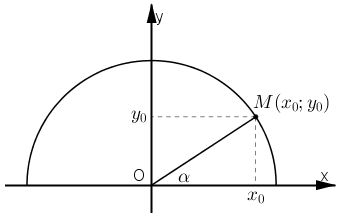
Vẽ đường tròn lượng giác (O; 1).

Với mọi α (0° ≤ α ≤ 180°), ta đều có điểm M(x₀; y₀) thuộc nửa đường tròn sao cho $\widehat{MOx}=\alpha$.

Khi đó ta có: sinα = y₀ và cosα = x₀.

Mà M thuộc đường tròn lượng giác nên $x_0^2+y_0^2=O{M}^2$.

⇔ sin²α + cos²α = 1.

Vậy ta có điều phải chứng minh.

Câu 19: Trong lớp 10C có 16 học sinh giỏi Toán, 15 học sinh giỏi Lí, 11 học sinh giỏi Hóa. Biết rằng có 9 học sinh vừa giỏi Toán và Lí, 6 học sinh vừa giỏi Lí và Hóa, 8 học sinh vừa giỏi Hóa và Toán, trong đó có 11 học sinh giỏi đúng 2 môn. Hỏi có bao nhiêu học sinh trong lớp:

a) Giỏi cả ba môn.

b) Giỏi đúng 1 môn.

Lời giải:

a) Gọi A là tập hợp số học sinh giỏi Toán. Tức là, n(A) = 16.

B là tập hợp số học sinh giỏi Lí. Tức là, n(B) = 15.

C là tập hợp số học sinh giỏi Hóa. Tức là, n(C) = 11.

Có 9 học sinh vừa giỏi Toán và Lí. Suy ra n(A ∩ B) = 9.

Có 6 học sinh vừa giỏi Lí và Hóa. Suy ra n(B ∩ C) = 6.

Có 8 học sinh vừa giỏi Hóa và Toán. Suy ra n(A ∩ C) = 8.

Ta có sơ đồ Ven:

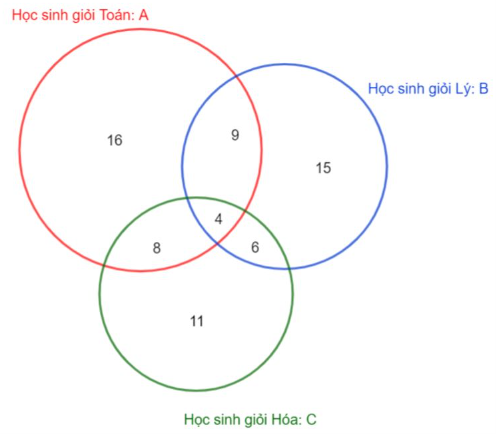
Vì có 11 học sinh chỉ giỏi đúng 2 môn nên ta có:

n(A ∩ B) + n(B ∩ C) + n(C ∩ A) – 3.n(A ∩ B ∩ C) = 11.

⇒ 9 + 6 + 8 – 3.n(A ∩ B ∩ C) = 11.

⇔ n(A ∩ B ∩ C) = 4.

Vậy có 4 học sinh trong lớp 10C giỏi cả ba môn.

b) Xét tổng n(A) + n(B) + n(C), có:

⦁ n(A ∩ B) + n(B ∩ C) + n(A ∩ C) được tính 2 lần nên ta phải trừ đi 1 lần;

⦁ n(A ∩ B ∩ C) được tính 3 lần nên ta phải trừ đi 2 lần.

Trong n(A ∩ B) + n(B ∩ C) + n(A ∩ C), có n(A ∩ B ∩ C) được tính 3 lần, trừ đi 1 lần n(A ∩ B) + n(B ∩ C) + n(A ∩ C) là trừ đi 3 lần n(A ∩ B ∩ C).

Như vậy, số học sinh chỉ giỏi một môn là:

n(A ∪ B ∪ C)

= n(A) + n(B) + n(C) – [n(A ∩ B) + n(A ∩ C) + n(B ∩ C)] + n(A ∩ B ∩ C).

= 16 + 15 + 11 – (9 + 8 + 6) + 4 = 23.

Câu 20: Có bao nhiêu số tự nhiên có 9 chữ số mà các chữ số của nó viết theo thứ tự giảm dần?

A. 5.

B. 15.

C. 55.

D. 10.

Lời giải:

Đáp án đúng là: D

Chọn 9 số từ 10 chữ số trong tập {0; 1; 2; 3; ...; 8; 9} thì có $C_{10}^9$ cách.

Sắp xếp 9 chữ số đó theo thứ tự giảm dần thì có 1 cách xếp.

Vậy ta có tất cả $C_{10}^9.1=10$ số tự nhiên thỏa mãn yêu cầu bài toán.

Do đó ta chọn phương án D.

Câu 21: Tập giá trị T của hàm số y = sin2x là

A. T = [–1; 1].

B. T = [0; 1].

C. T = (–1; 1).

D. T = [–2; 2].

Lời giải:

Đáp án đúng là: A

Ta có –1 ≤ sin2x ≤ 1.

Suy ra –1 ≤ y ≤ 1.

Do đó T = [–1; 1].

Vậy ta chọn phương án A.

Câu 22: Ngoặc vuông và ngoặc tròn trong toán học.

Lời giải:

Ngoặc vuông và ngoặc tròn trong toán học được sử dụng trong các trường hợp sau:

– Thứ tự thực hiện các phép tính trong biểu thức: ( ) → [ ] → { }.

– Biểu diễn một đoạn, khoảng, nửa đoạn, nửa khoảng.

Câu 23: Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh.

Lời giải:

Gọi x là số ha đất trồng ngô, y là số ha đất trồng đậu xanh.

Ta có các điều kiện ràng buộc đối với x, y như sau:

⦁ Hiển nhiên x ≥ 0, y ≥ 0.

⦁ Diện tích canh tác không vượt quá 8 ha nên ta có x + y ≤ 8.

⦁ Số ngày công sử dụng không vượt quá 180 ngày nên 20x + 30y ≤ 180.

⇔ 2x + 3y ≤ 18.

Từ đó, ta có hệ bất phương trình mô tả các điều kiện ràng buộc là:

$\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y\le 8\\ 2x+3y\le 18\end{array}\right.\left(*\right)$.

Yêu cầu bài toán ⇔ Tìm (x; y) thỏa (*) để F(x; y) = 40x + 50y đạt giá trị lớn nhất.

Vẽ và xác định miền nghiệm của (*):

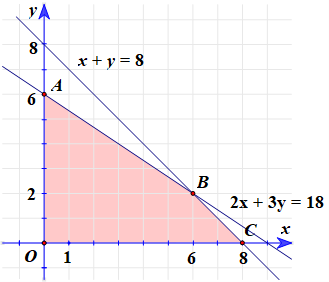
Ta có:

⦁ Miền nghiệm của (*) là tứ giác OABC (kể cả biên).

⦁ O(0; 0), A(0; 6), B(6; 2), C(8; 0).

⦁ F(O) = 0, F(A) = 300, F(B) = 340, F(C) = 320.

Suy ra maxF(x; y) = F(B) = 340 khi và chỉ khi x = 6, y = 2.

Vậy để thu được nhiều tiền nhất thì bác Năm cần trồng 6 ha ngô và 2 ha đậu xanh.

Câu 24: Lớp 10B có 45 học sinh. Trong kì thi học kì I có 20 em đạt loại giỏi môn Toán; 18 em đạt loại giỏi môn Tiếng Anh; 17 em đạt loại giỏi môn Ngữ văn; 5 em đạt loại giỏi cả ba môn học trên và 7 em không đạt loại giỏi môn nào trong ba môn học trên. Số học sinh chỉ đạt loại giỏi một trong ba môn học trên là:

A. 40.

B. 26.

C. 21.

D. 17.

Lời giải:

Đáp án đúng là: B

Gọi x, y, z lần lượt là số học sinh đạt loại giỏi một môn, hai môn và ba môn.

Lập sơ đồ Ven liên hệ giữa các tập hợp, ta có hệ phương trình:

$\left\{\begin{array}{l}x+y+z=45-7\\ x+2y+3z=20+18+17\\ z=5\end{array}\right.\iff \left\{\begin{array}{l}x=26\\ y=7\\ z=5\end{array}\right.$.

Vậy số học sinh chỉ đạt loại giỏi một trong ba môn học trên là 26 học sinh.

Do đó ta chọn phương án B.

Câu 25: Trong lớp 10B có 45 học sinh, 25 học sinh thích môn Văn, 20 học sinh thích môn Toán, 18 học sinh thích môn Sử, 6 học sinh không thích môn nào, 5 học sinh thích cả 3 môn. Hỏi số học sinh chỉ thích một trong 3 môn trên?

Lời giải:

Gọi x, y, z lần lượt là số học sinh thích một môn, hai môn và ba môn.

Lập sơ đồ Ven liên hệ giữa các tập hợp, ta có hệ phương trình:

$\left\{\begin{array}{l}x+y+z=45-6\\ x+2y+3z=25+20+18\\ z=5\end{array}\right.\iff \left\{\begin{array}{l}x=20\\ y=14\\ z=5\end{array}\right.$.

Vậy số học sinh chỉ thích một trong 3 môn trên là 20 học sinh.

Câu 26: Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8 km. Góc tạo bởi hai đoạn dây AC và CB là 70°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.

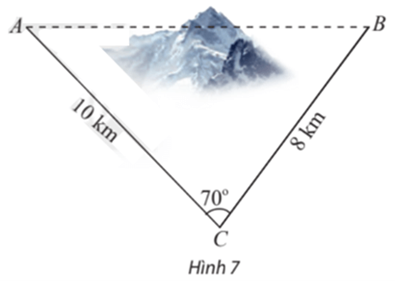
Lời giải:

Áp dụng định lí côsin cho tam giác ABC, ta được:

AB² = AC² + BC² – 2AC.BC.cosC

       = 10² + 8² – 2.10.8.cos70° ≈ 109,3.

Suy ra AB ≈ 10,5.

Ta có (AC + CB) – AB = (10 + 8) – 10,5 = 7,5.

Vậy vì không thể nối trực tiếp từ A đến B nên chiều dài dây tăng thêm 7,5 km.

Câu 27: Phương là gì, chiều là gì, hướng là gì trong toán học?

Lời giải:

Hai vectơ được gọi là cùng phương khi giá của chúng song song hoặc trùng nhau.

Hai vectơ được gọi là cùng hướng (cùng chiều) khi chúng là hai vectơ cùng phương và cùng xác định một hướng.

Câu 28: Tính nhanh: (2354 – 45) – 2354.

Lời giải:

Vận dụng quy tắc dấu ngoặc và tính chất giao hoán, kết hợp, ta có:

(2354 – 45) – 2354 = 2354 – 45 – 2354 = (2354 – 2354) – 45 = –45.

Câu 29: Ba bạn Hồng, Hoa, Lan có tất cả 134 cái bưu ảnh. Biết rằng số bưu ảnh của Hoa nhiều hơn Hồng 14 chiếc song lại kém Lan 16 chiếc. Tính số bưu ảnh của mỗi bạn.

Lời giải:

Ta có sơ đồ như hình vẽ.

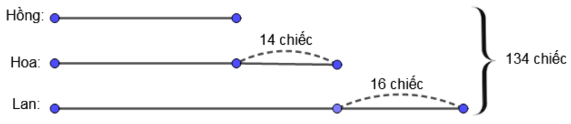
Quan sát sơ đồ, ta thấy nếu Hồng có thêm 14 chiếc bưu ảnh và Lan bớt đi 16 chiếc thì có số bưu ảnh bằng số bưu ảnh của Hoa.

Vậy nếu tổng số bưu ảnh của ba bạn cộng thêm 14 và bớt 16 thì được 3 lần số bưu ảnh của Hoa.

Số bưu ảnh của Hoa là:

(134 + 14 – 16) : 3 = 44 (bưu ảnh).

Số bưu ảnh của Hồng là:

44 – 14 = 30 (bưu ảnh).

Số bưu ảnh của Lan là:

44 + 16 = 60 (bưu ảnh).

Đáp số: Hoa: 44 bưu ảnh;

          Hồng: 30 bưu ảnh;

          Lan: 60 bưu ảnh.

Câu 30: Cách phân biệt góc so le trong và góc đồng vị.

Lời giải:

Cho đường thẳng a cắt hai đường thẳng b và c (b và c song song với nhau).

– Hai góc so le trong:

+ Hai góc không chung gốc.

+ Hai góc đó phải nằm ở phía trong hai đường thẳng b và c.

+ Hai góc đó phải nằm ở vị trí so le nhau, hay nói cách khác, hai góc đó phải nằm ở khác phía so với đường thẳng a.

– Hai góc đồng vị:

+ Hai góc không chung gốc.

+ Hai góc đó phải nằm cùng phía so với đường thẳng a và nằm ở vị trí giống nhau trên hai đường thẳng b và c.

Câu 31: Tính bằng cách thuận tiện: (–525) – [(475 + 245) – 45].

Lời giải:

(–525) – [(475 + 245) – 45]

= – (525 + 475) – (245 – 45)

= –1000 – 200

= –1200.

Câu 32: Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọc. Có bao nhiêu cách xếp hàng khác nhau nếu ông hay bà An đứng ở đầu hoặc cuối hàng.

A. 720;

B. 1440;

C. 18 720;

D. 40 320.

Lời giải:

Đáp án đúng là: B

• Trường hợp 1: Ông An đứng ở đầu hàng, bà An đứng ở cuối hàng và 6 người con đứng ở giữa.

Khi đó có tất cả 6! cách sắp xếp.

• Trường hợp 2: Ông An đứng ở cuối, bà An đứng ở đầu hàng và 6 người con đứng ở giữa.

Khi đó có tất cả 6! cách sắp xếp.

Số cách xếp hàng khác nhau nếu ông hay bà An đứng ở đầu hoặc cuối hàng là:

2 . 6! = 2 . 720 = 1 440 (cách)

Vậy có 1 440 cách cần tìm.

Do đó ta chọn phương án B.

Câu 33: Một tấm vải dài 36m. Lần đầu người ta cắt ra 16 mảnh vải, mỗi mảnh vải dài $1\frac{1}{5}$m. Lần thứ hai người ta cắt được 6 mảnh vải dài như nhau thì vừa hết tấm vải. Hỏi mỗi mảnh vải cắt ra ở lần thứ hai dài bao nhiêu mét?

Lời giải:

Đổi: $1\frac{1}{5}$ m = 1,2 m.

Số mét vải cắt ra lần đầu là:

1,2 × 16 = 19,2 (m)

Số mét vải cắt ra lần thứ hai là:

36 – 19,2 = 16,8 (m)

Mỗi mảnh vải cắt ra ở lần thứ hai dài số mét là:

16,8 : 6 = 2,8 (m)

Đáp số: 2,8 m.

Câu 34: Trước nửa đêm là bao nhiêu phút nếu trước đó 32 phút thời gian này gấp 3 lần số phút sau 22 giờ?

Lời giải:

Trước nửa đêm: 24 giờ.

Số phút trước nửa đêm cần tìm là: x.

Trước đó 30 phút, tức là x – 32.

Thời gian này gấp 3 lần số phút sau 22 giờ: x . 3 + 22 . 60.

Ta có phương trình: 24 . 60 – x – 32 = x . 3 + 22 . 60.

⇒ 1408 – x = x . 3 + 1320.

⇒ 4 . x = 88.

⇒ x = 88 : 4.

⇒ x = 22.

Vậy trước nửa đêm 22 phút thỏa mãn yêu cầu bài toán.

Câu 35: Một cửa hàng bán trái cây nhập khẩu 500 kg cam với giá 40 000 đồng/kg. Phí vận chuyển của chuyến hàng là 4 000 000 đồng. Giả sử rằng 10% số kg cam trên bị hư trong quá trình vận chuyển và số kg cam còn lại được bán hết. Hỏi giá bán của mỗi kg cam là bao nhiêu để công ty có lợi nhuận 20% so với tiền vốn ban đầu?

Lời giải:

Tổng số tiền mua cam là:

500 . 40 000 = 20 000 000 (đồng)

Tổng số tiền vốn ban đầu là:

20 000 000 + 4 000 000 = 24 000 000 (đồng)

Số lượng cam không bị hư là:

500 . (100% – 10%) = 450 (kg)

Số tiền thu được sau khi bán hết số cam nhập khẩu là:

(100% + 20%) . 24 000 000 = 28 800 000 (đồng)

Giá bán mỗi kg cam là:

28 800 000 : 450 = 64 000 (đồng)

Đáp số: 64 000 đồng.

Câu 36: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = x² – 2(m + 1)x – 3 đồng biến trên khoảng (4; 2018)?

Lời giải:

Hàm số đã cho có a = 1 > 0 và $\frac{-b}{2a}=m+1$ nên hàm số đã cho đồng biến trên khoảng (m + 1; +∞).

Do đó để hàm số đã cho đồng biến trên khoảng (4; 2018) thì (4; 2018) ⊂ (m + 1; +∞).

⇔ m + 1 ≤ 4 ⇔ m ≤ 3.

Mà m là số nguyên dương.

Suy ra m ∈ {1; 2; 3}.

Vậy có 3 giá trị nguyên dương của tham số m thỏa mãn yêu cầu bài toán.