Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 47)

Câu 1: Biểu diễn miền nghiệm của của bất phương trình hai ẩn 2x − y ≥ 0.

Lời giải:

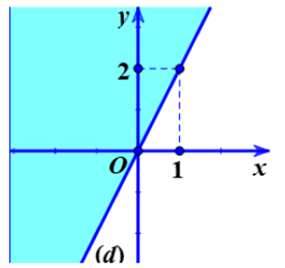
Trong mặt phẳng tọa độ Oxy, vẽ đường thẳng (d): 2x − y = 0.

Ta được đường thẳng (d) chia mặt phẳng Oxy thành hai nửa.

Chọn điểm M(1; 0) không thuộc đường thẳng (d), ta thấy M là nghiệm của bất phương trình bậc nhất 2 ẩn đã cho.

Vì vậy, miền nghiệm cần tìm chính là nửa mặt phẳng bờ (d) và chứa điểm M(1; 0) (miền không được tô màu xanh ở hình vẽ).

Câu 2: Phân tích đa thức sau thành nhân tử: (b − 2c)(a − b) − (a + b)(2c − b).

Lời giải:

(b − 2c)(a − b) − (a + b)(2c − b)

= (b − 2c)(a − b) + (a + b)(b − 2c)

= (b − 2c)(a − b + a + b) = 2a(b − 2c).

Câu 3: Cho góc a ∈ (90°; 180°). Khẳng định nào sau đây đúng?

A. sin a và cot a cùng dấu;

B. Tích sin a.cot a mang dấu âm;

C. Tích sin a.cos a mang dấu dương;

D. sin a và tan a cùng dấu.

Lời giải:

Đáp án đúng là: B

Với góc a ∈ (90°; 180°) thì sin a > 0; cos a < 0; tan a < 0 và cot a < 0

Khi đó:

• sin a và cot a trái dấu

Vậy khẳng định A là sai

• Tích sin a.cot a mang dấu âm

Vậy khẳng định B là đúng

• Tích sin a.cos a mang dấu âm

Vậy khẳng định C là sai

• sin a và tan a trái dấu

Vậy khẳng định D là sai

Chọn đáp án B.

Câu 4: Cho a là góc tù. Mệnh đề nào đúng trong các mệnh đề sau?

A. tan a < 0;

B. cot a > 0;

C. sin a < 0;

D. cos a > 0.

Lời giải:

Đáp án đúng là: A

Với góc a ∈ (90°; 180°) thì sin a > 0; cos a < 0; tan a < 0 và cot a < 0

Khi đó, mệnh đề đúng là tan a < 0.

Chọn đáp án A.

Câu 5: Gọi S là tổng các giá trị nguyên của tham số m để phương trình 4^x + 7 = 2^{x + 3} + m² + 6m có nghiệm x ∈ (1; 3). Chọn đáp án đúng.

A. S = −35;

B. S = 20;

C. S = 25;

D. S = −21.

Lời giải:

Ta có:

4^x + 7 = 2^{x + 3} + m² + 6m

⇔ 4^x − 8.2^x = m² + 6m − 7 (1)

Đặt 2^x = t, với x ∈ (1; 3) thì t ∈ (2; 8)

Phương trình đã cho trở thành

t² − 8t = m² + 6m − 7 (2)

Xét hàm số f (t) = t² − 8t, t ∈ (2; 8)

Lại có f (2) = 12; f (4) = −16; f (8) = 0

Mà hàm f (t) xác định và liên tục trên t ∈ (2; 8)

⇔ −16 < m² + 6m − 7 < 0

⇔ −7 < m < 1

Suy ra m ∈ {−6; −5; −4; −3; −2; −1; 0}

Vậy tổng các giá trị nguyên của tham số m để phương trình có nghiệm x ∈ (1; 3) là:

S = (−6) + (−5) + (−4) + (−3) + (−2) + (−1) + 0 = −21

Chọn đáp án D.

Câu 6: Phương trình 2^{2x + 1} = 32 có nghiệm là:

Lời giải:

Ta có: 2^{2x + 1} = 32

⇔ 2^{2x + 1} = 2⁵

⇔ 2x + 1 = 5

⇔ 2x = 4

⇔ x = 2

Vậy x = 2 là nghiệm của phương trình đã cho.

Câu 7: Tìm số a để:

a) Đa thức x³ + 3x² + 5x + a chia hết cho x + 3

b) Đa thức x³ − 3x + a chia hết cho đa thức x² − 2x + 1

Lời giải:

a) x³ + 3x² + 5x + a = x²(x + 3) + 5(x + 3) + a − 15

= (x + 3)(x² + 5) + a − 15

Vì (x + 3)(x² + 5) ⋮ x + 3 nên để x³ + 3x² + 5x + a ⋮ x + 3 thì

a − 15 = 0 ⇔ a = 15

Vậy a = 15.

b) Đa thức x³ − 3x + a chia hết cho đa thức x² − 2x + 1

x³ − 3x + a = x(x² − 2x + 1) + 2(x² − 2x + 1) + a − 2

= (x² − 2x + 1)(x + 2) + a − 2

Vì (x² − 2x + 1)(x + 2) ⋮ x² − 2x + 1 nên để x³ − 3x + a ⋮ x² − 2x + 1 thì

a − 2 = 0 ⇔ a = 2

Vậy a = 2.

Câu 8: Tìm a để đa thức x³ + 3x² + 5x + a chia hết cho đa thức x + 3

Lời giải:

Ta có: x³ + 3x² + 5x + a

= x²(x + 3) + 5(x + 3) + a − 15

= (x + 3)(x² + 5) + a − 15

Vì (x + 3)(x² + 5) ⋮ x + 3 nên để x³ + 3x² + 5x + a ⋮ x + 3 thì

a − 15 = 0 ⇔ a = 15

Vậy a = 15.

Câu 9: Tìm x, biết: 2 . 3^x = 10 . 3¹² + 8 . 27⁴.

Lời giải:

2 . 3^x = 10 . 3¹² + 8 . 27⁴

2 . 3^x = 10 . 3¹² + 8 . 3¹²

2 . 3^x = 18 . 3¹²

2 . 3^x = 2 . 3² . 3¹²

2 . 3^x = 2 . 3¹⁴

3^x = 3¹⁴

x = 14

Vậy x = 14.

Câu 10: Phân tích đa thức sau thành nhân tử:

a) 4x² + y² − 4xy

b) 27 + 9x² + 27x + x³

c) 8z³ + 1

d) (2z − 3)² − 16

e) (2x − 7)² − (x + 2)²

Lời giải:

a) 4x² + y² − 4xy

= (2x)² − 2.2x.y + y²

= (2x − y)²

b) 27 + 9x² + 27x + x³

= 3³ + 3.3.x² + 3.3².x + x³

= (3 + x)³

c) 8z³ + 1 = (2z)³ + 1

= (2z + 1)(4z² − 2z + 1)

d) (2z − 3)² − 16

= (2z − 3)² − 4²

= (2z − 3 − 4)(2z − 3 + 4)

= (2z − 7)(2z + 1)

e) (2x − 7)² − (x + 2)²

= (2x − 7 − x − 2)(2x − 7 + x + 2)

= (x − 9)(3x − 5)

Câu 11: Phân tích các đa thức sau thành nhân tử

a) 4x² − 4xy + y²

b) 9x³ − 9x²y − 4x + 4y

c) x³ + 2 + 3(x³ − 2)

Lời giải:

a) 4x² − 4xy + y²

= (2x)² − 2.2x.y + y²

= (2x − y)²

b) 9x³ − 9x²y − 4x + 4y

= 9x²(x − y) − 4(x − y)

= (x − y)(9x² − 4)

= (x − y)(3x − 2)(3x + 2)

c) x³ + 2 + 3(x³ − 2)

= x³ + 2 + 3x³ − 6

= 4x³ − 4

= 4(x³ − 1)

= 4(x − 1)(x² + x + 1)

Câu 12: Cho một điểm A cố định và một đường thẳng a cố định không đi qua A. Gọi O là một điểm thay đổi trên a. Chứng minh rằng các mặt cầu tâm O bán kính r = OA luôn luôn đi qua một đường tròn cố định.

Lời giải:

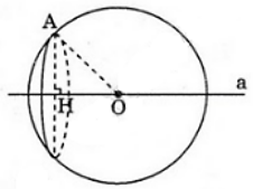
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng a tại H. Khi đó (P) và H cố định.

Ta có: (P) cắt mặt cầu S(O; R) theo đường tròn tâm H và bán kính HA không đổi.

Vậy các mặt cầu tâm O bán kính R = OA luôn đi qua đường tròn cố định tâm H bán kính bằng HA.

Câu 13: Cho hàm số f (x) có đạo hàm trên khoảng (a; b). Trong các mệnh đề sau, mệnh đề nào sai?

A. Nếu f '(x) < 0 với mọi x thuộc (a; b) thì hàm số f (x) nghịch biến trên (a; b);

B. Nếu hàm số f (x) đồng biến trên (a; b) thì f (x) > 0 với mọi x thuộc (a; b);

C. Nếu hàm số f (x) đồng biến trên (a; b) thì f (x) ≥ 0 với mọi x thuộc (a; b);

D. Nếu f '(x) > 0 với mọi x thuộc (a; b) thì hàm số f (x) đồng biến trên (a; b).

Lời giải:

Đáp án đúng là: B

Nếu f '(x) > 0 với mọi x thuộc (a; b) thì hàm số f (x) đồng biến trên (a; b)

Vậy mệnh đề D là đúng

Nếu f '(x) < 0 với mọi x thuộc (a; b) thì hàm số f (x) nghịch biến trên (a; b)

Vậy mệnh đề A là đúng

Nếu hàm số f (x) đồng biến trên (a; b) thì f (x) ≥ 0 với mọi x thuộc (a; b)

Vậy mệnh đề B là sai và mệnh đề C là đúng

Chọn đáp án B.

Câu 14: Cho hàm số y = f (x) có đạo hàm trên (a; b). Phát biểu nào sau đây sai?

A. Hàm số y = f (x) nghịch biến trên khoảng (a; b) khi và chỉ khi f ‘(x) ≤ 0, ∀x ∈ (a; b);

B. Hàm số y = f (x) nghịch biến trên khoảng (a; b) khi và chỉ khi f ‘(x) ≤ 0, ∀x ∈ (a; b) và f ‘(x) = 0 tại hữu hạn giá trị x ∈ (a; b);

C. Hàm số y = f (x) nghịch biến trên khoảng (a; b) khi và chỉ khi ∀x₁, x₂ ∈ (a; b): x₁ > x₂ ⇔ f (x₁) < f (x₂);

D. Nếu f ‘(x) < 0, ∀x ∈ (a; b) thì hàm số y = f (x) nghịch biến trên khoảng (a; b).

Lời giải:

Đáp án đúng là: A

Hàm số y = f (x) nghịch biến trên khoảng (a; b) khi và chỉ khi f ‘(x) ≥ 0, ∀x ∈ (a; b)

Vậy mệnh đề A là sai

Hàm số y = f (x) nghịch biến trên khoảng (a; b) khi và chỉ khi f ‘(x) ≤ 0, ∀x ∈ (a; b) và f ‘(x) = 0 tại hữu hạn giá trị x ∈ (a; b)

Vậy mệnh đề B là đúng

Hàm số y = f (x) nghịch biến trên khoảng (a; b) khi và chỉ khi ∀x₁, x₂ ∈ (a; b): x₁ > x₂ ⇔ f (x₁) < f (x₂)

Vậy mệnh đề C là đúng

Nếu f ‘(x) < 0, ∀x ∈ (a; b) thì hàm số y = f (x) nghịch biến trên khoảng (a; b)

Vậy mệnh đề D là đúng

Chọn đáp án A.

Câu 15: Cho hàm số y = e^{cos x}. Mệnh đề nào sau đây đúng?

A. y'.cos x + y.sin x + y² = 0;

B. y'.sin x + y.cos x + y² = 0;

C. y'.sin x − y².cos x + y' = 0;

D. y'.cos x − y.sin x − y² = 0.

Lời giải:

Đáp án đúng là: B

Ta có: $\left\{\begin{array}{l}{y}^{\text{'}}=-\sin x.e^{\cos x}\\ {y^{\text{'}}}^{\text{'}}={\sin }^{2}x.e^{\cos x}-\cos x.e^{\cos x}\end{array}\right.$

Thay lần lượt vào các đáp án thì ta được đáp án B đúng.

Thật vậy:

Ta có: y' . sin x + y . cos x + y²

= −sin x . e^{cos x}.sin x + e^{cos x} . cos x + sin² x . e^{cos x} − cos x . e^{cos x}  

= −sin² x . e^{cos x} + e^{cos x} . cos x + sin² x . e^{cos x} − cos x . e^{cos x} = 0

Chọn đáp án B.

Câu 16: Cho hàm số y = f (x) xác định và có đạo hàm trên K. Khẳng định nào sau đây là sai?

A. Nếu hàm số y = f (x) đồng biến trên khoảng K thì f ‘(x) ≥ 0, ∀x ∈ K;

B. Nếu f ‘(x) > 0, ∀x ∈ K thì hàm số f (x) đồng biến trên K;

C. Nếu f ‘(x) ≥ 0, ∀x ∈ K thì hàm số f (x) đồng biến trên K;

D. Nếu f ‘(x) ≥ 0, ∀x ∈ K và f ‘(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên K.

Lời giải:

Đáp án đúng là: C

Nếu hàm số y = f (x) đồng biến trên khoảng K thì f ‘(x) ≥ 0, ∀x ∈ K và nếu f ‘(x) > 0, ∀x ∈ K và f ‘(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên K

Vậy khẳng định C là sai

Chọn đáp án C.

Câu 17: Cho K là một khoảng và hàm số y = f (x) có đạo hàm trên K. Khẳng định nào sau đây là sai?

A. Nếu f ‘(x) = 0, ∀x ∈ K thì hàm số đồng biến trên K;

B. Nếu f ‘(x) > 0, ∀x ∈ K thì hàm số đồng biến trên K;

C. Nếu f ‘(x) ≥ 0, ∀x ∈ K thì hàm số đồng biến trên K;

D. Nếu f ‘(x) < 0, ∀x ∈ K thì hàm số nghịch biến trên K.

Lời giải:

Đáp án đúng là: C

Nếu f ‘(x) > 0, ∀x ∈ K và f ‘(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên K.

Nếu f ‘(x) < 0, ∀x ∈ K và f ‘(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên K.

Vậy khẳng định C là sai.

Câu 18: Giá trị lớn nhất và nhỏ nhất của hàm số y = x⁴ + 2x² − 1 trên [−1; 2] lần ượt là M, m. Tính giá trị của tích M . m.

Lời giải:

TXĐ: D = ℝ nên hàm số đã cho xác định và liên tục trên đoạn [−1; 2].

Ta có: y’ = 4x³ + 4x = 0 ⇔ x(x² + 1) = 0

⇔ x = 0 ∈ [−1; 2]

Lại có f (−1) = 2, f (0) = −1, f (2) = 23

Do đó $\left\{\begin{array}{l}M=\underset{\left[1;2\right]}{\max }f\left(x\right)=f\left(2\right)=23\\ m=\underset{\left[1;2\right]}{\min }f\left(x\right)=f\left(0\right)=-1\end{array}\right.$

Vậy M.m = 23.(−1) = −23.

Câu 19: Hình đa diện sau có bao nhiêu mặt?

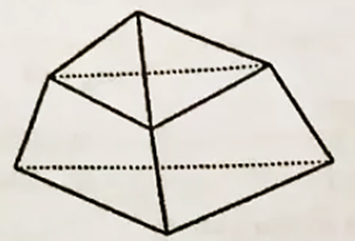
Lời giải:

Hình đa diện trên có 7 mặt.

Câu 20: Hình đa diện sau có bao nhiêu mặt?

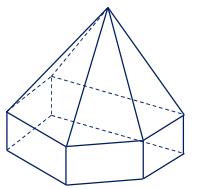
Lời giải:

Hình đa diện trên có 11 mặt.

Câu 21: Làm tính nhân:

a) 3x.(5x² − 2x − 1);

b) (x² + 2xy − 3).(− xy);

Lời giải:

a) 3x.(5x² − 2x − 1)

= 3x.5x² − 3x.2x − 3x.1

= 15x³ − 6x² − 3x 

b) (x² + 2xy − 3).(– xy)

= x².(− xy) + 2xy.(− xy) − 3.(− xy)

= − x³y − 2x²y² + 3xy

Câu 22: Phân tích các đa thức sau thành nhân tử:

a) (x + y)² − (x − y)²

b) x² − 2x − 4y² − 4y

c) x²(x − 1) + 16(1 − x)

Lời giải:

a) (x + y)² − (x − y)²

= (x² + 2xy + y²) − (x² − 2xy + y²)

= x² + 2xy + y² − x² + 2xy − y²

= 4xy

b) x² − 2x − 4y² − 4y

= (x² − 2x + 1) − (4y² + 4y + 1)

= (x − 1)² − (2y + 1)²

= (x − 1 − 2y − 1)(x − 1 + 2y + 1)

= (x − 2y − 2)(x + 2y)

c) x²(x − 1) + 16(1 − x)

= x²(x − 1) − 16(x − 1)

= (x − 1)(x² − 16)

= (x − 1)(x − 4)(x + 4)

Câu 23: Cho ab + bc + ca = 1. Khi đó (a² + 1)(b² + 1)(c² + 1) bằng

A. (a + c + b)²(a + b)²;

B. (a + c)²(a + b)²(b + c);

C. (a + c)² + (a + b)² + (b + c)²;

D. (a + c)²(a + b)²(b + c)².

Lời giải:

Đáp án đúng là: D

Vì ab + bc + ca = 1 nên

(a² + 1)(b² + 1)(c² + 1)

= (a² + ab + bc + ca)(b² + ab + bc + ca)(c² + ab + bc + ca)

= [a(a + b) + c(a + b)][b(a + b) + c(a + b)][b(a + c) + c(a + c)]

= (a + b)(a + c)(a + b)(b + c)(a + c)(b + c)

=  (a + c)²(a + b)²(b + c)²

Vậy (a² + 1)(b² + 1)(c² + 1) bằng (a + c)²(a + b)²(b + c)²

Chọn đáp án D.

Câu 24: Tính tổng tất cả các nghiệm của phương trình 3^2x − 2.3^{x + 2} + 27 = 0.

Lời giải:

3^2x − 2.3^{x + 2} + 27 = 0

⇔ 3^2x − 2.9.3^x + 27 = 0

⇔ 3^2x − 18.3^x + 27 = 0

Theo Vi-ét, ta có::

$3^{x_1}.3^{x_2}=27\Rightarrow 3^{x_1+x_2}=27\Rightarrow x_1+x_2=3$

Vậy tổng các nghiệm của phương trình là 3.

Câu 25: Điều tra thời gian hoàn thành một sản phẩm của 20 công nhân, người ta thu được mẫu số liệu sau (thời gian tính bằng phút).

Kích thước mẫu là bao nhiêu?

Lời giải:

Kích thước của mẫu là: 20.

Câu 26: Điều tra thời gian hoàn thành một sản phẩm của 20 công nhân, người ta thu được mẫu số liệu sau (thời gian tính bằng phút).

Có bao nhiêu giá trị khác nhau trong mẫu số liệu trên?

Lời giải:

Các giá trị khác nhau: 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 23.

Suy ra có 12 giá trị khác nhau.

Câu 27: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, AC = 3a và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ B đến mặt phẳng (SAC).

Lời giải:

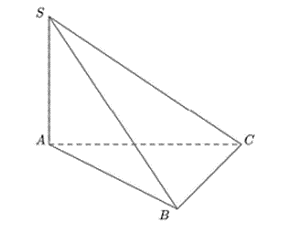
Ta có tam giác ABC vuông cân tại C nên BC ⊥ AC (1) và AC = BC = 3a

Mặt khác SA ⊥ (ABC) ⇒ SA ⊥ BC (2)

Từ (1) và (2) suy ra BC ⊥ (SAC) ⇒ d(B, (SAC)) = BC = 3a

Vậy khoảng cách từ B đến mặt phẳng (SAC) bằng 3a.

Câu 28: Tính đạo hàm của hàm số y = 2^x.

Lời giải:

y = 2^x ⇒ y’ = 2^x.ln 2.

Câu 29: Phân tích đa thức 4x² − 5x + 1 thành nhân tử.

Lời giải:

Ta có: 4x² − 5x + 1

= 4x² − 4x − x + 1

= 4x(x − 1) − (x − 1)

= (x − 1)(4x − 1)

Câu 30: Phân tích đa thức thành nhân tử:

a) 4x² + 5x − 9

b) 4x³ + 4x² − 5x − 3

Lời giải:

a) 4x² + 5x − 9

= 4x² − 4x + 9x − 9

= 4x(x − 1) + 9(x − 1)

= (x − 1)(4x + 9)

b) 4x³ + 4x² − 5x − 3

= 4x³ − 4x² + 8x² − 8x + 3x − 3

= 4x²(x − 1) + 8x(x − 1) + 3(x − 1)

= (x − 1)(4x² + 4x + 3)

Câu 31: Chứng minh x² + y² ≥ 2xy.

Lời giải:

Ta có: (x − y)² ≥ 0, ∀x, y ∈ ℝ

⇔ x² − 2xy + y² ≥ 0, ∀x, y ∈ ℝ

⇔ x² + y² ≥ 2xy, ∀x, y ∈ ℝ

Vậy x² + y² ≥ 2xy (đpcm).

Câu 32: Chứng minh đẳng thức: x² + y² = (x + y)² − 2xy.

Lời giải:

Ta có: VP = (x + y)² − 2xy

= x² + 2xy + y² − 2xy

= x² + y² + 2xy − 2xy

= x² + y² = VT

Suy ra x² + y² = (x + y)² − 2xy

Vậy đẳng thức được chứng minh.

Câu 33: Tìm x biết: 3^{x + 1} = 9^x

Lời giải:

3^{x + 1} = 9^x

⇔ 3^{x + 1} = 3^2x

⇔ x + 1 = 2x

⇔ 2x − x = 1

⇔ x = 1.

Vậy x = 1 là nghiệm cần tìm.

Câu 34: Tìm nghiệm của phương trình 3^{x − 1} = 9.

Lời giải:

3^{x − 1} = 9

⇔ 3^{x − 1} = 3²

⇔ x − 1 = 2

⇔ x = 2 + 1

⇔ x = 3

Vậy x = 3 là nghiệm của phương trình.

Câu 35: Cho tập A = {0; 1; 2; 3; 4; 5}, từ A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau, trong đó nhất thiết phải có chữ số 0 và 3. 

Lời giải:

Số tự nhiên thỏa mãn có dạng $\overline{abcd}$ với a, b, c, d ∈ A và đôi một khác nhau.

• TH1: d = 0

Có 5 cách chọn a; 4 cách chọn b và 3 cách chọn c nên theo quy tắc nhân có: 

5 . 4 . 3 = 60 (số).

• TH2: d ≠ 0

d có 2 cách chọn là 2, 4

Khi đó có 4 cách chọn a (vì a khác 0 và khác d); có 4 cách chọn b và 3 cách chọn c.

Theo quy tắc nhân có: 2 . 4 . 4 . 3 = 96 (số).

Vậy có tất cả: 96 + 60 = 156 (số).

Câu 36: Cho một cấp số cộng (u_n) có u₁ = 5 và tổng 50 số hạng đầu bằng 5150. Tìm công thức của số hạng tổng quát u_n.

Lời giải:

Sử dụng công thức: $S_{50}=\frac{\left(2u_1+49d\right).50}{2}$

⇔ 5150 = 25(2.5 + 49d)

⇔ d = 4.

Vậy công thức của số hạng tổng quát u_n là: u_n = u₁ + (n − 1)d = 5 + (n − 1).4 = 1 + 4n.

Câu 37: Cho dãy số (u_n) là một cấp số cộng, biết u₂ + u₂₁ = 50. Tính tổng của 22 số hạng đầu của dãy.

Lời giải:

Gọi cấp số cộng có công sai d và số hạng đầu u₁.

Khi đó u₂ = u₁ + d; u₂₁ = u₁ + 20d

Do đó u₂ + u₂₁ = 50 ⇔ u₁ + d + u₁ + 20d = 50

⇔ 2u₁ + 21d = 50

Tổng 22 số hạng đầu tiên của dãy là:

$$\begin{gathered} S_{22}=\frac{\left(u_1+u_{22}\right).22}{2}=\frac{\left(u_1+u_1+21d\right).22}{2} \\ =\frac{\left(2u_1+21d\right).22}{2}=\frac{50.22}{2}=550 \end{gathered}$$

Câu 38: Tìm số mặt cầu chứa một đường tròn cho trước.

Lời giải:

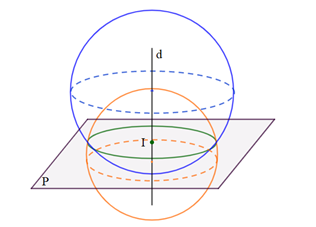
Có vô số mặt cầu chứa một đường tròn cho trước. Tâm các mặt cầu ấy nằm trên trục của đường tròn (đường thẳng đi qua tâm và vuông góc với mặt phẳng chứa đường tròn).

Câu 39: Có bao nhiêu mặt cầu chứa một đường tròn cho trước?

A. Chỉ có 2 mặt cầu;

B. Chỉ có một mặt cầu;

C. Có vô số mặt cầu;

D. Không có mặt cầu nào.

Lời giải:

Đáp án đúng là: C

Có vô số mặt cầu chứa một đường tròn cho trước.

Chọn đáp án C.

Câu 40: Tìm x, biết: 4x + 5 chia hết cho x + 1.

Lời giải:

4x + 5 = 4x + 4 + 1 = 4(x + 1) + 1

Vì 4(x + 1) ⋮ x + 1 nên để 4x + 5 chia hết cho x + 1 thì 1 ⋮ x + 1

⇒ x + 1 ∈ Ư(1) = {±1}

⇒ x ∈ {−2; 0}.

Vậy x ∈ {−2; 0} thì 4x + 5 chia hết cho x + 1.