Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 63)

Câu 1: Tính (7²⁰¹⁴ + 7²⁰¹²) : 7²⁰¹².

Lời giải:

(7²⁰¹⁴ + 7²⁰¹²) : 7²⁰¹²

= 7²⁰¹⁴ : 7²⁰¹² + 7²⁰¹² : 7²⁰¹²

= 7^{2014 – 2012} + 7^{2012 – 2012}

= 7² + 7⁰

= 49 + 1

= 50

Câu 2: Tìm chữ số tận cùng của 7⁹⁹.

Lời giải:

5 lần 7 nhân với nhau có tận cùng là 7, có số nhóm như vậy:

99 : 5  = 19 (dư 4)

Đang có tận cùng là 7 nhân thêm 1 số 7 nữa có tận cùng là 9.

Đang có tận cùng là 9 nhân thêm 1 số 7 nữa có tận cùng là 3.

Đang có tận cùng là 3 nhân thêm 1 số 7 nữa có tận cùng là 1. 

Vậy tận cùng của 7⁹⁹ là 1.

Câu 3: Tìm x:

a) 2(x – 5) – 3(x + 7) = 14;

b) 5(x – 6) – 2(x + 3) = 12;

c) −7(3x – 5) + 2(7x – 14) = 28;

d) 5(3 – 2x) + 5(x – 4) = 6 – 4x.

Lời giải:

a) 2(x – 5) – 3(x + 7) = 14

2x – 10 – 3x – 21 = 14

−x = 14 + 31

x = −45

Vậy x = −45

b) 5(x – 6) – 2(x + 3) = 12

5x – 30 – 2x – 6 = 12

3x = 12 + 36

3x = 48

x = 16

Vậy x = 16.

c) −7(3x – 5) + 2(7x – 14) = 28

−21x + 35 + 14x – 28 = 28

−7x = 28 – 7

−7x = 21

x = −3

Vậy x = −3

d) 5(3 – 2x) + 5(x – 4) = 6 – 4x

15 – 10x + 5x – 20 = 6 – 4x

−5x + 4x = 6 + 5

−x = 11

x = −11

Vậy x = −11

Câu 4: Tìm x:

a) −5(2 – x) + 4(x – 3) = 10x – 15;

b) 2(4x – 8) – 7(3 + x) = |−4|(3 – 2);

c) 8(x – |−7|) – 6(x – 2) = |−8|.6 – 50.

Lời giải:

a) −5(2 – x) + 4(x – 3) = 10x – 15

−10 + 5x + 4x – 12 = 10x – 15

9x – 22 = 10x – 15

10x – 9x = 15 – 22 

x= −7

Vậy x = −7

b) 2(4x – 8) – 7(3 + x) = |−4|(3 – 2)

8x – 16 – 21 – 7x = 4

x – 37 = 4

x = 41

Vậy x = 41

c) 8(x – |−7|) – 6(x – 2) = |−8|.6 – 50

8x – 56 – 6x + 12 = 48 – 50

2x = −2 + 44

2x = 42

x = 21

Vậy x = 21

Câu 5: Tìm m để bất phương trình x² – 2(m + 1) + m² + 2m ≤ 0 có nghiệm với mọi m ∈ [0; 1].

Lời giải:

Đặt x² – 2(m + 1) + m² + 2m = f(x)

Bất phương trình có nghiệm đúng với x ∈ [0; 1]

Phương trình f(x) = 0 có hai nghiệm thỏa mãn

x₁ ≤ 1 < 2 ≤ x₂ ⇔ $\left\{\begin{array}{l}kf\left(0\right)\le 0\\ kf\left(1\right)\le 0\end{array}\right.\iff \left\{\begin{array}{l}{m}^2+2m\le 0\\ m^2-1\le 0\end{array}\right.$

$\iff \left\{\begin{array}{l}-2\le m\le 0\\ -1\le m\le 1\end{array}\right.\iff -1\le m\le 0$

Vậy với −1 ≤ m ≤ 0 thỏa mãn yêu cầu bài toán.

Câu 6: Điền vào chỗ trống:

2,5 phút = …. phút … giây.

Lời giải:

2,5 phút = 2 phút 30 giây.

Câu 7: Cho đa thức P(x) = x⁴ – 4x² + 5 – 2x. Tìm đa thức Q(x) sao cho

P(x) + Q(x) = 2x² + 4x – 3.

Lời giải:

Ta có: P(x) + Q(x) = 2x² + 4x – 3.

⇔ Q(x) = 2x² + 4x – 3 – (x⁴ – 4x² + 5 – 2x) = −x⁴ + 6x² + 6x – 8.

Vậy Q(x) = −x⁴ + 6x² + 6x – 8.

Câu 8: Đa thức P(x) bậc 4 có hệ số bậc cao nhất là 1. Biết P(1) = 0; P(3) = 0; P(5) = 0. Hãy tính giá trị của biểu thức Q = P(−2) + 7P(6).

Lời giải:

P(1) = 0; P(3) = 0; P(5) = 0 nên 1 ; 3 ; 5 lần lượt là nghiệm của phương trình nên

P(x) chứa nhân tử (x – 1); (x – 3); (x – 5)

Vì P(x) bậc 4 có hệ số bậc cao nhất là một nên P(x) có dạng:

P(x) = (x – 1)(x – 3)(x – 5)(x – a)

Q = P(–2) + 7P(6)

= (–2 – 1)( –2 – 3)( –2 – 5)( –2 – a) + 7(6 – 1)(6 – 3)(6 – 5)(6 – a)

= 210 + 105a + 7(90 - 15a)

= 210 + 105a + 630 - 105a

= 840

Câu 9: Cho hình chóp SABCD, có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và SC. Tìm giao tuyến của (SMN) và (SBD).

Lời giải:

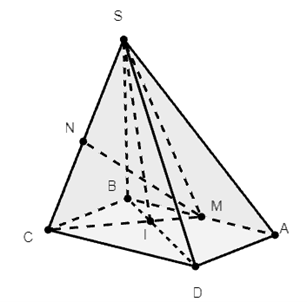
Ta có: M ∈ SM, N ∈ SC, SM ∩ SC = {S}

⇒ MN ∈ (SMC)

Gọi BD ∩ MC = {I}

⇒ I ∈ (SMC)

I ∈ BD, BD ∈ (SBD)

⇒ I ∈ (SBD)

Ta thấy: (SBD) và (SMC) có chung điểm S, BD ∩ MC = {I}

⇒ SI là giao tuyến của (SBD) và (SMC)

Hay SI là giao tuyến của (SBD) và (SMN).

Câu 10: Có một ca 1 l và một ca 300 ml. Chỉ dùng hai ca đó, làm thế nào để lấy được 400 ml từ xô nước.

Lời giải:

Lấy 1 l nước từ xô nước

Tiến hành đổ nước từ ca 1l vào ca 300 ml hai lần (cả hai lần đã đổ đi 600 ml nước)

Lượng nước còn lại trong ca 1 l khi đó sẽ còn 400 ml.

Câu 11: Liệt kê các số chẵn từ 0 đến 98.

Lời giải:

Các số chẵn từ 0 đến 98:

0; 2; 4; 6; 8;…; 96; 98.

 Quy luật số liền sau cách số liền trước hai đơn vị.

Câu 12: Một lớp có 7 học sinh giỏi Toán, 5 học sinh giỏi Văn, 6 học sinh giỏi Lịch Sử. Hỏi có bao nhiêu cách chọn ra

a) 3 học sinh giỏi?

b) 3 học sinh giỏi trong đó có tất cả học sinh giỏi của cả 3 môn?

c) 2 học sinh giỏi ở hai bộ môn khác nhau?

Lời giải:

a) Số cách chọn số học sinh giỏi là:

 (cách chọn)

b) Số cách chọn 3 học sinh giỏi trong đó có tất cả học sinh giỏi của cả 3 môn là:

7.5.6 = 210 (cách)

c) Số cách chọn 2 học sinh giỏi ở hai bộ môn khác nhau là:

7.5 + 5.6 + 7.6 = 107 (cách)

Đáp số:

a) 816 cách

b) 210 cách

c) 107 cách

Câu 13: Giải phương trình: log₂x + log₃x + log₄x = log₂₀x

Lời giải:

Điều kiện: x > 0

Ta có:

log₂x + log₃x + log₄x = log₂₀x

$$\begin{gathered} \iff {\log }_{2}x+\frac{{\log }_{2}x}{{\log }_{2}3}+\frac{{\log }_{2}x}{{\log }_{2}4}=\frac{{\log }_{2}x}{{\log }_{2}20} \\ \iff {\log }_{2}x\left(1+\frac{1}{{\log }_{2}3}+\frac{1}{2}-\frac{1}{{\log }_{2}20}\right)=0 \end{gathered}$$

⇔ log₂x = 0

⇔ x = 1 (thỏa mãn)

Vậy phương trình đã cho có nghiệm duy nhất x = 1.

Câu 14: Rút gọn biểu thức (a + b)³ – (a – b)³ – 2b³.

Lời giải:

(a + b)³ – (a – b)³ – 2b³

= a³ + 3a²b + 3ab² + b³ – (a³ – 3a²b + 3ab² – b³) – 2b³

= a³ + 3a²b + 3ab² + b³ – a³ + 3a²b – 3ab² + b³) – 2b³

= (a³ – a³) + (3a²b +3a²b) + (3ab² – 3ab²) + (b³ + b³– 2b³)

= 0 + 6a²b + 0 + 0 = 6a²b

Câu 15: Một hình chữ nhật có độ dài cạnh lần lượt là 15 cm, 12 cm, nếu giảm một cạnh đi 3 cm thì phải tăng cạnh kia bao nhiêu cm để diện tích chữ nhật không đổi.

Lời giải:

Diện tích ban đầu là: 15 × 12 = 180 (cm²)

Chiều dài sau giảm là: 15 – 3 = 12 (cm)

Cạnh còn lại phải có độ dài để diện tích không đổi là: 180 : 12 = 15 (cm)

Vậy chiều rộng tăng: 15 – 12 = 3 (cm)

Nếu giảm chiều rộng 3 cm thì chiều rộng còn: 12 – 3 = 9 (cm)

Cạnh còn lại phải có độ dài để diện tích không đổi là: 180 : 9 = 20 (cm)

Vậy chiều dài phải tăng: 20 – 15 = 5 (cm).

Câu 16: Tìm x, biết:

a) (8x² – 4x) : (−4x) – (x + 2) = 8;

b) (2x⁴ – 3x³ + x²) : (−x²) + 4(x – 1)² = 0.

Lời giải:

a) (8x² – 4x) : (−4x) – (x + 2) = 8

−2x + 1 – x – 2 = 8

−3x = 9

x = −3.

Vậy x = −3.

b) (2x⁴ – 3x³ + x²) : (−x²) + 4(x – 1)² = 0

−2x² + 3x – 1 + 4x² – 8x + 4 = 0

2x² – 5x + 3 = 0

2x² – 2x – (3x – 3) = 0

2x(x – 1) – 3(x – 1) = 0

(x – 1)(2x – 3) = 0

x – 1 = 0 hoặc 2x – 3 = 0

x = 1 hoặc $x=\frac{3}{2}$

Vậy $x\in \left\{1;\frac{3}{2}\right\}$ .

Câu 17: Rút gọn biểu thức:

4x²(5x² + 3) – 6x (3x² – 2x + 1) – 5x³(2x – 1)

Lời giải:

4x²(5x² + 3) – 6x (3x² – 2x + 1) – 5x³(2x – 1)

= 4x².5x² + 4x².3 + (–6x).3x² + (–6x).( –2x) + (–6x).1 + (–5x³).2x + (–5x³).( –1)

= 20x⁴ + 12x² + (–18x³) + 12x² + (–6x) + (–10x⁴) + 5x³

= 20x⁴ + 12x² – 18x³ + 12x² – 6x – 10x⁴ + 5x³

= (20x⁴ – 10x⁴) + (–18x³ + 5x³) + (12x² + 12x²) – 6x

= 10x⁴ + (–13x³) + 24x² – 6x

= 10x⁴ – 13x³ + 24x² – 6x.

Câu 18: 0.1 vs 0.125 cái nào lớn hơn

Lời giải:

Ta có: 0,1 = 0,100

Vì 0,100 < 0,125 nên 0,1 < 0,125.

Câu 19: Hình trụ có bán kính đáy bằng a và thiết diện qua trục là một hình vuông. Ta có thể tích khối trụ đó bằng bao nhiêu?

Lời giải:

Do thiết diện tạo thành là một hình vuông nên độ dài đường cao h của hình trụ bằng 2 bán kính r của đáy.

Do đó h = 2r = 2a.

Khi đó thể tích hình trụ là V = πr²h = πa²(2a) = 2a²π.

Câu 20: Một hình trụ có bán kính đáy bằng a, chu vi thiết diện qua trục bằng 10a. Thể tích của khối trụ đã cho bằng bao nhiêu?

Lời giải:

Gọi ABCD là thiết diện qua trục của hình trụ, ta có ABCD là hình chữ nhật.

Từ giả thiết ta có: AB = 2a và 2(AB + BC) = 10a

BC = 3a.

Vậy thể tích khổi trụ đã cho bằng V = πa² . 3a = 3πa³.

Câu 21: Người ta xếp các số tự nhiên vào nhóm (1); (2; 3); (4; 5; 6); (7; 8; 9; 10).... Hỏi số đầu tiên của nhóm thứ 100 là bao nhiêu?

Lời giải:

Số cuối cùng của nhóm thứ 99 là: (99 + 1) × 99 : 2 = 4 950

Số đầu tiên của nhóm thứ 100 là 4 951.

Câu 22: Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4 m còn kích thước cửa ở giữa là 3 m × 4 m. Hãy tính khoảng cách giữa hai điểm A và B.

Lời giải:

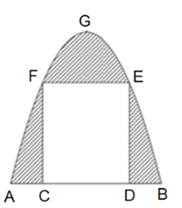
Đỉnh G có tọa độ (0; 4) nên

a . 0² + b . 0 + c = 4

Do đó c = 4.

Điểm D có tọa độ (2; 3) nên a . 2² + b . 2 + 4 = 3

⇒ 4a + 2b = −14  (1)

Điểm C có tọa độ (–2; 3) nên a . (−2)² + b . (−2) + 4 = 3

4a – 2b = −14 (2)

Từ (1) và (2) suy ra a = – 0,25; b = 0.

Khi đó parabol có dạng y = −0,25 . x² + 4

Điểm A và B có tung độ y = 0

⇒ −0,25 . x² + 4 = 0

⇒ x = 4 hoặc x = – 4

Suy ra điểm B có tọa độ (4; 0) và điểm A có tọa độ (– 4; 0).

Vậy khoảng cách giữa hai điểm A và B là 8.

Câu 23: Chiều rộng của một đám đất hình chữ nhật là 16,5m, chiều rộng bằng $\frac{1}{3}$ chiều dài. Trên thửa ruộng đó người ta trồng cà chua. Hỏi người ta thu hoạch được bao nhiêu tạ cà chua biết mỗi mét vuông thu hoạch được 6,8 kg cà chua?

Lời giải:

Chiều dài đám đất là 16,5 × 3 = 49,5 (m)

Diện tích đám đất là 49,5 × 16,5 = 816,75 (m²)

Người ta thu hoạch được là:

816,75 × 6,8 = 5 553,9 (kg)

Đổi: 5 553,9 kg = 55,539 tạ

Đáp số: 55,539 tạ.

Câu 24: Biện luận m để (1 + m)x² – 2mx + 2m = 0 có nghiệm.

Lời giải:

∆' = (–m)² – 2m(1 + m) = –m² – 2m

để pt có nghiệm thì ∆^’ ≥ 0

–m² – 2m ≥ 0

–m(m – 2) ≥ 0

m ≤ 0 hoặc m ≥ 2

vậy 0 ≥ m ≥ 2

Câu 25: Cho phương trình x²– 2mx² + m²– 2m = 0 có nghiệm x = 2. Tìm nghiệm còn lại.

Lời giải:

Thay x = 2 vào phương trình:

2² – 2m2² + m² – 2m = 0

m² – 10m + 4 = 0

$\iff \left\{\begin{array}{l}{m}_1=5+\sqrt{21}\\ m_2=5-\sqrt{21}\end{array}\right.$

Lâng lượt thay m vào ta được x₁ = 2, x₂ = – 2

Vậy nghiệm còn lại là – 2

Câu 26: Có bao nhiêu cách xếp 5 bạn nam và 5 bạn nữ vào 10 ghế được kê thành hàng ngang, sao cho:

a) Nam và nữ ngồi xen kẽ nhau.

b) Các bạn nam ngồi liền nhau.

Lời giải:

Để xác định, các ghế được đánh số từ 1 đến 10 tính từ trái sang phải.

Nếu các bạn nam ngồi ở các ghế ghi số lẻ thì các bạn nữ ngồi ở các ghế còn lại. Có 5! cách xếp bạn nam, 5! cách xếp bạn nữ. Tất cả có (5!)² cách xếp.

Nếu các bạn nam ngồi ở các ghế ghi số chẵn, các bạn nữ ngồi ở các ghế còn lại thì có (5!)² cách xếp nam và nữ.

Vậy có tất cả 2. (5!)² cách xếp nam nữ ngồi xen kẽ nhau.

Câu 27: Tìm số ước của số 10 000 (các ước là số tự nhiên)

Lời giải:

Ta có: 10 000 = 2⁴.5⁴
Do đó 10 000 có tất cả (4 + 1)(4 + 1) = 25 ước số tự nhiên.

Câu 28: Người thợ may lấy một tấm vải để cắt may 10 bộ quần áo thì còn thừa 1,5 m. Hỏi lúc đầu tấm vải đó dài bao nhiều mét? Biết rằng mỗi bộ quần áo may hết 2,35 m vải

Lời giải:

Tấm vải đó dài số mét là:

2,35 × 10 + 1,5 = 25 (m)

Đáp số: 25 m

Câu 29: Người thợ may lấy ra một tấm vải lớn để cắt may 25 bộ quần áo cho công ty, mỗi chiếc ao may hết 500 cm vải, mỗi chiếc quần may hết 685 cm vải. Sau khi cắt xong thì tấm vải còn lại 5 dam. Vậy tấm vải ban đầu dài là bao nhiêu?

Lời giải:

Đổi 5 dam = 5 000 cm

Số vải dùng để may 1 bộ quần áo là

500 + 685 = 1 185 (cm)

Số vải dùng để may 25 bộ quần áo là:

1 185 ×25 = 29 625 (cm)

Tấm vải ban đầu dài là:

29 625 + 5 000 = 34 625 (cm)

Đáp số: 34 625 cm vải.

Câu 30: Khi nào 4 + 9 = 1?

Lời giải:

4 giờ + 9 giờ = 13 giờ

Mà 13 giờ là 1 giờ chiều.

Câu 31: Khi nào 9 – 1 = 10?

Lời giải:

Khi số 9 được viết bằng số la mã IX.

IX bỏ đi 1 (I) sẽ được 10 (X).

Câu 32: Tổng hai số là 19,1. Nếu giảm số hạng thứ nhất đi 4 lần và giữ nguyên số hạng thứ hai thì được tổng mới là 7,4. Tìm hai số đó.

Lời giải:

Tổng cũ hơn tổng mới  là :

4 – 1 = 3 ( lần số hạng thứ nhất)

Giá trị của 3 lần số hạng thứ nhất là :

19,1 – 7,4 = 11,7

Số hạng thứ nhất là 11,7 : 3 × 4 = 15,6

Số thứ hai là:   19,1 – 15,6 = 3,5

Đáp số: Số thứ nhất: 15,6;

   Số thứ hai là 3,5.

Câu 33: Tổng hai số là 678. Nếu giảm số hạng thứ nhất đi 56, tăng số hạng thứ hai lên 39 thì tổng là bao nhiêu?

Lời giải:

Giảm số hạng thứ nhất đi 56 thì tổng giảm đi 56 đơn vị. Tổng mới lúc này là: 678 – 56 = 622

Sau đó, tăng số hạng thứ hai lên 39 thì tổng lại tăng lên 39 đơn vị.

Tổng mới là: 622 + 39 = 661

Đáp số: 661.

Câu 34: Người ta cần sử dụng 300 viên gạch hình vuông có cạnh 30 cm để lát kín một căn phòng. Hỏi căn phòng có diện tích bao nhiêu mét vuông? Biết diện tích mạch vữa không đáng kể.

Lời giải:

Diện tích một viên gạch là :

30 × 30 = 900 (cm²)

Diện tích căn phòng là:

900 × 300 = 270 000 (cm²)

Đổi: 270 000 cm² = 27 m².

Đáp số: 27 m².

Câu 35: Để lát một phòng họp người ta cần dùng hết 400 viên gạch lát nền hình vuông có cạnh 5 dm. Tính diện tích phòng họp (Biết diện tích mạch vữa không đáng kể).

Lời giải:

Diện tích một viên gạch là :

5 × 5 = 25 (dm²)

Diện tích căn phòng là:

25 × 400 = 10 000 (dm²)

Đổi: 10 000 dm² = 100 m²

Đáp số: 100 m².

Câu 36: 5 giờ 40 phút = … phút

Lời giải:

5 giờ 40 phút = 300 phút + 40 phút = 340 phút

Vậy 5 giờ 40 phút = 340 phút.

Câu 37: Tính 5 giờ 40 phút + 2,5 giờ – 38 phút

Lời giải:

5 giờ 40 phút + 2,5 giờ – 38 phút

= 300 phút + 40 phút + 150 phút – 38 phút

= 452 phút

Vậy 5 giờ 40 phút + 2,5 giờ – 38 phút = 452 phút

Câu 38: 7 m 10 dm = … dm

Lời giải:

Ta có 7 m 10 dm = 70 dm + 10 dm = 80 dm

Vậy 7 m 10 dm = 80 dm

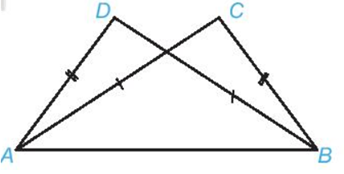
Câu 39: Cho hình vẽ dưới đây, biết AD = BC, AC = BD. Chứng minh

∆ADB = ∆BCA 

Lời giải:

Hai tam giác ADB và BCA có:

AD = BC (theo giả thiết)

BD = AC (theo giả thiết)

AB là cạnh chung

Vậy ∆ADB = ∆BCA (c.c.c)