Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 31)

Câu 1: Giải phương trình: x⁵ + x⁴ – x³ + x² – x + 2 = 0.

Lời giải:

x⁵ + x⁴ - x³ + x² – x + 2 = 0

⇔ x⁵ + 2x⁴ – x⁴ – 2x³ + x³ + 2x² – x² – 2x + x + 2 = 0

⇔ x⁴(x + 2) – x³(x + 2) + x²(x + 2) – x(x + 2) + (x + 2) = 0

⇔ (x + 2)(x⁴ – x³ + x² – x + 1) = 0      (1)

Ta xét phương trình: x⁴ – x³ + x² – x + 1 = 0            (2)

$\iff {\left(x^2-\frac{1}{2}x\right)}^2+{\left(\frac{\sqrt{3}}{2}x-\frac{2}{\sqrt{3}}\right)}^2+\frac{1}{3}=0$

Do ${\left(x^2-\frac{1}{2}x\right)}^2+{\left(\frac{\sqrt{3}}{2}x-\frac{2}{\sqrt{3}}\right)}^2+\frac{1}{3}>0\forall x$

Nên phương trình (2) vô nghiệm

Suy ra phương trình (1) tương đương với:

x + 2 = 0 ⇔ x = –2

Vậy tập nghiệm của phương trình là S = {2}.

Câu 2: Tổng của hai số bằng 10,45. Tìm hai số đó, biết rằng nếu số hạng thứ nhất cộng với 4 lần số hạng thứ hai thì được 22,45.

Lời giải:

Gọi số thứ nhất là a, số thứ hai là b 

Ta có a + b = 10,45

a + 4b = 22,45

3b = 22,45 – 10,45 

3b = 12,45 

b = 4,15 

Do đó a = 10,45 – 4,15 hay a = 6 ,3 

Vậy số thứ nhất là 6,3; số thứ hai là 4,15.

Câu 3: Giải phương trình: x . 3,9 + x . 0,1 = 2,7

Lời giải:

x . 3,9 + x . 0,1 = 2,7

⇔ x . (3,9 + 0,1) = 2,7

⇔ x = 2,7 : 4 

⇔ x = 0,625

Vậy nghiệm của phương trình là x = 0,625.

Câu 4: Trên quãng đường AC có điểm B. Lúc 7 giờ, người thứ nhất đi từ A, người thứ hai đi từ B, cả 2 người cùng đến C lúc 10 giờ. Trên đường đi, người thứ hai gặp một chiếc xe lửa đi từ C đến A vào lúc 8 giờ 30 phút, người thứ nhất gặp chiếc xe lửa đó vào lúc 8 giờ 40 phút. Biết rằng AB dài 30 km và vận tốc xe lửa gấp đôi người thứ nhất. Hỏi xe lửa đi từ C lúc mấy giờ, và quãng đường AC dài bao nhiêu?

Lời giải:

Xe lửa gặp người thứ hai lúc 8 giờ 30 phút ở D, gặp người thứ nhất lúc 8 giờ 40 phút ở E.

Thời gian người thứ nhất đi EC là:

10 giờ – 8 giờ 40 phút = 80 phút
Thời gian xe lửa đi CE là:

80 : 2 = 40 (phút)
Xe lửa khởi hành từ C lúc là:
8 giờ 40 phút – 40 phút = 8 giờ
Thời gian xe lửa đi CD là:
8 giờ 30 phút – 8 giờ = 30 phút
Thời gian người thứ hai đi CD là:

10 giờ – 8 giờ 30 phút = 90 phút
Tỉ số vận tốc xe lửa và vận tốc người thứ hai là:

90 : 30 = 3 (lần)

Tỉ số vận tốc người thứ nhất và vận tốc người thứ hai là:

3 : 2= 1,5 (lần)

Quãng đường AC gấp rưỡi quãng đường BC nên quãng đường AC gấp ba AB, tức là:

30 . 3 = 90 (km)

Câu 5: Tìm các số tự nhiên x sao cho: x ⋮ 15 và 0 < x < 40.

Lời giải:

Vì x ⋮ 15 nên x ∈ B(15) = {0; 15; 30; 45; 60; 75;…}.

Mà 0 < x < 40 nên x ∈ {15; 30}.

Câu 6: Hai ông bà Brain cùng đến một buổi gặp mặt với 4 cặp vợ chồng khác nhân dịp năm mới. Nhóm người này tiến hành bắt tay nhau (không nhất thiết phải bắt tay với tất cả), nhưng không ai bắt tay với vợ/chồng của mình. Sau khi bắt tay, ông Brain đến hỏi từng người xem họ bắt tay với bao nhiêu người. Tất cả đều trả lời trung thực và thật ngạc nhiên là mỗi người lại đưa ra một con số khác nhau. Hỏi vợ chồng ông bà Brain bắt tay với bao nhiêu người?

Lời giải:

Chúng ta có 10 người trong nhóm và mỗi người có thể bắt tay với 0; 1; 2; 3; 4; 5; 6; 7 hoặc 8 người.

• Người bắt tay với 8 người sẽ bắt tay với tất cả mọi người ngoại trừ vợ/chồng của chính mình.

Vì mọi người khác bắt tay với ít nhất 1 người, điều đó có nghĩa là vợ/chồng của người này phải là người bắt tay với người trả lời là 0.

Câu trả lời của 8 và 0 được ghép nối, và đây là một cặp vợ chồng.

• Người bắt tay với 7 người, có nghĩa là bắt tay với tất cả mọi người ngoại trừ người vợ/chồng của chính họ và người trả lời 0.

Bây giờ mọi người khác, ngoại trừ bạn đời và người trả lời 0, phải bắt tay với ít nhất 2 người, nghĩa là vợ/chồng của người đó phải là người bắt tay với 1 người.

Câu trả lời của 7 và 1 được ghép nối, và đây là một cặp vợ chồng.

• Tương tự có thể được tiếp tục cho thấy rằng câu trả lời của 6 và 2 là một cặp vợ chồng, cũng như câu trả lời của 5 và 3.

Theo phương pháp loại trừ, câu trả lời còn lại phải là câu trả lời của bà Brain, người đã bắt tay với 4 người.

Ông Brain sẽ bắt tay với những người đưa ra câu trả lời 8, 7, 6 và 5 nên ông ấy không thể bắt tay với người trả lời 4 (vợ anh ta).

Câu trả lời 3 bắt tay với câu trả lời 8, 7 và 6; câu trả lời 2 bắt tay với câu trả lời 8 và 7; và câu trả lời của 1 bắt tay với câu trả lời là 8.

Câu trả lời 0 không bắt tay ai.

Do đó, ông Brain bắt tay với đúng 4 người, giống như vợ mình.

Vậy vợ chồng ông Brain mỗi người bắt tay với 4 người.

Câu 7: Cho đường tròn tâm O đường kính 10 cm. Gọi H là trung điểm của dây AB. Tính độ dài đoạn OH, biết AB = 6 cm.

Lời giải:

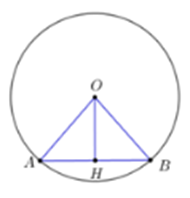
Xét đường tròn (O) ta có H là trung điểm của dây cung AB

Ta có OH ⊥ AB tại H (mối liên hệ giữa đường kính và dây cung).

Áp dụng định lý Py-ta-go cho tam giác OAH vuông tại H có:

OH² = OA² − AH² = $R^2-{\left(\frac{AB}{2}\right)}^2$= 5² – 3² = 4²

Do đó OH = 4 cm.

Câu 8: Khi nhân một số có 5 chữ số với 1000, Hồng cho kết quả là số có 9 chữ số còn Hà cho kết quả là số có chữ số hàng trăm là 6. Hỏi kết quả của ai đúng?

Lời giải:

Gọi số có 5 chữ số đó là $\overline{abc\text{d}e}$.

Ta có: $\overline{abc\text{d}e}\cdot 1000=\overline{abc\text{d}e000}$.

Xét chữ số hàng trăm của $\overline{abc\text{d}e000}$ bằng 0.

Xét số $\overline{abc\text{d}e000}$ có 8 chữ số

Vậy kết quả của cả 2 bạn đều sai.

Câu 9: Thu gọn: S = 1 + x + x² + x³ + …. + xⁿ

Lời giải:

S = 1 + x + x² + x³ + …. + xⁿ

⇔ S = x⁰ + x¹ + x² + x³ + ...... + xⁿ

⇒ xS = x¹ + x² + x³ + ...... + xⁿ⁺¹

⇒ xS – S = x¹ + x² + x³ + ...... + xⁿ⁺¹ - (x⁰ + x¹ + x² + x³ + ...... + xⁿ)

⇔ S(x - 1) = x¹ + x² + x³ + ...... + xⁿ⁺¹ - x⁰ - x¹ - x² - x³ - …... - xⁿ

⇔ S(x - 1) = xⁿ⁺¹ - x⁰

⇔ S(x-1) = xⁿ⁺¹ - 1

⇒ $S=\frac{x^{n+1}-1}{x-1}$

Câu 10: Một đơn vị bộ đội chuẩn bị một số gạo đủ cho 50 người ăn trong 10 ngày, 3 ngày sau được tăng thêm 20 người. Hỏi đơn vị cần chuẩn bị bao nhiêu suất gạo nữa để cả đơn vị đủ ăn trong những ngày sau đó? (Số gạo mỗi người ăn trong một ngày là một suất gạo)

Lời giải:

Số gạo đó đủ cho số người ăn trong 1 ngày là:

50 . 10 = 500 (người)

Số gạo đã ăn đủ cho số người ăn trong 1 ngày là:

50 . 3 = 150 (người)

Số gạo còn lại đủ cho số người ăn trong 1 ngày là:

500 – 150 = 350 (người)

Sau ngày thứ 3 thì có số người ăn là:

50 + 20 = 70 (người)

Số ngày còn lại là:

10 – 3 = 7 (ngày)

Số suất ăn cần là:

70 . 7 = 490 (suất)

Cần thêm số suất ăn là:

490 – 350 = 140 (suất)

Đáp số: 140 suất.

Câu 11: Cho biết 3 người làm cỏ một cánh đồng hết 6 giờ. Hỏi 12 người (có cùng năng suất) làm cỏ cánh đồng đó hết bao nhiêu thời gian?

Lời giải:

Với cùng một cánh đồng nên số người làm cỏ hết cánh đồng đó và số giờ là hai đại lượng tỉ lệ nghịch.

Hệ số tỉ lệ bằng: 3 . 6 = 18

Gọi số giờ để 12 người làm cỏ hết cánh đồng là x (giờ)

Theo tính chất của đại lượng tỉ lệ nghịch ta có x . 12 = 18 suy ra x = 1,5

Vậy 12 người làm cỏ cánh đồng hết 1,5 giờ (1 giờ 30 phút)

Câu 12: 7a + 4b = 26. Tìm a và b.

Lời giải:                

7a + 4b = 26

⇒ 7a = 26 - 4b ⇒ 7a = 2(13 - 2b)

⇒ 7a ⁝ 2 mà (2,7) = 1

⇒ a ⁝ 2

Vì 7a = 26 - 4b ⇒ 7a ≤ 26 ⇒ a < 4 ⇒ a = 0; 2

Xét a = 0 ⇒ 4b = 26 – 0 = 26 ⇒ b = $\frac{13}{4}$ (vô lí)

Xét a = 2 ⇒ 4b = 26 – 2 . 7 = 26 – 14 = 12 ⇒ a = 3

Vậy a = 2, b = 3

Câu 13: Cho a, b > 0 thỏa mãn: a + b = 4. Tìm GTNN của: $B=2\text{a}+3b+\frac{6}{a}+\frac{10}{b}$.
Lời giải:

Áp dụng BĐT AM-GM ta có:

$$\begin{gathered} B=2\text{a}+3b+\frac{6}{a}+\frac{10}{b}=a+b+a+2b+\frac{6}{a}+\frac{10}{b} \\ =4+a+\frac{4}{a}+2b+\frac{8}{b}+\frac{2}{a}+\frac{2}{b} \\ \ge 4+2\sqrt{a\cdot \frac{4}{a}}+2\cdot 2\sqrt{b\cdot \frac{4}{b}}+2\cdot \frac{4}{a+b} \end{gathered}$$

    = 4 + 2 . 2 + 2 . 2 . 2 + 2 . 1 = 4 + 2 . 2 + 2 . 2 . 2 + 2 . 1

    = 4 + 4 + 8 + 2 = 18.

Nên GTNN của B là 18 đạt được khi a = b = 2.

Câu 14: Cho các chữ số 3; 4; 5. Hãy viết các số thập phân gồm ba chữ số khác nhau trong đó, phần thập phân của các số đều có hai chữ số.

Lời giải:

Các số cần tìm là: 3,45; 3,54; 4,35; 4,53; 5,34; 5,43.

Câu 15: Cho nửa đường tròn (O) đường kính AD. Trên nửa đường tròn lấy hai điểm B và C. Biết AB = BC = $2\sqrt{5}$cm, CD = 6cm. Tính bán kính đường tròn.

Lời giải:

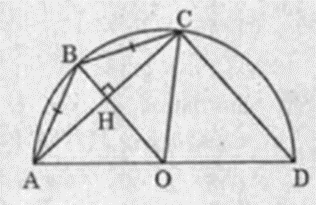
Dễ thấy OB là đường trung trực của AC nên $OB\perp AC$ tại H và HA = HC

OH là đường trung bình của ∆ABC, ta có $OH=\frac{1}{2}C\text{D}=3$

• Xét ∆OHC vuông tại H, ta có:

HC² = OC² – OH² = R² – 9        (1)

• Xét ∆BHA vuông ở H, ta có:

HC² = BC² – BH² = 20 – (R – 3)²        (2)

Từ (1) và (2) suy ra: R² – 9 = 20 – (R – 3)²

⇔ R² – 9 = 20 - R² + 6R – 9

⇔ 2R² – 6R – 20 = 0

⇔ (R – 5)(R + 2) = 0

⇔ R = 5 hoặc R = −2 (loại)

Vậy bán kính của đường tròn là 5 cm.

Câu 16: Một người đi từ A đến B gồm các đoạn AC, CD, DB vơi vận tốc theo thứ tự bằng 10 km/giờ, 12 km/giờ, 15 km/giờ. Lúc về, người đó đi BD, DC, CA với vận tốc theo thứ tự bằng 10 km/giờ, 12 km/giờ, 15 km/giờ. Tính quãng đường AB biết thời gian cả đi lẫn về là 3 giờ.

Lời giải:

Vận tốc trung bình đi và về trên đoạn AC là 12 km/giờ.

Do đó vận tốc trung bình đi và về trên DB cũng bằng 12 km/giờ và vận tốc trung bình cả đi lẫn về trên AB cũng bằng 12 km/giờ.

Quãng đường cả đi lẫn về trên AB là: 12 . 3 = 36 (km)

Quãng đường AB dài là: 36 : 2 = 18 (km)

Vậy quãng đường AB là 18 km.

Câu 17: Giải phương trình: y : 15 – 34,87 = 52,21 + 6

Lời giải:

y : 15 – 34,87 = 52,21 + 6

⇔ y : 15 – 34,87 = 58,21

⇔ y : 15 = 58,21 + 34,87

⇔ y : 15 = 83,08

⇔ y = 83,08 . 15

⇔ y = 1246,2.

Vậy phương trình đã cho có nghiệm y = 1246,2.

Câu 18: Tìm hai số, biết hiệu của chúng là 1554 còn tổng của chúng có dạng $\overline{2x3y}$ chia hết cho 2, cho 5 và cho 9.

Lời giải:

• $\overline{2x3y}$ ⁝ 2 và 5 nên y = 0 

• $\overline{2x3y}$ ⁝ 9 ⇒ 2 + x + 3 + y = 5 + x ⁝ 9 

Vì x là chữ số nên x = 4 . ta có tổng 2 số là 2430

Số lớn là: (2430 + 1554) : 2 = 1992

Số bé là: 2430 - 1992 = 438

Vậy 2 số cần tìm là 1992 và 438.

Câu 19: Hình chữ nhật ABCD được chia thành  5 hình chữ nhật bằng nhau như hình vẽ tính chu vi hình chữ nhật ABCD biết diện tích hình chữ nhật bằng 432 cm².

Lời giải:

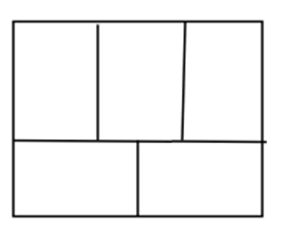
Ta chia hình chữ nhật nhỏ thành sáu hình vuông bằng nhau

Diện tích hình vuông là: 4320 : 5 : 6 = 144 (cm²)

Vì 144 = 12 . 12 nên cạnh hình vuông là 12 cm

Chiều dài hình chữ nhật nhỏ: 12 . 3 = 36 (cm)

Chiều rộng hình chữ nhật nhỏ: 12 . 2 = 24 (cm)

Chu vi hình chữ nhật ABCD:

(36 + 36) + (24 + 36) . 2 = 264 (cm).

Vậy chu vi hình chữ nhật ABCD là 264 cm.

Câu 20: Bạn Mai dùng 25 000 đồng mua bút. Có hai loại bút: Loại I giá 2000 đồng một chiếc, loại II giá 1500 đồng một chiếc. Bạn Mai mua được nhiều nhất bao nhiêu chiếc bút nếu:

a) Mai chỉ mua bút loại I;

b) Mai chi mua bút loại II;

c) Mai mua cả hai loại bút với số lượng như nhau.

Lời giải:

a) Ta có 25 000 : 2000 = 12 (dư 1000)

Vậy Mai mua được nhiều nhất 12 cây bút loại I.

b) Ta có 25 000 : 1500 = 16 (dư 1000)

Vậy Mai mua được nhiều nhất 16 cây bút loại II.

c) Ta có 25 000 : (2000 + 1500) = 7 (dư 500)

Vậy Mai mua được nhiều nhất 7 cây bút loại I và 7 cây bút loại II.

Câu 21: Có bao nhiêu số chia hết cho 3 và có 2 chữ số

Lời giải:

Số nhỏ nhất có hai chữ số chia hết cho 33 là: 12;

Số lớn nhất có hai chữ số chia hết cho 33 là: 99.

Do đó ta có dãy: 12; 15; 18; …...; 96; 99.

Dãy trên có số số hạng là:

(99 − 12) : 3 + 1 = 30(99 − 12) : 3 + 1 = 30  (số hạng)

Vậy có 30 số hạng chia hết cho 3 và có 2 chữ số.

Câu 22: Hai người đi từ A đến B. Người thứ nhất đi từ A đến B rồi quay lại ngay. Người thứ hai đi từ B đến A rồi quay lại ngay. Hai người này gặp nhau tại C cách A là 6 km. Tính AB biết vận tốc người thứ hai bằng $\frac{2}{3}$ người thứ nhất.

Lời giải:

Từ lúc khởi hành đến lúc gặp nhau lần thứ hai ở C, người thứ hai đi được quãng đường là BA + 6 km (1), cả hai người đi được 3AB

Vận tốc của người thứ hai bằng $\frac{2}{3}$ vận tốc người thứ nhất

Nên quãng đường của người thứ hai đi được bằng $\frac{2}{5}$ tổng quãng đường hai người đi được tức là bằng: $3\text{A}B\cdot \frac{2}{5}=\frac{6}{5}AB$  (2)

Từ (1) và (2) suy ra $\frac{1}{5}AB$ dài 16 km.

Quãng đường AB dài là

$6:\frac{1}{5}=30$  (km)

Vậy quãng đường AB là 30 km.

Câu 23: Khi nhân một số tự nhiên với 235 do sơ ý bạn Cúc đã đặt các tích riêng thứ 2 với thứ 3 thẳng cột nên cúc được kết quả là 10 285. Tìm tích đúng.

Lời giải:

Khi nhân số A với 235 do sơ ý bạn Cúc đã đặt các tích riêng thẳng cột nên được kết quả là 10 285. 

Tức là bạn Cúc đã nhân lần lượt với 5; 20; 30 rồi cộng các kết quả lại .

A . 5 + A . 20 + A . 30 = 10 285

A . 55 = 10 285

A = 10 285 : 55

A = 187

Vậy tích đúng là:

 235 . 187 = 43 945

Câu 24: Một đội công nhân làm 3 ngày, trung bình mỗi ngày sửa đc 1,5 km đường. Ngày thứ nhất và ngày thứ hai sửa đc 3,3 km. Ngày thứ hai và ngày thứ ba sửa đc 2,9 km. Tính mỗi km đường mà mỗi ngày đội đó sửa được.

Lời giải:

Cả 3 ngày làm được:

1,5 . 3 = 4,5 (km)

Ngày thứ 3 sửa được:

4,5 - 3,3 = 1,2 (km)

Ngày thứ nhất sửa được:

4,5 – 2,9 = 1,6 (km)

Ngày thứ 2 sửa được:

4,5 – 1,2 – 1,6 = 1,7 (km)

Đáp số: Ngày thứ nhất: 1,2 km;

   Ngày thứ hai: 1,7 km;

   Người thứ ba: 1,6 km.

Câu 25: Thắng viết lên bảng các số từ 10 đến 70. Mỗi lần, Linh xóa đi 5 số bất kì và viết lại lên bảng trung bình cộng của 5 số đã xóa. Hỏi sau bao nhiêu lần như thế thì Linh chỉ còn lại 1 số trên bảng?

Lời giải:

Từ 10 đến 70 có số các số là:

(70 − 10) : 1 + 1 = 61(70 − 10) : 1 + 1 = 61 (số)

Khi xóa đi 5 số, viết lại 1 số là số trung bình cộng của số đã xóa thì lúc đó trên bảng sẽ mất đi 4 số so với ban đầu

Sau n lần xóa thì trên bảng đã mất đi số các số là: 4.n (số)

Khi chỉ còn 1 số trên bảng thì trên bảng đã mất đi

61 – 1 = 60 (số)

Khi đó ta có số lần xóa là: 60 = 4 . n hay n = 15

Vậy sau 15 lần xóa.

Câu 26: Thắng viết lên bảng các số từ 10 đến 70. Mỗi lần, Linh xóa đi 5 số bất kì và viết lại lên bảng trung bình cộng của 5 số đã xóa. Hỏi bao nhiêu lần như thế thì Linh chỉ còn lại 1 số trên bảng?

Lời giải:

Từ 10 đến 70 có số số là: 70 – 10 +1 = 61

Khi xóa đi 5 số và viết lại lên bảng trung bình cộng của các số đã xóa thì lúc đó trên bảng sẽ mất đi: 4 số

Giả sử sau x (x ∈ ℕ*) lần xóa và viết lại như thế thì còn lại 1 số trên bảng

Khi đó trên bảng mất đi: 4x (số)

Trên bảng còn lại: 61 – 4x (số)

Vì còn lại 1 số trên bảng nên ta có:

61 – 4x = 1

4x = 60

x = 60 : 4

x = 15

Đáp số: 15 lần.

Câu 27: Thắng viết lên bảng các số tự nhiên từ 10 đến 20. Mỗi bước Linh xoá đi 2 số bất kì và viết lại lên bảng tổng của 2 số đã xoá. Cứ làm vậy cho tới khi trên bảng còn lại 1 số. Khi đó, số còn lại cuối cùng trên bảng là bao nhiêu?

Lời giải:

Sau mỗi bước, Linh xóa hai số a và b và viết lên bảng a + b.

Do đó tổng các số trên bảng không thay đổi.

Khi đó ta suy ra  số cuối cùng được viết trên bảng là tổng các số trên bảng lúc đầu.

Vậy số cuối cùng là:

(20 + 10).11 : 2 = 165.

Câu 28: Tìm y, biết:

y : 15 – 34,87 = 52,21 + 6

Lời giải:

y : 15 – 34,87 = 52,21 + 6

y : 15 = 58,21 + 34,87

y : 15 = 93,08

y = 93,08 ´ 15

y = 1396,2

Vậy y = 1396,2.

Câu 29: Tìm n ∈ ℕ sao cho:

a) 10 chia hết n;

b) (n + 2) là ước của 20 ;

Lời giải:

a) Vì 10 chia hết cho n nên n ∈ Ư(10).

Mà Ư(10) = {1; 2; 5; 10} nên n ∈ {1; 2; 5; 10}.

Vậy n ∈ {1; 2; 5; 10}.

b) Vì (n + 2)là ước của 20 nên (n + 2) = Ư(20)        (1)

Mà 20 = 1 . 2² . 5

Do đó Ư(20) = {1; 2; 4; 5;10; 20}       (2)

Từ (1) và (2) suy ra n ∈ {−1; 0 ; 2; 3; 8; 18}.

Mặt khác n ∈ ℕ suy ra n ∈ {0 ; 2; 3; 8; 18}.

Câu 30: Một người đi xe đạp trong 3 giờ đầu, mỗi giờ đi được 12,5 km; trong 2 giờ sau, mỗi giờ đi được 13,75 km. Hỏi trên cả quãng đường, trung bình mỗi giờ người đó đi được bao nhiêu ki-lô-mét?

Lời giải:

Quãng đường người đi xe đạp đi trong 3 giờ đầu là:

12,5 × 3 = 37,5 (km)

Quãng đường người đi xe đạp trong 2 giờ tiếp sau là:

13,75 × 2 = 27,5 (km)

Thời gian người đi xe đạp đi trên cả quãng đường là:

3 + 2 = 5 (giờ)

Trên cả quãng đường, trung bình mỗi giờ người đó đi được là:

(37,5 + 27,5) : 5 = 13 (km)

Đáp số: 13 km

Câu 31: Tìm các bội của 25 đồng thời là ước của 300

Lời giải:

Ta có:

B(25) = {0; 25; 50; 75; 100; 125; 150; 175; 200; 225; 250; 275; 300; 325;…}

300 = 1.2².3.5²

Ư(300) = {1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 25; 30; 50; 60; 75; 100; 150; 300}

Mà ta thấy {25; 50; 75; 100; 150} đều thuộc cả hai tập hợp trên.

Vậy các số 25; 50; 75; 100;1 50 vừa là bội của 25 vừa là ước của 300.

Câu 32: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm). Chứng minh rằng OA$\perp$MN.

Lời giải:

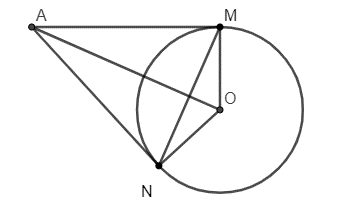
Ta có: AM = AN (tính chất hai tiếp tuyến cắt nhau)

Suy ra tam giác AMN cân tại A

Mặt khác AO là đường phân giác của $\widehat{MAN}$ (tính chất hai tiếp tuyến cắt nhau)

Suy ra AO là đường cao của tam giác AMN (tính chất tam giác cân)

Vậy OA ⊥ MN.

Câu 33: May 1 bộ quần áo hết 2 m 3 dm vải. Nếu đem 34 m vải may 10 bộ quần áo thì thừa bao nhiêu m vải?

Lời giải:

Đổi 2 m 3 dm = 2,3 m

Mau 18 bộ quần áo cần số mét vải là:

2,3 ´ 10 = 23 (m)

Thừa số mét vải là:

34 − 23 = 11 (m)

Đáp số: 11 m

Câu 34: Cho đường thẳng (d) : y = (m − 1)x + 2m − 3, trong đó m là tham số. Gọi M là điểm cố định mà (d) luôn đi qua với mọi m. Tính OM.

Lời giải:

Ta có: y = (m – 1)x + 2m – 3

⇔ y = m(x + 2) – x – 3

Ta thấy với x = −2 thì y = −1 $\forall m$.

Vậy M = (−2; −1) ⇒ $OM=\sqrt{{\left(-1\right)}^2+{\left(-2\right)}^2}=\sqrt{5}$.

Câu 35: Hãy cho biết có tất cả bao nhiêu số tự nhiên nhỏ hơn 56?

Lời giải:

Có tất cả các số tự nhiên nhỏ hơn 56 là:

(56 − 0):1+1 = 57 (số hạng)

Đáp số: 57 số.

Câu 36: Tìm x, biết:

a) |x – 2,3| – |−1,2| = 2,1;

b) |x| + |x – 1| = 0.

Lời giải:

 a) |x – 2,3| – |−1,2| = 2,1

|x – 2,3| − 1,2 = 2,1

|x – 2,3| = 2,1 + 1,2 = 3,3

x – 2,3 = 3,3 hoặc x – 2,3 = −3,3

• Xét x – 2,3 = 3,3 nên ta có x = 2,3 + 3,3 = 5,6;

• Xét x – 2,3 = −3,3 nên ta có x = 2,3 – 3,3 = −1.

Vậy x = 5,6 hoặc x = −1.

b) |x| + |x – 1| = 0

Ta có |x| ≥ 0 $\forall x$, |x – 1| ≥ 0 $\forall x$∈ ℝ

Do đó |x| + |x – 1| = 0; |x| = |x – 1| = 0

 x = 0 và x = 1 (vô lí)

Vậy không có giá trị x thỏa mãn.

Câu 37: May 1 bộ quần áo hết 2 m 3 dm vải. Nếu đem 43 m vải may 18 bộ quần áo thì thừa bao nhiêu m vải?

Lời giải:

Đổi 2 m 3 dm = 2,3 m

Mau 18 bộ quần áo cần số mét vải là:

2,3 ´ 18 = 41,4 (m)

Thừa số mét vải là:

43 − 41,4 = 1,6 (m)

Đáp số: 1,6 m

Câu 38: Cho dãy số 3;4;6;9;13;......

Tìm quy luật và tìm 3 số hạng tiếp theo của dãy số trên.

Lời giải:

Nhận xét:

+ Số thứ nhất: u₁​ = 3

 + Số thứ hai: u₂ ​= 4 = 3 + 1

 + Số thứ ba: u₃​ = 6 = 4 + 2

 + Số thứ tư: u₄​ = 9 = 6 + 3

 + Số thứ năm: u₅ ​= 13 = 9 + 4

 Quy luật: Mỗi số đều bằng số đằng trước nó cộng với số thứ tự của số đằng trước nó. Hoặc: u_n​ = u_{n – 1} + n − 1 

Ta có:

+ Số thứ sáu: u₆ ​= 13 + 5 = 18

+ Số thứ bảy: u₇​ = 18 + 6 = 24

+ Số thứ tám: u₈ ​= 24 + 7 = 31

Vậy 3 số hạng tiếp theo là: 18 ; 24 ; 31.

Câu 39: Số học sinh giỏi, khá, trung bình của khối 7 lần lượt tỉ lệ với 2 : 3 : 5. Tính số học sinh giỏi, khá, trung bình, biết tổng số học sinh khá và học sinh trung bình hơn học sinh giỏi là 180 em.

Lời giải:

Gọi số học sinh giỏi, khá, trung bình lần lượt là: a, b, c (học sinh. a, b, c ∈ ℕ*)

Theo bài cho ta có:

$\frac{a}{2}=\frac{b}{3}=\frac{c}{5}$ và b + c – a = 180.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

 $\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{b+c-a}{3+5-2}=\frac{180}{6}=30$

Suy ra:

a = 2.30 = 60 (thỏa mãn điều kiện)

b = 3.30 = 90 (thỏa mãn điều kiện)

c = 5.30 = 150 (thỏa mãn điều kiện)

Vậy số học sinh giỏi, khá, trung bình khối 7 lần lượt là: 60 em; 90 em; 150 em.

Câu 40: Để làm xong một công việc trong 5 giờ cần 12 công nhân. Nếu số công nhân tăng thêm 8 người thì thời gian hoàn thành công việc giảm được mấy giờ? (biết rằng năng suất của mỗi công nhân là như nhau)

Lời giải:

Số công nhân sau khi được tăng thêm là:

12 + 8 = 20 (công nhân)

Gọi thời gian 20 công nhân hoàn thành xong công việc là a.

Vì thời gian và số công nhân tỉ lệ nghịch với nhau nên:

5.12 = x.20

$x=\frac{5.12}{20}=3$

Thời gian hoàn thành công việc được giảm:

5 – 3 = 2 (giờ)

Đáp số: 2 giờ

Câu 41: Cho hình thoi ABCD có AC cắt BD tại O. Đáp án nào sau đây là đúng:

A. OA = OB, OC = OD;

B. OA = OD, OB = OC;

C. OA = OC, OB = OD;

D. Một đáp án khác.

Lời giải:

Đáp án đúng là: C

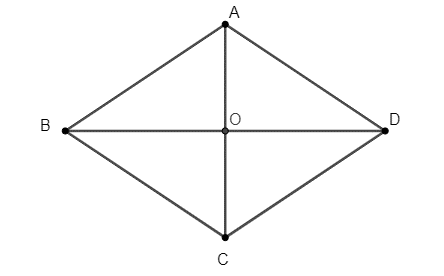
Theo tính chất của hình thoi ta có:

OA = OC, OB = OD.

Vậy đáp án đúng là C.

Câu 42: Một người làm 50 sản phẩm thì hết 8 giờ. Hỏi người đó làm được 12 giờ thì được bao nhiêu sảm phẩm ?

Lời giải:

12 giờ gấp 8 giờ số lần là:

$12:8=\frac{3}{2}$ (lần)

Người đó làm trong 12 giờ được số sản phẩm là:

$50\times \frac{3}{2}=75$ (sản phẩm)

Đáp số: 75 sản phẩm

Câu 43: Một thùng chứa gạo có khối lượng gạo là 43,8 kg. Một bao gạo có khối lượng 13,9 kg một người trút hết bao gạo vào trong thùng. Hỏi sau khi trút hết gạo từ bao vào thùng thì trong thùng có bao nhiêu kilôgam gạo?

Lời giải:

Vì trút hết gạo từ bao gạo chứa 13,9 kg  gạo vào thùng thì số gạo trong thùng được cộng thêm 13,9 kg.

Số gạo trong thùng lúc này là :

13,9 + 43,8 = 57,7 (kg)

Đáp số: 57,7 kg.

Câu 44: Một mảnh vườn hình chữ nhật chiều dài 120 m, chiều rộng 48 m. Người ta muốn trồng cây xung quanh vườn sao cho mỗi góc vườn có một cây và khoảng cách giữa hai cây liên tiếp bằng nhau. Tính khoảng cách lớn nhất giữa hai cây liên tiếp, khi đó tổng số cây trồng được là bao nhiêu?

Lời giải:

Gọi khoảng cách giữa hai cây liên tiếp là x (x > 0)

Vì 120  chia hết cho x, 48 chia hết cho x, x lớn nhất

x = ƯCLN(120, 48) = 2³.3 = 24

Vậy khoảng cách lớn nhất giữa 2 cây liên tiếp là 24 m.

Tổng số cây của chiều dài là:

(120 : 24) . 2 = 10 (cây)

Tổng số cây của chiều rộng là:

(48 : 24) . 2 = 4 (cây)

Tổng số cây của mảnh vườn là:

10 + 4 = 14 (cây)

Vậy khoảng cách lớn nhất giữa hai cây liên tiếp là 24 m, khi đó tổng số cây trồng được là 14 cây.

Câu 45: Cho dãy số: 2; 4; 8; 16; 32;....

a) Hãy nêu quy luật của dãy số đó.

b) Tính tổng 10 số hạng đó.

Lời giải:

a) Quy luật của dãy số trên là mỗi số hạng gấp đôi số đứng liền trước nó.

Hay u_n­ = 2.u_{n – 1}

b) 10 số hạng đầu tiên của dãy số đó là:

2; 4; 8; 16; 32; 64; 128; 256; 512; 1024.

 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512 + 1024 = 2046

Câu 46: Tìm 25% của 530.

Lời giải:

25% của 530 là:

530 : 100 ´ 25 = 132,5

Đáp số: 132,5

Câu 47: Tìm x biết:

x% : 3 + 45% = 0,7

Lời giải:

x% : 3 + 45% = 0,7

x% : 3 + 0,45 = 0,7

x% : 3 = 0,7 – 0,45 = 0,25

x% = 0,25 . 3 = 0,75

x% = 75%

x = 75.

Vậy x = 75.

Câu 48: Có 10 người bước vào phòng họp, tất cả đều bắt tay lẫn nhau. Hỏi có tất cả bao nhiêu cái bắt tay?

Lời giải:

1 người bắt tay với 9 người còn lại nên có số cái bắt tay là :

9 x 10  = 90 (cái)

Nhưng nếu tính như vậy thì mỗi cái bắt ta đã được tính 2 lần.

Vậy số cái bắt tay thực tế là:

90 : 2 = 45 (cái)

Đáp số : 45 cái

Câu 49: Chứng minh (2.5⁷ + 3.5⁶ + 4.5⁵) chia hết cho 69.

Lời giải:

2.5⁷ + 3.5⁶ + 4.5⁵

= 5⁵(2.5² + 3.5 + 4)

= 5⁵.69

Vì 69 ⁝ 69

⇒  5⁵.69 ⁝ 69

Vậy (2.5⁷ + 3.5⁶ + 4.5⁵) chia hết cho 69.

Câu 50: Trong 4 giờ xe máy đi được 121 km, trong 2 giờ ô tô đi được 111 km. Hỏi trung bình mỗi giờ ô tô đi được nhiều hơn xe máy bao nhiêu ki-lô-met?

Lời giải:

Trung bình mỗi giờ xe máy đi được số km là:

121 : 4 = 30,25 (km)

Trung bình mỗi giờ ô tô đi được số km là:

111 : 2 = 55,5 (km)

Trung bình mỗi giờ ô tô đi nhiều hơn xe máy số km là:

55,5 − 30,25 = 25,25 (km)

Đáp số: 25,25 km