Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 19)
Câu 1: Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng
.
Lời giải:
Ta có
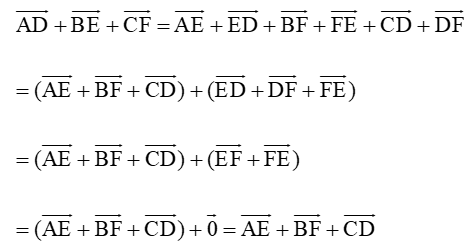
Ta có

a) sin5x + sin8x + sin3x = 0.
b)
Lời giải:
a) Ta có

Vậy , , .
b) Ta có:
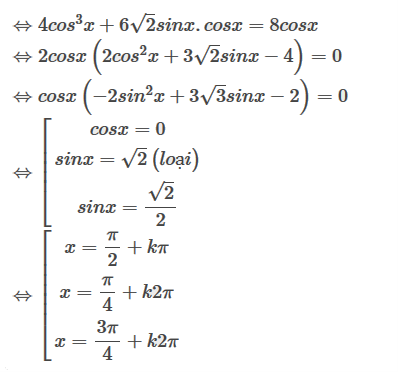
Vậy , , .
Câu 3: Cho bảng biến thiên hàm số y = f(x) như sau:
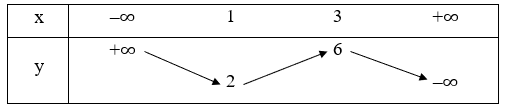
So sánh f(– 2021) và f(– 1); và f(2).
Lời giải:
Ta có – 2021; – 1 ∈ (– ∞; 1) và – 2021 < – 1
Mà trên khoảng (– ∞; 1) hàm số nghịch biến nên f(– 2021) > f(– 1)
Ta có và
Mà trên khoảng (1; 3) hàm số đồng biến nên
Vậy f(– 2021) > f(– 1) và .
Câu 4: Cho hàm số y = f(x) = – 3x.
a) Vẽ đồ thị hàm số y = – 3x.
b) So sánh f(–2) và f(5).
Lời giải:
a) Đồ thị hàm số y = – 3x đi qua gốc tọa độ O và điểm (– 1; 3)
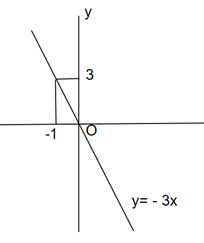
b) Ta có: f(–2) = –3 . (–2) = 6
f(5) = –3 . 5 = – 15
Vì 6 > – 15 nên f(–2) > f(5)
Vậy f(–2) > f(5).
Câu 5: Tìm m để hàm số y = có tập xác định là ℝ.
Lời giải:
y =
Điều kiện xác định của y là x2 + 4x + m ≥ 0
Để y có tập xác định là R
⇔ x2 + 4x + m ≥ 0 với mọi x ∈ R
⇔ Δ' < 0
⇔ 22 – 1 . m < 0
⇔ 4 – m < 0
⇔ m > 4
Vậy m > 4 thì hàm số y = có tập xác định là R.
Lời giải:
Để hàm số đạt giá trị nhỏ nhất bằng – 10 trên ℝ thì
Vậy m = 2.
Câu 7: Tìm đa thức M biết (x3 – 5x2 + x – 5) = (x – 5).M
Lời giải:
Ta có (x3 – 5x2 + x – 5) = (x – 5) . M
Vậy M = x2 + 1.
Câu 8: Cho a, b, c > 0. Chứng minh .
Lời giải:
Áp dụng bất đẳng thức Cô – si ta có:
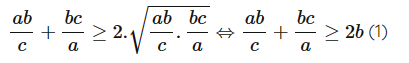
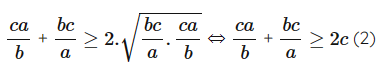
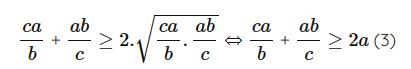
Suy ra
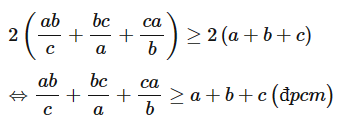
Vậy .
Câu 9: Cho tam giác ABC có a = 8, b = 10, . Độ dài cạnh c là
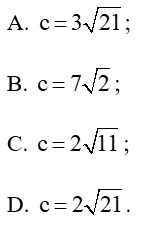
Lời giải:
Đáp án đúng là: D
Xét tam giác ABC có:
![]()
Vậy ta chọn đáp án D.
Câu 10: Cho các điểm A(1; – 2), B(– 2; 3) và C(0; 4). Diện tích tam giác ABC bằng bao nhiêu?
Lời giải:
Ta có A(1; – 2), B(– 2; 3) và C(0; 4)
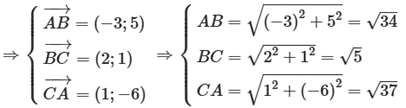
Nửa chu vi tam giác ABC là:
Suy ra:
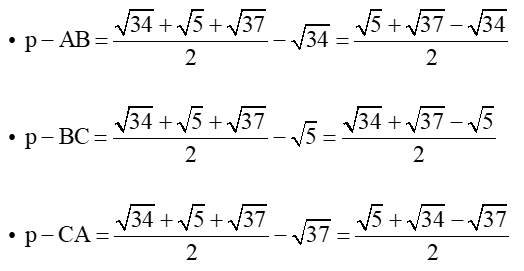
Diện tích tam giác ABC là:

Vậy diện tích tam giác ABC bằng .
Câu 11: Cho tập hợp A = (– ∞; 2023), B = [4 – 3m; + ∞). Tìm m để CRB ⊂ A.
Lời giải:
Ta có CRB = R ∖ B = (– ∞; 4 – 3m)
Để CRB ⊂ A thì 4 – 3m < 2023
⇔ – 3m < 2019
⇔ m > 673
Vậy m > 673.
A. 15;
B. 20;
C. 25;
D. 30.
Lời giải:
Đáp án đúng là B
Gọi a, b, c theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán
X là số học sinh chỉ thích hai môn là văn và toán
y là số học sinh chỉ thích hai môn là Sử và toán
z là số học sinh chỉ thích hai môn là văn và Sử
Ta có số em thích ít nhất một môn là 45 – 6 = 39
Dựa vào biểu đồ ven ta có hệ phương trình
Suy ra a + b + c + 2(x + y + z) + 15 = 25 + 18 +20
Hay a + b + c + 2(x + y + z) = 48 (2)
Từ (1) và (2) ta có
a + b + c + 2(39 – 5 – a – b − c) = 48
⇔ a + b + c = 20
Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.
Câu 13: Cho số phức z thỏa mãn + z = 3 + 4i. Mô đun của z bằng?
Lời giải:
Gọi số phức z có dạng z = a + bi (a, b ∈ ℝ)
Ta có + z = 3 + 4i
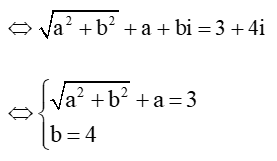
Do đó
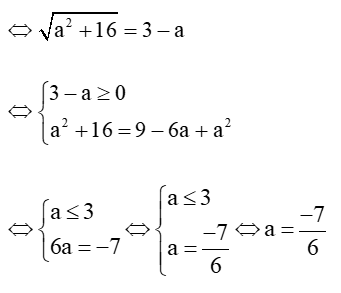
Vậy số phức cần tìm là .
Câu 14: Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị là A(1; – 7) và B (2; – 8). Tính y(– 1)
A. y(– 1) = 7;
B. y(– 1) = 11;
C. y(– 1) = – 11;
D. y(– 1) = – 35.
Lời giải:
Đáp án đúng là: D
Vì đồ thị hàm số đi qua A và B nên
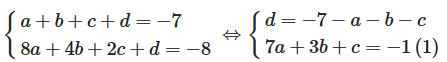
Ta có y’ = 3ax2 + 2bx + c có hai nghiệm x = 1, x = 2 nên
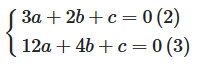
Từ (1), (2) và (3) suy ra
Suy ra d = – 12
Khi đó y(– 1) = – a + b – c + d = – 35
Vậy ta chọn đáp án D.
1/ (– 37) + 14 + 26 + 37;
2/ (– 24) + 6 + 10 + 24;
3/ 15 + 23 + (– 25) + ( – 23);
4/ 60 + 33 + (– 50) + (– 33);
5/ (– 16) + ( – 209) + ( – 14) + 209;
6/ (– 12) + ( – 13) + 36 + (– 11);
7/ 300 – (– 200) – (– 120) + 18;
8/ – (– 299) + (– 219) – 401 + 12;
9/ 555 – (– 333) – 100 – 80;
10/ 34 + 35 + 36 + 37 – 14 – 15 – 16 – 17;
11/ 1+ (– 2) + 3 + (– 4) + ..... + 19 + (– 20);
12/ 1 – 2 + 3 – 4 + ... + 99 – 100.
Lời giải:
1/ (– 37) + 14 + 26 + 37
= [(– 37) + 37] + (14 + 26)
= 0 + 40 = 40
2/ (– 24) + 6 + 10 + 24
= (– 24 + 24) + (6 + 10)
= 0 + 16 = 16
3/ 15 + 23 + (– 25) + ( – 23)
= [15 + (– 25) + [23 + (– 23)]
= – 10 + 0 = – 10
4/ 60 + 33 + (– 50) + (– 33)
= [60 + (– 50)] + [33 + (– 33)]
= 10 + 0 = 10
5/ (– 16) + ( – 209) + ( – 14) + 209
= [(– 16) + (– 14)] + [(– 209) + 209]
= – 20 + 0 = – 20
6/ (– 12) + ( – 13) + 36 + (– 11)
= (– 25) + (– 11) + 36
= – 36 + 36 = 0
7/ 300 – (– 200) – (– 120) + 18
= 300 + 200 + 120 + 18
= 500 + 120 + 18
= 620 + 18
= 638
8/ – (– 299) + (– 219) – 401 + 12
= 299 – 219 – 401 + 12
= 80 – 401 + 12
= – 321 + 12 = – 309
9/ 555 – (– 333) – 100 – 80
= 555 + 333 – 180
= 888 – 180
= 708
10/ 34 + 35 + 36 + 37 – 14 – 15 – 16 – 17
= (34 – 14) + (35 – 15) + (36 – 16) + (37 – 17)
= 20 + 20 + 20 + 20
= 80
11/ 1+ (– 2) + 3 + (– 4) + ..... + 19 + (– 20)
=[1 + (– 2)] . [(20 – 1) : 1 + 1] : 2 = – 1 . 10 = – 10
12/ 1 – 2 + 3 – 4 + ... + 99 – 100
= (1 – 2) . [(100 – 1) : 1 + 1] : 2 = –1 . 50 = – 50
Câu 16: Tìm điểm thuộc đồ thị y = – x + 2 có hoành độ gấp 3 lần tung độ.
Lời giải:
Gọi A(xA; yA) là điểm cần tìm
Theo đề bài ta có xA = 3yA
Vì A thuộc đồ thị hàm số y = – x + 2
Nên yA = – xA + 2
⇔ yA = – 3yA + 2
⇔ 4yA = 2
Suy ra
Vậy .
Câu 17: Cho a và b là hai số dương khác nhau thỏa mãn .
Chứng minh a2 + b2 = 1.
Lời giải:
Ta có
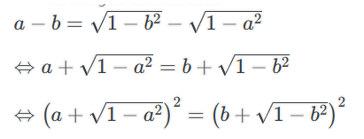
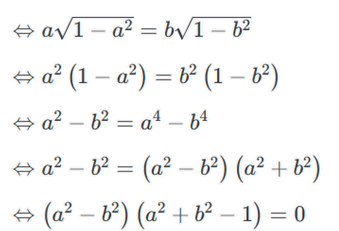
Mà a ≠ b
Suy ra a2 + b2 = 1.
Câu 18: Cho A (– 1; 2); B(2; 0); C(3; 4).
a) Tính tọa độ trung điểm I của AC.
b) Tính tọa độ trọng tâm G của tam giác ABC.
c) Tính tọa độ D: ABCD theo thứ tự là hình bình hành.
d) Tìm tọa độ E sao cho: .
Lời giải:
a) Vì I là trung điểm của AC nên
Vậy I (1; 3)
b) Vì G là trọng tâm tam giác ABC nên
Vậy G ( ; 2)
c) Vì ABCD là hình bình hành nên
Vậy D(0; 6)
d) Gọi K là trung điểm của AB
Suy ra và
Ta có
Mà nên
Suy ra
Vậy .
Câu 19: Cho tam giác đều cạnh a, trọng tâm G . Tính .
Lời giải:
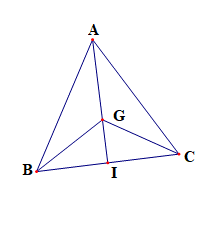
Vì G là trọng tâm tam giác ABC nên
Suy ra
Gọi giao điểm của AG và BC là I
Vì ABC là tam giác đều nên AI ⊥ BC
Hay tam giác ABI vuông tại I
Suy ra AI =
Do đó AG = AI =
Vậy .
a) (x2 – x + 7) ⋮ (x – 1);
b) (x2 – 9x + 7) ⋮ (x – 9).
Lời giải:
a) (x2 – x + 7) ⋮ (x – 1)
⇔ x(x – 1) + 7 ⋮ (x – 1)
Vì x(x – 1) ⋮ (x – 1) nên 7 ⋮ (x – 1)
Suy ra x – 1 ∈ Ư(7) = {1; – 1; 7; – 7}
Do đó x ∈ {2; 0; 8; – 6}
b) (x2 – 9x + 7) ⋮ (x – 9)
⇔ x(x – 9) + 7 ⋮ (x – 9)
Vì x(x – 9) ⋮ (x – 9) nên 7 ⋮ (x – 9)
Suy ra x – 9 ∈ Ư(7) = {1; – 1; 7; – 7}
Do đó x ∈ {10; 8; 16; 2}
Lời giải:
Vì đồ thị hàm số y = ax + b song song với đường thẳng y = 2x – 3
Nên a = 2; b ≠ − 3
Vì đồ thị hàm số y = ax + b cắt trục tung tại điểm có tung độ là 5
nên x = 0 ; y = 5
⇔ 5 = 2 . 0 + b
⇔ 5 = b ( thỏa mãn )
Vậy y = 2x + 5 là hàm số cần tìm.
Lời giải:
Cần số người để làm xong việc đó trong 1 ngày là
10 × 8 = 80 (người)
Cần số người để làm xong việc đó trong 5 ngày là
80 : 5 = 16 (người)
Vậy cần 16 người để hoàn thành công việc trong 5 ngày.
Lời giải:
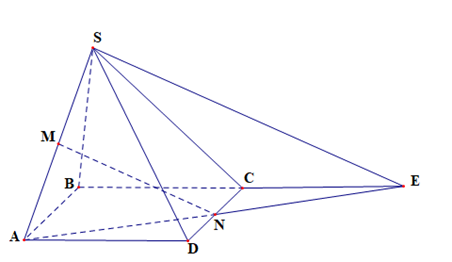
Trong mp(ABCD) nối AN kéo dài cắt BC kéo dài tại E
Suy ra E ∈ (SBC)
Vì N là trung điểm của CD nên NC = ND
Vì AD // BE nên (Định lí Ta – let)
Suy ra AN = EN
Do đó N là trung điểm của AE
Xét tam giác SAE có
N là trung điểm của AE
M là trung điểm của AS
Suy ra MN là đường trung bình
Do đó MN // SE
Vậy MN // (SBC).
Câu 24: Cho A = (– ∞; m], B = [3 – 2m; + ∞). Tìm m để
a) A giao B bằng rỗng, A giao B khác rỗng, A hợp B bằng ℝ.
b) A giao B là 1 tập hợp có 1 phần tử.
Lời giải:
a) • A ⋂ B = ∅
⇔ m < 3 – 2m
⇔ 3m < 3
⇔ m < 1
• A ⋂ B ≠ ∅
⇔ m ≥ 3 – 2m
⇔ 3m ≥ 3
⇔ m ≥ 1
• A ∪ B = ℝ
⇔ m ≥ 3 – 2m
⇔ 3m ≥ 3
⇔ m ≥ 1
b) A giao B là 1 tập hợp có 1 phần tử
⇔ m = 3 – 2m
⇔ 3m = 3
⇔ m = 1
Lời giải:
Gọi I(x; y)
Ta có ; và
Ta có
Vậy .
Câu 26: Cho tam giác ABC nhọn. Chứng minh rằng BC2 = AB2 + AC2 – 2AB.AC.cosA.
Lời giải:
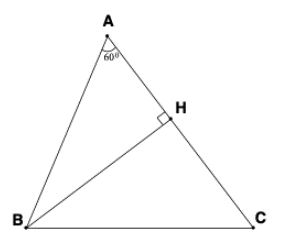
Kẻ đường cao BH
Xét tam giác ABH vuông ở H có AH = AB.cosA
Theo định lí Pytago ta có
AB2 = AH2 + BH2
Xét tam giác ACH vuông ở H có AC2 = AH2 + CH2 (định lí Pytago)
Ta có AB2 + AC2 – 2AB.AC.cosA
= AB2 + AC2 – 2AC.AH
= AH2 + BH2 + AC2 – 2AC.AH
= BH2 + (AC – AH)2
= BH2 + HC2
= BC2
Vậy BC2 = AB2 + AC2 – 2AB.AC.cosA.
a) Chứng minh MN // CD.
b) Tìm giao điểm P của SC và (AND).
c) Gọi I là giao điểm của AN và DP. Chứng minh SI // AB // CD.
Lời giải:
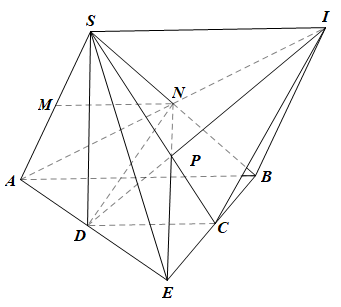
a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB
Suy ra MN là đường trung bình của tam giác
Do đó MN // AB (tính chất đường trung bình của tam giác)
Mà AB // CD (do ABCD là hình thang).
Suy ra MN // CD.
b) Trong mp(ABCD), gọi E là giao điểm của BC và AD.
Khi đó E ∈ AD ⊂ (AND) nên mp(AND) chính là mp(ANE);
E ∈ BC ⊂ (SBC) nên mp(SBC) chính là mp(SBE).
Trong mp(SBE), gọi P là giao điểm của EN và SC.
Ta có: (ANE) ∩ (SBE) = NE;
NE ∩ SC = P
Suy ra SC ∩ (ANE) = P.
Do đó P là giao điểm của SC và (AND).
c) Do AN ∩ DP = {I} nên ta có:
• I ∈ DP, DP ⊂ (SCD) do đó I ∈ (SCD).
• I ∈ AN, AN ⊂ (SAB) do đó I ∈ (SAB).
Ta có: S ∈ (SAB) và S ∈ (SCD) nên (SAB) ∩ (SCD) = S;
I ∈ (SAB) và I ∈ (SCD) nên (SAB) ∩ (SCD) = I.
Do đó (SAB) ∩ (SCD) = SI.
Lại có AB // CD; AB ⊂ (SAB) và CD ⊂ (SCD)
Suy ra SI // AB // CD.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN).
Lời giải:
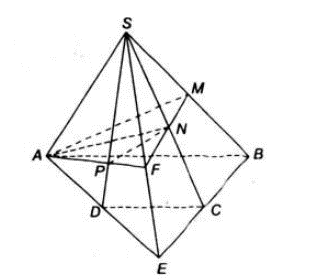
a) Gọi E là giao điểm của AD và BC.
Ta có
Do đó E = (SAD) ∩ (SBC)
Mà S = (SAD) ∩ (SBC)
Suy ra SE = (SAD) ∩ (SBC).
b) Trong mp(SBE) gọi giao điểm của MN và SE là F.
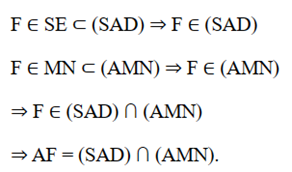
Trong mp(SAD) gọi giao điểm của AF là SD là P.
Suy ra P = SD ∩ (AMN).
c) Ta có
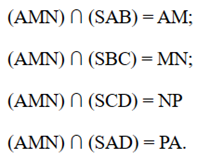
Vậy thiết diện thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN) là tứ giác AMNP.
Lời giải:
Số học sinh thích đúng 2 môn bóng đá và bơi: 14 – 10 = 4 (học sinh)
Số học sinh thích đúng hai môn bơi và bóng chuyền: 13 – 10 = 3 (học sinh)
Số học sinh thích đúng hai môn bóng đá và bóng chuyền: 15 – 10 = 5 (học sinh)
Số học sinh chỉ thích bóng đá: 20 – (4 + 10 + 5) = 1 (học sinh)
Số học sinh chỉ thích bơi: 17 – (4 + 10 + 3) = 0 (học sinh)
Số học sinh chỉ thích bóng chuyền: 36 – (5 + 10 + 3) = 18 (học sinh)
Vậy số học sinh của lớp là: 1 + 0 + 18 + 4 + 10 + 5 + 3 + 12 + = 53 (học sinh).
Lời giải:
• Vì đồ thị của hàm số y = ax + b song song với đường thẳng y = 2x + 3 nên .
Khi đó ta có hàm số y = 2x + b (b ≠ 3).
• Vì đồ thị của hàm số y = 2x + b cắt trục hoành tại điểm có hoành độ là – 2 nên điểm A(– 2; 0) thuộc đồ thị hàm số y = 2x + b
Suy ra 0 = 2 . (– 2) + b
Hay b = 4 (thỏa mãn b ≠ 3)
Vậy y = 2x + 4.
Câu 31: Số tự nhiên thích hợp để điền vào dãy số sau: 3, 17, 59, 185, 563, ... là số nào?
Lời giải:
Ta thấy
Hiệu giữa 3 và 17 là 14
Hiệu giữa 17 và 59 là 42 = 14 . 3
Hiệu giữa 59 và 185 là 126 = 42 . 3
Hiệu giữa 185 và 563 là 378 = 126 . 3
Suy ra quy luật hiệu của hai số sau sẽ gấp 3 lần hiệu của hai số trước (có lặp lại số ở giữa 2 số kia)
Vậy số cần điền là : 378 . 3 + 563 = 1697.
Câu 32: Phân tích các đa thức sau thành nhân tử:
a) 4x2 – 4xy + y2;
b) 9x3 – 9x2y – 4x + 4y;
c) x3 + 2 + 3(x3 – 2).
Lời giải:
a) 4x2 – 4xy + y2
= (2x – y)2
b) 9x3 – 9x2y – 4x + 4y
= 9x2(x – y) – 4(x – y)
= (x – y)(9x2 – 4)
c) x3 + 2 + 3(x3 – 2)
= x3 + 2 + 3x3 – 6
= 4x3 – 4
= 4(x3 – 1)
= 4(x – 1)(x2 + x + 1)
Lời giải:
Hiền có số quyển vở là :
56 – 14 = 42 (quyển)
Cả 2 bạn có số quyển vở là :
56 × 2 = 112 (quyển)
Hương có số quyển vở là :
112 – 42 = 70 (quyển)
Hương có nhiều hơn Hiền số quyển vở là :
70 – 42 = 28 (quyển)
Vậy Hương có nhiều hơn Hiền 28 quyển vở.
Câu 34: Cho tam giác ABC. Tìm điểm M thỏa mãn .
A. M là trung điểm cạnh IC, với I là trung điểm cạnh AB.
B. M trùng với đỉnh C của tam giác ABC.
C. M là trọng tâm của tam giác ABC.
D. M là đỉnh của hình bình hành MCAB.
Lời giải:
Đáp án đúng là A
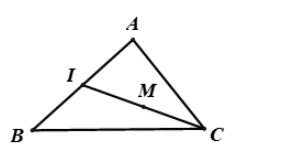
Gọi I là trung điểm của cạnh AB
Ta có
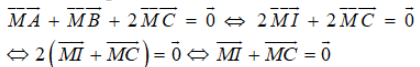
Suy ra M là trung điểm cạnh IC
Vậy ta chọn đáp án A.
A. 40%;
B. 45%;
C. 60%;
D. 66,66%.
Lời giải:
Đáp án đúng là D
Mẹ mua số lít nước mắm loại hai là:
10 – 4 = 6 (lít)
Tỉ số phần trăm giữa nước mắm loại một và nước mắm loại hai là:
4 : 6 = 0,6666 = 66,66%
Vậy ta chọn đáp án D.
Lời giải:
Số tiền được lãi của người đó là :
300 000 – 250 000 = 50 000 ( đồng )
Người đó được lãi số phần trăm là :
50 000 : 250 000 × 100 % = 20 %
Vậy người đó lãi được 20%.
Câu 37: Cho biết . Chứng minh x : y : z = a : b : c.
Lời giải:
Ta có
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
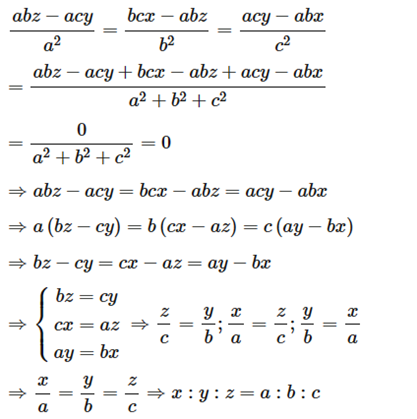
Vậy x : y : z = a : b : c.
Câu 38: Cho tam giác ABC. Vẽ điểm D thỏa mãn . Tứ giác ABCD là hình gì?
Lời giải:
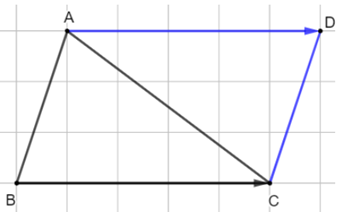
Cách vẽ:
+) Vẽ tam giác ABC bất kì
+) Trên nửa mặt phẳng bờ AB có chứa điểm C, vẽ một phần đường thẳng d đi qua A, song song với BC
+) Trên d, lấy điểm D sao cho AD = BC
Khi đó ta có hai vectơ cùng hướng và cùng độ dài nên
+) Tứ giác ABCD có AD // BC và AD = BC nên ABCD là hình bình hành.
Câu 39: Cho hai khoảng A = (m; m + 1) và B = (3; 5)
Tìm m để A ∪ B là một khoảng. Hãy xác định khoảng đó.
Lời giải:
Để A hợp B là một khoảng thì
Trường hợp 1: A ⊂ B, tức (m; m + 1) ⊂ (3; 5)
Khi đó A ∪ B = (3; 5).
Trường hợp 2: B ⊂ A, tức (3; 5) ⊂ (m; m + 1)
(loại)
Do đó không xảy ra trường hợp này.
Khi đó A ∪ B = (3; 5).
Trường hợp 3: A ∪ B = (m; 5) thì
Trường hợp 4: A ∪ B = (3; m +1) thì
Vậy thì A ∪ B = (m; 5);
thì A ∪ B = (3; 5);
thì A ∪ B = (3; m +1).
Lời giải:
Dây dài nhất đi qua M chính là đường kính đi qua M của đường tròn.
Như vậy độ dài của dây dài nhất bằng 26 (cm).
Dây ngắn nhất đi qua M là dây đi qua M và vuông góc với MO.
Độ dài dây ngắn nhất bằng
(cm).
Suy ra dây có độ dài là số nguyên thì có độ dài là 24, 25, 26 (cm)
Vậy có 3 dây có độ dài là một số tự nhiên đi qua M.
Câu 41: Giải phương trình sinx + cosx = 1.
Lời giải:
Ta có
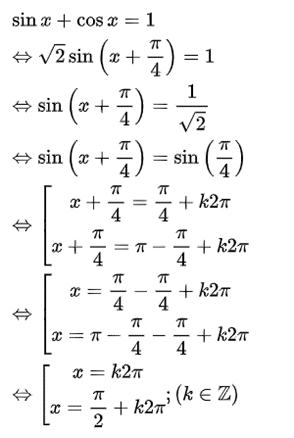
Vậy phương trình có nghiệm là x = k2π hoặc .
Lời giải:
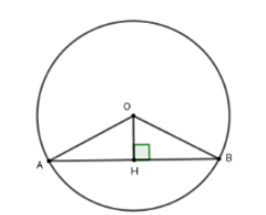
Xét tam giác OAB có OA = OB nên tam giác OAB cân tại O
Mà OH là trung tuyến
Suy ra OH là đường cao
Hay tam giác OAH vuông tại H
Suy ra AO2 = OH2 + AH2
Hay
Suy ra
Vậy H di động trên đường tròn tâm O bán kính 1,5 cm.
Câu 43: Tìm GTNN của A = x4 – 2x3 + 3x2 + 4x + 5.
Lời giải:
Ta có
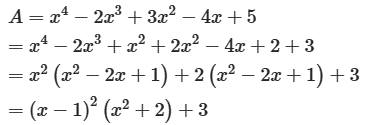
Vì (x – 1)2 ≥ 0 với mọi x
x2 + 2 ≥ 0 với mọi x
suy ra A ≥ 3 với mọi x
Dấu “ = ” xảy ra khi x = 1
Vậy giá trị nhỏ nhất của A bằng 3 khi x = 1.
A. Phép tịnh tiến vectơ ;
B. Phép đối xứng trục MP;
C. Phép quay tâm A góc quay 180°;
D. Phép quay tâm O góc quay – 180°.
Lời giải:
Đáp án đúng là: D
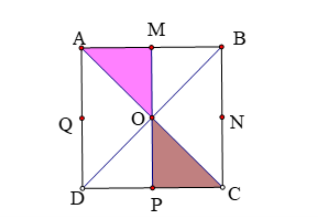
Ta có: phép dời hình biến DAMO thành DCPO tức biến điểm A thành điểm C, biến điểm O thành chính nó sao cho OA = OC.
Do đó C = Q(O; –180°)(A).
Phép dời hình biến DAMO thành DCPO tức biến điểm M thành điểm P, biến điểm O thành chính nó sao cho OM = OP.
Do đó P = Q(O; –180°)(M).
Mà O = Q(O; –180°)(O).
Suy ra phép dời hình biến DAMO thành DCPO là phép quay tâm O, góc quay – 180°.
Vậy ta chọn đáp án D.
Câu 45: Phương trình sinx = a luôn có nghiệm khi nào?
Lời giải:
Vì – 1 ≤ sinx ≤ 1
Nên phương trình sinx = a có nghiệm khi – 1 ≤ a ≤ 1
Vậy – 1 ≤ a ≤ 1.
Lời giải:
Đổi 300 000 m = 300 km
300 km gấp 100 km số lần là :
300 : 100 = 3 (lần)
Ô tô đi quãng đường 300 km thì tiêu thụ hết số xăng là :
13 x 3 = 39 (lít)
Vậy đi 300 000 m ô tô cần 39 lít xăng.
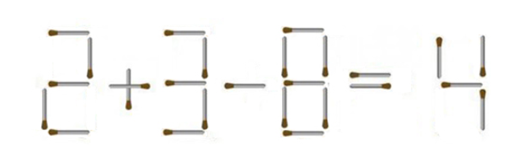
Lời giải:
Ta dịch chuyển 1 que diêm từ số 8 sang trước số 4 để có phép tính đúng là:
2 + 3 – 9 = – 4
Ta dịch chuyển 1 que diêm từ dấu = sang dấu – để có phép tính đúng là:
2 + 2 = 8 – 4
Câu 48: Cho A = 5 + 70 + x với x thuộc ℕ. Tìm x để:
a) A chia hết cho 5;
b) A không chia hết cho 5.
Lời giải:
a) Ta có: A = 5 + 70 + x = 75 + x
Để A chia hết cho 5 thì 75 + x chia hết cho 5
Mà 75 chia hết cho 5 nên x chia hết cho 5
Suy ra x ∈ B(5)
Vậy x ∈ B(5) thì A chia hết cho 5.
b) Ta có: A = 75 + x
Để A không chia hết cho 5 thì 75 + x không chia hết cho 5
Mà 75 chia hết cho 5 nên x không chia hết cho 5
Suy ra x ∉ B(5)
Vậy x ∉ B(5) thì A không chia hết cho 5.
Lời giải:
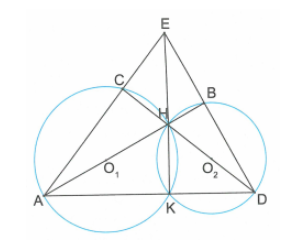
Gọi giao điểm của AC và BD là E
Các tam giác ACH, AKH nội tiếp đường tròn (O1) có cạnh HA là đường kính nên tam giác ACH vuông tại C, tam giác AHK vuông tại K
Suy ra
Các tam giác HDK, HDB nội tiếp đường tròn (O2) có cạnh HD là đường kính nên tam giác HDK vuông tại K, tam giác HBD vuông tại B
Suy ra
Từ (2) và (3) suy ra A, K, D thẳng hàng
Do đó HK ⊥ AD
Từ (1) và (4) suy ra H là trực tâm tam giác AED
Do đó HE ⊥ AD
Suy ra H thuộc EK
Vậy BC, BD, HK đồng quy tại 1 điểm.
Câu 50: Cho tana = 2. Tính giá trị của biểu thức .
Lời giải:
Vì tana = 2 nên cosa ≠ 0.
Ta có:
Câu 51: Cho tanα = – 2. Tính giá trị biểu thức .
Lời giải:
Vì tanα = – 2 nên cosα ≠ 0.
Ta có
(vì )
Thay tanα = – 2 vào biểu thức trên ta được:
Nên .
Vậy A = 5.