Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 9)

Câu 46: Một trang trại cần thuê xe vận chuyển 450 con lợn và 35 tấn cám. Nơi cho thuê xe chỉ có 12 xe lớn và 10 xe nhỏ. Một chiếc xe lớn có thể chở 50 con lợn và 5 tấn cám. Một chiếc xe nhỏ có thể chở 30 con lợn và 1 tấn cám. Tiền thuê một xe lớn là 4 triệu đồng, một xe nhỏ là 2 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thuê xe là thấp nhất?

Lời giải:

Gọi x, y (xe) lần lượt là số xe loại lớn, số xe loại nhỏ cần thuê (x, y ≥ 0, x, y ∈ ℤ).

Suy ra T = 4x + 2y (triệu đồng) là số tiền thuê xe.

Do đó yêu cầu bài toán ⇔ T nhỏ nhất.

Theo đề, ta có hệ: $\left\{\begin{array}{l}0\le x\le 12\\ 0\le y\le 10\\ 50x+30y\ge 450\\ 5x+y\ge 35\end{array}\right.$ (*)

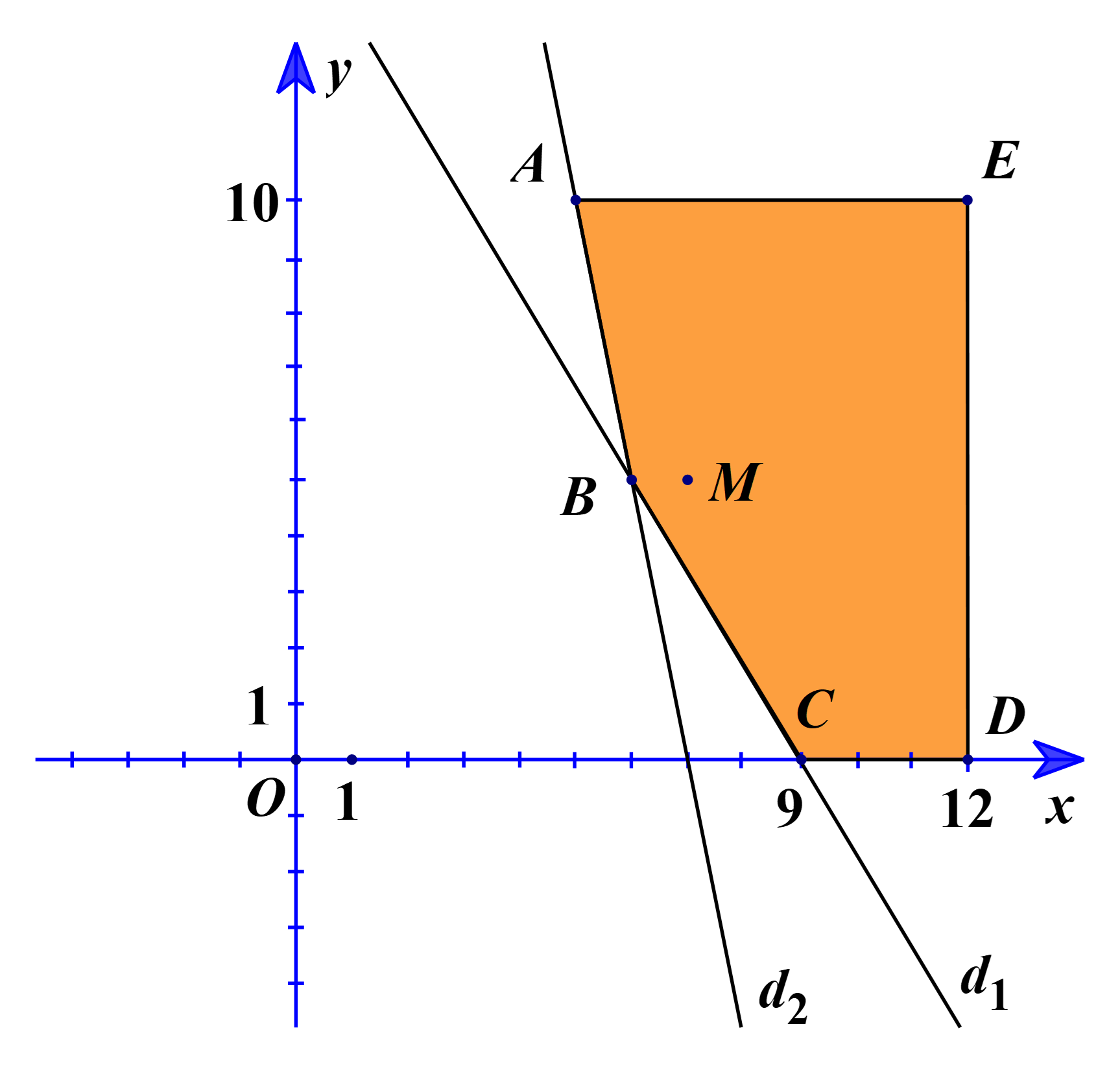
Vẽ các đường thẳng d₁: 50x + 30y = 450 và d₂: 5x + y = 35 trên cùng một hệ trục tọa độ.

Tiếp theo, ta lấy điểm M(7; 5). Khi đó ta có: $\left\{\begin{array}{l}0\le 7\le 12\\ 0\le 5\le 10\\ 50.7+30.5\ge 450\\ 5.7+5\ge 35\end{array}\right.$  (đúng).

Suy ra miền nghiệm của hệ (*) là phần ngũ giác ABCDE, kể cả các đoạn thẳng AB, BC, CD, DE, EA, với A(5; 10), B(6; 5), C(9; 0), D(12; 0), E(12; 10).

Ta có T_A = 40, T_B = 34, T_C = 36, T_D = 48, T_E = 68.

Do đó T nhỏ nhất ⇔ x = 6, y = 5.

Vậy trang trại phải thuê 6 xe lớn, 5 xe nhỏ để chi phí thuê xe là thấp nhất.

Phương pháp giải:

- Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng: $ax+by+c<0,ax+by+c>0,ax+by+c\le 0,ax+by+c\ge 0$ trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0; x và y là các ẩn số. 

- Để xác định miền nghiệm của bất phương trình $ax+by+c\le 0$, ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình như sau: 

Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng d: $ax+by+c =0$ 

Bước 2: Lấy điểm $M\left(x_0;y_0\right)$ không thuộc d. 

Bước 3: Tính $a{x}_0+b{y}_0+c$ và so sánh $a{x}_0+b{y}_0+c$ với 0.

Bước 4: Kết luận:

Nếu $a{x}_0+b{y}_0+c<0$  thì nửa mặt phẳng bờ d chứa điểm M là miền nghiệm của bất phương trình $ax+by+c\le 0$ . 

Nếu $a{x}_0+b{y}_0+c>0$ thì nửa mặt phẳng bờ d không chứa điểm M là miền nghiệm của bất phương trình $ax+by+c\le 0$ .