Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 71)

Câu 1: Tìm số lớn nhất có 4 chữ số khác nhau, chữ số hàng trăm là chữ số 5. Số này phải chia hết cho 2 và chia hết cho 5.

Lời giải:

Gọi số cần tìm có dạng $\overline{abcd}$

Vì số đã cho có chữ số hàng trăm là 5 nên b = 5

Số đã cho chia hết cho cả 2 và 5 nên phải có chữ số tận cùng là 0, hay d = 0

Khi đó ta có số  $\overline{a5c0}$

Vì số cần tìm là số lớn nhất có 4 chữ số khác nhau nên suy ra a = 9 và c = 8.

Vậy số cần tìm là 9580.

Câu 2: Tìm x, y thỏa mãn 2x² + y² + 9 = 6x + 2xy.

Lời giải:

2x² + y² + 9 = 6x + 2xy

⇔ 2x² + y² + 9 – 6x – 2xy = 0

⇔ (x – 3)² + (x – y)² = 0

Ta thấy: (x – 3)² + (x – y)² ≥ 0 với mọi x, y

Nên để đẳng thức xảy ra thì: $\left\{\begin{array}{l}x-3=0\\ x-y=0\end{array}\right.$  ⇔ x = y = 3

Vậy x = y = 3.

Câu 3: Tổ 1 và tổ 2 chăm sóc 28500 m² rừng. Sau khi chuyển 2500 m² rừng của tổ 1 sang tổ 2 thì tổ 2 chăm sóc nhiều hơn tổ 1400 m² rừng. Hỏi lúc đầu mỗi tổ chăm sóc bao nhiêu m² rừng?

Lời giải:

Tổ 1 chăm sóc nhiều hơn tổ 2 số mét vuông rừng là:

2500 + 400 = 2900 (m²)

Lúc đầu tổ 2 chăm sóc số mét vuông rừng là:

(28500 – 2900) : 2 = 12800 (m²)

Lúc đầu tổ 1 chăm sóc số mét vuông rừng là:

28500 – 12800 = 15700 (m²).

Câu 4: Các số thực a,b,c,d thỏa mãn đồng thời các điều kiện abc – d = 1, bcd – a = 2, cda – b = 3 và dab – c = –6. Chứng minh: a + b + c + d  ≠  0.

Lời giải:

Giả sử a + b + c + d = 0 ⇒ b + c = −(a + d)

Cộng từng vế các điều kiện trên ta được

abc + bcd + cda + dab − (a + b + c + d) = 0

⇒ abc + bcd + cda + dab = 0

⇔ bc(a + d) + ad(b +c) = 0

⇔ bc(a + d) − ad(a + d) = 0

⇔ (a + d)(bc − ad) = 0

TH1: a + d = 0

Từ : abc – d = 1,bcd – a = 2, ta cộng lại ta được

abc + bcd−(a + d) = 3

⇔ bc(a + d)−(a + d) = 3

⇔ (a + d)(bc − 1) = 3

⇔ 0 = 3 (Vô lí)

Th2 : bc – ad = 0

Nếu b = 0 ⇒ a + c + d = 0(1)

Từ abc –d = 1 ⇒ 0 −d = 1 ⇒ d = −1

Từ bcd – a =2 ⇒ a = −2

Từ dab – c =−6 ⇒ c = 6

Lúc này ⇒ a + c + d = − 2 + 6 + (−1) = 3 ≠ 0 (Trái với (1)

Do đó b ≠ 0, tương tự d ≠ 0

Từ bc – ad = 0 ⇒ ab = cd (b, d ≠ 0)

Áp dụng tính chất dãy tỉ số bằng nhau

⇒ $\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}=\frac{-\left(b+d\right)}{b+d}=-1$

⇒ a = −b ⇒ a + b = 0

Tương tụ như với a + d = 0 ⇒ Vô lí

Vậy a + b + c + d ≠ 0 (đpcm).

Câu 5: Cho dãy số (u_n) có u₁ = 4 và u_n+1 = 3u_n – 2. Tìm số hạng thứ 5 của dãy.

Lời giải: 

Ta có: u₂ = 3u₁ – 2 = 3.4 – 2 = 10

u₃ = 3u₂ – 2 = 3.10 – 2 = 28

u₄ = 3u₃ – 2 = 3.28 – 2 = 82

u₅ = 3u₄ – 2 = 3.82 – 2 = 244.

Câu 6: Tìm số hạng đầu tiên của cấp số nhân, biết rằng công bội là 3, tổng các số hạng là 728 và số hạng cuối là 486.

Lời giải: 

Gọi số hạng đầu là u₁, công bội là q

Ta có: q = 3

u_n = u₁ . q^n–1 = u₁ . 3^n–1 = 486

Suy ra: u¹ . 3ⁿ = 486 . 3 = 1458

728 = $\frac{u_1.\left(1-3^n\right)}{1-3}=\frac{u_1.\left(1-3^n\right)}{-2}=\frac{u_1.\left(3^n-1\right)}{2}$

⇔ u₁(3ⁿ – 1) = 728 . 2 = 1456

⇔ u₁ . 3ⁿ – u₁ = 1456

⇔ 1458 – u₁ = 1456

⇔ u₁ = 1458 – 1456 = 2

Vậy số hạng đầu của cấp số nhân là 2.

Câu 7: Một người bán 120kg gạo, trong đó có 65% là gạo tẻ, còn lại là gạo nếp. Hỏi người đó bán được bao nhiêu ki–lô–gam gạo nếp?

Lời giải: 

Số gạo tẻ là:

120 . 65% : 100% = 78 (kg)

Số gạo nếp là:

 120 – 78 = 42 (kg)

Câu 8: Bác Vinh mua 1425 viên gạch bông để lát nền nhà. Bác dự tính sẽ thừa ra 125 viên đủ để lát 5m² khu vệ sinh. Hỏi diện tích nền nhà cần lát gạch bông của bác Vinh là bao nhiêu mét vuông?

Lời giải: 

Số viên gạch bông đủ để lát 1m² nền nhà là: 125 : 5 = 25 (viên)

Nền nhà của bác Vinh lát hết số viên gạch bông là: 1425 – 125 = 1300 (viên)

Diện tích nền nhà của bác Vinh là: 1300 : 25 = 52 (m²).

Câu 9: Cho các chữ số 0;1;2;3;4;5. Từ các chữ số này ta có thể lập được bao nhiêu số có 3 chữ số khác nhau từng đôi một và chia hết cho 9 ?

Lời giải: 

+ Gọi số có 3 chữ số khác nhau có dạng: $\overline{abc}$

+ Để số có 3 chữ số chia hết cho 9 ⇒ Tổng a + b + c phải chia hết cho 9

+ Tập hợp các số mà tổng của chúng chia hết cho 9 là:

A = {0, 5, 4}

⇒ Các số đó là: 540, 450, 504, 405 ⇒ Vậy có 4 số

B = {2, 3, 4}⇒ Đảo vị trí 3 số ta có: 3!

C = {1, 3, 5}⇒ Đảo vị trí 3 số ta có: 3!

Vậy có: 4 + 3! + 3! = 16 số.

Câu 10: Một biển báo giao thông như hình vẽ. Tính diện tích phần tô đậm của biển báo, biết biển báo hình tròn có đường kính 50cm; diện tích hình chữ nhật bằng 20% diện tích hình tròn

Lời giải: 

Bán kính biển báo là : 50 : 2 = 25 (cm)

Diện tích biển báo là : 25 x 25 x 3,14 = 1962,5 (cm²)

Diện tích hình chữ nhật là : 1962,5 x 20 : 100 = 392,5 (cm²)

Diện tích phần tô đậm là : 1962,5 – 392,5 = 1570 (cm²).

Câu 11: Một cấp số cộng (u_n) có u₉ = 47; công sai d = 5. Số 10092 là số hạng thứ mấy trong cấp số cộng?

Lời giải: 

Ta có: u₉ = u₁ + 8d = 47

Suy ra: u₁ = 47 – 8.5 = 7

Gọi số 10092 là số hạng thứ n trong cấp số cộng

Ta có: 10092 = u₁ + (n – 1)d

⇔ 10092 = 7 + (n – 1).5

⇔ 5n – 5 + 7 = 10092

⇔ 5n = 10090

⇔ n = 2018

Vậy 10092 là số hạng thứ 2018 của cấp số cộng.

Câu 12: Một người nuôi ong thu hoạch được 40 lít mật ong. người đó muốn đổ vào các chai, mỗi chai chứa 0,72 lít cần ít nhất bao nhiêu chai để chứa hết số dầu đó?

Lời giải: 

Để đựng hết 40 lít mật ong thì người đó cần số chai là:

40 : 0,72 = 55 (chai) và dư 0,4 lít

Do thừa 0,4 lít mật ong nên cần thêm 1 chai nữa.

Vậy tổng số chai người đó cần là:

55 + 1 = 56 (chai).

Câu 13: Tuần này lớp 6A và 6B gồm 40 học sinh nữ và 36 học sinh nam được phân công đi thu gom rác làm sạch bờ biển ở địa phương. Nếu chia nhóm sao cho số học sinh nam và nữ trong các nhóm bằng nhau thì:

a) Có thể chia được thành bao nhiêu nhóm học sinh?

b) Có thể chia nhiều nhất bao nhiêu nhóm học sinh?

Lời giải: 

Để số học sinh nam và nữ trong các nhóm bằng nhau thì số học sinh nam bằng số học sinh nữ và phải là ước chung của 36 và 40

Ta có:

36 = 2² . 3² và 40 = 2³ . 5

⇒ ƯC (36; 40) = 2² = 4

a) Có thể chia nhóm như sau:

+) Chia được 2 nhóm. Nhóm có 18 nam và 20 nữ.

+) Chia được 4 nhóm. Nhóm có 9 nam và 10 nữ.

b) Có thể chia nhiều nhất 4 nhóm với mỗi nhóm có 9 nam và 10 nữ.

Câu 14: Tìm số dư trong phép chia 0,6159 : 0,52 ( số thương chỉ lấy đến hai chữ số ở phần thập phân).

Lời giải: 

Ta có: 0,6159 : 0,52 = 1,18 (dư 0,0023)

Vậy số dư của phép chia khi lấy 2 chữ số ở phần thập phân là 0,0023.

Câu 15: Tìm x biết: x(x + 2)(x² + 2x + 2) + 1 = 0.

Lời giải: 

x(x + 2)(x² + 2x + 2) + 1 = 0

⇔ (x² + 2x)(x² + 2x + 2) + 1 = 0

Đặt x² + 2x = t

Ta có: t(t + 2) + 1 = 0

⇔ t² + 2t + 1 = 0

⇔ (t + 1)² = 0

⇔ t = – 1

Khi đó: x² + 2x = – 1

⇔ x²  + 2x + 1 = 0

⇔ (x + 1)² = 0

⇔ x = – 1

Vậy x = –1.

Câu 16: 5,34 km² = …ha.

Lời giải: 

1 km² = 100 ha

Nên 5,34 km² = 534 ha.

Câu 17: Diện tích hình vuông tăng lên gấp 4 lần, hỏi độ dài mỗi cạnh hình vuông tăng lên gấp mấy lần?

Lời giải: 

Gọi cạnh hình vuông ban đầu là: a (a > 0)

Diện tích hình vuông ban đầu là: a.a  (đon vị đo)

Diện tích hình vuông lúc sau là: a . a . 4 (đơn vị đo) = a . a . 2 . 2 = (a . 2) . (a . 2)

Cạnh của hình vuông lúc sau là: a . 2 (đơn vị đo)

Cạnh hình vuông đó tăng số lần là: 

a . 2 : a = 2 (lần)

Vậy cạnh hình vuông ban đầu phải tăng 2 lần thì diện tích hình vuông mới gấp 4 được.

Câu 18: Năm nay bố 32 tuổi và gấp 4 lần tuổi con. Hỏi sau 4 năm nữa tuổi bố gấp mấy lần tuổi con?

Lời giải: 

Năm nay con có số tuổi là:

32 : 4 = 8 (tuổi)

4 năm nữa bố có số tuổi là:

32 + 4 = 36 (tuổi)

4 năm nữa con có số tuổi là:

8 + 4 = 12 (tuổi)

4 năm nữa tuổi bố gấp tuổi con số lần là:

36 : 12 = 3 (lần)

Câu 19: Sắp xếp 6 nam sinh và 5 nữ sinh vào một dãy ghế hàng ngang có 11 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau?

Lời giải: 

Coi 5 nữ sinh là X .

Số cách sắp xếp X và nam sinh là 7!

Số cách sắp xếp 5 nữ sinh trong X là 5!

Số cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau: 7!.5! = 604800.

Câu 20: Tìm x để 3 số: 1 − x, x², 1 + x theo thứ tự lập thành một cấp số cộng?

Lời giải: 

Do 3 số đã cho lập thành một cấp số cộng nên số ở giữa phải bằng trung bình cộng của 2 số còn lại. Do đó ba số: 1 − x, x², 1 + x  lập thành một cấp số cộng khi và chỉ khi 

x² − (1 − x) = 1 + x – x²

⇔ 2x² = 2

⇔ x = ±1.

Câu 21: Tính diện tích hình thang có tổng đọ dài của chiều cao và đáy bé bằng 28,7 dm, 3 lần đáy bé bằng 4 lần chiều cao, đáy lớn hơn đáy bé 1,2 dm.

Lời giải: 

Vì 3 lần đáy bé bằng 4 lần chiều cao nên tỉ số giữa chiều cao và đáy bé là $\frac{3}{4}$

Tổng số phần bằng nhau là:

3 + 4 = 7 (phần)

Đáy bé của hình thang đó là:

28,7 : 7 × 4 = 16,4 (dm)

Chiều cao của hình thang đó là:

28,7 – 16,4 = 12,3 (dm)

Đáy lớn của hinhg thang đó là:

16,4 + 1,2 = 17,6 (dm)

Diện tích hình thang là:

(17,6 + 16,4) . 12,3 : 2 = 209,1 (dm²).

Câu 22: Tính diện tích phần tô đậm biết AB = 16 cm.

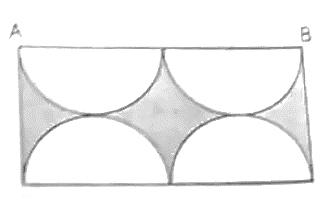
Lời giải: 

Độ dài đường kính nửa đường tròn là:

16 : 2 = 8 (cm)

Bán kính nửa đường tròn là:

8 : 2 = 4 (cm)

Diện tích 4 nửa đường tròn là:

3,14 . 4² . 2 = 100,48 (cm²)

Ta thấy chiều rộng hình chữ nhật bằng 1 nửa AB nên chiều rộng hình chữ nhật là: 16 : 2 = 8 (cm)

Diện tích hình chữ nhật là:

16 . 8 = 128 (cm²)

Diện tích phần tô đậm là:

128 – 100,48 = 27,52 (cm²)

Câu 23: Tính nhanh 1152 – (374 + 1152) + (–65 + 374).

Lời giải: 

1152 − (374 + 1152) + (−65 + 374)

= 1152 – 374 – 1152 – 65 + 374

= (1152 − 1152) + (−374 + 374) + (−65)

= 0 + 0 + (−65)

= −65.

Câu 24: Một người mua 600 cái bát khi chuyên chở đã có 69 cái bát bị vỡ mỗi cái bát còn lại người đó bán với giá 6000 đồng và được lãi 18% so với số tiền mua bát hỏi giá tiền mua mỗi tá bát là bao nhiêu đồng.

Lời giải: 

Số cái bát đem bán là:

600 – 69 = 531 (cái)

Sô tiền bán 531 cái bát với giá 6000 đồng là:

531 . 6000 = 3186000 (đồng)

Coi giá vốn mua bát là 100%

Số tiền bán bát chiếm số phần trăm số tiền vốn là:

100% + 18% = 118% (tiền vốn)

Số tiền vốn là:

3186000 : 118 . 100 = 2700000 (đồng)

Số tiền mua 1 cái bát là:

2700000 : 600 = 4500 (đồng)

Ta có 1 tá = 12 cái

Số tiền mua mỗi tá bát là:

4500 . 12 = 54000 (đồng)

Đáp số: 54000 đồng.

Câu 25: Biết chu vi của hình chữ nhật là 26m và tỉ số hai cạnh là 1,6. Hỏi diện tích của hình chữ nhật là bao nhiêu?

Lời giải: 

Nửa chu vi hình chữ nhật là: 26 : 2 = 13 (m)

Gọi chiều dài hình chữ nhật là a (m) thì chiều rộng hình chữ nhật là 13 – a (m)

Theo bài ra ta có:

a : (13 – a) = 1,6

⇔ a = 1,6 (13 – a)

⇔ a = 20,8 – 1,6a

⇔ 2,6a = 20,8

⇔ a = 8

Suy ra: chiều dài hình chữ nhật là 8m

Chiều rộng hình chữ nhật là:

13 – 8 = 5 (m)

Diện tích hình chữ nhật là:

8 . 5 = 40 (m²).

Câu 26: Giá niêm yết một bộ quần áo thể thao tại một cửa hàng A là 780000 đồng. Nhân dịp khai trương, cửa hàng giảm tất cả các bộ quần áo thể thao loại bộ quần ảo thể thao là 20% theo giá niêm yết.

a) Hỏi giá một bộ quần áo thể thao sau khi được giảm là bao nhiêu tiền ?

b) Để tri ân khách hàng, cửa hàng đã giảm thêm 10% nữa (so với giá giảm lần đầu). Trong đợt khuyển mãi lần thứ hai này, của hàng đã bán được 25 bộ quần áo thể thao thì lời được 2750000 đồng . Hỏi giá vốn một bộ quần áo thể thao là bao nhiêu tiền?

Lời giải: 

a) Giá một bộ quần áo thể thao sau khi được giảm là:

7800000 . (100% – 20%) = 6240000 (đồng)

b) Giá một bộ quần áo thể thao sau khi giảm thêm 10% là:

6240000 . (100% – 10%) = 5616000 (đồng)

Một bộ quần áo thể thao lời được số tiền là:

27500000 : 25 = 1100000 (đồng)

Giá vốn của một bộ quần áo là:

5616000 – 1100000 = 4516000 (đồng)

Câu 27: Tam giác thường có cạnh huyền không?

Lời giải: 

Tam giác thường không có cạnh huyền.

Tam giác có cạnh huyền là tam giác vuông.

Câu 28: Theo kế hoạch hai tổ sản xuất 600 sản phẩm trong một thời gian nhất định. Do áp dụng kĩ thuật mới nên tổ I đã vượt mức 18% và tổ II đã vượt mức 21%. Vì vậy trong thời gian quy định họ đã hoàn thành vượt 120 sản phẩm. Hỏi số sản phẩm được giao của mỗi tổ kế hoạch?

Lời giải: 

Gọi số sản phẩm được giao của mỗi tổ theo kế hoạch lần lượt là a và b (sản phẩm, 0 ≤ a, b ≤ 600)

Theo kế hoạch hai tổ sản xuất 600 sản phẩm nên ta có a + b = 600 (1)

Do áp dụng kĩ thuật mới nên tổ I vượt mữa 18% và tổ hai vược mức 21%, vì vậy họ đã hoàn thành vượt 120 sản phẩm nên ta có:

0,18a + 0,21b = 120(2)

Từ (1) và (2) ta có hệ phương trình, nhân cả hai vế của phương trình (1) với 0,21 rồi trừ đi (2) ta được:

0,03a = 6 ⇔ a = 200

⇒ b = 400

Vậy theo kế hoặc tổ I được giao 200 sản phầm, tổ II được giao 400 sản phẩm.

Câu 29: Bài toán Ủng hộ miền Trung năm 2020: Một chuyến hàng ủng hộ miền Trung có 300 thùng mì tôm, 240 thùng nước ngọt và 420 lốc sữa. Các cô chú muốn chia thành các phần quà đều nhau về số lượng mì, nước và sữa. Con hãy giúp các cô chú chia sao cho số lượng các phần quà là nhiều nhất.

Lời giải: 

Gọi phần quà chia được nhiều nhất là x

Theo bài ra, ta có:

300 chia hết cho x

240 chia hết cho x

420 chia hết cho x

⇒ x ∈ ƯCLN(300; 240; 420) 

Ta lại có:

300 = 2².3.5²

240 = 2⁴.3.5

420 = 2².3.5.7

⇒ x ∈ ƯCLN (300; 240; 420) = 2².3.5 = 60

Vậy có thể chia được nhiều nhất 60 phần quà.

Câu 30: Cho a + b + c = 0. Chứng minh a³ + b³ + c³ = abc.

Lời giải: 

Từ a + b + c = 0 suy ra: a = –(b+c)

a³ = –(b + c)³ = –[b³ + c³ + 3bc(b + c)] = –b³ – c³ + 3abc

⇒  a³ + b³ + c³ = abc.

Câu 31: Cho hàm số y = (m – 2)x + m + 1 (d)

a) Với giá trị nào của m thì hàm số đã cho là hàm số bậc nhất ?

b) Với giá trị nào của m thì hàm số đã cho là hàm số đồng biến?

c) Tìm m để (d) song song với (d₁): y = 3x + 2.

d) Vẽ đồ thị hàm số với m = 5.

Lời giải: 

a) Hàm số bậc nhất khi m – 2 ≠ 0

⇔ m ≠ 2

b) Hàm số đồng biến khi m – 2 > 0

⇔ m > 2

c) (d)//(d1):y=3x+2 khi m – 2 = 3; m + 1  ≠ 2

⇔ m = 5; m ≠ 1

⇒ m = 5

d) Khi m = 5 ta có: y = (5 – 2)x + 5 + 1 = 3x + 6

Đường thẳng y = 3x + 6 đi qua A(0;6), B(–2;0)

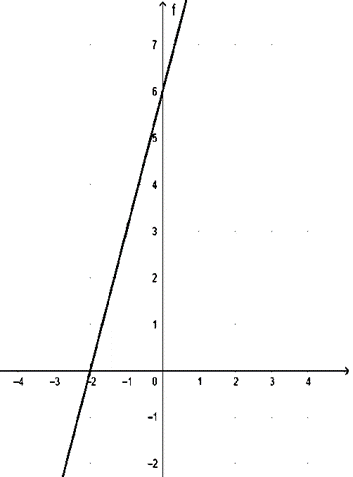
Câu 32: Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của BC, BD. (P) là mp qua IJ và cắt AC, AD lần lượt tại N, M. Chứng minh tứ giác IJMN là hình thang. Nếu M là trung điểm AD thì tứ giác IJMN là hình gì?

Lời giải:

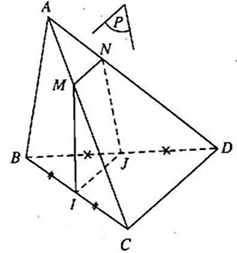
Ba mặt phẳng (ACD) , ( BCD) , (P) đôi một cắt nhau theo các giao tuyến CD, IJ, MN.

Vì IJ // CD ( IJ là đường trung bình của tam giác BCD) nên theo định lí 2 ta có IJ // MN.

Vậy tứ giác IJNM là hình thang.

Nếu M là trung điểm của AC thì N là trung điểm của AD.

Khi đó tứ giác IJNM có một cặp cạnh đối vừa song song vừa bằng nhau nên là hình bình hành.

Câu 33: Một cái lều hình vuông được dựng ở trung tâm của một mảnh vườn hình vuông. Khoảng cách từ mỗi mép ngoài cái lều tới tường bao quanh khu vườn là 8 m. Biết tổng diện tích của phần mảnh vườn không tính cái lều là 448m², tính diện tích cái lều, theo m²?

Lời giải: 

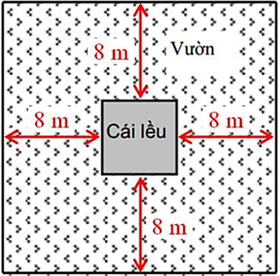
Gọi cạnh của cái lều là a (m)

Diện tích cái lều là a²

Cạnh của mảnh vườn hình vuông là: 8 + 8 + a = a + 16

Ta có: (a + 16)² – a² = 448

⇔ a² + 32a + 256 – a² – 448 = 0

⇔ 32a – 192 = 0

⇔ a = 6

Vậy cạnh của cái lều là 6 m.

Diện tích cái lều là:

6 . 6 = 36 (m²).

Câu 34: Một mảnh đất hình chữ nhật có chiều dài 26m, chiều rộng bằng $\frac{1}{4}$  chiều dài trong đó diện tích để làm nhà chiếm 62,5⁰/₀. Tính diện tích đất làm nhà.

Lời giải:

Chiều rộng mảnh đất hình chữ nhật đó là:

26 : 4 = 6,5 (m) 

Diện tích mảnh đất hình chữ nhật đó là:

6,5 . 26 = 169 (m²)

Coi mảnh đất hình chữ nhật đó là 100% thì diện tích đất làm nhà là

169 : 100 . 62,5 = 105,625 (m²)

Đáp số: 105,625 m².

Câu 35: Một lớp học gồm 16 nam và 24 nữ. Muốn chia thành các tổ sao cho số nam, số nữ ở mỗi tổ đều bằng nhau.

a) Có mấy cách chia ?

b) Nhiều nhất có bao nhiêu tổ. Lúc đó số nam, số nữ trong mỗi tổ là bao nhiêu ?

Lời giải:

a) Gọi số tổ chia được là x (tổ), x > 1, x thuộc ℕ

Ta có: 16 ⋮ x; 24 ⋮ x

⇒ x ∈ ƯC (16, 24)

Ta có: 16 = 2⁴; 24 = 2³.3

ƯCLN (16, 24) = 2³ = 8

ƯC (16, 24) = {1; 2; 4; 8} có 4 số

x ∈ ƯC (16, 24) = Ư(8) > 1 = {2; 4; 8}

Vậy có 3 cách chia.

b) Ta có: ƯCLN (16, 24) = 2³ = 8

Nên số tổ chia được nhiều nhất chính là ƯCLN(16, 24) = 8

Lúc đó số nam mối tổ là:

16 : 8 = 2 (bạn)

Số nữ mỗi tổ là:

24 : 8 = 3 (bạn).

Câu 36: Sau khi xem bảng báo giá ở siêu thị, mẹ bạn Tín đưa cho bạn 1200000 đồng nhờ bạn ra siêu thị mua 1 bàn ủi và 1 bộ lau nhà. Hôm nay đúng đợt khuyến mãi, bàn ủi có giá niêm yết 350000 đồng được giảm 20% bộ lau nhà có giá niêm yết 280000 đồng được giảm 25%.

a) Số tiền bạn Tín mang theo có đủ để mua bàn ủi và bộ lau nhà hay không? Vì sao?

b) Giá niêm yết của ba lô là 630000 đồng và được giảm 10%. Giả sử số tiền bạn Tín mang theo đủ để mua ba loại hàng trên bảng giá. Hãy cho biết nếu mua ba loại hàng trên, bạn Tín phải trả bao nhiêu tiền và được giảm bao nhiêu % ? (làm tròn đến chữ số thập phân thứ nhất)

Lời giải: 

a) Số tiền 1 bàn ủi (sau khi khuyến mãi) là:

350000 – 350000 . 20% = 280000 (đồng)

Số tiền 1 bộ lau nhà (sau khi khuyến mãi) là:

280000 – 280000 . 25% = 210000 (đồng)

Tổng số tiền là:

280000 + 210000 = 490000 (đồng) < 1200000 đồng

Vậy số tiền bạn Tín mang theo đủ để mua bàn ủi và bộ lau nhà.

b) Số tiền 1 balô (sau khi khuyến mãi) là:

630000 – 630000 . 10% = 567000 (đồng)

Tổng số tiền mua đồ (khi chưa giảm giá) là:

350000 + 280000 + 630000 = 1260000 (đồng)

Tổng số tiền mua đồ (sau khi giảm) là:

490000 + 567000 =  1057000 (đồng)

Bạn Tín được giảm số % khi đi mua đồ là:

(1260000 – 1057000) : 1260000 . 100% = 16.1%.

Câu 37: Sân bóng đá tại trung tâm thể thao quần Tây Hồ là một hình chữ nhật có chiều dài là 105m, chiều rộng 68m. Ban quản lý muốn thay cỏ mới cho sân. Tính số tiền ban quản lý phải trả để mua cỏ? Biết mỗi mét vuông cỏ có giá 120000 đồng.

Lời giải: 

Diện tích sân bóng đó là:

105 . 68 = 7140 (m²)

Số tiền ban quản lý phải trả để mua cỏ là:

120000 . 7140 = 856800000 (đồng)

Câu 38: 1. Xây dựng các học liệu số phục vụ cho một hoạt động học trong kế hoạch bài dạy môn Toán có ứng dụng CNTT ở cấp Tiểu hoc đã có.

2. Mô tả cách sử dụng học liệu số trong hoạt động dạy học.

Lời giải: 

1. Các học liệu số phục vụ cho hoạt động học trong kế hoạch bài dạy môn Toán bài: Hình thoi Toán lớp 4.

– Hoạt động: Củng cố kiến thức , ôn luyện.

– Mục đích:

+ Giúp học sinh nhận dạng được thế nào là hình thoi.

+ Cách tính diện tích, chu vi của hình thoi.

+ Các tính chất của hình thoi.

– Các học liệu:

+ Powpoint.

+ Video.

+ Các nguồn web / link phục vụ trò chơi học tập: Quizz.

2. Mô tả sử dụng học liệu số:

– Đối với powpoint : Trình chiếu , mô tả những hình ảnh sinh động nhiều màu sắc giúp học sinh tiếp thu nhanh, nhớ lâu.

– Video: Xem những video liên quan đến hình thoi có ứng dụng liên quan đến thực tế cuộc sống xung quanh.

– Quizz: Kết hợp với việc học , tạo game trên hình thức học qiuzz giúp học sinh hứng thú, là công cụ tốt để triển khai kiểm tra năng lực nhận thức và vận dụng của học sinh cuối buổi học.

Vai trò của học liệu trong giáo dục:

– Tạo động lực cho giáo viên.

– Hỗ trợ và góp phần cải thiện các phương pháp giáo dục.

– Giúp người học có động lực và trách nhiệm hơn trong việc tự học.

Câu 39: Diện tích bề mặt Trái đất có bao nhiêu ki lô mét vuông?

Lời giải: 

Diện tích bề mặt Trái đất khoảng 510 100 000 km².

Câu 40: Tìm góc tạo bởi đường thẳng y = 2x – 1 với trục Ox.

Lời giải: 

Đường thẳng y = 2x – 1 cắt trục Ox tại điểm A(12;0); B(0;−1)

Vì hệ số của đường thẳng là 2 > 0 nên góc tạo bởi đường thẳng với Ox là góc nhọn.

tan α = $\frac{1}{\frac{1}{2}}=2$  ⇒ α ≈ 63,43°.

Câu 41: Tính tổng S = 1 + 2 + 3 + ... + n.

Lời giải: 

Ta thấy: 2 – 1 = 1, 3 – 2 = 1. Vậy khoảng cách giữa hai số hạng bằng 1

Số hạng đầu dãy là 1

Số hạng cuối dãy là n

Số các số hạng là: (n – 1) : 1 + 1 = n

Tổng S = $\frac{n\left(n+1\right)}{2}$ .

Câu 42: Tổng số học sinh của 1 trường THCS là 600 em học sinh. Tính số học sinh mỗi khối biết rằng số học sinh bốn khối 6, 7, 8, 9 cửa trường đó tỉ lệ nghịch với các số 9, 8, 7, 6.

Lời giải: 

Gọi số học sinh của bốn khối 6, 7, 8, 9 là a, b, c, d (a, b, c, d ∈ ℕ^*)

Theo bài ra ta có: a + b + c + d = 600

Vì a, b, c, d tỉ lệ nghịch với 9, 8, 7, 6 nên ta có:

$\frac{a}{9}=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}=\frac{a+b+c+d}{9+8+7+6}=\frac{600}{30}=20$

Suy ra: a = 20.9 = 180

b = 20.8 = 160

c = 20.7 = 140

d = 20.6 = 120

Vậy số học sinh của bốn khối 6, 7, 8, 9 lần lượt là 180, 160, 140, 120 học sinh.

Câu 43: Từ các số 0, 1, 2, 7, 8, 9 lập được bao nhiêu số chẵn có năm chữ số khác nhau?

Lời giải: 

Gọi số cần tìm có dạng $\overline{abcde}$  (a ≠ 0; a ≠ b ≠ c ≠ d ≠ e)

Từ các số đã cho, để lập được số chẵn thì e ∈ {0; 2; 8}

TH1: Nếu e = 0

Có 5 cách chọn a

Có 4 cách chọn b

Có 3 cách chọn c

Có 2 cách chọn d

Suy ra có: 5 . 4 . 3 . 2 = 120 (cách)

TH2: Nếu e = 2 hoặc e = 8

Có 4 cách chọn a (vì a khác 0)

Có 4 cách chọn b

Có 3 cách chọn c

Có 2 cách chọn d

Suy ra có: 4 . 4 . 3 . 2 . 2 = 192 (cách)

Vậy có: 120 + 192 = 312 (cách) lập được số thỏa mãn yêu cầu bài toán.

Câu 44: Vào tháng 5, giá niêm yết một cái tủ lanh tại một siêu thị điện máy là 10000000 đồng. Đến tháng 6, siêu thị giảm 5% cho mỗi chiếc. Sang tháng 7 siêu thị tiếp tục giảm thêm 10% (so với giá tháng 6). Hỏi giá tháng 7 chênh lệch so với giá niêm yết là bao nhiêu tiền?

Lời giải: 

Giá của chiếc tủ lạnh vào tháng 6 là:

10000000 – 10000000 . 5% = 9500000 (đồng)

Giá của chiếc tủ lạnh vào tháng 7 là:

9500000 – 9500000 . 10% = 8550000 (đồng)

Giá tiền chênh lệch vào tháng 7 so với giá niêm yết là:

10000000 – 8550000 = 1450000 (đồng).

Câu 45: Để lát nền một căn phòng người ta đã sử dụng hết 200 viên gạch hình vuông có cạnh 30cm . Hỏi căn phòng đó có diện tích báo nhiêu mét vuông, biết diện tích phần mạch vữa không đáng kể?

Lời giải: 

Diện tích một viên gạch là:

30 . 30 = 900 (cm²)

Diện tích của căn phòng là:

900 . 200 = 180000 (cm²)

Đổi: 180000 cm² = 18 m².

Câu 46: Cho x – y = 1. Chứng minh x³ – y³ = 1 + 2xy.

Lời giải: 

Xét x³ – y³ = (x – y)(x² + xy + y²)

= x² + xy + y²

= (x– y)² + 2xy

= 1 + 2xy

Vậy x³ – y³ = 1 + 2xy.

Câu 47: Cho đường tròn (O) và một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB với đường tròn (O) (A và B là hai tiếp điểm). Gọi I là giao điểm của OM và AB. Kẻ đường kính BC của (O). Chứng minh OI.OM = OA²

Lời giải: 

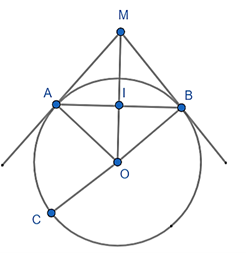
Ta có: OA = OB  (bán kính)

MA = MB (tính chất hai tiếp tuyến cắt nhau)

⇒ OM là trung trực của AB ⇒ OM ⊥ AB tại I.

ΔOAM vuông tại A đường cao AI

⇒ OI.OM = OA² (hệ thức giữa cạnh và đường cao).

Câu 48: Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7 và 8 quả cầu vàng được đánh số từ 1 đến 8. Hỏi có bao nhiêu cách lấy ra 3 quả cầu khác màu và khác số.

Lời giải: 

Ta chọn các quả cầu theo trình tự sau:

Công đoạn 1, Chọn quả cầu xanh: 7 cách chọn (Vì cầu xanh được chọn tuỳ ý từ 1 đến 7)

Công đoạn 2, Chọn quả cầu vàng: có 7 cách chọn (Vì số đánh trên cầu vàng không được chọn lại số đã đánh trên quả cầu xanh đã chọn)

Công đoạn 3, Chọn quả cầu đỏ: có 8 cách chọn (Vì số trên quả cầu đỏ chọn không được chọn lại các số mà quả cầu xanh và quả cầu vàng đã chọn)

Tổng kết, số cách lấy ra 3 quả cầu khác màu và khác số là 7.7.8 = 392 cách chọn.

Câu 49: Tăng cạnh hình vuông thêm 25 % ta được một hình vuông mới có chu vi là 15 cm. Tính chu vi hình vuông ban đầu 

Lời giải: 

Gọi cạnh hình vuông ban đầu là a(cm)

Ta có: (a + 25%) . 4 = 15

⇔ (a + 0,25) . 4 = 15

⇔ 4a + 1 = 15

⇔ 4a = 14

⇔ a = 3,5 (cm)

Chu vi hình vuông ban đầu là:

3,5 . 4 = 14 (cm)

Câu 50: Trong điều kiện thích hợp (khoảng 40 độ C) một con vi khuẩn trong không khí cứ 20 phút sau lại nhân đôi một lần. Giả sử bạn đầu có 1 con vụ khuẩn. Hỏi sau 6 giờ sẽ sinh ra bao nhiêu con vi khuẩn trong không khí?

Lời giải: 

6 giờ = 360 phút

Số lần nhân đôi là: 360 : 20 = 18 (lần)

Số vi khuẩn sinh ra là: 2¹⁸ = 262144.