Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 70)

Câu 1: Tìm ước chung lớn nhất của 64, 72, 448, 100.

Lời giải:

Ta có: 64 = 2⁶

72 = 2³.3²

448 = 2⁶.7

100 = 2².5²

ƯCLN (64; 72; 448; 100) = 2² = 4.

Câu 2: Tìm x biết (4x – 3)² – 3x(3 – 4x) = 0.

Lời giải:

(4x – 3)² – 3x(3 – 4x) = 0

⇔ (3 – 4x)² – 3x(3 – 4x) = 0

⇔ (3 – 4x)(3 – 4x – 3x) = 0

⇔ (3 – 4x)(3 – 7x) = 0

⇔ $\left[\begin{array}{l}3-4x=0\\ 3-7x=0\end{array}\right.$

⇔ $\left[\begin{array}{l}x=\frac{3}{4}\\ x=\frac{3}{7}\end{array}\right.$

Vậy S = $\left\{\frac{3}{4};\frac{3}{7}\right\}.$

Câu 3: Trong các hình bình hành có tổng độ dài đáy và chiều cao là 18 cm, hình bình hành nào có diện tích lớn nhất và diện tích đó là bao nhiêu ?

Lời giải:

Hình bình hành có diện tích lớn nhất là khi hình bình hành có chiều cao bằng độ dài đáy.

Mà tổng độ dài đáy và chiều cao là 18 cm

Suy ra: chiều cao = độ dài đáy = 18 : 2 = 9 (cm)

Diện tích lớn nhất của hình đó là: S_max = 9 . 9 = 81 (cm²).

Câu 4: 2022 là hợp số hay số nguyên tố?

Lời giải:

Ta thấy: 2022 là hợp số vì 2022 chia hết cho 2; 3; 6; ….

Số nguyên tố chỉ có 2 ước là 1 và chính nó.

Vậy 2022 là hợp số.

Câu 5: A = {1; 2; 3; …; 16}. Bốc ngẫu nhiên 3 phần tử trong A. Tính xác suất để tổng 3 số bốc ra chia hết cho 3.

Lời giải:

n$\left(\Omega \right)$  = 16³

Các số tự nhiên từ 1 đến 16 chia thành 3 nhóm:

- Nhóm I gồm các số tự nhiên chia hết cho 3 gồm 55 số

- Nhóm II gồm các số tự nhiên cho 3 dư 1 gồm 66 số.

- Nhóm III gồm các số tự nhiên cho 3 dư 2 gồm 5 số.

Để ba số có tổng chia hết cho 3 thì xảy ra các trường hơp sau:

- Cả ba bạn viết được số thuộc nhóm I có 5353 cách.

- Cả ba bạn viết được số thuộc nhóm II có 6363 cách.

- Cả ba bạn viết được số thuộc nhóm III có 5353 cách.

Mỗi bạn viết được một số thuộc một nhóm có 3! . (5.6.5).

Vậy có tất cả: 5³ + 6³ + 5³ + 3! . (5.6.5) = 1366

Xác suất cần tính bằng: $\frac{1366}{{16}^3}=\frac{683}{2048}$

Câu 6: Cho dãy số (un) bởi: u₁ = 1 và u_n+1 = 5u_n + 8 với mọi n ≥ 1.

a) Chứng minh rằng dãy số (v_n) với v_n = u_n +2 là một cấp số nhân.

b) Dựa vào kết quả phần a) hãy tìm số hạng tổng quát của dãy số (u_n).

 Lời giải:

Ta có: u_n+1 = 5u_n + 8

v_n = u_n + 2

Suy ra: v_n+1 = u_n+1 + 2 = 5u_n + 8 + 2 = 5u_n + 10 = 5(u_n + 2) = 5v_n (*)

Vậy v_n là cấp số nhân với công bội q = 5.

b) Từ (*) ta có:

v₁ = u₁ + 2 = 1 + 2 = 3

v₂ = 5v₁ = 5.3 = 15

…

v_n = 5v_n–1

Số hạng tổng quát của v_n là: v_n = u₁.q^n–1 = 3.5^n–1

⇒ u_n = v_n – 2 =  3.5^n–1 – 2.

Câu 7:  Có bao nhiêu số tự nhiên có hai chữ số mà hai chữ số của nó đều chẵn?

Lời giải:

Chữ số hàng chục có thể chọn trong các chữ số 2,4,6,8 do đó có 4 cách chọn.

Chữ số hàng đơn vị có thể chọn trong các chữ số 0,2,4,6,8 do đó có 5 cách chọn.

Vậy theo quy tắc nhân ta có 4.5 = 20 số có hai chữ số mà hai chữ số của nó đều chẵn.

Câu 8: Giá trị của chữ số 6 ở phần thập phân trong số 63,546 là?

Lời giải:

Giá trị của chữ số 6 ở phần thập phân là: 6 phần nghìn tức là $\frac{6}{1000}=\mathrm{0,006}$ .

Câu 9: Lãi suất tiết kiệm là 1.2% một tháng. Một người gửi tiết kiệm 8000000 đồng. Hỏi sau hai tháng , cả tiền gửi và tiền lãi là bao nhiêu đồng?

Lời giải:

Số tiền lãi người đó có sau tháng thứ nhất là:

8000000 . 1,2 : 100 = 96000(đồng)

Tổng số tiền cả gốc lẫn lãi người đó có sau tháng thứ nhất là:

8000000 + 96000 = 8096000(đồng)

Số tiền lãi người đó có sau tháng thứ hai là:

8096000 . 1,2 : 100 = 97152(đồng)

Tổng số tiền cả gốc lẫn lãi người đó có sau tháng thứ hai là:

8096000 + 97152 = 8193152(đồng)

Câu 10: Một người bỏ ra 4 500 000 đồng tiền vốn mua hoa. Biết rằng người đó lãi 12% tiền vốn. Tính số tiền lãi.

Lời giải:

Số tiền lãi là:

4500000 . 12 : 100 = 540000 (đồng)

Đáp số: 540000 đồng.

Câu 11: Một số chia cho 9 có số dư là 6. Hỏi số đó có chia hết cho 3 không ?

Lời giải:

Giả sử số đó là x, thương là n

Ta có: x : 9 = n (dư 6)

x = 9n + 6

Vì 9n chia hết cho 3 và 6 chia hết cho 3 nên 9n + 6 chia hết cho 3

Hay x chia hết cho 3

Vậy số đó chia hết cho 3.

Câu 12: Cho ba đường thẳng y = 2x + 1 (d₁); y = x – 1 (d₂) và u = (m + 1)x – 2. Tìm điều kiện của tham số m để ba đường thẳng đồng quy.

Lời giải:

Hoành độ giao điểm của d₁ và d₂ là nghiệm của phương trình:

2x + 1 = x – 1

⇒ x = –2

Với x = –2 ⇒ y = –2 – 1 = –3

Suy ra hai đường thẳng d₁ và d₂ cắt nhau tại điểm A(–2; –3)

Để ba đường thẳng đồng quy thì điểm A(–2; –3) thuộc đồ thị hàm số y = (m + 1)x – 2. Khi đó ta có:

–3 = (m + 1).(–2) – 2

⇒ $m=\frac{-1}{2}$

Vậy với $m=\frac{-1}{2}$ thì ba đường thẳng đã cho đồng quy.

Câu 13: Tìm tham số m để ba đường thẳng y = x – 2; y = 2x + m + 1 và y = 3x – 2 đồng quy.

Lời giải:

Hoành độ giao điểm của y = x – 2 và y = 3x – 2 là nghiệm của phương trình:

x – 2 = 3x – 2

⇒ x = 0

Với x = 0 ⇒ y = 0 – 2 = –2

Suy ra hai đường thẳng y = x – 2 và y = 3x – 2 cắt nhau tại điểm B(0; –2)

Để ba đường thẳng đồng quy thì điểm B(0; –2) thuộc đồ thị hàm số y = 2x + m + 1. Khi đó ta có:

0 = 2.(–2) + m + 1

⇒ m – 3 = 0

⇒ m = 3

Vậy với m = 3 thì ba đường thẳng đã cho đồng quy.

Câu 14: Cho hình đa diện đều loại {4;3} có cạnh bằng a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Tính S?

Lời giải:

Khối đa diện đều loại {4;3} là hình lập phương.

Khối lập phương có 6 mặt là hình vuông cạnh a.

Diện tích một mặt là a²

Vậy tổng diện tích các mặt của hình lập phương đó là: S = 6a².

Câu 15: Tính nhanh: A = 1 + 3 – 5 – 7 + 9 + 11  – … – 397 – 399.

Lời giải:

Biểu thức đã cho có (399 – 1) : 2 + 1 = 200 số

1 + 3 – 5 – 7 + 9 + 11 – 13 – 17 + ... + 393 + 395 – 397 – 399

= (1 + 3 – 5 – 7) + (9 + 11 – 13 – 15) + ..... + (393 + 395 – 397 – 399)

= (–8) + (–8) + ... + (–8)

Ta suy biểu thức ban đầu có 200 số, chia ra các cặp số, mỗi cặp gồm 4 số.

Vậy có số cặp là: 200 : 4 = 50 (cặp)

Vậy A = (–8) × 50 = – 400.

Câu 16: Một chiếc đồng hồ đánh chuông, số tiếng chuông được đánh đúng bằng số mà kim giờ chỉ tại thời điểm đánh chuông. Hỏi một ngày đêm đồng hồ đó đánh bao nhiêu tiếng chuông?

Lời giải:

Trong một ngày đêm kim giờ quay hai vòng

Vậy trong một ngày đêm đồng hồ đó đánh

(1 + 2 + ... + 12) . 2 = 12 . (12 + 1) = 156 tiếng.

Câu 17: Tìm tập hợp số nguyên x biết 3x + 2 chia hết cho x – 1.

Lời giải:

Ta có: 3x + 2 chia hết cho x – 1

3x + 2 = 3x – 3 + 5 = 3(x – 1) + 5

Vì 3(x – 1) chia hết cho x – 1 nên để 3x + 2 chia hết cho x – 1 thì 5 chia hết cho x–1

⇒ x – 1 thuộc Ư(5) = {1; –1; 5; –5}

⇒ x ∈ {2; 0; 6; –4}

Vậy x ∈{2; 0; 6; –4}.

Câu 18: Đặt dấu ngoặc một cách thích hợp để tính tổng đại số sau:

a) 942 – 2567 + 2563 – 1942.

b) 13 – 12 + 11 + 10 – 9 + 8 – 7 – 6 + 5 – 4 + 3 + 2 – 1.

Lời giải:

a) 942 – 2567 + 2563 – 1942

= (942 – 1942) – (2567 – 2563)

= –1000 – 4

= –1004

b) 13 – 12 + 11 – 10 – 9 + 8 – 7 – 6 + 5 – 4 – 3 + 2 – 1

= ( 13 – 12 ) + ( 11 – 10 ) – ( 9 – 8 ) – 7 – ( 6 – 5 ) – 4 – ( 3 – 2 ) – 1

= 1 + 1 – 1 – 7 – 1 – 4 – 1 – 1

= –13.

Câu 19: Cha hơn con 32 tuổi. Biết 4 năm nữa tổng số tuổi của 2 cha con là 64 tuổi. Tính tuổi 2 cha con hiện nay ?

Lời giải:

Tuổi của 2 cha con hiện nay là:

64 – 4 . 2 = 56(tuổi)

Tuổi của con là:

(56 − 32) : 2 = 12 (tuổi)

Tuổi của cha là:

56 – 12 = 44 (tuổi)

Đáp số: Con: 12 tuổi, Cha: 44 tuổi.

Câu 20: Một công nhân phải làm một số dụng cụ trong một thời gian. Nếu mỗi ngày tăng 3 dụng cụ thì hoàn thành sớm 2 ngày, nếu mỗi ngày làm giảm 3 dụng cụ thì thời gian phải kéo dài 3 ngày. Tính số dụng cụ được giao.

Lời giải:

Gọi số dụng cụ mỗi ngày người đó làm là x

        số ngày người đó làm việc là y

⇒ Tổng số dụng cụ được giao là x.y

Nếu mỗi ngày tăng 3 dụng cụ thì hoàn thành sớm 2 ngày 

 ⇒(x + 3)(y – 2) = xy

⇔ xy + 3y – 2x – 6 = xy

⇔ –2x + 3y = 6 (1)

Nếu mỗi ngày làm giảm 3 dụng cụ thì tg kéo dài 3 ngày 

⇒ (x – 3)(y – 3) = xy

⇔ xy – 3y + 3x – 9 = xy

⇔ 3x – 3y = 9

⇔ x – y = 3

⇔ x = 3 + y    (2)

Từ (1) và (2) ta có: –2(3 + y) + 3x = 6

⇔ –6 – 2y + 3y = 6

⇔ y = 12 (ngày)

⇒ x = 3 + y = 12 + 3 = 15 (dụng cụ)

Tổng số dụng cụ là:  12.15 = 180 (dụng cụ).

Câu 21: Một thửa ruộng hình chữ nhật có chu vi là 120m. Tính diện tích thửa ruộng đó nếu biết tăng chiều rộng 5m và giảm chiều dài 5m thì thua ruộng đó thành hình vuông.

Lời giải:

Nếu tăng chiều rộng và giảm chiều dài 5m thì thửa rộng đó thành hình vuông, hay là nếu tăng chiều rộng và giảm chiều dài 5m thì ta được 2 đoạn bằng nhau

Ta có sơ đồ như hình vẽ:

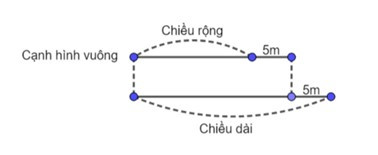
Hiệu của chiều dài và chiều rộng của thửa ruộng đó là:

5 + 5 = 10 (m)

Nửa chu vi thửa ruộng đó là:

120 : 2 = 60 (m)

Chiều dài của thửa ruộng đó là:

(60 + 10) : 2 = 35 (m)

Chiều rộng của thửa ruộng là:

(60 – 10) : 2 = 25 (m)

Diện tích của thửa ruộng đó là:

35 . 25 = 875 (m²)

Câu 22: Gọi M là tập hợp các số tự nhiên có ba chữ số lập được từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7. Lấy ngẫu nhiên đồng thời 2 số từ tập M. Xác suất để cả 2 số lấy được đều có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và hàng đơn vị là?

Lời giải:

Số lượng số tự nhiên có 3 chữ số lập từ 8 chữ số trên là 7 . 8 . 8 = 448 số

⇒ Tập M có 448 số

Gọi số thỏa mãn đề là $\overline{abc}$

Ta có: b < a, b < c

+) b = 0 ⇒ Có 7 cách chọn chữ số a, c

⇒ Có tất cả: 7 . 7 = 49 số cần tìm 

+) b = 1 ⇒ Có 6 cách chọn chữ số a, c

+) b = 2 ⇒ Có 5 cách chọn chữ số a, c

+) b = 3 ⇒ Có 4 cách chọn chữ số a, c

+) b = 4 ⇒ Có 3 cách chọn chữ số a, c

+) b = 5 ⇒Có 2 cách chọn chữ số a, c

+) b = 6 ⇒ Có 1 cách chọn chữ số a, c

+) b = 7 ⇒ Có 0 cách chọn chữ số a, c

⇒ Số cách chọn a, b, c thỏa mãn đề là:

7 . 7 + 6 . 6 + 5 . 5 + 4 . 4 + 3 . 3 + 2 . 2 + 1 . 1 = 140

⇒ Xác suất để cả 2 số lấy được đều có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và hàng đơn vị là: $\frac{140.139}{448.447}=\frac{695}{7152}$ .

Câu 23: Một nhà máy dự định sản xuất một số chi tiết máy trong một thời gian đã định, với năng suất 300 chi tiết máy trong một ngày. Nhưng thực tế mỗi ngày đã làm được 400 chi tiết nên đã sản xuất thêm được 600 chi tiết và hoàn thành kế hoạch trước 1 ngày. Tính số chi tiết máy dự định sản xuất.

Lời giải:

Gọi thời gian đự định sản xuất xong là x (ngày) , điều kiện x > 1

Thời gian thực tế đã sản xuất được là x – 1 (ngày)

Số chi tiết máy dự định sản xuất là 300x (chi tiết)

Số chi tiết thực tế sản xuất được là 400.(x–1) (chi tiết )

Theo đề ta có phương trình: 300x + 600 = 400(x–1)

300x + 600 = 400x – 400

⇔ 100x = 1000

⇔ x = 10

Vậy số chi tiết dự định sản xuất là 300.10 = 3000.

Câu 24: Bảng giá cước của hãng taxi được cho như sau: Giá mở cửa 11 000 đồng. Giá tiếp theo từ 0,8km đến 30km là 15 800 đồng/1km. Từ km thứ 31 trở đi giá 12 500 đồng/1km. Quí thời gian chờ từ 5 phút đến 1 giờ là 3000 đồng. Giá trên đã bao gồm thuế VAT.

a) Gọi y (đồng) là số tiền khách phải trả sau khi đi x (km). Lập hàm số của y theo x. (Giả sử không tính thời gian chờ và phí cầu đường, bến bãi).

b) Một hàn khách thuê taxi quãng đường 40km phải trả số tiền là bao nhiêu?

Lời giải:

a) + Nếu 0 < x < 0,8:

y = 11000 (đồng)

+ Nếu 0,8 ≤ x ≤ 30

y = 11000 + 15800(x − 0,8) = 15800x – 1640 (đồng)

+ Nếu x ≥ 31:

y = 11000 + 15800.(30 − 0,8) + 12500(x − 30) = 12500x + 97360(đồng)

b) Khi x = 40:

y = 12500 . 40 + 97360 = 597360 (đồng) 

Vậy số tiền phải trả là 597360 đồng.

Câu 25: Cho một số có 4 chữ số khác nhau biết tổng các chữ số là 9. Tính tích của các chữ số đó?

Lời giải:

Ta thấy: 9 = 6 + 2 + 1 + 0.

Số có 4 chữ số khác nhau và tổng các chữ số bằng 9 là 6210; 6120; 1260; 1620 ; 2160; 2610; ….

Tích các chữ số là: 2 . 6 . 1 . 0 = 0

Vậy tích của các chữ số là 0.

Câu 26: Cho đoạn thẳng AB và điểm C thuộc đoạn AB sao cho 3AC = 2BC. Biết AB = 10 cm, tính độ dài AC, CB?

Lời giải:

Vì 3AC = 2BC nên coi AC là 2 phần thì BC là 3 phần

Tổng số phần bằng nhau là:

2 + 3 = 5 (phần)

Độ dài AC là:

10 : 5 . 2 = 4 (cm)

Độ dài BC là:

10 – 4 = 6 (cm)

Câu 27: Một hình vuông có chu vi là 24dm thì diện tích hình vuông đó là?

Lời giải:

Cạnh hình vuông là:

24 : 4 = 6 (dm)

Diện tích hình vuông là:

6 . 6 = 36 (dm²).

Câu 28: Có bao nhiêu cách để bỏ 4 lá thư vào 5 hộp thư?

Lời giải:

Lá thư thứ nhất có 5 cách xếp vào 5 hộp thư

Lá thư thứ hai có 5 cách xếp vào 5 hộp thư

Lá thư thứ ba có 5 cách xếp vào 5 hộp thư

Lá thư thứ tư có 5 cách xếp vào 5 hộp thư

Suy ra: có tất cả 5 . 5 . 5 . 5 = 625 cách xếp 4 lá thư vào 5 hộp thư

Câu 29: Một người đang dự định đi mua xe máy mà muốn chọn 1 trong hai loại xe sau:

Loại 1: Có giá 27 000 000 (đồng) và trung bình số ki–lô–mét đi được mỗi lít xăng là 58 km/lít xăng.

Loại 2: Có giá 30 000 000 (đồng) và trung bình số ki–lô–mét đi được mỗi lít xăng là 62,5 km/lít xăng.

Biết rằng giá trung bình của 1 lít xăng là 18 000 (đồng). Người ta dự tính mua xe máy để sử dụng khoảng 8 năm. Biết rằng mỗi năm người đó đi được khoảng 7 250 km.

 Gọi s (đồng) là chi phí từng năm theo thời gian t (năm) của mỗi loại xe (bao gồm tiền mua xe và tiền xăng). Lập hàm số của s theo t.

Lời giải:

Đối với xe loại 1, mỗi năm xe tiêu thụ hết:

7 250 : 58 = 125 (lít)

Suy ra mỗi năm, xe loại 1 tiêu thụ hết:

125.18 000 = 2 250 000 (đồng)

Hàm số của s theo t đối với xe loại 1:

s = 27 000 000 + 2 250 000.t

Đối với xe loại 2, mỗi năm xe tiêu thụ hết:

7 250 : 62,5 = 116 (lít)

Suy ra mỗi năm, xe loại 2 tiêu thụ hết:

116. 18 000 = 2 088 000 (đồng)

Hàm số của s theo t đối với xe loại 2:

s = 30 000 000 + 2 088 000.t

Câu 30: Một lớp có 40 học sinh,trong đó nam nhiều hơn nữ.Trong giờ ra chơi,cô giáo đưa cho cả lớp 260000 đồng để mỗi bạn nam mua ly Coca giá 5000 đồng/ly , mỗi mỗi bạn nữ mua một bánh phô mai giá 8000 đồng/cái và được căn tin thối lại 3000 đồng. Hỏi lớp có bao nhiêu học sinh nam và nữ?

Lời giải:

Gọi số bạn nam là: x (x > 20) (bạn)( Do số bạn nam nhiều hơn nữ nên sô bạn nam nhiều hơn một nửa tổng số thành viên trong lớp)

Số bạn nữ là 40 − x (bạn)

Số tiền mua là: 260000 – 3000 = 257000( Đồng)

Số tiền bạn các bạn nam mua là: 5000x (Đồng)

Số tiền bạn các nữ mua là: 8000(40 − x) (Đồng)

Ta có phương trình sau:

5000x + 8000(40 − x) = 257000

⇔ 5000x + 320000 − 8000x = 257000

⇔ −3000x = 257000 − 320000

⇔ −3000x = −63000

⇔ x = 21

Vậy số bạn nam là: 21 bạn

Số bạn nữ là: 40 – 21 = 19 bạn.

Câu 31: Tìm x biết 5x³ – 20x = 0.

Lời giải:

5x³ – 20x = 0

⇔ x(5x² – 20) = 0

⇔ 5x(x² – 4) = 0

⇔ 5x(x – 2)(x + 2) = 0

⇔ $\left[\begin{array}{l}x=0\\ x=2\\ x=-2\end{array}\right.$

Vậy x ∈ {–2; 0; 2}.

Câu 32: Tìm x biết (x – 5)(x + 5) + 3(3 – x) = –11 + 10x.

Lời giải:

x² – 25 + 9 − 3x + 11 − 10x = 0

⇔ x² − 13x – 14 = 0

⇔ x² + x − 14x – 14 = 0

⇔ x(x + 1) − 14(x + 1) = 0

⇔ (x + 1)(x − 14) = 0

⇔ $\left[\begin{array}{l}x+1=0\\ x-14=0\end{array}\right.$

⇔ $\left[\begin{array}{l}x=-1\\ x=14\end{array}\right.$

Vậy x = –1 hoặc x = 14

Câu 33: Bà Minh có 3 530 000 đồng với tổng cộng có 74 tờ tiền gồm 3 loại: loại 20 000 đồng loại 50 000 đồng và loại 100 000 đồng . Hỏi mỗi loại có mấy tờ biết rằng số tờ tiền loại 20 000 đồng gấp đôi số tờ tiền loại 100 000 đồng.

Lời giải:

Gọi 2x là số tờ tiền 20000 đồng thì x là số tờ tiền 100000 đồng

y là số tờ tiền 50000 đồng (x, y ∈ N^*) 

Tổng số tờ là 74 ⇒ 2x + x + y = 74   (1) 

Tổng giá trị tiền là 3530 nghìn đồng

⇒ 20.2x + 100x + 50y = 3530        (2) 

Từ (1), (2) ta có ⇒ x = 17; y = 23 (thỏa mãn)

Vậy số tờ tiền 20000 đồng là 34, số tờ tiền 50000 đồng là 23, số tờ tiền 100000 đồng là 17.

Câu 34: Ba xe ô tô chở 118 tấn hàng tổng cộng hết 50 chuyến. Số chuyến xe thứ nhất chở gấp rưỡi số chuyến thứ 2. Mỗi chuyến xe thứ nhất chở 2 tấn, xe thứ 2 chở 2,5 tấn, xe thứ 3 chở 3 tấn. Hỏi mỗi ô tô chở bao nhiêu chuyến?

Lời giải:

Gọi số chuyến của xe thứ nhất, thứ hai, thứ ba lần lượt là x, y, z (0<x; y; z<500)

Theo bài ra ta có:

– Ba xe ô tô chở tổng cộng 50 chuyến ⇒ x + y + z = 50 (1)

– Số chuyến xe thứ nhất chở gấp rưỡi số chuyến thứ hai ⇒ x = 1,5y (2)

– Mỗi chuyến xe thứ nhất chở 2 tấn, xe thứ 2 chở 2,5 tấn, xe thứ 3 chở 3 tấn mà ba xe chở tổng cộng 118 tấn hàng

⇒ 2x + 2,5y + 3z = 118 (3)

Thay (2) vào (1) và (2) vào (3) ta có hệ phương trình:

$\left\{\begin{array}{l}\mathrm{2,5}y+z=50\\ \mathrm{5,5}y+3z=118\end{array}\right.$

⇔ $\left\{\begin{array}{l}y=16\\ z=10\end{array}\right.$

và x = 1,5y = 1,5.16 = 24.

Vậy xe thứ nhất chở 24 chuyến, xe thứ hai chở 16 chuyến, xe thứ 3 chở 10 chuyến.

Câu 35: Kết quả đo chiều dài của một cây cầu được ghi là 152m ± 0,2m, điều đó có nghĩa là gì? Tìm sai số tương đối.

Lời giải:

Gọi a là chiều dài đúng của cây cầu

Suy ra: a = 152m ± 0,2m

⇒ 152 – 0,2 ≤ a ≤ 152 + 0,2

⇒ 151,8 ≤ a ≤ 152,2

Vậy chiều dài đúng của cây cầu là một số nằm trong khoảng 151,8m đến 152,2m

Sai số tương đối = 0,2 : 152 . 100% ≈ 0,13%.

Câu 36: Một phân xưởng có 20 máy đóng gói tự động, trong một ngày đóng gói được 400 sản phẩm. Để đóng gói được 600 sản phẩm một ngày thì phân xưởng đó cần đầu tư thêm bao nhiêu máy? Giả thiết rằng năng suất của các máy là như nhau.

Lời giải:

Gọi x (máy) là số máy mà phân xưởng cần đầu tư thêm (x ∈ ℕ^*).

Số máy để đóng gói 600 sản phẩm là x + 20 (máy)

Ta có tỉ lệ thức: $\frac{20}{400}=\frac{x+20}{600}$

⇔ 20.600 = 400.(x + 20)

⇔ 400(x + 20) = 12 000

⇔ x + 20 = 30

Do đó x = 30 − 20 = 10 (máy)

Vậy phân xưởng đó cần đầu tư thêm 10 máy.

Câu 37: Một người bắt đầu đi làm được nhận được số tiền lương là 7 000 000 đồng một tháng. Sau 36 tháng người đó được tăng lương 7%. Hằng tháng người đó tiết kiệm 20% lương để gửi vào ngân hàng với lãi suất 0,3%/tháng theo hình thức lãi kép (nghĩa là lãi của tháng này được nhập vào vốn của tháng kế tiếp). Biết rằng người đó nhận lương vào đầu tháng và số tiền tiết kiệm được chuyển ngay vào ngân hàng. Hỏi sau 36 tháng tổng số tiền người đó tiết kiệm được (cả vốn lẫn lãi) là bao nhiêu? (làm tròn đến hàng nghìn).

Lời giải:

Đặt a = 70000000, m = 20%, n = 0,3%, t = 7%

Hết tháng thứ nhất, người đó có tổng số tiền tiết kiệm là:

T₁ = am(1 + n)¹

Hết tháng thứ hai, người đó có tổng số tiền tiết kiệm là:

T₂ = (T₁ + am)(1 + n) = am(1 + n)² + am(1 + n)¹

Hết tháng thứ 36, người đó có tổng số tiền tiết kiệm là:

T₃₆ = am(1 + n)³⁶ + am(1 + n)³⁵ + … + am(1 + n) = am(1 + n)$\frac{{\left(1+n\right)}^{36}-1}{n}$

Thay số vào ta được: T₃₆ ≈ 53297684,73 (đồng).

Câu 38: Một xưởng sản xuất nước mắm đã sản xuất được 1230 lít nước mắm, người ta muốn đóng vào các can như nhau. Hãy tính và nêu số can nước mắm đóng được trong các trường hợp sau:

Số lít mỗi can	2 lít	3 lít	5 lít
Số can	?	?	?

Lời giải:

Xưởng sản xuất nước mắm đã sản xuất được 1230 lít nước mắm.

Mỗi can 2 lít thì cần số can là:

1230 : 2 = 615 (can)

Mỗi can 3 lít thì cần số can là:

1230 : 3 = 410 (can)

Mỗi can 5 lít thì cần số can là:

1230 : 5 = 246 (can)

Vậy ta hoàn thành bảng sau:

Số lít mỗi can	2 lít	3 lít	5 lít
Số can	615	410	246

Câu 39: Phép tính với tổng sigma là gì? Cho ví dụ.

Lời giải:

Σ là chữ cái Hi Lạp (Sigma viết hoa, phân biệt sigma viết thường σ) 

Đây là phép tổng, cộng liên tiếp nhiều hạng tử

Ví dụ: Cần tính A = 1 + 2 + 3 + 4 + … + 50 thì ta chỉ cần tính theo tổng sigma:

$\sum _i^{50}=1275$.

Câu 40: Tìm số chia cho 3 được 4 dư 9.

Lời giải:

Ta thấy trong 1 phép chia có dư thì số dư luôn nhỏ hơn số chia

Trong bài toán này số dư là 9 lớn hơn số chia là 3.

Vậy không tồn tại phép chia thỏa mãn 1 số chia 3 được thương là 4, dư 9.