Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 18)
Lời giải:
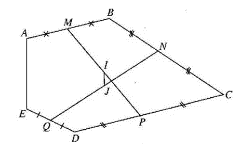
Ta có:
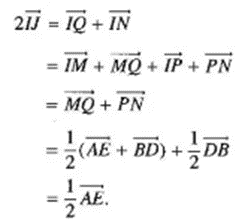
Hay
Suy ra IJ // AE và IJ = AE
Vậy IJ // AE và IJ = AE.
a) Rút gọn biểu thức P.
b) Tìm x để P = 3.
Lời giải:
a) Điều kiện xác định
Ta có :
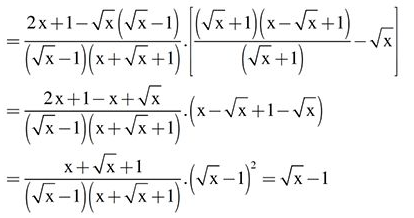
Vậy với thì .
b) Với để P = 3 thì
(thỏa mãn)
Vậy x = 16 thì P = 3.
a) Xác định tập xác định của biểu thức.
b) Rút gọn biểu thức.
Lời giải:
a) Biểu thức P xác định khi
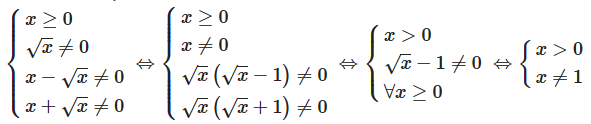
b) Ta có :
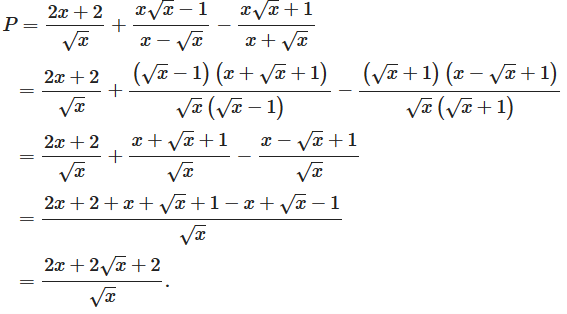
Lời giải:
Số gạo kho thứ nhất nhiều hơn số gạo kho thứ hai là:
17 – 8 = 9 (tấn)
Số gạo lúc đầu của kho thứ nhất là:
(155 + 9) : 2 = 82 (tấn)
Số gạo lúc đầu của kho thứ hai là
155 – 82 = 73 (tấn)
Vậy lúc đầu kho thứ nhất có 82 tấn gạo, kho thứ hai có 73 tấn gạo.
Lời giải:
Ta có sơ đồ:
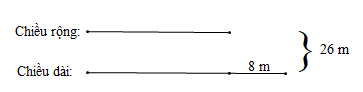
Theo sơ đồ, hai lần chiều dài hình chữ nhật là:
26 + 8 = 34 (cm)
Chiều dài hình chữ nhật là:
34 : 2 = 17 (cm)
Chiều rộng hình chữ nhật là:
17 – 8 = 9 (cm)
Diện tích hình chữ nhật là:
17 × 9 = 153 (cm2)
Vậy diện tích hình chữ nhật là 153 cm2.
Câu 6: Không tính cụ thể các giá trị của A và B, hãy cho biết số nào lớn hơn và lớn hơn bao nhiêu?
A = 32 . 53 – 31; B = 53 . 31 + 32.
Lời giải:
Ta có:
A = 32 . 53 – 31
A = 31 . 53 + 53 – 31
A = 31 . 53 + (53 – 31)
A = 31 . 53 + 22
Vì 22 < 32
Suy ra A < B và nhỏ hơn 32 – 22 = 10
Vậy A < B.
Câu 7: Không tính cụ thể các giá trị của A và B, hãy cho biết số nào lớn hơn và lớn hơn bao nhiêu?
a, A = 1998 . 1998 ; B = 1996 . 2000.
b, A = 2000 . 2000 ; B = 1990 . 2010.
c, A = 25 . 33 – 10 ; B = 31 . 26 + 10.
d, A = 32 . 53 – 31 ; B = 53 . 31 + 32.
Lời giải:
a, Ta có:
A = 1998 . 1998 = (1996 + 2) . 1998 = 1996 . 1998 + 2 . 1998
B = 1996 . 2000 = 1996 . (2 + 1998) = 1996 . 2 + 1996 . 1998
Vì 2 . 1998 > 1996 . 2 nên 2 . 1998 + 1996 . 1998 > 1996 . 2 + 1996 . 1998
Vậy A > B.
b, Ta có:
A = 2000 . 2000
B = 1990 . 2010 = (2000 – 10) . (2000 + 10) = 2000 . 2000 – 10 . 10
Suy ra A > B.
c, Ta có:
A = 25 . 33 – 10 = (26 – 1) . 33 – 10 = 26 . 33 – 33 – 10 = 26 . 33 – 43
B = 31 . 26 + 10 = (33 – 2) . 26 + 10 = 33 . 26 – 2 . 26 + 10 = 26 . 33 – 42
Vì 42 < 43 nên 26 . 33 – 42 > 26 . 33 – 43 hay B > A.
Nên A < B
d, Ta có:
A = 32 . 53 – 31
A = 31 . 53 + 53 – 31
A = 31 . 53 + (53 – 31)
A = 31 . 53 + 22
Vì 22 < 32 nên 31 . 53 + 22 < 53 . 31 + 32 hay A < B.
Vậy A < B.
Câu 8: Cho biết log25 7 = a và log2 5 = b. Tính theo a, b.
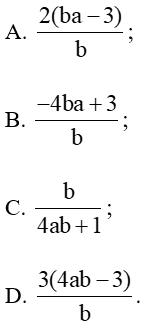
Lời giải:
Đáp án đúng là: D
Ta có:
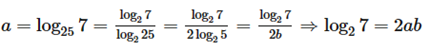
Do đó :
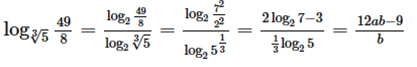
Vậy ta chọn đáp án D.
Lời giải:
Đổi 2dam2 60m2 = 260 m2
Diện tích để làm nhà là :
260 : 5 × 2 = 104 (m2)
Diện tích còn lại sau khi làm nhà là:
260 – 104 = 156 (m2)
Diện tích để trồng rau là :
156 : 3 × 1 = 52 (m2)
Diện tích đất làm chuồng trại chăn nuôi là :
156 – 52 = 104 (m2)
Vậy diện tích phần làm chuồng trại chăn nuôi là 104 m2.
Lời giải:
Chu vi khu đất hình chữ nhật là :
(48 + 25) x 2 = 146 (m)
Đổi : 146 m = 1460 dm và 2 m = 20 dm
Số dm rào ông Tư cần là :
1460 – 20 = 1440 (dm)
Số tiền ông Tư cần là :
1440 × 2 500 = 3 600 000 (đồng)
Vậy ông Tư tốn tất cả 3 600 000 đồng.
Lời giải:
Tổng số học sinh tiên tiến của cả hai lớp là : 22 × 2 = 44 ( học sinh )
Lớp 4B có số học sinh tiên tiến là : 44 – 24 = 20 ( học sinh )
Vậy lớp 4B có 20 học sinh tiên tiến.
Câu 12: Số trung bình cộng của hai số bằng 8 . Biết một trong hai số kia là 9 .tìm số kia ?
Lời giải:
Tổng của hai số là: 8 × 2 = 16
Số kia là: 16 – 9 = 7
Vậy số còn lại là 7.
Lời giải:
Số kg chè chị hái được là:
27 – 12 = 15 (kg)
Số kg chè em hái được là:
15 – 6 = 9 (kg)
Trung bình mỗi người hái được số kg chè là:
(27 + 15 + 9) : 3 = 17 (kg)
Vậy trung bình mỗi người hái được 17 kg chè.
Lời giải:
Phương trình hoành độ giao điểm của (d) và Ox là
(m – 3)x + 3m + 2 = 0
⇔ (m – 3)x = – 3m – 2
Để x đạt giá trị nguyên thì nguyên
⇔ 11 ⋮ 3 – m
⇔ 3 – m ∈ Ư(11)
⇔ 3 – m ∈ {1; 11; – 1; – 11}
⇔ m ∈ {2; – 8; 4; 14}
Vậy m ∈ {2; – 8; 4; 14} thì (d) cắt trục hoành tại điểm có hoành độ nguyên.
Câu 15: Chứng minh: sin 2a = 2sin a cos a.
Lời giải:
Ta có
sin 2a = sin (a + a) = sin a cos a + cos a sin a = 2sin a cos a
Vậy sin 2a = 2sin a cos a.
Câu 16: Diện tích miếng bìa có kích thước theo hình vẽ bên là:
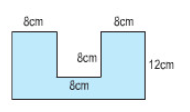
A. 96 cm2;
B. 192 cm2;
C. 224 cm2;
D. 288 cm2.
Lời giải:
Đáp án đúng là C
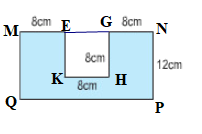
Chiều dài hình chữ nhật MNPQ là:
8 + 8 + 8 = 24 (cm)
Diện tích hình chữ nhật MNPQ là:
24 × 12 = 288 (cm2)
Diện tích hình vuông EGHK là:
8 × 8 = 64 (cm2)
Diện tích miếng bìa là :
288 – 64 = 224 (cm2)
Vậy ta chọn đáp án C.
Câu 17: Tính diện tích miếng bìa có kích thước theo hình vẽ bên.
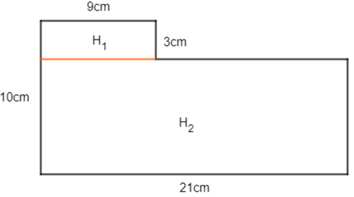
Lời giải:
Chia miếng bìa ra thành hai miếng bìa nhỏ. Từ đó ta có hai miếng bìa hình chữ nhật.
Diện tích của miếng bìa thứ nhất (H1) là:
9 × 3 = 27 (cm2)
Chiều rộng của miếng bìa thứ hai (H2) là:
10 – 3 = 7 (cm)
Diện tích của miếng bìa thứ hai (H2) là:
21 × 7 = 147 (cm2)
Diện tích cả miếng bìa là:
27 + 147 = 174 (cm2 )
Vậy diện tích miếng bìa là 174 cm2.
Câu 18: Cho hàm số y = (m – 2)x + m + 1 (d). Tìm m để (d) đi qua gốc tọa độ.
Lời giải:
Để (d) đi qua gốc tọa độ thì (d) đi qua điểm O(0; 0)
Suy ra m + 1 = 0
Hay m = – 1
Vậy với m = – 1 thì (d) đi qua gốc tọa độ.
Câu 19: Chu kì của hàm số y = 3 + 2sin2 2x là
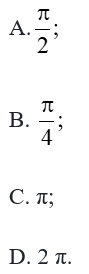
Lời giải:
Đáp án đúng là: A
Ta có: y = 3 + 2sin2 2x
Do đó chu kì của hàm số trên là
Vậy ta chọn đáp án A.
Lời giải:
Số tiền dùng để mua kẹo Trung thu là:
5000 × 18 = 90 000 (đồng)
Số gói kẹo mua được nếu mua kẹo loại 7 500 đồng 1 gói là:
90 000 : 7 500 = 12 (gói)
Vậy mua được 12 gói kẹo loại 7 500 đồng.
Lời giải:
Số mét đường ống cần phải lắp là:
200 x 15 = 3000 (m)
Nếu cải tiến kỹ thuật thì mỗi ngày đội công nhân đó lắp được số ống là:
200 + 50 = 250 (m)
Số ngày cần có để đội công nhân lắp xong đường ống đó là:
3000 : 250 = 12 (ngày)
Vậy cần 12 ngày để đội nhân công đố lắp xong đường ống.
Lời giải:
Trong 5 giờ vòi nước chả được số phần bể là
(bể)
Trung bình mỗi giờ vòi nước chảy được là
(bể)
Vậy trung bình mỗi giờ vòi nước đó chảy được bể nước.
Câu 23: Trên mặt phẳng tọa độ Oxy cho hai điểm A(1; 2) và B(3; 4)
a) Tìm hệ số a của đường thẳng đi qua A và B.
b) Xác định hàm số biết đồ thị của nó là đường thẳng đi qua A và B.
Lời giải:
a) Đường thẳng đi qua hai điểm A và B có dạng: y = ax + b
Đường thẳng đi qua hai điểm A và B nên tọa độ A và B nghiệm đúng phương trình
Ta có:
Tại A: 2 = a + b ⇔ b = 2 – a (1)
Tại B: 4 = 3a + b (2)
Thay (1) và (2) ta có: 4 = 3a + 2 – a ⇔ 2a = 2 ⇔ a = 1
Vậy hệ số a của đường thẳng đi qua A và B là 1
b) Ta có: b = 2 – a = 2 – 1 = 1
Vậy đường thẳng đi qua A và B là y = x + 1.
Câu 24: Giải phương trình: x2 – 4x + xy – 4y = 0.
Lời giải:
Ta có x2 – 4x + xy – 4y = 0
⇔ (x2 – 4x) + (xy – 4y) = 0
⇔ x(x – 4) + y(x – 4) = 0
⇔ (x – 4)(x + y) = 0
Vậy phương trình có nghiệm (x;y) = (4; – 4).
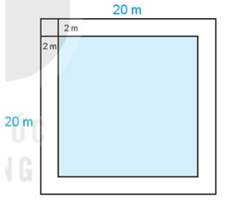
Phần còn lại để trồng trọt là hình vuông có cạnh là:
20 – 2 – 2 = 16 (m)
Diện tích trồng trọt của mảnh vườn là:
16 × 16 = 256 (m2)
Vậy diện tích trồng trọt của mảnh vườn là 256 m2.
Lời giải:
Ta có (x – 1)2 ≥ 0
⇔ x2 + 1 ≥ 2x
(y – 1)2 ≥ 0
⇔ y2 + 1 ≥ 2y
(z – 1)2 ≥ 0
⇔ z2 + 1 ≥ 2z
(x – y – z)2 ≥ 0
⇔ 2(x2 + y2 + z2 ) ≥ 2(xy + yz + zx)
Suy ra 3(x2 + y2 + z2) + 3 ≥ 2(x + y + z + xy + yz + xz)
Hay 3P + 3 ≥ 2 . 6
⇔ P ≥ 3
Dấu “ = ” xảy ra khi x = y = z =1
Vậy P đạt giá trị nhỏ nhất bằng 3 khi x = y = z =1.
Lời giải:
Vì hàm số y = (m – 1)x + 3 là hàm số bậc nhất
Nên m – 1 ≠ 0
Hay m ≠ 1
Vì đường thẳng (d) song song với đường thẳng y = – x + 1
Nên m – 1 = –1
Hay m = 0
Vậy m = 0 thì đường thẳng (d) song song với đường thẳng y = – x + 1.
a) Viết công thức biểu diễn y theo x.
b) Hỏi nhà máy A phải bán bao nhiêu cái áo để đạt được số tiền lời trên 15 000 000 (đồng)?
Lời giải:
a) Ta có:
b) Để số tiền lời trên 15 000 000 đồng
⇔ y > 15 000 000
⇔ 400 000x – 500 000 000 > 15 000 000
⇔ 400 000x > 515 000 000
⇔ x > 1 287,5
⇔ x = 1288
Vậy nhà máy A phải bán 1288 cái áo để đạt được số tiền lời trên 15 000 000 (đồng).
Câu 29: So sánh: 1218 và 2716 . 169.
Lời giải:
Ta có
1218 = (22 . 3)18 = 236 . 318
2716 . 169 = (33)16 . (24)9 = 348 . 236
Vì 318 < 348 nên 1218 < 2716 . 169
Vậy1218 < 2716 . 169
Lời giải:
Ta có △’ = (m + 1)2 – 4m = m2 + 2m + 1 – 4m = m2 – 2m + 1 = (m – 1)2
△’ ≥ 0 nên phương trình có 2 nghiệm là
Ta có: (x1 + m)(x2 + m) = 3m2 + 12
⇔ (2m + m)(2 + m) = 3m2 + 12
⇔ 4m + 2m2 + 2m + m2 = 3m2 + 12
⇔ 6m + 3m2 = 3m2 + 12
⇔ 6m = 12
⇔ m = 2
Vậy m = 2.
Câu 31: Trong hai số – 1 và – 6, số nào lớn hơn?
Lời giải:
Vì 1 < 6 nên – 1 > – 6
Vậy – 1 > – 6.
Câu 32: Tìm tất cá các giá trị thực của tham số m để hàm số đồng biến trên ℝ.
A. 0 < m < 1;
B. – 1 ≤ m ≤ 1;
C. 0 ≤ m ≤ 1;
D. – 1 < m < 1.
Lời giải:
Đáp án đúng là: B
Ta có: y’ = x2 – 4mx + 4
△’ = (– 2m)2 – 4 = 4m2 – 4
Để làm số đồng biến trên ℝ thì y’ ≥ 0, ∀x ∈ ℝ
⇔ ⇔
⇔ m2 – 1 ≤ 0
⇔ – 1 ≤ m ≤ 1
Vậy – 1 ≤ m ≤ 1.
Câu 33: Biết 20% của một số là 25 số đó là bao nhiêu?
Lời giải:
Số cần tìm là
25 × 100 : 20 = 125
Vậy số đó là 125.
Câu 34: Cho 4 điểm A, B, C, D bất kì. Chứng minh .
Lời giải:
Ta có:
![]()
Vậy .
A. 2;
B. 3;
C. 4;
D. 1.
Lời giải:
Đáp án đúng là: A
Ta có
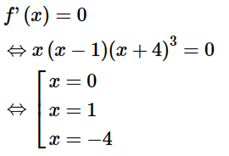
Ta có bảng xét dấu của f’(x)

Dựa vào bảng xét dấu của f'(x) suy ra hàm số đã cho có 2 điểm cực tiểu.
Vậy ta chọn đáp án A.
A. 2;
B. 0;
C. 1;
D. 3.
Lời giải:
Đáp án đúng là C
Ta có:
f’(x) = 0 ⇔ x(x − 1)2 = 0 ⇔
Ta xét dấu của f’ (x)

Ta thấy đạo hàm đổi dấu đúng 1 lần nên hàm số đã cho có đúng 1 cực trị
Vậy ta chọn đáp án C.
a) Chứng minh A, B , C, D cùng thuộc 1 đường tròn và gọi đường tròn đó có tâm O
b) Chứng minh CD < AB.
c) Giả sử 2 đoạn thẳng CD cắt AB tại M. Chứng minh OM = .
Lời giải:
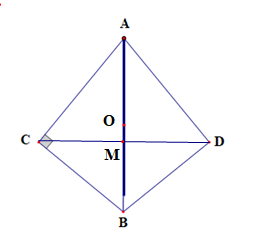
a) Gọi O là trung điểm của AB
Vì tam giác ABC vuông tại C
Nên C thuộc đường tròn (O) đường kính AB
Vì tam giác ABD vuông tại D
Nên D thuộc đường tròn (O) đường kính AB
Suy ra A, B, C, D cùng thuộc đường tròn (O)
b) Xét (O) có
AB là đường kính
CD là dây cung
Do đo: CD < AB
c) Ta có MA + MB = AB = 2OM (vì O là trung điểm của AB)
Suy ra OM =
Vậy OM = .
A. 3
B. 2
C. 5
D. 1.
Lời giải:
Đáp án đúng là A
Ta có f’(x) = 0 ⇔ x(x – 1)(x + 2)3 = 0
⇔
Vì các nghiệm này đều là nghiệm bội bậc lẻ nên hàm số đã cho có 3 điểm cực trị
Vậy ta chọn đáp án A.
Lời giải:
Gọi Ai là biến cố “bộ phận thứ i của thiết bị hoạt động tốt trong khoảng thời gian T” (i = 1, 2, 3 )
Gọi A là biến cố “thiết bị hoạt động tốt trong khoảng thời gian T”
Như vậy: A = A1 . A2 . A3
Vì A1, A2, A3 độc lập toàn phần với nhau, do đó:
P(A) = P(A1) . P(A2) . P(A3)
Các biến cố “bộ phận thứ i hoạt động tốt”và “bộ phận thứ i bị hỏng” là đối lập với nhau, cho nên:
P(A1) = 1 – 0,1 = 0,9
P(A2) = 1 – 0,2 = 0,8
P(A3) = 1 – 0,3 = 0,7
Vậy P(A) = 0,9 . 0,8 . 0,7 = 0,504.
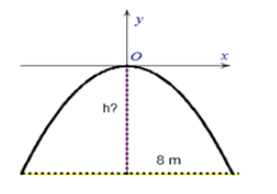
Lời giải:
Đường thẳng chứa chiều rộng d = 8 m cắt (P) tại A(4; – h) nằm bên phải trục tung.
Điểm A thuộc (P) suy ra – h =
Hay h = 8
Vậy chiều cao h của cổng là 8 m.
Lời giải:
Đổi 45 phút = 0,75 giờ
Theo đề ta có:
V . t = (v - v' )(t' + t) (km)
Hay: 54t' = 45(t' + 0,75)
⇔ 54 t' – 45 t' = 33,75
⇔ t' = 3,75 (giờ)
Suy ra quãng đường AB là:
s = 54t' = 3,75 . 54 = 202,5 (km)
Vậy quãng đuong AB dài 202,5km; thời gian dự tính là 3,75 giờ.
A. 0,26 . 10-3
B. 0,52 . 10-3
C. 0,37 . 10-3
D. 0,41 . 10-3
Lời giải:
Đáp án đúng là A
Số cách chia 20 bạn thành 4 nhóm, mỗi nhóm 5 bạn là
n(Ω) =
Gọi A là biến cố “5 bạn nữ thuộc cùng một nhóm”
Xét 5 bạn nữ thuộc nhóm A có cách chia các bạn nam vào nhóm còn lại
Do vai trò của các nhóm như nhau nên
Khi đó
Vậy ta chọn đáp án A.
Lời giải:
Ta có:
![]()
Theo bài ra
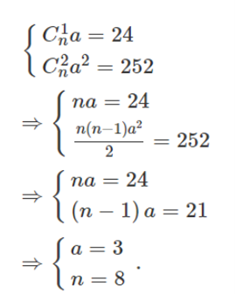
Vậy a = 3 và n = 8.
a) 2 phế phẩm
b) không quá 2 phế phẩm.
Lời giải:
a) Xác xuất để trong 12 sản phẩm do do nhà máy đó sản xuất ra có 2 phế phẩm là
P = . 0,052 . 0,9510 = 66 . 0,0025 . 0,599 = 0,099
b) Xác xuất để trong 12 sản phẩm do do nhà máy đó sản xuất ra có không quá 2 phế phẩm là
P = P(0) + P(1) = 0,9512 + . 0,05 . 0,9511 = 0,54 + 0,34 = 0,88.
Câu 45: Tìm x, y biết x : y : z = 3 : 8 : 5 và 3x + y – 2z = 14.
Lời giải:
Ta có x : y : z = 3 : 8 : 5
Suy ra
Hay
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra
Vậy x = 6, y = 16, z = 10.
Câu 46: Điền số thích hợp vào chỗ trống: 271 km 25m = ....m.
Lời giải:
Ta có:
271 km 25m = 271 025 m.
Câu 47: Phân số cần những điều kiện gì để trở thành 1 số nguyên?
Lời giải:
Ta có phân số , điều kiện phân số là một số nguyên là:
+) a và b khác 0
+) a > b và a chia hết cho b
Câu 48: Một số nếu giảm xuống 3 lần rồi bớt đi 14,6 thì được kết quả là 30,4. Tìm số đó.
Lời giải:
Gọi số phải tìm là: x
Theo đề bài, ta có:
x : 3 − 14,6 = 30,4
⇔ x : 3 = 30,4 + 14,6
⇔ x : 3 = 45
⇔ x = 45 x 3
⇔ x = 135
Vậy số phải tìm là 135.
Lời giải:
Ta có:
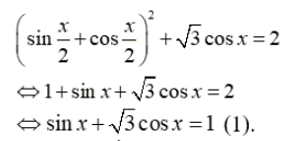
Chia cả hai vế của phương trình (1) cho 2 ta được:
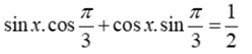
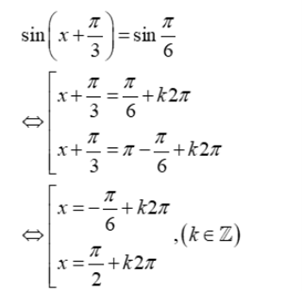
Vậy phương trình có nghiệm là x = , x = .
Câu 50: Tìm x, y, z biết và 5z – 3x – 4y = 50.
Lời giải:
Ta có:
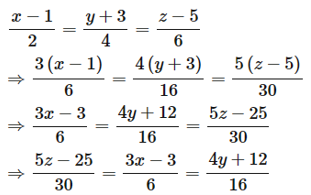
Áp dụng tính chất dãy tỉ số bằng nhau
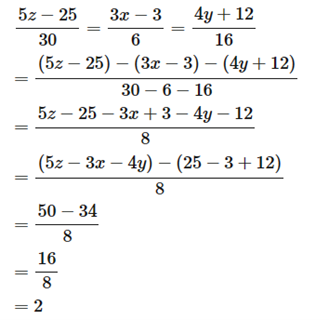
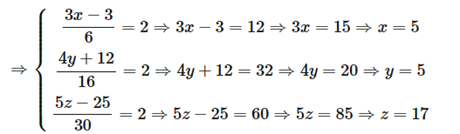
Vậy x = 5, y = 5, z = 17.