Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 67)

Câu 1: Điền vào chỗ trống: 789g = …kg.

Lời giải:

Ta có: 1kg = 1000g hay 1g = 0,001 kg

Vậy 789g = 0,789 kg.

Câu 2: Tìm x biết: 6x² – (2x – 3)(3x + 2) – 1 = 0.

Lời giải:

6x² – (2x – 3)(3x + 2) – 1 = 0

⇔ 6x² – (6x² – 5x – 6) – 1 = 0

⇔ 6x² – 6x² + 5x + 6 – 1 = 0

⇔ 5x + 5 = 0

⇔ x = – 1

Vậy x = – 1.

Câu 3: Tính tổng A = 3 + 6 + 12 + 24 + … + 3072.

Lời giải:

Ta thấy: 6 = 3.2

12 = 6.2

24 = 12.2

Do đó, đây là cấp số nhân có số hạng đầu là 3 và công bội là 2.

Số hạng cuối cùng có dạng: 3072 = 3.2^n–1

⇒ 2^n–1 = 1024 = 2¹⁰

⇒ n – 1 = 10 hay n =11

Vậy dãy A có 11 số hạng

Tổng A = $\frac{3\left(2^{11}-1\right)}{2-1}=6141$ .

Câu 4: Chứng minh rằng: A = n³ + (n+1)³ + (n+2)³ chia hết cho 9 với mọi n thuộc ℕ.

Lời giải:

Áp dụng hằng đẳng thức (a+b)³ = a³ + 3a²b + 3ab² + b³ ta có

A = n³ + (n+1)³ + (n+2)³

= n³ + n³ + 3n² + 3n + 1 + n³ + 6n² + 12n + 8

= 3n3 + 9n2 + 15n + 9

= 3(n³ + 5n) + 9(n² + 1)

Vậy để chứng minh A chia hết cho 9 thì ta sẽ chứng minh 3(n³ + 5n) chia hết cho 9 hay n³ + 5n³ chia hết cho 3.

Nếu n chia hết cho 3 thì hiển nhiên n³ + 5n = n(n² + 5) chia hết cho 3. Do đó A chia hết cho 9.

Giả sử n chia 3 dư 1, khi đó tồn tại một số tự nhiên k sao cho n = 3k + 1. Thay vào ta có

n³ + 5n = n(n² + 5)

= (3k + 1)[(3k + 1)² + 5]

= (3k + 1)(9k² + 6k + 1 + 5)

= (3k + 1)(9k² + 6k + 6)

= (3k + 1).3.(3k² + 2k + 2)

Vậy n³ + 5n chia hết cho 3, do đó 3(n³ + 5n) chia hết cho 9 nên A chia hết cho 9.

Với n chia 3 dư 2, tồn tại một số tự nhiên k sao cho n = 3k + 2. Thay vào ta có

n³ + 5n = n(n² + 5)

= (3k + 2)[(3k + 2)² + 5]

= (3k + 2)(9k² + 12k + 4 + 5)

= (3k + 2)(9k² + 12k + 9)

= (3k + 2).3.(3k² + 4k + 3)

Vậy n³ + 5n chia hết cho 3, do đó 3(n³ + 5n) chia hết cho 9 nên A chia hết cho 9.

Vậy trong mọi trường hợp với n, A đều chia hết cho 9.

Câu 5: Một nhà máy sản xuất sản phẩm với 40% sản phẩm loại I, 50% sản phẩm loại II, còn lại là phế phẩm. Lấy ngẫu nhiên 1 sản phẩm của nhà máy. Tính xác suất sản phẩm lấy ra là loại I hoặc loại II?

Lời giải:

Xác suất sản phẩm là phế phẩm là: 1 – 0,4 – 0,5 = 0,1

Xác suất lấy ra sản phẩm là loại I hoặc loại II là: 0,4 + 0,5 = 0,9.

Câu 6: Một chiếc thuyền dự định đi từ vị trí A bên bờ sông này đến vị trí B bên bờ sông kia. AB vuông góc với 2 bờ sông. Do dòng nước chảy xiết nên chiếc thuyền đã đi lệch góc so với AB và đến vị trí C bên bờ bên kia. Biết khoảng cách giữa 2 bờ sông là 160 m. Tính thời gian chuyển động của thuyền, biết vận tốc nước chảy so với bờ là 2 m/s.

Lời giải:

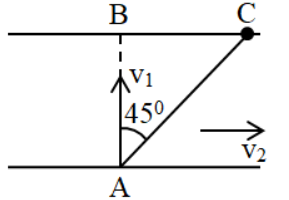
Xét tam giác vuông ABC, ta có:

BC = AB . tan45° = 160 . 1 = 160 (m)

Nhận xét: Thời gian thuyền sang sông từ A đến C bằng thời gian nước chảy từ B đến C

Thời gian chuyển động của thuyền là: $\frac{AC}{v_1}=\frac{BC}{v_2}=\frac{160}{2}=80$ (s).

Câu 7: Tìm hệ số của x¹⁵ trong khai triển (x² + 8)¹².

Lời giải:

(x² + 8)¹² = $\sum _{k=0}^{12}{C}_{12}^k.{\left(x^2\right)}^k{.8}^{12-k}$ .

Ta thấy (x²)^k luôn có số mũ chẵn do đó không xuất hiện x¹⁵ trong khai triển này.

Câu 8: Hai người đi xe từ A đến C. Người thứ nhất đi theo đường từ A đến B rồi từ B đến C. Người thứ hai đi thẳng từ A đến C. Cả hai đều về đích cùng lúc. Tính quãng đường và độ dịch chuyển của người thứ nhất và người thứ hai, so sánh và nhận xét kết quả.

Lời giải:

Ta thấy: AB + BC > AC (theo tính chất tam giác)

Suy ra: người thứ nhất đi dài hơn người thứ hai

Mà 2 người đi đến đích cùng lúc nên tốc độ người thứ nhất nhanh hơn người thứ hai.

Câu 9: Hiện nay anh hơn em 13 tuổi biết sau 7 năm nữa tuổi anh gấp 2 lần tuổi em. Tìm tuổi em và tuổi anh hiện nay?

Lời giải:

Gọi tuổi em hiện nay là x, thì tuổi anh là x + 13

Ta có: x + 13 + 7 = 2 (x + 7)

⇔ x + 20 = 2x + 14

⇔ x = 6

Vậy tuổi em hiện nay là 6 tuổi.

Tuổi anh hiện nay là: 6 + 13 = 19 (tuổi).

Câu 10: Trung bình cộng số ngô ở hai thùng là 225 kg .Thùng B nhiều hơn thùng A là 120 kg.Tìm tỉ số phần trăm số ngô giữa thùng A và thùng B.

Lời giải:

Tổng khối lượng ngô của 2 thùng A và B là:

225 . 2 = 450 (kg ngô)

Thùng A có số kg ngô là:

(450 − 120) : 2=165 (kg ngô)

Thùng B có số kg ngô là:

450 – 165 = 285(kg ngô)

Tỉ số phần trăm số ngô giữa thùng A và thùng B là:

165 : 285 . 100% = $\frac{1100}{19}\%$

Đáp số: $\frac{1100}{19}\%$ .

Câu 11: ​Phân tích đa thức thành nhân tử: 81x⁴ + 4y⁴.

Lời giải:

81x⁴ + 4y⁴

= (9x²)² + (2y²)²

= (9x²)² + (2y²)² + 2.9x².2y² – 36x²y²

= (9x² + 2y²)² – (6xy)²

= (9x² + 2y² – 6xy)(9x² + 2y² + 6xy).

Câu 12: ​Thực hiện phép tính: (6²⁰⁰⁷ – 6²⁰⁰⁶) : 6²⁰⁰⁶.

Lời giải:

(6²⁰⁰⁷ – 6²⁰⁰⁶) : 6²⁰⁰⁶

= 6²⁰⁰⁶ (6 – 1) : 6²⁰⁰⁶

= 6²⁰⁰⁶ . 5 : 6²⁰⁰⁶

= 5.

Câu 13: ​Có bao nhiêu cách xếp 3 quả bóng giống nhau vào 5 chỗ khác nhau (mỗi chỗ xếp không quá một quả bóng)?

Lời giải:

Xếp 3 quả bóng  giống nhau, mỗi quả vào 1 chỗ nên ta sẽ lấy 3 quả bóng bất kỳ trong 5 chỗ khác nhau để xếp bóng.

Vậy số cách xếp bóng bằng số cách chọn 3 quả bóng từ 5 chỗ – và bằng số  tổ hợp chập 3 của 5 phần tử (chỗ).

Như vậy, ta có $C_5^3=\frac{5!}{2!.3!}$ = 10 cách.

Câu 14: ​Hai người khách du lịch xuất phát đồng thời từ hai thành phố cách nhau 38 km. Họ đi ngược chiều và gặp nhau sau 4 giờ.Hỏi vận tốc của mỗi người biết rằng đến khi gặp nhau, người thứ nhất đi được nhiều hơn người thứ hai là 2 km.

Lời giải:

Gọi vận tốc người đi từ A và B lần lượt là x và y. (x, y > 0)

Họ đi ngược chiều gặp nhau sau 4 giờ nên

4x + 4y = 38 (1)

Người thứ nhất đi nhiều hơn người thứ 2 là 2km nên

4x − 4y = 2 (2)

Từ (1) và (2) ⇒ ta có hệ phương trình:

$\left\{\begin{array}{l}4x+4y=38\\ 4x-4y=2\end{array}\right.$ ⇔ $\left\{\begin{array}{l}8x=40\\ 4x-4y=2\end{array}\right.$

⇔ $\left\{\begin{array}{l}x=5\\ 4x-4y=2\end{array}\right.$ ⇔ $\left\{\begin{array}{l}x=5\\ y=\mathrm{4,5}\end{array}\right.$

Vậy vận tốc người thứ nhất là 5km/h, vận tốc người thứ hai là 4,5 km/h.

Câu 15: Gieo 3 con súc sắc cân đối và đồng chất. Xác suất để số chấm xuất hiện trên 3 con súc sắc đó bằng nhau.

Lời giải:

Số phần tử của không gian mẫu là:

|Ω| = 6³ = 216

A: “số chấm xuất hiện trên 3 con súc sắc đó bằng nhau”.

A = {(1,1,1) ; (2,2,2) ; (3,3,3) ; (4,4,4) ; (5,5,5) ; (6,6,6)}

Xác suất để số chấm  xuất hiện trên 3 con súc sắc đó bằng nhau là:

P = $\frac{6}{216}=\frac{1}{36}$ .

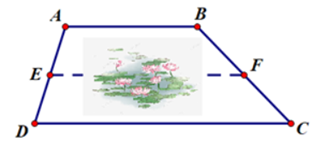
Câu 16: Tại môt khu nghỉ dưỡng người ta muốn xây một cây cầu bắc qua ao sen (đoạn EF để du khách có thể đi bộ ngắm sen và đàn cá KOI bơi, cây cầu đi bộ này song song với hai con đường AB và DC. Em hãy tính độ dài cây cầu EF, biết con đường AB và DC dài lần lượt là 30m và 50m, E và F là điểm chính giữa AD và BC.

Lời giải:

Ta thấy: EF là đường trung bình của hình thang ABCD do E, F lần lượt là trung điểm của AD và BC.

Nên: $EF=\frac{AB+CD}{2}=\frac{30+50}{2}=40$ (m).

Câu 17: Một bể bơi có chiều dài 25m, chiều rộng 10m và sâu 1,5m. Bể đó đc lát đáy và xung quanh bằng gạch men hình vuông có cạnh 5dm. Tính số gạch dùng để lát bể bơi đó.

Lời giải:

5dm = 0,5m

Diện tích được lát gạch:

(25 + 10) . 2 . 1,5 + 25 . 10 = 355(m²)

Diện tích mỗi viên gạch:

0,5 . 0,5 = 0,25 (m²)

Cần số viên gạch là:

355 : 0,25 = 1420 (viên)

Đáp số: 1420 viên gạch.

Câu 18: Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần?

Lời giải:

Vì số có chín chữ số viết theo thứ tự giảm dần nên chỉ có thể là chữ số 9 hoặc chữ số 8 đứng đầu.

+ Trường hợp 1, số 9 đứng đầu

Từ các số 0; 1; 2; 3; 4; 5; 6; 7; 8 mỗi một lần ta bỏ đi một số ta sẽ lập được 1 số có 9 chữ số viết theo thứ tự giảm dần mà số 9 đứng đầu.

Vậy trường hợp 1 có 9 số được lập

+ Trường hợp 2, số 8 đứng đầu

Vì từ 0 đến 8 có chín chữ số nên ta chỉ lập được 1 số có 9 chữ số viết theo thứ tự giảm đần

Vậy cả 2 trường hợp có 9 + 1 = 10 số.

Câu 19: trên cạnh BC của hình tam giác ABC có các điểm M,N sao cho BM = MN = NC. So sánh diện tích các hình tam giác AMN, AMN, ANC. Tính diện tích mỗi hình tam giác đó, biết diện tích hình tam giác ABC là 77,4m²

Lời giải:

Kí hiệu S là diện tích.

Ta có :

S_ABM​ = S_AMN​ = S_ANC​ (BM = MN = NC, chung chiều cao hạ từ A xuống BC )

Diện tích của mỗi hình là:

77,4 : 3 = 25,8 (m²).

Câu 20: Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log₂(4x + 4) + x = y + 1 + 2^y?

Lời giải:

log₂(4x + 4) +x = y + 1 + 2^y

⇔ log₂[4(x + 1)] + x = y + 1 + 2^y

⇔ log₂4 + log₂(x + 1) + x = y + 1 + 2^y

⇔ log₂(x + 1) + 2 + x  = 2^y + y + 1 (*)

Xét f(a) = 2^a + a + 1

f'(a) = 2^a. ln2 + 1 > 0

Suy ra f(a) là hàm số đồng biến trên R

Phương trình (*) tương đương với:

f(log₂(x+1)) = f(y)

⇒ log₂(x + 1) = y

⇔ x + 1 = 2^y

⇔ x = 2^y – 1

Do 0 ≤ x ≤ 2020 suy ra: 0 ≤ 2^y – 1 ≤ 2020

⇔ 1 ≤ 2^y  ≤ 2021

⇔ 0 ≤ y ≤ 10,98

Vậy y ∈ {0;1;2;3;4;5;6;7;8;9;10} (có 11 số nguyên y)

Tương ứng có 11 số nguyên x

Vậy có 11 cặp số nguyên (x; y) thỏa mãn.

Câu 21: Có bao nhiêu số tròn nghìn có 5 chữ số?

Lời giải:

Các số có 5 chữ số tròn nghìn là : 

10000, 11000, 12000 ,..., 99000

Ta có : (99000 − 10000) : 1000 + 1 = 90 (số)

Vậy có 90 số trong nghìn có năm chữ số.

Câu 22: Bác Năm mới mua miếng đất hình vuông có diện tích 3600 m². Bác tính làm hàng rào bằng dây kẽm gai hết tất cả 5000000 đồng bao gồm cả chi phí dây kẽm và tiền công làm. Gọi x là giá mỗi mét dây kẽm (x > 0), y là số tiền công làm hàng rào.

a) Hãy viết hàm số tính công làm hàng rào.

b) Hỏi bác Năm phải trả bao nhiêu tiền công để thợ rào hết hàng rào. Biết rằng giá mỗi mét dây kẽm là 15.000 đồng.

Lời giải:

a) Ta có cạnh hình vuông là: 60 m

Chu vi hình vuông là: 60 . 4 = 240 (m)

Có 240x + y = 5000000

⇒ y = 5000000 – 240x

b) Bác Nam phải trả số tiền là:

5000000 – 240 . 1500 = 1400000 (đồng).

Câu 23: Ta có thể trừ đi 1 từ số 1111 bao nhiêu lần?

Lời giải:

Chỉ một lần duy nhất.

Vì sau khi lấy 1111 trừ đi 1, chúng ta sẽ không còn số 1111 nữa, mà là 1110 (1111 – 1 = 1110), và tiếp tục các lần tiếp theo là lần lượt các số 1109, 1108, 1107,…

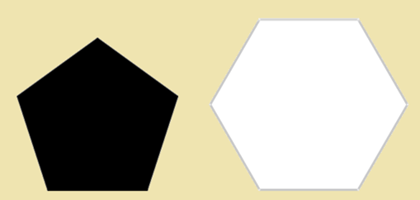
Câu 24: Một quả bóng được khâu từ 32 miếng da gồm hai loại như hình vẽ:

Biết rằng mỗi miếng màu đen chỉ giáp với 5 miếng màu trắng và mỗi miếng màu trắng giáp với 3 miếng màu đen. Hỏi có bao nhiêu miếng da màu trắng?

Lời giải:

Gọi số miếng trắng là: a

Gọi số miếng đen là: b

Ta có: a + b = 32

Vì mỗi miếng màu đen chỉ giáp với 5 miếng màu trắng và mỗi miếng màu trắng giáp với 3 miếng màu đen ⇒ 3a = 5b

⇔ $\frac{a}{5}=\frac{b}{3}=\frac{a+b}{5+3}=\frac{32}{8}=4$

⇔ a = 4 . 5 = 20 miếng

⇒ b = 32 − 20 = 12 miếng.

Câu 25: Tìm x biết 12x + 9,28 . 12 = 240

Lời giải:

12x + 9,28 . 12 = 240

⇔ 12(x + 9,28) = 240

⇔ x + 9,28 = 240:12

⇔ x + 9,28 = 20

⇔ x = 20 − 9,28

⇔ x = 10,72

Vậy x = 10,72.

Câu 26: Nêu cách vẽ tam giác cân?

Lời giải:

Tam giác cân là tam giác có hai cạnh bằng nhau.

Ví dụ vẽ tam giác cân bằng compa và thước

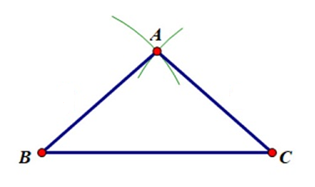
Tam giác ABC cân tại A, ta có:

AB, AC là các cạnh bên, BC là cạnh đáy, Góc A là góc ở đỉnh, góc B và góc C là các góc ở đáy.

Cách vẽ tam giác ABC cân tại A:

Đầu tiên, ta vẽ cạnh BC

Tiếp theo vẽ cung tròn tâm B, bán kính r

Tiếp theo vẽ cung tròn tâm C, bán kính r

Hai cung tròn cắt nhau tại A.

Như vậy, tam giác ABC là tam giác cần vẽ.

Câu 27: Khi đo chiều dài của chiếc bàn học, một học sinh viết được kết quả: C = 118 ± 2 (cm). Sai số tỉ đối phép đo đó bằng?

Lời giải:

Sai số tỉ đối của phép đo đó là:

ε = $\frac{2}{118}.100\%$  = 1,67%.

Câu 28: Tại cửa hàng giá niêm yết một cái áo là 300000 đồng. Nếu bán với giá bằng ba phần tư giá niêm yết thì được lãi 20%. Hỏi để lãi 40% thì cửa hàng bán giấ niêm yết là bao nhiêu?

Lời giải:

Giá niêm yết  là 300000 đồng nếu bán với giá bằng $\frac{3}{4}$ giá niêm yết thì giá bán là:

34.300000 = 225000 (đồng)

Với giá 225000 đồng thì cửa hàng khi đó lãi 20%

⇒ Giá gốc là: 225000 : 120 . 100 = 187500 (đồng)

Để lãi 40% thì cửa hàng bán giá niêm yết là:

187500 : 100 . 140= 262500 (đồng).

Câu 29: Một trường có 1030 học sinh. Số học sinh nam chiếm 40%. Tính số học sinh nữ.

Lời giải:

Số học sinh nữ chiếm số phần trăm là:

100% − 40% = 60%

Số học sinh nữ của trường đó là :

1030 . 60 : 100 = 618 (học sinh)

Đáp số: 618 học sinh.

Câu 30: Có bao nhiêu số tự nhiên gồm 5 chữ số chia hết cho 10?

Lời giải:

Gọi số cần tìm có dạng : $\overline{abcde}$ (a ≠ 0)

Công đoạn 1, chọn số e có 1 cách chọn (vì số $\overline{abcde}$  chia hết cho 10 nên e chỉ có thể chọn là số 0)

Công đoạn 2, chọn số a có 9 cách chọn (vì a ≠ 0 nên a chỉ được chọn một trong 9 số 1; 2; 3 ; 4; 5; 6; 7; 8; 9)

Công đoạn 3, chọn số b có 10 cách chọn (vì b chọn tuỳ ý nên b có thể chọn 1 trong 10 số 0; 1; 2; 3 ; 4; 5; 6; 7; 8; 9)

Công đoạn 4, chọn số c có 10 cách chọn (vì c chọn tuỳ ý nên c có thể chọn 1 trong 10 số 0; 1; 2; 3 ; 4; 5; 6; 7; 8; 9)

Công đoạn 5, chọn số d có 10 cách chọn (vì d chọn tuỳ ý nên d có thể chọn 1 trong 10 số 0; 1; 2; 3 ; 4; 5; 6; 7; 8; 9)

Tổng kết, theo quy tắc nhân ta có Số các số tự nhiên gồm 5 chữ số chia hết cho 10 là: 1.9.10.10.10 = 9000 (số).

Câu 31: Trong số 423,15 phần thập phân là?

Lời giải:

Phần thập phân là 0,15 = $\frac{15}{100}$ .

Câu 32: Cho nửa đường tròn tâm O đường kính AB =2R và điểm M nằm trên đường tròn đó (M ≠ A, B) tiếp tuyến tại điểm M của nửa đường tròn tâm O cắt các tiếp tuyến tại A và B. Lần lượt tại các điểm C, D. Gọi E là giao điểm của OC với AM, gọi F là giao điểm của OD và BM.

a) Chứng minh CD = AC + BD.

b) Chứng minh EF vuông góc BD và EF là tiếp tuyến đường tròn đi qua các điểm M, D, F.

Lời giải:

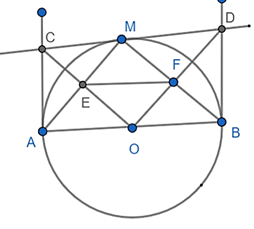
a) Vì CA, CM là tiếp tuyến của (O) nên AC = CM

Tương tự: DM = DB

Suy ra: CM + DM = AC + BD ⇒ CD = AC + BD

b) Vì CA, CM là tiếp tuyến của (O) nên OC ⊥ AM tại E là trung điểm AM

Tương tự: OF ⊥ BM tại F là trung điểm BM

Suy ra: EF là đường trung bình của ∆MAB

⇒ EF // AB mà AB ⊥ BD nên EF ⊥ BD

Vì MB ⊥ OD tại F nên G là trung điểm DM, là tâm đường tròn ngoại tiếp ∆MDF

Mà GF là đường trung bình ∆MBD

Suy ra: GF // BD ⇒ GF ⊥ EF

Vậy EF là tiếp tuyến của đường tròn đi qua M, D, F.

Câu 33: Chứng minh giá trị của biểu thức sau không phụ thuộc vào biến x.

A = x(3x² – x + 5) – (2x³ + 3x – 25) – x(x² – x + 2).

B = x(2x + 1) – x²(x + 2) + (x³ – x + 10).

Lời giải:

A = x(3x² – x + 5) – (2x³ + 3x – 25) – x(x² – x + 2)

= 3x³ – x² + 5x – 2x³ – 3x + 25 – x³ + x² – 2x

= (3x³ – 2x³ – x³) + (x² – x²) + (5x – 3x – 2x) + 25

= 25.

Vậy A = 25, không phụ thuộc giá trị vào x.

B = x(2x + 1) – x²(x + 2) + (x³ – x + 10)

= 2x² + x – x³ – 2x² + x³ – x + 10

= (2x² – 2x²) + (x³ – x³) + (x – x) + 10

= 10.

Vậy B = 10, không phụ thuộc giá trị vào x.

Câu 34: Cho hàm số bậc nhất y = m – 1 + (m + 2)x. Tìm tọa độ điểm cố định mà đường thẳng y luôn đi qua.

Lời giải:

Gọi điểm cố định mà hàm số đi qua là N(x₀; y₀)

Ta có: y₀ = (m + 2)x₀ + m – 1

⇔ m(x₀ + 1) + (2x₀ – 1 – y₀) = 0

Vậy để đồ thị hàm số luôn đi qua N thì:

$\left\{\begin{array}{l}{x}_0+1=0\\ 2x_0-y_0-1=0\end{array}\right.$ ⇔ $\left\{\begin{array}{l}{x}_0=-1\\ y_0=-3\end{array}\right.$

Vậy điểm cố định mà đường thẳng y luôn đi qua là N(–1; –3).

Câu 35: Tìm tập giá trị T của hàm số y = sin2x.

Lời giải:

Ta thấy: –1 ≤ sin2x ≤ 1

Nên tập giá trị T của hàm số y = sin2x là [–1; 1].

Câu 36: Có 3 học sinh nữ và 2 học sinh nam. Ta muốn sắp xếp vào 1 bàn dài có 5 ghế ngồi. Hỏi có bao nhiêu cách xếp cho 3 học sinh nữ ngồi liền nhau.

Lời giải:

Gọi theo thứ tự 5 ghế là $\overline{abcde}$

Vậy 33 bạn nữ có thể ngồi bắt đầu từ a, b hoặc c

Do đó có 3 cách chọn. Hơn nữa, ta có thể đảo vị trí 3 bạn đó. Cuối cùng xếp 2 bạn nam vào 2 chỗ còn lại.

Vậy số cách là

3 . 3! . 2 = 36 (cách)

Cách 2:

Cho 3 bạn nữ là 1 nhóm nữ, xếp 3 bạn nữ có 3! cách

Sắp xếp nhóm nữ và 2 bạn nam vào 3 vị trí có 3! cách

Như vậy có tất cả 3!.3! = 36 cách.

Câu 37: Làm tròn số 45,29 với độ chính xác d = 6.

Lời giải:

Độ chính xác d = 6 tức là làm tròn đến hàng chục

Vì phía sau số 4 là số 5 nên ta cộng thêm 1 đơn vị vào chữ số 4 và thay các chữ số bên phải số 4 thành 0

Vậy làm tròn số 45,29 với độ chính xác d = 6 là 50.

Câu 38: Số thập phân có 5 chữ số khác nhau lớn nhất mà số đó nhỏ hơn 100?

Lời giải:

Để số thập phân là lớn nhất thì trước dấu phẩy gồm 2 số trước dấu phẩy

Gọi số thập phân cần tìm có dạng $\overline{ab,cde}$

Muốn số thập phân lớn nhất thì a = 9

Do theo giả thiết 5 chữ số khác nhau nên b = 8, c = 7, d = 6, e = 5.

Vậy số thập phân cần tìm là 98,765.

Câu 39: Cho x + 2y = 5. Tính giá trị biểu thức A= x² + 4y² – 2x + 10 + 4xy – 4y.

Lời giải:

A = x² + 4y² – 2 + 10 + 4xy – 4y

⇔ A = x² + (2y)² – 2 + 10 + 4xy – 4y

⇔ A = [x² + 4xy + (2y)²] – 2 + 10 – 4y

⇔ A = (x + 2y)² + 8 – 4y

⇔ A = 5² + 8 – 4y

⇔ A = 25 + 8 – 4y

⇔ A = 33 – 4y

Câu 40: Xét mệnh đề kéo theo P: “Nếu 18 chia hết cho 3 thì tam giác cân có 2 cạnh bằng nhau” và Q: “Nếu 17 là số chẵn thì 25 là số chính phương”. Xét tính đúng, sai của mệnh đề P và Q?

Lời giải:

+ Xét mệnh đề P:

Ta thấy: 18 chia hết cho 3 là đúng và tam giác cân có 2 cạnh bằng nhau là đúng nên mệnh đề P là mệnh đề đúng

+ Xét mệnh đề Q:

Ta thấy: 17 không phải là số chẵn và 25 là số chính phương nên mệnh đề Q là mệnh đề sai.

Câu 41: 3m 6cm = … dm.

Lời giải:

Ta có: 1m = 10dm = 100cm

Nên 3m 6cm = 306cm = 30,6 dm.

Câu 42: Cho tập hợp A={1;2;3;...;n} trong đó n là số nguyên dương lớn hơn 1. Hỏi có bao nhiêu cặp sắp thứ tự (x;y) thõa mãn: x và y thuộc A; x lớn hơn y?

Lời giải:

• Nếu x = y: có n số thuộc A nên có n cặp 

• Nếu x > y:

Mỗi cách lấy hai số bất kỳ thuộc A đều có 1 cách xếp (x; y)

⇒ $C_n^2=\frac{n!}{2\left(n-2\right)!}=\frac{n\left(n-1\right)}{2}=\frac{n^2-n}{2}$ cách

Vậy tổng số cặp là: $n+\frac{n^2-n}{2}=\frac{n^2+n}{2}$ .

Câu 43: Có bao nhiêu tập hợp X thỏa mãn điều kiện {0; 1; a} hợp với X = {0; 1; a; b; c}.

Lời giải:

Ta có các tập hợp sau thỏa mãn:

X = {0; 1; a; b; c}; X = {1; a; b; c}; X = {a; b; c}; X = {b; c}; X = {0; a; b; c}; X = {0; b; c}. 

Vậy có 6 tập hợp thỏa mãn.

Câu 44: Một mảnh đất hình chữ nhật có chu vi 180m, chiều dài hơn chiều rộng 22m.

a) Tính chiều dài và chiều rộng của mảnh đất đó.

b) Tính diện tích của mảnh đất đó.

Lời giải:

a) Nửa chu vi mảnh đất hình chữ nhật hay tổng chiều dài và chiều rộng của hình chữ nhật là:

180 : 2 = 90 (m)

Chiều rộng của mảnh đất hình chữ nhật là:

(90 − 22) : 2 = 34 (m)

Chiều dài của mảnh đất hình chữ nhật là:

34 + 22 = 56 (m)

b) Diện tích của mảnh đất hình chữ nhật là:

34 . 56 = 1904(m²)

Đáp số: a) 34m và 56m

b) 1904m²

Câu 45: Một hình tam giác có diện tích là 8m² và độ dài cạnh đáy là 32dm. Tìm chiều cao của hình tam giác tương ứng với cạnh đáy đó.

Lời giải:

Đối: 8m² = 800dm²

Chiều cao của hình tam giác là:

800 . 2 : 32 = 50 (dm)

Đáp số: 50dm.

Câu 46: Một xí nghiệp đóng giày dự định hoàn thành kế hoạch trong 26 ngày. Nhưng do cải tiến kĩ thuật nên mỗi ngày đã vượt mức 6000 đôi giày, do đó chẳng những đã hoàn thành kế hoạch đã định trong 24 ngày mà còn vượt mức 104000 đôi giày. Tính số đôi giày phải làm theo kế hoạch?

Lời giải:

Gọi năng suất sản xuất giầy trong một ngày xí nghiệp phải làm theo kế hoạch là x (giầy/ngày), x > 0

Theo dự định hoàn thành kế hoạch trong 26 ngày nên tổng số đôi giầy phải làm theo kế hoạch là 26x (đôi giầy)

Do cải tiến kỹ thuật nên mỗi ngày xí nghiệp vượt mức 6000 đôi giầy suy ra năng suất mỗi ngày là x + 6000 (đôi giầy/ngày)

Cho nên đã hoàn thành trong 24 ngày nên tổng số đôi giày làm được là: 24(x + 6000) (đôi giầy)

Vì thực tế xí nghiệp vượt mức dự định 104000 đôi giầy nên ta có phương trình:

24(x + 6000) – 26x = 104000

⇔ 24x + 144000 – 26x = 104000

⇔ 2x = 40000

⇔ x = 20000

Vậy theo kế hoạch xí nghiệp phải sản xuất: 26x = 20000 . 26 = 520000 đôi giầy.

Câu 47: Tại cửa hàng bán hoa giá bán ban đầu của một bó hoa là 60 000 đồng. Vào ngày quốc tế phụ nữ 8/3, giá mỗi bó được giảm 20% và nếu khách mua 10 bó trở lên thì từ bó thứ 10 trở đi khách hàng sẽ chỉ trả một nửa giá đang bán. Một vị khách mua hoa đã trả 648 000 đồng. Hỏi khách này đã mua bao nhiêu bó hoa ?

Lời giải:      

Giá tiền của 9 bó đầu tiên:

9. 60 000. ( 1 – 20% ) = 432 000 (đồng)

Số tiền còn lại:

648 000 – 432 000 = 216 000 (đồng)

Số bó hoa được giảm một nửa sau khi đã giảm lần 1:

216 000 : [ ( 60 000. (1 – 20%) : 2 ] = 9 (bó)

Số bó hoa khách hàng đã mua là:

9 + 9 = 18 (bó)

Vậy khách hàng đã mua 18 bó hoa.

Câu 48: Phân tích đa thức thành nhân tử: x⁴y – xy⁴.

Lời giải:      

x⁴y – xy⁴

= xy (x³ – y³)

= xy (x – y)(x² + xy + y²).

Câu 49: Cho hàm số y = (m–1)x + m – 4 (m là tham số và m khác 1).

a) Tìm giá trị của m để đồ thị hàm số đi qua điểm A(2; 3).

b) Vẽ đồ thị hàm số với giá trị của m tìm được ở phần a.

c) Tìm m biết đồ thị hàm số cắt đường thẳng y = 3x + 2 tại điểm có hoành độ là –2.

Lời giải:      

a) Thay A(2;3) vào ta có:

(m−1).2 + m – 4 = 3

⇔ 2m – 2 + m – 4 = 3

⇔ 3m – 6 = 3

⇔ 3m = 9

⇔ m = 3 (thỏa mãn)

Vậy m = 3 được: y=2x−1

b) y = 2x – 1

x = 0⇒ y = –1

x = 2 ⇒ y = 3

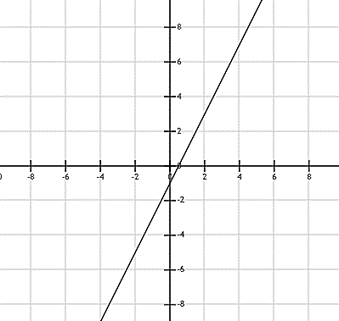
c) Thay x = −2 vào y = 3x + 2 được: y = 3.(−2) + 2 = −4

Suy ra: B(−2;−4)

Thay B(−2;−4) vào ta có:(m−1).(−2) + m – 4 = −4

⇔ −2m + 2 + m = 0

⇔ −m + 2 = 0

⇔ m = 2

Vậy m = 20.

Câu 50: Để sản xuất một tờ giấy A5 lần 5 lít nước. Một cuốn sổ A5 có 300 trang. Hỏi để sản xuất ra cuốn sổ đó cần bao nhiêu mét khối nước?

Lời giải:      

Cuốn sổ A5 dày 300 trang có số tờ là:

300 : 2 = 150 (tờ)

Lượng nước cần thiết để sản xuất ra số tờ giấy đó là:

150 . 5 = 750 (lít)

Đổi 750 lít = 0,75 m³

Đáp số: 0,75 m³.

Câu 51: Tìm ước chung lớn nhất của 1 và 2019.

Lời giải:

Ta có: Ư(1) = {1; –1}

Ư(2019) = {1; –1; 3; –3; 673; –673; 2019; –2019}

Câu 52: 1,2 ha = … m².

Lời giải:

1 ha = 10000 m²

1,2 ha = 1,2 . 10000 = 12000 m².

Câu 53: Một bồn hoa có dạng hình vuông có độ dài cạnh là 2m. Để làm lối đi rộng hơn, người ta thu nhỏ bồn hoa vẫn có dạng hình vuông nhưng độ dài cạnh giảm đi 50cm .

a) Tính diện tích bồn hoa sau khi thu nhỏ.

b) Lối đi được tăng thêm bao nhiêu diện tích?

Lời giải:

Đổi 2m = 200cm

a) Diện tích bồn hoa sau khi giảm là

(200 – 50).(200 – 50) = 22500 (cm²).

b) Diện tích bồn hoa trước khi giảm là:

200.200 = 40000 (cm²).

 Lối đi được tăng thêm là 

40000 – 22500 = 17500 (cm²).

Câu 54: Công thức nào sau đây cho ta quan hệ với tỉ lệ thuận?

A. y = –3x

B. y = 2x – 1

C. y = $\frac{3}{x}$

D. y = –2x²

Lời giải:

Đáp án đúng là: A

y tỉ lệ thuận với x theo hệ số là −3

Công thức của 2 đại lượng tỉ lệ thuận : y = kx (k≠0)

Do đó : y = −3x là quan hệ giữa 2 đại lượng tỉ lệ thuận.

Câu 55: Tìm x thoả mãn: x : 12 ; x ⋮ 18 và x < 250.

Lời giải:      

x chia hết 12 và x chia hết 18

Suy ra x ∈ BC(12;18) và x < 250

Ta có:

12 = 2².3

18 = 2.3²

⇒ B(12; 18) = 2² . 3² = 36

⇒ BC(12; 18) = B(36) = {0; 36; 72; 108; 144; 180; 216; 252; …}

Vì x < 250 nên x ∈{ 0; 36; 72; 108; 144; 180; 216}.

Câu 56: Bán kính của một bánh xe ô tô là 0,25m. Tính chu vi bánh xe đó. Nếu ô tô đó đi hết quãng đường dài 4,71km thì bánh xe lăn trên mặt đất được bao nhiêu vòng?

Lời giải:

Chu vi xe ô tô là:

0,25 . 2 . 3,14 = 1,57 (m)

Đổi: 4,71km = 4710m

Nếu ô tô đó đi hết quãng đường dài 4,71 km thì bánh xe lăn trên mặt đất được:

4710 : 1,57 = 3000 (vòng)

Đáp số: 3000 vòng.