Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 45)

Câu 1: 1 cửa hàng có số gạo tẻ hơn số gạo nếp  là 168 kg. Số gạo nếp bằng $\frac{1}{2}$  số gạo tẻ. Hỏi cửa hàng đó có bao nhiêu kg gạo nếp và gạo tẻ?

Lời giải:

Số kg gạo nếp là: 

168 : (2 – 1) = 168 (kg)

Số kg gạo tẻ là:

168 × 2 = 336 (kg)

Đáp số: Gạo nếp: 168 kg;

   Gạo tẻ: 336 kg.

Câu 2: Một cửa hàng có số gạo tẻ nhiều hơn gạo nếp là 115,6 kg. Sau khi bán đi 13,5 kg mỗi loại thì số gạo tẻ còn lại gấp 5 lần số gạo nếp còn lại. Vậy lúc đầu cửa hàng đó có bao nhiêu kg gạo nếp, có bao nhiêu kg gạo tẻ.

Lời giải:

Vì bán đi gạo mỗi loại nên hiệu số giữa gạo tẻ còn lại và gạo nếp còn lại vẫn không thay đổi và bằng 115,6 kg.

Ta có sơ đồ biểu diễn số gạo còn lại sau khi bán:

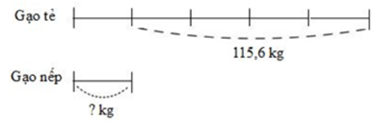
Theo sơ đồ, hiệu số phần bằng nhau là:

5 − 1 = 4 (phần)

Giá trị một phần hay số gạp nếp còn lại sau khi bán là:

115,6 : 4 = 28,9 (kg)

Lúc đầu cửa hàng có số ki-lô-gam gạo nếp là:

28,9 + 13,5 = 42,4 (kg)

Lúc đầu cửa hàng có số ki-lô-gam gạo tẻ là:

42,4 + 115,6 = 158 (kg)

Đáp số: Gạo nếp: 42,4kg;

   Gạo tẻ: 158kg.

Câu 3: Một hình chữ nhật có nửa chu vi là 61,5 m, chiều rộng bằng $\frac{2}{3}$  chiều dài. Tính diện tích hình chữ nhật đó.

Lời giải:

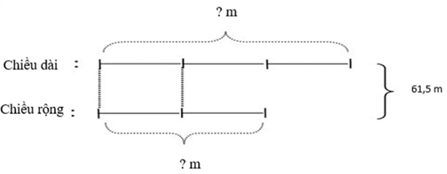
Theo sơ đồ, tổng số phần bằng nhau là:

2 + 3 = 5 (phần)

Chiều rộng hình chữ nhật là:

(61,5 : 5) × 2 = 12,3 (m)

Chiều dài hình chữ nhật là:

61,5 − 12,3 = 49,2 (m)

Diện tích hình chữ nhật là:

12,3 × 49,2 = 605,16 (m²)

Đáp số: 605,16 m².

Câu 4: Một mảnh vườn hình chữ nhật có chiều dài 20 m và chiều rộng 15 m. Người ta dành 20% diện tích mảnh vườn để trồng rau muống, 10% diện tích để trồng rau cải. Tính diện tích phần đất trồng rau muống, diện tích phần đất trồng rau cải.

Lời giải:

Diện tích mảnh đất hình chữ nhật là:

20 × 15 = 300 (m²)

Diện tích phần đất trồng rau muống là:

300 : 100 × 25 = 75 (m²)

Diện tích phần đất trồng rau cải là:

300 : 100 × 10 = 30 (m²)

Đáp số: 75 m² đất trồng rau muống;

    30 m² đất trồng rau cải.

Câu 5: Một can nhựa chứa 10 lít dầu. Biết một lít dầu cân nặng 0,8 kg, can rỗng cân nặng 1,3 kg. Hỏi can dầu đó cân nặng bao nhiêu ki-lô-gam?

Lời giải:

10 lít dầu cân nặng là:

10 × 0,8 = 8 (kg)

Can dầu cân nặng là:

8 + 1,3 = 9,3 (kg)

Đáp số: 9,3 kg.

Câu 6: Tính tổng sau một cách hợp lí: 34 + 35 + 36 + 37 - 24 - 25 - 26 - 27.

Lời giải:

34 + 35 + 36 + 37 - 24 - 25 - 26 - 27

= (34 - 24) + (35 - 25) + (36 - 26) + (37 - 27)

= 10 + 10 + 10 + 10

= 10 × 4 = 40.

Câu 7: Một mảnh đất hình thoi có tổng độ dài hai đường chéo là 76,4 m. Tính diện tích mảnh đất đó, biết đường chéo thứ nhất hơn đường chéo thứ hai là 4,4 m.

Lời giải:

Đường chéo lớn hơn có độ dài là: (76,4 + 4,4) : 2 = 40,4 (m)

Đường chéo nhỏ hơn có độ dài là: 40,4 - 4,4 = 36 (m)

Diện tích mảnh đất đó là: 40,4 . 36 : 2 = 727,2 (m²)

Đáp số: 727,2 m².

Câu 8: Một mảnh vườn hình thoi có tổng hai đường chéo bằng 71 m, đường chéo thứ nhất hơn đường chéo thứ hai 10 m.

a) Tìm độ dài của mỗi đường chéo.

b) Tính diện tích mảnh vườn.

c) Trên mảnh đất người ta dành 25% diện tích đất để trồng rau 46,5% diện tích để trồng ngô. Hỏi diện tích còn lại chiếm bao nhiêu diện tích mảnh vườn.

Lời giải:

a) Độ dài đường chéo nhỏ của mảnh vườn là:

(71 - 10) : 2 = 30,5 (m)

Độ dài đường chéo lớn của mảnh vườn là:

71 - 30,5 = 40,5 (m)

b) Diện tích của mảnh vườn là:

30,5 × 40,5 : 2 = 617,625 (m²)

c) Số phần trăm diện tích còn lại của mảnh vườn là:

100 - (25 + 46,5) = 28,5 %

Diện tích miếng đất còn lại của mảnh vườn là:

617,625 × 28 : 100 = 176, 023125 (m²)

Đáp số:

a) Đường chéo bé: 30,5 m;

Đường chéo lớn: 40,5 m.

b) 617,625 m².

c) 176, 023125 m².

Câu 9: Tính bằng cách thuận tiện nhất

a) 38,25 - 18,25 + 21,64 - 11,64 + 9,93;

b) 45,28 + 52,17 - 15,28 - 12,17;

c) 72,9 × 99 + 72 + 0,9;

d) 0,8 × 96 + 1,6 × 2.

Lời giải:

a) 38,25 - 18,25 + 21,64 - 11,64 + 9,93

= (38,25 - 18,25) + (21,64 - 11,64) + 9,93

= 10 + 10 + 9,93 = 29,93

b) 45,28 + 52,17 - 15,28 - 12,17

= (45,28 - 15,28) + (52,17 - 12,17)

= 30 + 40 = 70

c) 72,9 × 99 + 72 + 0,9

= 72,9 × 99 + (72 + 0,9)

= 72,9 × 99 + 72,9

= 72,9 × 99 + 72,9 × 1

= 72,9 × (99 + 1)

= 72,9 × 100 = 7290

d) 0,8 × 96 + 1,6 × 2

= 0,8 × 96 + 0,8 × 2 × 2

= 0,8 × (96 + 2 × 2)

= 0,8 × 100 = 80

Câu 10: Bán một cái quạt máy với giá 336 000 đồng thì được lãi 12% so với tiền vốn. Tính tiền vốn của cái máy quạt đó.

Lời giải:

Giá của chiếc quạt bằng:

100% + 12% = 112% (so với tiền vốn)

Vậy chiếc quạt máy có giá vốn:

336 000 : 112 . 100 = 300 000 (đồng)

Đáp số: 300 000 đồng.

Câu 11: Hình chữ nhật và hình bình hành cùng có những đặc điểm?

Lời giải:

Hình chữ nhật và hình bình hành có chung những đặc điểm sau: Có từng cặp cạnh đối diện song song và bằng nhau.

Nói thêm: Từ nhận xét có thể thấy hình chữ nhật có các đặc điểm của hình bình hành, nên có thể hình chữ nhật là hình bình hành đặc biệt.

Câu 12: May 15 bộ quần áo như nhau hết 45 m vải. Hỏi may 25 bộ quần áo cùng loại hết bao nhiêu mét vải?

Lời giải:

Số mét may 1 bộ quần áo là:

45 : 15 = 3 (m)

Số mét may 25 bộ quần áo là:

3 × 25 = 75 (m)

Đáp số: 75 m .

Câu 13: Chia 129 cho một số ta được số dư là 10. Chia 61 cho số đó ta cũng được số dư là 10. Tìm số chia.

Lời giải:

Gọi số chia là b, theo bài ra ta có:

129 = b.q₁ + 10 ⇒ b.q₁ = 119 = 119.1 = 17.7

(với q₁ là thương)

61 = b.q₂ + 10 ⇒ b.q₂ = 51 = 51.1 = 17.3 (với q₂ là thương và q₂ ≠ q₁)

Vì b > 10 và q₂ ≠ q₁ nên ta có b = 17.

Câu 14: Kiểm tra một sản phẩm của một xưởng may, người ta thấy có 732 sản phẩm đạt chuẩn, chiếm 91,5% tổng số sản phẩm. Tính tổng số sản phẩm.

Lời giải:

Tổng sản phẩm của xưởng đó là:

732 : 91,5 × 100 = 800 (sản phẩm)

Đáp số: 800 sản phẩm.

Câu 15: Một cửa hàng trong một ngày bán được 3 tạ rưỡi gạo. Buổi sáng bán được 1 tạ rưỡi gạo, buổi chiều bán kém buổi tối là 60 kg. Hỏi buổi chiều và buổi tối, mỗi buổi bán được bao nhiêu tạ gạo ?

Lời giải:

Đổi: 3 tạ rưỡi = 350 kg;

1 tạ rưỡi = 150 kg

Buổi chiều và buổi tối bán được số gạo là:

350 - 150 = 200 (kg)

Buổi chiều bán số gạo là:

(200 - 60) : 2 = 70 (kg)

Buổi tối bán số gạo là:

200 - 70 = 130 (kg)

Đổi: 70 kg = 0,7 tạ; 130 kg = 1,3 tạ

Đáp số: Buổi chiều: 0,7 tạ;

   Buổi tối: 1,3 tạ.

Câu 16: Một hình chữ nhật có chiều dài là 150 m, chiều rộng là 90 m được chia thành các hình vuông có diện tích bằng nhau. Tính độ dài cạnh hình vuông lớn nhất trong các cách chia trên (số đo cạnh là số tự nhiên với đơn vị là m).

Lời giải:

Theo đề bài, độ dài các cạnh hình vuông lớn nhất có thể chia là ƯCLN(150, 90).

Ta có 150 = 2 . 3 . 5²; 90 = 2 . 3² . 5.

Do đó ƯCLN(150, 90) = 2.3.5 = 30.

Vậy độ dài cạnh hình vuông lớn nhất trong các cách chia trên là 30 m.

Câu 17: Một thửa ruộng hình chữ nhật có chu vi là 120 m. Tính diện tích thửa ruộng đó nếu biết tăng chiều rộng 5 m và giảm chiều dài 5 m thì thửa ruộng đó thành hình vuông.

Lời giải:

Nếu tăng chiều rộng và giảm chiều dài 5 m thì thửa ruộng đó thành hình vuông, hay là nếu tăng chiều rộng và giảm chiều dài 5 m thì ta được 2 đoạn bằng nhau

Hiệu của chiều dài và chiều rộng của thửa ruộng đó là:

5 + 5 = 10 (m)

Nửa chu vi thửa ruộng đó là:

120 : 2 = 60 (m)

Chiều dài của thửa ruộng đó là:

(60 + 10) : 2 = 35 (m)

Chiều rộng của thửa ruộng là:

(60 - 10) : 2 = 25 (m)

Diện tích của thửa ruộng đó là:

35 × 25 = 875 (m²)

Đáp số: 875 m².

Câu 18: Tìm thương và số dư trong phép chia 9,5 cho 2,35 (phần thập phân của thương lấy đến hai chữ số)

A. 9,5 : 2,35 = 4,04 (dư 6);

B. 9,5 : 2,35 = 4,04 (dư 0,6);

C. 9,5 : 2,35 = 4,04 (dư 0,06);

D. 9,5 : 2,35 = 4,04 (dư 0,006).

Lời giải:

Đáp án đúng là: D

Giải thích: Vì 4,04 × 2,35 = 9,494 mà 9,5 - 9,494 = 0,006.

Câu 19: Tìm 3 số nguyên tố a, b, c sao cho abc = 3(a + b + c).

Lời giải:

Ta có: abc = 3(a + b + c) nên abc chia hết cho 3.

Do a, b, c là các số nguyên tố nên phải có ít nhất 1 số chia hết cho 3.

Giả sử số đó là a, a chia hết cho 3 và a là số nguyên tố nên a = 3

Vậy ta có: 3.b.c = 3.(3 + b + c) ⇔ bc = 3 + b + c ⇔ bc - b - c = 3

⇔ (b - 1)(c - 1) = 4

Vậy b - 1 là ước của 4

b - 1	1	2	4
c - 1	4	2	1
b	2	3	5
c	5	3	2

 Vậy có các số a, b, c thoả mãn là: (a, b, c) = (3, 2, 5) ; (3, 5, 2) ; (3, 3, 3).

Câu 20: Tìm tất cả các bộ ba số nguyên tố a, b, c sao cho abc < ab + bc + ca.

Lời giải:

Vì a, b, c có vai trò như nhau nên giả sử a £ b £ c.

Khi đó: ab + bc + ca £ 3bc

⇔ abc £ 3bc

⇔ a £ 2 ⇒ a = 2 (vì a là số nguyên tố)

Với a = 2, ta có: 2bc < 2b + 2c + bc

⇔ bc < 2(b + c) £ 4c

⇒ b < 4$\Rightarrow \left[\begin{array}{l}b=2\\ b=3\end{array}\right.$

Nếu b = 2 thì 4c < 2 + 4c thoả mãn với c là số nguyên tố bất kì

Nếu b = 3 thì 6c < 6b + 5c suy ra c < 6 vậy c = 3 hoặc c= 5

Vậy các cặp số (a, b, c) cần tìm là (2, 2, p) ; (2, 3, 3) ; (2, 5, 5) và các hoán vị của chúng, với p là số nguyên tố

Câu 21: Tính bằng cách thuận tiện nhất: (72,69 + 18,47) - (8,47 + 22,69).

Lời giải:

(72,69 + 18,47) - (8,47 + 22,69)

= (72,59 + 22,69) + (18,47 - 8,47)

= 50 + 10 = 60.

Câu 22: Mảnh vải thứ nhất dài hơn mảnh vải thứ hai là 3,6 mét. Tỉ số phần hai mảnh vải là 40%. Tính độ dài mỗi mảnh vải.

Lời giải:

Ta có: 40% = $\frac{40}{100}=\frac{2}{5}$.

Hiệu số phần bằng nhau là:

5 - 2 = 3 (phần)

Độ dài của mảnh vải thứ nhất là:

3,6 : 3 × 5 = 6 (m)

Độ dài của mảnh vải thứ hai là:

3.6 : 3 × 2 = 2,4 (m)

Đáp số: Mảnh vải thứ nhất: 6 m;

   Mảnh vải thứ hai: 2,4 m.

Câu 23: Tính bằng cách thuận tiện nhất: 45,28 + 52,17 - 15,18 - 12,17.

Lời giải:

45,28 + 52,17 - 15,18 - 12,17

= (45,28 - 15,18) + (52,17 - 12,17)

= 30 + 40 = 70

Câu 24: Tính bằng cách thuận tiện nhất:

a) [461 + (-78) + 40] + (-461);

b) [53 + (-76)] - [-76 -(-53)];

c) -564 + [(-724) + 564 + 224];

d) -87 + (-12) - (-487) + 512;

e) 942 - 2567 + 2563 - 1942;

f) 17 + (-20) + 23 + (-26) + .... + 53 + (-56);

g) 1152 - (374 + 1152) + (-65 + 374);

h) -2005 + (-21 + 75 + 2005).

Lời giải:

a) [461 + (-78) + 40] + (-461)

= 461 + (-78) + 40 + (-461)

= (461 - 461) + (-78 + 40)

= 0 - 38 = -38.

b) [53 + (-76)] - [-76 -(-53)]

= 53 + (-76) + 76 - (-53)

= [(-76) + 76] + [53 + (-53)]

= 0 + 0 = 0.

c) -564 + [(-724) + 564 + 224]

= -564 + (-724) + 564 + 224   

= (-564 + 564) + (-724 + 224)

= 0 - 500 = -500.

d) -87 + (-12) - (-487) + 512

= -87 + (-12) + 487 + 512

= (-87 + 487) + (-12 + 512)

= 400 + 500 = 900.

e) 942 - 2567 + 2563 - 1942

= (942 - 1942) + (-2567 + 2563)

= -1000 + (-4) = -1004.

f) 17 + (-20) + 23 + (-26) + .... + 53 + (-56)

= [17 + (-20)] + [23 + (-26)] + .... + [53 + (-56)]

= -3 + (-3) + ... + (-3) (7 số -3)

= -3 × 7 = -21.

g) 1152 - (374 + 1152) + (-65 + 374)

= 1152 - 374 - 1152 + -65 + 374

= (1152 - 1152) + (-374 + 374) - 65

= 0 + 0 - 65 = -65.

h) -2005 + (-21 + 75 + 2005)

= -2005 + -21 + 75 + 2005

= (-2005 + 2005) + (-21 + 75)

= 0 + 54 = 54.

Câu 25: Cho hình tam giác ABC có cạnh đáy BC = 15 cm. Nếu kéo dài cạnh đáy 7 cm thì diện tích tăng thêm 38,5 cm². Tính diện tích tam giác ABC.

Lời giải:

Chiều cao của hình tam giác là:

38,5 : 7 = 5,5 (cm)

Diện tích tam giác ABC là:

$\frac{\mathrm{15.5,5}}{2}=\mathrm{41,25}$ (cm²)

Vậy diện tích tam giác ABC là 41,25 cm².

Câu 26: Học sinh khối 6 có 195 nam và 117 nữ tham gia lao động. Thầy phụ trách muốn chia ra thành các tổ sao cho số nam và số nữ ở mỗi tổ đều bằng nhau. Hỏi có thể chia nhiều nhất thành mấy tổ? Mỗi tổ bao nhiêu nam, bao nhiêu nữ?

Lời giải:

Gọi số tổ là a (a Î ℕ*)

Khi đó ta có: 195 ⋮ a, 117 ⋮ a và a lớn nhất

Do đó a là ƯCLN(195, 117)

Ta có 195 = 3.5.13; 117 = 3².13

Do đó a = 3.13 = 39

Vậy có thể chia nhiều nhất 39 tổ, mỗi tổ gồm:

Khi đó, số học sinh nam của tổ đó là: 195 : 39 = 5 (học sinh)

Số học sinh nam của tổ đó là: 117 : 39 = 4 (học sinh)

Vậy có thể chia nhiều nhất 39 tổ, mỗi tổ có 6 học sinh nam và 4 học sinh nữ.

Câu 27: Học sinh khối 6 của một trường có từ 200 đến 300 em. Nếu xếp thành hàng 4, hàng 5 hoặc hàng 7 đều dư 1 em. Tìm số học sinh khối 6 của trường đó.

Lời giải:

Gọi số học sinh khối 6 là x (x Î ℕ*, 200 £ x £ 300)

Nếu xếp thành hàng 4, hàng 5 hoặc hàng 7 đều dư 1 em nên ta có:

• (x - 1) ⋮ 4;

• (x - 1) ⋮ 5;

• (x - 1) ⋮ 7.

Do đó (x - 1) Î BC(4, 5, 7).

Mà BCNN(4, 5, 7) = 2².5.7 = 140.

Suy ra (x - 1) Î BC(4, 5, 7) = B(140) = {0; 280; 420; ...}.

Hay x Î {1; 281; 421; ... } mà 200 £ x £ 300 nên x = 281.

Vậy số học sinh khối 6 là 281 học sinh.

Câu 28: Một can chứa 27 lít dầu cân nặng 21,65 kg. Hỏi sau khi lấy đi 10 lít dầu thì lượng dầu còn lại cân nặng bao nhiêu ki-lô-gam, biết rằng cái can rỗng cân nặng 1,4 kg.

Lời giải:

Số lít dầu trong can cân nặng là:

21,65 - 1,4 = 20,25 (kg)

1 lít dầu cân nặng là:

20,25 : 27 = 0,75 (kg)

10 lít dầu cân nặng là:

0,75 × 10 = 7,5 (kg)

Sau khi lấy đi thì lượng dầu còn lại cân nặng là:

20,25 - 7,5 = 12,75 (kg)

Đáp số: 12,75 kg.

Câu 29: Một người vay 10 000 000 đồng với lãi suất 1% tháng. Hỏi sau 3 tháng người đó phải trả bao nhiêu tiền ? (Biết lãi được nhập vốn để tính lãi tiếp tháng sau).

Lời giải:

Sau 1 tháng số tiền vốn cộng với số tiền lãi so với số tiền vốn ban đầu là:

100% + 1% = 101%.

Sau 1 tháng người đó phải trả số tiền là:

10 000 000 × 101 : 100 = 10 100 000 (đồng)

Sau 2 tháng người đó phải trả số tiền là:

10 100 000 × 101 : 100 = 10 200 000 (đồng)

Sau 3 tháng người đó phải trả số tiền là:

10 200 000 × 101 : 100 = 10 300 000 (đồng)

Đáp số: 10 300 000 đồng.

Câu 30: Một cửa hàng mua về một số nước mắm. Ngày thứ nhất cửa hàng bán được 78 lít nước mắm, chiếm 60% tổng số nước mắm. Ngày thứ hai cửa hàng bán được 42 lít nước mắm. Hỏi sau hai ngày cửa hàng còn lại bao nhiêu lít nước mắm?

Lời giải:

Tổng số lít nước mắm cửa hàng đó là:

78 × 100 : 60 = 130 (lít)

Sau hai ngày cửa hàng còn lại số lít nước mắm là:

130 - 78 - 42 = 10 (lít)

Đáp số: 10 lít nước mắm.

Câu 31: Một người bán một món hàng thu được tiền lãi bằng 15% tiền vốn. Nếu tăng tiền lãi thêm 109 600 đồng thì lúc đó tiền lãi bằng 19% tiền bán. Tính số tiền lãi của người đó.

Lời giải:

Phần trăm mà số tiền 109 600 đồng tương ứng là:

19% - 15% = 4%

Tiền lãi khi tăng thêm là:

109 600 : 4 × 19 = 520 600 (đồng)

Tổng số tiền lãi của người đó là:

109 600 + 520 600 = 630 200 (đồng)

Đáp số: 630 200 đồng.

Câu 32: Tính bằng cách thuận tiện nhất: 45,83 - 8,46 - 7,37.

Lời giải:

45,83 - 8,46 - 7,37

= (45,83 - 7,37) - 8,46

= 38,46 - 8,46 = 30.

Câu 33: Cho 2 đa thức P(x) = x³ - x² - 5x - 8 và Q(x) = x - 3.

a) Tìm thương và dư trong phép chia P(x) cho Q(x).

b) Tìm các giá trị nguyên của x để giá trị của P(x) chia hết cho giá trị của Q(x).

Lời giải:

a) Ta có: (x³ - x² - 5x - 8) : (x - 3) = x² + 2x + 1 + $\frac{-5}{x-3}$

Vậy thương là x² + 2x + 1, dư là - 5.

b) Ta có dư là 1 hằng số ko phụ thuộc vào x

Suy ra không tồn tại x để giá trị P(x) chia hết cho giá trị Q(x).

Câu 34: Cho các đa thức sau: P(x) = x³ + 3x² + 3x - 2 và Q(x) = -x³ - x² - 5x + 2.

a) Tính P(x) + Q(x);

b) Tính P(x) - Q(x);

c) Tìm nghiệm của đa thức H(x) biết H(x) = P(x) + Q(x).

Lời giải:

a) P(x) + Q(x) = x³ + 3x² + 3x - 2 - x³ - x² - 5x + 2 = 2x² - 2x.

b) P(x) - Q(x) = (x³ + 3x² + 3x - 2) -(- x³ - x² - 5x + 2)

= x³ + 3x² + 3x - 2 + x³ + x² + 5x - 2

= 2x³ + 4x² + 8x - 4.

c) Ta có H(x) = 0

⇔ 2x² - 2x = 0

⇔ 2x(x - 1) = 0

$\iff \left[\begin{array}{l}2x=0\\ x-1=0\end{array}\right.$

$\iff \left[\begin{array}{l}x=0\\ x=1\end{array}\right.$

Vậy tập nghiệm của đa thức H(x) là S = {0; 1}.

Câu 35: Tính một cách hợp lí:

a) 112 + (-12) + (-487) + 512;

b) 24 - 4² : 4 . 2 + 3;

c) 21 - 21.[(2 . 9 + 64 : 32) - 52].

Lời giải:

a) 112 + (-12) + (-487) + 512

= 112 - 12 + 512 - 487

= 100 + 25 = 125

b) 24 - 4² : 4 . 2 + 3

= 24 - 16 : 8 + 3

= 24 - 2 + 3

= 22 + 3 = 25.

c) 21 - 21.[(2 . 9 + 64 : 32) - 52]

= 21 - 21 . [(18 + 2) - 52]

= 21 - 21 . (20 - 52)

= 21 - 21 . (-32)

= 21 . [1 - (-32)]

= 21 . 33 = 693.

Câu 36: Tính bằng hai cách: 18,64 - (6,24 + 10,5).

Lời giải:

Cách 1: 18,64 - (6,24 + 10,5)

= 18,64 - 16,74 = 1,9.

Cách 2: 18,64 - (6,24 + 10,5)

= 18,64 - 6,24 - 10,5

= 12,4 - 10,5 = 1,9.

Câu 37: Tính hợp lí: [53 - (-76)] + [-76 - (-53)].

Lời giải:

[53 - (-76)] + [-76 - (-53)]

= (53 + 76) + (-76 + 53)

= 53 + 76 - 76 + 53

= (53 + 53) + (76 - 76)

= 106 + 0 = 106

Câu 38: Tính (phần thập phân của thương lấy đến hai chữ số).

23 : 24

461 : 45

24 : 7,35

32 : 45,6

Lời giải:

23 : 24 = 0,95

461 : 45 = 10,24

24 : 7,35 = 3,26

32 : 45,6 = 0,70

Câu 39: Một trường học dự trữ gạo cho 150 học sinh ăn trong 20 ngày. Nay có 25 học sinh không ăn nữa. Hỏi số gạo đó đủ ăn cho tất cả ăn trong bao nhiêu ngày? (mức ăn của mỗi người như nhau)

Lời giải:

Có tất cả số suất ăn là:

150 × 20 = 3000 (suất)

Vì có 25 học sinh chuyển đi nên còn số học sinh là:

150 - 25 = 125 (học sinh)

Số gạo dự trữ đủ ăn trong số ngày là:

3000 : 125 = 24 (ngày)

Đáp số: 24 ngày

Câu 40: Một đội công nhân có 18 người nhận sửa xong một quãng đường trong 20 ngày. Hỏi muốn làm xong trong 12 ngày thì cần thêm bao nhiêu người?

Lời giải:

Muốn công việc đó làm xong trong 1 ngày thì cần số người là:

18 × 20 = 360 (người)

Muốn công việc đó làm xong trong 12 ngày thì cần số người là:

360 : 12 = 30 (người)

Đội công nhân đó cần thêm số người là :

30 - 18 = 12 (người)

Đáp số: 12 người

Câu 41: Một đội công nhân có 18 người dự định hoàn thành một công việc trong 25 ngày. Sau khi làm được 5 ngày thì đội bổ sung thêm 6 người nữa. Hỏi đội công nhân hoàn thành công việc đó sớm hơn dự định bao nhiêu ngày ? (Sức làm mỗi người như nhau).

Lời giải:

Số ngày còn lại sau khi làm đc 5 ngày là:

25 - 5 = 20 (ngày)

Số người sau khi thêm 6 người là:

18 + 6 = 24 (người)

Số ngày để 1 công nhân làm hết công việc còn lại là:

20 × 18 = 360 (ngày)

Số ngày để 24 công nhân làm hết công việc còn lại là:

360 : 24 = 15 (ngày)

Đội công nhân hoàn thành công việc sớm hơn so với dự định là:

20 - 15 = 5 (ngày)

Đáp số: 5 ngày

Câu 42: Viết các số thập phân gồm:

Ba chục đơn vị, năm phần mười, bảy phần nghìn: ...................

Hai trăm linh ba đơn vị, một trăm sáu mươi bảy phần nghìn: ................................

Không đơn vị, mười tám phần nghìn: ..............................

Năm mươi lăm đơn vị, hai mươi lăm phần trăm: ..................................

Một trăm ba mươi lăm đơn vị, hai mươi lăm phần trăm: ..................................

Một nghìn hai trăm đơn vị, ba mươi bảy phần nghìn: .................................

Sáu đơn vị, chín phần mươi nghìn: ..........................................

Lời giải:

Ba chục đơn vị, năm phần mười, bảy phần nghìn: 30, 507

Hai trăm linh ba đơn vị, một trăm sáu mươi bảy phần nghìn: 203, 167

Không đơn vị, mười tám phần nghìn: 0,018

Năm mươi lăm đơn vị, hai mươi lăm phần trăm: 55,1056

Một trăm ba mươi lăm đơn vị, hai mươi lăm phần trăm: 135,25

Một nghìn hai trăm đơn vị, ba mươi bảy phần nghìn: 1200,037

Sáu đơn vị, chín phần mươi nghìn: 6,0009