Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 105)
Phương pháp giải:
Phân tích thành rồi tính tổng còn lại .
Tổng .
Thay vào biểu thức: và tính kết quả.
Lời giải:
Đặt
Đặt
Vậy:
Câu 2: Chứng minh rằng: A = không là số chính phương với mọi n thuộc N*
Phương pháp giải:
Số chính phương là số bằng bình phương của một số tự nhiên (ví dụ 0, 1, 4, 9, 16, ...).
Tính chữ số tận cùng của từng lũy thừa trong biểu thức .
Tìm chữ số tận cùng của tổng dựa trên các chữ số tận cùng đã tính.
Lời giải:
luôn có chữ số tận cùng là 6, luôn có chữ số tận cùng là 1, luôn có chữ số tận cùng là 6, luôn có chữ số tận cùng là 5.
luôn có chữ số tận cùng là 8.
Mà số chính phương không bao giờ có chữ số tận cùng là 8
A không phải là số chính pơng.
Câu 3: Cho . Chứng minh rằng trong ba số a, b, c tồn tại hai số bằng nhau?
Phương pháp giải:
Quy đồng phân số về dạng cùng mẫu số.
Phân tích đa thức thành nhân tử và kết luận.
Lời giải:
=> a = b hoặc b = c hoặc a = c (dpcm)
Câu 4: a. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3
b. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Phương pháp giải:
Phần a: Sử dụng bất đẳng thức cơ bản và phân tích biểu thức.
Đầu tiên, áp dụng bất đẳng thức để suy ra .
Sau đó, thêm điều kiện để suy ra các giá trị lớn nhất và nhỏ nhất của biểu thức .
Cuối cùng, xác định khi .
Phần b: Sử dụng cách biểu diễn để đưa ra kết luận.
Phân tích biểu thức và tiếp tục áp dụng bất đẳng thức cho các biểu thức liên quan.
Kết luận dựa trên bất đẳng thức, và cuối cùng là rút ra kết quả mong muốn.
Lời giải:
a. Với mọi a;b ta có:
khi
b.
Do
Mà
Mặt khác với mọi a;b ta có:
Từ đó:
khi .
a) Tính diện tích hinh thang ABCD.
b) So sánh diện tích hai tam giác AOD và BOC.
c) So sánh OA và OC.
Phương pháp giải:
a) Áp dụng công thức tính diện tích hình thang:
Thay giá trị của , , và vào để tính diện tích.
b) Kẻ AH vuông góc với DC; BK vuông góc với DC và chứng minh thông qua trung gian.
c) Theo cách làm câu b sẽ tìm so sánh được OA và OC
Lời giải:
a: Độ dài đáy lớn là 5,2*2=10,4(cm)
Diện tích hình thang ABCD là:
b: Kẻ AHDC; BKDC
=> AH//BK
Xét tứ giác ABKH có:
AB // KH
AH // BK
Do đó: ABKH là hình bình hành
=> AH = BK(1)
Vì ΔADC có AH là đường cao
nên
Vì ΔBDC có BK là đường cao
nên
Từ (1), (2), (3) suy ra
Vì AB // CD
nên
OA/OC=1/2 nên
=>
Vì OB/OD = 1/2 nên
=>
Từ (4), (5), (6) suy ra
c) Vì
nên OA < OC
Câu 6: Khi nào dùng suy ra và khi nào dùng tương đương?
Phương pháp giải:
Nêu lí do khi nào có thể dùng tương đương hoặc suy ra.
Lời giải:
+ Dấu tương đương được dùng trong khi mình suy ra được và suy ngược lại được. Hay nói cách khác là tương đương với nhau.
+ Dấu suy ra được dùng khi một mệnh đề hoặc kết quả có thể được rút ra từ một mệnh đề hoặc kết quả khác, nhưng không đảm bảo rằng điều ngược lại là đúng
Mở rộng:
Dùng "suy ra" khi chỉ muốn kết luận một chiều và không đảm bảo rằng kết luận ngược lại cũng đúng.
Dùng "tương đương" khi hai mệnh đề hoặc kết quả liên hệ chặt chẽ, đảm bảo rằng cả hai đều có thể rút ra từ nhau.
Câu 7: a. Giải hệ phương trình:
b. Rút gọn biểu thức:
B = với x > 0; x4
Phương pháp giải:
a) Tính x theo y, thay vào phương trình dưới tìm y. Sau đó tìm x.
b) Quy đồng đưa về cùng mẫu và tối giản biểu thức đó.
Lời giải:
a) Ta có:
b) Ta có:
Phương pháp chung:
Phương pháp giải hệ phương trình:
Phương pháp 1: Phương pháp thế.
Bước 1: Từ một phương trình của hệ đã cho (coi là phương trình thức nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy để thay thế cho phương trình thức hai trong hệ (phương trình thứ nhất cũng thường được thay thế bởi hệ thức biểu diễn một ẩn theo ẩn kia có được ở bước 1).
Bước 3: Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ đã cho.
Bước 4: Kết luận.
Phương pháp 2: Phương cộng đại số.
Bước 1: Nhân hai vế của mỗi phương trình với một số thích hợp( nếu cần) sao cho các hệ số của một ẩn nào đó( ẩn x hay y) trong hai phương trình của hệ bằng nhau hoặc đối nhau.
Bước 2: Cộng hay trừ từng vế hai phương trình của hệ phương trình đã cho để được một phương trình mới
Bước 3: Dùng phương trình mới ấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia)
Bước 4: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.
Bước 5: Kết luận
Phương pháp 3: Phương đặt ẩn phụ.
Bước 1: Đặt điều kiện của phương trình.
Bước 2: Đặt ẩn phụ, điều kiện của ẩn phụ. Đưa hệ ban đầu về hệ mới.
Bước 3: Giải hệ mới tìm ẩn phụ.
Bước 4: Thay giá trị vào ẩn phụ tìm x và y.
Bước 5: Kết luận.
Phương pháp rút gọn biểu thức:
Bước 1: Vận dụng thích hợp các phép tính và các phép biến đổi đã biết làm xuất hiện căn thức cùng loại;
+ Đưa thừa số A2 ra ngoài dấu căn: với B ≥ 0;
+ Đưa thừa số vào tròn dấu căn: 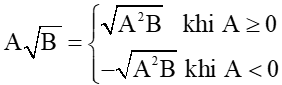
+ Khử căn ở mẫu: với B ≠ 0, AB ≥ 0;
+ Trục căn thức ở mẫu: ; .
Bước 2: Cộng, trừ, các căc thức bậc hai cùng loại.
Phương pháp giải:
- Bước 1: Đưa các phân số về dạng tối giản. Phân số tối giản (hay phân số không rút gọn được nữa) là phân số mà tử và mẫu chỉ có ước chung là 1 và -1.
- Bước 2: Áp dụng quy tắc cộng, trừ và các tính chất để tính
● Quy tắc cộng, trừ: Đưa các số hữu tỉ về cùng mẫu (quy đồng, rút gọn,…) rồi cộng, trừ tử số, giữ nguyên mẫu số.
● Tính chất:
Tính chất giao hoán: x + y = y + x
Tính chất kết hợp: (x + y) + z = x + (y + z)
Tính chất cộng với 0: x + 0 = 0 + x = x
- Bước 3: Rút gọn kết quả (nếu có thể)
Lời giải:
Phương pháp giải:
Đặt là nhân tử chung của bài toán.
Tính tổng số hạn trong ngoặc.
Lời giải:
Phương pháp giải
Tử số bằng hiệu hai thừa số ở mẫu số. Ta tách như sau:
Ví dụ:
Câu 10: Cho hình thang cân ABCD có AB song song với CD và AB < CD biết AD = AB
a) Chứng minh AB = BC
b) Chứng minh DB là phân giác ADC
Phương pháp giải:
a. Chứng minh thông qua AD.
b. Chứng minh góc ADB = góc CDB
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
Lời giải:
a/
ABCD là hình thang cân => AD = BC
Mà AD = AB (gt)
=> AB = BC
b/
ABCD là hình thang cân
(Hai góc trong cùng phía)
=> ABCD là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bù nhau là tứ giác nt)
Ta có
Cung AB và cung BC có hai dây trương cung bằng nhau
AB = BC (cmt) => sđ cung AB = sđ cung BC (1)
(góc nội tiếp) (2)
(góc nội tiếp) (3)
Từ (1) (2) (3) => DB là phân giác của
Theo bạn chiều rộng và chiều dài của lá cờ có thể bao nhiêu mét?
Phương pháp giải:
Gọi chiều dài của lá cờ là (m) và chiều rộng là (m).
Ta biết rằng diện tích của lá cờ là mét vuông.
Theo đề bài, chiều rộng bằng chiều dài, tức là .
Lời giải:
Ta có: gọi A,B lần lượt là chiều dài, chiều rộng của lá cờ đó
Vì diện tích lá cờ bằng 54cm2 => A x B = 54
Mà chiều rộng bằng chiều dài => B = A
Thay vào ta được: A x A = 54
<=> A2 = 81 <=> A = 9(cm) => B = 6(cm)
Vậy chiều dài bằng 9cm, chiều rộng bằng 6cm
Phương pháp giải:
Tách thành 2 phân số .
Rút gọn 2 phân số và tính toán.
Lời giải:
A =
A =
A =
A =
Câu 13: Tìm số nguyên n biết: 2n + 13 là bội của n + 1
Phương pháp giải:
Bài toán yêu cầu tìm sao cho là bội của . Ta có , nên phải là ước của 11. Các ước của 11 là 1 và 11, suy ra hoặc .
Lời giải:
2n + 13 là bội của n + 1
=> ( 2n + 13 ) ( n+ 1 )
Ta có: ( 2n+13 ) = [ 2(n+1 ) + 11 ]
mà 2(n+1 ) ( n+1)
Để ( 2n+13 ) ( n+1 ) thì => 11 ( n+ 1 )
hay n+ 1 thuộc ước của 11
Ư(11) = { 1;11 }
Ta có bảng sau
n+1 1 11
n 0 10
Vậy n { 0;10 }
Câu 14: Cho x; y là 2 số dương thỏa mãn x + y = 1. CMR:
Phương pháp giải:
Áp dụng BDT Cauchy:
Với hai số thực không âm ta có a+b≥2√ab. Dấu bằng xảy ra khi và chỉ khi a = b.
Lời giải:
(*)
Áp dụng BĐT cauchy cho 2 số > 0 và > 0 ta đc:
(**)
Từ (*),(**) =>
Vậy với x + y = 1 thì
Câu 15: Biến đổi thành tổng biểu thức sau: 4sin3x.sin2x.cosx
Phương pháp giải:
Áp dụng công thức biến đổi tích thành tổng
![\begin{aligned}
&\cos a \cdot \cos b=\frac{1}{2}[\cos (a+b)+\cos (a-b)] \\
&\sin a \cdot \sin b=-\frac{1}{2}[\cos (a+b)-\cos (a-b)] \\
&\sin a \cdot \cos b=\frac{1}{2}[\sin (a+b)+\sin (a-b)]
\end{aligned}](https://o.rada.vn/data/image/blank.png)
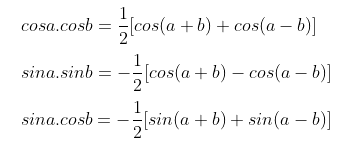
Lời giải:
Câu 16: Tìm x: 5.x + 3.(10 - x) + x = 45
Phương pháp giải:
Phân phối và giản ước các hạng tử trong phương trình
Gom các hạng tử có chứa lại với nhau
Giải phương trình đơn giản
Lời giải:
5x + 3.(10 - x) + x = 45
5x + 30 - 3x + x = 45
5x - 3x + x = 45 - 30
x.(5 - 3 + 1) = 15
=> 3x = 15
=> x =15 : 3
=> x = 5
Câu 17: Chứng minh a2 + b2 + c2 lớn hơn hoặc bằng ab + bc + ca với mọi số a, b, c
Phương pháp giải:
Bước 1: Viết lại bất đẳng thức cần chứng minh dưới dạng hiệu giữa hai biểu thức.
Bước 2: Đưa biểu thức vào dạng tổng các bình phương.
Bước 3: Kết luận
Lời giải:
a2 + b2 + c2 ≥ ab + bc + ac (1)
Xét hiệu
a2 + b2 + c2 - ab - bc - ac ≥ 0
<=> 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ac ≥ 0
<=> (a2 - 2ab + b2) + (b2 - 2bc + c2) + (c2 - 2ac + a2) ≥ 0
<=> (a - b)2 + (b - c)2 + (c - a)2 ≥ 0 (luôn đúng với mọi a,b,c)
=> (1) đccm
Phương pháp giải:
Đưa các phân số về cùng mẫu số.
Đưa về dạng biểu thức không có mẫu rồi tìm x.
Lời giải:
ĐKXĐ :
Ta có :
Vậy ...
Câu 19: Cho . Chứng minh rằng A chia hết cho 13
Phương pháp giải:
Biến đổi tổng thành các nhóm ba số liên tiếp. Nhận thấy mỗi nhóm có yếu tố chung , ta rút ra ngoài yếu tố 13. Do đó, , chứng tỏ chia hết cho 13.
Lời giải:
Câu 20: Cho . Chứng tỏ S không phải là số tự nhiên
Phương pháp giải:
Biểu diễn dưới dạng tổng của các phân số.
Chứng minh rằng tổng các phần tử này không phải là một số tự nhiên:
là một tổng của các phân số với các mẫu số khác nhau, và các phân số này không thể rút gọn thành một số nguyên duy nhất.
Ngoài ra, do các phần tử trong tổng là các số phân số có phần thập phân không bằng 0, tổng của chúng sẽ không phải là một số tự nhiên.
Lời giải:
+, Ta thấy:
Suy ra:
(1)
+, Lại có:
Suy ra:
(2)
Từ (1) và (2)
S không phải là số tự nhiên
Câu 21: So sánh: A = 333444 và B = 444333
Phương pháp giải:
Tách 2 số về dạng mũ 111 và 111n
So sánh hai số đó và kết luận.
Lời giải:
Ta có :
Vì và
nên
Vậy
Câu 22: Tìm các số nguyên x và y biết : x . y = -15
Phương pháp giải:
Ta tìm ước của -15 và kẻ bảng các trường hợp.
Lời giải:
Ta có :
là ước của -15
Ta có bảng :
Vậy
Phương pháp giải:
Gọi số cần tìm là , với là phần số khi bỏ chữ số tận cùng.
Sử dụng điều kiện để thiết lập phương trình.
Giải phương trình và tìm số .
Lời giải:
Gọi số tự nhiên đó là abc3 ; nếu bỏ chữ số tận cùng thì số mới là abc
Ta có
abc3 - abc = (1000a + 100b + 10c + 3) - (100a + 10b + c)
=> 900a + 90b + 9c + 3 = 1992
=> 900a + 90b + 9c = 1989
=> 9(100a + 10b + c) = 1989
=> 100a + 10b + c = 221
=> abc = 221
=> abc3 = 2213
Vậy số đó là 2213
Câu 24: Tìm tất cả các số nguyên dương x, y, z thỏa mãn : và
Phương pháp giải:
Thiết lập phương trình: Ta có hệ phương trình . Gọi là giá trị chung của các biểu thức này và lập các phương trình tương ứng.
Giải hệ phương trình: Giải các phương trình bậc nhất theo , , và để tìm các giá trị thỏa mãn.
Kiểm tra điều kiện : Sau khi có các giá trị , , và , kiểm tra xem các giá trị này có thỏa mãn điều kiện trên không.
Lời giải:
mà
Vì z là số nguyên dương
mà y là số nguyên dương và
Thế vào và
+) Với
Với
Vậy ta có các cặp nghiệm là:
a, Tính vận tốc dự định và quãng đường AB
b, Nếu sau khi đi được 1h , do có công việc người ấy phải ghé lại 30 phút . Hỏi đoạn đường còn lại người ấy phải đi với vận tốc bao nhiêu để đến nơi như đự định
Phương pháp giải:
Thiết lập phương trình: Gọi là vận tốc dự định, lập phương trình về thời gian đi từ A đến B theo hai đoạn đường với vận tốc đã thay đổi.
Giải hệ phương trình để tìm và quãng đường .
Giải quyết tình huống ở câu b: Tính vận tốc cần thiết để bù đắp thời gian đã mất khi nghỉ giữa chừng.
Lời giải:
Đổi 2 giờ 10 phút = 2 (giờ)
Vì là chuyển động thẳng đều theo dự định nên đi quãng đường sẽ hết 2 giờ
Nhưng sau đó tăng tốc lên 3km/giờ thì quãng đường hết
2 (2 - )
Ta có phương trình:
Vận tốc dự định*2 = (V dự định+3)*(2 - )(do chúng đều = S/2)
=> Vận tốc dự định =15km/h
=> Quãng đường = 60km
b) Người đó đi với vận tốc 15km/h.
<=> Đi 1h được 15 km còn 60 -15 = 45 (km)
Nếu dự định là 4h thi thời gian còn lại là: (giờ)
=> Vận tốc là 45 : 2.5=18 (km/giờ)
a) 9x2 +y2 + 2z2 – 18x +4z – 6y +20 = 0
b) 5x2 +5y2 +8xy+2y – 2x+2 = 0
c) 5x2 +2y2 + 4xy – 2x + 4y +5 = 0
d) x2 + 4y2 + z2 =2x + 12y – 4z – 14
e) x2 +y2 – 6x + 4y +2= 0
Phương pháp giải:
Đưa về hằng đẳng thức đáng nhớ:
(A + B)2 = A2 + 2AB + B2
(A – B)2 = A2 – 2AB + B2
Lời giải:
PT vô nghiệm vì 11 không phải là tổng 2 số chính phương
Câu 27: Tìm x: x [(- 2x)2+ 5x] = 16
Phương pháp giải:
Mở ngoặc và sắp xếp lại phương trình để đưa về dạng phương trình bậc hai.
Rút gọn và sắp xếp phương trình theo và .
Giải phương trình bậc hai tìm nghiệm .
Lời giải:
Vậy
Phương pháp giải:
Tính nửa chu vi của hình chữ nhật.
Từ đó tính được chiều dài và chiều rộng của hình chữ nhật.
Tìm diện tích bằng công thức chiều dài nhân chiều rộng.
Lời giải:
Nửa chu vi hình chữ nhật là :
60 : 2 = 30 (m)
Chiều dài hình chữ nhật là :
24 x 2 : 2 = 24 (m)
Chiều rộng hình chữ nhật là :
30 - 24 = 6 (m)
Diện tích hình chữ nhật là :
24 x 6 = 144 (m2)
Đáp số : 144 m2
Câu 29: Điền vào chỗ trống: 4m2 5dm2 = .......... dm2
Phương pháp giải:
Đổi đơn vị: Chuyển tất cả về đơn vị .
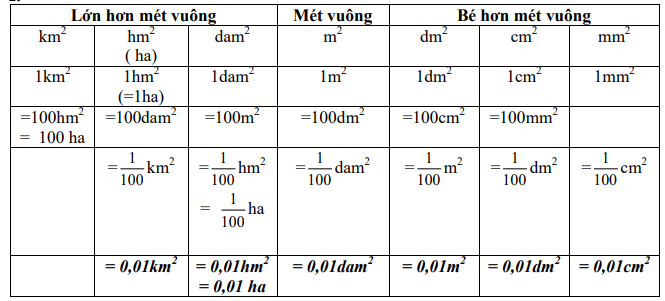
Nhận xét:
- Mỗi đơn vị đo diện tích gấp 100 lần đơn vị bé hơn tiếp liền.
- Mỗi đơn vị đo diện tích bằng đơn vị lớn hơn tiếp liền.
Tính tổng: Cộng các diện tích sau khi đã quy đổi.
Lời giải:
4m2 5dm2 = 405 dm2
Câu 30: Một ô tô có công suất 75kW
a.Tính công do ô tô thực hiện trong 1,5 giờ
b.Biết xe chuyển động với vận tốc 10m/s.Tính lực kéo của động cơ
Phương pháp giải:
Đổi đơn vị.
Sử dụng công thức sau:
Công thức tính công của dòng điện.
A = Pt = UIt
Trong đó: U đo bằng vôn (V),
I đo bằng ampe (A),
t đo bằng giây (s),
A của dòng điện đo bằng jun (J).
Công Suất Của Lực Kéo
Công suất (P) = Lực kéo (F) x Vận tốc (v)
Trong đó:
Lực kéo (F): đơn vị Newton (N)
Vận tốc (v): đơn vị mét trên giây (m/s)
Công suất (P): đơn vị Watt (W)
Lời giải:
1,5 h = 5400s
75 kW = 75000W
Công là
Lực kéo là