Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 53)

Câu 1: Xác định a, b, c biết parabol y = ax² + bx + c đi qua điểm A(8; 0) và có đỉnh là I(6; −12).

Lời giải:

+ Parabol y = ax² + bx + c đi qua điểm A(8; 0)

⇒ 0 = a.8² + b.8 + c ⇒ 64a + 8b + c = 0 (1).

+ Parabol y = ax² + bx + c có đỉnh là I (6; –12) suy ra:

$\frac{-b}{2a}=6\Rightarrow b=-12a$ (2).

$\frac{-\Delta }{4a}=-12\Rightarrow \Delta =48a\Rightarrow b^2-4ac=48a$ (3) .

Thay (2) vào (1) ta có: 64a − 96a + c = 0 ⇒ c = 32a.

Thay b = −12a và c = 32a vào (3) ta được:

(−12a)² − 4a.32a = 48a

⇒ 144a² − 128a² = 48a

⇒ 16a² = 48a

⇒ a = 3 (vì a ≠ 0).

Từ a = 3 ⇒ b = −36 và c = 96.

Vậy a = 3; b = −36 và c = 96.

Câu 2: Biết giá bán 1 kg cam cao hơn 10% so với giá 1 kg xoài. Hỏi giá 1 kg xoài thấp hơn giá 1 kg cam bao nhiêu %.

2²²²

Lời giải:

Vì 1 kg cam cao hơn 10% so với giá 1 kg xoài

Do đó giá 1 kg xoài thấp hơn giá 1 kg cam 10%

Đáp số: 10%.

Câu 3: Bạn Hoa ra chợ mua hoa quả. Giá tiền 1 kg Cam hơn giá 1 kg Ổi là 17 000 đồng. Bạn Hoa đã mua 3 kg Cam và 8 kg Ổi, tổng cộng hết 139 000 đồng. Em hãy tính giùm bạn Hoa xem mỗi kg trái cây có giá bao nhiêu tiền?

2²²²

Lời giải:

Gọi x (đồng) là giá tiền 1 kg cam (0 < x < 17 000)

Do đó x − 17 000 là giá tiền 1 kg ổi

Ta lập được phương trình: 3x + 8(x − 17 000) = 139 000

⇔ 3x + 8x − 136 000 = 139 000

⇔ 11x = 275 000

⇔ x = 25 000 (TMĐK)

Suy ra giá tiền 1 kg ổi là:

 25 000 − 17 000 = 8 000 (đồng)

Vậy 1 kg cam có giá 25 000 đồng; 1 kg ổi có giá 8 000 đồng.

Câu 4: Một tàu hỏa cần chở 920 hành khách đi du lịch. Biết rằng mỗi toa có 10 khoang, mỗi khoang có 5 chỗ ngồi. Hỏi cần ít nhất bao nhiêu toa để chở hết số hành khách đi du lịch.

Lời giải:

Số người mỗi toa có là:

5.10 = 50 (người)

Ta có: 920 : 50 = 18 (dư 20)

Nên cần thêm 1 toa nữa để chở hết 20 người còn lại.

Vậy cần ít nhất: 18 + 1 = 19 (toa)

Câu 5: Dấu hiệu chia hết cho 2, 3, 5, 9, 4, 8, 25, 125, 11.

Lời giải:

- Dấu hiệu chia hết cho 2: Các số có chữ số tận cùng chia hết cho 2.

- Dấu hiệu chia hết cho 5: Có chữ số tận cùng là 0 hoặc 5.

- Dấu hiệu chia hết cho 3: Tổng các chữ số chia hết cho 3.

- Dấu hiệu chia hết cho 9: Tổng các chữ số chia hết cho 9.

- Dấu hiệu chia hết cho 4: Hai chữ số tận cùng chia hết cho 4.

- Dấu hiệu chia hết cho 25: Hai chữ số tận cùng chia hết cho 25.

- Dấu hiệu chia hết cho 8: Ba chữ số tậ cùng chia hết cho 8.

- Dấu hiệu chia hết cho 125: Ba chữ số tận cùng chia hết cho 125.

- Dấu hiệu chia hết cho 11: Tổng accs chữ số hàng lẻ bằng tổng các chữ số hàng chẵn.

Câu 6: Trên mặt phẳng Oxy cho 2 điểm A(−2; −2) và B(5; −4).

a) Tìm tọa độ trọng tâm của tam giác OAB.

b) Tìm tọa độ điểm C sao cho tam giác ABC có trọng tâm là điểm G(2; 0).

 Lời giải:

a) Trọng tâm G có tọa độ

 $\left\{\begin{array}{l}x=\frac{x_O+x_A+x_B}{3}=1\\ y=\frac{y_O+y_A+y_B}{3}=-2\end{array}\right.$

Vậy G(1; −2).

b) Gọi C(x_C; y_C) là tọa độ điểm C thì ta có:

 $\left\{\begin{array}{l}\frac{x_C-2+5}{3}=2\\ \frac{y_C-2-4}{3}=0\end{array}\right.\iff \left\{\begin{array}{l}{x}_C=3\\ y_C=6\end{array}\right.$

Vậy C(3; 6)

Câu 7: Cho a, b, c là 3 cạnh của tam giác ABC. Biết a³(b − c) + b³(c − a) + c³(a − b) = 0. Chứng minh: tam giác ABC cân.

Lời giải:

a³(b − c) + b³(c − a) + c³(a − b) = 0

⇔ a³b − a³c + b³c − ab³ + c³(a − b) = 0

⇔ a³b − a³c + b³c − ab³ + c³(a − b) = 0

⇔ ab(a² − b²) − c(a³ − b³) + c³(a − b) = 0

⇔ ab(a − b)(a + b) − c(a − b)(a² + ab + b²) + c³(a − b) = 0

⇔ (a − b)[ab(a + b) − c(a² + ab + b²) + c³] = 0

⇔ (a − b)[ab(a + b) − c(a² + ab + b²) + c³] = 0

⇔ (a − b)[ab(a + b) − ac(a + b) + b²c + c³] = 0

⇔ (a − b)[a(a + b)(b − c) − c(b² − c²)] = 0

⇔ (a − b)[a(a + b)(b − c) − c(b − c)(b + c)] = 0

⇔ (a − b)(b − c)[a(a + b) − c(b + c)] = 0

⇔ (a − b)(b − c)[(a² − c²) + (ab − bc)] = 0

⇔ (a − b)(b − c)[(a − c)(a + c) + b(a − c)] = 0

⇔ (a − b)(b − c)(a − c)(a + b + c) = 0

⇒ (a − b)(b − c)(a − c) = 0

 $\Rightarrow \left[\begin{array}{l}a-b=0\\ b-c=0\\ a-c=0\end{array}\right.\iff \left[\begin{array}{l}a=b\\ b=c\\ a=c\end{array}\right.$

Vậy ABC là tam giác cân.

Câu 8: Cho a + b + c = 0. Chứng minh: a³ + b³ + c³ = 3abc.

Lời giải:

a + b + c = 0

⇒ (a + b + c)³ = 0

⇔ a³ + b³ + c³ + 3a²b + 3ab² + 3b²c + 3bc² + 3a²c + 3ac² + 6abc = 0

⇔ a³ + b³ + c³ + (3a²b + 3ab² + 3abc) + (3b²c + 3bc² + 3abc) + (3a²c + 3ac² + 3abc) − 3abc = 0

⇔ a³ + b³ + c³ + 3ab(a + b + c) + 3bc(a + b + c) + 3ac(a + b + c) = 3abc

Do a + b + c = 0

⇒ a³ + b³ + c³ = 3abc (đpcm)

Câu 9: Có bao nhiêu số tự nhiên có 3 chữ số khác nhau. Biết tổng của 3 chữ số này là 18.

Lời giải:

Gọi số tự nhiên có 3 chữ số là $\overline{abc}\left(a\ne 0;a\ne b\ne c\right)$ .

Theo đề, ta có a + b + c = 18

⇒ (a; b; c) = {(1; 8; 9); (2; 7; 9); (3; 6; 9); (4; 5; 9); (3; 7; 8); (4; 6; 8); (5; 6; 7)}.

Vậy số tự nhiên có 3 chữ số mà tổng bằng 18 là 7.3! = 42 (số).

Câu 10: Tìm nghiệm của  đa thức: D(x) = 2x² − 13x + 15.

Lời giải:

Xét phương trình D(x) = 2x² − 13x + 15 = 0

⇔ 2x² − 10x − 3x + 15 = 0

⇔ 2x(x − 5) − 3(x − 5) = 0

⇔ (2x − 3)(x − 5) = 0

 $\iff \left[\begin{array}{l}2x-3=0\\ x-5=0\end{array}\right.\iff \left[\begin{array}{l}x=\frac{3}{2}\\ x=5\end{array}\right.$

Vậy nghiệm của phương trình là  $x=\frac{3}{2};x=5.$

Câu 11: Dùng hệ thức Vi-ét để tìm nghiệm x₂ của phương trình rồi tìm giá trị của m trong mỗi trường hợp sau: Phương trình x² + mx − 35 = 0 có nghiệm  x₁ = 7.
Lời giải:

Theo hệ thức Vi-ét, ta có:

 $\left\{\begin{array}{l}{x}_1+x_2=-m\\ x_1.x_2=-35\end{array}\right.\iff \left\{\begin{array}{l}7+x_2=-m\\ 7x_2=-35\end{array}\right.\iff \left\{\begin{array}{l}m=-7+5=-2\\ x_2=-5\end{array}\right.$

Vậy m = −2 là giá trị thỏa mãn.

Câu 12: Tính A = cos² 10° + cos² 20° + ... + cos² 70° + cos² 80°.

Lời giải:

A = cos² 10° + cos² 20° + ... + cos² 70° + cos² 80°

= sin² 80° + sin² 70° + sin² 60° + sin² 50° + cos² 50° + cos² 60°  + cos² 70° + cos² 80°

= (sin² 80° + cos² 80°) + (sin² 70° + cos² 70°) + (sin² 60° + cos² 60°) + (sin² 50° + cos² 50°)

= 1 + 1 + 1 + 1 = 4

Câu 13: Rút gọn biểu thức: cos² 10° + cos² 20° + cos² 30° + ... + cos² 180°.

Lời giải:

Ta có: cos x = − cos (180° − x) ⇒ cos² x = cos² (180° − x)

sin x = cos (90° − x)

sin² x + cos² x = 1

A = cos² 10° + cos² 20° + cos² 30° + ... + cos² 180°

= cos² 10° + cos² 20° + cos² 30° + ... + cos² 180°

= cos² 10° + cos² 20° + ... + cos² 80° + cos² 90° + cos² 80° + cos² 70° + ... + cos² 0°

= cos² 0° + cos² 90° + 2(cos² 10° + cos² 20° + ... + cos² 80°)

= 1 + 0 + 2(cos² 10° + cos² 20° + cos² 30° + cos² 40° + sin² 40° + sin² 30° + sin² 20° + sin² 10°)

= 1 + 0 + 2 . 4 = 9.

Câu 14: Từ các chữ số 0, 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau?

Lời giải:

Gọi số tự nhiên có 5 chữ số khác nhau cần tìm có dạng:

 $\overline{abcde}\left(a\ne b\ne c\ne d\ne e,a\ne 0\right)$

Lập số có 5 chữ số phân biệt bất kì: 5! cách

Lập số 5 chữ số phân biệt trong đó số 0 đứng đầu: 4! cách

⇒ Có 5! − 4! = 96 số thỏa mãn

Câu 15: Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên có 5 chữ số?

Lời giải:

Gọi số tự nhiên có 5 chữ số khác nhau cần tìm có dạng: $\overline{abcde}\left(a\ne 0\right)$

Lập số a có 5 cách

Lập số b có 6 cách

Lập số c có 6 cách

Lập số d có 6 cách

Lập số e có 6 cách

⇒ Có 5.6.6.6.6 = 6 480 số thỏa mãn

Câu 16: 7% của 100 là bao nhiêu?

Lời giải:

7% của 100 là:

100 : 100 × 7 = 7

Đáp số: 7.

Câu 17: Trong mặt phẳng tọa độ Oxy cho 4 điểm A(0; 1); B(1; 3); C(2; 7) và D(0; 3). Tìm giao điểm của 2 đường thẳng AC và BD.

Lời giải:     

Phương trình đường thẳng đi qua hai điểm A(0; 1); C(2; 7) có dạng:

 $\frac{x}{2}=\frac{y-1}{6}\iff 3x-y=-1$

Phương trình đường thẳng đi qua hai điểm B(1; 3) và D(0; 3) có dạng:

y = 3

Giao điểm của 2 đường thẳng AC và BD có tọa độ là nghiệm của hệ phương trình:

 $\left\{\begin{array}{l}3x-y=-1\\ y=3\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{2}{3}\\ y=3\end{array}\right.$

Vậy $I\left(\frac{2}{3};3\right)$  là điểm cần tìm.

Câu 18: Cho 4 điểm A(1; 2) và B(−1; 4); C(2; 2); D(−3; 2). Tìm tọa độ giao điểm của 2 đường thẳng AB và CD.

Lời giải:     

Phương trình đường thẳng đi qua hai điểm A(1; 2) và B(−1; 4) có dạng:

 $\frac{x-1}{-2}=\frac{y-2}{2}\iff x+y=3$

Phương trình đường thẳng đi qua hai điểm C(2; 2); D(−3; 2) có dạng:

y = 2

Giao điểm của 2 đường thẳng AB và CD có tọa độ là nghiệm của hệ phương trình:

 $\left\{\begin{array}{l}x+y=3\\ y=2\end{array}\right.\iff \left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$

Vậy I(1; 2) là điểm cần tìm

Câu 19: Vẽ hai đường thẳng xy và zt cắt nhau tại O. Lấy A thuộc tia Ox, B thuộc tia Ot, C thuộc tia Oy, D thuộc tia Oz sao cho OA = OC = 3cm, OB = 2cm, OD = 2OB.

Lời giải:

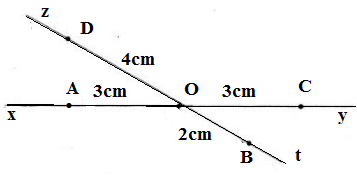
Các bạn vẽ hình theo các bước:

• Vẽ hai đường thẳng xy và zt cắt nhau tại O

• Trên đường thẳng xy:

Lấy A thuộc tia Ox, lấy C thuộc tia Oy sao cho OA = OC = 3 cm.

• Trên đường thẳng zt:

+ Lấy B thuộc tia Ot sao cho OB = 2 cm

+ Lấy D thuộc tia Oz sao cho OD = 2OB = 2 . 2 = 4 (cm).

Câu 20: Giải phương trình: sin 5x − sin 3x + sin 8x = 0

Lời giải:

sin 5x − sin 3x + sin 8x = 0

⇔ 2cos 4x.sin x + 2sin 4x.cos 4x = 0

⇔ 2cos 4x(sin x + sin 4x) = 0

 $$\begin{gathered} \iff 4\cos 4x.\sin \frac{5x}{2}\cos \frac{3x}{2}=0 \\ \iff \left[\begin{array}{l}\cos 4x=0\\ \sin \frac{5x}{2}=0\\ \cos \frac{3x}{2}=0\end{array}\right. \\ \iff \left[\begin{array}{l}4x=\frac{\pi }{2}+k\pi \\ \frac{5x}{2}=k\pi \\ \frac{3x}{2}=\frac{\pi }{2}+k\pi \end{array}\right. \\ \iff \left[\begin{array}{l}x=\frac{\pi }{8}+\frac{k\pi }{4}\\ x=\frac{k2\pi }{5}\\ x=\frac{\pi }{3}+\frac{k2\pi }{3}\end{array}\right. \end{gathered}$$

Vậy $x=\frac{\pi }{8}+\frac{k\pi }{4},x=\frac{k2\pi }{5},x=\frac{\pi }{3}+\frac{k2\pi }{3}\left(k\in \mathbb{Z}\right)$

Câu 21: Một kho gạo có 246,75 tấn gạo người ta chuyển đi $\frac{4}{5}$  số gạo của kho. Hỏi kho còn lại bao nhiêu ki lô gam gạo?

Lời giải:

Người ta đã chuyển đi số tấn gạo là:

$\mathrm{246,75}\times \frac{4}{5}=\mathrm{197,4}$ (tấn)

Trong kho còn lại số tấn gạo là:

246,75 − 197,4 = 49,35 (tấn)

Đáp số: 49,35 tấn gạo

Câu 22: Một kho chứa 246,75 tấn gạo. Người ta chuyển đến một số lượng gạo bằng $\frac{3}{5}$  số gạo hiện có của kho. Hỏi kho đó có tất cả bao nhiêu kg gạo?

Lời giải:

Người ta đã chuyển đến số tấn gạo là:

$\mathrm{246,75}\times \frac{3}{5}=\mathrm{148,05}$ (tấn)

Trong kho còn lại số tấn gạo là:

246,75 + 148,05 = 394,8 (tấn) = 394 800 (kg)

Đáp số: 394 800 kg gạo.

Câu 23: Chứng tỏ giá trị biểu thức sau không phụ thuộc vào biến:

(x + y + z)² + (x − y)² + (x − z)² + (y − z)² − 3(x² + y² + z²)

Lời giải:

(x + y + z)² + (x − y)² + (x − z)² + (y − z)² − 3(x² + y² + z²)

= x² + y² + z² + 2xy + 2yz + 2zx + x² − 2xy + y² + x² − 2xz + z² + y² + y² − 2yz + z² − 3(x² + y² + z²)

= 3(x² + y² + z²) − 3(x² + y² + z²) = 0

Vậy biểu thức trên không phụ thuộc vào biến.

Câu 24: Rút gọn biểu thức: (x + 1)² − (x − 1)² − 3(x + 1)(x − 1).

Lời giải:

(x + 1)² − (x − 1)² − 3(x + 1)(x − 1)

= (x + 1 + x − 1)(x + 1 − x + 1) − 3(x² − 1)

= 2x . 2 − 3x² + 3

= −3x² + 4x + 3

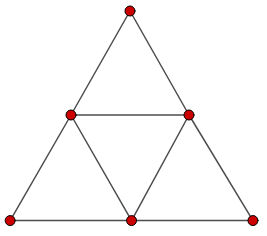
Câu 25: Vẽ 5 hình tam giác có 9 que diêm.

Lời giải:

Từ 9 que diêm vẽ được 5 hình tam giác như sau:

Câu 26: Giải phương trình: x³ − 6x² + 5x + 12 = 0.

Lời giải:

x³ − 6x² + 5x + 12 = 0

⇔ x³ + x² − 7x² − 7x + 12x + 12 = 0

⇔ x²(x + 1) − 7x(x + 1) + 12(x + 1) = 0

⇔ (x + 1)(x² − 7x + 12) = 0

⇔ (x + 1)(x² − 4x − 3x + 12) = 0

⇔ (x + 1)[x(x − 4) − 3(x − 4)] = 0

⇔ (x + 1)(x − 4)(x − 3) = 0

 $\Rightarrow \left[\begin{array}{l}x+1=0\\ x-4=0\\ x-3=0\end{array}\right.\iff \left[\begin{array}{l}x=-1\\ x=4\\ x=3\end{array}\right.$

Vậy tập nghiệm của phương trình là S = {−1; 3; 4}.

Câu 27: Sắp xếp các số đo khối lượng: 1 kg 512 g; 1 kg 5 hg; 1 kg 51 dag; 10 hg;  50 g theo thứ tự từ bé đến lớn.

Lời giải:

Đổi: 1 kg 512 g = 1512 g;

1 kg 5 hg = 1500 g;

1 kg 51 dag = 1510 g;

10 hg = 100 g.

Vì 50 g < 100 g < 1500 g < 1510 g < 1512 g.

Sắp xếp các số đo khối lượng theo thứ tự từ bé đến lớn là: 

50 g, 100 g, 1500 g, 1510 g, 1512 g.

Hay 50 g, 10 hg, 1kg 5hg, 1 kg 51 hg, 1 kg 512 g.

Vậy sắp xếp các số đo khối lượng theo thứ tự từ bé đến lớn là: 

50 g, 10 hg, 1kg 5hg, 1 kg 51 hg, 1 kg 512 g.

Câu 28: Điền số thích hợp vào chỗ chấm: 10 hg 5g = ..... g

Lời giải:

Ta có 10 hg = 1 000 g

Suy ra 10 hg 5g = 1 005 g.

Câu 29: Tính sin² 20° + sin² 30° + sin² 40° + sin² 50° + sin² 60° + sin² 70° + sin² 36° + sin² 54° − 2tan 25°.tan 65°.

Lời giải:

sin² 20° + sin² 30° + sin² 40° + sin² 50° + sin² 60° + sin² 70° + sin² 36° + sin² 54° − 2tan 25°.tan 65°

= (sin² 20° + sin² 70°) + (sin² 30° + sin² 60°) + (sin² 40° + sin² 50°) + (sin² 36° + sin² 54°)  − 2tan 25°.tan 65°

= (sin² 20° + cos² 20°) + (sin² 30° + cos² 30°) + (sin² 40° + cos² 40°) + (sin² 36° + cos² 36°)  − 2tan 25°.cot 25°

= 1 + 1 + 1 + 1 − 2.1 = 2

Câu 30: Hãy tính biểu thức sau: A = 2.sin 30° − 2.cos60° + tan 45°.

Lời giải:

A = 2.sin 30° − 2.cos60° + tan 45°

$=2.\frac{1}{2}-2.\frac{1}{2}+1=1$.

Câu 31: Cho A = [−4; 7], B = (−∞; −2) ∪ (3; +∞). Tìm A ∩ B.

Lời giải:

Ta có: A = [−4; 7], B = (−∞; −2) ∪ (3; +∞)

Do đó A ∩ B = [−4; −2) ∪ (3; 7].

Vậy A ∩ B = [−4; −2) ∪ (3; 7].

Câu 32: Cho tam giác ABC cân tại A, M là trung điểm của BC. ME vuông góc với AB, MF vuông góc với AC. Chứng minh AM là trung trực của BC.

Lời giải:

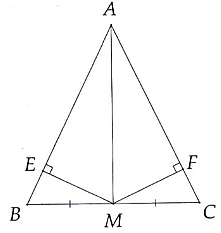
ΔABC cân tại A nên AB = AC

M là trung điểm của BC nên MB = MC

⇒ AM là đường trung trực của BC (tính chất đường trung trực của đoạn thẳng)

Vậy AM là đường trung trực của BC.

Câu 33: Chứng minh rằng a⁵ – a chia hết cho 30.

Lời giải:

a⁵ – a = a(a⁴ – 1) = a(a² – 1)(a² + 1) = a(a – 1)(a + 1)(a² – 4 + 5)

= a(a – 1)(a + 1)(a² – 4) + 5a(a – 1)(a + 1)

= a(a – 1)(a + 1)(a – 2)(a + 2) + 5a(a – 1)(a + 1)

Do a(a – 1)(a + 1)(a – 2)(a + 2) là tích 5 số nguyên liên tiếp nên tồn tại 1 số chia hết cho 2; 1 số chia hết cho 3 và 1 số chia hết cho 5

⇒ a(a – 1)(a + 1)(a – 2)(a + 2) chia hết cho 30

Mặt khác, a(a – 1)(a + 1) là tích 3 số nguyên liên tiếp nên a(a – 1)(a + 1) chia hết cho 6

⇒ 5a(a – 1)(a + 1) chia hết cho 30

⇒ a(a – 1)(a + 1)(a – 2)(a + 2) + 5a(a – 1)(a + 1) chia hết cho 30

Vậy a⁵ – a chia hết cho 30.

Câu 34: Đoạn đường AB dài 1km gồm hai đoạn AM và MB. Đoạn AM = $\frac{2}{3}$ đoạn MB. Hãy tính độ dài của đoạn đường MB.

Lời giải:

Đổi: 1 km = 1000 m

Ta có sơ đồ:

$\frac{2}{3}$

Độ dài đoạn đường  MB là:

1000 : (2 + 3) × 3 = 600 (m)

Đáp số: 600 m

Câu 35: Câu Tìm trung bình cộng của các số 10; 30; 50; 70.

Lời giải:

Trung bình cộng của 4 số đó là:

(10 + 30 + 50 + 70) : 4 = 40

Đáp số: 40

Câu 36: Tìm trung bình cộng của dãy số sau: 14; 20; 26; 32; … ; 86.

Lời giải:

Số số hạng của dãy số trên là:

(86 – 14) : 6 + 1 = 13 (số)

Tổng của dãy số trên là:

(14 + 86) × 13 : 2 = 650

Trung bình cộng của dãy số trên là:

650 : 13 = 50

Đáp số: 50

Câu 37: Có bao nhiêu cách sắp xếp 20 thí sinh vào một phòng thi có 20 bàn mỗi bàn một thí sinh.

Lời giải:

Mỗi cách xếp 20 thí sinh vào 20 vị trí của một phòng thi là một hoán vị của 20 phần tử,

Số cách xếp là:

P₂₀ = 20! (cách)

Vậy có 20! cách sắp xếp thoả mãn đề bài.

Câu 38: Cho A là tập hợp các học sinh lớp 10 đang học ở trường em và B là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Hãy diễn đạt bằng lời các tập hợp sau: A ∪ B; A ∩ B; A \ B; B \ A.

Lời giải:

A ∪ B: tập hợp các học sinh hoặc học lớp 10 hoặc học môn Tiếng Anh của trường em.

A ∩ B: tập hợp các học sinh lớp 10 học môn Tiếng Anh của trường em.

A \ B: tập hợp các học sinh học lớp 10 nhưng không học môn Tiếng Anh của trường em.

B \ A: tập hợp các học sinh học môn Tiếng Anh của trường em nhưng không học lớp 10 của trường em.

Câu 39: Cho hai tập hợp:

A = {1; 3}

B = {1; 2}

Tìm A ∪ B ; A ∩ B ; A \ B ; B \ A.

Lời giải:

Ta có: A = {1; 3} và B = {1; 2}

A ∪ B={1; 2; 3}

A ∩ B = {1}

A \ B = {3}

B \ A = {2}

Câu 40: Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh giỏi Toán và Lý, 5 học sinh giỏi Hoá và Lý, 4 học sinh giỏi Toán và Hoá, 3 học sinh giỏi cà 3 môn. Hỏi số học sinh giỏi ít nhất 1 môn trong 3 môn là bao nhiêu em?

Lời giải:

Theo giả thiết đề bài cho, ta có biểu đồ Ven:

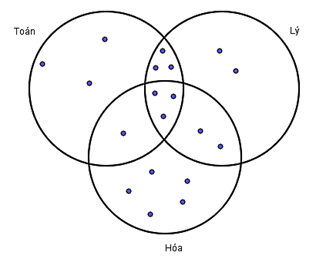
Dựa vào biểu đồ Ven ta thấy:

Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: 

6 – 3 = 3 (em)

Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: 

4 – 3 = 1 (em)

Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là: 

5 – 3 = 2 (em)

Số học sinh chỉ giỏi một môn Toán là: 

10 – 3 – 3 – 1 = 3 (em)

Số học sinh chỉ giỏi một môn Lý là: 

10 – 3 – 3 – 2 = 2 (em)

Số học sinh chỉ giỏi một môn Hóa là: 

11 – 1 – 3 – 2 = 5 (em)

Số học sinh giỏi ít nhất một trong ba môn là:

3 + 2 + 5 + 1 + 2 + 3 + 3 =19 (em)

Đáp số: 19 em

Câu 41: Có 40 học sinh giỏi, mỗi em giỏi ít nhất 1 môn. Có 22 em giỏi Văn, 25 em giỏi Toán, 20 em giỏi Anh. Có 8 em giỏi đúng hai môn Văn, Toán. Có 7 em giỏi đúng hai môn Toán, Anh. Có 6 em giỏi đúng hai môn Anh, Văn. Hỏi có bao nhiêu em giỏi cả ba môn Văn, Toán, Anh?

Lời giải:

Ta có sơ đồ Ven:

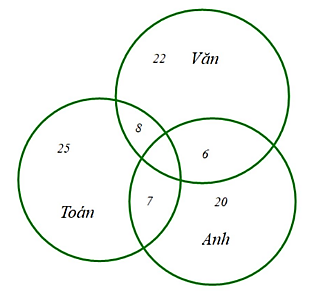
Số học sinh giỏi ít nhất hai môn là:

7 + 6 + 8 = 21 (em)

Vậy số học sinh giỏi cả ba môn Toán, Văn, Anh là:

22 + 25 + 20 – 40 – 21 = 6 (em)

Đáp số: 6 em.

Câu 42: Giải phương trình: cos² 3x = 1.

Lời giải:

cos² 3x = 1

⇔ sin² 3x = 0

⇔ sin 3x = 0

$$\begin{gathered} \iff 3x=k\pi (k\in \mathbb{Z}) \\ \iff x=\frac{k\pi }{3}(k\in \mathbb{Z}) \end{gathered}$$

Vậy $x=\frac{k\pi }{3}(k\in \mathbb{Z})$.

Câu 43: Tìm x, biết: 4^{2x – 3} = 2¹⁴.

Lời giải:

4^{2x – 3} = 2¹⁴

4^{2x – 3} = (2²)⁷

4^{2x – 3} = 4⁷

⇔ 2x – 3 = 7

⇔ 2x = 10

⇔ x = 5

Vậy x = 5.

Câu 44: Xác định các tập hợp A ∪ B và A ∩ B với: A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím}.

Lời giải:

Tập A ∪ B = {đỏ; cam; vàng; lục; lam; chàm; tím}.

Các phần tử vừa thuộc tập hợp A và B là: lục; lam.

Do đó A ∩ B = {lục; lam}.

Vậy A ∪ B = {đỏ; cam; vàng; lục; lam; chàm; tím} và A ∩ B = {lục; lam}.

Câu 45: Xác định các tập hợp A ∪ B và A ∩ B với: A là tập hợp các tam giác đều, B là tập hợp các tam giác cân.

Lời giải:

Vì mọi tam giác đều là tam giác cân nên tập A là tập hợp con của B.

Khi đó A ∪ B = B và A ∩ B = A.

Vậy A ∪ B = B và A ∩ B = A.

Câu 46: Cho a + b + c = 0. Chứng minh a³ + b³ + c³ = 3abc.

Lời giải:

Từ giả thiết a + b + c = 0

⇒ c = −(a + b), thay vào đẳng thức cần chứng minh ta được 

a³ + b³ − (a + b)³ = −3ab(a + b)

⇔ −3ab² − 3a²b = −3ab² − 3a²b

Vậy a³ + b³ + c³ = 3abc.

Câu 47: Cho A = (2; +∞), B =  (m; +∞). Điều kiện cần và đủ của m sao cho B là tập con của A là.

Lời giải:

Ta có: B Ì A ⇔ (m; +∞) Ì (2; +∞)

Do đó ∀x ∈ B

⇒ x ∈ A

⇒ m ³ 2.

Câu 48: Tìm tập hợp A giao B biết A = (–1; +∞) và B = (1; 2).

Lời giải:

Ta có:

• A Ç B = {x ∈ ℝ | 1 < x < 2}.

• A È B = {x ∈ ℝ | x > –1}.

Câu 49: Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm. Tính BH, CH.

Lời giải:

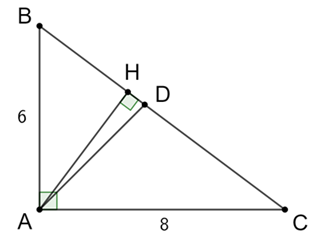
Áp dụng hệ thức lượng trong tam giác vuông, ta có:

AB² = BA.BC

⇔ 6² = BH.10

⇔ BH = 3,6 cm

⇒ HC = BC − BH = 10 − 3,6 = 6,4 (cm)

Vậy BH = 3,6 cm, HC = 6,4 cm.

Câu 50: Cho tập hợp A={0; 1; 2; 3; 4; 5}. Có thể lập bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau?

Lời giải:

Số tự nhiên thỏa mãn có dạng $\overline{abcd}$  với a, b, c, d ∈ A  và đôi một khác nhau.

Trường hợp 1: d = 0

Có 5 cách chọn a; 4 cách chọn b và 3 cách chọn c nên theo quy tắc nhân có  5.4.3 = 60 số.

Trường hợp 2: d ≠ 0 ; d có 2 cách chọn là 2, 4

Khi đó có 4 cách chọn a (vì a khác 0 và khác d); có 4 cách chọn b và 3 cách chọn c.

Theo quy tắc nhân có: 2.4.4.3 = 96 số

Có tất cả số số là: 96 + 60 = 156 (số)

Vậy có 156 số.