Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 32)

Câu 1: Tính tổng: A = 1 + 3 + 5 + 7 + … + (2n – 1)

Lời giải:

Ta thấy A chính là tổng số của các số lẻ.

Áp dụng công thức:

Tổng của dãy số cách đều = [(số hạng đầu + số hạng cuối). số các số hạng] : 2.

Từ đó, ta tính tổng của A như sau:

A = [(1 + 2n − 1) . n] : 2 = (2n . n) : 2 = 2n² : 2  = n².

Câu 2: Số 46 có phải số chính phương không?

Lời giải:

Ta có số 46 chia hết cho 2.

Nhưng không chia hết cho 2² = 4 nên suy ra số 46 không phải là số chính phương.

Câu 3: Với mọi số tự nhiên n thì a_n = n(n + 1)(n + 2)(n + 3) + 1 là số chính phương.

Lời giải:

Ta có: a_n  =  n(n + 1)(n + 2)(n + 3) + 1

= n(n + 3)(n + 1)(n + 2) + 1

= (n² + 3n)(n²  + 3n + 2) + 1

= (n²  + 3n)²  + 2(n²  + 3n) + 1

= (n² + 3n + 1)².

Với n là một số tự nhiên thì (n² + 3n + 1)² cũng sẽ là một số tự nhiên.

Vậy nên a_n là một số chính phương.

Câu 4: Có 8 viên bi giống nhau. Trong đó có 7 viên có trọng lượng bằng nhau, một viên có khối lượng khác. Nêu cách tìm ra viên bi có khối lượng khác đó với số lần cân bi nhỏ nhất.

Lời giải:

Cần tối thiểu 3 lần cân để xác định viên bi có khối lượng khác.

Chia đều 8 viên bi vào 2 mặt cân lấy bên nặng hơn.

Chia đều 4 viên bi nặng hơn vào 2 mặt cân lấy bên nặng hơn.

 Chia đều 2 viên bi nặng hơn vào 2 mặt cân lấy bên nặng hơn.

Viên bi đó chính là viên có khối lượng khác.

Câu 5: Cho dãy số 4; 7; 10; 13; 16;....

a) Tìm số thứ 100 của dãy.

b) Tính tổng của 100 số hạng đầu tiên của dãy.

Lời giải:

a) Khoảng cách giữa các số trong dãy số là 3 đơn vị.

Suy ra ta có: u_n = u_n-1 + 3 = u₁ + (n – 1).3

Số thứ 100 là: 3 ´ (100 − 1) + 4 = 301

b) Ta có tổng 100 số hạng đầu tiên của dãy số:

 4 + 7 + 10 + ... + 301 = (301 + 4) ´ 100 : 2 = 15 250

Đáp số: a) 301

b) 15 250

Câu 6: Hãy cho biết có tất cả bao nhiêu số tự nhiên có 2 chữ số nhỏ hơn 68?

Lời giải:

Số số tự nhiên có 2 chữ số nhỏ hơn 68 là:

(67 – 10) + 1 = 58 (số)

Đáp số: 58 số.

Câu 7: Có 15 công nhân dự định làm công việc trong 20 ngày. Sau khi làm được 6 ngày có 5 người phải chuyển đi nơi khác. Hỏi họ cần mấy ngày nữa để làm xong công việc đó?

Lời giải:

Một công nhân có thể hoàn thành công việc trong số ngày là:

15 x 20 = 300 (ngày)

Sau 6 ngày số công việc đã làm được là:

15 x 6 = 90 (ngày)

Số người còn lại sau khi đi bớt:

15 – 5 = 10 (người)

Vậy số ngày cần để hoàn thành xong công việc là:

(300 – 90) : 10 = 21 (ngày)

Đáp số: 21 ngày.

Câu 8: Một kho chứa 672 bao, mỗi bao chứa 50 kg thóc.Người ta lấy đi $\frac{1}{7}$ số thóc đó. Hỏi người ta đã lấy đi bao nhiêu tạ thóc?

Lời giải:

Trong kho có tất cả số ki-lô-gam thóc là:

672 x 50 = 33 600 (kg)

Người ta lấy đi số ki-lô-gam thóc là:

$33600\times \frac{1}{7}=4800$ (kg)

Đáp số: 4800 kg.

Câu 9: Một liên đội thiếu niên khi xếp hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người. Tính số đội viên của liên đội biết rằng số đội viên khoảng từ 100 đến 150?

Lời giải:

Gọi số đội viên là a. (100 ≤ a ≤ 150)

Ta có: a chia 2; 3; 4; 5 đều dư 1 suy ra  (a – 1) chia hết cho 2; 3; 4; 5 

⇒ a − 1 ∈ BC(2, 3, 4, 5)

Mà BCNN(2, 3, 4, 5) = 60 

⇒ (a – 1) ∈ B(60) = {0; 60; 120; 180; 240....} (*)

Theo bài cho:

100 ≤ a ≤ 150

⇒101 ≤ a −1 ≤ 151

Kết hợp với (*) ta có: 

a – 1 = 120

⇒a = 121.

Vậy số đội viên của đội là 121 người.

Câu 10: Kết quả của phép chia: (6xy² + 4x²y – 2x³) : 2x là:

A. 3y² + 2xy – x²;

B. 3y² + 2xy + x²;

C. 3y² – 2xy – x²;

D. 3y² + 2xy.

Lời giải:

Đáp án đúng là: A

(6xy² + 4x²y – 2x³) : 2x

= 6xy² : 2x + 4x²y : 2x – 2x³ : 2x

=  3y² + 2xy – x²

Câu 11: Rút gọn biểu thức: Q = (2x + 3y)(4x² – 6xy + 9y²)

Lời giải:

Q = (2x + 3y)(4x² – 6xy + 9y²)

= (2x + 3y)[(2x)² – 2x.3y + (3y)²]

= (2x)³ + (3y)³

Câu 12: Tìm 25% của 300.

Lời giải:

25% của 300 là:

300 x 25 : 100 = 75

Đáp số: 75.

Câu 13: Xếp các số thập phân sau theo thứ tự từ bé đến lớn: 8,09; 8,9; 8,89; 8,8.

Lời giải:

Thứ tự từ bé đến lớn của các số thập phân: 8,09; 8,8; 8,89; 8,9.

Câu 14: Số hạng tiếp theo của dãy số:

a) 1,2; 0,36; 0,108; 0,0324; ....

b) 1,2; 2,4; 7,2; 28,8;.....

Lời giải:

a) Quy luật của dãy số là: u_n = u_{n – 1} . 0,3

 Vậy số hạng tiếp theo của dãy số là:

0,0324. 0,3 = 0,00972.

b) Quy luật của dãy số là: u_n = u_{n – 1} . n

 Vậy số hạng tiếp theo của dãy số là:

28,8. 5 = 144.

Câu 15: Phân tích đa thức thành nhân tử: x⁴ + 6x³ + 7x² – 6x + 1.

Lời giải:

x⁴ + 6x³ + 7x² – 6x + 1

= x⁴ + 6x³ + 9x² – 2x² – 6x + 1

= (x²)² + 2x².3x + (3x)² – 2.(x² + 3x) + 1

= (x² + 3x)² – 2(x² + 3x).1 + 1²

= (x² + 3x – 1)²

Câu 16: Rút gọn biểu thức: P = 12.(5² + 1)(5⁴ + 1)(5⁸ + 1)(5¹⁶ + 1).

Lời giải:

Ta có: (5² – 1).P = (5² – 1).12.(5² + 1)(5⁴ + 1)(5⁸ + 1)(5¹⁶ + 1)

= 12.(5² – 1)(5² + 1)(5⁴ + 1)(5⁸ + 1)(5¹⁶ + 1)

= 12.(5⁴ – 1)(5⁴ + 1)(5⁸ + 1)(5¹⁶ + 1)

= 12.(5⁸ – 1)(5⁸ + 1)(5¹⁶ + 1)

= 12.(5¹⁶ – 1)(5¹⁶ + 1)

= 12.(5³² – 1)

Câu 17: Chứng minh rằng: 35x – 14y + 2⁹ – 1 chia hết cho 7.

Lời giải:

Ta có: 35x – 14y + 2⁹ – 1

= 35x – 14x + 511

= 7(5x – 2y + 73) ⁝ 7 ∀x, y ∈ ℝ (đpcm)

Câu 18: Cho tam giác ABC. Gọi H là trực tam của tam giác. Chứng minh rằng: AH² + BC² = BH² + AC²

Lời giải:

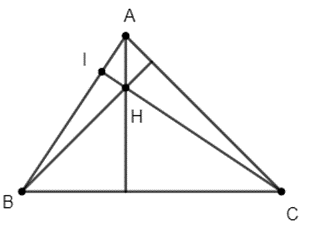
Gọi I là giao điểm của CH và AB.

Áp dụng định lý Py-ta-go cho các tam giác vuông ∆AHI, ∆BHI, ∆ACI, ∆BCI ta có:

AH² = AI² + HI² ⇒ AH² – AI² = HI²

BH² = IH² + BI² ⇒ BH² – BI² = IH²

AC² = AI² + IC² ⇒ AC² – AI² = IC²

BC² = BI² + IC² ⇒ BC² – BI² = IC² 

Suy ra:

AH² – AI² = BH² – BI² (1)

AC² – AI² = BC² – BI² (2)

Trừ (2) cho (1) ta được:

AC² – AH² = BC² – BH²

⇒ AH² + BC² = BH² + AC² (đpcm)

Câu 19: Cho f(x) = ax³ + 4x(x² – x) – 4x + 8; g(x) = x³ – 4x(bx + 1) + c – 3

Trong đó a, b, c là hằng số. Xác định a, b, c để f(x) = g(x).

Lời giải:

Ta có: f(x) = ax³ + 4x(x² – x) – 4x + 8

= (a + 4)x³ − 4x² – 4x + 8

g(x) = x³ – 4x(bx + 1) + c – 3

= x³ – 4bx² – 4x + c – 3

Để f(x) = g(x) thì:

$\left\{\begin{array}{l}a+4=1\\ -4=-4b\\ 8=c-3\end{array}\right.\iff \left\{\begin{array}{l}a=-3\\ b=1\\ c=11\end{array}\right.$

Vậy a = −3; b = 1; c = 11.

Câu 20: Một mảnh vườn hình chữ nhật có chiều dài 60 m, chiều rộng bằng $\frac{3}{5}$ chiều dài. Tính chu vi và diện tích mảnh vườn đó.

Lời giải:

Chiều rộng của mảnh vườn hình chữ nhật là:

$60\times \frac{3}{5}=36\left(m\right)$

 Chu vi của mảnh vườn hình chữ nhật là:

(60 + 36) x 2 = 192 (m)

Diện tích của mảnh vườn hình chữ nhật là:

60 x 36 = 2160 (m²)

Đáp số: 192 m; 2160 m².

Câu 21: Một mảnh vườn có chu vi là 120 m. Chiều dài hơn chiều rộng 20 m. Tính diện tích mảnh vườn.

Lời giải:

Nửa chu vi của mảnh vườn là:

120 : 2 = 60 (m)

Chiều dài của mảnh vườn là:

(60 + 20) : 2 = 40 (m)

Chiều rộng của mảnh vườn là:

40 – 20 = 20 (m)

Diện tích của mảnh vườn là:

40 x 20 = 800 (m²)

Đáp số: 800 m²

Câu 22: Một căn phòng ngủ hình chữ nhật cần lát gạch có chiều dài 8 m. Chiều rộng bằng $\frac{3}{4}$ chiều dài. Để lát kín căn phòng đó người ta dùng loại gạch men hình vuông cạnh 4 dm. Hỏi để lát kín căn phòng người ta cần dùng bao nhiêu viên gạch?

Lời giải:

Chiều rộng căn phòng hình chữ nhật là:

$8\times \frac{3}{4}=6\left(m\right)$

Diện tích căn phòng hình chữ nhật là:

8 x 6 = 48 (m²)

Đổi: 48 m² = 4800 dm²

Diện tích viên gạch men hình vuông là:

4 x 4 = 16 (dm²)

Số viên gạch để lát kín căn phòng là:

4800 : 16 = 300 (viên)

Đáp số: 300 viên gạch

Câu 23: Một căn phòng khách hình chữ nhật của nhà Mai có tỉ số giữa chiều dài và chiều rộng là $\frac{4}{3}$. Chiều dài hơn chiều rộng 2 m. Người ta lát nền căn phòng đó bằng loại gạch hình vuông cạnh 2 dm. Vậy để lát kín căn phòng cần bao nhiêu viên gạch?

Lời giải:

Ta có sơ đồ:

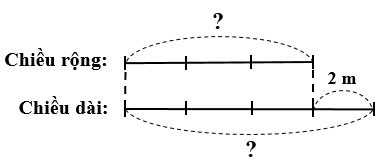
Hiệu số phần bằng nhau là:

4 – 3 = 1 (phần)

Chiều dài căn phòng là:

2 : 1 x 4 = 8 (m)

Chiều rộng căn phòng là:

8 – 2 = 6 (m)

Diện tích căn phòng là:

8 x 6 = 48 (m²)

Diện tích viên gạch là:

2 x 2 = 4 (dm²)

Đổi 48 m² = 4800 dm²

Số viên gạch cần để lát kín căn phòng là:

4800 : 4 = 1200 (viên)

Đáp số: 1200 viên gạch

Câu 24: Một viên gạch có dạng hình hộp chữ nhật có chiều dài 22 cm, chiều rộng 10 cm, chiều cao 5,5 cm. Tính diện tích xung quanh và diện tích toàn phần của khối gạch dạng hình hộp chữ nhật do 6 viên gạch xếp thành 3 hàng, mỗi hàng 2 viên.

Lời giải:

Trường hợp 1: Xếp mỗi hàng 2 viên gạch sao cho chiều dài không đổi.

Chiều rộng khối gạch là:

10 x 2 = 20 (cm)

Chiều cao khối gạch là:

5,5 x 3 = 16,5 (cm)

Diện tích xung quanh khối gạch là:

(22 + 20) x 2 x 16,5 = 1386 (cm²)

Diện tích toàn phần của khối gạch là:

1386 + 22 x 20 x 2 = 2266 (cm²)

Trường hợp 2: Xếp mỗi hàng 2 viên gạch sao cho chiều rộng không đổi.

Chiều dài khối gạch là:

22 x 2 = 44 (cm)

Chiều cao khối gạch là:

5,5 x 3 = 16,5 (cm)

Diện tích xung quanh khối gạch là:

(44 + 10) x 2 x 16,5 = 1782 (cm²)

Diện tích toàn phần của khối gạch là:

1782 + 44 x 10 x 2 = 2662 (cm²)

Đáp số: Trường hợp 1: 1386 cm²; 2266 cm²

             Trường hợp 2: 1782 cm²; 2662 cm²

Câu 25: Tính diện tích xung quanh của hình hộp chữ nhật có chiều dài 5 m, chiều rộng 3 m, chiều cao 4,5 m.

Lời giải:

Chu vi mặt đáy là:

(5 + 3) x 2 = 16 (m)

Diện tích xung quanh là:

16 x 4,5 = 72 (m²)

Đáp số:  72 m²

Câu 26: Trong một phép trừ biết tổng của số bị trừ, số trừ và hiệu bằng 7652 và hiệu số lớn hơn số trừ 798. Tìm số bị trừ, số trừ, hiệu của phép trừ đó?

Lời giải:

Số bị trừ là:

7652 : 2 = 3826

Tổng của số trừ và hiệu bằng 3826.

Ta có sơ đồ:

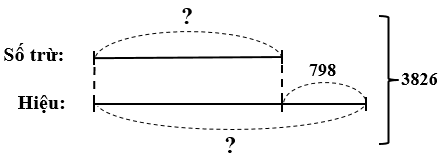
Hiệu là:

(3826 + 798) : 2 = 2312

Số trừ là:

3826 – 2312 = 1514

Đáp số: 3826; 1514; 2312

Câu 27: Trong một phép trừ biết tổng của số bị trừ, số trừ và hiệu bằng 2000. Tìm số bị trừ và số trừ trong phép tính đó, biết rằng số trừ lớn hơn hiệu là 200.

Lời giải:

Số bị trừ là:

2000 : 2 = 1000

Tổng của số trừ và hiệu bằng 1000.

Ta có sơ đồ:

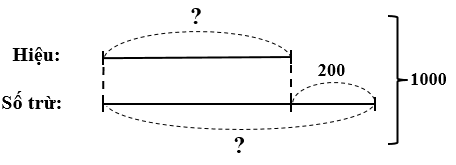
Số trừ là:

(1000 + 200) : 2 = 600

Hiệu là:

1000 – 600 = 400

Đáp số: 1000; 600; 400

Câu 28: Tìm số tự nhiên a bé nhất trong các số 1, 2, 3, 4 sao cho 3 nhân a lớn hơn 6.

Lời giải:

Thay a lần lượt bằng 1, 2, 3, 4 vào biểu thức 3 ´ A > 6

Chọn a = 1 ta được 3 x 1 = 3 < 6

Chọn a = 2 ta được 3 x 2 = 6

Chọn a = 3 ta được 3 x 3 = 9 > 6

Chọn a = 4 ta được 3 x 4 = 12 > 6

Vậy số tự nhiên a bé nhất thỏa mãn yêu cầu bài toán là 3.

Câu 29: Tìm số tự nhiên x bé nhất trong các số 4, 5, 6, 7, 8 sao cho 0,5 nhân x nhỏ hơn 4.

Lời giải:

Thay x lần lượt bằng 4, 5, 6, 7, 8 vào biểu thức 0,5 . x < 4

Chọn x = 4 ta được 0,5 . 4= 2 < 4

Chọn x = 5 ta được 0,5 . 5 = 2,5 < 4

Chọn x = 6 ta được 0,5 . 6 = 3 < 4

Chọn x = 7 ta được 0,5 . 7 = 3,5 < 4

Chọn x = 8 ta được 0,5 . 8 = 4

Vậy số tự nhiên x bé nhất thỏa mãn yêu cầu bài toán là 4.

Câu 30: Phân tích đa thức thành nhân tử:  A = xyz + xz – yz –  z + xy + x – y – 1.

Lời giải:

A = xyz + xz – yz – z + xy + x – y – 1

= z(xy + x – y – 1) + (xy + x – y – 1)

= (z + 1)(xy + x – y – 1)

= (z + 1)[x(y + 1) – (y + 1)]

= (z + 1)(y + 1)(x – 1)

Vậy A = (z + 1)(y + 1)(x – 1)

Câu 31: Tính giá trị biểu thức B với x = 11; y = 19; z = 29. B = xyz + xz – yz –  z + xy + x – y – 1.

Lời giải:

B = xyz + xz – yz –  z + xy + x – y – 1

= z(xy + x – y – 1) + (xy + x – y – 1)

= (z + 1)(xy + x – y – 1)

= (z + 1)[x(y + 1) – (y + 1)]

= (z + 1)(y + 1)(x – 1)

Thay x = 11; y = 19; z = 29 ta có:

B = (29 + 1)(19 + 1)(9 – 1)

= 30. 20. 10

= 600. 10

= 6000

Vậy B = 6000

Câu 32: Một ô tô trung bình mỗi giờ đi được 40 km. Hỏi trong 4 giờ ô tô đi được bao nhiêu km?

Lời giải:

Số km mà ô tô đi được trong 4 giờ là:

40 × 4 = 160 (km)

Đáp số: 160 km

Câu 33: Một ô tô trung bình mỗi giờ đi được 50 km. Ô tô đi từ điểm A đến B hết 4 giờ. Hỏi quãng đường A B dài bao nhiêu km?

Lời giải:

Chiều dài quãng đường A B là:

50 × 4 = 200 (km)

Đáp số: 200 km.

Câu 34: 6 giờ 25 phút bằng bao nhiêu phút?

Lời giải:

Đổi 6 giờ = 6 × 60 = 360 (phút)

6 giờ 25 phút = 360 + 25 = 385 (phút)

Đáp số: 385 phút.

Câu 35: 180 phút bằng bao nhiêu giờ?

Lời giải:

180 phút = 180 : 60 = 3 (giờ)

Đáp số: 3 giờ.

Câu 36: 8 người sơn được 3 cái nhà trong 6 giờ. Hỏi với 12 người sẽ sơn được bao nhiêu cái nhà trong 12 giờ?

Lời giải:

8 người trong 1 giờ sơn được số cái nhà là:

$3:6=\frac{1}{2}$ (cái nhà)

8 người trong 12 giờ sơn được số cái nhà là:

$\frac{1}{2}\times 12=6$ (cái nhà)

12 người trong 12 giờ sơn được số cái nhà là:

$6:8\times 12=9$ (cái nhà)

Đáp số: 9 cái nhà

Câu 37: Cho số 650. Tìm xem số đó có chia hết cho 13 không?

Lời giải:

Áp dụng quy tắc chia hết cho 13 ta có:

65 + (0 × 4) = 65 (chia hết cho 13)

Vậy 650 chia hết cho 13.

Câu 38: Cho một số là 2,453,674. Tìm xem nó có chia hết cho 13 hay không?

Lời giải:

Áp dụng quy tắc chia hết cho 13 ta có:

674 – 453 + 2 = 223 (không chia hết cho 13)

Vậy 2,453,674 không chia hết cho 13.

Câu 39: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng: AD.AB = AE.AC = HC.HB

Lời giải:

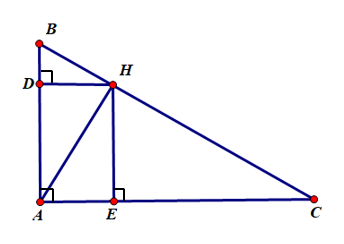
Xét ΔAHB vuông tại H có HD là đường cao nên:

AD.AB = AH²     (1)  (hệ thức lượng trong tam giác vuông)

Xét ΔAHC vuông tại H có HE là đườg cao nên:

AE.AC = AH²    (2) (hệ thức lượng trong tam giác vuông)

Xét ΔABC vuông tại A có AH là đường cao nên:

HB⋅HC = AH²  (3) (hệ thức lượng trong tam giác vuông)

Từ (1), (2) và (3) suy ra AD.AB = AE.AC = HB.HC.

Câu 40: Cho tam giác ABC vuông tại A, đường cao AM. Gọi H, K lần lượt là hình chiếu của M trên AB, AC. Biết AM = 4 cm. Tính HA.HB + KA.KC.

Lời giải:

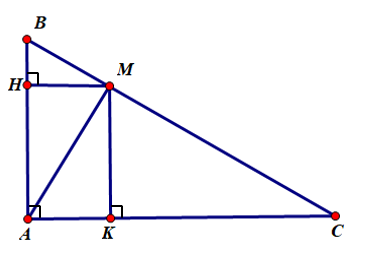
Xét ΔAMB vuông tại M có MH là đường cao nên:

HA.HB = HM²     (1)  (hệ thức lượng trong tam giác vuông)

Xét ΔAMC vuông tại M có MK là đường cao nên:

KA.KC = KM²    (2) (hệ thức lượng trong tam giác vuông)

Tứ giác AHMK có:

$\widehat{AHM}=\widehat{MKA}=\widehat{HAK}=90°$

Suy ra AHMK là hình chữ nhật

Do đó AH = KM

Từ (1) và (2) ta có:

HA.HB + KA.KC = HM² + KM²

HA.HB + KA.KC = HM² + AH²

HA.HB + KA.KC = AM² (áp dụng định lý Pythagore cho tam giác vuông AHM)

HA.HB + KA.KC = 4² = 16

Vậy HA.HB + KA.KC = 16.

Câu 41: Cạnh thứ nhất của một hình tam giác dài 11,5 cm. Cạnh thứ nhất ngắn hơn cạnh thứ hai 0,6 cm và dài hơn cạnh thứ ba 0,9 cm. Tính chu vi hình tam giác đó.

Lời giải:

Cạnh thứ hai dài là:

11,5 + 0,6 = 12,1 (cm)

Cạnh thứ ba dài là:

11,5 – 0,9 = 10,6 (cm)

Chu vi hình tam giác đó là:

11,5 + 12,1 + 10,6 = 34,2 (cm)

Đáp số: 34,2 cm

Câu 42: Cạnh thứ nhất của một hình tam giác dài 5 cm. Cạnh thứ hai dài gấp 2,4 lần cạnh thứ nhất. Biết chu vi tam giác bằng 30 cm. Tính cạnh thứ ba.

Lời giải:

Cạnh thứ hai dài là:

5 x 2,4 = 12 (cm)

Cạnh thứ ba dài là:

30 – 12 – 5 = 13 (cm)

Đáp số: 13 cm.

Câu 43: Mảnh vải thứ nhất dài 2,75 m. Mảnh vải thứ hai dài gấp 3 lần mảnh vải thứ nhất và dài hơn mảnh vải thứ ba 0,86 m. Hỏi cả ba mảnh vải dài bao nhiêu mét?

Lời giải:

Ta có sơ đồ:

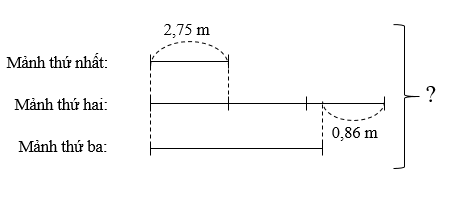
Độ dài mảnh vải thứ 2 là:

2,75 × 3 = 8,25 (m)

Độ dài mảnh vải thứ 3 là

8,25 – 0,86 = 7,39 (m)

Tổng độ dài của 3 mảnh vải là

2,75 + 8,25 + 7,39 = 18,39 (m)

Đáp số: 18,9 m

Câu 44: Mảnh vải thứ nhất dài hơn mảnh vải thứ hai 2,7 m, biết tỉ số phần trăm giữa mảnh vải thứ hai và mảnh vải thứ nhất là 40%. Tính độ dài mỗi mảnh vải.

Lời giải:

Ta có: $40\%=\frac{40}{100}=\frac{2}{5}$

Ta có sơ đồ:

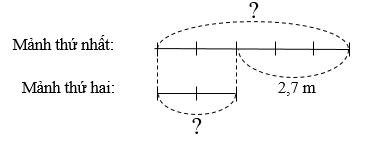
Tỉ số giữa mảnh vải thứ nhất và mảnh vải thứ hai bằng $\frac{2}{5}$

Theo đề bài ta có:

Hiệu số phần bằng nhau:

5 – 2 = 3

Mảnh vải thứ nhất dài:

2,7 × 3 = 1,8 (m)

Mảnh vải thứ hai dài:

1,8 + 2,7 = 4,5 (m)

Đáp số: 1,8 m; 4,5 m

Câu 45: Một can nhựa chứa 10 lít dầu hỏa. Biết một lít dầu hỏa cân nặng 0,8 kg, can rỗng cân nặng 1,3 kg. Hỏi can dầu hỏa đó cân nặng bao nhiêu ki-lô-gam?

Lời giải:

Cân nặng của 10 lít dầu hoả là:

10 × 0,8 = 8 (kg)

Sô cân nặng của cả can dầu là:

8 + 1,3 = 9,3 (kg)

Đáp số: 9,3 kg

Câu 46: Một xô nhựa chứa 20 lít nước. Biết mỗi một lít nước nặng 1 kg, xô rỗng nặng 0,5 kg. Hỏi can nước đó nặng bao nhiêu kg?

Lời giải:

Cân nặng của 10 lít nước là;

10 × 1 = 10 (kg)

Số cân nặng của cả xô nước là:

10 + 0,5 = 10,5 (kg)

Đáp số: 10,5 kg

Câu 47: Một mảnh vườn hình chữ nhật có chiều dài 24 m, chiều rộng bằng $\frac{1}{2}$ chiều dài. Tính chu vi và diện tích của mảnh vườn đó?

Lời giải:

Chiều rộng mảnh vườn hình chữ nhật là:

24 × $\frac{1}{2}$ = 12 (m)

Chu vi mảnh vườn hình chữ nhật là:

(24 + 12) × 2 = 72 (m)

Diện tích mảnh vườn hình chữ nhật là:

24 × 12 = 288 (m²)

Đáp số: Chu vi: 72 m, Diện tích: 288 m²

Câu 48: Mảnh vườn hình chữ nhật có chiều rộng bằng 8 m và diện tích bằng 120 m². Tính chu vi hình chữ nhật đó.

Lời giải:

Chiều dài của mảnh vườn hình chữ nhật là:

120 : 8 = 15 (m)

Chu vi của mảnh vườn hình chữ nhật là:

(8 + 15) × 2 = 46 (m)

Đáp số: 46 m

Câu 49: Số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 21, 20, 22. Tính số học sinh của mỗi lớp. Biết rằng lớp 7C nhiều hơn lớp 7A 2 học sinh.

Lời giải:

Gọi số học sinh của ba lớp 7A, 7B, 7C lần lượt là x, y, z (học sinh) (x, y, z Î ℕ^*)

Vì số học sinh của ba lớp 7A, 7B, 7C tỉ lệ với 21, 20, 22 nên:

$\frac{x}{21}=\frac{y}{20}=\frac{z}{22}$

Vì số học sinh lớp 7C nhiều hơn lớp 7A 2 học sinh nên: z – x = 2

Áp dụng dãy tỉ số bằng nhau ta có:

$\frac{x}{21}=\frac{y}{20}=\frac{z}{22}=\frac{z-x}{22-21}=2$

Suy ra x = 21. 2 = 42 (tmđk), y = 20. 2 = 40 (tmđk), z = 22. 2 = 44 (tmđk)

Vậy số học sinh lớp 7A, 7B, 7C lần lượt là 42, 40, 44 học sinh.

Câu 50: Trung bình cộng của 3 số là 25,42. Tổng của số thứ hai và số thứ ba là 58,5. Biết số thứ ba hơn số thứ nhất là 7,4. Tìm ba số đó.

Lời giải:

Tổng của 3 số đó là:

25,42 × 3 = 76,26

Số thứ nhất là:

76,26 – 58,5 = 17,76

Số thứ 2 là:

17,76 + 7,4 = 24,8

Số thứ 3 là:

58,5 – 24,8 = 33,7

Đáp số: số thứ nhất: 17,76

Số thứ 2: 24,8

Số thứ 3: 33,7.