Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 108)
Câu 1: Cho tam giác ABC vuông tại A, biết AB = 12cm, tanB = . Tính độ dài BC, AC và số đó góc C
Phương pháp giải:
Áp dụng công thức tangens góc B: Dựa vào điều kiện và , ta tính được độ dài của cạnh bằng cách giải phương trình.
Áp dụng định lý Pythagore: Dùng định lý Pythagore để tính độ dài cạnh trong tam giác vuông ABC.
Tính góc C: Sử dụng công thức và .
Kết luận.
Lời giải:
Ta có:
(cm)
(cm) - theo định lý Pitago
Chứng minh các hệ thức trên
Phương pháp giải:
Chuyển đổi vế trái (VT):
Sử dụng các công thức lượng giác cơ bản:
Biến đổi vế trái thành dạng phân số:
Tách biểu thức tử số: Sử dụng hằng đẳng thức:
Rút gọn phân số: Sau khi tách tử số, tiến hành rút gọn với mẫu số:
Đưa về dạng liên quan đến : Chia cả tử và mẫu cho (với ):
Kết luận: VT bằng với vế phải (VP), hoàn thành chứng minh.
Lời giải:
VT = (với cos #0)
Câu 3: Chứng minh: a5 - b5 = (a - b)(a4 + a3b + a2b2 + ab3 + b4)
Phương pháp giải:
Khai triển vế phải sao cho về dạng giống với vế trái và kết luận.
Lời giải:
Phương pháp chung
Áp dụng phép nhân đơn thức với đơn thức, nhân đa thức với đơn thức và nhân đa thức với đa thức với đa thức. Chúng ta biến đổi:
+ Cách 1: Vế trái và chứng minh bằng vế phải
+ Cách 2: Vế phải và chứng minh bằng vế trái
+ Cách 3: Vế trái và vế phải cùng bằng một biểu thức.
Câu 4: 415 x 530 bằng bao nhiêu và tại sao?
Phương pháp giải:
Phân tích cơ số, sử dụng tính chất lũy thừa và kết luận.
Tính chất của lũy thừa với số mũ thực:
Cho a, b là những số thực dương; α, β là những số thực tùy ý. Khi đó ta có:
Lời giải:
415 x 530
= (22)15 x 530
= 230 x 530
= (2x5)30
= 1030
a)
b)
c)
d)
Phương pháp giải:
Thực hiện các phép tính cộng, trừ, nhân, chia phân số căn bản và rút gọn (nếu có).
Lời giải:
a)
b)
c)
d)
a) Phép cộng hai phân số:
⦁ Cộng hai phân số cùng mẫu: (với a, b, m ∈ ℤ và m ≠ 0).
⦁ Cộng hai phân số khác mẫu: Quy đồng mẫu số của phân số để đưa về phép cộng hai phân số cùng mẫu.
b) Phép trừ hai phân số:
⦁ Số đối: (với a, b ∈ ℤ và b ≠ 0).
⦁ Trừ hai phân số cùng mẫu: (với a, b, m ∈ ℤ và m ≠ 0).
⦁ Trừ hai phân số khác mẫu: Quy đồng mẫu số của phân số để đưa về phép trừ hai phân số cùng mẫu.
Chú ý:
– Muốn trừ hai phân số ta có thể cộng số bị trừ với số đối của số trừ.
(với a, b, c, d ∈ ℤ và b, d ≠ 0).
– Sau khi thực hiện phép cộng và phép trừ phân số, ta rút gọn kết quả (nếu có).
c) Phép nhân hai phân số
Quy tắc: Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Lưu ý:
+) Sau khi làm phép nhân hai phân số, nếu thu được phân số chưa tối giản thì ta phải rút gọn thành phân số tối giản.
+) Khi nhân hai phân số, sau bước lấy tử số nhân tử số, mẫu số nhân mẫu số, nếu tử số và mẫu số cùng chia hết cho một số nào đó thì ta rút gọn luôn, không nên nhân lên sau đó lại rút gọn.
d) Các tính chất của phép nhân phân số
+) Tính chất giao hoán: Khi đổi chỗ các phân số trong một tích thì tích của chúng không thay đổi.
+) Tính chất kết hợp: Khi nhân một tích hai phân số với phân số thứ ba, ta có thể nhân phân số thứ nhất với tích của hai phân số còn lại.
+) Tính chất phân phối: Khi nhân một tổng hai phân số với phân số thứ ba, ta có thể nhân lần lượt từng phân số của tổng với phân số thứ ba rồi cộng các kết quả đó lại với nhau.
+) Nhân với số 1: Phân số nào nhân với 1 cũng bằng chính phân số đó.
Lưu ý: ta thường áp dụng các tính chất của phép nhân phân số trong các bài tính nhanh.
e) Phép chia hai phân số
Quy tắc: Muốn chia một phân số cho một phân số, ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Câu 6: Cho hệ phương trình . Tìm m thuộc Z để hệ có nghiệm duy nhất là các số nguyên
Phương pháp giải:
Kiểm tra điều kiện có nghiệm duy nhất.
Do 3m + 2 thuộc Ư(7). Kẻ bảng và tìm từng giá trị của m.
Kiểm tra điều kiện và kết luận m.
Lời giải:
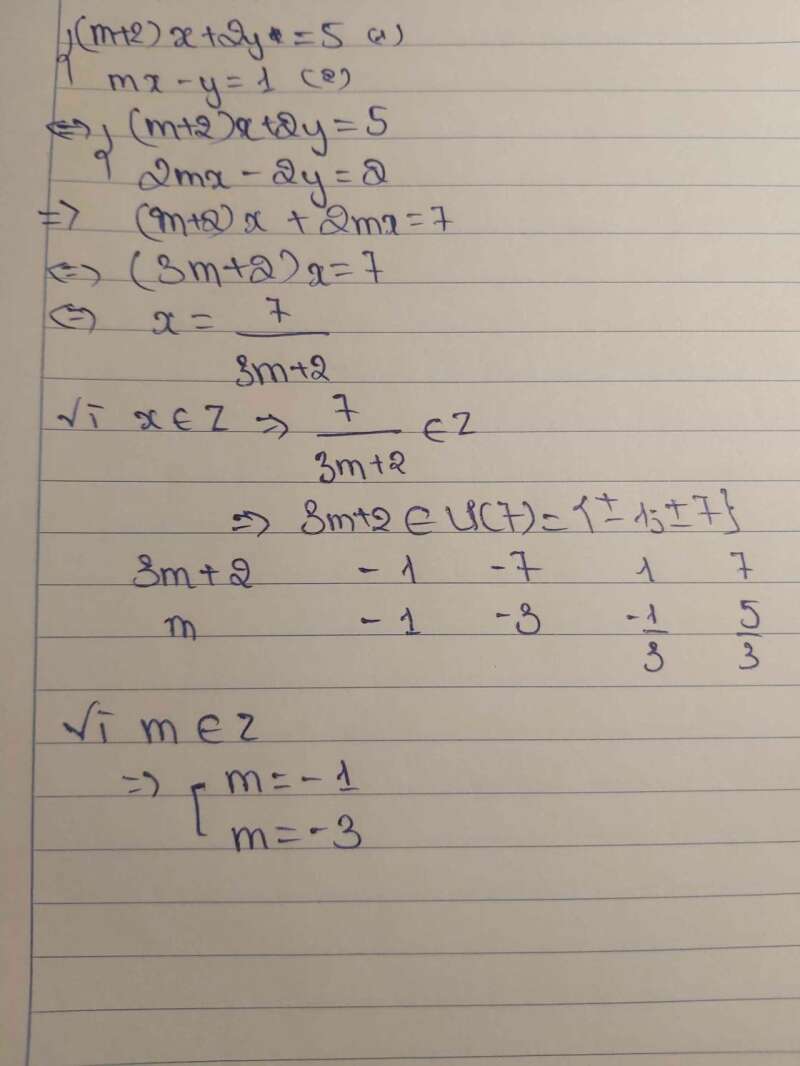
Phương pháp giải hệ phương tình
• Bước 1: Từ một phương trình của hệ phương trình đã cho, ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình còn lại để được một phương trình mới (chỉ còn một ẩn).
• Bước 2: Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ phương trình đã cho.
Chú ý:
+ Để có lời giải đơn giản, ta thường chọn các phương trình có hệ số không quá lớn (bằng 1 hoặc -1) và biểu diễn ẩn có hệ số nhỏ hơn qua ẩn còn lại.
+ Thay một phương trình trong hệ bởi phương trình một ẩn vừa tìm ta được hệ phương trình mới tương đương với hệ phương trình đã cho.
Phương pháp giải:
Gọi hai số tự nhiên cần tìm là (số thứ nhất) và (số thứ hai). Ta có hệ phương trình.
Giải hệ phương trình và tìm x, y.
Lời giải:
Gọi số tự nhiên thứ nhất là , số tự nhiên thứ hai là
Vì 4 lần số thứ hai cộng với 5 lần số thứ nhất bằng 18040 nên ta có:
Vì 3 lần số thứ nhất hơn 2 lần số thứ hai là 2002 nên ta có:
Từ (1) và (2) ta có hệ phương trình:
Phương pháp chung
Trình tự các bước giải bài toán bằng cách lập hệ phương trình
• Bước 1: Lập hệ phương trình.
+ Biểu diễn hai đại lượng phù hợp bằng ẩn số x và y. Đặt đơn vị và điều kiện của ẩn.
+ Biểu thị các đại lượng chưa biết qua ẩn.
+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng và thành lập hệ hai ẩn từ các phương trình vừa tìm.
• Bước 2: Giải hệ phương trình nói trên.
• Bước 3: Kiểm tra nghiệm tìm được thỏa mãn điều kiện của bài toán và nêu kết luận của bài toán.
Câu 8: So sánh các phân số sau
a) và
b) và
Phương pháp giải:
Quy đồng sao cho cùng mẫu số và so sánh.
Kết luận.
Lời giải:
a) và MC(4161)
nên
b) và MC(36)
nên
Phương pháp: So sánh các phân số khác mẫu
a) Quy đồng mẫu số
Quy tắc: Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó rồi so sánh các tử số của hai phân số mới.
Phương pháp giải:
Bước 1: Quy đồng mẫu số hai phân số.
Bước 2: So sánh hai phân số có cùng mẫu số đó.
Bước 3: Rút ra kết luận.
b) Quy đồng tử số
Điều kiện áp dụng: Khi hai phân số có mẫu số khác nhau nhưng mẫu số rất lớn và tử số nhỏ thì ta nên áp dụng cách quy đồng tử số để việc tính toán trở nên dễ dàng hơn.
Quy tắc: Muốn so sánh hai phân số khác tử số, ta có thể quy đồng tử số hai phân số đó rồi so sánh các mẫu số của hai phân số mới.
Phương pháp giải:
Bước 1: Quy đồng tử số hai phân số.
Bước 2: So sánh hai phân số có cùng tử số đó.
Bước 3: Rút ra kết luận.
Câu 9: Tính nhanh 28 + 62 x a x (a x 1 – a : 1) + 28 x 8 + 28
Phương pháp giải:
Phân tích biểu thức bên trong dấu ngoặc.
Thay thế vào biểu thức gốc.
Tính các phần còn lại.
Tính tổng.
Lời giải:
= 28 + 62 x a x ( a x 1 - a : 1 ) + 28 x 8 + 28
= 28 + 62 x a x ( a - a ) + 28 x 8 + 28
= 28 + 62 xa x 0 + 28 x 8 + 28
= 28 + 0 + 28 x 8 + 28
= 28 x (1 + 8 + 1)
= 28 x 10
= 280
Phương pháp chung
* Các tính chất của phép cộng như sau:
+ Tính giao hoán: a + b = b + a.
+ Tính kết hợp: (a + b) + c = a + (b + c).
+ Cộng với số 0: a + 0 = 0 + a = a
+ Cộng với số đối: a + (-a) = 0
* Để tính nhanh, tính hợp lí giá trị một biểu thức ta có thể làm theo các cách sau:
- Áp dụng các tính chất của phép cộng để nhóm các số lại với nhau sao cho tổng của mỗi nhóm là một số tròn trục, tròn trăm…
- Nhóm các số lại với nhau sao cho mỗi nhóm có cùng kết quả, sau đóthực hiện cộng các số đã nhóm.
Câu 10: Tính nhanh 27 : 0,125 + 27 : 0,5 + 27 : 0,2 + 27 : 0,25 + 27
Phương pháp giải:
Tính từng phép chia
Cộng các kết quả lại
Kết luận
Lời giải:
27 : 0,125 + 27 : 0,5 + 27 : 0,2 + 27 : 0,25 + 27
= 27 : (0,125 + 0,5 + 0,2 + 0,25 + 1)
= 27 : 2,075
= 13,01
Phương pháp chung
* Các tính chất của phép cộng như sau:
+ Tính giao hoán: a + b = b + a.
+ Tính kết hợp: (a + b) + c = a + (b + c).
+ Cộng với số 0: a + 0 = 0 + a = a
+ Cộng với số đối: a + (-a) = 0
* Để tính nhanh, tính hợp lí giá trị một biểu thức ta có thể làm theo các cách sau:
- Áp dụng các tính chất của phép cộng để nhóm các số lại với nhau sao cho tổng của mỗi nhóm là một số tròn trục, tròn trăm…
- Nhóm các số lại với nhau sao cho mỗi nhóm có cùng kết quả, sau đóthực hiện cộng các số đã nhóm.
Phương pháp giải:
Đưa các phân số về dạng cùng tử số
Nhóm phần chung vào 1 nhóm và tìm x.
Lời giải:
Có:
Mà
Phương pháp chung
+ Bước 1: Quy đồng và khử mẫu ( nếu có mẫu thức).
+ Bước 2: Áp dụng quy tắc chuyển vế đổi dấu.
+ Bước 3. Nhân phá các ngoặc, rút gọn hai vế, tìm giá trị của ẩn thỏa mãn
Chú ý: a.b = 0 khi a = 0 hoặc b = 0
Phương pháp giải:
Đổi đơn vị: 1 phút = 60 giây
Tìm chiều dài nửa quãng đường AB
Thời gian xe đi nửa quãng đường sau và lập phương trình
Giải phương trình và kết luận
Lời giải:
Ta có :10p = 600s
Chiều dài nửa quãng đường AB là :
S =
Thời gian xe đi nửa quãng đường đầu là :
t1 = (h)
Thời gian xe đi nửa quãng đường sau là :
t2 = (h)
Ta có : t1+t2=t
(m/s) = 21,6km/h
v2 = v1 = = 10,8(km/h)
Câu 13: CMR với mọi a, b, c > 0 ta có
Phương pháp giải:
Áp dụng bất đẳng thức Cô-si để giải bài toán trên:
Với ba số thực không âm ta có a + b + c ≥ . Dấu bằng xảy ra khi và chỉ khi a = b = c.
Lời giải:
Áp dụng cô si ta có :
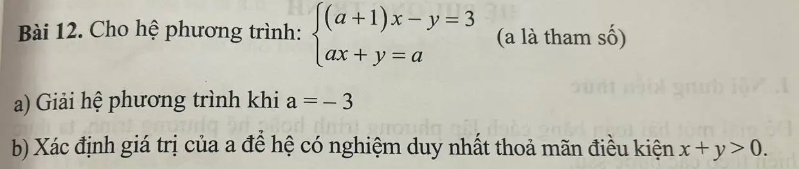
Phương pháp giải:
a) Đặt a = - 3 vào hệ phương trình, ta được hệ phương trình mới. Giải hệ phương trình này ta được nghiệm (x, y) = (1, -1).
b) Để hệ phương trình có nghiệm duy nhất, ta cần đảm bảo rằng hệ số của x và y trong hai phương trình không tỷ lệ với nhau. Từ đó, ta có:
Giải phương trình trên ta được a ≠ -1.
Để thoả mãn điều kiện x + y > 0, ta cần giải hệ phương trình và tìm giá trị của a sao cho x+y>0.
Lời giải:
a) Khi a = -3, hệ phương trình trở thành:
Giải hệ phương trình trên ta được nghiệm (x, y) = (1, -1).
b)
Điều kiện để hệ có nghiệm duy nhất:
Hệ phương trình:
Hệ có nghiệm duy nhất khi định thức khác 0:
Điều kiện: , tức .
Giải:
Giải hệ phương trình:
Sử dụng phương pháp thế hoặc cộng đại số:
Điều kiện :
Tổng:
Điều kiện :
Tử số:
Mẫu số:
khi biểu thức cùng dấu ở tử và mẫu.
Nghiệm:
Giá trị thỏa mãn:
Câu 15: Tính nhanh 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
Phương pháp giải:
Để tính tổng dãy số từ , có thể nhóm các số thành các cặp sao cho tổng mỗi cặp bằng nhau và tính toán.
Lời giải:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
= (1 + 9) + (2 + 8) + (7 + 3) + (4 + 6) + 5
= 10 + 10 + 10 + 10 + 5
= 10 x 4 + 5
= 40 + 5
= 45
Phương pháp tính nhanh giá trị biểu thức
Dạng 1: Nhóm các số hạng trong biểu thức thành từng nhóm có tổng (hoặc hiệu) là các số tròn chục, tròn trăm, tròn nghìn... rồi cộng (hoặc trừ) các kết quả lại.
Trong một bài toán về tính giá trị biểu thức, học sinh cần quan sát xem có nhóm các số nào có tổng hoặc hiệu là các số tròn chục, tròn trăm, tròn nghìn hay không, từ đó nhóm các số đó lại để tính một cách thuận tiện nhất.
Công thức tổng quát: a + b + c = (a + b) + c
a - b - c = (a - b) - c
Dạng 2: Vận dụng tính chất một số nhân với một tổng, một số nhân với một hiệu, một tổng chia cho một số, một hiệu chia cho một số.
Trong các phép tính tổng (hoặc hiệu), tích ( hoặc thương), học sinh cần chú ý các tính chất giao hoán, tính chất kết hợp của các số để có thể tính một cách thuận tiện nhất.
Công thức tổng quát:
- Một số nhân với một tổng: a x (b + c) = a x b + a x c
a x b + a x c = a x (b + c)
- Một số nhân với một hiệu: a x (b - c) = a x b - a x c
a x b - a x c = a x (b - c)
- Một tổng chia cho một số: (a + b + c) : d = a : d + b : d + c : d
Ví dụ: Tính nhanh giá trị của biểu thức sau
(18 + 45 + 63) : 9
= 18 : 9 + 45 : 9 + 63 : 9
= 2 + 5 + 7
= 14
- Một hiệu chia cho một số: (a - b - c) : d = a : d - b : d - c : d
Với các biểu thức chưa có thừa số chung, cần xem xét có thể phân tích một số ra một tích hoặc phân tích một tích ra các thừa số, từ đó làm xuất hiện thừa số chung được không.
Dạng 3: Vận dụng các tính chất: một số nhân với 0, một số nhân với 1, một số chia cho 1, 0 chia cho một số.
Trong các phép tính giá trị biểu thức, học sinh cần chú ý quan sát có biểu thức nào kết hợp các số có cho kết quả đặc biệt như 0 hoặc 1 hay không, từ đó tính bằng cách thuận tiện nhất.
Tính chất đặc biệt:
Một số nhân với 0 luôn cho kết quả bằng 0
Một số nhân với 1 luôn cho kết quả bằng chính số đó
Một số chia cho 1 luôn cho kết quả bằng chính số đó
Số 0 chia cho một số luôn cho kết quả bằng 0
Công thức tổng quát:
a x 0 = 0
a x 1 = a
a : 1 = a
0 : a = 0
Dạng 4: Vận dụng kiến thức về dãy số để tính giá trị biểu thức bằng cách thuận tiện nhất.
Vận dụng chủ yếu trong các dạng bài toán nâng cao về dãy số cách đều.
Công thức tổng quát:
Cách tìm số hạng của một dãy số cách đều: Số các số hạng = (Số cuối - Số đầu) : Khoảng cách + 1
Cách tính nhanh tổng của một dãy số cách đều:
Bước 1: Tính số các số hạng của dãy số cách đều (Theo công thức nêu trên)
Bước 2: Tính số cặp số của dãy số bằng cách lấy kết quả ở bước 1 chia cho 2 (Trường hợp dư 1 thì xem xét không ghép cặp 1 số)
Bước 3: Nhóm các cặp số hạng và tính tổng giá trị của cặp số (Chú ý có cặp số nào cho kết quả đặc biệt không, thông thường hay nhóm số đầu với số cuối)
Bước 4: Tính tổng dãy số bằng cách nhân kết quả ở bước 2 với kết quả ở bước 3, cộng thêm số không ghép cặp nếu có (tính tích số các cặp số nhân với tổng của một cặp số).
a)
b)
c)
Phương pháp giải:
Rút gọn biểu thức: Đưa về dạng đơn giản nhất bằng cách thực hiện các phép cộng/trừ, nhân/chia phân số.
Chuyển vế và nhân phá dấu ngoặc: Đưa về một vế và các số về vế còn lại.
Giải phương trình: Tìm bằng cách chia hoặc nhân theo đúng quy tắc.
Lời giải:
b)
c)
Phương pháp chung:
Áp dụng các quy tắc
Đối với phép cộng: Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết
Đối với phép trừ:
+ Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ
+ Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu
Đối với phép nhân: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết
Đối với phép chia:
+ Muốn tìm số bị chia ta thấy thương nhân với số chia
+ Muốn tìm số chia ta thấy số bị chia thương
a, Tìm n để A có giá trị nguyên ?
b, Chứng minh phân số A tối giản ?
Phương pháp giải:
Phân tích yêu cầu chia hết cho hoặc kiểm tra điều kiện để là số nguyên hoặc tối giản.
Sử dụng phép chia và hiệu để đưa về điều kiện chia hết cho , hoặc kiểm tra
Xác định các giá trị hoặc chứng minh là phân số tối giản dựa vào tính chất ước số.
Lời giải:
a) Để A có giá trị là số nguyên
Suy ra 2n-3 chia hết cho n-2
Mà n-2 chia hết cho n-2
Suy ra 2(n-2) chia hết cho n-2
Suy ra 2n-4chia hết cho n-2
Mà 2n-3 chia hết cho n-2
Suy ra [(2n-3)-(2n-4)]chia hết cho n-2
(2n-3-2n+4) chia hết cho n-2
Suy ra 1 chia hết cho n-2
n-2 thuộc Ư(1)
n-2 thuộc {1;-1}
Ta có bảng
| n-2 | 1 | -1 |
| n | 3 | 1 |
| Nhận định | Chọn | Chọn |
Vậy n thuộc {3;1}
b) Gọi ƯCLN (2n-3:n-2)=d
Suy ra 2n-3chia hết cho d
n-2 chia hết cho d
Suy ra 2n-3 chia hết cho d
2(n-2) chia hết cho d
Suy ra 2n-3 chia hết cho d
2n-4 chia hết cho d
Suy ra [(2n-3)-(2n-4)] chia hết cho d
(2n-3-2n+4) chia hết cho d
1 chia hết cho d
Suy ra d thuộc Ư(1)
d thuộc {1;-1}
Vậy phân số A là phân số tối giản
Câu 18: Tính nhanh 532 + 472 + 2.47.53
Phương pháp giải:
Nhận dạng bài toán sử dụng hằng đẳng thức:
Lời giải:
532+472+2.47.53
= 532+472+94.53
= 472+2.47.53+532
= (47+53)2
= 1002
= 10 000
Câu 19: Số các cặp số nguyên (x;y) thỏa mãn là:
A. 2
B. 3
C. 1
D. 4
Phương pháp giải:
Quy đồng mẫu số chung để dễ tính toán.
Xét tính chia hết.
Xét thứ tự
Lời giải:
Đáp án cần chọn là: B
MSC:36
Khi đó:
⇒ ⇒ 2 < x .3 < y .4 < 9
Mà (x.3)⋮3 và (y.4)⋮4 nên x.3∈{3;6} và y.4∈{4;8}
Mà x.3 < y.4 nên:
+ Nếu x.3 = 3 thì y.4 = 4 hoặc y.4 = 8
Hay nếu x = 1 thì y = 1 hoặc y = 2
+ Nếu x.3 = 6 thì y.4 = 8
Hay nếu x = 2 thì y = 2
Vậy các cặp số nguyên (x;y) là (1;1), (1;2), (2;2)
Câu 20: Tính nhanh: 11 + 12 + 13 + ... + 109 = ?
Phương pháp giải:
Xác định số số hạng: Dùng công thức
Tính tổng: Áp dụng công thức tổng dãy số:
Lời giải:
11 + 12 + 13 + ... + 109
Số số hạng của dãy số trên là :
(109 - 11) : 1 + 1 = 99 (số hạng)
Tổng của dãy số là :
(109 + 11) . 99 : 2 = 5940
Vậy 11 + 12 + 13 + ... + 109 = 5940
Câu 21: Tìm số đo của góc nhọn biết
Phương pháp giải:
Sử dụng hằng đẳng thức:
Lời giải:
Ta có:
=> =>
=>
=>
Xong bạn giải phương trình bậc 2 => =>
Phương pháp giải:
Chuyển đổi số hỗn hợp sang phân số:
Chuyển , , và thành phân số.
Tính toán vế phải:
Thực hiện phép trừ .
Tìm .
Lời giải:
Phương pháp giải:
Đài quan sát, điểm chiếu của máy bay xuống mặt đất, và máy bay tạo thành một tam giác vuông. Góc nhìn 25° là góc giữa mặt đất và đường ngắm máy bay.
Độ cao là cạnh đối diện góc 25°, khoảng cách cần tìm là cạnh huyền.
Dùng công thức: sin = đối/huyền
Lời giải:
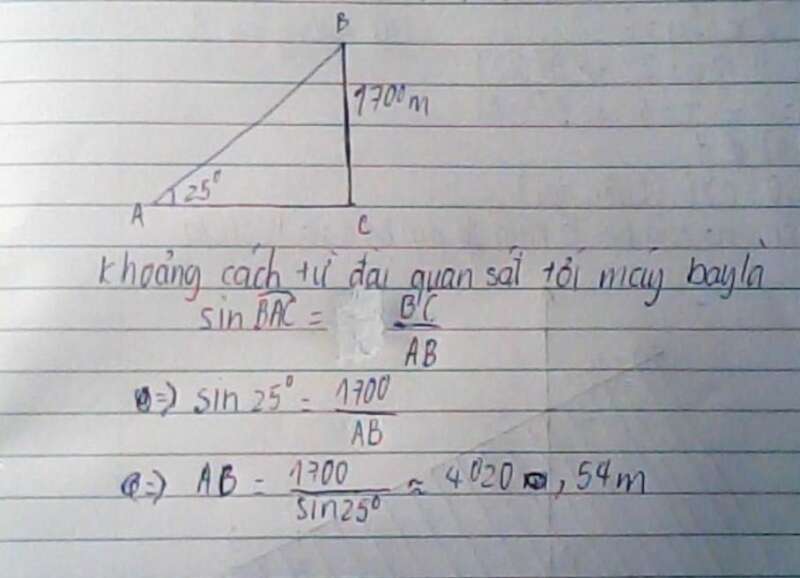
Câu 24: Phân tích đa thức thành nhân tử: (a + 1)(a + 2)(a + 3)(a + 4) + 3
Phương pháp giải:
Gộp nhóm: Nhóm các hạng tử của biểu thức thành từng cặp để đơn giản hóa.
Phân tích tích các cặp: Tính và , sau đó nhân chúng lại.
Thêm 3 vào biểu thức đã gộp: Thực hiện các phép tính và phân tích thành nhân tử cuối cùng.
Lời giải:
Ta có:
Phương pháp giải:
Mỗi mẫu số là bội số của 2, có thể nhận dạng theo công thức .
Áp dụng công thức chuỗi rút gọn, chỉ còn lại hai hạng tử đầu và cuối, từ đó tính tổng.
Lời giải:
=
=
=
=
Câu 26: Chỉ ra tính chất đặc trưng của tập hợp B = {-4; 1 ; 6; 11; 16}
Phương pháp giải:
Dãy số có sự thay đổi đều giữa các hạng tử. Ta nhận thấy dãy số này là một cấp số cộng với công sai .
Xác định công thức tổng quát cho hạng tử thứ
Lời giải:
B = {-4; 1; 6; 11; 16}
Xét dãy số: -4; 1; 6; 11; 16
st1 = - 4 = 5.0 - 4 = 5.(1 - 1) - 4
st2 = 1 = 5.1 - 4 = 5.(2 - 1) - 4
st3 = 6 = 5.2 - 4 = 5.(3 - 1) - 4
st4 = 11 = 5.3 - 4 = 5.(4 - 1) - 4
st5 = 16 = 5.4 - 4 = 5.(5 - 1) - 4
...................................................
stn = 5.(n - 1) - 4
B = {5.(n - 1) - 4/ n N; 1 ≤ n ≤ 6}
Câu 27: Chứng minh bất đẳng thức sau A = (a + b)() >= 4
Phương pháp giải:
Sử dụng bất đẳng thức giữa trung bình cộng và trung bình nhân (AM - GM)
Lời giải:
BĐT
Do BĐT cuối luôn đúng nên ta có đpcm. Dấu "=" xảy ra khi a = b
Câu 28: Tìm số hạng thứ 100 của các dãy được viết theo quy luật :
a) 3, 8, 15, 24, 35, .... ( 1 )
b) 3, 24, 63, 120, 195, .... ( 2 )
c) 1, 3, 6, 10, 15, .... ( 3 )
d) 2, 5, 10, 17, 26, .... ( 4 )
Phương pháp giải:
a) Số hạng thứ 100 là tổng của các số lẻ, công thức tổng của dãy số lẻ: n =
Trong đó là số hạng cuối cùng, là số đầu tiên, và là số hạng cần tìm.
b) Áp dụng công thức tổng các số có khoảng cách đều, tổng của các số hạng có khoảng cách đều : n =
Trong đó là số đầu tiên, là số hạng cuối cùng, và là số hạng cần tìm.
c) Đây là dãy số tam giác, công thức tổng của dãy tam giác: S_n =
Dãy số d) Sử dụng công thức tổng số hạng cách đều: n =
Trong đó là số đầu tiên, là số hạng cuối cùng, là số hạng cần tìm, và là hằng số cộng.
Lời giải:
a) Gọi số hạng thứ 100 của dãy là n, n là số tự nhiên.
Ta có 3 = 3
8 = 3 + 5
15 = 3 + 5 + 7
24 = 3 + 5 + 7 + 9
35 = 3 + 5 + 7 + 9 + 11
n = 3 + 5 + 7 + 9 + 11 + ... + n1
n1 = (100 - 1) x 2 + 3 = 201
=> n = (201 + 3) x 100 : 2 = 10200
Số hạng thứ 100 của dãy là 10 200
b) Gọi số hạng thứ 100 của dãy là n, n là số tự nhiên.
Ta có: 3 = 3
24 = 3 + 21
63 = 3 + 21 + 39
120 = 3 + 21 + 39 + 57
195 = 3 + 21 + 39 + 57 + 75
n = 3 + 21 + 39 + 57 + 75 + ... + n1 (Tổng dãy số cách đều có khoảng cách 18 đơn vị)
n1 = (100 - 1) x 18 + 3 = 1785
n = (3 + 1785) x 100 : 2 = 89400
Số hạng thứ 100 của dãy là 89400
c) Dãy này có quy luật là số thứ n của dãy là tổng từ 1 đến n (dãy số tự nhiên).
- Số hạng thứ nhất: 1.
- Số hạng thứ hai: 1 + 2 = 3.
- Số hạng thứ ba: 1 + 2 + 3 = 6.
- Và tiếp tục.
Áp dụng quy luật trên, ta tính được số hạng thứ 100:
1 + 2 + 3 + ... + 100 = 5,050.
d) Gọi số hạng thứ 100 của dãy là n, n là số tự nhiên.
Có 2 = 2
5 = 2 + 3
10 = 2 + 3 + 5
17 = 2 + 3 + 5 + 7
26 = 2 + 3 + 5 + 7 + 9
n = 2 + 3 + 5 + 7 + 9 + ... + n1 (Kể từ số hạng thứ 2 đến n là dãy số cách đều có khoảng cách 2 đơn vị và có 99 số trong dãy đó)
n1 = (99 - 1) x 2 + 3 = 199
n = (3 + 199) x 99 : 2 + 2 = 10 001
Số hạng thứ 100 của dãy là 10 001
Câu 29: Cho dãy số: 3; 18; 48; 93; 153; ...
a) Tìm số hạng thứ 100 của dãy
b) Số 11703 là số hạng thứ bao nhiêu của dãy
Phương pháp giải:
Dãy số có dạng
Số hạng thứ 100 là
Số 11703 là số hạng thứ 40, do và giải phương trình tam giác.
Lời giải:
a) Ta có: 3 = 15 x 0 + 3; 18 = 15 x 1 + 3; 48 = 15 x 3 + 8; 93 = 15 x 6 + 3; 153 = 15 x 10 + 3, .....
Như vậy, bản chất là tìm số hạng thứ 100 của dãy số: 0, 1, 3, 6, 10,....Bỏ qua số 0 (1, 3, 6, 10,....) thì dãy số này, bắt đầu từ số thứ 2 bằng tổng của số liền trước cộng với số thứ tự của nó. Số hạng thứ 100 cần tìm của dãy 0, 1, 3, 6, 10,....chính là số hạng thứ 99 của dãy 1, 3, 6, 10,.... và bằng: 1 + 2 + 3 + ... + 98 + 99 = (99 + 1) x 99 : 2 = 4950.
Vậy số hạng thứ 100 cần tìm là: 15 x 4950 + 3 = 74253.
b) Ta có: (11703 – 3) : 15 = 780; Mà 780 x 2 = 1560 = 39 x 40 = (39 + 1) x 39.
Vậy số 11703 là số hạng thứ 40 của dãy