Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 89)

Đề bài. Chứng minh rằng A = 1.5 + 2.6 + 3.7 + … + 2023.2027 chia hết cho 11, 23 và 2023.

Lời giải:

Ta thấy các số hạng có dạng tổng quát là k.(k + 4) = k² + 4k

Do đó: A = 1.5 + 2.6 + 3.7 + … + 2023.2027

A = (1² + 2² + 3² + … + 2023²) + 4.(1 + 2 + 3 +… + 2023)

Mà ta có công thức: 1² + 2² + 3² + … + n² = $\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

Nên A = $\frac{\mathrm{2023.2024.4047}}{6}+4.\frac{2023.\left(1+2023\right)}{2}=\frac{\mathrm{2023.2024.4047}}{6}+\mathrm{2.2024.2023}$

Ta thấy: 2024 chia hết cho cả 11, 23 nên $\frac{\mathrm{2023.2024.4047}}{6}$ chia hết cho 11, 23, 2023 đồng thời 2.2024.2023 chia hết cho 11, 23, 2023.

Vậy A chia hết cho 11, 23, 2023.

Đề bài. Chứng minh rằng $\frac{2}{\sin 4x}-\tan 2x=\cot 2x$.

Lời giải:

$\frac{2}{\sin 4x}-\tan 2x=\frac{2}{2\sin 2x.\cos 2x}-\frac{\sin 2x}{\cos 2x}$

$=\frac{1}{\sin 2x.\cos 2x}-\frac{\sin 2x}{\cos 2x}$

$=\frac{\cos 2x-\cos 2x.{\sin }^{2}2x}{\sin 2x.{\cos }^{2}2x}$

$=\frac{\cos 2x\left(1-{\sin }^{2}2x\right)}{\sin 2x.{\cos }^{2}2x}$

$=\frac{\cos 2x.{\cos }^{2}2x}{\sin 2x.{\cos }^{2}2x}$

$=\frac{\cos 2x}{\sin 2x}$

= cot2x.

Đề bài. Tìm x biết: $x-\sqrt{x-1}=3$.

Lời giải:

Điều kiện xác định: x – 1 ≥ 0 hay x ≥ 1.

$x-\sqrt{x-1}=3$

⇔ $\left(x-1\right)-\sqrt{x-1}-2=0$

Đặt $\sqrt{x-1}=t\left(t\ge 0\right)$

Ta có: t² – t – 2 = 0

⇔ $\left[\begin{array}{l}t=-2\left(L\right)\\ t=1\end{array}\right.$

Với t = 1 thì $\sqrt{x-1}=1$

⇔ x – 1 = 1

⇔ x = 2.

Vậy x = 2.

Đề bài. Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD

a) Chứng minh rằng AF // CE.

b) Gọi M, N theo thứ tự là giao điểm của BD và AF, CE. Chứng minh rằng DM = MN = NB.

Lời giải:

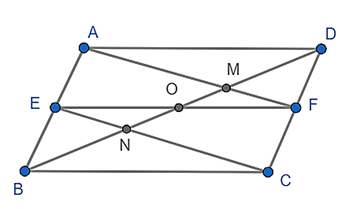
a) Ta có: AB // CD và AB = CD vì ABCD là hình bình hành

Nên AE // CF và AE = CF = $\frac{1}{2}AB=\frac{1}{2}CD$

Suy ra: AECF là hình bình hành

Vậy AF // CE

b) Xét ΔAEM có E là trung điểm của AB

EN // AM

Do đó N là trung điểm của BM

⇒ BN = NM (1)

Xét ΔDNC có F là trung điểm của DC

FM // NC

Do đó: M là trung điểm của DN

⇒ DM = MN (2)

Từ (1) và (2) suy ra DM = MN = NB.

Đề bài. Tìm số tự nhiên n sao cho 2n + 3 chia hết cho n – 2.

Lời giải:

Ta có: 2n + 3 = 2(n – 2) + 7

Vì 2(n – 2) chia hết cho n – 2 nên để 2n + 3 chia hết cho n – 2 thì 7 chia hết cho (n – 2)

Hay (n – 2) ∈ Ư(7)

⇒ n – 2 ∈ {1;7} (vì n là số tự nhiên)

⇒ n ∈ {3; 9}

Vậy n = 3 hoặc n = 9.

Đề bài. Cho $\sin 2\alpha =\frac{3}{4}$. Tính giá trị biểu thức A = tanα + cotα.

Lời giải:

A = tanα + cotα = $\frac{\sin \alpha }{\cos \alpha }+\frac{\cos \alpha }{\sin \alpha }=\frac{{\sin }^2\alpha +{\cos }^2\alpha }{\sin \alpha \cos \alpha }=\frac{1}{\frac{1}{2}\sin 2\alpha }=\frac{1}{\frac{1}{2}.\frac{3}{4}}=\frac{8}{3}$.

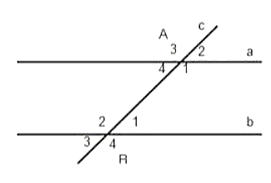
Đề bài. Cho biết a // b và góc $\widehat{A_1}$= 120°.

a) Tính góc $\widehat{B_1}$.

b) So sánh góc $\widehat{A_1}$ và góc $\widehat{B_4}$.

c) Tính $\widehat{B_2}$

Lời giải:

a) Vì a // b nên $\widehat{A_1}+\widehat{B_1}=180°$ (2 góc trong cùng phía)

Suy ra: $\widehat{B_1}=180°-120°=60°$

b) Lại có: $\widehat{A_1}=\widehat{B_4}=120°$(2 góc đồng vị)

c) $\widehat{A_1}=\widehat{B_2}=120°$(2 góc so le trong).

Đề bài. Cho tam giác ABC cân tại A lấy điểm D bất kì trên AB, lấy điểm E trên tia đối của tia CA sao cho CE = BD. Từ D kẻ đường thẳng song song với AC cắt BC tại F

a) Tam giác DBF là tam giác gì?

b) Chứng minh tứ giác DCEF là hình bình hành.

Lời giải:

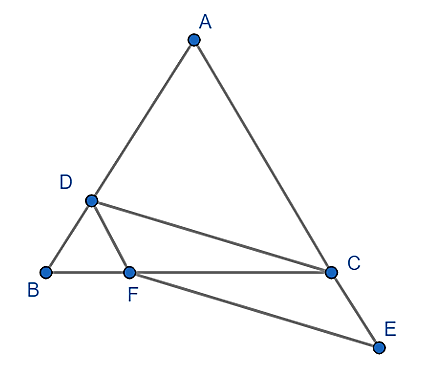
a) Ta có: DF // AC nên: $\widehat{DFB}=\widehat{ACB}=\widehat{B}$

Suy ra: tam giác DBF cân tại D

b) Từ câu a ta có: DB = DF

Mà DB = CE theo giả thiết nên DF = CE

Lại có: DF // AC nên DF // CE

Xét tứ giác DCEF có: DF // CE và DF = CE

Vậy DCEF là hình bình hành.

Đề bài. Chứng minh 3n + 11 và 3n + 2 là hai số nguyên tố cùng nhau với mọi số tự nhiên n.

Lời giải:

Gọi d = ƯCLN(3n + 11, 3n + 2)

⇒ 3n + 11 ⋮ d; 3n + 2 ⋮ d

Suy ra: (3n + 11) – (3n + 2) ⋮ d

Hay 9 ⋮ d

Suy ra: d = 1; 3; 9

Ta có: 3n chia hết cho 3 và 11 không chia hết cho 3 nên 3n + 11 không chia hết cho 3

Tức là 3n + 11 cũng không chia hết cho 9

Suy ra: d = 1.

⇒ ƯCLN(3n + 11, 3n + 2) = 1

Vậy 3n + 11 và 3n + 2 là hai số nguyên tố cùng nhau .

Đề bài. Cho n thuộc ℕ. Chứng minh rằng n² + n + 1 không chia hết cho 4.

Lời giải:

n² + n + 1 = n(n + 1) + 1

Vì n(n + 1) là tích của 2 số tự nhiên liên tiếp nên n(n + 1) chia hết cho 2 hay n(n + 1) là một số chẵn

Do đó n(n + 1) + 1 là một số lẻ

Mà số lẻ thì không chia hết cho 4.

Vậy n² + n + 1 không chia hết cho 4.

Đề bài. Tính tổng sau: 7²⁰²² – 7²⁰²¹ + 7²⁰²⁰ – 7²⁰¹⁹ + … + 7² – 7.

Lời giải:

A = 7²⁰²² – 7²⁰²¹ + 7²⁰²⁰ – 7²⁰¹⁹ + … + 7² – 7

⇔ 7A = 7²⁰²³ – 7²⁰²² + 7²⁰²¹ – 7²⁰²⁰ + … + 7³ – 7²

⇔ 7A + A = 7²⁰²³ – 7²⁰²² + 7²⁰²¹ – 7²⁰²⁰ + … + 7³ – 7² + 7²⁰²² – 7²⁰²¹ + 7²⁰²⁰ – 7²⁰¹⁹ + … + 7² – 7

⇔ 8A = 7²⁰²³ – 7

⇔ $A=\frac{7^{2023}-7}{8}$

Đề bài. Tìm số tiếp theo trong dãy:1; 5; 14; 33; 72; ...

Lời giải:

Ta thấy:

5 = 1.2 + 3

14 = 5.2 + 4

33 = 14.2 + 5

72 = 33.2 + 6

Số tiếp theo là: 72.7 + 7 = 151.

Đề bài. Cho hệ phương trình: $\left\{\begin{array}{l}x+my=2\\ mx-2y=1\end{array}\right.$. Giải hệ phương trình khi m = 2.

Lời giải:

Với m = 2 ta có hệ: $\left\{\begin{array}{l}x+2y=2\\ 2x-2y=1\end{array}\right.$

⇔ $\left\{\begin{array}{l}3x=3\\ 2x-2y=1\end{array}\right.$

⇔ $\left\{\begin{array}{l}x=1\\ 2-2y=1\end{array}\right.$

⇔ $\left\{\begin{array}{l}x=1\\ y=\frac{1}{2}\end{array}\right.$

Vậy khi m = 2 thì phương trình có nghiệm (x; y) = $\left(1;\frac{1}{2}\right)$.

Đề bài. Chứng minh $\frac{{\sin }^{2}x-{\cos }^{2}x+{\cos }^{4}x}{{\cos }^{2}x-{\sin }^{2}x+{\sin }^{4}x}={\tan }^{4}x$.

Lời giải:

$\frac{{\sin }^{2}x-{\cos }^{2}x+{\cos }^{4}x}{{\cos }^{2}x-{\sin }^{2}x+{\sin }^{4}x}$

$=\frac{{\cos }^{4}x+1-2{\cos }^{2}x}{{\sin }^{4}x+2{\cos }^{2}x-1}=\frac{{\cos }^{4}x-\cos 2x}{{\sin }^{4}x+\cos 2x}=\frac{{\left({\cos }^{2}x\right)}^2-\cos 2x}{{\left({\sin }^{2}x\right)}^2+\cos 2x}$

$=\frac{\frac{{\left(\cos 2x+1\right)}^2}{4}-\cos 2x}{\frac{{\left(1-\cos 2x\right)}^2}{4}+\cos 2x}$

$=\frac{{\cos }^{2}2x-2\cos 2x+1}{1+2\cos 2x+{\cos }^{2}2x}$

$=\frac{{\left(\cos 2x-1\right)}^2}{{\left(1+\cos 2x\right)}^2}$

$=\frac{{\left(-2{\sin }^{2}x\right)}^2}{{\left(2{\cos }^{2}x-1+1\right)}^2}=\frac{{\sin }^{4}x}{{\cos }^{4}x}={\tan }^{4}x$.

Đề bài. Cho hình thang cân ABCD (AB // CD) có $\widehat{A}=3\widehat{D}$. Tính góc A, B, C, D.

Lời giải:

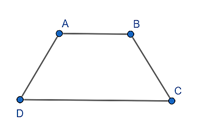
Ta có: ABCD là hình thang cân, AB // CD nên: $\widehat{A}+\widehat{D}=180°$

Mà $\widehat{A}=3\widehat{D}$ nên $4\widehat{D}=180°\Rightarrow \widehat{D}=45°$

Suy ra: $\widehat{A}=3\widehat{D}=3.45°=135°$

Do ABCD là hình thang cân nên $\widehat{A}=\widehat{B}=135°;\widehat{C}=\widehat{D}=45°$.

Đề bài. Chứng minh rằng với mọi số nguyên n ta có: A = 1⁵ + 2⁵ + … + n⁵ chia hết cho B = 1 + 2 + 3 + … + n.

Lời giải:

Ta xét B = 1 + 2 + 3 + … + n = $\frac{n\left(n+1\right)}{2}$

2A = (n⁵ + 1) + [(n – 1)⁵ + 2⁵] + [(n – 2)⁵ + 3⁵] + … + (1 + n⁵)

Nhận thấy mỗi số hạng của 2A đều chia hết cho (n + 1) nên 2A ⋮ (n + 1) (1)

Lại có: 2A – 2n⁵ = [(n – 1)⁵ + 1⁵] + [(n – 2)⁵ + 2⁵] + … chia hết cho n

Do 2n⁵ ⋮ n nên 2A ⋮ n (2)

Từ (1) và (2) suy ra: 2A ⋮ n(n + 1) do đó 2A ⋮ 2B hay A ⋮ B.

Đề bài. Một đợt bán xe đạp ở cửa hàng sau khi giảm giá lần đầu là 10% và lần thứ hai giảm 5% thì bây giờ lại tăng 8%. Biết giá giảm hay tăng tính dựa theo giá đang bán. Hiện tại giá mỗi chiếc xe đạp là 7387200 đồng. Tính giá gốc ban đầu khi chưa tăng giảm của đợt bán xe đạp này.

Lời giải:

Gọi x (triệu đồng) là giá ban đầu của xe

Sau hai lần giảm 10% và 5%, giá tiền là:

x.(100 − 10)%. (100 − 5)% = 0,855x

Sau lần tăng 8%, giá tiền là:

0,855x.(100 + 8)% = 0,9234x

Giá hiện tại là 7,3872 triệu đồng nên ta có:

0,9234x = 7,3872

⇔ x = 8

Vậy giá xe ban đầu là 8 triệu đồng.

Đề bài. Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến. Chứng minh:

a. Tam giác ADE cân tại A.

b. ∆ABD = ∆ACE.

c. BCDE là hình thang cân.

Lời giải:

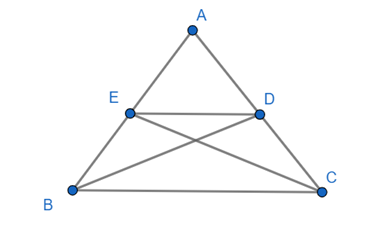
a. BD và CE là 2 đường trung tuyến.

⇒ EA = EB, DA = DC

Có ΔABC cân tại A ⇒ AB=AC

⇒ AE =AD

⇒ ΔAED cân tại A

b. Xét ΔABD và ΔACE có:

$\widehat{A}$ chung

AB = AC (GT)

AD = AE (chứng minh trên)

⇒ ΔABD = ΔACE (c.g.c)

c. EA = EB, DA=DC

⇒ ED là đường trung bình của ΔABC

⇒ ED //BC

⇒ tứ giác BCDE là hình thang

Lại có: ΔABD = ΔACE ⇒ BD = CE (Hai cạnh tương ứng)

⇒ BCDE là hình thang cân.

Đề bài. Tính hợp lý: 5 – (1997 – 2005) + 1997.

Lời giải:

5 – (1997 – 2005) + 1997

= 5 – 1997 + 2005 + 1997

= 5 + 2005

= 2010.

Đề bài. Nếu $\tan \frac{\beta }{2}=4\tan \frac{\alpha }{2}$ thì $\tan \frac{\beta -\alpha }{2}$ bằng bao nhiêu?

Lời giải:

$\tan \frac{\beta -\alpha }{2}=\frac{\tan \frac{\beta }{2}-\tan \frac{\alpha }{2}}{1+\tan \frac{\beta }{2}.\tan \frac{\alpha }{2}}=\frac{3\tan \frac{\alpha }{2}}{1+4{\tan }^2\frac{\alpha }{2}}=\frac{3\sin \frac{\alpha }{2}\cos \frac{\alpha }{2}}{1+3{\sin }^2\frac{\alpha }{2}}=\frac{3\sin \alpha }{5-3\cos \alpha }$

Đề bài. Thực hiện phép tính: $\sqrt[3]{45+29\sqrt{2}}+\sqrt[3]{45-29\sqrt{2}}$.

Lời giải:

$\sqrt[3]{45+29\sqrt{2}}+\sqrt[3]{45-29\sqrt{2}}$

$=\sqrt[3]{27+27\sqrt{2}+18+2\sqrt{2}}+\sqrt[3]{27-27\sqrt{2}+18-2\sqrt{2}}$

$=\sqrt[3]{27+27\sqrt{2}+18+2\sqrt{2}}+\sqrt[3]{27-27\sqrt{2}+18-2\sqrt{2}}$

$=\sqrt[3]{{\left(3+\sqrt{2}\right)}^3}+\sqrt[3]{{\left(3-\sqrt{2}\right)}^3}$

$=3+\sqrt{2}+3-\sqrt{2}=6$.

Đề bài. Cho x, y, z khác 0 và x khác y khác z thỏa mãn x² – xy = y² – yz = z² – zx = a.

a) Chứng minh rằng a khác 0.

b) Chứng minh: $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0$.

Lời giải:

a) a = x² – xy = x(x – y)

Vì x khác 0 vì x khác y nên x – y ≠ 0

Suy ra: x(x – y) ≠ 0

Vậy a ≠ 0.

b) Ta có: $\left\{\begin{array}{l}{x}^2-xy=y^2-yz\left(1\right)\\ y^2-yz=z^2-zx\left(2\right)\\ z^2-zx=x^2-xy\left(3\right)\end{array}\right.$

Lấy (3) trừ (1): 2xy = xz + yz – z² + 2x² – y²

Lấy (3) trừ (2): 2zx = xy + yz + 2z² – x² – y²

Lấy (2) trừ (1): 2yz = 2y² + xy + xz – x² – z²

Cộng lại ta được: yz + xz + xy = 0 do đó: $\frac{yz+xz+xy}{xyz}=0\iff \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0$.

Đề bài. Cho hình thang vuông ABCD ($\widehat{A}=\widehat{D}=90°$), có CD = 2AB, gọi H là hình chiếu của D trên AC, M là trung điểm của HC. Chứng minh $\widehat{BMD}=90°$.

Lời giải:

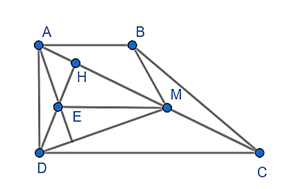
Gọi E là trung điểm HD

Ta có: EM là đường trung bình của tam giác HDC

Nên: EM // DC và EM = $\frac{1}{2}DC=AB$

Xét tứ giác ABME có: AB // EM // CD

AB = EM

Nên ABME là hình bình hành

Suy ra: BM // AE (1)

Lại có: Xét trong tam giác ADM có: DH ⊥ AM (giả thiết); EM ⊥ AD (vì AD ⊥ AB mà AB // EM)

Nên E là trực tâm của tam giác ADM

Suy ra: AE ⊥ DM (2)

Từ (1) và (2): BM ⊥ DM hay $\widehat{BMD}=90°$.

Đề bài. Người ta đã dùng 400 viên gạch hình vuông có cạnh dài 60 cm để lát nền cho một căn phòng hình vuông (coi các mảnh ghép là không đáng kể). Hỏi nền căn phòng hình vuông đó có cạnh dài bao nhiêu mét?

Lời giải:

Diện tích viên gạch hình vuông là: 60.60 = 3600 (cm²)

Diện tích nền căn phòng hình vuông là: 3600.400 = 1440000 (cm²)

Đổi 1440000 cm² = 144 m²

Vì 144 = 12.12 nên cạnh nền căn phòng hình vuông đó là 12m.

Đề bài. Giải phương trình: x² – 4x + 4 = 25.

Lời giải:

x² – 4x + 4 = 25

⇔ x² – 4x – 21 = 0

⇔ x² – 7x + 3x – 21 = 0

⇔ x(x – 7) + 3(x – 7) = 0

⇔ (x – 7)(x + 3) = 0

⇔ $\left[\begin{array}{l}x=7\\ x=-3\end{array}\right.$

Vậy x = 7 hoặc x = -3.

Đề bài. Thực hiện phép tính: $\left(\frac{1}{4.9}+\frac{1}{9.14}+\mathrm{...}\frac{1}{44.49}\right)\frac{1-3-5-7-\mathrm{...}-49}{89}$.

Lời giải:

$\left(\frac{1}{4.9}+\frac{1}{9.14}+\mathrm{...}\frac{1}{44.49}\right)\frac{1-3-5-7-\mathrm{...}-49}{89}$

$=\frac{1}{5}\left(\frac{1}{4}-\frac{1}{9}+\frac{1}{9}-\frac{1}{14}+\mathrm{...}+\frac{1}{44}-\frac{1}{49}\right)\frac{2-\left(1+3+5+7+\mathrm{...}+49\right)}{89}$

$=\frac{1}{5}\left(\frac{1}{4}-\frac{1}{49}\right)\frac{2-\left(12.50+25\right)}{89}$

$=-\frac{\mathrm{5.9.7.89}}{\mathrm{5.4.7.7.89}}=\frac{-9}{28}$.

Đề bài. Chứng minh rằng với mọi n ∈ ℕ^*, n ≥ 2 ta có: $1+\frac{1}{2^2}+\mathrm{...}+\frac{1}{n^2}<2-\frac{1}{n}$

Lời giải:

Xét: $\frac{1}{2^2}+\mathrm{...}+\frac{1}{n^2}<\frac{1}{1.2}+\frac{1}{2.3}+\mathrm{...}+\frac{1}{n\left(n-1\right)}$

$\frac{1}{2^2}+\mathrm{...}+\frac{1}{n^2}<1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\mathrm{...}+\frac{1}{n-1}-\frac{1}{n}$

$\frac{1}{2^2}+\mathrm{...}+\frac{1}{n^2}<1-\frac{1}{n}$

Suy ra: $1+\frac{1}{2^2}+\mathrm{...}+\frac{1}{n^2}<1+1-\frac{1}{n}$

Hay $1+\frac{1}{2^2}+\mathrm{...}+\frac{1}{n^2}<2-\frac{1}{n}$.

Đề bài. Cô giáo muốn chia 240 bút bi, 210 bút chì và 180 tập giấy thành một số phần thưởng như nhau. Hỏi có thể chia được nhiều nhất là bao nhiêu phần thưởng, mỗi phần thưởng có bao nhiêu bút bi, bút chì tập giấy?

Lời giải:

Do trong mỗi phần thưởng, số bút bi, số bút chì và số tập giấy trong mỗi phần thưởng phải bằng nhau nên số bút bi, số bút chì và số tập giấy phải chia hết cho số bút bi, số bút chì và số tập giấy trong mỗi phần thưởng.

Vậy số phần thưởng phải là ước chung của 240, 210, và 180.

Do số phần thưởng là lớn nhất nên số phần thưởng sẽ là

ƯCLN(240,210,180)

Ta có:

240 = 2⁴.3.5

210 = 2.3.5.7

180 = 2².32.5

Vậy ƯCLN(240,210,180) = 2.3.5 = 30

Mỗi phần thưởng có số bút bi là

240 : 30 = 8 (cái)

Mỗi phần thưởng có số bút chì là

210 : 30 = 7 (cái)

Mỗi phần thưởng có số tập giấy là

180 : 30 = 6 (tập)

Vậy có thể chia nhiều nhất thành 30 phần thưởng, mỗi phần thưởng có 8 bút bi, 7 bút chì, và 6 tập giấy.

Đề bài. Tính tỉ số $\frac{A}{B}$ biết $A=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\mathrm{...}+\frac{1}{2009}$; $B=\frac{2008}{1}+\frac{2007}{2}+\mathrm{...}\frac{2}{2007}+\frac{1}{2008}$.

Lời giải:

$B=1+\left(\frac{2007}{2}+1\right)+\mathrm{...}+\left(\frac{2}{2007}+1\right)+\left(\frac{1}{2008}+1\right)$

$B=\frac{2009}{2009}+\frac{2009}{2}+\frac{2009}{3}+\mathrm{...}+\frac{2009}{2008}$

$B=2009.\left(\frac{1}{2}+\frac{1}{3}+\mathrm{...}+\frac{1}{2009}\right)$

$\frac{A}{B}=\frac{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\mathrm{...}+\frac{1}{2009}}{2009.\left(\frac{1}{2}+\frac{1}{3}+\mathrm{...}+\frac{1}{2009}\right)}=\frac{1}{2009}$.

Đề bài. Cho a là số thập phân có hai chữ số ở phần thập phân. Biết rằng khi làm tròn a đến hàng đơn vị thì được kết quả là 56. Tìm giá trị lớn nhất của a.

Lời giải:

Khi làm tròn a đến hàng đơn vị thì bằng 56 vậy a có số đơn vị là 56

Gọi số chữ số thập phân của a là x

Ta có 56 < 56,x < 56,5 với x lớn nhất vậy x là 49.

Số cần tìm là 56,49.

Đề bài. Rút gọn biểu thức sau A = sinx.cosx.cos2x.cos4x.cos8x.

Lời giải:

A = sinx.cosx.cos2x.cos4x.cos8x

$A=\frac{1}{2}.2\sin x.\cos x.\cos 2x.\cos 4x.\cos 8x$

$A=\frac{1}{2}.\sin 2x.\cos 2x.\cos 4x.\cos 8x$

$A=\frac{1}{4}.\left(2.\sin 2x.\cos 2x\right).\cos 4x.\cos 8x$

$A=\frac{1}{4}.\sin 4x.\cos 4x.\cos 8x$

$A=\frac{1}{8}.\left(2.\sin 4x.\cos 4x\right)\cos 8x$

$A=\frac{1}{8}.\sin 8x.\cos 8x$

$A=\frac{1}{16}\mathrm{.2.}\sin 8x.\cos 8x$

$A=\frac{1}{16}.\sin 16x$.

Đề bài. Cho cota = 15. Tính giá trị sin2a.

Lời giải:

cota = 15

⇔ $\frac{{\cos }^{2}a}{{\sin }^{2}a}+1={15}^2+1=226$

⇔ $\frac{1}{{\sin }^{2}a}=226$

⇔ $\left\{\begin{array}{l}{\sin }^{2}a=\frac{1}{226}\\ {\cos }^{2}a=\frac{225}{226}\end{array}\right.$

Suy ra: sin2a = 2sina.cosa = $\pm \frac{15}{113}$.

Đề bài. Một khu vườn hình vuông có cạnh bằng 20m, người ta làm một lối đi xung quanh vườn có bể rộng x (m).

a) Viết biểu thức biểu diễn diện tích đất còn lại của khu vườn.

b) Tìm x biết diện tích dùng làm lối đi là 144m².

Lời giải:

Điều kiện:

20 − 2x ≥ 0

⇔ 2x ≤ 20

⇔ x ≤ 10

a) Cạnh khu đất còn lại là:

20 − 2x (m)

Diện tích khu đất còn lại là:

(20 − 2x)(20 − 2x) = 4x² − 80x + 400 (m²)

b) Diện tích khu vườn là:

20.20 = 400 (m²)

Diện tích khu đất còn lại là:

400 – 144 = 256 (m²)

Ta có: 4x² – 80x + 400 = 256

⇔ 4x² – 80x + 144 = 0

⇔ $\left[\begin{array}{l}x=18\\ x=2\end{array}\right.$

Kết hợp với điều kiện: x = 2

Vậy x = 2.

Đề bài. Cho hình bình hành ABCD có $\widehat{A}=120°$. Tính số đo các góc còn lại của hình bình hành.

Lời giải:

Trong tính chất của hình bình hành:

Định lí: Trong hình bình hành:

+ Các cạnh đối bằng nhau.

+ Các góc đối bằng nhau.

+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường

Suy ra: $\widehat{A}=\widehat{C}=120°$

Khi đó ta có: $\left\{\begin{array}{l}\widehat{B}=\widehat{D}\\ \widehat{B}+\widehat{D}=120°\end{array}\right.\Rightarrow \widehat{B}=\widehat{D}=60°$.

Đề bài. Số chính phương khi chia cho 5 thì số dư có thể bằng?

Lời giải:

Số chính phương có dạng n² là số có tận cùng bằng 0; 1; 4; 5; 6; 9.

Xét n² có tận cùng là 0, mà 0 : 5 = 0 dư 0

Tận cùng là 1; 1 : 5 = 0 dư 1

Tận cùng là 4; 4 : 5 = 0 dư 4

Tận cùng là 5; 5 : 5 = 1 dư 0

Tận cùng là 6; 6 : 5 = 1 dư 1

Tận cùng là 9; 9 : 5 = 1 dư 4

Vậy một số chính phương khi chia cho 5 có thể có số dư là 0, 1, 4.

Đề bài. Tìm hai số biết tổng hai số là số lớn nhất có hai chữ số. Hiệu hai số là số lẻ bé nhất có 2 chữ số.

Lời giải:

Tổng 2 số là số lớn nhất chữ số: 99

Hiệu 2 số là số lẻ bé nhất có 2 chữ số: 11

Số lớn là: (99 + 11) : 2 = 55

Số bé là: (99 − 11) : 2 = 44.

Vậy số lớn là 55, số bé là 44.

Đề bài. Một mảnh vườn hình vuông cạnh 20 m. Người ta làm một lối đi xung quanh vườn rộng 2 m thuộc đất của vườn. Phần đất còn lại dùng để trồng trọt. Tính diện tích trồng trọt của mảnh vườn.

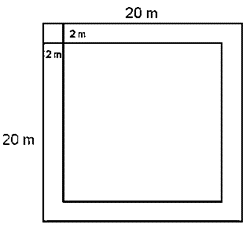
Lời giải:

Phần còn lại để trồng trọt là hình vuông có cạnh:

20 - 2 - 2 = 16 (m)

Diện tích trồng trọt của mảnh vườn là:

16. 16 = 256 (m²)

Vậy diện tích trồng trọt của mảnh vườn là 256m².

Đề bài. Tìm hai số có tổng là số bé nhất có 4 chữ số và hiệu là số chẵn lớn nhất có 2 chữ số.

Lời giải:

Số bé nhất có 4 chữ số là 1000. Vậy tổng là 1000

Số chẵn lớn nhất có 2 chữ số là 18. Vậy hiệu là 18.

Số lớn là:

(1000 + 18) : 2 = 509

Số bé là:

1000 – 509 = 491.

Vậy số lớn là 509, số bé là 491.

Đề bài. Tổng 2 số là số lớn nhất có 3 chữ số, hiệu của chúng là số lẻ nhỏ nhất có 2 chữ số. Tìm mỗi số.

Lời giải:

Số lớn nhất có 3 chữ số là 999. Nên tổng là 999.

Số lẻ nhỏ nhất có 2 chữ số là 11. Nên hiệu là 11.

Số lớn là: (999 + 11) : 2 = 505

Số bé là: 505 – 11 = 494.

Vậy số lớn là 505, số bé là 494.

Đề bài. Cho tam giác ABC có AB = 6, AC = 8, $\widehat{A}=100°$ . Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).

Lời giải:

Xét tam giác ABC, có:

BC² = AB² + AC² – 2.AB.AC.cosA (định lí côsin)

⇔ BC² = 6² + 8² – 2.6.8.cos100°

⇔ BC² ≈ 116,7

⇔ BC ≈ 10,8.

Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{BC}{\sin A}=2R$

⇔ R = $\frac{10,8}{2\sin 100°}\approx 5,5$.

Đề bài. Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y = x² và đường thẳng (d) có phương trình y = mx + 3 (với m là tham số).

1. Chứng minh đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A và B.

2. Gọi x₁, x₂ lần lượt là hoành độ của A và B. Tính tích các giá trị của m để 2x₁ + x₂ = 1

Lời giải:

1. Xét phương trình hoành độ giao điểm:

x² – mx – 3 = 0 (*)

∆ = m² + 12 > 0 với mọi m

Nên (*) luôn có 2 nghiệm phân biệt hay đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A và B.

2. Áp dụng hệ thức Vi-ét ta có: $\left\{\begin{array}{l}{x}_1+x_2=m\left(2\right)\\ x_1{x}_2=-3\left(3\right)\end{array}\right.$

Theo đề bài: 2x₁ + x₂ = 1 (4)

Từ (2) và (4) ta có hệ phương trình:

$\left\{\begin{array}{l}{x}_1+x_2=m\\ 2x_1+x_2=1\end{array}\right.\iff \left\{\begin{array}{l}{x}_1=1-m\\ x_1+x_2=m\end{array}\right.\iff \left\{\begin{array}{l}{x}_1=1-m\\ x_2=2m-1\end{array}\right.$

Thay vào (3) ta được: (1 – m)(2m – 1) = -3

⇔ 2m² – 3m – 2 = 0

⇔ $\left[\begin{array}{l}m=2\\ m=-\frac{1}{2}\end{array}\right.$

Tích các giá trị của m là: $2.\left(\frac{-1}{2}\right)=-1$.

Đề bài. Cho hai số a, b thỏa mãn a + b = 1.

Tính giá trị của biểu thức P = 2a³ + 6ab + 2b³ – 2024.

Lời giải:

P = 2a³ + 6ab + 2b³ – 2024

P = 2[(a + b)³ – 3ab(a + b)] + 6ab – 2024

P = 2[1 – 3ab(a + b)] + 6ab – 2024

P = 2(1 – 3ab) + 6ab – 2024

P = 2 – 6ab + 6ab – 2024

P = – 2022.

Đề bài. Cho tam giác ABC vuông tại A và đường cao AH (H ∈ BC).

1) Cho AH = 6; BH = 3. Tính BC và số đo $\widehat{ABC}$ (góc làm tròn đến phút).

2) Đường thẳng vuông góc với BC tại B cắt tia CA tại K. Hạ AE ⊥ BK (E ∈ BK). Chứng minh rằng: AK.AC = EH², từ đó suy ra BH.HC + BE.EK = AK.AC.

Lời giải:

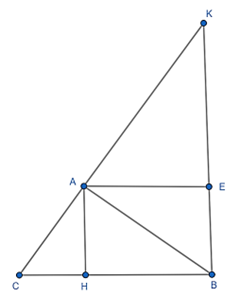
1) Áp dụng hệ thức lượng giác vào tam giác ABC vuông tại A có đường cao AH

AH² = BH.HC

⇒ 6²= 3. HC ⇒ HC = 6² : 3= 12cm

Ta có : BC = BH + HC = 3 + 12 =15 cm

$\frac{1}{A{H}^2}=\frac{1}{A{B}^2}+\frac{1}{A{C}^2}\Rightarrow AC=6\sqrt{5}$

$AB=\sqrt{A{H}^2+B{H}^2}=\sqrt{3^2+6^2}=3\sqrt{5}$

Xét tam giác BAC vuông tại A có: sin$\widehat{ABC}=\frac{AC}{BC}=\frac{6\sqrt{5}}{15}=\frac{2\sqrt{5}}{5}\Rightarrow \widehat{ABC}=63°$

2) Xét tam giác BAK và tam giác CAB có:

$\widehat{BAK}=\widehat{BAC}=90°$

$\widehat{BKA}=\widehat{ABC}$(cùng phụ với $\widehat{KBA}$)

Suy ra: ∆BAK ∽ ∆CAB (g.g)

⇒ $\frac{BA}{AC}=\frac{AK}{AB}\Rightarrow A{B}^2=AK.AC$

Lại có: ABHE là hình chữ nhật vì $\widehat{H}=\widehat{B}=\widehat{E}=90°$ nên AB = HE

Suy ra: EH² = AK.AC (1)

Xét tam giác BEA và tam giác AEK có:

$\widehat{BEA}=\widehat{AEK}=90°$

$\widehat{ABE}=\widehat{KAE}=90°-\widehat{EAB}$

Suy ra: ∆BEA ∽ ∆AEK (g.g)

⇒ $\frac{BE}{AE}=\frac{AE}{EK}$⇒ BE.EK = AE²

Xét tam giác BHA và tam giác AHC có:

$\widehat{BHA}=\widehat{CHA}=90°$

$\widehat{ABH}=\widehat{CAH}=90°-\widehat{ACH}$

Suy ra: ∆BHA ∽ ∆AHC (g.g)

⇒ $\frac{BH}{AH}=\frac{AH}{HC}$ ⇒ AH² = BH.HC

⇒ BH.HC + BE.EK = AE² + AH² = EH² (2)

Từ (1) và (2) suy ra: BH.HC + BE.EK = AK.AC.

Đề bài. Chứng minh rằng m + 2014n chia hết cho 2015 khi và chỉ khi n + 2014m chia hết cho 2015.

Lời giải:

Ta có: m + 2014n = 2015(m + n) – (n + 2014m)

Do 2015(m + n) ⋮ 2015 và m + 2014n ⋮ 2015

Nên: n + 2014m chia hết cho 2015.

Đề bài. Giải phương trình: $\sqrt{x^2-4x+3}=2\sqrt{25-4x^2}$ (*).

Lời giải:

ĐKXĐ: $\left\{\begin{array}{l}{x}^2-4x+3\ge 0\\ 25-4x^2\ge 0\end{array}\right.\iff \left\{\begin{array}{l}\left[\begin{array}{l}x\le 1\\ x\ge 3\end{array}\right.\\ \frac{-5}{2}\le x\le \frac{5}{2}\end{array}\right.\iff \frac{-5}{2}\le x\le 1$

Bình phương 2 vế (*) ta được:

x² – 4x + 3 = 4(25 – 4x²)

⇔ x² – 4x + 3 = 100 – 16x²

⇔ 17x² – 4x – 97 = 0

∆ = 16 + 6596 = 6612

Suy ra phương trình có 2 nghiệm: $\left[\begin{array}{l}x=\frac{4+\sqrt{6612}}{34}\\ x=\frac{4-\sqrt{6612}}{34}\end{array}\right.$.

Đề bài. Cho ΔABC cân tại A có AB = 5cm; BC = 6cm. Kẻ phân giác trong AM (M ∈ BC). Gọi O là trung điểm của AC và K là điểm đối xứng của M qua O.

a) Tính diện tích tam giác ABC.

b) Tứ giác ABMO là hình gì? Vì sao?

c) Để tứ giác AMCK là hình vuông thì tam giác ABC phải có thêm điều kiện gì?

Lời giải:

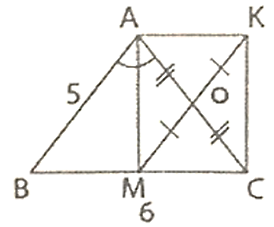
a) Vì M là trung điểm của BC nên:

BM = $\frac{1}{2}BC=\frac{1}{2}.6=3\left(cm\right)$

Tam giác ABC cân tại A, lại có AM là đường phân giác nên AM cũng là đường cao. Do đó tam giác AMB vuông tại M.

Suy ra: AM² = AB² - BM² (Định lí Pytago)

= 52 - 32 = 16(cm)

Suy ra AM = 4cm

S_ABC = $\frac{1}{2}.AM.BC=\frac{1}{2}\mathrm{.4.6}=12\left(c{m}^2\right)$

ΔAMC vuông tại M có MO là đường trung tuyến nên OM = OA.

Suy ra $\widehat{OAM}=\widehat{OMA}$( ΔAMO cân tại O)

Lại có $\widehat{OAM}=\widehat{MAB}$(AM là tia phân giác góc BAC)

Suy ra $\widehat{OMA}=\widehat{MAB}$

Mà đây là 2 góc ở vị trí so le trong

Suy ra OM // AB

Vậy tứ giác ABMO là hình thang.

c) Tứ giác AMCK có OA = OC; OM = OK nên tứ giác AMCK là hình bình hành .

Lại có $\widehat{AMC}=90°$ (chứng minh trên) nên tứ giác AMCK là hình chữ nhật.

Hình chữ nhật AMCK là hình vuông

⇔ AM = MC = BM

⇔ AM = $\frac{1}{2}BC$

Suy ra tam giác ABC vuông cân tại A.

Đề bài. Xác định các hệ số a, b, c biết: (a – 1)(x² – bx + 3) = 2x² + 5x + c.

Lời giải:

(a – 1)(x² – bx + 3) = 2x² + 5x + c

⇔ (a – 1)x² – (a – 1)bx + 3(a – 1) = 2x² + 5x + c

Suy ra ta có: $\left\{\begin{array}{l}a-1=2\\ -\left(a-1\right)b=5\\ 3\left(a-1\right)=c\end{array}\right.\iff \left\{\begin{array}{l}a=3\\ b=\frac{-5}{2}\\ c=6\end{array}\right.$.

Đề bài. Chứng minh rẳng A = 1 + 4 + 4² + 4³ + … + 4²⁰²¹ chia hết cho 21.

Lời giải:

Dựa vào số mũ ta có thể thấy A có tất cả 2022 số hạng nên chia làm 674 nhóm, mỗi nhóm 3 hạng tử

Ta có: A = 1 + 4 + 4² + 4³ + … + 4²⁰²¹

A = (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + … + (4²⁰¹⁹ + 4²⁰²⁰ + 4²⁰²¹)

A = (1 + 4 + 4²) + 4³(1 + 4 + 4²) + … + 4²⁰¹⁹(1 + 4 + 4²)

A = (1 + 4 + 4²)(1 + 4³ + … + 4²⁰¹⁹)

A = 21.(1 + 4³ + … + 4²⁰¹⁹)

Vì 21 chia hết cho 21 nên 21.(1 + 4³ + … + 4²⁰¹⁹) chia hết cho 21.

Vậy A chia hết cho 21.

Đề bài. Một can xăng đựng 8,5 lít xăng cân nặng 8,22 kg, vỏ can cân nặng 1,25kg. Hỏi một thùng xăng cùng loại có 28,3 lít xăng cân nặng bao nhiêu kg, biết vỏ thùng cân nặng 3,08 kg?

Lời giải:

8,5 lít xăng nặng số kg là:

8,22 – 1,25 = 6,97 (kg)

1 lít xăng nặng số kg là:

6,97 : 8,5 = 0,82 (kg)

28,3 lít xăng nặng số kg là:

28,3 . 0,82 = 23,206 (kg)

Một thùng xăng chứa 28,3 lít xăng nặng số kg là:

23,206 + 3,08 = 26,286 (kg)

Đáp số: 26,286 kg.

Đề bài. Tìm dư khi chia x⁹⁹ + x⁵⁵ + x¹¹ + x + 7 cho x² + 1.

Lời giải:

x⁹⁹ + x⁵⁵ + x¹¹ + x + 7

= x(x⁹⁸ + 1) + x(x⁵⁴ + 1) + x(x¹⁰ + 1) – 2x + 7

Chú ý rằng (x²)⁴⁰ + 1, (x²)²⁷ + 1, (x²)²⁵ + 1 chia hết cho x² + 1.

Như vậy số dư cần tìm là –2x + 7.

Đề bài. Tam giác ABC có BC = $\sqrt{5}$; AC = 3 và cotC = -2. Tính cạnh AB.

Lời giải:

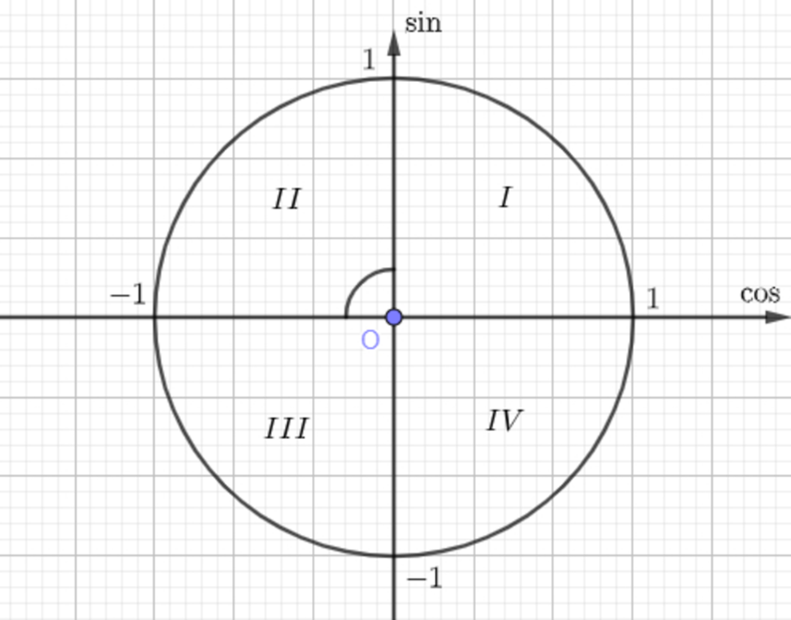
cotC = – 2

⇔ cot²C = 4

⇔ $\frac{{\cos }^{2}C}{{\sin }^{2}C}=4$

⇔ $\frac{{\cos }^{2}C}{1-{\cos }^{2}C}=4$

⇔ cos²C = 4 – 4cos²C

⇔ cos²C = $\frac{4}{5}$

⇔ cosC = $-\frac{2}{\sqrt{5}}$(vì cotC = – 2 < 0 nên cosC và sinC trái dấu)

Mà $0°<\widehat{C}<180°$nên C thuộc góc phần tư thứ II nên cosC < 0

AB² = AC² + BC² – 2.AC.BC.cosC

$A{B}^2=5+9-\mathrm{2.3.}\sqrt{5}.\left(-\frac{2}{\sqrt{5}}\right)=26$

Suy ra: $AB=\sqrt{26}$.

Đề bài. Tìm hệ số a để x⁴ + ax³ + bx – 1 chia hết cho x² – 1.

Ta có:

x⁴ + ax³ + bx – 1

= x⁴ + ax³ + x² – x² + bx – 1

= x²(x² + ax + 1) – (x² + ax + 1) + bx – ax

= (x² + ax + 1)(x² – 1) + x(b – a)

Ta thấy: (x² + ax + 1)(x² – 1) ⋮ x² – 1 nên để x⁴ + ax³ + bx – 1 chia hết cho x² – 1 thì x(b – a) chia hết cho x² – 1

Suy ra: b – a = 0 hay a = b

Vậy a = b thì x⁴ + ax³ + bx – 1 chia hết cho x² – 1.

Đề bài. Tìm x thuộc B(12) và 30 < x < 100.

Lời giải:

x thuộc B(12) ={12; 24; 36; 48; 60; 72; 84; 96; 108;...}

+ Mà 30 < x < 100

⇒ x = {36; 48; 60; 72; 84; 96}

Vậy x ={36; 48; 60; 72; 84; 96}.

Đề bài. Cho n điểm phân biệt trên mặt phẳng (n ∈ ℕ, n > 2). Số véctơ khác có cả điểm đầu và điểm cuối là các điểm đã cho bằng.

Lời giải:

Hai điểm bất kì trong n điểm trên tạo thành hai véctơ thỏa mãn yêu cầu bài toán. Nên số các véctơ đó là: $2.C_n^2=2.\frac{n!}{2!\left(n-2\right)!}=n\left(n-1\right)$

Nhận xét: Có thể hiểu mỗi véctơ là một chỉnh hợp chập 2 của n điểm.

Nên số véctơ là:$A_n^2=\frac{n!}{\left(n-2\right)!}=n\left(n-1\right)$.

Đề bài. Cho đoạn thẳng MN = 24cm và điểm O nằm giữa hai điểm M và N. Gọi E là trung điểm của đoạn thẳng OM, F là trung điểm của đoạn thẳng ON, I là trung điểm đoạn thẳng EF. Độ dài đoạn thẳng IE là ...cm.

Lời giải:

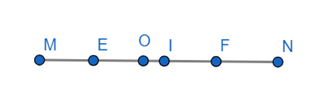
O là trung điểm MN nên OM = ON = $\frac{1}{2}MN=\frac{24}{2}=12\left(cm\right)$

OE = $\frac{1}{2}OM=\frac{12}{2}=6\left(cm\right)$

OF = $\frac{1}{2}ON=\frac{12}{2}=6\left(cm\right)$

Mà EF = OE + OF = 6 + 6 = 12(cm)

IE = IF = $\frac{1}{2}EF=\frac{12}{2}=6\left(cm\right)$.

Đề bài. Giải phương trình cos3x = cos7x.

Lời giải:

cos3x = cos7x

⇔ $\left[\begin{array}{l}3x=7x+k2\pi \\ 3x=-7x+k2\pi \end{array}\right.$

⇔ $\left[\begin{array}{l}x=-k\frac{\pi }{2}\\ x=k\frac{\pi }{5}\end{array}\right.\left(k\in \mathbb{Z}\right)$.

Đề bài. Cho đoạn thẳng AB và điểm I sao cho $2\overrightarrow{IA}+3\overrightarrow{IB}=\overrightarrow{0}$.

a) Tìm hệ số k sao cho $\overrightarrow{AI}=k\overrightarrow{AB}$.

b) Chứng minh với mọi M ta có $\overrightarrow{MI}=\frac{2}{5}\overrightarrow{MA}+\frac{3}{5}\overrightarrow{MB}$.

Lời giải:

a) $2\overrightarrow{IA}+3\overrightarrow{IB}=\overrightarrow{0}$

⇔ $-2\overrightarrow{AI}+3\left(\overrightarrow{AB}-\overrightarrow{AI}\right)=\overrightarrow{0}$

⇔ $-5\overrightarrow{AI}=-3\overrightarrow{AB}$

⇔ $\overrightarrow{AI}=\frac{3}{5}\overrightarrow{AB}$

⇔ $k=\frac{3}{5}$

b) $\overrightarrow{MI}=\frac{2}{5}\overrightarrow{MA}+\frac{3}{5}\overrightarrow{MB}$

⇔ $\overrightarrow{MI}=\frac{2}{5}\left(\overrightarrow{MI}+\overrightarrow{IA}\right)+\frac{3}{5}\left(\overrightarrow{MI}+\overrightarrow{IB}\right)$

⇔ $\overrightarrow{MI}=\frac{2}{5}\overrightarrow{MI}+\frac{3}{5}\overrightarrow{MI}+\frac{2}{5}\overrightarrow{IA}+\frac{3}{5}\overrightarrow{IB}$

⇔ $\overrightarrow{MI}=\overrightarrow{MI}+\frac{1}{5}\left(2\overrightarrow{IA}+3\overrightarrow{IB}\right)$

⇔ $\overrightarrow{MI}=\overrightarrow{MI}$ (Luôn đúng).

Đề bài. Cho a, b, c là 3 số dương. Chứng minh: $\sqrt{\frac{a^3}{b^3}}+\sqrt{\frac{b^3}{c^3}}+\sqrt{\frac{c^3}{a^3}}\ge \frac{a}{b}+\frac{b}{c}+\frac{c}{a}$.

Lời giải:

Đặt $\sqrt{\frac{a}{b}}=x;\sqrt{\frac{b}{c}}=y;\sqrt{\frac{c}{a}}=z$

BĐT cần chứng minh trở thành: x³ + y³ + z³ ≥ x² + y² + z² với xyz = 1

Thật vậy, áp dụng BĐT Côsi:

(x³ + y³ + z³)(x + y + z) ≥ (x² + y² + z²)²

⇔ x³ + y³ + z³ ≥ $\frac{{\left(x^2+y^2+z^2\right)}^2}{x+y+z}\left(1\right)$

Theo BĐT AM-GM có:

x² + y² + z² ≥ xy + yz + xz

⇔ 3(x² + y² + z²) ≥ (x + y + z)²

⇔ x² + y² + z² ≥ $\frac{{\left(x+y+z\right)}^2}{3}\ge \frac{\left(x+y+z\right).3\sqrt[3]{xyz}}{3}=x+y+z$(2)

Từ (1) và (2) suy ra: x³ + y³ + z³ ≥ x² + y² + z² (đpcm)

Dấu “=” xảy ra khi x = y = z = 1 hay a = b = c.

Đề bài. Giải phương trình: $\cos \left(4x+\frac{\pi }{3}\right)-\sin \left(x-\frac{\pi }{4}\right)=0$.

Lời giải:

$\cos \left(4x+\frac{\pi }{3}\right)-\sin \left(x-\frac{\pi }{4}\right)=0$

⇔$\cos \left(4x+\frac{\pi }{3}\right)=\sin \left(x-\frac{\pi }{4}\right)$

⇔$\cos \left(4x+\frac{\pi }{3}\right)=\cos \left(\frac{\pi }{2}-x+\frac{\pi }{4}\right)$

⇔$\cos \left(4x+\frac{\pi }{3}\right)=\cos \left(\frac{3\pi }{4}-x\right)$

⇔$\left[\begin{array}{l}4x+\frac{\pi }{3}=\frac{3\pi }{4}-x+k2\pi \\ 4x+\frac{\pi }{3}=-\frac{3\pi }{4}+x+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

⇔ $\left[\begin{array}{l}x=\frac{\pi }{12}+k\frac{2\pi }{5}\\ x=-\frac{13\pi }{36}+k\frac{2\pi }{3}\end{array}\right.\left(k\in \mathbb{Z}\right)$.

2

Đề bài. Cho hình chóp SABCD có đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm AB, SC.

a) Xác định giao điểm I, K của AN, MN với (SBD).

b) Tính tỉ số $\frac{IA}{IN};\frac{KM}{KN}$.

c) Chứng minh B, I, K thẳng hàng. Tính tỉ số $\frac{IB}{IK}$.

Lời giải:

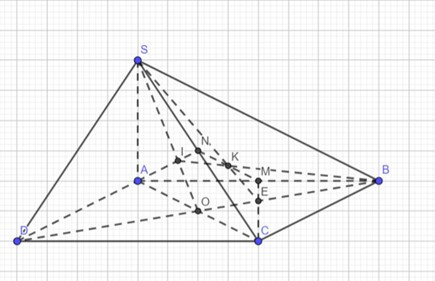
a) Gọi AC ∩ BD = O, SO ∩ AN = I

⇒ AN ∩ (SBD) = I

CM ∩ BO = E, SE ∩ MN = K ⇒ MN ∩ (SBD) = K

b, c) Ta có M, N là trung điểm AB, SC; O là trung điểm AC, BD

⇒ I, E là trọng tâm SAC, BAC

⇒ $\frac{IA}{IN}=2$

Ta có: M, K, N thẳng hàng; M ∈ CE, K ∈ SE, N ∈ SC

Suy ra: $\frac{MC}{ME}.\frac{KE}{KS}.\frac{NS}{NC}=1$

⇒ $3.\frac{KE}{KS}.1=1$

⇒ $\frac{KE}{KS}=\frac{1}{3}$

⇒ $\frac{BO}{BE}.\frac{KE}{KS}.\frac{IS}{IO}=\frac{3}{2}.\frac{1}{3}.2=1$

Vậy B, I, K thẳng hàng (định lý Menelauyt)

Ta có: S, K, E thẳng hàng nên $\frac{SC}{SN}.\frac{KN}{KM}.\frac{EM}{EC}=1$

⇒

⇒

Lại có từ S, K, E thẳng hàng nên $\frac{SO}{SI}.\frac{KI}{KB}.\frac{EB}{EO}=1$

⇒ $\frac{3}{2}.\frac{KI}{KB}.2=1$

⇒ $\frac{KI}{KB}=\frac{1}{3}$

⇒ $\frac{KI}{KB+KI}=\frac{1}{3+1}$

Hay $\frac{KI}{IB}=\frac{1}{4}$

Suy ra: $\frac{IB}{IK}=4$.

Đề bài. Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A(−1;1); B(3;1); C(2;4). Tính chu vi và diện tích tam giác ABC.

Lời giải:

$\overrightarrow{AB}=\left(4;0\right),\overrightarrow{AC}=\left(3;3\right),\overrightarrow{BC}=\left(-1;3\right)$

AB =$\sqrt{4^2+0}=4$

AC = $\sqrt{3^2+3^2}=3\sqrt{2}$

BC =$\sqrt{{\left(-1\right)}^2+3^2}=\sqrt{10}$

Chu vi tam giác ABC = AB + AC + BC =$4+3\sqrt{2}+\sqrt{10}$

$\overrightarrow{BC}=\left(-1;3\right)\Rightarrow \overrightarrow{n_{BC}}=\left(-3;-1\right)$

Phương trình đường thẳng BC là: -3(x – 3) + -1(y – 1) = 0 hay -3x – y + 10 = 0

d(A, BC) = $\frac{\left|\left(-1\right).\left(-3\right)+1.\left(-1\right)+10\right|}{\sqrt{{\left(-3\right)}^2+{\left(-1\right)}^2}}=\frac{12}{\sqrt{10}}$

S_ABC = $\frac{1}{2}d\left(A;BC\right).BC=\frac{1}{2}.\frac{12}{\sqrt{10}}.\sqrt{10}=6\left(dvdt\right)$.

Đề bài. Một chữ nhật hình có chiều dài gấp 4 lần chiều rộng. Tăng chiều dài và chiều rộng lên 2m thì diện tích tăng thêm 94m². Tinh chu vi và diện tích ban đầu của hình chữ nhật đó?

Lời giải:

Gọi chiều rộng là a, thì chiều dài là 4a.

Diện tích ban đầu là: 4a.a = 4a²

Ta có: (4a + 2)(a + 2) = 4a.a + 94

⇔ 4a² + 10a + 4 = 4a² + 94

⇔ 10a + 4 = 94

⇔ 10a = 90

⇔ a = 9

Vậy chiều rộng là 9m

Chiều dài là: 9.4 = 36 (m)

Chu vi hình chữ nhật là: (36 + 9).2 = 90 (m)

Diện tích hình chữ nhật là: 36.9 = 324 (m²).

Đề bài. Cho tam giác ABC có AB = 2, BC = 3, AC = 4. Tính độ dài đường trung tuyến MA với M là trung điểm của BC.

Lời giải:

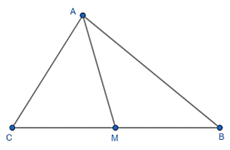
Ta có công thức tính độ dài đường trung tuyến:

MA² = $\frac{A{B}^2+A{C}^2}{2}-\frac{B{C}^2}{4}=\frac{2^2+4^2}{2}-\frac{3^2}{4}=\frac{31}{4}$

Suy ra: MA = $\frac{\sqrt{31}}{2}$.

Đề bài. Cho A = 1 + 2¹ + 2² + 2³ + … + 2²⁰²¹. Tìm x thuộc ℕ sao cho 2^x = A + 1.

Lời giải:

A = 1 + 2¹ + 2² + 2³ + … + 2²⁰²¹

2A = 2(1 + 2¹ + 2² + … + 2²⁰²¹) = 2 + 2² + … + 2²⁰²²

2A – A = (2 + 2² + … + 2²⁰²²) – (1 + 2¹ + 2² + 2³ + … + 2²⁰²¹)

A = 2²⁰²² – 1

Lại có: 2^x = A + 1 = 2²⁰²² – 1 + 1 = 2²⁰²²

Vậy x = 2022.

Đề bài. Tìm giá trị của m để (m + 1)x² – 2(m + 1)x + 4 ≥ 0 với mọi x thuộc ℝ.

Lời giải:

Với m = -1 ta có: 4 ≥ 0 với mọi x thuộc ℝ (thỏa mãn)

Với m khác -1, ta có:

(m + 1)x² – 2(m + 1)x + 4 ≥ 0, ∀x ∈ ℝ khi và chỉ khi:

$\left\{\begin{array}{l}m+1>0\\ \Delta \text{'}={\left(m+1\right)}^2-4\left(m+1\right)\le 0\end{array}\right.$

⇔ $\left\{\begin{array}{l}m>-1\\ \left(m+1\right)\left(m-3\right)\le 0\end{array}\right.$

⇔ $\left\{\begin{array}{l}m>-1\\ -1\le m\le 3\end{array}\right.$

⇔ -1 < m ≤ 3.

Kết hợp lại ta được: -1 ≤ m ≤ 3.

Đề bài. Cho tam giác ABC cân tại A. Gọi D, E, F lần lượt là trung điểm của AB, AC, BC. Điểm I đối xứng với F qua E. Chứng minh tứ giác BDEC là hình thang cân.

Lời giải:

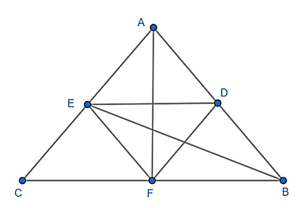
Xét ΔABC, ta có:

AD = DB (gỉa thiết)

AE = EC (gỉa thiết)

⇒ DE là đường trung bình của ΔABC

⇒ DE // BC

⇒ Tứ giác DECB là hình thang

mà (vì ΔABC cân tại A)

⇒ Tứ giác DECB là hình thang cân.

Đề bài. Cho tanα = $\frac{1}{2}$. Tính $\frac{\cos \alpha +\sin \alpha }{\cos \alpha -\sin \alpha }$.

Lời giải:

$\tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{1}{2}$. ⇒ cosα = 2sinα

Ta có: $\frac{\cos \alpha +\sin \alpha }{\cos \alpha -\sin \alpha }=\frac{2\sin \alpha +\sin \alpha }{2\sin \alpha -\sin \alpha }=\frac{3\sin \alpha }{\sin \alpha }=3$.

Đề bài. Cho tam giác ABC có trung tuyến AM , Gọi I là trung điểm AM , D là giao điểm BI và AC. Chứng minh AD = $\frac{1}{3}AC$.

Lời giải:

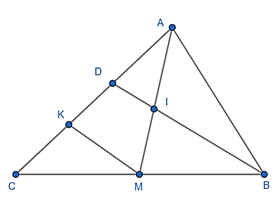
Gọi K là trung điểm của CD

Xét ΔBDC có:

M là trung điểm của BC

K là trung điểm của CD

Do đó: MK là đường trung bình của ΔBDC

⇒ MK // BD

hay ID // MK

Xét ΔAMK có:

I là trung điểm của AM

ID // MK

Do đó: D là trung điểm của AK

⇒ AD = DK = KC

Vậy AD = $\frac{1}{3}AC$.

Đề bài. Tìm điều kiện của tham số m dể phương trình cos²x − 4cosx + m = 0 có nghiệm.

Lời giải:

Xét phương trình: cos²x – 4cosx + m = 0 (1)

Đặt t = cosx (|t| ≤ 1)

Khi đó phương trình (1) trở thành: t² – 4t + m = 0 (2)

Để phương trình (1) có nghiệm khi phương trình (2) có nghiệm thỏa mãn |t| ≤ 1

Phương trình (2) có nghiệm khi:

Δ′ ≥ 0 ⇔ 4 – m ≥ 0 ⇔ m ≤ 4

Khi đó phương trình có nghiệm là: $\left[\begin{array}{l}t=2+\sqrt{4-m}\\ t=2-\sqrt{4-m}\end{array}\right.$

Mà |t| ≤ 1

⇔ $\left[\begin{array}{l}\left|2+\sqrt{4-m}\right|\le 1\\ \left|2-\sqrt{4-m}\right|\le 1\end{array}\right.$

⇔ $\left[\begin{array}{l}\sqrt{4-m}\le -1\left(L\right)\\ \left|2-\sqrt{4-m}\right|\le 1\end{array}\right.$

⇔ $\left|2-\sqrt{4-m}\right|\le 1$

⇔ $\left[\begin{array}{l}2-\sqrt{4-m}\le 1\\ 2-\sqrt{4-m}\ge -1\end{array}\right.$

⇔ $\left[\begin{array}{l}\sqrt{4-m}\ge 1\\ \sqrt{4-m}\le 3\end{array}\right.$

⇔ $\left[\begin{array}{l}\sqrt{4-m}\ge 1\\ \sqrt{4-m}\le 3\end{array}\right.$

⇔ $\left[\begin{array}{l}m\le 3\\ m\ge -5\end{array}\right.$

⇔ -5 ≤ m ≤ 3.

Kết hợp với điều kiện (*) ta được: −5 ≤ m ≤ 3

Vậy với −5 ≤ m ≤ 3 thì phương trình đã cho có nghiệm.

Đề bài. Tính C = $\frac{1}{2}+\frac{1}{2^3}+\frac{1}{2^5}+\mathrm{...}+\frac{1}{2^{99}}$.

Lời giải:

C = $\frac{1}{2}+\frac{1}{2^3}+\frac{1}{2^5}+\mathrm{...}+\frac{1}{2^{99}}$

4C = $2+\frac{1}{2}+\frac{1}{2^3}+\mathrm{...}+\frac{1}{2^{97}}$

4C – C = $\left(2+\frac{1}{2}+\frac{1}{2^3}+\mathrm{...}+\frac{1}{2^{97}}\right)-\left(\frac{1}{2}+\frac{1}{2^3}+\frac{1}{2^5}+\mathrm{...}+\frac{1}{2^{99}}\right)$

3C = $2-\frac{1}{2^{99}}$

C = $\frac{2}{3}-\frac{1}{{3.2}^{99}}=\frac{3.\left(2^{100}-1\right)}{3^2{.2}^{99}}=\frac{2^{100}-1}{{3.2}^{99}}$.

Đề bài. Cho đường tròn (O) đường kính AB, lấy điểm C thuộc đường tròn (O), với C không trùng A và B. Gọi I là trung điểm của đoạn AC. Vẽ tiếp tuyến của đường tròn (O) tại tiếp điểm C cắt tia OI tại điểm D.

a) Chứng minh OI song song với BC.

b) Chứng minh DA là tiếp tuyến của đường tròn (O).

c) Vẽ CH vuông góc với AB, H ∈ AB và vẽ BK vuông góc với CD, K ∈ CD. Chứng minh CK² = HA.HB.

Lời giải:

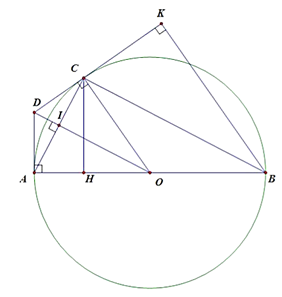
a) Vì DC = DA (tính chất hai tiếp tuyến cắt nhau tại D) và OA = OC = R

Nên OD là trung trực AC nên OD ⊥ AC

Mà I là trung điểm AC nên I thuộc OD

Lại có: $\widehat{ACB}=90°$ (góc nội tiếp chắn nửa đường tròn)

⇒ AC ⊥ CB

Suy ra: OD // BC hay OI // BC

b) Xét tam giác OCD và OAD có:

OC = OA = R

OD chung

DA = DC

⇒ ∆OCD = ∆OAD (c.c.c)

⇒ $\widehat{DCO}=\widehat{DAO}=90°$

⇒ DA ⊥ AB và A trên (O) nên DA là tiếp tuyến của (O).

c) $\widehat{OCB}=\widehat{OBC}$

OC // BK (cùng vuông góc với CD)

Nên $\widehat{OCB}=\widehat{CBK}$

Suy ra: $\widehat{OBC}=\widehat{CBK}$

Xét tam giác CHB và CKB có:

$\widehat{H}=\widehat{K}=90°$

Cạnh BC chung

$\widehat{HBC}=\widehat{OBC}=\widehat{CBK}$

Vậy ∆CHB = ∆CKB (g.c.g)

Suy ra: CK = CH

Áp dụng hệ thức lượng trong tam giác ABC vuông có: CH² = HA.HB

Mà CH = CK nên CK² = HA.HB.

Đề bài. Gọi M là trung điểm của đoạn thẳng AB. Trên 2 nửa phẳng đối nhau bờ AB lần lượt vẽ 2 tia Ax, By vuông góc AB. Trên Ax lấy điểm P, Trên Ay lấy Q sao cho AP = BQ. Chứng minh P, Q, M thẳng hàng.

Lời giải:

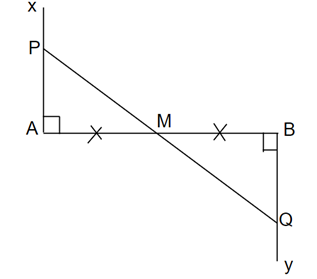
Xét tam giác APM và tam giác BQM có:

AP = BQ (giả thiết)

$\widehat{PAM}=\widehat{QBM}=90°$

AM = MB (giả thiết)

⇒ ∆APM = ∆BQM (c.g.c)

⇒ $\widehat{AMP}=\widehat{BMQ}$ (2 góc tương ứng)

Mà ta có: $\widehat{AMP}+\widehat{PMB}=180°$

⇒ $\widehat{BMQ}+\widehat{PMB}=180°$

Hay P, Q, M thẳng hàng.

Đề bài. Cho tam giác ABC, gọi BM và CN lần lượt là các đường trung tuyến sao cho BM vuông góc với CN. Chứng minh cotA = 2 (cotB + cotC).

Lời giải:

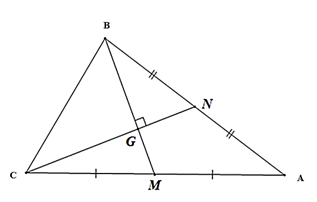
Theo định lý cosin: cosA = $\frac{b^2+c^2-a^2}{2bc}$

Và sinA = $\frac{a}{2R}$

cotA = $\frac{\cos A}{\sin A}=\frac{b^2+c^2-a^2}{2bc}:\frac{a}{2R}=\frac{b^2+c^2-a^2}{abc}.R=\frac{b^2+c^2-a^2}{4S}$ (*)

Lại có theo công thức tính độ dài đường trung tuyến của tam giác ta có:

BM² = $\frac{a^2+c^2}{2}-\frac{b^2}{4}$

CN² = $\frac{c^2+b^2}{2}-\frac{a^2}{4}$

Suy ra: a² = BC² = BG² + GC² = $\frac{4}{9}B{M}^2+\frac{4}{9}C{N}^2$= $\frac{4}{9}\left(\frac{a^2+c^2}{2}-\frac{b^2}{4}\right)+\frac{4}{9}\left(\frac{c^2+b^2}{2}-\frac{a^2}{4}\right)$

⇔ a² = $\frac{4}{9}\left(\frac{b^2+c^2}{4}+a^2\right)$

⇔ 9a² = b² + c² + 4a²

⇔ 5a² = b² + c² (**)

Thay (**) vào (*): cotA = $\frac{5a^2-a^2}{4S}=\frac{4a^2}{4S}=\frac{a^2}{S}\left(1\right)$

Mặt khác cotB + cotC = $\frac{a^2+c^2-b^2}{4S}+\frac{a^2+b^2-c^2}{4S}$

⇒ cotB + cotC = $\frac{2a^2}{4S}=\frac{a^2}{2S}$(2)

Từ (1) và (2) suy ra: cotA = 2 (cotB+cotC) = $\frac{a^2}{S}$

Vậy cotA = 2 (cotB + cotC).

Đề bài. Chứng tỏ rằng các số có dạng $\overline{aa}$ chia hết cho 11.

Lời giải:

$\overline{aa}$ = 10a + a = 11a

Vì 11 chia hết cho 11 nên 11a ⋮ 11

Vậy $\overline{aa}$⋮ 11.

Đề bài. Tìm 2 số tự nhiên nhỏ nhất a và b thỏa mãn ƯCLN(a, b) = 12 và a – b = 84.

Lời giải:

Từ a – b = 84 ta thấy a > b

Vì ƯCLN(a;b) = 12 nên a ⋮ 12, b ⋮ 12

Ta giả sử a = 12m, b = 12n (m, n ∈ ℕ^*) (m > n)

Ta có: a – b = 84

⇔ 12m – 12n = 84

⇔ m – n = 7

Để a, b là số tự nhiên nhỏ nhất thì m, n nhỏ nhất

Suy ra: n = 1; m = 8.

Vậy a = 96; b = 12.

Đề bài. Cho ba số x, y, z thỏa mãn x² + y² + z² = xy + yz + zx và x + y + z = -3. Tính giá trị biểu thức B = x²⁰²² + y²⁰²³ + z²⁰²⁴.

Lời giải:

x² + y² + z² = xy + yz + zx

⇔ 2x² + 2y² + 2z² = 2xy + 2yz + 2zx

⇔ (x – y)² + (y – z)² + (z – x)² = 0 (*)

Mà (x – y)² + (y – z)² + (z – x)² ≥ 0 với mọi x, y, z nên để đẳng thức (*) xảy ra thì:

$\left\{\begin{array}{l}x-y=0\\ y-z=0\\ z-x=0\end{array}\right.$ hay x = y = z

Mà x + y + z = -3

⇔ x = y = z = -1

B = x²⁰²² + y²⁰²³ + z²⁰²⁴ = 1 – 1 + 1 = 1.

Đề bài. Viết $\frac{3}{2}$ thành 3 phân số thập phân rồi chuyển 3 phân số đó thành số thập phân.

Lời giải:

$\frac{3}{2}=\frac{15}{10}=\frac{150}{100}=\frac{1500}{1000}$

$\frac{15}{10}=\frac{150}{100}=\frac{1500}{1000}=1,5$.

Đề bài. Cho a, b, c là các số thực dương thỏa mãn a + b + c + ab + bc + ac = 6. Chứng minh rằng: $\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\ge 3$.

Lời giải:

Đặt P = $\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}$

Có a, b, c là các số thực dương, theo bất đẳng thức AM-GM có:

$\left\{\begin{array}{l}\frac{a^3}{b}+ab\ge 2a^2\\ \frac{b^3}{c}+bc\ge 2b^2\\ \frac{c^3}{a}+ac\ge 2c^2\end{array}\right.$

Suy ra: P = $\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\ge 2\left(a^2+b^2+c^2\right)-\left(ab+bc+ca\right)$

Mà a + b + c + ab + bc + ac = 6

⇒ P ≥ 2(a² + b² + c²) + a + b + c – 6

Có (a – b)² + (b – c)² + (c – a)² ≥ 0

⇒ 2(a² + b² + c²) ≥ 2(ab + bc + ca)

Suy ra: P ≥ $\frac{2}{3}{\left(a+b+c\right)}^2+\left(a+b+c\right)-6$

Có ab + bc + ca ≤ a² + b² + c²

⇒ 3(ab + bc + ca) ≤ (a + b + c)²

Do đó: 6 = a + b + c + ab + bc + ac ≤ a + b + c + $\frac{1}{3}{\left(a+b+c\right)}^2$

⇒ $\frac{1}{3}{\left(a+b+c\right)}^2$+ (a + b + c) – 6 ≥ 0

⇒ a + b + c ≥ 3(a + b + c)² ≥ 9

Suy ra: P ≥ $\frac{2}{3}.9+3-6=3$

Dấu “=” xảy ra khi a = b = c.

Đề bài. Một can nếu đựng đầy dầu cân nặng 72 kg, nếu đựng nửa số dầu đó thì cân nặng 38kg. Hỏi cái can rỗng thì nặng bao nhiêu ki-lô-gam?

Lời giải:

Can + dầu = 72kg

Can + nửa số dầu = 38 kg

Nửa số dầu nặng là: 72 – 38 = 36 (kg)

Cái can rỗng nặng là: 38 – 36 = 2 (kg).

Đề bài. Bác Bình gửi tiết kiệm 500 triệu đồng kì hạn 1 tháng với lãi suất 6% một năm theo hình thức lãi suất kép. Nếu sau đúng một năm bác Bình mới đến ngân hàng rút tiền thì số tiền lãi là bao nhiêu?

Lời giải:

Lãi suất một kỳ hạn của bác Bình là: 6% : 12 = 0,5%

Vì bác Bình sau đúng 1 năm mới rút tiền nên số tiền lãi bác nhận được là:

A_lãi = A – A_gốc = A_gốc(1 +r%)ⁿ - A_gốc

= 500.10⁶(1 + 0,5%)¹² – 500.10⁶

= 30,83 (triệu đồng)

Vậy sau đúng một năm bác Bình mới đến ngân hàng rút tiền thì số tiền lãi là 30,83 triệu.

Đề bài. Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên đường tròn (M khác A; B) vẽ tiếp tuyến với nửa đường tròn, cắt Ax và By lần lượt tại C và D.

a) Chứng minh $\widehat{COD}=90°$.

b) Chứng minh AC.BD không đổi.

Lời giải:

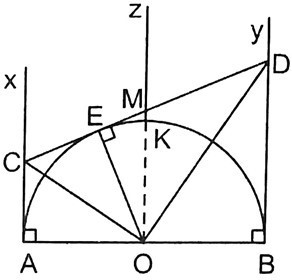
Theo tính chất của hai tiếp tuyến cắt nhau ta có:

• OC là tia phân giác của $\widehat{AOM}$

• OD và tia phân giác của $\widehat{BOM}$

Khi đó, OC và OD là các tia phân giác của hai góc kề bù $\widehat{AOM}$ và $\widehat{BOM}$

Do đó OC ⊥ OD.

Vậy $\widehat{COD}=90°$ (đpcm)

b) Ta có: AC = CM, BD = DM nên AC . BD = CM . MD.

Xét ΔCOD vuông tại O, ta có:

CM . MD = OM² = R² (R là bán kính đường tròn O).

Vậy AC . BD = R² (không đổi).

Đề bài. Cho tam giác ABC( AB < AC ) có hai đường phân giác CM, BN cắt nhau ở D. Qua A kẻ AE và AF vuông góc với BN và CM. Các đường thẳng AE và AF cắt BC ở I; K.

a) Chứng minh AFDE nội tiếp.

b) Chứng minh AB.NC = AN.BC.

Lời giải:

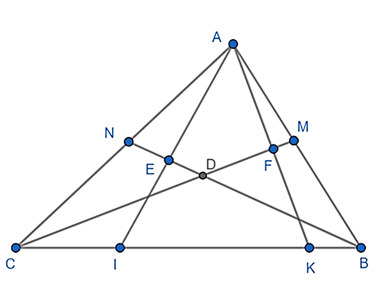
a) Xét tứ giác AFDE có: $\widehat{AED}=\widehat{AFD}=90°$

Suy ra: $\widehat{AED},\widehat{AFD}$ cùng nhìn AD dưới 1 góc 90 độ không đổi

Hay tứ giác AFDE nội tiếp.

b) Vì BN, CM cắt nhau tại D nên AD là đường phân giác thứ ba của tam giác ABC.

Áp dụng tính chất đường phân giác, ta có:

Xét ∆ABN có AD là phân giác: $\frac{BD}{DN}=\frac{AB}{AN}\left(1\right)$

Xét ∆CBN có CD là phân giác: $\frac{BD}{BN}=\frac{BC}{CN}\left(2\right)$

Từ (1) và (2) suy ra: $\frac{BC}{CN}=\frac{AB}{AN}$

Vậy AB.NC = AN.CB.

Đề bài. Cho tam giác ABC có đường cao AH và BD cắt nhau tại I.

a) Chứng minh 4 điểm C, D, I, H cùng thuộc 1 đường tròn.

b) Chứng minh 4 điểm A, B, H, D cùng thuộc 1 đường tròn.

c) Tính bán kính đường tròn đi qua 4 điểm C, D, H, I nếu biết CH = 4cm và $\widehat{HAB}$ = 30°.

Lời giải:

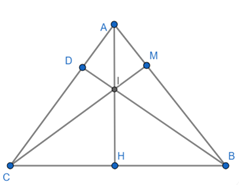
a) Xét tam giác DIC vuông tại D (BD ⊥ AC)

⇒ D, I, C cùng thuộc đường tròn đường kính IC

Xét tam giác HIC vuông tại H (AH ⊥ BC)

⇒ H, I, C cùng thuộc đường tròn đường kính IC

Vậy D, I, C, H cùng thuộc đường tròn đường kính IC

b) Xét tam giác ABH vuông tại H (AH ⊥ BC)

⇒ A, B, H cùng thuộc đường tròn đường kính AB

Xét tam giác ABD vuông tại D (BD ⊥ AC)

⇒ A, B, D cùng thuộc đường tròn đường kính AB

Vậy A, B, H, D cùng thuộc đường tròn đường kính AB

c) Gọi M là giao điểm của CI và AB

Xét tam giác BAC có: AH và BD là đường cao, AH ∩ BD ={I}

Nên I là trực tâm của tam giác BAC

Vậy AM là đường cao thứ 3 của tam giác ABC

Xét ∆ABH và ∆CBM có:

$\widehat{B}$ chung

$\widehat{AHB}=\widehat{CMB}=90°$

⇒ ∆ABH ~ ∆CBM (g.g)

⇒ $\widehat{BCM}=\widehat{HAB}$ = 30°

Xét ∆HCI vuông tại H có: cos$\widehat{HCI}=\frac{CH}{CI}\Rightarrow \cos 30°=\frac{4}{CI}\Rightarrow CI=\frac{8\sqrt{3}}{3}\left(cm\right)$

Mà đường tròn đi qua D, I, C, H là đường tròn đường kính IC

Suy ra bán kính đường tròn là $\frac{1}{2}CI=\frac{4\sqrt{3}}{3}\left(cm\right).$

Đề bài. Cho tam giác vuông ABC vuông ở A có đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB và AC.

a. So sánh AH và EF.

b. Tính độ dài HF biết AB = 6 cm, BC = 10 cm và BH = 3,6 cm.

Lời giải:

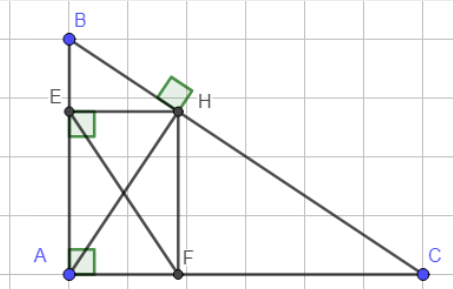
a) Xét tứ giác AEHF có: $\widehat{A}=\widehat{E}=\widehat{F}=90°$

Nên AEHF là hình chữ nhật

Suy ra: AH = EF

b) Xét tam giác AHE và tam giác AHB có:

$\widehat{A}$ chung

$\widehat{AEH}=\widehat{AHB}=90°$

⇒ ∆AEH ∽ ∆AHB (g.g)

⇒ $\frac{AE}{AH}=\frac{AH}{AB}$

⇒ AE = $\frac{A{H}^2}{AB}=\frac{A{B}^2-B{H}^2}{AB}=\frac{6^2-3,6^2}{6}=3,84\left(cm\right)$.

Đề bài. Rút gọn M = sin(x – y)cosy + cos(x – y)siny

Lời giải:

M = sin(x – y)cosy + cos(x – y)siny

M = sin[(x – y) + y]

M = sin x.

Đề bài. Cho tam giác ABC vuông tại A. Trên tia đối của tia AC kẻ tia Ax. Trên Ax lấy điểm D sao cho AD = AB. Kẻ tia Ay nằm trong BAD. Kẻ DH vuông góc với Ay tại H, kẻ BI vuông góc với Ay tại I.

a) Chứng minh rằng DH = AI; AH = BI.

b) Gọi M là trung điểm của BD. Chứng minh rằng Tam giácMDH = tam giác AMI.

c) Chứng minh rằng MHI là tam giác vuông.

Lời giải:

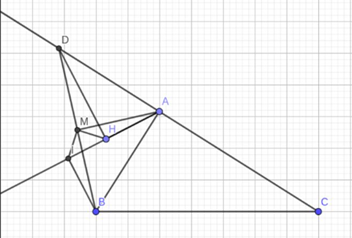
a) Xét tam giác ABI, ADH có:

$\widehat{I}=\widehat{H}=90°$

AB = AD

$\widehat{IAB}=90°-\widehat{HAD}=\widehat{D}$

⇒ ΔABI = ΔDAH (cạnh huyền-góc nhọn)

⇒ AI = DH, BI = AH

Ta có: AI = DH, BI = AH

b) Ta có: AD = AB, AD ⊥ AB

⇒ ΔADB vuông cân tại A

M là trung điểm BD

⇒ ΔABM, ΔAMD vuông cân tại M

⇒ MA = MD = MB

Xét ΔMDH và ΔMAI có:

MD = MA

$\widehat{MDH}=\widehat{MDA}-\widehat{HDA}=45°-\widehat{HDA}=45°-\widehat{IAB}=\widehat{MAB}-\widehat{IAB}=\widehat{MAI}$

DH = AI

⇒ ΔMDH = ΔMAI (c.g.c)

c) Từ câu b, suy ra: MI = MH, $\widehat{IMA}=\widehat{DMH}$

$\widehat{IMH}+\widehat{HMA}=\widehat{DMA}+\widehat{HMA}$

⇒ $\widehat{IMH}=\widehat{AMD}=90°$

Suy ra: Tam giác MHI vuông cân tại M.

Đề bài. Cho tam giác ABC vuông tại A, đường cao AH biết BH = 3.6 cm; CH = 6.4 cm

a) Tính AH, AB và số đo góc $\widehat{HCA}$.

b) Gọi M và N lần lượt là hình chiếu của H lên AB, AC. Chứng minh AM.AB = AN.AC và tam giác AMN đồng dạng với tam giác ACB.

Lời giải:

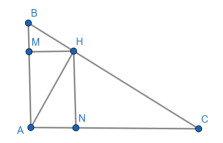
a) Áp dụng hệ thức lượng trong tam giác vuông ta có:

AH² = BH.CH = 3,6 . 6,4 = 23,04

Suy ra: AH = 4,8 cm

AB² = AH² + HB² = 4,8² + 3,6²

⇒ AB = 6 cm

AC = $\sqrt{A{H}^2+H{C}^2}=8\left(cm\right)$

$\tan \widehat{HCA}=\tan \widehat{ACB}=\frac{AB}{AC}=\frac{6}{8}$

⇒ $\widehat{HCA}\approx 36,9°$

b) Xét tam giác AMH và tam giác AHB có:

Chung $\widehat{A}$

$\widehat{AMH}=\widehat{AHB}=90°$

⇒ ∆AMH ~ ∆AHB (g.g)

⇒ $\frac{AM}{AH}=\frac{AH}{AB}$

⇒ AM.AB = AH² (1)

Chứng minh tương tự: ∆ANH ~ ∆AHC (g.g)

⇒ $\frac{AN}{AH}=\frac{AH}{AC}$

⇒ AN.AC = AH² (2)

Từ (1) và (2): AM.AB = AN.AC.

Đề bài. Với mỗi số thực r, ta gọi số nguyên lớn nhất nhỏ hơn hoặc bằng r là phần nguyên của r và kí hiệu là |r|. Có bao nhiêu số nguyên không âm x thỏa mãn $\left|\frac{x}{2023}\right|=\left|\frac{x}{2024}\right|$.

Lời giải:

+ Với x > 0 ta có: $\frac{x}{2023}>\frac{x}{2024}$ nên không có x thỏa mãn

+ Với x < 0 ta có: $\left|\frac{x}{2023}\right|=-\frac{x}{2023};\left|\frac{x}{2024}\right|=-\frac{x}{2024}$ mà $-\frac{x}{2023}>-\frac{x}{2024}$ nên không có x thỏa mãn

+ Với x = 0 thì ta có: $\frac{0}{2023}=\frac{0}{2024}=0$(thỏa mãn)

Vậy x = 0.

Đề bài. Tìm số dư của 2²⁰¹⁷ khi chia cho 11.

Lời giải:

Ta có 2²⁰¹⁷ = 2^{2015 + 2} = 2²⁰¹⁵. 2² = 2^{5 . 403} . 4 = (2⁵)⁴⁰³ . 2.

Vì 2⁵ = 32 chia cho 11 dư – 1 nên (2⁵)⁴⁰³ chia cho 11 dư (– 1)⁴⁰³ = – 1.

Suy ra (2⁵)⁴⁰³ . 4 chia cho 11 dư – 1 . 4 = – 4 hay 2²⁰¹⁷ chia cho 11 dư 7.

Vậy số dư của 2²⁰¹⁷ khi chia cho 11 là 7.

Đề bài. Cho khối chóp S.ABCD đáy là hình chữ nhật, cạnh AB = a, AD = 2a. Hình chiếu vuông góc của S xuống ABCD là trung điểm H của AB. Biết SD = 3a. Tính thể tích khối chóp S.ABCD.

Lời giải:

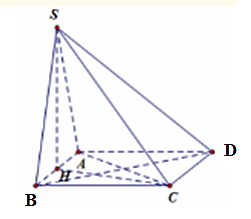
Vì SH vuông góc với đáy nên SH ⊥ HD

Áp dụng định lý Pytago vào tam giác AHD, SHD có:

HD² = AH² + AD² = ${\left(\frac{1}{2}AB\right)}^2+A{D}^2={\left(\frac{a}{2}\right)}^2+{\left(2a\right)}^2=\frac{a^2}{4}+4a^2=\frac{17a^2}{4}$

⇒ HD = $\frac{a\sqrt{17}}{2}$

SD² = SH² + HD²

⇒ SH = $\sqrt{S{D}^2-S{H}^2}=\sqrt{9a^2-\frac{17a^2}{4}}=\frac{a\sqrt{19}}{2}$

Ta có V_S.ABCD = $\frac{1}{3}.SH.S_{ABCD}=\frac{1}{3}.\frac{a\sqrt{19}}{2}.2a.a=\frac{a^3\sqrt{19}}{3}$.