Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 50)

Câu 1: Chứng minh rằng n(n + 1)(2n + 1) chia hết cho 6 với n thuộc mọi số tự nhiên.

Lời giải:

Ta có: n(n + 1)(2n + 1)

= n(n + 1)(2n + 2 – 1)

= n(n + 1)(n + 2 + n – 1)

= n(n + 1)(n + 2) + n(n + 1)(n – 1)

Vì n; n + 1; n + 2 là 3 số tự nhiên liên tiếp và n – 1; n; n + 1 cũng là 3 số tự nhiên liên tiếp.

Ta có: 3 số tự nhiên liên tiếp chắc chắn có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2. Do đó, tích 3 số tự nhiên liên tiếp chia hết cho 3.

Vì 3 số tự nhiên liên tiếp luôn có 2 chẵn 1 lẻ hoặc 2 lẻ 1 chẵn. Do đó, tích 3 số tự nhiên liên tiếp cũng chia hết cho 2.

Vì tích 3 số tự nhiên liên tiếp vừa chia hết cho 2 vừa chia hết cho 3 nên chia hết cho 6.

Vậy n(n + 1)(2n + 1) chia hết cho 6 với n thuộc mọi số tự nhiên.

Câu 2: Cúc đang làm một phép tính mà khi nhân 342 với 1 số có 2 chữ số giống nhau, Cúc đã đặt các tích riêng thẳng cột như trong phép cộng nên Cúc đã tìm ra kết quả ít hơn tích đúng là 12312. Tìm số có 2 chữ số giống nhau đó.

Lời giải:

Gọi số cần tìm là $\overline{aa}$  (0 < a < 10; a ∈ ℕ*)

Ta có:

Khi nhân 342 với $\overline{aa}$  mà đặt các tích riêng thẳng hàng thì tức là ta nhân 342 với lần lượt a và a.

Ta sẽ có: (342 $\overline{aa}$) – (342.a.2) = 12312

⇔ 342.a.11 – 342.a.2 = 12312

⇔ 342.a.(11 – 2) = 12312

⇔ 342.a.9 = 12312

⇔ 342.a = 1368

⇔ a = 4 (thỏa mãn)

Vậy số cần tìm là 44.

Câu 3: Chứng minh rằng với mọi số nguyên n thì n⁷ – n chia hết cho 7.

Lời giải:

Đặt A_n = n⁷ – n.

Khi n = 1 thì A₁ = 0 và chia hết cho 7.

Giả sử đã có A_k = (k⁷ – k) ⋮ 7 (giả thiết quy nạp)

Ta phải chứng minh A_{k + 1} ⋮ 7, tức là (k + 1)⁷ – (k + 1) ⋮ 7.

Áp dụng công thức Nhị thức Niu – tơn ta có:

A_{k + 1} = (k + 1)⁷ – (k + 1)

= k⁷ + 7k⁶ + 21k⁵ + 35k⁴ + 35k³ + 21k² + 7k + 1 – k – 1

= k⁷ – k + 7(k⁶ + 3k⁵ + 5k⁴ + 5k³ +3k² + k).

Theo giả thiết quy nạp thì A_k = k⁷ – k chia hết cho 7, do đó A_{k + 1} ⋮ 7.

Vậy n⁷ – n chia hết cho 7 với mọi số nguyên n.

Câu 4: Bỏ ngoặc rồi tính: 25 – (−17) + 24 – 12.

Lời giải:

25 – (−17) + 24 – 12

= 25 + 17 + 24 – 12

= 54.

Câu 5: Cho hình trụ có bán kính đáy bằng 3 và thể tích bằng 18π. Tính diện tích xung quanh S_xq của hình trụ.

Lời giải:

Ta có: V = πr²h ⇔ 18π = π3²h ⇔ h = 2.

Khi đó S_xq = 2πrh = 12π.

Câu 6: Cho tam giác ABC có A(−5; 6), B(1; −3), C(−1; 1). Tìm tọa độ trung điểm H của BC.

Lời giải:

Trung điểm H của BC có tọa độ là $H\left(\frac{x_B+x_C}{2};\frac{y_B+y_C}{2}\right)$

⇔ $H\left(\frac{1-1}{2};\frac{-3+1}{2}\right)$  ⇔ H(0; −1)

Vậy H(0; −1).

Câu 7: Làm phép tính sau: 2 357 × 24.

Lời giải:

2357 × 24 = 2357 × (20 + 4)

= 2357 × 20 + 2357 × 4

= 47 410 + 9 428

= 56 838.

Vậy 2 357 × 24 = 56 838.

Câu 8: Một mảnh đất hình chữ nhật có chiều dài là 38m, chiều rộng bằng $\frac{3}{4}$  chiều dài, trong đó diện tích đất làm nhà chiếm 25%. Tính:

a) Diện tích của mảnh đất đó.

b) Diện tích đất làm nhà là bao nhiêu mét vuông?

Lời giải:

a) Chiều rộng mảnh đất là:

 $38\times \frac{3}{4}=\mathrm{28,5}$ (m)

Diện tích mảnh đất là:

28,5 ´ 38 = 1083 (m²)

b) Diện tích đất làm nhà:

1083 ´ 25% = 270,75 (m²)

Đáp số:

a) 1083 m.

b) 270,75 m².

Câu 9: Một mảnh đất hình chữ nhật có chiều dài là 40m, chiều rộng bằng $\frac{1}{2}$  chiều dài, trong đó diện tích đất làm nhà chiếm 30%. Tính:

a) Diện tích của mảnh đất đó.

b) Diện tích đất làm nhà là bao nhiêu mét vuông?

Lời giải:

a) Chiều rộng mảnh đất là:

 $40\times \frac{1}{2}=20$(m)

Diện tích mảnh đất là:

20 ´ 40 = 800 (m²)

b) Diện tích đất làm nhà:

800 ´ 30% = 240 (m²)

Đáp số: a) 800 m;

    b) 240 m².

Câu 10: Để lát nền một căn phòng có dạng hình vuông có chu vi là 80 dm. Người ta phải dùng các viên gạch hình vuông để lát, mỗi viên gạch có độ dài cạnh 2 dm và có giá là 25 000 đồng/viên. Tính số viên gạch cần dùng và số tiền mua gạch để lát nền căn phòng đó.

Lời giải:

Độ dài cạnh của căn phòng là:

80 : 4 = 20 (dm)

Diện tích căn phòng là:

20 ´ 20 = 400 (dm²)

Diện tích 1 viên gạch là:

2 ´ 2 = 4 (dm²)

Để lát nền căn phòng cần số viên gạch là:

400 : 4 = 100 (viên)

Số tiền mua gạch để lát nền là:

25 000 ´ 100 = 2500 000 (đồng)

Đáp số: 2 500 000 đồng

Câu 11: Một khu đất hình chữ nhật có diện tích 256 m², chiều rộng là 8 m. Xung quanh khu đất người ta đóng cọc để rào xung quanh, biết rằng khoảng cách giữa hai cọc liền nhau là 4 m. Hỏi cần bao nhiêu cọc để đủ rào xung quanh khu đất đó.

Lời giải:

Chiều dài là: 256 : 8 = 32 (m)

Chu vi hình chữ nhật là: (8 + 32).2 = 80 (m)

Cần số cọc là: 80 : 4 = 20 (cọc)

Đáp số: 20 cọc.

Câu 12: Nếu gửi tiết kiệm theo kì hạn là 12 tháng thì lãi suất hàng tháng là 0,7%. Hỏi 1 người gửi 50 000 000 đồng trong 1 năm thì thu được bao nhiêu tiền lãi? (Tiền lãi của tháng không được cộng vào tiền gửi).

Lời giải:

Một năm thu được số tiền lãi là:

50 000 000 ´ 0,7% ´ 12 = 4 200 000 (đồng)

Đáp số: 4 200 000 đồng.

Câu 13: Bạn Sơn tạo các hình bằng những chiếc tăm giống nhau theo sơ đồ nhứ hình trên (Hình thứ n có n² ô vuông giống nhau và mỗi cạnh hình vuông là một chiếc tăm). Hỏi Sơn phải thêm bao nhiêu chiếc tăm vào hình thứ 2018 để được hình thứ 2019.

A. 8076;

B. 7698;

C. 5346;

D. 6782.

Lời giải:

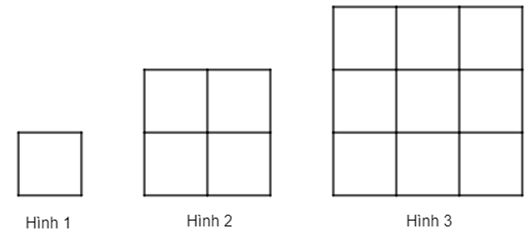
• Với n = 1 ta có hình 1² = 1 ô vuông và cần dùng 4 = 2.1.(1 + 1) (chiếc tăm).

• Với n = 2 ta có hình 2² = 4 ô vuông và cần dùng 12 = 2.2.(2 + 1) (chiếc tăm).

• Với n = 3 ta có hình 3² = 9 ô vuông và cần dùng 24 = 2.3.(3 + 1) (chiếc tăm).

…

Như vậy mỗi số n ta có n² và cần dùng 2n(n + 1) chiếc tăm để tạo thành.

• Với n = 2018 ta có: 2018² ô vuông và cần 2 . 2018 . 2019 (chiếc tăm).

• Với n = 2019 ta có: 2019² ô vuông và cần 2 . 2019 . 2020 (chiếc tăm).

Vậy từ hình thứ 2018 đến 2019 ta cần thêm số chiếc tăm là:

2 . 2019 . 2020 – 2 . 2018 . 2019 = 8 076 (chiếc tăm)

Đáp số: 8076 chiếc tăm

Câu 14: Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là:

A. Đường thẳng qua Svà song song với AD;

B. Đường thẳng quaSvà song song với CD;

C. Đường SO với O là tâm hình bình hành;

D. Đường thẳng qua S và cắt AB.

Lời giải:

Đáp án đúng là: B

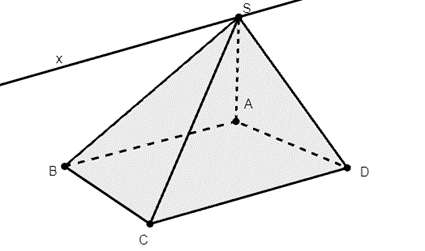
Vì AB//CD nên (SAB) cắt (SCD) theo giao tuyến là đường thẳng Sx, Sx//AB//CD.

Câu 15: Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của mp(SAD) và mp(SBC) là đường thẳng song song với đường thẳng nào trong số các đường thẳng sau?

A. AC;

B. BD;

C.AD;

D. SC.

Lời giải:

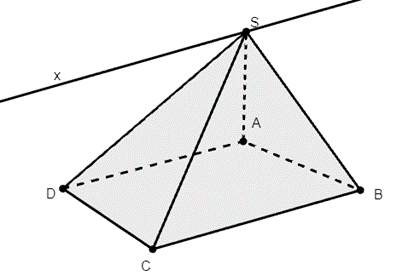
Xét (SAD) và (SBC) có:

S là điểm chung

AD // BC

Do đó giao tuyến của (SAD) và (SBC) là đường thẳng đi qua S và song song với AD.

Câu 16: Tìm điểm cố định mà đường thẳng y = (m – 2)x + 3 luôn đi qua với mọi giá trị của m.

Lời giải:

y = (m – 2)x + 3 (d)

Giả sử I(x₀; y₀) là điểm cố định mà (d) luôn đi qua.

Khi đó ta có:

y₀ = (m – 2)x₀ + 3

⇔ y₀ = mx₀ – 2x₀ + 3

⇔ mx₀ = y₀ + 2x₀ – 3

⇔ $\left\{\begin{array}{l}{x}_0=0\\ 2x_0+y_0-3=0\end{array}\right.\iff \left\{\begin{array}{l}{x}_0=0\\ y_0=3\end{array}\right.$

Câu 17: Cho hàm số y = (2m – 3)x + m – 1. Chứng minh rằng đồ thị hàm số đi qua điểm cố định với mọi giá trị của m. Tìm điểm cố định ấy.

Lời giải:

Gọi M(x₀; y₀) là điểm cố định mà đường thẳng (d) luôn đi qua. Khi đó ta có:

y₀ = (2m – 3)x₀ + m – 1

⇔ y₀ = 2mx₀ – 3x₀ + m – 1

⇔ y₀ – 2mx₀ – 3x₀ + m – 1 = 0

⇔ m(–2x₀ + 1) + (y₀ – 3x₀ – 1) = 0

$$\begin{gathered} \Rightarrow \left\{\begin{array}{l}-2x_0+1=0\\ y_0-3x_0-1=0\end{array}\right.\iff \left\{\begin{array}{l}{x}_0=\frac{1}{2}\\ y_0=\frac{5}{2}\end{array}\right. \\ \Rightarrow M\left(\frac{{\displaystyle 1}}{{\displaystyle 2}};\frac{{\displaystyle 5}}{{\displaystyle 2}}\right) \end{gathered}$$

Vậy với mọi m, họ các đường thẳng (d) có phương trình y = (m + 1)x + 2x – m luôn đi qua mọt điểm M cố định có tọa độ $M\left(\frac{1}{2};\frac{5}{2}\right)$ .

Câu 18: Viết kết quả phép tính dưới dạng một lũy thừa.

a) 3².9³;

b) 2².5²;

c) 8⁵.2³;

d) 9⁸ : 3².

Lời giải:

a) 3² . 9³ = 3² . (3²)³ = 3² . 3⁶ = 3⁸;

b) 2².5² = (2.5)² = 10²;

c) 8⁵ . 2³ = (2³)⁵ . 2³ = 2¹⁵ . 2³ = 2¹⁸;

d) 9⁸ : 3² = (3²)⁸ : 3² = 3¹⁶ : 3² = 3¹⁴.

Câu 19: Cho hàm số y = mx³ – mx² – (m +4)x + 2. Xác định m để hàm số đã cho nghịch biến trên ℝ.

Lời giải:

Ta xét trường hợp hàm số suy biến. Khi m = 0, hàm số trở thành y = −x + 2. Đây là hàm bậc nhất nghịch biến trên ℝ. Vậy m = 0 thỏa mãn yêu cầu bài toán.

Với m ≠ 0, hàm số là hàm đa thức bậc 3.

Y’ = 3mx² – 2mx² – (m + 4)

Do đó hàm số nghịch biến trên ℝ khi và chỉ khi:

$$\begin{gathered} \left\{\begin{array}{l}m<0\\ \Delta \text{'}\le 0\end{array}\right.\iff \left\{\begin{array}{l}m<0\\ m^2+3m\left(m+4\right)\le 0\end{array}\right. \\ \iff \left\{\begin{array}{l}m<0\\ 4m^2+12m\le 0\end{array}\right.\iff \left\{\begin{array}{l}m<0\\ -3\le m\le 0\end{array}\right. \\ \iff \left\{\begin{array}{l}m<0\\ -3\le m\le 0\end{array}\right. \end{gathered}$$

 ⇔ −3 ≤ m < 0.

Kết hợp 2 trường hợp ta được −3 ≤ m ≤ 0 0 thỏa mãn yêu cầu bài toán.

Câu 20: Cho hàm số y = x³ – (m + 1)x² – (m² – 2m)x + 2020. Tìm m để hàm số nghịch biến trên khoảng (0; 1).

Lời giải:

Ta có:

Y’ = 3x² – 2(m + 1)x – (m² – 2m)

Khi đó y’ = 0

⇔ 3x² – 2(m + 1)x – (m² – 2m) = 0

$\iff \left[\begin{array}{l}x=m\\ x=\frac{m-2}{3}\end{array}\right.$

Hàm số đã cho nghịch biến trên khoảng (0; 1) khi và chỉ khi:

$\left[\begin{array}{l}m\le 0<1\le \frac{m-2}{3}\\ \frac{m-2}{3}\le 0<1\le m\end{array}\right.\iff 1\le m\le \frac{3}{2}$

Vậy với $1\le m\le \frac{3}{2}$  thỏa mãn yêu cầu bài toán.

Câu 21: Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn z(1 + i) là số thực là:

A. Đường trong bán kính bằng 1;

B. Trục Ox;

C. Đường thẳng y = −x;

D. Đường thẳng y = x.

Lời giải:

Đáp án đúng là: C.

Giả sử ta có số phức z = x + yi. Ta có:

Z(1 + i) = (x + yi)(1 + i) = (x – y) + (x + y)i

Z(1 + i) là số thực khi x + y = 0 hay y = −x.

Câu 22: Cho hình chóp S.ABCD, đáy là hình bình hành tâm O. Gọi M, N, P, Q lần lượt là trung điểm SA, SB, SC và SD. Tìm giao tuyến của (MNPQ) và (SAC).

A. MN;

B. QM;

C. SO;

D.MP.

Lời giải:

Đáp án đúng là: D.

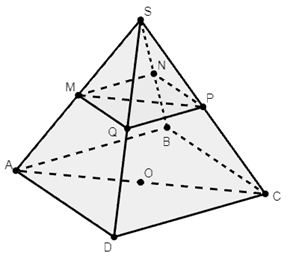
Ta có: M ∈ SA ⇒ M ∈ (SAC)

M ∈ (MNPQ)

⇒ M ∈ (SAC) ∩ (MNPQ)         (1)

Mặt khác:

P ∈ (SC) ⇒ P ∈ (SAC)

P ∈ (MNPQ)

⇒ P ∈ (SAC) ∩ (MNPQ)          (2)

Từ (1) và (2) suy ra (MNPQ) ∩ (SAC) = MP.

Câu 23: Cho hình chóp S.ABCD là hình bình hành tâm O. M, N, P lần lượt là trung điểm của AD, SA, SB.

a) Tìm giao tuyến của (MNP) và (SAB).

b) Tìm giao tuyến của (MNP) và (SBD).

Lời giải:

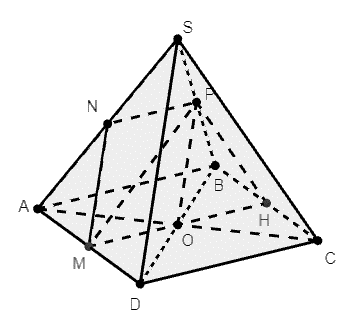
a) Xét tam giác SAB có NP là đường trung bình nên NP ∈ (SAB)

Mà NP ∈ (MNP).

Do đó NP là giao tuyến của (MNP) và (SAB).

b) Gọi H là trung điểm của BC

Suy ra MH là đường trung bình ở hình bình hành ABCD đi qua tâm O.

Mà (MNP) ⊂ (MNPH)

MH ∩ DB = {O}

Mà MH ∈ (MNPH) và DB ∈ (SDB)

Do đó (MNPH) ∩ (SDB) = O

Mặt khác ta có P   SB ∈ (SDB)

Vậy PO là giao tuyến của (MNP) và (SBD).

Câu 24: Xác định hàm số bậc hai y = ax² + bx + c biết đồ thị của nó có đỉnh I(1; −1) và đi qua điểm A(2; 0)

A. y = x² − 3x + 2;

B. y = 2x² − 4x + 3;

C. y = x² − 2x;

D. y = x² + 2x.

Lời giải:

Đáp án đúng là: C

Ta có đỉnh I(1; −1)  ⇒ $-\frac{b}{2a}=1$  (1)

a + b + c = −1 (2)

Đồ thị hàm số đi qua A(2 ; 0)

⇒ 4a + 2a + c = 0 (3)

Từ (1); (2) và (3) ta có: a = 1; b = −2; c = 0.

Vậy hàm số cần tìm là: y = x² – 2x.

Câu 25: Xác định hàm số bậc hai y = 2x² + bx + c biết đồ thị của nó có đỉnh I(−1; −2).

A. y = 2x² – 4x + 4;

B. y = 2x² – 4x;

C. y = 2x² – 3x + 4;

D. y = 2x² + 4x.

Lời giải:

Đáp án đúng là: D

Vì hàm số cần tìm có đỉnh là I(−1; −2) nên $\left\{\begin{array}{l}-\frac{b}{2a}=-1\\ 2-b+c=-2\end{array}\right.$

Mà a = 2 nên $\left\{\begin{array}{l}b=4\\ c=0\end{array}\right.$

Vậy hàm số cần tìm là: 2x² + 4x.

Câu 26: Cho tam giác ABC vuông tại A. Về phía ngoài tam giác vẽ các hình vuông ABDE, ACFG và BCHI. Ta có:

A. S_ACFG = S_BCHI + S_ABDE;

B. S_BCHI = S_ABDE + S_ACFG;

C. S_ABDE = S_BCHI + S_ACFG;

D. S_BCHI = S_ACFG − S_ABDE.

Lời giải:

Đáp án đúng là: B

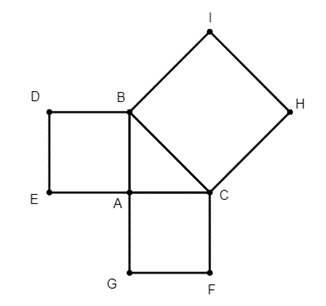
Ta có: S_BCHI = BC²; S_ACFG = AC²; S_ABDE = AB².

Theo định lý Py-ta-go cho tam giác ABC vuông tại A ta có: BC² = AB² + AC²

⇒ S_BCHI = S_ACFG + S_ABDE

Câu 27: Biết đồ thị hàm số y = (k − 3)x − 4 cắt đường thẳng y = −3x + 2 tại điểm có tung độ bằng 5. Tìm tham số k

Lời giải:

A là điểm có tung độ bằng 5 và A thuộc đường thẳng y = −3x + 2 nên ta có:

5 = −3x + 2 ⇔ x = −1

Suy ra A(−1; 5) thuộc đường thẳng y = (k − 3)x – 4 nên ta có:

5 = (k − 3)(−1) – 4 ⇔ k = −6

Vậy k = −6 là giá trị cần tìm.

Câu 28: Tìm m để đồ thị hàm số bậc nhất y = mx − 4 cắt đường thẳng y = −3x + 2 tại điểm có tung độ bằng 5.

Lời giải:

A là điểm có tung độ bằng 5 và A thuộc đường thẳng y = −3x+2 nên ta có:

5 = −3x+2 ⇔ x = −1

Suy ra A(−1; 5) thuộc đường thẳngy = mx − 4 nên ta có:

5 = m(−1) – 4 ⇔ m = −9

Vậy m = −9 là giá trị cần tìm.

Câu 29: Cho phương trình: x² − (m − 2)x− m − 1 = 0 (với m là tham số)

a) Chứng tỏ phương trình trên luôn có 2 nghiệm phân biệt x₁, x₂ với mọi m.

b) Tìm m thỏa mãn hệ thức: (x₁ − x₂)² − 3x₁x₂ = 21

Lời giải:

x² − (m − 2)x − m − 1 = 0

Δ=(m−2)²+4m+ 4 =m²+8> 0, ∀m

⇒ Phương trình luôn có 2 nghiệm phân biệt

Theo Viet ta có: 

$\left\{\begin{array}{l}{x}_1+x_2=m-2\\ x_1{x}_2=-m-1\end{array}\right.$

(x₁−x₂)²−3x₁x₂= 21

⇔(x₁+x₂)²− 7x₁x₂− 21 = 0

⇔(m−2)²+7m+7− 21 =0

⇔m²+3m− 10 =0

$\Rightarrow \left[\begin{array}{l}m=2\\ m=-5\end{array}\right.$

Vậy m = 2 và m =−5 là các giá trị thỏa mãn.

Câu 30: Cho hai hàm số y=x² và y=2x − m+2.Tìm m để đồ thị hai hàm số trên chỉ có một điểm chung? Tìm tọa độ điểm chung đó?

Lời giải:

Phương trình hoành độ giao điểm là:

x² = 2x − m + 2

⇔ x² − 2x + m − 2 = 0

Để hai đồ thị hàm số chỉ có một điểm chung thì Δ’ = 0

⇔ 1 − m + 2 = 0 ⇔ m = 3

Vậy hoành độ giao điểm đó là nghiệm của phương trình

x² − 2x + 1 = 0 ⇔ x = 1

⇒ y = 1

Vậy tọa độ điểm chung đó là (1; 1).

Câu 31: Một cửa hàng bán vải được 2 160 000 đồng tính ra được lãi 160 000 đồng . Hỏi số tiền lãi bằng bao nhiêu phần trăm tiền vốn?

Lời giải:

Số tiền vốn là:

2160000 − 160000 = 2 000 000 (đồng)

Tỉ số phần trăm tiền lãi với tiền vốn là:

160 000 : 2 000 000 × 100 = 8%

Đáp số: 8%.

Câu 32: Một cửa hàng bán vải được 2 160 000 đồng. Tính gia cửa hàng lãi 8% so với tiền vốn. Hỏi số tiền lãi là bao nhiêu tiền?

Lời giải:

Tiền bán ứng:

100% + 8% = 108%

Tiền vốn là:

2160 000 : 108% = 2000 000 (đồng )

Tiền lãi là:

2160 000 − 2000 000 = 160 000 (đồng )

Đáp số: 160 000 đồng.

Câu 33: Tìm x biết |x − 1| = 3x + 2.

Lời giải:

|x − 1| = 3x + 2

• TH1: x − 1 ≥ 0 ⇔ x ≥ 1

x − 1 = 3x + 2

⇔ 3x − x = −1 − 2

⇔ 2x = −3

 (loại)

• TH2: x − 1 < 0 ⇔ x < 1

−x + 1 = 3x + 2

⇔ 3x + x = 1 − 2

⇔ 4x = −1

$\Rightarrow x=-\frac{1}{4}$ (thỏa mãn)

Vậy $x=-\frac{1}{4}$  là nghiệm của phương trình.

Câu 34: Thực hiện phép tính:

a) 483 + (−56) + 263 + (−64)

b) 371 + (−531) + (−271) + 731

c) 3251 − 243 − 3250

d) 279 − (145 + 279)

Lời giải:

a) 483 + (−56) + 263 + (−64)

= 427 + 263 + (−64)

= 690 + (−64) = 262

b) 371 + (−531) + (−271) + 731

= (371 − 271)  + (731 − 531)

= 100 + 200 = 300

c) 3251 − 243 − 3250

= 3251 − 3250 − 243

= 1 – 243 = −242

d) 279 − (145 + 279)

= 279 – 421 = −142.

Câu 35: Cho tập hợp A = {−3;−2; 0; 6; 9}.Trong các 1 tập hợp sau tập hợp nào không phải là tập hợp con của A?

A. {−3; 9};

B. {−2; 0; −9};

C. {−3; 0; 6; 9};

D. {−2}.

Lời giải:

Vì −9 ∉ A nên suy ra {−2; 0; −9} không phải là tập hợp con của A.

Vậy ta chọn đáp án B.

Câu 36: Tìm ước chung của 9 và 15.

A. {1;3};

B. {0; 3};

C. {1; 5};

D. {1; 3; 9}.

Lời giải:

Ta có: Ư(9) = {1; 3; 9} và Ư(15)  = {1; 3; 5; 15}

Vậy ƯC(9, 15) = Ư(9) ∩ Ư(15)={1; 3}

Vậy ta chọn đáp án A.

Câu 37: Hàm số y = cos 2x đồng biến trên khoảng nào?

Lời giải:

Để hàm số y = cos 2x đồng biến thì

$2x\in \left(\pi +k2\pi ;2\pi +k2\pi \right)\Rightarrow x\in \left(\frac{\pi }{2}+k\pi ;\pi +k\pi \right),k\in \mathbb{Z}$

Vậy hàm số cos 2x đồng biến trên các khoảng $\left(\frac{\pi }{2}+k\pi ;\pi +k\pi \right),k\in \mathbb{Z}$

Câu 38: Hàm số y = cos 2x nghịch biến trên khoảng nào?

Lời giải:

Để hàm số y = cos 2x nghịch biến thì

$2x\in \left(k2\pi ;\pi +k2\pi \right)\Rightarrow x\in \left(k\pi ;\frac{\pi }{2}+k\pi \right),k\in \mathbb{Z}$.

Vậy hàm số cos 2x đồng biến trên các khoảng $\left(\frac{\pi }{2}+k\pi ;\pi +k\pi \right),k\in \mathbb{Z}$ .

Câu 39: Trên một bản đồ tỉ lệ 1 : 1 000 có hình vẽ một khu đất hình chữ nhật với chiều dài 6 cm và chiều rộng 4 cm. Tính diện tích khu đất đó bằng đơn vị ha.

Lời giải:

Chiều dài thật khu đất đó là:

 6 × 1 000 = 6 000 (cm)

Chiều rộng thật khu đất đó là:

4 × 1 000 = 4 000 (cm)

Diện tích khu đất đó là:

6 000 × 4 000 = 24 000 000 (cm²)

Đổi: 24 000 000 cm² = 0,24 ha

Đáp số: 0,24 ha.

Câu 40: Hình vẽ một mảnh đất hình chữ nhật trên bản đồ tỉ lệ 1 : 1000 có chiều dài 8 cm, chiều rộng 6 cm. Vậy diện tích thực tế của mảnh đất đó là bao nhiêu?

Lời giải:

Chiều dài thật mảnh đất đó là:

 8 × 1 000 = 8 000 (cm)

Chiều rộng thật mảnh đất đó là:

6 × 1 000 = 6 000 (cm)

Diện tích mảnh đất đó là:

8 000 × 6 000 = 48 000 000 (cm²)

Đổi: 48 000 000 cm² = 0,48 ha

 Đáp số: 0,48 ha.