Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 103)
Phương pháp giải:
Sử dụng tính chất của tia phân giác và các góc tạo bởi các tia để tìm góc mOn.
Lời giải:
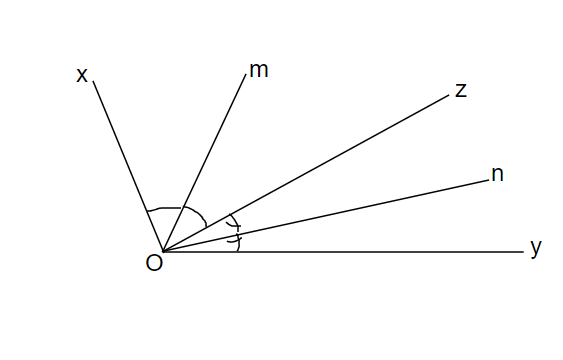
Vì tia Oz nằm giữa hai tia Ox và Oy
Mà Om và On lần lượt là tia phân giác của và
Nên tia Oz cũng nằm giữa hai tia Om và On.
Mà Om và On lần lượt là tia phân giác của và .
và
Hay .
Câu 2: Cho 2 đường thẳng MN và PQ cắt nhau tại O biết . Tính số đo các góc được tạo thành
Phương pháp giải:
Khi hai đường thẳng cắt nhau, các góc kề nhau là hai góc kề bù, tổng số đo của chúng bằng .
Các góc đối đỉnh có số đo bằng nhau.
Sử dụng các mối quan hệ góc để tính toán dựa vào điều kiện bài toán.
Lời giải:
Vì MOQ và MOP là 2 góc kề bù
nên MOP + MOP = 1800 (1)
Ta có: MOP = 2MOQ (2)
Từ 1,2 => MOP + 2MOP = 1800
3MOP = 1800
MOP = 1800/3
MOP = 600 (3)
Từ 2,3 => MOP = 2.600 = 1200
Vì 2 đường thẳng MN và PQ cắt nhau tại D
*) nên MOP và NOQ là 2 góc đối đỉnh nhau
hay MOP = NOQ = 1200
*) nên MOQ và NOP là 2 góc đối đỉnh nhau
hay MOQ = NOP = 600
Vậy MOP = NOQ = 1200; MOQ = NOP = 600
Phương pháp giải:
Tìm x bằng cách: Lấy số bị chia chia cho thương.
Để thực hiện phép chia hai phân số, ta làm như sau: Lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải:
=
Phương pháp giải:
Quan sát: Phương trình có hai trường hợp cần xét:
Trường hợp 1: .
Trường hợp 2: , khi đó mũ hai vế phải bằng nhau, tức (vô lý).
Kết luận: Chỉ cần xét trường hợp .
Lời giải:
Phương pháp giải:
Điều kiện chia đều:
Số học sinh nam (24) và số học sinh nữ (18) phải được chia đều vào mỗi tổ.
Do đó, số tổ phải là ước chung của 24 và 18.
Tìm ước chung:
Xác định tất cả các ước của 24 và 18.
Tìm ước chung lớn nhất (UCLN) và các ước chung khác.
Lời giải:
Để số nam và số nữ được chia đều vào các tổ thì số HS nam và HS nữ phải thuộc UCLN(24;18)
Ư(24)={1; 2; 3; 4; 6; 12; 24}
Ư(18)={1; 2; 3; 6; 9;18}
ƯC(24;18)={1; 2; 3; 6}
Vậy có 4 cách chia tổ: chia thành 1, 2, 3 hoặc 6 tổ
Cách 1: 24 nam;18 nữ (gồm 1 tổ)
Cách 2: 12 nam; 9 nữ (gồm 2 tổ)
Cách 3 : 8 nam ; 6 nữ (gồm 3 tô)
Cách 4 : 4 nam; 3 nữ (gồm 6 tổ)
Câu 6: Tính nhanh: 210. 15 + 210. 85
Phương pháp giải:
Nhận dạng bài toán: Đây là bài toán có thể áp dụng phân tích thừa số chung để tính nhanh.
Đưa ra ngoài làm thừa số chung.
Tính tổng các hệ số còn lại, sau đó nhân với .
Lời giải:
210. 15 + 210. 85
= 210. (15 + 85)
= 210. 100
= 1024 . 100
= 102400
Phương pháp giải:
Biểu thức diện tích tam giác ABE
Mối quan hệ giữa và
Liên hệ diện tích tam giác với diện tích hình vuông
Tính diện tích hình vuông
Lời giải:
AB = BC = CD = AD
S(ABE) = BC x AB : 2 = BC x AB : 2 = x BC x AB = 16,35 cm2
Mà BC x AB = S(ABCD)
Nên S(ABCD) = 16,35 x 6 = 98,1 cm2
A. 5
B. 7
C. 8
D. 6
Phương pháp giải:
Xác định công thức cấp số nhân:
Số lá sen mỗi ngày tăng theo cấp số nhân với công bội , bắt đầu với 9 lá (ngày đầu).
Công thức tính số lá sen:
Số lá sen ngày thứ là:
Giải phương trình để tìm ngày đầy hồ:
Để hồ đầy 39 lá, ta giải phương trình , tìm được .
Lời giải:
Chọn C.
+) Nếu số lá sen ngày đâù là 1= 30 thì số lá sen ngày thứ 2 là 1.3 = 31; số lá sen ngày thứ ba là 3.3 = 32 ...số lá sen ngày thứ 10 là 39.
Như vậy để hồ đầy lá sen thì cần 39 lá.
+) Nếu ngày đầu có u1 = 9 lá thì ngày thứ 2 có: 9.3 = 27 lá; ngày thứ 3 có: 27.3 = 81 lá...
Do đó; số lá sen mỗi ngày có trong hồ là 1 cấp số nhân với u1 = 9, q = 3.
Số hạng thứ n là un = u1.qn-1 = 9.3n-1.
Để hồ đầy lá sen thì cần 39 lá
⇒ 9.3n-1 = 39 => 32.3n-1 = 39
=> 3n+1 = 39
⇒ n + 1 = 9 ⇒ n = 8
Vậy đến ngày thứ 8 thì hồ sẽ đầy lá.
Câu 9: ngày bằng bao nhiêu giờ?
Phương pháp giải:
Đổi 1 ngày = 24 giờ
Thực hiện nhân và kết luận
Lời giải:
1 ngày = 24 giờ
ngày bằng số giờ là:
24 x = 8 giờ
Đáp số: 8 giờ.
Bảng đơn vị đo thời gian
1 thế kỉ = 100 năm 1 tuần lễ = 7 ngày
1 năm = 12 tháng 1 ngày = 24 giờ
1 năm = 365 ngày 1 giờ = 60 phút
1 năm nhuận = 366 ngày 1 phút = 60 giây
Cứ 4 năm lại có 1 năm nhuận.
Tháng một, tháng ba, tháng năm, tháng bảy, tháng tám, tháng mười, tháng mười hai có 31 ngày.
Tháng tư, tháng sáu, tháng chín, tháng mười một có 30 ngày.
Tháng hai có 28 ngày (vào năm nhuận có 29 ngày)
Câu 10: Có bao nhiêu cách sắp xếp 6 người vào một bàn tròn?
Phương pháp giải:
Khi sắp xếp các đối tượng vào bàn tròn, thứ tự sắp xếp là tính theo chu vi, nên một cách xếp có thể xoay vòng tạo ra kết quả giống nhau.
Để loại bỏ tính đối xứng, ta cố định một người làm mốc.
Sắp xếp người còn lại vào các vị trí, số cách sắp xếp là .
Lời giải:
Do đây là bàn tròn nên khi xếp ta chọn 1 người làm mốc,
ếp 5 người còn lại có 5! cách
Vậy có tất cả 5!.1 = 120 cách xếp 6 người vào 1 bàn tròn.
Lý thuyết Hóa vị
- Cho tập A gồm n phần tử (n ≥ 1). Khi xếp n phần tử này theo một thứ tự, ta được một hoán vị các phần tử của tập hợp A, (gọi tắt là một hoán vị của A).
- Số hoán vị của một tập hợp có n phần tử là Pn = n! = n(n – 1)(n – 2)…3.2.1.
- Đặc điểm: Đây là sắp xếp có thứ tự và số phần tử sắp xếp đúng bằng số phần tử trong nhóm (bằng n).
- Chú ý: Giai thừa: n! = n(n – 1)(n – 2)…3.2.1
Quy ước: 0! = 1; 1! = 1.
Phương pháp giải:
Nêu khái niệm và chỉ ra các số có trong tập hợp Z và N.
Lời giải:
Tập hợp Z là tập hợp các số nguyên âm, số nguyên dương và số 0.
Z = {...; -2; -1; 0; 1; 2; ...}
Tập hợp các số nguyên dương là Z+
Z+ = {1, 2, 3, ......}
Tập hợp các số nguyên dương là Z-
Z- = { -1, -2, -3, ........}
Tập hợp N là tập hợp các số tự nhiên (trong đó có 0)
N = {0; 1; 2; 3; ...}
Tập hợp các số tự nhiên khác 0 là N*
N* = {1, 2, 3, ......}
Số 0 không là số nguyên âm, cũng không phải là số nguyên dương.
Câu 12: Tính 7 phút = ...... giây
Phương pháp giải:
Đổi từ phút sang giây bằng cách nhân số phút với 60 (vì 1 phút = 60 giây).
Lời giải:
7 phút = 7 x 60 = 420 giây
Bảng đơn vị đo thời gian
1 thế kỉ = 100 năm 1 tuần lễ = 7 ngày
1 năm = 12 tháng 1 ngày = 24 giờ
1 năm = 365 ngày 1 giờ = 60 phút
1 năm nhuận = 366 ngày 1 phút = 60 giây
Cứ 4 năm lại có 1 năm nhuận.
Tháng một, tháng ba, tháng năm, tháng bảy, tháng tám, tháng mười, tháng mười hai có 31 ngày.
Tháng tư, tháng sáu, tháng chín, tháng mười một có 30 ngày.
Tháng hai có 28 ngày (vào năm nhuận có 29 ngày)
Phương pháp giải:
Số có bốn chữ số, chữ số đầu tiên không thể là , nên chữ số đầu tiên có cách chọn (từ ).
Các chữ số có thể là nên mỗi chữ số có cách chọn.
Quy tắc nhân
Giả sử một công việc phải hoàn thành qua hai công đoạn liên tiếp nhau:
- Công đoạn một có m1 cách thực hiện,
- Với mỗi cách thực hiện công đoạn một, có m2 cách thực hiện công đoạn hai.
Khi đó số cách thực hiện công việc là m1 . m2 cách.
Lời giải:
Gọi số có 4 chữ số thỏa mãn là . Khi đó a có 4 cách chọn (từ 1 đến 4). Còn các chữ số b, c, d đều có 5 cách chọn (từ 0 đến 4).
Do đó có tất cả số thỏa mãn ycbt.
Câu 14: Năm nhuận là năm mà tháng Hai có 29 ngày.
a) Biết rằng các năm nhuận của thế kỉ XXI là: 2004, 2008, 2012, ..., 2096. Hỏi thế kỉ XXI có bao nhiêu năm nhuận?
b) Năm cuối cùng của thế kỉ XX là một năm nhuận. Hỏi năm đó là năm nào?
Phương pháp giải:
Xác định số năm nhuận trong thế kỷ XXI:
Các năm nhuận từ 2004 đến 2096 là dãy số cách đều với công sai . Số năm nhuận được tính bằng:
Xác định năm cuối cùng của thế kỷ XX:
Năm cuối cùng của thế kỷ XX là năm 2000.
Năm nhuận là năm chia hết cho , nhưng năm tròn thế kỷ (chia hết cho 100) chỉ là năm nhuận nếu chia hết cho . Năm 2000
thỏa mãn điều kiện này.
Lời giải:
a) Thế kỉ XXI có số năm nhuận là:
(2096 – 2004) : 4 + 1 = 24 (năm)
b) Năm cuối cùng là năm nhuận của thế kỉ XX là năm 2000.
bình mỗi ngày mua được bao nhiêu lít sữa?
Phương pháp giải:
Tính tổng số lít sữa đã mua trong 5 ngày.
Trong 2 ngày đầu: Mỗi ngày mua 1200 lít, tổng cộng là .
Trong 3 ngày sau: Mỗi ngày mua 2100 lít, tổng cộng là .
Tính trung bình mỗi ngày mua được bao nhiêu lít sữa
Lời giải:
Trong 2 ngày đầu thu hoạch được tất cả số lít sữa là:
1200 x 2 = 2400 (l sữa)
Trong 3 ngày sau thu hoạch được tất cả số l sữa là:
2100 x 3 = 6300 (l sữa)
Trung bình mỗi gày thu được số lít sữa là:
(2400 + 6300) : (2 + 3) = 1740 (l sữa)
Đáp số: 1740 l sữa
Tìm số trung bình cộng
Muốn tìm trung bình cộng của nhiều số, ta tính tổng các số đó, rồi đem tổng vừa tính chia cho số các số hạng.
Phương pháp giải bài toán trung bình cộng:
Bước 1: Xác định các số hạng có trong bài toán.
Bước 2: Tính tổng các số hạng vừa tìm được.
Bước 3: Trung bình cộng = Tổng các số hạng vừa tìm được : số các số hạng có trong bài toán.
Phương pháp giải:
Phân tích điều kiện:
Ta biết chia hết cho 4, tức là:
Tính các tổng liên quan:
đều là tổng của 2 số trong . Khi cộng các tổng này, ta thu được , vẫn chia hết cho 4.
Xét biểu thức :
Phân tích và sử dụng tính chất chia hết để chứng minh .
Lời giải:
Ta có:
Ta thấy:
nên chẵn. Do đó phải tồn tại ít nhất 1 trong 3 số là số chẵn.
Từ
Ta có đpcm.
Câu 17: Hiệu hai số tự nhiên là 6. Nếu gấp số bị trừ lên 4 lần thì hiệu sẽ là 54. Tìm hai số đó.
Phương pháp giải:
Đặt hai số:
Gọi hai số tự nhiên là (số bị trừ) và (số trừ).
Theo đề bài, ta có:
Nếu gấp số bị trừ lên 4 lần, hiệu sẽ là 54:
Giải hệ phương trình:
Từ phương trình (1), ta có .
Thay vào phương trình (2) và giải để tìm .
Lời giải:
Gọi 2 số đó là a và b. Theo bài ra, ta có:
a - b = 6 => a = b + 6 (1)
a.4 - b = 54 (2)
Từ (1) và (2), ta có:
(b + 6) .4 - b = 54
b.4 + 24 - b = 54
b.3 = 54 - 24
b.3 = 30
b = 30:3
b = 10
=> a = 10 + 6 = 16
Vậy 2 số đó là 10 và 16
Phương pháp giải:
Áp dụng định lý Pythagore trong tam giác vuông
Tính và (dùng đường cao )
Tính (sử dụng tính chất phân giác)
Lời giải:
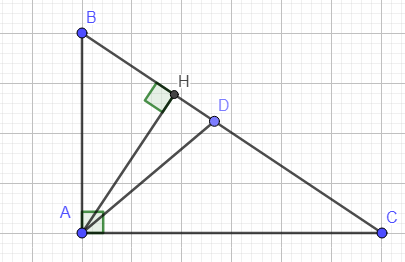
Áp dụng định lý Pitago:
(cm)
Áp dụng tính chất tia phân giác:
Mà:
(cm)
Theo hệ thức lượng của tam giác vuông:
(cm)
(cm)
(cm)
Câu 19: Giải phương trình: 3x2 - 7x + 8 = 0
Phương pháp giải:
Đưa phương trình về dạng bình phương của một hiệu.
Do lớn hơn 0 nên phương trình vô nghiệm.
Lời giải:
Cách 1:
=
=
=
VP luôn lớn hơn 0, VT = 0
=> Phương trình vô nghiệm
Cách 2:
Xét phương trình
Δ = b2 − 4ac = (−7)2 − 4⋅3⋅8 = 49 − 96 = −47
=> Δ < 0
=> phương trình vô nghiệm
Phương pháp giải:
Sử dụng hiệu số tuổi không đổi:
Hiệu số tuổi của hai mẹ con luôn là 28 tuổi, kể cả sau 3 năm.
Lập tỉ lệ tuổi sau 3 năm:
Theo đề bài, sau 3 năm, tuổi con bằng tuổi mẹ. Sử dụng tỉ lệ này để tính tuổi con sau 3 năm.
Tính tuổi con và mẹ hiện tại:
Từ tuổi con sau 3 năm, suy ra tuổi con hiện tại bằng cách trừ đi 3.
Tính tuổi mẹ hiện tại bằng cách cộng thêm hiệu số tuổi (28 tuổi) vào tuổi con hiện tại.
Lời giải:
3 năm sau hiệu số tuổi của hai mẹ con không thay đổi và bằng: 28 tuổi
Tuổi con 3 năm sau là:
28 : (7 - 3) x 3 = 21( tuổi)
Tuổi con hiện nay là:
21 - 3 = 18 (tuổi)
Tuổi mẹ hiện nay là:
18 + 28 = 46 (tuổi)
Đáp số: Con: 18 tuổi
Mẹ : 46 tuổi
Phương pháp giải:
Khởi tạo biến:
Khai báo các biến cần thiết: (tổng), (biến đếm), và (giá trị giới hạn được nhập từ bàn phím).
Duyệt từ 1 đến :
Sử dụng vòng lặp để duyệt qua các số từ 1 đến .
Kiểm tra nếu số đó là số chẵn (chia hết cho 2) thì cộng vào biến tổng .
In kết quả:
Sau khi hoàn tất vòng lặp, in ra tổng các số chẵn nhỏ hơn .
Lời giải:
uses crt;
var
m, n, s, i: integer;
begin
clrscr;
writeln('Nhap so tu nhien n: ');
readln(n);
s := 0;
for i := 1 to n - 1 do
if i mod 2 = 0 then
s := s + i;
writeln('Tong cac so chan nho hon ', n, ' la: ', s);
readln;
end.
Phương pháp giải:
Rút gọn các phân số:
Đơn giản hóa các phân số trong phương trình nếu có thể.
Tìm mẫu số chung:
Xác định mẫu số chung để quy đồng các phân số trong phương trình, từ đó chuyển phương trình thành phương trình dạng đa thức.
Giải phương trình bậc nhất:
Sau khi quy đồng, ta sẽ có một phương trình tuyến tính (bậc nhất) theo .
Giải phương trình bậc nhất để tìm .
Kết luận:
Đưa ra giá trị của tìm được.
Lời giải:
Vậy nghiệm của phương trình là x = -100
Câu 23: Cho Biểu Thức . Tìm giá trị nguyên của x để:
a) E có giá trị nguyên
b) E có giá trị nhỏ nhất
Phương pháp giải:
Xác định điều kiện của :
Biểu thức xác định khi (để tránh mẫu số bằng 0).
Biến đổi biểu thức để phân tích giá trị của :
Ta viết lại biểu thức dưới dạng khác nếu cần, nhằm hiểu rõ hơn về cách thay đổi khi thay đổi.
Tìm giá trị nguyên của để nhỏ nhất:
Thử thay các giá trị nguyên của vào để tìm giá trị nhỏ nhất có thể.
Nếu biểu thức là dạng phân số có mẫu chứa , có thể khảo sát dấu của tử và mẫu để xác định khi nào đạt giá trị nhỏ nhất.
Kết luận:
Ghi lại giá trị của mà tại đó đạt giá trị nhỏ nhất.
Lời giải:
a) Ta có :
Vì
Mà
Lại có :
Lập bảng xét 2 trường hợp ta có :
Vậy
Câu 24: rút gọn được bao nhiêu
Phương pháp giải:
Tìm ƯCLN của tử số (15) và mẫu số (35) bằng cách phân tích ra thừa số nguyên tố
Rút gọn phân số bằng cách chia cả tử và mẫu cho
Lời giải:
ƯCLN là .
Phương pháp chung:
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lưu ý: Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn 1, hay phân số tối giản là phân số không thể rút gọn được nữa.
Câu 25: Giải hệ phương trình bằng phương pháp thế
Phương pháp giải:
Chọn phương trình đơn giản hơn để biểu diễn một ẩn theo ẩn còn lại
Thế vào phương trình còn lại
Giải phương trình với một ẩn
Lời giải:
=>
=>
=>
Câu 26: Tính bằng cách hợp lý:
a) - (-253) + 178 - 216 + (-156) - (-21)
b) - (-239) + 115 + (-27) + (-125) -121
Phương pháp giải:
Đổi dấu khi gặp , hoặc giữ nguyên khi .
Kết hợp các số có dấu hoặc có giá trị gần nhau để dễ tính toán.
Tính từng nhóm nhỏ trước, sau đó cộng/trừ để có kết quả cuối cùng.
Lời giải:
a)
b)
b. Viết 4 phân số khác nhau sao cho mỗi phân số lớn hơn và bé hơn
Phương pháp giải:
Biến đổi phương trình và tìm x.
Bài toán yêu cầu tìm các phân số có mẫu số bằng 35 và có tử số từ 26 đến 29. Biến đổi các phân số về mẫu số chung 35.
Lời giải:
a.
b. Ta có :
Vậy 4 phân số thỏa mãn là
Phương pháp chung:
Áp dụng các quy tắc
Đối với phép cộng: Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết
Đối với phép trừ:
+ Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ
+ Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu
Đối với phép nhân: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết
Đối với phép chia:
+ Muốn tìm số bị chia ta thấy thương nhân với số chia
+ Muốn tìm số chia ta thấy số bị chia thương
Câu 28: Dãy số tự nhiên liên tiếp từ 218 đến 436 có bao nhiêu số chẵn, bao nhiêu số lẻ?
Phương pháp giải:
Tính tổng số các số tự nhiên trong dãy từ 218 đến 436.
Tính số lượng các số chẵn.
Tính số lượng các số lẻ.
Lời giải:
Dãy STN liên tiếp từ 218 đến 436 có số các số tự nhiên là:
( 436 - 218 ) : 1 + 1 = 219 (số)
Dãy STN liên tiếp từ 218 đến 436 có số các số chẵn là:
( 436 - 218 ) : 2 + 1 = 110 (số)
Dãy STN liên tiếp từ 218 đến 436 có số các số lẻ là:
219 - 110 = 109 (số)
Đ/S: 110 số chẵn, 109 số lẻ
Câu 29: Chứng minh rằng đa thức f(x) có ít nhất 2 nghiệm biết rằng: x.f(x+1) = (x+3).f(x)
Phương pháp giải:
Để chứng minh rằng đa thức có ít nhất 2 nghiệm, ta sử dụng phương trình với mọi giá trị của .
Xét 2 trường hợp: x = 0 và x = -3
Lời giải:
Vì x.f(x+1) = (x+3).f(x) với mọi x nên:
* Khi x = 0 thì 0.f(0-1) = (0+3).f(0) tương đương f(0)=0.
Vậy 0 là nghiệm của đa thức f(x)
* Khi x = -3 suy ra -3.f(-3+2) = (-3 +3).f(-3)
-3f(-2) = 0f(-3) tương đương f(-2) = 0.
Vậy -2 cũng là một nghiệm của f(x)
Do đó đa thức f(x) có ít nhất 2 nghiệm là 0 và 2
Câu 30: Cho số thập phân 135,27. Hỏi giá trị của chữ số 3 gấp giá trị của chữ số 2 bao nhiêu lần?
Phương pháp giải:
Bước 1: Xác định giá trị của chữ số 3
Bước 2: Xác định giá trị của chữ số 2
Bước 3: Tính tỷ lệ giữa giá trị của chữ số 3 và chữ số 2
Lời giải:
Chữ số 3 trong số 135,27 có giá trị là 3x10 = 30.
Chữ số 2 trong phần thập phân (0,27) có giá trị là 2x0,1 = 0,2.
Giá trị của chữ số 3 gấp giá trị của chữ số 2 là
30 : 0,2 = 150 (lần)
a. Tính số áo dạ và áo phao mà cửa hàng đó cần chuẩn bị
b. Số áo trắng chiếm bao nhiêu phần trăm, số áo len chiếm bao nhiêu phần trăm
Phương pháp giải:
a. Tính số áo dạ và áo phao:
Số áo dạ: Tính 30% của 20 cái áo
Số áo phao: Số áo phao chiếm 35% của 20 cái áo
b. Tính phần trăm áo trắng và áo len:
Số áo trắng: Trong đơn hàng có 5 cái áo trắng.
Số áo len: Tổng số áo là 20 cái, do đó tính số áo len.
Tính tỷ lệ phần trăm của áo trắng; Tính tỷ lệ phần trăm của áo len
Lời giải:
a, Số áo dạ:
35% x 20 = 7 (cái)
Số áo phao:
30% x 20 = 6 (cái)
b, Số áo len:
20 - (5 + 7 + 6) = 2 (cái)
Số áo trắng chiến số phần trăm là:
Số áo len chiến số phần trăm là:
hoặc 100% - 35% - 30% - 25% = 10%
Câu 32: Tìm a để đa thức A chia hết cho đa thức B
A = và B =
A = và B =
Phương pháp giải:
Câu a: Chia cho , phần dư là , giải , ta có .
Câu b: Chia cho , phần dư là , giải , ta có .
Kết luận.
Lời giải:
Cách 1:
Chỉ có thể C =
Cách 2:
a)
= (x - 5)(2x2 + 3x + 4) + a + 12
=> A : B dư a + 12 để A chia hết cho B thì a + 12 = 0
=> a = -12
b)
= (2 - x)( - x2 - x + 3) + a - 4
=> A : B dư a - 4 để A chia hết cho B thì a - 4 = 0
=> a = 4
Phương pháp giải:
Áp dụng các quy tắc
Đối với phép cộng: Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết
Đối với phép trừ:
+ Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ
+ Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu
Đối với phép nhân: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết
Đối với phép chia:
+ Muốn tìm số bị chia ta thấy thương nhân với số chia
+ Muốn tìm số chia ta thấy số bị chia thương
Lời giải:
Phương pháp giải:
Sử dụng Quy tắc thương số có cùng cơ số:
Lời giải:
= 25 + 5x24 - 3x25
Phương pháp giải:
Tính vận tốc:
Vận tốc = Quãng đường / Thời gian.
Tính thời gian đi quãng đường 30,5 km:
Thời gian = Quãng đường / Vận tốc.
Lời giải:
Vận tốc xe đạp là:
18,3 : 1,5 = 12,2(km/giờ).
Thời gian để đi hết quãng đường 30,5km là:
30,5 : 12,2 = 2,5 (giờ).
Đáp số: 2,5 giờ.
Phương pháp giải:
Đưa phương trình về dạng lũy thừa
Rút gọn phương trình
Biến đổi về cơ số 5
Lời giải: