Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 85)
Lời giải:
Xếp 6 người chồng quanh bàn tròn có 5! cách.
Xếp các bà vợ vào ngồi cạnh chồng của mình, mỗi bà vợ có 2 vị trí ngồi nên có 26 cách.
Vậy số cách xếp là 5!.26 = 7680 cách.
Lời giải:
Tiến hành theo các bước sau:
Bước 1: Xếp 6 nam ngồi quanh bàn tròn, có 5! cách xếp
Bước 2: Vì 6 nam ngồi quanh bàn tròn nên có 6 khoảng trống để xếp 6 người nữa, vậy có 6! cách xếp
Theo quy tắc nhân ta có: 5!.6! = 86 400 (cách).
Lời giải:
Gọi A là biến cố “Người thứ nhất bắn trúng”
Gọi B là biến cố “Người thứ hai bắn trúng”
Suy ra P (A) = 0,8 và P (B) = 0,7
Và C là biến cố “Cả hai người đều bắn trúng”
Ta có: P (C) = P (A).P (B) = 0,8.0,7 = 0,56.
Câu 4: Phát biểu nào sau đây là đúng?
A. Nếu f ‘(x) đổi dấu từ dương sang âm khi x qua điểm x0 và f (x) liên tục tại x0 thì hàm số y = f (x) đạt cực đại tại điểm x0;
B. Hàm số y = f (x) đạt cực trị tại x0 khi và chỉ khi x0 là nghiệm của f ‘(x) = 0;
C. Nếu f ‘(x0) = 0 và f ‘‘(x0) = 0 thì x0 không là điểm cực trị của hàm số y = f (x);
D. Nếu f ‘(x0) = 0 và f ‘‘(x0) > 0 thì hàm số đạt cực đại tại x0.
Lời giải:
Đáp án đúng là: A
Phát biểu A là đúng vì theo lý thuyết SGK
Các mệnh đề còn lại sai vì:
Phát biểu B thiếu điều kiện f ‘(x) đổi dấu khi qua x0
Phát biểu C sai, ví dụ hàm y = x4 có f ‘(0) = 0 và f ‘‘(0) = 0 nhưng x = 0 là điểm cực tiểu của hàm số
Phát biểu D sai vì nếu f ‘(x0) = 0 và f ‘‘(x0) > 0 thì hàm số đạt cực tiểu tại x0.
Câu 5: Hai véctơ bằng nhau khi hai véctơ đó có
A. Cùng hướng và có độ dài bằng nhau;
B. Song song và có độ dài bằng nhau;
C. Cùng phương và có độ dài bằng nhau;
D. Thỏa mãn cả 3 tính chất trên.
Lời giải:
Đáp án đúng là: A
Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
Câu 6: Hai tia phân giác của hai góc kề bù là
A. Hai tia trùng nhau;
B. Hai tia vuông góc;
C. Hai tia đối nhau;
D. Hai tia song song.
Lời giải:
Đáp án đúng là: B
Theo định lý của hai đường phân giác ta có: Hai đường phân giác của hai góc kề bù thì vuông góc với nhau.
A. 72 cm2;
B. 82 cm2;
C. 92 cm2;
D. 102 cm2.
Lời giải:
Đáp án đúng là: A
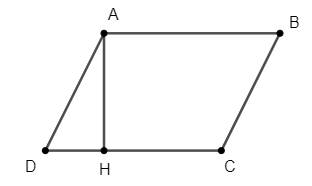
Ta có: SABCD = AH.CD = 6.12 = 72 (cm2)
A. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến;
B. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì điểm đó cách đều hai tiếp điểm;
C. Tiếp tuyến của một đường tròn thì vuông góc với mọi bán kính của đường tròn đó;
D. Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
Lời giải:
Đáp án đúng là: C
Theo tính chất của tiếp tuyến của đường tròn ta có:
Tiếp tuyến của một đường tròn thì vuông góc với mọi bán kính của đường tròn đó.
Câu 9: Có bao nhiêu loại khối đa diện đều mà mỗi mặt của nó là một tam giác đều?
A. 3;
B. 1;
C. 5;
D. 2.
Lời giải:
Đáp án đúng là: A
Có ba loại khối đa diện đều mà mỗi mặt của nó là một tam giác đều là: khối tứ diện đều, khối bát diện đều và khối hai mươi mặt đều.
A. 0,42;
B. 0,58;
C. 0,12;
D. 0,88.
Lời giải:
Đáp án đúng là: D
Xác suất bắn trượt của hai xạ thủ lần lượt là 0,4 và 0,3.
Xác suất để cả hai người cùng bắn trượt là: 0,4.0,3 = 0,12
Xác suất để có ít nhất 1 trong 2 người bắn trúng (xác suất mục tiêu bị hạ) là
1 – 0,12 = 0,88
Vậy xác suất để có ít nhất 1 trong 2 người bắn trúng (xác suất mục tiêu bị hạ) là 0,88.
Câu 11: Đúng ghi Đ, sai ghi S:
A. Hình thoi có 2 cặp cạnh đối diện song song bằng nhau.
B. Hai đường chéo của hình thoi vuông góc với nhau.
C. Diện tích hình thoi bằng tích độ dài hai đường chéo.
D. Bốn cạnh của hình thoi luôn bằng nhau.
Lời giải:
A. Hình thoi có 2 cặp cạnh đối diện song song bằng nhau Đ
B. Hai đường chéo của hình thoi vuông góc với nhau. Đ
C. Diện tích hình thoi bằng tích độ dài hai đường chéo. S
Vì diện tích hình thoi bằng tích độ dài hai đường chéo chia 2.
D. Bốn cạnh của hình thoi luôn bằng nhau. Đ
Lời giải:
Một người làm công việc hết số ngày là:
16 × 15 = 240 (ngày)
24 người làm công việc hết số ngày là:
240 : 24 = 10 (ngày)
Đáp số: 10 ngày
Câu 13: Gieo một đồng xu 5 lần liên tiếp. Số phần tử của không gian mẫu là
A. 10;
B. 16;
C. 32;
D. 64.
Lời giải:
Đáp án đúng là: C
Kết quả của 5 lần gieo là dãy abcde, trong đó a, b, c, d, e nhận một trong hai giá trị S, N.
Do đó số phần tử của không gian mẫu là:
2.2.2.2.2 = 32.
Câu 14: Gieo một đồng xu 5 lần liên tiếp. Gọi A là biến cố “Lần đầu tiên xuất hiện mặt sấp”. Khi đó:
A. n(A) = 16;
B. n(A) = 18;
C. n(A) = 20;
D. n(A) = 22.
Lời giải:
Đáp án đúng là: A
Lần đầu tiên xuất hiện mặt sấp nên lần đầu chỉ nhận giá trị S
Các lần gieo thứ hai, ba, bốn và năm có thể nhận S hoặc N nên:
n(A) = 1.2.2.2.2 = 16
Câu 15: Phân tích đa thức thành nhân tử: x2 + 2xy + y2 – x – y – 12.
Lời giải:
x2 + 2xy + y2 – x – y – 12
= (x + y ) 2 – (x + y) – 12
= (x + y) 2 – 4(x + y ) + 3(x + y ) – 12
= (x + y)(x + y – 4) + 3(x + y – 4)
= (x + y – 4)(x + y + 3).
Lời giải:
Số tự nhiên có 5 chữ số khác nhau lập được là: 5! = 120 số
Gọi S(5) là tổng của tất cả các số tự nhiên đó
Mỗi chữ số trong một số có 5 chữ số được lặp lại 4! lần
Khi đó ta có
S(5) = 4! . (1 + 2 + 3 + 4 + 5)(104 + 103 + 102 + 10 + 1) = 24 . 15 . 11111 = 3 999 960
Vậy lập được 120 số có tổng là 3 999 960.
Câu 17: Trong các hình sau đây, hình nào có 4 trục đối xứng?
A. Hình bình hành
B. Hình chữ nhật
C. Hình thoi
D. Hình vuông.
Lời giải:
Đáp án đúng là: D
Hình vuông có 4 trục đối xứng: đường chéo và đường thẳng đi qua trung điểm của cặp cạnh đối diện
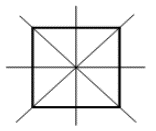
Vậy ta chọn đáp án D.
A. 20
B. 30
C. 35
D. 25.
Lời giải:
Đáp án đúng là: B
Số bạn đạt học lực giỏi nhưng không có hạnh kiểm tốt là:
15 – 10 = 5 (bạn)
Số bạn đạt hạnh kiểm tốt nhưng khôgn có học lực giỏi là:
25 – 10 = 15 (bạn)
Số bạn được khen thưởng là:
5 + 15 + 10 = 30 (bạn)
Vậy ta chọn đáp án B.
Câu 19: Phân tích đa thức thành nhân tử: (a – b)3 + (b – c)3 + (c – a)3.
Lời giải:
Ta có:
(a – b)3 + (b – c)3 + (c – a)3
= a3 – 3a2b + 3ab2 – b3 + b3 – 3b2c + 3bc2 – c3 + c3 – 3c2a + 3ca2 – a3
= 3ab2 – 3a2b – 3b2c + 3bc2 – 3c2a + 3ca2
= 3[(ab2 – a2b) + (bc2 – c2a) + (ca2 – b2c)]
= 3[ab(b – a) + c2(b – a) + c(a2 – b2)]
= 3[ab(b – a) + c2(b – a) + c(a – b)(a + b)]
= 3(b – a)[(ab + c2 – c(a + b)]
= 3(b – a)(ab + c2 – ca – cb)
= 3(b – a)[(ab – ca)+ (c2 – cb)]
= 3(b – a)[a(b – c)+ c(c – b)]
= 3(b – a)(a – c)(b – c).
Câu 20: Góc nội tiếp chắn nửa đường tròn bẳng bao nhiêu độ?
A. 45°
B. 90°
C. 60°
D. 120°.
Lời giải:
Đáp án đúng là: B
Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông nên bằng 90°
Vậy ta chọn đáp án B.
Câu 21: Tính nhanh giá trị của đa thức: 3(x – 3)(x + 7) + (x – 4)2 + 48 với x = 0,5.
Lời giải:
Ta có:
3(x – 3)(x + 7) + (x – 4)2 + 48
= 3(x2 + 7x – 3x – 21) + x2 – 8x + 16 + 48
= 3(x2 + 4x – 21) + x2 – 8x + 64
= 3x2 + 12x – 63 + x2 – 8x + 64
= 4x2 + 4x + 1
= (2x + 1)2
Thay x = 0,5 vào biểu thức ta được
(2 . 0,5 + 1)2 = (1 + 1)2 = 22 = 4
Vậy biểu thức có giá trị bằng 4.
Câu 22: Phân tích nhân tử ab(a – b) + bc(b – c) + ca(c – a).
Lời giải:
Ta có:
ab(a – b) + bc(b – c) + ca(c – a)
= ab(a – b) + b2c – bc2 + c2a – a2c
= ab(a – b) + (b2c – ca2) + (c2a – c2b)
= ab(a – b) + c(b2 – a2) + c2(a – b)
= ab(a – b) – c(a – b)(a + b) + c2(a – b)
= (a – b)(ab – ca – cb + c2)
= (a – b)[(ab – cb) + (–ca + c2)]
= (a – b)[b(a – c) + c(c – a)]
= (a – b)(a – c)(b – c).
Câu 23: Hãy chứng minh 1 + 1 = 3.
Lời giải:
Ta có:
1 + 1 = 3 ⟺ 2 = 3
Giả sử ta có đẳng thức:
14 + 6 – 20 = 21 + 9 – 30
Đặt thừa số chung ta có
2 × (7 + 3 – 10) = 3 × (7 + 3 – 10)
Theo toán học thì hai tích bằng nhau và có thừa số thứ hai bằng nhau thì thừa số thứ nhất bằng nhau
Do đó 2 = 3
Phản biện:
+) Sự thật 2 không thể bằng 3. Bài toán này sai trong lí luận của chúng ta là ở chỗ ta kết luận rằng: Hai tích bằng nhau và có thừa số thứ hai bằng nhau thì thừa số thứ nhất cũng bằng nhau. Điều đó không phải bao giờ cũng đúng.
+) Kết luận đó đúng khi và chỉ khi hai thừa số bằng nhau đó khác 0. Khi đó ta có thể chia 2 vế của đẳng thức cho số đó. Trong trường hợp thừa số đó bằng 0, thì luôn luôn có a × 0 = b × 0 với bất kì giá trị nào của a và b.
Ta có: 1 + 1 = 2 + 1
Mà (1 + 1) × 0 = (2 + 1 ) × 0
Vậy 1 + 1 = 3.
A. Sxq = 2πa2
B. Sxq = 4πa2
C. Sxq = 8πa2
D. Sxq = 4a2.
Lời giải:
Đáp án đúng là: B
Thiết diện qua trục của một hình trụ là hình vuông có chu vi là 8a
Suy ra cạnh hình vuông là 2a
Chiều cao của hình trụ là cạnh của thiết diện qua trục: h = 2a
Bán kính đáy của hình trụ là nửa cạnh của thiết diện qua trục: R = a
Diện tích xung quanh của hình trụ đó là:
Sxq = 2πRh = 2π . a . 2a = 4πa2
Vậy ta chọn đáp án B.
Câu 25: Cho điểm M có hoành độ là –2 và điểm M thuộc đồ thị hàm số y = –2x2. Xác định tọa độ điểm M.
Lời giải:
Vì M thuộc đồ thị hàm số y = –2x2 và M có hoành độ bằng –2
Nên y = –2 . (–2)2 = –2 . 4 = –8
Vậy M(–2; –8).
Câu 26: Trả lời các câu hỏi sau:
a) Thế nào là hai đường thẳng trùng nhau? Thế nào là hai đường thẳng phân biệt?
b) Thế nào là một tia? Thế nào là hai tia đối nhau? Thế nào là hai tia trùng nhau?
Lời giải:
a) Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm A và B. Từ đó suy ra:
Hai đường thẳng có 2 điểm chung thì trùng nhau.
Hai đường thẳng khồn trùng nhau gọi là 2 đường thẳng phân biệt.
b) Hình gồm một điểm O và một phần đường thẳng bị chia ra bởi O là một tia gốc O. Khi viết(đọc) tên một tia, phải đọc hay viết tên gốc trước.
Hai tia chung gốc Ox và Oy tạo thành một đường thẳng xy gọi là hai tia đối nhau.
Hai tia trùng nhau là hai tia chung gốc và cùng nằm 1 phía trên 1 đường thẳng.
Câu 27: Chứng minh bất đẳng thức: a2 + b2 + c2 ≥ ab + bc + ca.
Lời giải:
Ta có:
a2 + b2 + c2 ≥ ab + bc + ca
⇔ 2(a2 + b2 + c2) ≥ 2(ab + bc + ca)
⇔ (a2 – 2ab + b2) + (b2 – 2cb + c2) + (a2 – 2ac + c2) ≥ 0
⇔ (a – b)2 + (b – c)2 + (a – c)2 ≥ 0
Vì (a – b)2 ≥ 0 với mọi a, b
(b – c)2 ≥ 0 với mọi b, c
(a – c)2 ≥ 0 với mọi a, c
Nên (a – b)2 + (b – c)2 + (a – c)2 ≥ 0 với mọi a, b, c
Vậy a2 + b2 + c2 ≥ ab + bc + ca.
a) (a + b + c)2 ≤ 3(a2 + b2 + c2)
b) (a + b)2 ≤ 2(a2 + b2).
Lời giải:
a) Ta có :
(a + b + c)2 ≤ 3(a2 + b2 + c2)
⇔ a2 + b2 + c2 + 2ab + 2ac + 2bc ≤ 3a2 + 3b2 + 3c2
⇔ – 2a2 – 2b2 – 2c2 + 2ab + 2ac + 2bc ≤ 0
⇔ – (a – b)2 – (b – c)2 – (a – c)2 ≤ 0
Vì (a – b)2 ≥ 0 với mọi a, b
(b – c)2 ≥ 0 với mọi b, c
(a – c)2 ≥ 0 với mọi a, c
Nên – (a – b)2 – (b – c)2 – (a – c)2 ≤ 0 với mọi a, b, c
Dấu " = " xảy ra khi a = b = c
Vậy (a + b + c)2 ≤ 3(a2 + b2 + c2)
b) Ta có: (a + b)2 ≤ 2(a2 + b2)
⇔ a2 – 2ab + b2 ≤ 2a2 + 2b2
⇔ – a2 – 2ab – b2 ≤ 0
⇔ – (a + b)2 ≤ 0
Vì (a – b)2 ≥ 0 với mọi a, b
Nên – (a + b)2 ≤ 0 với mọi a, b
Dấu "=" xảy a khi a = – b
Vậy (a + b)2 ≤ 2(a2 + b2).
Câu 29: Phân tích đa thức thành nhân tử: x2 – 2x – 15.
Lời giải:
Ta có:
x2 – 2x – 15 = x2 + 3x – 5x – 15
= x(x + 3) – 5(x + 3)
= (x + 3)(x – 5).
Câu 30: Phân tích đa thức thành nhân tử: x2 + 2y2 – 3xy + x – 2y.
Lời giải:
Ta có:
x2 + 2y2 – 3xy + x – 2y
= x2 – 2xy + 2y2 – xy + x – 2y
= x(x – 2y) + y(2y – x) + (x – 2y)
= (x – 2y)(x – y + 1).
Câu 31: Chứng minh đẳng thức sau: (x + y + z)3 = x3 + y3 + z3 + 3(x + y)(y + z)(z + x).
Lời giải:
Ta có:
x3 + y3 + z3 + 3(x + y)(y + z)(z + x)
= x3 + y3 + z3 + (3xy + 3xz + 3y2 + 3yz)(z + x)
= x3 + y3 + z3 + 3xyz + 3x2y + 3xz2 + 3x2z + 3y2z + 3y2x + 3yz2 + 3xyz
= x3 + y3 + z3 + 3x2y + 3xz2 + 3x2z + 3y2z + 3y2x + 3yz2 + 6xyz
= x3 + 3x2y + 3y2x + y3 + 3x2z + 6xyz + 3y2z + 3xz2 + 3yz2 + z3
= (x + y)3 + 3z(x2 + 2xy + y2) + 3z2(x + y) + z3
= (x + y)3 + 3z(x + y)2 + 3z2(x + y) + z3
= (x + y + z)3
Vậy (x + y + z)3 = x3 + y3 + z3 + 3(x + y)(y + z)(z + x).
Câu 32: 4 giờ 30 phút đổi ra thập phân?
Lời giải:
Vì 1 giờ = 60 phút
Nên 4 giờ 30 phút = 4,5 giờ.
A. 480
B. 460
C. 246
D. 260.
Lời giải:
Đáp án đúng là: A
Số cách xếp 6 người vào 6 ghế là 6!
Ta tính số cách xếp sao cho A và F ngồi cạnh nhau:
Xem AF là một phần tử X, ta có 5! = 120 cách xếp 5 người X; B; C; D; E
Khi hoán vị A; F ta có thêm được một cách xếp
Vậy có 2 . 120 = 240 cách xếp để A và F ngồi cạnh nhau
Do đó, số cách xếp để A và F không ngồi cạnh nhau là:
6! – 240 = 480 cách
Vậy ta chọn đáp án A.
Câu 34: Khi nào dùng denta và denta phẩy?
Lời giải:
Phương trình dạng ax2 + bx + c = 0
• Denta: Dùng cho mọi trường hợp
Công thức denta: ∆ = b2 – 4ac
• Denta phẩy: Nên dùng khi hệ số b chia hết cho 2
Công thức denta phẩy: ∆’ = b’2 – ac trong đó b' = b2.
Câu 35: Chứng minh rằng: Nếu P là số nguyên tố lớn hơn 3 thì (P – 1)(P + 1) chia hết cho 24.
Lời giải:
Vì P là số nguyên tố lớn hơn 3
Nên P không chia hết cho 2 và 3
Ta có: P không chia hết cho 2
Suy ra P – 1 và P + 1 là 2 số chẵn liên tiếp
Do đó (P – 1)(P + 1) chia hết cho 8 (1)
Mặt khác: P không chia hết cho 3
+) Nếu P = 3k +1 thì P – 1 = 3k ⋮ 3
Suy ra (P – 1)(P + 1) chia hết cho 3
+) Nếu P = 3k + 2 thì P + 1 = 3k + 3 ⋮ 3
Suy ra (P – 1)(P + 1) chia hết cho 3
Do đó P không chia hết cho 3 thì (P – 1)(P + 1) chia hết cho 3 (2)
Từ (1) và (2) suy ra (P – 1)(P + 1) chia hết cho 8 và 3
Mà (8; 3) = 1
Suy ra (P – 1)(P + 1) chia hết cho 24
Vậy nếu P là số nguyên tố lớn hơn 3 thì (P – 1)(P + 1) chia hết cho 24.
Câu 36: Với các số thực dương a, b, c chứng minh rằng: a3 + b3 + c3 ≥ ab2 + bc2 + ca2.
Lời giải:
Áp dụng bất đẳng thức Cô – si ta có:
a3 + b3 + b3 ≥ 3ab2
b3 + c3 + c3 ≥ 3bc2
a3 + a3 + c3 ≥ 3ca2
Cộng vế với vế của các bất đẳng thức trên ta được
3(a3 + b3 + c3) ≥ 3(ab2 + bc2 + ca2)
⇔ a3 + b3 + c3 ≥ ab2 + bc2 + ca2
Dấu “=” xảy ra khi a = b = c
Vậy a3 + b3 + c3 ≥ ab2 + bc2 + ca2.
Câu 37: Phân tích đa thức sau thành nhân tử: 2ab2 – a2b – b3.
Lời giải:
Ta có:
2ab2 – a2b – b3
= –b(b2 – 2ab + a2)
= –b(b – a)2.
Câu 38: Chứng minh bất đẳng thức: a2 + b2 ≥ 2ab.
Lời giải:
Ta có:
(a – b)2 ≥ 0 với mọi a, b
⇔ a2 – 2ab + b2 ≥ 0 với mọi a, b
⇔ a2 + b2 ≥ 2ab với mọi a, b
Dấu “=” xảy ra khi a = b
Vậy a2 + b2 ≥ 2ab.
Lời giải:
(y – 5)(y + 8) – (y + 4)(y – 1)
= y2 + 8y – 5y – 40 – y2 + y – 4y + 4
= –36
Vậy giá trị biểu thức trên không phụ thuộc vào biến y.
Câu 40: Tổng 2 số tự nhiên là 1987 biết giữa chúng có 200 số chẵn. Tìm hai số đó.
Lời giải:
Vì giữa chúng có 200 số chẵn nên hiệu của nó là:
200 × 2 + 1 = 401
Số lớn là :
(1987 + 401) : 2 = 1194
Số bé là :
1194 – 401 = 793
Vậy hai số cần tìm là 1194 và 793.
Câu 41: Phân tích đa thức thành nhân tử: x4 + 6x3 + 7x2 – 6x + 1.
Lời giải:
Ta có:
x4 + 6x3 + 7x2 – 6x + 1
= x4 + 6x3 + 9x2 – 2x2 – 6x + 1
= (x2)2 + 2 . x2 . 3x + (3x)2 – 2(x2 + 3x) + 1
= (x2 + 3x)2 – 2(x2 + 3x) + 1
= (x2 + 3x – 1)2
Câu 42: Thực hiện chứng minh –x2 – 4x – 7 luôn âm với mọi x.
Lời giải:
Ta có:
–x2 – 4x – 7 = –x2 – 4x – 4 – 3 = –(x2 + 4x + 4) – 3 = –(x + 2)2 – 3
Vì (x + 2)2 ≥ 0 với mọi x
Nên –(x + 2)2 ≤ 0 với mọi x
Suy ra –(x + 2)2 – 3 < 0 với mọi x
Vậy –x2 – 4x – 7 luôn âm với mọi x.
Câu 43: Số giao điểm của đồ thị hai hàm số y = x2 – 3x – 1 và y = x3 – 1 là:
A. 1
B. 0
C. 2
D. 3.
Lời giải:
Đáp án đúng là: A
Xét phương trình hoành độ giao điểm:
x2 – 3x – 1 = x3 – 1
⇔ x3 – x2 + 3x = 0
⇔ x(x2 – x + 3) = 0
⇔ x = 0 (vì x2 – x + 3 > 0)
Suy ra 2 đồ thị hàm số cắt nhau tại 1 điểm
Vậy ta chọn đáp án A.
A. Stp = 2πR2
B. Stp = 4πR2
C. Stp = 6πR2
D. Stp = 3πR2.
Lời giải:
Đáp án đúng là C
Thiết diện qua trục của hình trụ là một hình vuông nên chiều cao của hình trụ là h =2R
Diện tích toàn phần của hình trụ bằng
Stp = 2πR2 + 2πR . h = 2πR2 + 2πR . 2R = 6πR2
Vậy ta chọn đáp án C.
Câu 45: Chứng minh 62n + 19n – 2n+1 chia hết cho 17.
Lời giải:
Ta có:
62n + 19n – 2n+1
= 62n + 19n – 2.2n
= (36n – 2n ) + (19n – 2n)
Vì 36n – 2n = (36 – 2) . a (a là 1 số dương)
19n – 2n = (19 – 2) . b (b là 1 số dương)
Nên 36n – 2n ⋮ (36 – 2) = 34 = 2 . 17
19n – 2n ⋮ (19 – 2) = 17
Suy ra 62n + 19n – 2n+1 = (36n – 2n ) + (19n – 2n) ⋮ 17
Vậy 62n + 19n – 2n+1 chia hết cho 17.
A. 62
B. 72
C. 720
D. 144.
Lời giải:
Đáp án đúng là: B
Chọn vị trí cho hai nhóm 3 nam và 3 nữ có 2 cách chọn (1 nhóm ở vị trí chẵn và nhóm còn lại ở vị trí lẻ)
Xếp 3 nam có: 3 . 2 . 1 = 6 cách xếp
Xếp 3 nữ có: 3 . 2 . 1 = 6 cách xếp
Suy ra có 2 . 6 . 6 = 72 cách xếp
Vậy ta chọn đáp án B.
Câu 47: Trong các mệnh đề sau, mệnh đề nào đúng?
I. “ Mỗi phép vị tự tỉ số k là một phép đồng dạng tỉ số k”
II. “ Mỗi phép đồng dạng là một phép dời hình”
III. “Thực hiện liên tiếp hai phép đồng dạng ta được một phép đồng dạng”
A. Chỉ I
B. Chỉ II
C. Chỉ III
D. Cả I và III.
Lời giải:
Đáp án đúng là: C
Mệnh đề I sai vì nếu k < 0 thì phép đồng dạng có tỉ số |k|
Mệnh đề II sau vì phép đồng dạng tỉ số k ≠ 1 không phải phép dời hình
Mệnh để III đúng
Vậy ta chọn đáp án C.
Câu 48: Tìm giá trị nhỏ nhất của biểu thức:
a) A = x2 – 2x + 5
b) B = x2 – 8x + 10
c) C = x2 – 6x + 11.
Lời giải:
a) A = x2 – 2x + 5
= x2 – 2x + 1 + 4
= (x – 1)2 + 4 ≥ 4
Dấu "=" xảy ra khi x – 1 = 0 ⇔ x = 1
Vậy GTNN của biểu thức A bằng 4 khi x = 1.
b) B = x2 –8x +10
= x2 – 2x.4 + 16 – 6
= (x – 4)2 – 6 ≥ –6
Dấu "=" xảy ra khi x = 4
Vậy giá trị nhỏ nhất của B là –6 khi x = 4.
c) C = x2 – 6x + 11
= x2 – 6x + 9 + 2
= (x – 3)2 + 2 ≥ 2
Dấu "=" xảy ra khi x = 3
Vậy giá trị nhỏ nhất của C bằng 2 khi x = 3.
Câu 49: Đồ thị hàm số x = 0 là như nào nêu định nghĩa. Lấy ví dụ.
Lời giải:
Đồ thị hàm số x = 0 là đồ thị được biểu diễn bởi tập hợp các điểm có hoành độ bằng 0 và tung độ bất kỳ.
Hay chính là trục tung.
Câu 50: Giải phương trình x4 + 2x2 – 24 = 0.
Lời giải:
Đặt t = x2 (t ≥ 0)
Ta có t2 + 2t – 24 = 0 (1)
∆ = 22 – 4 . 1 . (– 24) = 100
Vì ∆ > 0 nên phương trình (1) có hai nghiệm phân biệt là
Mà t ≥ 0 nên t = 4
Suy ra x2 = 4
Hay x = ± 2
Vậy x = 2, x = –2.