Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 95)

Đề bài. Cho x + y = 15. Tìm min, max $B=\sqrt{x-4}+\sqrt{y-3}$

Lời giải:

Áp dụng bất đẳng thức cho a, b > 0 $\sqrt{a}\mathrm{ }+\sqrt{b}\ge \sqrt{a+b}$ ta có:

$B=\sqrt{x-4}\mathrm{ }+\sqrt{y-3}\mathrm{ }\ge \sqrt{x-4+y-3}\mathrm{ }=\sqrt{x+y-7}$

Bình phương 2 vế được: B² ≥ x + y – 7 = 15 – 7 = 8

Suy ra: $B\ge 2\sqrt{2}$

Vậy minB = $2\sqrt{2}$ khi (x;y) = (4;11), (12;3)

Lại có: Áp dụng bất đẳng thức Bunhiacopxki:

$B^2={(1.\sqrt{x-4}\mathrm{ }+1.\sqrt{y-3})}^2\le (1+1)(x-4+y-3)=2.(15-7)=16$

Suy ra: maxB = 4

Dấu “=” xảy ra khi $\{\begin{array}{c}x\ge 4\\ y⩾3\\ x-4=\sqrt{y-3}\\ x+y=15\end{array}\iff (x;y)=(8;7)$

Đề bài. Cho x,y,z là các số nguyên thỏa mãn: (x - y)(y - z)(z – x) = x + y + z. Chứng minh x + y + z chia hết cho 27.

Lời giải:

- Nếu x,y,z khác số dư khi chia cho 3

+ Nếu có 2 số chia hết cho 3. Số còn lại không chia hết cho 3.

Giả sử đều chia hết cho 3, z không chia hết cho 3

Do x, y đều chia hết cho 3 nên

⇒ (x − y)(y − z)(z – x) ⋮ 3 (Vô lý)

+ Nếu có 1 số chia hết cho 3, 2 số còn lại khác số chia khi chia cho 3, không chia hết cho 3. Tương tự dẫn đến vô lý.

Vậy cả 3 số có cùng số dư khi chia cho 3

⇒(x − y)(y − z)(z − x) ⋮ 27

⇒ x + y + z ⋮ 27

Đề bài. Cho x, y, z thỏa mãn đk x + y + z = a. Tìm GTNN của $P=(1+\frac{a}{x})(1+\frac{a}{y})(1+\frac{a}{z})$

Lời giải:

$P=(1+\frac{a}{x})(1+\frac{a}{y})(1+\frac{a}{z})=(1+\frac{x+y+z}{x})(1+\frac{x+y+z}{y})(1+\frac{x+y+z}{z})$

$=\frac{(x+x+y+z)(x+y+y+z)(x+y+z+z)}{xyz}\ge \frac{4\sqrt[4]{x^{2}yz}.4\sqrt[4]{y^{2}xz}.4\sqrt[4]{z^{2}xy}}{xyz}=\frac{64xyz}{xyz}=64$

Vậy min P = 64 khi $x=y=z=\frac{a}{3}$

Đề bài. Cho x + 3y – 4 = 0, tính x³ - x² + 9x²y - 9y² + 27xy² + 27y³ - 6xy

Lời giải:

Ta có:

x³ - x² + 9x²y - 9y² + 27xy² + 27y³ - 6xy

= x³ + 3x²y – 4x² + 3x² + 9xy – 12x + 6x²y + 18xy² – 24xy + 9xy² + 27y³ – 36y² + 9xy + 27y² + 12x

= x²(x + 3y – 4) + 3x(x + 3y – 4) + 6xy(x + 3y – 4) + 9y²(x + 3y – 4) + 9y(x + 3y) + 12x

= 0 + 0 + 0 + 0 + 0 + 9y.4 + 12x

= 36y + 12x

= 12(x + 3y)

= 12.4

= 48.

Đề bài. Chứng tỏ rằng (2²⁰²² + 2²⁰²¹ + 2²⁰²⁰) chia hết cho 7.

Lời giải:

2²⁰²² + 2²⁰²¹ + 2²⁰²⁰ = 2²⁰²⁰(2² + 2 + 1) = 2²⁰²⁰.7

Ta thấy 7 ⋮ 7 nên 2²⁰²⁰.7 ⋮ 7

Vậy (2²⁰²² + 2²⁰²¹ + 2²⁰²⁰) chia hết cho 7.

Đề bài. Tìm các hệ số a, b, c biết: (ax + b)(x² – cx + 2) = x³ + x² – 2 với mọi x

Lời giải:

(ax + b)(x² – cx + 2) = x³ + x² – 2

⇔ (ax + b)(x² – cx + 2) = x³ – x² + 2x² – 2

⇔ (ax + b)(x² – cx + 2) = x²(x – 1) + 2(x – 1)(x + 1)

⇔ (ax + b)(x² – cx + 2) = (x – 1)(x² + 2x + 2)

Suy ra: $\{\begin{array}{c}a=1\mathrm{ }\\ b=-1\\ c=-2\end{array}$

Đề bài. Chứng minh $\frac{1}{2\sqrt{1}}+\frac{1}{3\sqrt{2}}+\frac{1}{4\sqrt{3}}+\mathrm{\dots }+\frac{1}{2005\sqrt{2004}}<2$

Lời giải:

Với mọi n thuộc ℕ ta có: $\frac{1}{(n+1)\sqrt{n}}<2(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}})$

Thật vậy, $1<2(n+1).\sqrt{n}(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}})$

⇔ $0<(n+1)-2\sqrt{n+1}.\sqrt{n}+n={(\sqrt{n+1}-\sqrt{n})}^2$(luôn đúng)

Áp dụng vào bài toán

$\frac{1}{2\sqrt{1}}+\frac{1}{3\sqrt{2}}+\frac{1}{4\sqrt{3}}+\mathrm{\dots }+\frac{1}{2005\sqrt{2004}}<2(\frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+\mathrm{\dots }+\frac{1}{\sqrt{2004}}-\frac{1}{\sqrt{2005}})$

$=2(1-\frac{1}{\sqrt{2005}})<2$

Đề bài. Chứng minh $\frac{1}{65}<\frac{1}{5^3}+\frac{1}{6^3}+\mathrm{\dots }+\frac{1}{{2004}^3}<\frac{1}{40}$

Lời giải:

Ta xét bài toán tổng quát: Với mọi n thuộc ℕ^* ta có:

$\frac{1}{n^3}<\frac{1}{n^3-n}=\frac{1}{n(n^2-1)}=\frac{1}{(n-1).n.(n+1)}$

$\frac{1}{n^3}>\frac{1}{n^3+3n^2+2n}=\frac{1}{n.(n+1).(n+2)}$

Áp dụng vào bài toán ta có:

$\frac{1}{5^3}+\frac{1}{6^3}+\mathrm{\dots }+\frac{1}{{2004}^3}<\frac{1}{\mathrm{4.5.6}}+\frac{1}{\mathrm{5.6.7}}+\mathrm{\dots }+\frac{1}{\mathrm{2003.2004.2005}}$

$\frac{1}{5^3}+\frac{1}{6^3}+\mathrm{\dots }+\frac{1}{{2004}^3}<\frac{1}{2}(\frac{2}{\mathrm{4.5.6}}+\frac{2}{\mathrm{5.6.7}}+\mathrm{\dots }+\frac{2}{\mathrm{2003.2004.2005}})$

$\frac{1}{5^3}+\frac{1}{6^3}+\mathrm{\dots }+\frac{1}{{2004}^3}<\frac{1}{2}(\frac{1}{4.5}-\frac{1}{5.6}+\frac{1}{5.6}-\frac{1}{6.7}+\mathrm{\dots }+\frac{1}{2003.2004}-\frac{1}{2004.2005})$

$=\frac{1}{2}(\frac{1}{4.5}-\frac{1}{2003.2004})=\frac{1}{40}-\frac{1}{\mathrm{2.2003.2004}}<\frac{1}{40}$

Vậy $\frac{1}{5^3}+\frac{1}{6^3}+\mathrm{\dots }+\frac{1}{{2004}^3}<\frac{1}{40}$

Lại có: $\frac{1}{5^3}+\frac{1}{6^3}+\mathrm{\dots }+\frac{1}{{2004}^3}>\frac{1}{\mathrm{5.6.7}}+\frac{1}{\mathrm{6.7.8}}+\mathrm{\dots }+\frac{1}{\mathrm{2004.2005.2006}}$

$\frac{1}{5^3}+\frac{1}{6^3}+\mathrm{\dots }+\frac{1}{{2004}^3}>\frac{1}{2}(\frac{1}{5.6}-\frac{1}{6.7}+\frac{1}{6.7}-\frac{1}{7.8}+\mathrm{\dots }+\frac{1}{2004.2005}-\frac{1}{2005.2006})$

$\frac{1}{5^3}+\frac{1}{6^3}+\mathrm{\dots }+\frac{1}{{2004}^3}>\frac{1}{2}(\frac{1}{5.6}-\frac{1}{2005.2006})$

$\frac{1}{5^3}+\frac{1}{6^3}+\mathrm{\dots }+\frac{1}{{2004}^3}>\frac{1}{65}$

Đề bài. Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng: Tổng $\frac{1}{D{I}^2}+\frac{1}{D{K}^2}$ không đổi khi I thay đổi trên cạnh AB.

Lời giải:

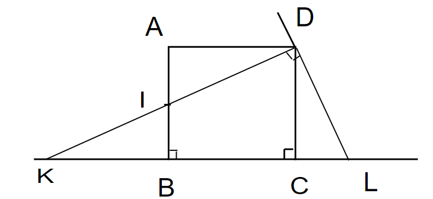
Trong tam giác DKL vuông tại D với đường cao DC. Theo hệ thức lượng trong tam giác vuông ta có: $\frac{1}{D{L}^2}+\frac{1}{D{K}^2}=\frac{1}{D{C}^2}$

Vì DI = DL nên $(\frac{1}{D{I}^2}+\frac{1}{D{K}^2}=\frac{1}{D{C}^2}$

DC không đổi nên tổng $\frac{1}{D{I}^2}+\frac{1}{D{K}^2}$ không đổi khi I thay đổi trên cạnh AB. (đpcm)

Đề bài. Chứng minh rằng F = 10²⁸ + 8 chia hết cho 72

Lời giải:

F = 10²⁸ + 8 ⋮ 9 vì tổng các chữ số bằng 9

F = 10²⁸ + 8 ⋮ 8 vì có tận cùng là 008

Do đó: F = 10²⁸ + 8 ⋮ 72 vì cùng chia hết cho 8 và 9.

Đề bài. Chứng minh $\frac{1-2{\sin }^{2}x}{1+\sin 2x}=\frac{1-\tan x}{1+\tan x}$

Lời giải:

$\frac{1-2{\sin }^{2}x}{1+\sin 2x}=\frac{1-{\sin }^{2}x-{\sin }^{2}x}{{\sin }^{2}x+{\cos }^{2}x+2\sin x.\cos x}=\frac{{\cos }^{2}x-{\sin }^{2}x}{{(\cos x+\sin x)}^2}=\frac{\cos x-\sin x}{\cos x+\sin x}\left(1\right)$

$\frac{1-\tan x}{1+\tan x}=\frac{1-\frac{\sin x}{\cos x}}{1+\frac{\sin x}{\cos x}}=\frac{\frac{\cos x-\sin x}{\cos x}}{\frac{\cos x+\sin x}{\cos x}}=\frac{\cos x-\sin x}{\cos x+\sin x}\left(2\right)$

Từ (1) và (2) suy ra:$\frac{1-2{\sin }^{2}x}{1+\sin 2x}=\frac{1-\tan x}{1+\tan x}$

Đề bài. Chứng minh tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình bình hành.

Lời giải:

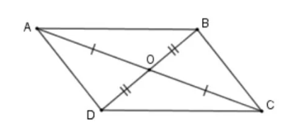
Gọi O là giao điểm của hai đường chéo.

Theo giả thiết ta có: OA = OC; OB = OD

Xét tam giác AOD và tam giác BOC có:

OA = OC

$\widehat{AOD}=\widehat{BOC}$ (đối đỉnh)

OB = OD

⇒ ∆AOD = ∆BOC (c.g.c)

Suy ra: AD = BC và $\widehat{ADO}=\widehat{BCO}$

Mà $\widehat{ADO},\widehat{BCO}$ ở vị trí so le trong nên AD // BC
Suy ra: ABCD là hình bình hành vì AD = BC và AD // BC.

Đề bài. Chứng minh n + 1 và 2n + 3 là hai số nguyên tố cùng nhau.

Lời giải:

Gọi d = ƯCLN (n + 1; 2n + 3)

Suy ra: n + 1 ⋮ d; 2n + 3 ⋮ d

⇒ $\{\begin{array}{c}2n+2\mathrm{⋮}d\\ 2n+3:d\end{array}\Rightarrow (2n+3)-(2n+2)\mathrm{⋮}d$ hay 1 ⋮ d

Suy ra: d = 1

Vậy (n + 1; 2n + 3) = 1 tức n + 1 và 2n + 3 là hai số nguyên tố cùng nhau.

Đề bài. Chứng minh rằng nếu 5(m + n)² + mn ⋮ 441 thì mn ⋮ 441 (m, n ∈ ℤ)

Lời giải:

Từ giả thiết 5(m + n)² + mn ⋮ 441

Mà 441 = 21² nên 5(m + n)² + mn ⋮ 21

Ta có: 5(m + n)² + mn = 5m² + 11mn + 5n² = 5m² – 10mn + 5n² + 21mn ⋮ 21

Hay 5(m – n)² + 21mn ⋮ 21

Mà 21mn ⋮ 21 nên 5(m –n)² ⋮ 21

Và (5;21) = 1 nên (m – n)² ⋮ 21

Suy ra: m – n ⋮ 21

⇒ (m – n)² ⋮ 441

⇒ 5(m – n)² ⋮ 441

Kết hợp với 5(m + n)² + mn ⋮ 441

⇒ 5(m + n)² + mn - 5(m – n)² ⋮ 441

Hay 21mn ⋮ 441, suy ra mn ⋮ 441

Đề bài. Cho $\frac{a}{b}=\frac{c}{d}$ với a, b, c, d khác 0. Chứng minh $\frac{a}{a-b}=\frac{c}{c-d}$

Lời giải:

Từ $\frac{a}{b}=\frac{c}{d}$ suy ra $\frac{a}{b}.bd=\frac{c}{d}.bd\iff ad=bc\iff \frac{b}{a}=\frac{d}{c}$

Suy ra: $1-\frac{b}{a}=1-\frac{d}{c}$

⇔ $\frac{a-b}{a}=\frac{c-d}{c}$

⇔ $\frac{a}{a-b}=\frac{c}{c-d}$

Đề bài. Cho tứ giác ABCD. Chứng minh $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$

Lời giải:

$\overrightarrow{AB}+\overrightarrow{CD}=(\overrightarrow{AD}\mathrm{ }+\overrightarrow{DB})+(\overrightarrow{CB}+\overrightarrow{BD})$

$=\overrightarrow{AD}+\overrightarrow{CB}\mathrm{ }+(\overrightarrow{BD}\mathrm{ }+\overrightarrow{DB})$

$=\overrightarrow{AD}+\overrightarrow{CB}+\overrightarrow{BB}$

$=\overrightarrow{AD}\mathrm{ }+\overrightarrow{CB}$

Vậy $\overrightarrow{AB}+\overrightarrow{CD}\mathrm{ }=\overrightarrow{AD}\mathrm{ }+\overrightarrow{CB}$

Đề bài. Cho tam giác ABC có BC = a, AC = b, Ab = c, đường phân giác AD.

1. Tính độ dài BD, DC.

2. Tia phân giác của góc B cắt AD tại I. Tính tỉ số AI : ID.

3. Cho BC bằng trung bình cộng của AB và AC, gọi G là trọng tâm của tam giác ABC. Chứng minh IG song song BC.

Lời giải:

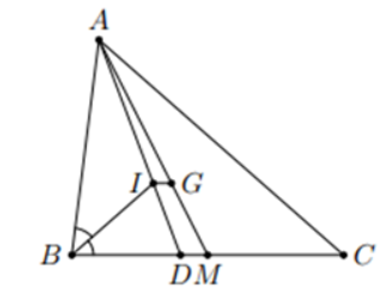1. Vì AD là phân giác của tam giác ABC nên $\frac{DB}{AB}=\frac{DC}{AC}=\frac{DB+DC}{AB+AC}=\frac{a}{b+c}$

Vậy $DB=\frac{ac}{b+c};DC=\frac{ab}{b+c}$

2. Vì BI là đường phân giác của tam giác BAD nên: $\frac{AI}{ID}=\frac{AB}{BD}=c:\frac{ac}{b+c}=\frac{b+c}{a}$

3. Ta có: $a=\frac{b+c}{2}\Rightarrow \frac{AI}{ID}=2$

Mặt khác $\frac{AG}{GM}=2$

Do đó: $\frac{AG}{GM}=\frac{AI}{ID}=2$

Suy ra: IG // BC.

Đề bài. Chứng minh biểu thức $A=-x^2+\frac{2}{3}x-1$ luôn âm với mọi giá trị của biến

Lời giải:

$A=\mathrm{ }-x^2+\frac{2}{3}x-1=-(x^2-\frac{2}{3}x+1)=-{(x-\frac{1}{3})}^2-\frac{8}{9}\le \mathrm{ }-\frac{8}{9}<0$ với mọi x

Đề bài. Chứng minh biểu thức sau luôn âm với mọi x: –x² – 6x – 15

Lời giải:

–x² – 6x – 15 = –(x² + 6x + 15) = –(x + 3)² – 6

Vì –(x + 3)² ≤ 0 với mọi x nên –(x + 3)² – 6 ≤ -6 với mọi x

Vậy –x² – 6x – 15 luôn âm với mọi x.

Đề bài. Chứng minh với a, b dương thì $\sqrt{a+b}\mathrm{ }<\sqrt{a}+\sqrt{b}$

Lời giải:

$\sqrt{a+b}<\sqrt{a}\mathrm{ }+\sqrt{b}$

⇒ ${\left(\sqrt{a+b}\right)}^2<{(\sqrt{a}\mathrm{ }+\sqrt{b})}^2$

⇒ $a+b<a+2\sqrt{ab}+b$

⇔ $2\sqrt{ab}>0$

⇔ $\sqrt{ab}\mathrm{ }>0$ (luôn đúng với a, b > 0)

Vậy $\sqrt{a+b}\mathrm{ }<\sqrt{a}+\sqrt{b}$

Đề bài. Có tồn tại hay không một dãy gồm 2019 số tự nhiên liên tiếp mà các số đó đều là hợp số?

Lời giải:

Có tồn tại.

Chứng minh:

Đặt: A = 2 . 3 . 4... 2019. 2020

Xét 2019 số tự nhiên liên tiếp:

A + 2; A + 3; ... ; A + 2020.

Ta có: A + 2 = 2 . 3 . 4... 2019. 2020 + 2 = 2 . ( 3 . 4... 2019. 2020 + 1 ) là hợp số.

A + 3 = 2 . 3 . 4... 2019. 2020 + 3 = 3 . ( 2 . 4... 2019. 2020 + 1 ) là hợp số.

...

A + 2020 = 2 . 3 . 4... 2019. 2020 + 2020 = 2020 . ( 2 . 3. 4... 2019 + 1 ) là hợp số.

Vậy tồn tại dãy số gồm 2019 số tự nhiên liên tiếp là hợp số.

Đề bài. Chứng minh đẳng thức sau: $\frac{(\sin x+\cos x)}{{\sin }^{3}x}={\cot }^{3}x+{\cot }^{2}x\cot x+1$

Lời giải:

cot³x + cotx + 1 = cot²x(cotx + 1) + (cotx + 1)

= (cotx + 1)(cot²x + 1)

$=\frac{\cos x+\sin x}{\sin x}.\frac{{\cos }^{2}x+{\sin }^{2}x}{{\sin }^{2}x}$

$=\frac{\cos x+\sin x}{\sin x}.\frac{1}{{\sin }^{2}x}$

$=\frac{\cos x+\sin x}{{\sin }^{3}x}$

Vậy $\frac{(\sin x+\cos x)}{{\sin }^{3}x}={\cot }^{3}x+{\cot }^{2}x\cot x+1$

Đề bài. Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc (O). Tiếp tuyến tại A của (O) cắt đường thẳng BC tại D. Gọi E là trung điểm của AD. Chứng minh EC là tiếp tuyến của (O).

Lời giải:

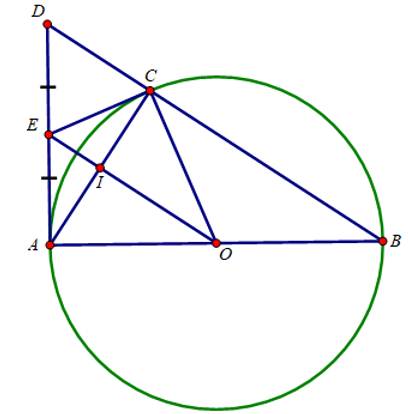a) Ta có: $\widehat{ACB}={90}^{\circ }$(góc nội tiếp chắn nửa đường tròn)

⇒ AC ⊥ BD

ΔACD vuông tại C có CE là trung tuyến nên:

CE = EA = $\frac{1}{2}AD$

Xét ΔAEO và ΔCEO có:

AE = CE

EO : cạnh chung

AO = CO

⇒ ΔAEO = ΔCEO (c.c.c)

⇒ $\widehat{EAO}=\widehat{ECO}={90}^{\circ }$

⇒ CE là tiếp tuyến của (O)

Đề bài. Chứng minh tam giác ABC có h_a = 2R.sinB.sinC

Lời giải:

TH1: Tam giác ABC nhọn hoặc tam giác ABC tù ở A

Ta có: $\widehat{AHC}={90}^{\circ }$

Suy ra: h_a = AH = AC.sinC = b.sinC

Mà theo định lý sin: $\frac{b}{\sin B}=2R$ hay b = 2R.sinB

Suy ra: h_a = 2R.sinB.sinC.

TH2: Tam giác ABC tù ở B hoặc C

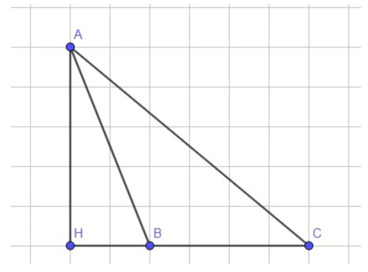Ta có: $\widehat{AHB}={90}^{\circ }$

Suy ra: h_a = AH = AB.sin$\widehat{ABH}$

h_a = AB.sin$({180}^{\circ }\mathrm{ }-\widehat{B})$

h_a = AB.sinB = c.sin B

Mà theo định lý sin: $\frac{c}{\sin C}=2R$ hay c = 2R.sinC

Vậy h_a = 2R.sinB.sinC.

Đề bài. Chứng minh n⁵ – n chia hết cho 30 với mọi số nguyên n.

Lời giải:

n⁵ – n = n(n⁴ – 1)

= n(n² – 1)(n² + 1)

= n(n – 1)(n + 1)(n² + 1)

= n(n – 1)(n + 1)(n² – 4 + 5)

= n(n – 1)(n + 1)(n – 2)(n + 2) + 5n(n – 1)(n +1)

Vì n(n – 1)(n + 1)(n – 2)(n + 2) là tích của 5 số nguyên liên tiếp nên n(n – 1)(n + 1)(n – 2)(n + 2) chia hết cho 5

Và 5n(n – 1)(n +1) chia hết cho 5

Nên: n(n – 1)(n + 1)(n – 2)(n + 2) + 5n(n – 1)(n +1) ⋮ 5 (1)

Lại có: n(n – 1)(n + 1) là tích của 3 số nguyên liên tiếp nên chia hết cho 2 và 3

Suy ra: n(n – 1)(n + 1)(n – 2)(n + 2) + 5n(n – 1)(n +1) ⋮ 6 (2)

Từ (1) và (2) ta có: n(n – 1)(n + 1)(n – 2)(n + 2) + 5n(n – 1)(n +1) ⋮ 30

Vậy n⁵ – n chia hết cho 30 với mọi số nguyên n.

Đề bài. Nếu ab chia hết cho c và ƯCLN (a,c) = 1 thì b chia hết cho c

Lời giải:

Ta có: ab ⋮ c suy ra: $[\begin{array}{c}a⋮c\\ b⋮c\end{array}$

Nếu a ⋮ c: theo giả thiết ƯCLN (a,c) = 1 tức a và c là hai số nguyên tố cùng nhau

Suy ra vô lý

Vậy b ⋮ c.

Đề bài. Cho (O) và A là điểm nằm ngoài (O). Qua A vẽ tiếp tuyến AB, AC với (O) với B,C là tiếp điểm. OA cắt BC tại DA

a) Chứng minh OA là đường trung trực BC.

b) Chứng minh OD.DA = BD²

c) Vẽ đường kính BE, AE cắt (O) tại F. Gọi G là trung điểm của EF, đường thẳng OG cắt đường thẳng BC tại H. Chứng minh OD.OA = OG.OH

d) Chứng minh EH là tiếp tuyến của (O)

Lời giải:

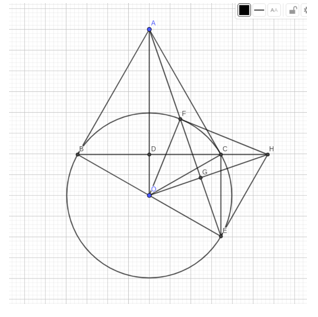a) Ta có: AB, AC là tiếp tuyến của (O) nên AB = AC

Mà OB = OC = R

Nên AO là trung trực BC

b) AB ⊥ OB, BD ⊥ OA nên OB² = OD.OA

BD² = OD.DA (hệ thức lượng trong tam giác ABO vuông tại B, BD là đường cao)

c) Xét tam giác OAG và tam giác OHD có:

Chung $\widehat{O}$

$\widehat{OGA}=\widehat{HDO}={90}^{\circ }$

⇒ ΔOAG ∼ ΔOHD (g.g)
⇒ $\frac{OA}{OH}=\frac{OG}{OD}$ hay OA.OD = OH.OG

d) Ta có: OA.OD = OH.OG = OB² = OE²

Suy ra: $\frac{OE}{OH}=\frac{OG}{OE}$

⇒ ΔOGE ∼ ΔOEH (c.g.c)

Nên: $\widehat{OEH}=\widehat{OGE}={90}^{\circ }$

Vậy EH là tiếp tuyến của (O).

Đề bài. Chứng tỏ rằng số có dạng $\overline{aaa}$ bao giờ cũng chia hết cho 37.

Lời giải:

Ta có: $\overline{aaa}$= 100.a + 10.a + a = (100 + 10 + 1).a = 111.a = 3.37.a ⋮ 37 (điều phải chứng minh)

Vậy số có dạng $\overline{aaa}$ bao giờ cũng chia hết cho 37.

Đề bài. Chứng minh rằng: Nếu p là một số nguyên tố lớn hơn 3 và 2p + 7 cũng là số nguyên tố thì 4p + 7 là một hợp số.

Lời giải:

Vì p và 2p + 7 đều là số nguyên tố lớn hơn 3 nên cả hai đều không chia hết cho 3.

Giả sử: p chia 3 dư 1, giả sử p = 3k + 1 thì 2p + 7 = 2(3k + 1) + 7 = 6k + 9 ⋮ 3 nên mâu thuẫn

Vậy p chia 3 dư 2, giả sử p = 3k + 2

Khi đó 4p + 7 = 4(3p + 2) + 7 = 12p + 15 ⋮ 3, mà 4p + 7 lớn hơn 3

Vậy 4p + 7 là hợp số.

Đề bài. Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu cùa H lên AB và AC.

a) Chứng minh: AM.AB = AN.AC.

b) Chứng minh: $\frac{S_{AMN}}{S_{ACB}}={\sin }^{2}B.{\sin }^{2}C$

Lời giải:

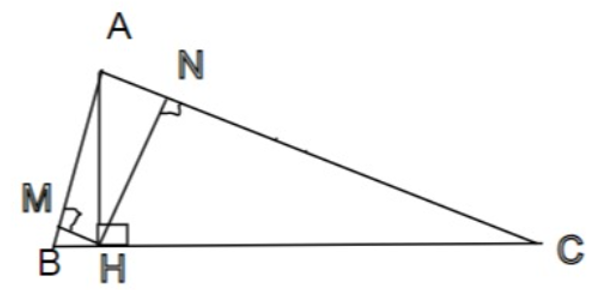a) Có : AH là đường cao của tam giác ABC ⇒ $\widehat{AHB}={90}^{\circ }$

Tam giác AHB vuông tại H có AM là đường cao

⇒ AM.AB = AH²

Tam giac AHC vuông tai H có AN là đường cao

⇒ AN.AC = AH²

Nên AM.AB =AN.AC

b) Tam giác AHB vuông tại H nên $\sin B=\frac{AH}{AB}$

Tam giác AHC vuông tại H ⇒ $\sin C=\frac{AH}{AC}$

Áp dụng công thức tính diện tích theo định lý sin, ta có:

Lại có: $S_{ABC}=\frac{1}{2}.AB.AC.\sin A$

$S_{AMN}=\frac{1}{2}.AM.AN.\sin A$

Suy ra: $\frac{S_{AMN}}{S_{ABC}}=\frac{\frac{1}{2}.AM.AN.\sin A}{\frac{1}{2}.AB.AC.\sin A}=\frac{AM.AN}{AB.AC}=\frac{A{H}^2.A{H}^2}{A{B}^2.A{C}^2}={\left(\frac{AH}{AB}\right)}^2.{\left(\frac{AH}{AC}\right)}^2={\sin }^{2}B.{\sin }^{2}C$

Đề bài. Cho tam giác ABC vuông tại A, đường cao AH. Trên AC lấy điểm K ( K khác A và C), gọi D là hình chiếu của A trên BK. Cho biết BC = 4BH.

Chứng minh rằng: $S_{BHD}=\frac{1}{4}{S}_{BKC}.{\cos }^2\widehat{ABD}$

Lời giải:

Ta có: $S_{ABC}=\frac{1}{2}.AC.AB=\frac{1}{2}.AC.AB.1=\frac{1}{2}.AC.AB.\sin {90}^{\circ }Â\mathrm{ }=\frac{1}{2}.AC.AB.\sin \widehat{A}$

$S_{BHD}=\frac{1}{2}.BH.BD.\sin \widehat{DBH}$

$S_{BKC}=\frac{1}{2}.BK.BC.\sin \widehat{KBC}$

$\frac{S_{BHD}}{S_{BKC}}=\frac{BH.BD}{BK.BC}=\frac{1}{4}.\frac{BD}{BK}=\frac{1}{4}.\frac{B{D}^2}{BK.BD}=\frac{1}{4}.\frac{B{D}^2}{B{A}^2}=\frac{1}{4}.{\cos }^2\widehat{ABD}$

Đề bài. Chứng minh $\frac{1-\cos 2x}{\sin 2x}=\tan x$

Lời giải:

$\frac{1-\cos 2x}{\sin 2x}=\frac{1-(2{\cos }^{2}x-1)}{2\sin x.\cos x}=\frac{2-2{\cos }^{2}x}{2\sin x.\cos x}=\frac{2(1-{\cos }^{2}x)}{2\sin x.\cos x}=\frac{2.{\sin }^{2}x}{2\sin x.\cos x}=\frac{\sin x}{\cos x}=\tan x$

Vậy $\frac{1-\cos 2x}{\sin 2x}=\tan x$

Đề bài. Chứng minh rằng trong tam giác ABC ta có: sinC = sin (A + B).

Lời giải:

Trong tam giác ABC có: $\widehat{A}+\widehat{B}+\widehat{C}={180}^{\circ }$

⇒ $\widehat{A}+\widehat{B}={180}^{\circ }\mathrm{ }-\widehat{C}$

Ta có: sinα = sin(180° – α ) nên sinC = sin(180° – C ) = sin (A + B).

Vậy sinC = sin (A + B).

Đề bài. Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh:

a) ∆ABH = ∆ACH

b) AH là tia phân giác của góc BAC.

Lời giải:

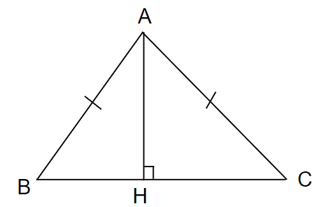a) Xét ∆ABH và ∆ACH có:

Chung AH

$\widehat{AHB}=\widehat{AHC}={90}^{\circ }$

AB = AC (vì tam giác ABC cân)

⇒ ∆ABH = ∆ACH (c.g.c)

b) Theo phần a có ∆ABH = ∆ACH nên $\widehat{BAH}=\widehat{HAC}$(2 góc tương ứng)

Suy ra: AH là tia phân giác của $\widehat{BAC}$

Đề bài. Chứng minh rằng trong 1 tam giác vuông, trung tuyến ứng với cạnh huyền nửa cạnh huyền

Lời giải:

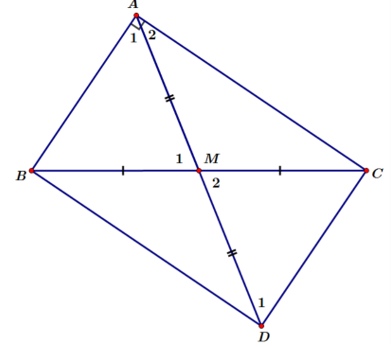Lấy D đối xứng với A qua M

Xét tam giác ABM và tam giác CDM ta có:

$\widehat{M_1}=\widehat{M_2}$ (đối đỉnh)

MB = MC

MA = MD

Suy ra: ∆ABM = ∆DCM (c.g.c)

Suy ra: AB = CD và $\widehat{A_1}=\widehat{D_1}$

Mặt khác ta có: $\widehat{A_1}+\widehat{A_2}=\widehat{BAC}={90}^{\circ }$

⇒ $\widehat{D_1}+\widehat{A_2}={90}^{\circ }\Rightarrow \widehat{ACD}={90}^{\circ }$

Xét tam giác ABC và tam giác ACD có:

AB = CD

$\widehat{BAC}=\widehat{ACD}={90}^{\circ }$

AC chung

⇒ ∆ABC = ∆CDA (c.g.c)

⇒ BC = AD

Mà theo cách dựng điểm D có: $MA=MD=\frac{1}{2}AD$

Suy ra: $AM=\frac{1}{2}BC$

Vậy trong 1 tam giác vuông, trung tuyến ứng với cạnh huyền bằng $\frac{1}{2}$ cạnh huyền.

Đề bài. Chứng minh rằng với mọi n ∈ ℕ thì n(2n + 7)(7n + 1) chia hết cho 6

Lời giải:

Vì (7n + 1) - n = 6n + 1 là số lẻ nên trong hai số 7n + 1 và n có đúng một số chẵn

⇒ A = n(2n + 7)(7n + 1) ⋮ 2 (1)

Xét 3 TH:

+) n = 3k (k ∈ ℕ): Khi đó n ⋮⋮ 3 ⇒⇒ A = n(2n + 7)(7n + 1) ⋮⋮ 3

+) n = 3k + 1 (k ∈ ℕ): Khi đó 2n + 7 = 2(3k + 1) + 7 = 6k + 9 ⋮ 3

⇒ A = n(2n + 7)(7n + 1) ⋮ 3

+) n = 3k + 2 (k ∈ ℕ): Khi đó 7n + 1 = 7(3k + 2) + 1 = 21k + 15 ⋮ 3

⇒ A = n(2n + 7)(7n + 1) ⋮ 3

Từ đó suy ra A = n(2n + 7)(7n + 1) ⋮ 3 (2)

Từ (1) và (2) suy ra A ⋮ 6 (đpcm)

Đề bài. Chứng tỏ rằng A = 1 + 4 + 4² + … + 4²⁰²¹ chia hết cho 21.

Lời giải:

Dựa vào số mũ ta có thể thấy A có tất cả 2022 hạng tử nên chia làm 674 nhóm, mỗi nhóm 3 hạng tử.

A = 1 + 4 + 4² + … + 4²⁰²¹

A = (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + … + (4²⁰¹⁹ + 4²⁰²⁰ + 4²⁰²¹)

A = (1 + 4 + 4²) + 4³(1 + 4 + 4²) + … + 4²⁰¹⁹(1 + 4 + 4²)

A = (1 + 4 + 4²)(1 + 4³ + … + 4²⁰¹⁹)

A = 21.(1 + 4³ + … + 4²⁰¹⁹) ⋮ 21

Vậy A ⋮ 21.

Đề bài. Chứng minh rằng A = 3^{5n + 2} + 3^{5n + 1} – 3⁵ⁿ chia hết cho 11 với mọi n ∈ ℕ

Lời giải:

A = 3^{5n + 2} + 3^{5n + 1} – 3⁵ⁿ

A = 3⁵ⁿ.3² + 3⁵ⁿ.3¹ – 3⁵ⁿ

A = 3⁵ⁿ(3² + 3 – 1)

A = 3⁵ⁿ.11 ⋮ 11

Vậy A ⋮ 11.

Đề bài. Chứng minh rằng A = 2 + 2² + 2³ + … + 2⁶⁰ chia hết cho 3 và 7.

Lời giải:

A = 2 + 2² + 2³ + … + 2⁶⁰

A = (2 + 2²) + (2³ + 2⁴) + … + (2⁵⁹ + 2⁶⁰)

A = 2(1 + 2) + 2³(1 + 2) +… + 2⁵⁹(1 + 2)

A = (1 + 2)(2 + 2³ + … + 2⁵⁹)

A = 3.(2 + 2³ + … + 2⁵⁹) ⋮ 3

Vậy A ⋮ 3

Lại có:

A = 2 + 2² + 2³ + … + 2⁶⁰

A = (2 + 2² + 2³) +( 2⁴ + 2⁵ + 2⁶) + … + (2⁵⁸ + 2⁵⁹ + 2⁶⁰)

A = 2.(1 + 2 + 2²) + 2⁴.(1 + 2 + 2²) + … + 2⁵⁸.(1 + 2 + 2²)

A = (1 + 2 + 2²)(2 + 2⁴ + … + 2⁵⁸)

A = 7.(2 + 2⁴ + … + 2⁵⁸) ⋮ 7

Vậy A ⋮ 7.

Đề bài. Chứng minh rằng số dư trong phép chia một số nguyên tố cho 30 chỉ có thể là 1 hoặc là số nguyên tố. Khi chia cho 60 thì kết quả ra sao

Lời giải:

Giả sử p là số nguyên tố và p = 30k + r (0 < r < 30)

Nếu r là hợp số thì r co ước nguyên tố q ≤ $\sqrt{30}$

⇒ q = 2, 3, 5

Nhưng với q = 3, 3, 5 thì p lần lượt chia hết cho 2, 3, 5 vô lí . Vậy r = 1 hoặc r là số nguyên tố.

Khi chia cho 60 thì kết quả không còn đúng nữa

Chẳng hạn p = 109 = 60.1 + 49 (49 là hợp số)

Đề bài. Cho a, b, c > 0. Chứng minh $\frac{a^5}{b^2}+\frac{b^5}{c^2}+\frac{c^5}{a^2}\ge a^3+b^3+c^3$

Lời giải:

Áp dụng bất đẳng thức Cauchy ta được:

$\frac{a^5}{b^2}+\frac{a^5}{b^2}+\frac{a^5}{b^2}+b^3+b^3\ge 5\sqrt[5]{\frac{a^5}{b^2}.\frac{a^5}{b^2}.\frac{a^5}{b^2}.b^3.b^3}=5a^3$

⇒ $\frac{3a^5}{b^2}+2b^3\ge 5a^3$

Tương tự ta được: $\frac{3b^5}{c^2}+2c^3\ge 5b^3$

$\frac{3c^5}{a^2}+2b^3\ge 5c^3$

Cộng vế theo vế ta được:

$\frac{3a^5}{b^2}+2b^3+\frac{3b^5}{c^2}+2c^3+\frac{3c^5}{a^2}+2b^3\ge 5a^3+5b^3+5c^3=5(a^3+b^3+c^3)$

Suy ra: $3(\frac{a^5}{b^2}+\frac{b^5}{c^2}+\frac{c^5}{a^2})+2(a^3+5b^3+5c^3)\ge 5(a^3+b^3+c^3)$

$3(\frac{a^5}{b^2}+\frac{b^5}{c^2}+\frac{c^5}{a^2})\ge 3(a^3+b^3+c^3)$

Vậy $\frac{a^5}{b^2}+\frac{b^5}{c^2}+\frac{c^5}{a^2}\ge a^3+b^3+c^3$

Dấu ‘=” xảy ra khi a = b = c.

Đề bài. Chứng minh rằng với mọi số tự nhiên n thì (n + 2022)(n + 2023) chia hết cho 2

Lời giải:

Có (n + 2022)(n + 2023) là 2 số tự nhiên liên tiếp (n ∈ ℕ).

⇒ Luôn có 1 số chia hết cho 2

⇒ (n + 2022)(n + 2023)`⋮ 2

Đề bài. Cho 3 số tự nhiên a b c không chia hết cho 4. Khi chia a b c cho 4 thì có số dư khác nhau. Chứng minh a + b + c chia hết cho 2

Lời giải:

Giả sử a chia 4 dư 1; b chia 4 dư 2; c chia 4 dư 3 ta có

(a − 1) ⋮ 4; (b − 2) ⋮ 4; (c − 3) ⋮ 4

⇒ (a −1) + (b − 2) + (c − 3) ⋮ 4

⇒ (a + b + c) – 2 – 4 ⋮ 4

⇒ (a + b + c) – 2 ⋮ 4

⇒ (a + b + c) – 2 ⋮ 2

⇒ a + b + c ⋮ 2

Vậy a + b + c chia hết cho 2

Đề bài. Có 35 viên bi trong đó có 7 viên màu xanh 8 viên màu đỏ và 20 viên bi màu vàng vậy số bi màu xanh chiếm bao nhiêu phần của tổng số bi ?

Lời giải:

Tổng số bi là: 35 bi

Số bi màu xanh chiếm: $\frac{7}{35}=\frac{1}{5}$ (tổng số bi).

Đề bài. Có 5 công nhân làm trong 6 giờ được 120 sản phẩm. Hỏi 4 công nhân làm trong bao nhiêu giờ thì được 96 sản phẩm? (mức làm mỗi người như nhau)

Lời giải:

1 giờ 5 người làm được số sản phẩm là

120 : 6 = 20 (sản phẩm )

1 giờ 1 người làm được số sản phẩm là

20 : 5 = 4 (sản phẩm )

4 người làm trong 1 giờ được số sản phẩm là

4 . 4 = 16 (sản phẩm)

96 sản phẩm làm trong số giờ là

96 : 16 = 6 (giờ)

Đáp số: 6 giờ.

Đề bài. Có 6 học sinh sẽ được sắp xếp ngồi vào 6 chỗ đã được ghi số thứ tự trên 1 bàn dài.

1.Tìm số cách sắp xếp 6 học sinh này ngồi vào bàn.

2. Tìm số cách sắp xếp 6 học sinh này ngồi vào bàn sao cho 2 học sinh A và B không ngồi cạnh nhau.

Lời giải:

Ta có :

1) 6 người vào 6 chỗ.

Có 6! cách xếp.

2) Xếp học sinh A ngồi cạnh học sinh B

Ghép học sinh A và B thành 1 người.

Xếp 5 học sinh vào 5 chỗ ngồi ta có 5! cách xếp.

Bản thân 2 học sinh A và học sinh B có thể đổi chỗ cho nhau.

Do đó có: 2.5! cách để xếp 2 học sinh A và B ngồi cạnh nhau.

Có : 6! − 2.5! = 480 cách xếp 22 học sinh A và B không ngồi cạnh nhau.

Đề bài. Cho tam giác ABC, D và I là các điểm được xác định bởi

$3\overrightarrow{DB}-2\overrightarrow{DC}=\overrightarrow{0};\overrightarrow{IA}+3\overrightarrow{IB}\mathrm{ }-2\overrightarrow{IC}=\overrightarrow{0}$.

a) Biểu diễn AD theo $\overrightarrow{AB},\overrightarrow{AC}$

b) Chứng minh A, I, D thẳng hàng

Lời giải:

a) Theo quy tắc 3 điểm, từ $3\overrightarrow{DB}\mathrm{ }-2\overrightarrow{DC}\mathrm{ }=\overrightarrow{0}$ ta có:

$3\overrightarrow{DA}\mathrm{ }+3\overrightarrow{AB}\mathrm{ }-2\overrightarrow{DA}-2\overrightarrow{AC}\mathrm{ }=\overrightarrow{0}$

⇔ $\overrightarrow{DA}\mathrm{ }=2\overrightarrow{AC}\mathrm{ }-3\overrightarrow{AB}$

⇔ $\overrightarrow{AD}=3\overrightarrow{AB}-2\overrightarrow{AC}$ (*)

b) Theo a có $\overrightarrow{AD}\mathrm{ }=3\overrightarrow{AB}-2\overrightarrow{AC}$

⇔ $\overrightarrow{AD}=2.(\frac{3}{2}\overrightarrow{AB}\mathrm{ }-\overrightarrow{AC})$

Mà $\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}\mathrm{ }=\overrightarrow{0}$

⇔ $2\overrightarrow{IA}+3\overrightarrow{AB}\mathrm{ }-2\overrightarrow{AC}\mathrm{ }=\overrightarrow{0}$

⇔ $2\overrightarrow{IAI}\mathrm{ }=3\overrightarrow{AB}\mathrm{ }-2\overrightarrow{AC}$ (**)

Từ (*) và(**) suy ra: $\overrightarrow{AD}\mathrm{ }=2\overrightarrow{AI}$

Vậy A, I, D thẳng hàng.

Đề bài. Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm.

a) Chứng minh tam giác ABC vuông.

b) Tính góc B và góc C.

Lời giải:

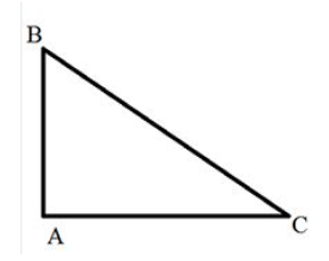a) Xét tam giác ABC thấy: 6² + 8² = 10² hay AB² + AC² = BC²

Áp dụng định lý Pytago đảo ta có tam giác ABC vuông tại A

b) $\sin \widehat{B}=\frac{AC}{BC}=\frac{8}{10}=\frac{4}{5}\Rightarrow \widehat{B}\approx {53}^{\circ }$

$\widehat{A}+\widehat{B}+\widehat{C}={180}^{\circ }\Rightarrow \widehat{C}={180}^{\circ }-{90}^{\circ }\mathrm{ }-{53}^{\circ }={37}^{\circ }$

Đề bài. Tam giác ABC có AB = 3, AC = 4 và $\tan \widehat{A}=2\sqrt{2}$. Tính cạnh BC.

Lời giải:

Ta thấy: $\tan \widehat{A}=2\sqrt{2}\mathrm{ }>0$

Nên: $\cos \widehat{A}>0$

$\frac{1}{{\cos }^2\widehat{A}}=\frac{1}{{\tan }^2\widehat{A}+1}$

⇒ $\cos \widehat{A}=\sqrt{\frac{1}{{\tan }^2\widehat{A}+1}}=\frac{1}{3}$

Áp dụng định lý cos: BC² = AB² + AC² – 2.AB.AC.$\cos \widehat{A}$

⇒ $BC=\sqrt{A{B}^2+A{C}^2-2.AB.AC.\cos \widehat{A}}\mathrm{ }=\sqrt{17}$

Đề bài. Cho tam giác ABC có AB = 4, AC = 6 và trung tuyến BM = 3. Tính cạnh BC?

Lời giải:

Tính BC dựa vào công thức tính độ dài đường trung tuyến BM.

$B{C}^2=2(B{M}^2+\frac{A{C}^2}{4})-A{B}^2=2(3^2+\frac{6^2}{4})-4^2=20$

Suy ra: $BC=2\sqrt{5}$

Đề bài. Cho tam giác ABC có $\widehat{B}+\widehat{C}={60}^{\circ }$; AB = 3; AC = 6. Tính độ dài đường phân giác AD?

Lời giải:

Qua D kẻ DE // AB (E thuộc AB)

Vì AD là phân giác góc A của tam giác ABC

$\frac{DC}{DB}=\frac{AC}{AB}$ (1)

Ta có AB là phân giác góc $\widehat{A}$ nên $\widehat{A_1}=\widehat{A_2}=\frac{1}{2}\widehat{BAC}={60}^{\circ }$

Mà $\widehat{A_1}=\widehat{D_1}={60}^{\circ }$ (so le trong DE//AB)

Suy ra: $\widehat{A_1}=\widehat{A_2}=\widehat{D_1}={60}^{\circ }$

⇒ Tam giác ADE đều

⇒ AD = DE

Vì DE // AB( cách dựng )

Xét tam giác ABC theo hệ quả của định lí Ta - lét ta có

$\frac{DE}{AB}=\frac{DC}{BC}$ (2)

Từ (1) và (2) ta có: $\frac{DE}{AB}=\frac{2}{3}\iff \frac{DE}{3}=\frac{2}{3}$

⇒ DE = 2 (cm)

Suy ra: DE = AD = 2cm

Đề bài. Tam giác ABC có $BC=\sqrt{5};AC=3;\cot C=-2$. Tính cạnh AB?

Lời giải:

Ta có: cotC = -2

Suy ra: cot²C = 4

⇔ $\frac{{\cos }^{2}C}{{\sin }^{2}C}=4$

⇔ $\frac{{\cos }^{2}C}{1-{\cos }^{2}C}=4$

⇔ cos²C = 4 – 4cos²C

⇔ ${\cos }^{2}C=\frac{4}{5}\Rightarrow \cos C=-\frac{2}{\sqrt{5}}$

mà 0°< $\widehat{C}$ < 180° ⇒ C ∈ góc phần tư thứ II, nên cosC < 0)

AB² = AC² + BC² – 2.AC.BC.cos$\widehat{C}$

AB² = 5 + 9 - $2.\sqrt{5}.3.\frac{-2}{\sqrt{5}}=26$

Suy ra: $AB=\sqrt{26}$

Đề bài. Tam giác ABC có BC = 12, CA = 9, AB = 6. Điểm M nằm trên cạnh BC sao cho BM = 4. Độ dài AM bằng bao nhiêu?

Lời giải:

Xét tam giác ABC có: $\cos \widehat{B}=\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}=\frac{11}{16}$

Xét tam giác ABM có: $\cos \widehat{B}=\frac{A{B}^2+B{M}^2-A{M}^2}{2.AB.BM}=\frac{11}{16}$

⇔ $\frac{11}{16}=\frac{6^2+4^2-A{M}^2}{\mathrm{2.6.4}}$

⇔ $AM=\sqrt{19}$

Đề bài. Cho tam giác ABC có BC = a, AC = b, AB = c. Đường trung tuyến AM = AB = c. Chứng minh rằng a² = 2(b² – c²)

Lời giải:

Ta có công thức tính đường trung tuyến AM:

$AM=\sqrt{\frac{A{B}^2+A{C}^2}{2}-\frac{B{C}^2}{4}}=\sqrt{\frac{c^2+b^2}{2}-\frac{a^2}{4}}$

Mà AM = c nên: c² = $\frac{c^2+b^2}{2}-\frac{a^2}{4}$

⇔ $\frac{2(c^2+b^2)-a^2}{4}=c^2$

⇔ 2(c² + b²) – a² = 4c²

⇔ 2b² – 2c² = a²

⇔ a² = 2(b² – c²)

Vậy a² = 2(b² – c²)

Đề bài. Cho tam giác ABC nhọn AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Kẻ Bx, Cy lần lượt vuông góc với AB, AC chúng cắt nhau tại K.

1. Chứng minh tứ giác BHCK là hình bình hành và H, M, K thẳng hàng

2. Gọi I là điểm đối xứng với H qua BC. Chứng minh tứ giác BIKC là hình thang cân

3. Gọi G là giao điểm của BK và HI, tam giác ABC phải có thêm điều kiện gì để tứ giác GHCK là hình thang cân.

Lời giải:

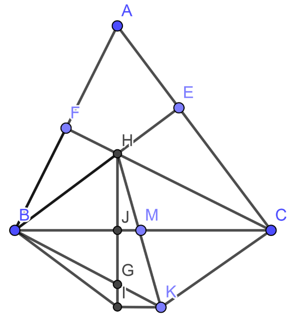1) Ta có: BH vuông góc với AC

CK vuông góc với AC

⇒ BH // CK

Chứng minh tương tự ta có: CH // BK

Xét tứ giác BHCK có: BH // CK; CH//BK

⇒ Tứ giác BHCK là hình bình hành

Có M là trung điểm của BC⇒ M là trung điểm của HK

⇒ M, H, K thẳng hàng

2. Gọi HI cắt BC tại J

Xét tam giác HIK có: J là trung điểm của HI; M là trung điểm của HK

⇒ JM là đường trung bình trong tam giác HIK

⇒ IK // MJ hay IK // BC

Xét tam giác BHJ và tam giác BIJ có;

HJ = JI

$\widehat{BJH}=\widehat{BJI}={90}^{\circ }$

BJ chung

⇒ ∆BHJ = ∆BIJ (c.g.c)

⇒ $\widehat{HBJ}=\widehat{IBJ}$

Mà $\widehat{HBJ}=\widehat{BCK}$(do BH//CK)

Xét tứ giác BIKC có: KI // BC

$\widehat{IBC}=\widehat{KCB}$

⇒Tứ giác BIKC là hình thang cân

3. Xét tứ giác GHCK có: GK//HC (do BK // HC)

⇒ Tứ giác GHCK là hình thang

Để GHCK là hình thang cân ⇒ $\widehat{GHC}=\widehat{KCH}$(1)

mà $\widehat{GHC}+\widehat{HCB}={90}^{\circ }$

$\widehat{KCH}+\widehat{HCA}={90}^{\circ }$

⇒ (1) $\widehat{HCB}=\widehat{HCA}$CH là phân giác của góc $\widehat{ACB}$

Xét tam giác ABC có : CH là phân giác của góc $\widehat{ACB}$

CH là đường cao trong tam giác ABC

⇒ Tam giác ABC cân tại C

Vậy tứ giác GHCK là hình thang cân

⇒ Tam giác ABC cân tại C

Đề bài. Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho.

Lời giải:

Gọi M là trung điểm của AC suy ra $AM=\frac{AC}{2}=\frac{a}{2}$.

Do tam giác BAM vuông tại A nên $BM=\sqrt{A{B}^2+A{M}^2}\mathrm{ }=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}$

Đề bài. Cho tam giác ABC vuông tại A có AB = 6cm , BC = 10cm. Tính sinC, tan C, cos C, cotC, sinB, cosB, tanB, cotB

Lời giải:

Xét ΔABC vuông tại A có :

AB² + AC² = BC²

⇒ AC = 8(cm)

- Ta có: $\sin C=\frac{AB}{BC}=\frac{6}{10}=\frac{3}{5}$

$\cos C=\frac{AC}{BC}=\frac{8}{10}=\frac{4}{5}$

$\tan C=\frac{AB}{AC}=\frac{6}{8}=\frac{3}{4}$

$\cot C=\frac{4}{3}$

$\sin B=\frac{AC}{BC}=\frac{8}{10}=\frac{4}{5}$

$\cos B=\frac{AB}{BC}=\frac{3}{5}$

$\tan B=\frac{AC}{AB}=\frac{4}{3}$

$\cot B=\frac{3}{4}$

Đề bài. Cho ΔABC có hai trung tuyến CM, BN bằng nhau và cắt nhau tại G. Chứng minh tam giác ABC cân.

Lời giải:

Vì G là giao điểm của hai đường trung tuyến BN và CM của tam giác ABC nên G là trọng tâm tam giác ABC.

Do đó $CG=\frac{2}{3}CM;BG=\frac{2}{3}BN$

Mà CM = BN (giả thiết) nên CG = BG.

Δ∆BGC có CG = BG nên Δ∆BGC cân tại G.

Suy ra $\widehat{GBC}=\widehat{GCB}$ (tính chất tam giác cân)

Xét Δ∆BMC và Δ∆CNB có:

MC = NB (theo giả thiết),

$\widehat{MCB}=\widehat{NBC}$ (do $\widehat{GBC}=\widehat{GCB}$)

BC là cạnh chung.

Do đó Δ∆BMC = Δ∆CNB (c.g.c).

Suy ra $\widehat{MBC}=\widehat{NCB}$ (hai góc tương ứng).

Tam giác ABC có $\widehat{ABC}=\widehat{ACB}$ nên Δ∆ABC cân tại A.

Vậy nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Đề bài. Cho tam giác có ba cạnh lần lượt là 5,6,7. Tìm độ dài đường cao ứng với cạnh có độ dài bằng 6.

Lời giải:

Giả sử a = BC = 5; b = AC = 6; c = AB = 7.

Ta cần tính độ dài đường cao ứng với cạnh AC

$p=\frac{a+b+c}{2}=\frac{5+6+7}{2}=9$

$S=\sqrt{p(p-a)(p-b)(p-c)}=6\sqrt{6}$

Mà $S=\frac{1}{2}{h}_b.b=6\sqrt{6}\Rightarrow h_b=2\sqrt{6}$

Đề bài. Tìm tất cả các giá trị thực của m để đồ thị hàm số y = x³ − 3mx² + 4m³ có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ.

Lời giải:

Ta có: y’ = 3x² – 6mx = 3x(x – 2m)

Xét y’ = 0 ⇒ $[\begin{array}{c}x=0\\ x=2m\end{array}\Rightarrow [\begin{array}{c}y=4m^3\\ y=0\end{array}\Rightarrow [\begin{array}{c}A(0;4m^3)\in Oy\\ B(2m; 0) \in Ox\end{array}$

Do ba điểm O, A, B không thẳng hàng nên 2m ≠ 0 hay m ≠ 0

Ta có: $S_{OAB}=\frac{1}{2}.OA.OB=\frac{1}{2}|4m^3|.|2m|=4m^4=4$

Suy ra: m = ±1.

Đề bài. Trên đoạn thẳng AB lấy một điểm M (MA > MB). Trên cùng một nửa mặt phẳng có bờ AB, vẽ các tam giác đều AMC, BMD. Gọi E, F, I, K theo thứ tự là trung điểm của CM, CB, DM, DA. Chứng minh rằng EFIK là hình thang cân và $KF=\frac{1}{2}CD$

Lời giải:

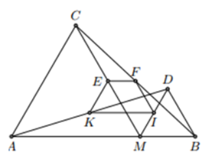Gọi EK giao AB tại P

Xét Δ CMB có EF là đường trung bình của Δ

⇒ EF // MB ⇒ EF // AB. (1)

Xét ΔΔADM có KI là đường trung bình của Δ

⇒ KI // AM ⇒⇒ KI // AB. (2)

Từ (1) và (2) ⇒ Tứ giác EFIK là hình thang (*)

Gọi P; Q lần lượt là trung điểm của AM và BN.

Xét Δ ACM có PE là đường trung bình của ΔΔ.

⇒ PE // AC mà AC // MD (Do $\widehat{A}=\widehat{M}={60}^{\circ }$ở vị trí đồng vị)

⇒ PE // MD (3)

Mặt khác ΔΔADM có PK là đường trung bình của ΔΔ.

⇒ PK // MD (4)

Từ (3) và (4) ⇒ P; E; K thẳng hàng mà PE // AC nên KE // AC (5).

Từ (2) và (5) ⇒ $\widehat{CAB}=\widehat{EKI}$ (Hai góc nhọn có cạnh tương ứng song song)

Mà $\widehat{CAB}={60}^{\circ }$(**)

Chứng minh tương tự ta được F; I; Q thẳng hàng mà QF // MC nên IF // MC;

Lại có MC // BD nên FI // BD (6).

Từ (2) và (6) ⇒ $\widehat{DBA}=\widehat{FIK}$ (Hai góc nhọn có cạnh tương ứng song song)

Mà $\widehat{DAB}={60}^{\circ }$

⇒ $\widehat{FIK}={60}^{\circ }$

Từ (*); (**) và (***)

⇒ EFIK là hình thang cân (Hình thang có 2 góc ở đáy bằng nhau là hình thang cân)

⇒ đcpm

Đề bài. Trong tam giác ABC lấy điểm O sao cho $\widehat{ABO}=\widehat{ACO}$. Gọi H, K lần lượt là hình chiếu của O lên AB, AC. Gọi M là trung điểm của BC. Chứng minh tam giác MHK là tam giác cân.

Lời giải:

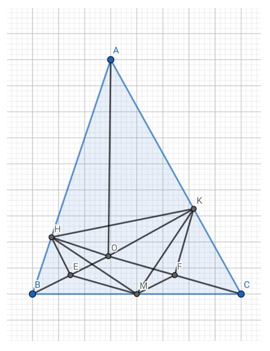ΔHOB vuông tại H và ΔKOC vuông tại K có:

$\widehat{HBO}=\widehat{KCO} (\widehat{ABO}=\widehat{ACO}):gt)$

⇒ $\widehat{HOB}=\widehat{KOC}$ (1)

Gọi E, F lần lượt là trung điểm OB, OC

Xét ΔHOB vuông tại H có:

E là trung điểm cạnh huyền OB

⇒ EO = EH = EB

⇒ΔEOH cân tại E

⇒ $\widehat{HEO}={180}^{\circ }-2\widehat{EOH}$(2)

Xét ΔKOC vuông tại K có:

F là trung điểm cạnh huyền OC

⇒ FO = FK = FC

⇒ΔFOK cân tại F

⇒ $\widehat{KFO}={180}^{\circ }-2\widehat{FOK}$(3)

(1), (2), (3) ⇒ $\widehat{KFO}=\widehat{HEO}$

Mặt khác:

ΔOBC có: M,E,F lần lượt là trung điểm BC,OB,OC

⇒ OEMF là hình bình hành

⇒ OE = MF; OF = ME; $\widehat{OEM}=\widehat{OFM}$

⇒ HE = MF, KF = ME; $\widehat{HEO}+\widehat{OEM}=\widehat{KFO}+\widehat{OFM}$

⇒ $\widehat{HEM}=\widehat{KFM}$

Xét ΔHEM và ΔMFK có:

HE = MF(cmt)

$\widehat{HEM}=\widehat{KFM}$

ME = KF(cmt)

Do đó ΔHEM = ΔMFK (c.g.c)

⇒ MH = MK

⇒ ΔMHK cân tại M

Đề bài. Trong tam giác ABC, nếu có 2h_a​ = h_b ​+ h_c​ thì:

A. $\frac{2}{\sin A}=\frac{1}{\sin B}+\frac{1}{\sin C}$

B. 2sinA = sinB + sinC

C. sinA = 2sinB + 2sinC

D. $\frac{2}{\sin A}=\frac{1}{\sin B}-\frac{1}{\sin C}$

Lời giải:

Chọn A

2h_a​ = h_b ​+ h_c

⇔ $\frac{4S_{ABC}}{a}=\frac{2S_{ABC}}{b}+\frac{2S_{ABC}}{c}$

⇔ $\frac{2}{a}=\frac{1}{b}+\frac{1}{c}$

Áp dụng định lí sin ta có:

$\frac{1}{\sin B}+\frac{1}{\sin C}=\frac{2R}{b}+\frac{2R}{c}=2R(\frac{1}{b}+\frac{1}{c})=2R.\frac{2}{a}=\frac{2}{\sin A}$

Vậy $\frac{2}{\sin A}=\frac{1}{\sin B}+\frac{1}{\sin C}$

Đề bài. Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc AC, từ B kẻ tia By song song AC. Gọi M là giao điểm của tia Ax và tia By. Nối M là trung điểm P của AB, đường thẳng MP cắt AC tại Q và đường thẳng BQ cắt AI tại H

a) Tứ giác AMBQ là hình gì?

b) Chứng minh CH vuông góc AB

c) Chứng minh tam giác PIQ cân

Lời giải:

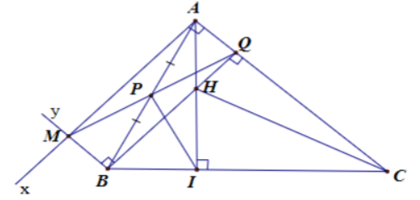a) AM vuông góc AC và BM // AC nên AM ⊥ BM

Xét AMBQ có: $\widehat{AQB}=\widehat{MAQ}=\widehat{MBQ}={90}^{\circ }$

Nên AMBQ là hình chữ nhật

b, AMBQ là hình chữ nhật nên BQ⊥AC mà BQ ∩ AI = H

Suy ra H là trực tâm của tam giác ABC

Do đó: CH⊥ AB

c, Tam giác ABI vuông tại I có đường trung tuyến IP nên $IP=\frac{1}{2}AB$

Do AMBQ là hình chữ nhật nên $PQ=\frac{1}{2}MQ=\frac{1}{2}AB$

Suy ra IP = PQ

Hay tam giác IPQ cân tại P

Đề bài. Cho tam giác ABC vuông tại A (AB < AC) đường cao AH

1) Giả sử AB = 9cm, AC = 12cm. Tỉnh độ dài các đoạn thẳng BC, BH và AH.

2) Gọi M và N lần lượt là chân các đường vuông góc kẻ từ điểm H đến các đường thẳng AB và AC. Chứng minh AM.AB = AN.AC.

3) Đường thẳng đi qua điểm A và song song với đường MN cắt đường thẳng đi qua điểm C và song song với đường AH tại điểm K. Gọi I là giao điểm của AH và BK. Chứng minh ba điểm M, L, N là ba điểm thẳng hàng.

Lời giải:

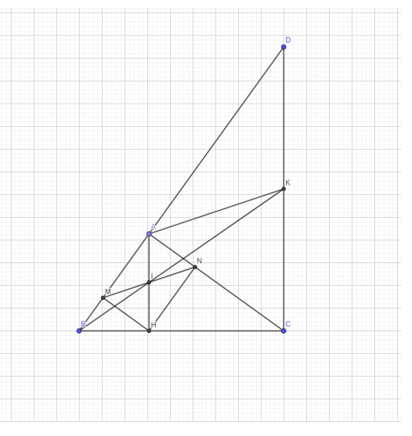1) $BC=\sqrt{A{B}^2+A{C}^2}=15$

ΔABC vuông tại A, AH ⊥ BC nên AH.BC = AB.AC

Suy ra: $AH=\frac{AB.AC}{BC}=7,2$

$BH=\sqrt{A{B}^2-A{H}^2}=5,4$

2) Áp dụng hệ thức lượng trong tam giác vuông AHB, AHC có:

AH² = AM.AB

AH² = AN.AC

Suy ra: AM.AB = AN.AC

3) Gọi AB ∩ CK = D

Vì HM ⊥ AB, HN ⊥ AC, AB ⊥ AC

⇒ AMHN là hình chữ nhật

MN // AK, KC // AH

⇒ $\widehat{KCA}=\widehat{CAH}=\widehat{HAN}=\widehat{ANM}=\widehat{CAK}$

⇒ ΔKAC cân tại K

⇒ AK = KC

Ta có: AB ⊥ AC⇒ AD ⊥ AC

⇒$\widehat{KAD}={90}^{\circ }-\widehat{KAC}={90}^{\circ }\mathrm{ }-\widehat{KCA}=\widehat{D}$

⇒ΔKAD cân tại K

⇒ AK = KD

⇒ KD = KC

Ta có: AH // CD (⊥BC)

⇒ $\frac{AI}{KD}=\frac{BI}{BK}=\frac{IH}{KC}$

⇒ IA = IH

⇒ I là trung điểm AH

Mà AMHN là hình chữ nhật

⇒ AH ∩ MN tại trung điểm mỗi đường
⇒ I là trung điểm MN

⇒ M, I, N thẳng hàng

Đề bài. Trong hình tam giác đều, khẳng định nào sau đây là đúng?

A. Ba cạnh bằng nhau và bằng 3 cm.

B. Ba góc bằng nhau và bằng 90°.

C. Ba cạnh bằng nhau, ba góc không bằng nhau.

D. Ba cạnh bằng nhau, ba góc bằng nhau và bằng 60°.

Lời giải:

Chọn D

+ Tam giác đều là tam giác có 3 cạnh bằng nhau

+ Tam giác đều là tam giác có 3 cạnh bằng nhau

+ Tổng 3 góc trong tam giác bằng 180° mà 3 góc trong tam giác đều bằng nhau mà 3 góc trong tam giác đều bằng nhau nên mỗi góc trong tam giác đều bằng nên mỗi góc trong tam giác đều bằng 180° : 3 = 60°

Đề bài. Khi quay 1 hình tam giác vuông một vòng quanh một cạnh góc vuông cố định ta được hình gì?

Lời giải:

Khi quay một tam giác vuông (kể cả các điểm trong của tam giác vuông đó) quanh đường thẳng chứa một cạnh góc vuông ta được một khối nón.

Chọn đáp án C.

Chú ý: Một số em nhầm sang đáp án A là hình nón. Ở đây chúng ta lưu ý rằng khi quay tất cả các điểm bên trong tam giác quanh cạnh góc vuông thì ta sẽ được một khối đặc nên ta được một khối nón chứ không phải hình nón.

Đề bài. Cho tam giác ABC vuông tại A (AB <AC), M là trung điểm của BC. Kẻ ME vuông góc AB (E thuộc AB), kẻ MF vuông góc AC (F thuộc AC ).

a) Tứ giác AEMF là hình gì? Vì sao?

b) Chứng minh EF = $\frac{1}{2}BC$

c) Gọi K là chân đường vuông góc kẻ từ A đến BC. Chứng minh rằng tứ giác EKMF là hình thang cân.

Lời giải:

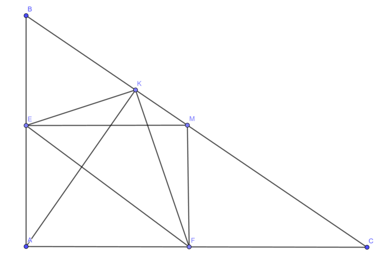a. Tứ giác AEFM có 3 góc vuông $(\widehat{A},\widehat{E},\widehat{F})$ nên AEFM là hình chữ nhật

b. ΔABC là tam giác vuông tại A, có AM là đường trung tuyến nên AM = MC = MB

ΔCMA là tam giác cân tại M (do MC = MA) nên MF là đường cao cũng là đường trung tuyến

⇒ F là trung điểm AC (1)

ΔBMA là tam giác cân tại M (do MA = MB) nên ME là đường cao cũng là đường trung tuyến
⇒ E là trung điểm AB (2)

Từ (1) và (2) suy ra: EF là đường trung bình của ΔABC

⇒ EF = $\frac{1}{2}BC$ (đpcm)

c, EF là đường trung bình của ΔABC ⇒ EF // BC

⇒ Tứ giác EKMF là hình thang

ΔAKC vuông tại K có KF là trung tuyến ứng với cạnh huyền

⇒ KF = FA mà FA = ME (do AEMF là hình chữ nhật)

⇒ KF = ME

⇒ Hình thang EKMF là hình thang cân (đpcm).

Đề bài. Nhà bạn Thu có một đèn trang trí có dạng hình chóp tam giác đều như Hình 10.16. Các cạnh của hình chóp đều bằng nhau và bằng 20 cm. Bạn Thu dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu. Tính diện tích giấy bạn Thu sử dụng (coi như mép dán không đáng kể). Cho biết $\sqrt{300}\approx 17,32$

Lời giải:

Mỗi mặt của đèn trang trí là một tam giác đều có cạnh bằng 20 cm.

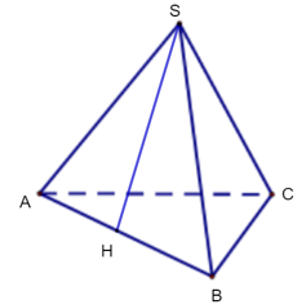Hình chóp S.ABC trên mô tả chiếc đèn trang trí, gọi H là trung điểm của AB.

Khi đó SH là trung đoạn của hình chóp tam giác đều S.ABC.

Ta có AH = HB = 20 : 2 = 10 (cm).

Sử dụng định lí Pythagore trong tam giác vuông SAH, ta suy ra

SH² = SA² – AH² = 20² – 10² = 300.

Suy ra SH = $\sqrt{300}\approx 17,32$ cm

Nửa chu vi mặt đáy ABC là p = $\frac{1}{2}$(20 + 20 + 20) = 30(cm).

Tổng diện tích các mặt bên của hình chóp đều S.ABC là:

S_xq = 30 . 17,32 = 519,6 (cm²).

Vậy diện tích giấy màu bạn Thu cần sử dụng là 519,6 cm².

Đề bài. Cho tam giác ABC có góc B bằng 120°, BC = 12cm, AB = 6cm. Đường phân giác của góc B cắt cạnh AC tại D.

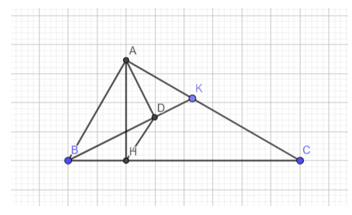
a) Tính độ dài đường phân giác BD

b) Gọi M là trung điểm của BC. Chứng minh AM ⊥ BD

Lời giải:

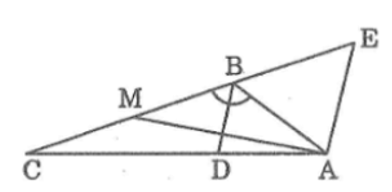a) Ta có: $\widehat{ABD}=\widehat{CBD}=\frac{1}{2}\widehat{ABC}={60}^{\circ }$

Từ A kẻ đường thẳng song song với BD cắt CD tại E

Lại có: $\widehat{BAE}=\widehat{ABD}={60}^{\circ }$(so le trong)

$\widehat{CBD}=\widehat{ABE}={60}^{\circ }$(đồng vị)

Suy ra: tam giác ABE đều ⇒ AB = BE = EA = 6 (cm) (1)

Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)

Tam giác ACE có AE // BD nên suy ra:

$\frac{BC}{CE}=\frac{BD}{AE}\Rightarrow BD=\frac{BC.AE}{CE}=\frac{12.6}{18}=4(cm)$

b) MB = MC = $\frac{1}{2}BC=6(cm)$ vì M là trung điểm BC

Mà AB = 6cm nên AB = BM

⇒ Δ∆ABM cân tại B

Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân).

Vậy BD ⊥ AM.

Đề bài. Cho (O ; 4cm) có 2 đường kính AB và CD vuông góc tại O. Lấy I trên OC sao cho OI = 3cm. AI cắt (O) tại M. Tính AM và đường cao MH của ΔAMB

Lời giải:

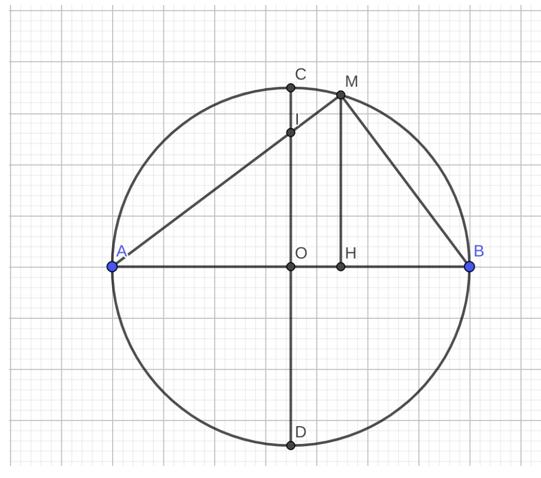Ta có $AI=\sqrt{A{O}^2+O{I}^2}\mathrm{ }=5$

Vì AB là đường kính của (O)

⇒ AM ⊥ MB

Xét ΔAOI, ΔAMB có:

Chung $\widehat{A}$

$\widehat{AOI}=\widehat{AMB}$

⇒ΔAOI ∼ ΔAMB(g.g)

⇒ $\frac{AO}{AM}=\frac{AI}{AB}$

⇒AI.AM = AO.AB

⇒ 5.AM = 4.8

⇒ $AM=\frac{32}{5}$

Ta có MA ⊥ MB, MH ⊥ AB

Suy ra: AM² = AH.AB

⇒ $AH=\frac{A{M}^2}{AB}=\frac{128}{25}$

⇒ $MH=\sqrt{A{M}^2-A{H}^2}=\frac{96}{25}$

Đề bài. Nêu tính chất đường trung tuyến trong tam giác vuông.

Lời giải:

Đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC. Đôi khi, đường thẳng AM cũng gọi là đường trung tuyến của tam giác ABC.

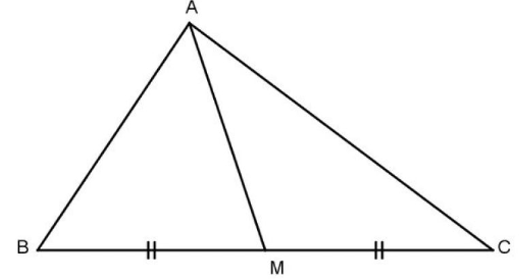Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng $\frac{1}{2}$ cạnh huyền.

Một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông.

Đường trung tuyến của tam giác vuông có đầy đủ các tính chất của một đường trung tuyến tam giác.

Đề bài. Giải tam giác vuông ABC khi biết độ dài hai cạnh

Lời giải:

Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c.

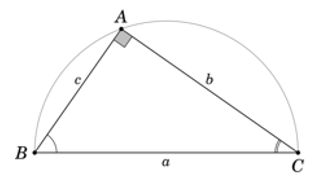1. Định lý: Trong một tam giác vuông, mỗi cạnh góc vuông bằng

- Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

- Cạnh góc vuông kia nhân với tan góc đối hoặc nhân với cot góc kề.

2. Như vậy, trong tam giác ABC vuông tại A, ta có hệ thức

• b = a.sinB = a.cosC = c.tanB = c.cotC

• c = a.sinC = a.cosB = b.tanC = b.cotB

Phương pháp giải:

Áp dụng định lý Py-ta-go để tìm cạnh còn lại.

• Xác định cạnh kề, cạnh đối, viết tỉ số lượng giác.

• Tính góc nhọn còn lại nhờ quan hệ phụ nhau.

Đề bài. Cho hình chóp tứ giác S.ABCD, M là một điểm trên cạnh SB. Gọi E, F là hai điểm lần lượt thuộc miền trong tam giác ABD và tam giác BCD. Tìm giao tuyến của mặt phẳng (MEF) và mặt phẳng (SCD).

Lời giải:

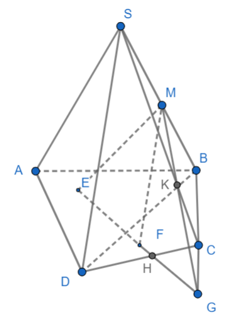Vì E,F lần lượt nằm ở miền trong của ABD, BCD nên EF ⊂ (ABCD)

Trong (ABCD) ta cho EF cắt CD, BC lần lượt tại H,G

Ta có H ∈ CD

⇒ H ∈ (MEF) ∩ (SCD)

Trong (SBC), ta có MG ⊂ (SCD), SC ⊂ (SCD) nên MG cắt SC tại K

⇒ K ∈ (SCD) ∩ (MEF) do K ∈ MG ⊂ (MEF)

Vậy (SCD) ∩ (MEF) = KH

Đề bài. Chu vi của một tam giác là 81cm. Các cạnh của nó tỉ lệ với 2, 3, 4. Tính độ dài mỗi cạnh.

Lời giải:

Gọi độ dài 3 cạnh tam giác lần lượt là a;b;;c (a;b;c > 0)

Theo bài ra ta có : a + b +c = 81

Lại có:

$\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{81}{9}=9$

Suy ra: a = 2.9 = 18;

b = 3.9 = 27 ;

c = 4.9 = 36

Vậy độ dài 3 cạnh tam giác là 18 cm ; 27 cm ; 36 cm.

Đề bài. Chứng minh rằng $\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}(n\in N^{*})$

Lời giải:

Xét $\frac{1}{n}-\frac{1}{n+1}=\frac{n+1-n}{n(n+1)}=\frac{1}{n(n+1)}$

Vậy $\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}(n\in N^{*})$

Đề bài. Giả sử AB là một dây cung của đường tròn (O). Trên cung nhỏ AB lấy các điểm C và D sao cho $\stackrel{⏜}{AC}=\stackrel{⏜}{BD}$. Chứng minh AB và CD song song.

Lời giải:

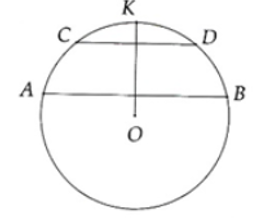Ta lấy K là điểm chính giữa cung nhỏ $\stackrel{⏜}{AB}$

Ta có: $\stackrel{⏜}{AK}=\stackrel{⏜}{KB}$

Mà $\stackrel{⏜}{AC}=\stackrel{⏜}{BD}$ nên $\stackrel{⏜}{AK}-\stackrel{⏜}{AC}=\stackrel{⏜}{BD}-\stackrel{⏜}{KB}$

Suy ra: $\stackrel{⏜}{CK}=\stackrel{⏜}{BD}$

Từ đó ta có OK⊥CD, OK ⊥AB ⇒ CD // AB.

Đề bài. Cho 10a² – 3b² + ab = 0 với b > a > 0. Tính $M=\frac{2a-b}{3a-b}+\frac{5b-a}{3a+b}$.

Lời giải:

10a² – 3b² + ab = 0

⇔ 10a² + 6ab – 5ab – 3b² = 0

⇔ (2a – b)(5a + 3b) = 0

⇔ $[\begin{array}{c}2a-b=0\\ 5a+3b=0\end{array}\iff [\begin{array}{c}2a=b\\ 5a=-3b\end{array}$ (loại 5a = - 3b vì b > a > 0).

Vậy 2a = b.

Khi đó $M=\frac{2a-b}{3a-b}+\frac{5b-a}{3a+b}=\frac{2a-2a}{3a-2a}+\frac{5.2a-a}{3a+2a}=0+\frac{9}{5}=\frac{9}{5}$.

Đề bài. Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.

a) Chứng minh E và F đối xứng với nhau qua AB.

b) Chứng minh tứ giác MEBF là hình thoi.

c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.

Lời giải:

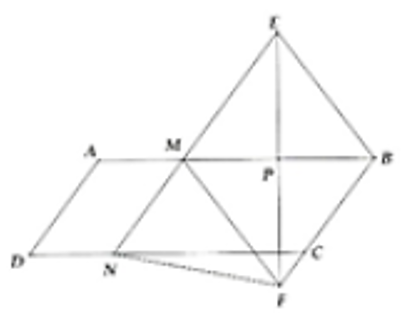a) Do AM = DN suy ra: MADN là hình bình hành

⇒$\widehat{D}=\widehat{AMN}=\widehat{EMB}=\widehat{MBC}$

Ta có ∆MPE = ∆BPE nên EP = FP.

Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.

b) Tứ giác MEBF có MB ∩ EF = P

Lại có P trung điểm BM, P là trung điểm EF, MB ⊥ EF.

Suy ra: MEBF là hình thoi.

c) Để BNCE là hình thang cân thì $\widehat{CNE}=\widehat{BEN}$

Mà $\widehat{D}=\widehat{CNE}=\widehat{EMB}=\widehat{MBC}$ nên ∆MEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì $\widehat{ABC}={60}^{\circ }$.

Đề bài. Cho $\overline{abc}-\overline{\mathrm{deg}}$ chia hết cho 7. Chứng minh $\overline{abcdeg}$ chia hết cho 7.

Lời giải:

$\overline{abc\mathrm{deg}}\mathrm{ }=1000\overline{abc}\mathrm{ }+\overline{\mathrm{deg}}\mathrm{ }=1001\overline{abc}\mathrm{ }-(\overline{abc}-\overline{\mathrm{deg}})$

Ta thấy: $1001\overline{abc}\mathrm{ }\mathrm{⋮}7;(\overline{abc}\mathrm{ }-\overline{\mathrm{deg}})\mathrm{⋮}7$

Nên: $\overline{abc\mathrm{deg}}=1001\overline{abc}-(\overline{abc}-\overline{\mathrm{deg}})\mathrm{⋮}7$

Vậy $\overline{abcdeg}$ chia hết cho 7.

Đề bài. Cho hình bình hành ABCD có $\widehat{A}={120}^{\circ }$. Tia phân giác của $\widehat{D}$ qua trung điểm I của AB. Kẻ AH vuông góc với DC. Chứng minh rằng:

a) AB = 2AD.

b) DI = 2AH.

c) AC vuông góc với AD.

Lời giải:

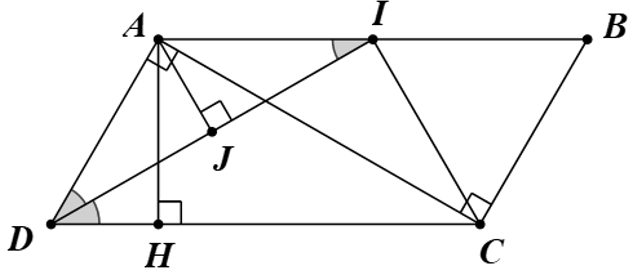a) Hình bình hành ABCD có $\widehat{BAD},\widehat{ADC}$ ở vị trí trong cùng phía.

Suy ra $\widehat{ADC}={180}^{\circ }\mathrm{ }-\widehat{BAD}={60}^{\circ }$

Khi đó $\widehat{ADI}=\widehat{IDC}=\frac{\widehat{ADC}}{2}={30}^{\circ }$ (do DI là tia phân giác của \(\widehat {ADC}\)).

Mà $\widehat{AID}=\widehat{IDC}$(cặp góc so le trong).

Vì vậy $\widehat{AID}=\widehat{ADI}$

Suy ra tam giác ADI cân tại A.

Do đó AD = AI.

Mà AB = 2AI (I là trung điểm của AB).

Vậy AB = 2AD (điều phải chứng minh).

b) Gọi J là trung điểm của DI.

Tam giác ADI có AJ là đường trung tuyến.

Suy ra AJ vừa là đường phân giác, vừa là đường cao của tam giác ADI.

Khi đó $\widehat{JAI}=\widehat{DAJ}=\frac{\widehat{DAI}}{2}={60}^{\circ }$

Xét ∆AJD và ∆DHA, có:

$\widehat{AJD}=\widehat{DHA}={90}^{\circ }$

AD là cạnh chung;

$\widehat{DAJ}=\widehat{ADH}={60}^{\circ }$

Do đó ∆AJD = ∆DHA (cạnh huyền – góc nhọn).

Suy ra DJ = AH (cặp cạnh tương ứng).

Mà DI = 2DJ (J là trung điểm của DI).

Vậy DI = 2AH (điều phải chứng minh).

c) Ta có BI = BC $(\frac{1}{2}AB)$

Suy ra tam giác IBC cân tại B.

Mà $\widehat{IBC}=\widehat{ADC}={60}^{\circ }$

Do đó tam giác IBC đều.

Vì vậy IC = IB = IA.

Khi đó tam giác ABC vuông tại C hay $\widehat{ACB}={90}^{\circ }$

Suy ra $\widehat{DAC}=\widehat{ACB}={90}^{\circ }$

Vậy AD ⊥ AC (điều phải chứng minh).

Đề bài. Cho 3 số nguyên tố lớn hơn 3 trong đó số sau lớn hơn số trước d đơn vị. Chứng minh rằng d chia hết cho 6.

Lời giải:

Các số nguyên tố > 3 có dạng: 3k + 1 hoặc 3k + 2 (k ∈ ℕ)

Có 3 số mà chỉ có 2 dạng nên tồn tại 2 số thuộc cùng 1 dạng, hiệu của chúng là d hoặc 2d chia hết cho 3,

Do đó d chia hết cho 3. (1)

Mặt khác: d chia hết cho 2 (vì d là hiệu của 2 số lẻ) (2)

Từ (1) & (2) ⇒ d chia hết cho 6 (đpcm).

Đề bài. Cho Parabol (P): y = x² và đường thẳng (d) : y = 2(m + 3)x – 2m + 2 (m là tham số, m thuộc R).

a) Với m = - 5 tìm tọa độ giao điểm của parabol (P) và đường thẳng (d).

b) Chứng minh rằng: Parabol (P) và đường thẳng (d) cắt nhau tại hai điểm phân biệt với mọi m. Tìm m để (d) cắt (P) tại hai điểm cùng nằm bên phải trục tung.

Lời giải:

a) m = -5 thì (d): y = -4x + 12

Xét phương trình hoành độ giao điểm:

x² = -4x + 12

⇒ $x^2$ + 4x-12= 0

⇒ x= 2 hoặc x= -6

Với x = 2 ⇒ y = 4

Với x = -6 ⇒ y = 36

Vậy 2 điểm cần tìm là (2; 4) và (-6; 36).

b) Phương trình hoành độ giao điểm (d) và (P) là:

x² = 2(m + 3)x – 2m + 2

⇔ x² – 2(m + 3)x + 2m – 2 = 0 (*)

∆' = (m + 3)² – (2m – 2) = m² + 4m + 11 = (m + 2)² + 7 > 0 với mọi m

Nên phương trình (*) luôn có 2 nghiệm phân biệt

Theo định lý Vi-ét: $\{\begin{array}{c}{x}_1+x_2=2(m+3)\\ x_1{x}_2=2m-2\end{array}$

Để (d) cắt (P) tại hai điểm cùng nằm bên phải trục tung thì hai điểm có hoành độ dương

Suy ra: $\{\begin{array}{c}{x}_1+x_2=2(m+3)>0\\ x_1{x}_2=2m-2>0\end{array}\Rightarrow \{\begin{array}{c}m-3\\ m>1\end{array}\Rightarrow m>1$.

Vậy m > 1 thì (d) cắt (P) tại hai điểm cùng nằm bên phải trục tung.

Đề bài. Từ điểm A ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC đến (O) (B, C là các tiếp điểm).

a) Chứng minh: OA vuông góc với BC tại H.

b) Vẽ đường thẳng vuông góc với OB tại O cắt cạnh AC tại E. Chứng minh: ∆OAE là tam giác cân.

c) Trên tia đối của tia BC lấy điểm Q. Vẽ hai tiếp tuyến QM, QN đến (O) (M, N là tiếp tuyến). Chứng minh: 3 điểm A, M, N thẳng hàng.

Lời giải:

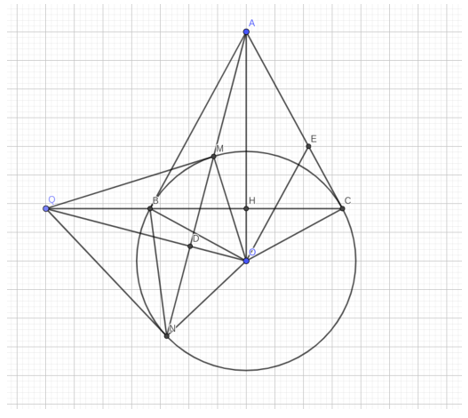a. Vì AB, AC là tiếp tuyến của (O)
⇒ AO ⊥ BC = H

b. Ta có: OE ⊥ OB

⇒ OE // AB vì AB là tiếp tuyến của (O)

⇒ OB ⊥ AB

⇒ $\widehat{CAO}=\widehat{OAB}=\widehat{AOE}$

⇒ΔOAE cân tại E

c.Ta có : AB,AC là tiếp tuyến của (O)

⇒ OB ⊥ AB mà BC⊥AB = H

⇒ OH.OA = OB² = R²

Tương tự QM, QN là tiếp tuyến của (O)

Gọi QO ∩ MN = D

⇒ OD.OQ = OM² = R² vì OM ⊥ QM

⇒ OH.OA = OD.OQ

⇒ $\frac{OH}{OD}=\frac{OQ}{OA}$

⇒ΔODA ∽ ΔOHQ(c.g.c)

$\Rightarrow \widehat{ADO}=\widehat{QHO}\Rightarrow \widehat{ADO}={90}^{\circ }$

⇒ AD ⊥ OQ

Mà MN ⊥ OQ = D
⇒ A, M, D, N thẳng hàng

Đề bài. Gọi M là trung điểm của đoạn thẳng AB. Trên 2 nửa phẳng đối nhau bờ AB lần lượt vẽ 2 tia Ax, By vuông góc AB. Trên Ax lấy điểm P, Trên Ay lấy Q sao cho AP = BQ. Chứng minh P, Q, M thẳng hàng.

Lời giải:

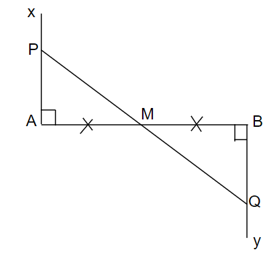Xét tam giác APM và tam giác BQM có:

AP = BQ (GT)

$\widehat{PAM}=\widehat{QBM}={90}^{\circ }$

AM = MB (GT)

⇒ tam giác APM = tam giác BQM (c.g.c)

⇒ $\widehat{AMP}=\widehat{BMQ}$(2 góc tương ứng)

Mà ta có: $\widehat{AMP}+\widehat{PMB}={180}^{\circ }$(kề bù)

⇒ $\widehat{BMQ}+\widehat{PMB}={180}^{\circ }$ hay P, Q, M thẳng hàng.

Đề bài. Cho M = 2 + 2² + 2³ + … + 2²⁰. Chứng minh M chia hết cho 10.

Lời giải:

Ta thấy từng số hạng của M đều chia hết cho 2

Nên M = 2 + 2² + 2³ + … + 2²⁰ chia hết cho 2 (1)

Lại có: M = 2 + 2² + 2³ + … + 2²⁰

M = (2 + 2³) + (2² + 2⁴) + … + (2¹⁷ + 2¹⁹) + (2¹⁸ + 2²⁰)

M = 2(1 + 2²) + 2²(1 + 2²) + … + 2¹⁷(1 + 2²) + 2¹⁸(1 + 2²)

M = (1 + 2²)(2 + 2² + … + 2¹⁷ + 2¹⁸)

M = 5.(2 + 2² + … + 2¹⁷ + 2¹⁸) ⋮ 5 (2)

Từ (1) và (2) suy ra: M chia hết cho 10.

Đề bài. Cho tam giác ABC vuông tại A có AH là đường cao chia cạnh huyền BC thành hai đoạn BH = 4cm; HC = 6cm.

a) Gọi M là trung điểm của AC. Tính số đo góc $\widehat{AMB}$ (làm tròn đến độ).

b) Kẻ AK vuông góc với BM (K thuộc BM). Chứng minh BK.BM = BH.BC.

Lời giải:

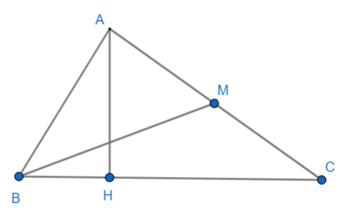a) $\cos \widehat{AMB}=\frac{A{M}^2+M{B}^2-A{B}^2}{2.AM.MB}$ (*)

Áp dụng hệ thức lượng trong tam giác vuông:

AH² = BH.HC = 4.6 = 24 ⇒ $AH=\sqrt{24}=2\sqrt{6}$cm

$AB=\sqrt{A{H}^2+B{H}^2}=2\sqrt{10}$cm

$AC=\sqrt{A{H}^2+C{H}^2}\mathrm{ }=2\sqrt{15}$cm

$BC=\sqrt{A{B}^2+A{C}^2}\mathrm{ }=10$cm

BM là đường trung tuyến nên ta có:

$B{M}^2=\frac{A{B}^2+B{C}^2}{2}-\frac{A{C}^2}{4}=52\Rightarrow BM=2\sqrt{13}cm$

$AM=MC=\frac{1}{2}AC=\sqrt{10}cm$

Thay số vào (*) ta có: $\cos \widehat{AMB}=\frac{{\left(\sqrt{10}\right)}^2+{(2\sqrt{13})}^2-{(2\sqrt{10})}^2}{2.\sqrt{10}.2\sqrt{13}}=0,15$

Suy ra: $\widehat{AMB}\approx 81,{22}^{\circ }$

b) Xét ΔABM vuông tại A có AK là đường cao nên BK.BM = AB² (1)

Xét ΔABC vuông tại A có AH là đường cao nên BH.BC = AB² (2)

Từ (1) và (2) suy ra BK.BM = BH.BC.

Đề bài. Cho a, b, c thuộc ℕ^*: a² + b² = c². Chứng minh abc chia hết cho 60.

Lời giải:

Giả sử cả 3 số trên đều không chia hết cho 3

⇒ a² ≡ 1 (mod3) và b² ≡ 1 (mod3) (bình phương 1 số chia hết cho 3 hoặc chia 3 dư 1)

⇒ a² + b² ≡ 2 (mod3) nhưng c² ≡ 1 (mod3) ⇒ mâu thuẫn

Vậy có ít nhất 1 số chia hết cho 3 (1)

+ Tương tự, có ít nhất 1 số chia hết cho 4, vì giả sử cả 3 số a, b, c đều không chia hết cho 4

⇒ a² ≡ 1 (mod4) và b² ≡ 1 (mod4)

⇒ a² + b² ≡ 2 (mod 4) nhưng c² ≡ 1 (mod 4) ⇒ mâu thuẫn

Vậy có ít nhất 1 số chia hết cho 4 (2)

+ Tương tự a² = 1 (mod 5) hoặc a² = -1 (mod 5) hoặc a² = 4 (mod 5) và -1 + 1 = 0,1 + 4 = 5,-1 + 4 = 3

⇒ phải có ít nhất 1 số chia hết cho 5 (3)

Từ (1), (2) và (3) ⇒ abc chia hết cho BCNN(3, 4, 5) = 60 hay abc chia hết 60.

Đề bài. Tam giác ABC có a = 7, b = 5, góc $\widehat{C}$ = 60°. Độ dài cạnh c bằng bao nhiêu?

Lời giải:

c² = a² + b² − 2ab.cos$\widehat{C}$

= 7² + 5² − 2.5.7.cos60° = 74 – 35 = 39

⇒ c =$\sqrt{39}$.

Đề bài. Cho tam giác ABC vuông tại A, đường cao AH.

a) Biết 3AB = 2AC. Tính $sin\widehat{ACB},tan\widehat{ACB}$.

b) Vẽ đường phân giác CK của tam giác AHC. Biết AH = 2,4 cm; BH = 1,8 cm. Tính CH, AC, CK, $cos\widehat{HCK}$.

Lời giải:

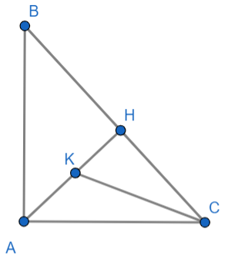a) $sin\widehat{ACB}=\frac{AB}{BC}=\frac{AB}{\sqrt{A{B}^2+A{C}^2}}=\frac{AB}{\sqrt{A{B}^2+\frac{9}{4}A{B}^2}}=\frac{\sqrt{13}}{2}AB$

$tan\widehat{ACB}=\frac{AB}{AC}=\frac{AB}{\frac{3}{2}AB}=\frac{2}{3}$

b) Tam giác ABC vuông tại A, AH là đường cao

AH² = BH.CH

⇒ $CH=\frac{A{H}^2}{BH}=\frac{2,4^2}{1,8}=3,2(cm)$

$AC=\sqrt{A{H}^2+H{C}^2}\mathrm{ }=4(cm)$

Tam giác AHC có CK là đường phân giác nên$\frac{HK}{AK}=\frac{HC}{AC}=\frac{3,2}{4}\Rightarrow HK=\frac{4}{5}AK=\frac{4}{9}AH$

HK = $\frac{4}{9}.2,4=1,067cm$

$cos\widehat{HCK}=\frac{HC}{KC}=\frac{HC}{\sqrt{H{C}^2+K{H}^2}}=\frac{3,2}{\sqrt{3,2^2+1,{067}^2}}=0,948$.

Đề bài. Cho hình vẽ sau biết $\widehat{xAB}={60}^{\circ };\widehat{ABy}={120}^{\circ };\widehat{BCz}={150}^{\circ }$. Chứng minh

a) Ax // By.

b) Biết $\widehat{ABC}={90}^{\circ }$, chứng minh Cz // By.

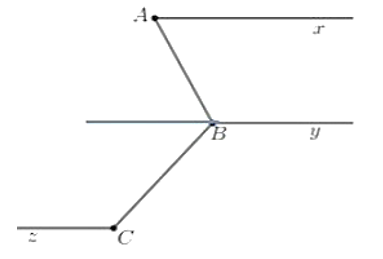Lời giải:

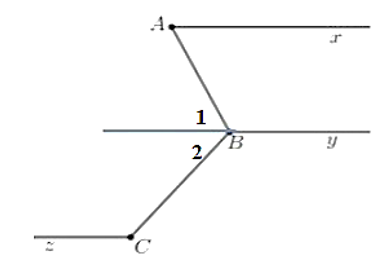a) $\widehat{ABy}+\widehat{B_1}={180}^{\circ }\Rightarrow \widehat{B_1}={180}^{\circ }-{120}^{\circ }\mathrm{ }=60$

$\widehat{B_1}=\widehat{xAB}={60}^{\circ }$

Nên Ax // By vì 2 góc ở vị trí so le trong

b) Vì $\widehat{ABC}=\widehat{B_1}+\widehat{B_2}={90}^{\circ }\mathrm{ }\Rightarrow \widehat{B_2}={90}^{\circ }-{60}^{\circ }\mathrm{ }={30}^{\circ }$

Ta có: $\widehat{BCz}+\widehat{B_2}={30}^{\circ }+{150}^{\circ }\mathrm{ }={180}^{\circ }$

Mà 2 góc $\widehat{BCz};\widehat{B_2}$ là 2 góc trong cùng phía

Nên Cz // By.