Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 38)

Câu 1: A = 2 + 2² + 2³ + … + 2¹⁰⁰. Tìm x biết 2(A + 2) = 2^2x.

Lời giải:

Ta có: 2A = 2² + 2³ + … + 2¹⁰¹

2A – A = (2² + 2³ + … + 2¹⁰¹) – (2 + 2² + 2³ + … + 2¹⁰⁰)

A = 2¹⁰¹ – 2

Thay A vào 2 (A + 2) = 2^2x ta có:

2(2¹⁰¹ – 2 + 2) = 2^2x

Hay 2¹⁰² = 2^2x

Vậy x = 102 : 2 = 51.

Câu 2: 1 con bò nặng $\frac{4}{7}$ con bò đó và 9 yến. Hỏi con bò đó nặng bao nhiêu tạ, bao nhiêu kg?

Lời giải:

9 yến tương đương với số phần con bò là:

1 – $\frac{4}{7}$ = $\frac{3}{7}$ (con bò)

Con bò nặng số yến là:

9 : $\frac{3}{7}$  = 21 (yến)

Đổi 21 yến = 210 kg = 2,1 tạ.

Câu 3: Một hình bình hành có cạnh đáy dài hơn chiều cao 12 cm. Chiều cao bằng $\frac{5}{7}$ cạnh đáy. Hãy tính diện tích hình bình hành đó.

Lời giải:

Cạnh đáy hình bình hành là: 12 : (7 – 5)  . 7 = 42 (cm)

Chiều cao hình bình hành là : 42 – 12 = 30 (cm)

Diện tích hình bình hành: 42 . 12 = 504 (cm²).

Câu 4: Một viên gạch hình vuông cạnh 40 cm. Tính diện tích 10 viên gạch đó?

Lời giải:

Diện tích một viên gạch là:

40 . 40 = 1600 (cm²)

Diện tích 10 viên gạch đó là:

1600 . 10 = 16000 (cm²)

Câu 5: Nêu định nghĩa n!.

Lời giải:

n! ta gọi là n giai thừa, là tích gồm các thừa số từ 1 đến n

n! = 1.2.3.4….n

Câu 6: Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a chia hết 21, a chia hết 35 và a chia hết 99.

Lời giải:

Ta có:

a ∈ BCNN (21; 35; 99)

Ta có:

21 = 3 . 7

35 = 5 . 7

99 = 3² . 11

Suy ra: BCNN (21; 35; 99) = 3² . 5 . 7 . 11 = 3465.

Vì a nhỏ nhất khác 0 nên a = 3465.

Vậy a = 3465.

Câu 7: Tìm số tự nhiên x sao cho 10 chia hết cho x – 1.

Lời giải:

Ta có: 10 chia hết cho x – 1

Suy ra: x – 1 là Ư(10) và x là số tự nhiên

Nên x – 1 ∈ {1; 2; 5; 10}

Vậy x ∈ {2; 3; 6; 11}.

Câu 8: Chứng minh rằng: (x^m + xⁿ + 1) chia hết cho x² + x + 1 khi và chỉ khi (mn – 2) chia hết cho 3.

Lời giải:

Đặt m = 3k + r với 0 ≤ r ≤ 2

n = 3t + s với 0 ≤ s ≤ 2

Ta có: x^m + xⁿ + 1

= x^3k+r + x^3t+s + 1

= x^3kx^r – x^r + x^3tx^s – x^s + x^r + x^s + 1

= x^r (x^3k – 1) + x^s (x^3t – 1) + x^r + x^s + 1

Ta thấy: (x^3k – 1) ⋮ (x² + x + 1) và (x^3t – 1) ⋮ (x² + x + 1)

Vậy để (x^m + xⁿ + 1) ⋮ x² + x + 1 thì (x^r + x^s + 1) ⋮ (x² + x + 1) với 0 ≤ r, s ≤ 2

Hay khi: $\left[\begin{array}{l}r=2;s=1\\ r=1;s=2\end{array}\right.$

⇔ $\left[\begin{array}{l}m=3k+2;n=3t+1\\ m=3k+1;n=3t+2\end{array}\right.$

⇔ $\left[\begin{array}{l}mn-2=\left(3k+2\right)\left(3t+1\right)-2=9kt+3k+6t=3\left(3kt+k+2t\right)\\ mn-2=\left(3k+1\right)\left(3t+2\right)-2=9kt+6k+3t=3\left(3kt+2k+t\right)\end{array}\right.$

Suy ra: mn – 2 ⋮ 3.

Câu 9: Hai người đi bộ cùng chiều, cùng một lúc từ hai địa điểm A và B để đi đến điểm M cách A 12 km và cách B 9 km, với tốc độ lần lượt là 30 km/giờ và 10 km/giờ. Hai người gặp nhau tại đâu?

Lời giải:

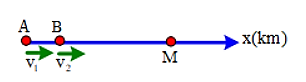
Chọn gốc thời gian và gốc tọa độ tại A, chiều dương từ A đến B

– Người đi từ A: x₁ = v₁t + x₀₁

Với: v₁ = 30 km/giờ; x₀₁ = 0 →  x₁ = 30t

– Người đi từ B: x₂ = v₂t + x₀₂

Với: v₂ = 10 km/giờ; x₀₂ = AB = MA − MB = 3 km →  x₂ = 10t + 3 (km)

– Hai người gặp nhau ta có: x₁ = x₂ →  30t = 10t + 3 →  t = 0,15 (giờ)

⇒ x₁ = x₂ =4,5 km

Suy ra, hai người gặp nhau cách A 4,5 km và gặp nhau trước khi đến M.

Câu 10: Tìm x, y thuộc ℕ biết: 36 – y² = 8(x – 2010)².

Lời giải:

Ta có: 36 – y² = 8(x – 2010)²

⇒ y² + 8(x–2010)² = 36

Vì y² ≥ 0 nên 8(x–2010)² ≤ 36

Suy ra: (x–2010)² ≤ $\frac{36}{8}$

Mặt khác: (x–2010)² là số chính phương nên

$\left[\begin{array}{l}{\left(x-2010\right)}^2=\text{ 0}\\ {\left(x-2010\right)}^2=1\\ {\left(x-2010\right)}^2=4\end{array}\right.$

Với (x–2010)² = 0, ta có: y² = 36. Suy ra y = 6 (vì y ∈ ℕ).

Với (x–2010)² = 1, ta có: y² = 28 (loại).

Với (x–2010)² = 4, ta có: y² = 4. Suy ra: y = 2 (vì y ∈ ℕ).

Vậy (x, y) = (2012; 2), (2008; 2), (2010; 6).

Câu 11: Tìm các số tự nhiên n  sao cho 3n + 7 chia hết cho n – 2 .

Lời giải:

Ta có: 3n + 7 = 3(n – 2) + 13

Để 3n + 7 chia hết cho n – 2 thì n – 2 thuộc Ư(13)

Vậy n – 2 = 1 hoặc n – 2 = 13 hay n = 3 hoặc n = 15.

Câu 12: Cho a – b = 10. Hãy tính A = (2a – 3b)² + 2(2a – 3b)(3a – 2b) + (2b – 3a)².

Lời giải:

A = (2a – 3b)² + 2(2a – 3b)(3a – 2b) + (2b – 3a)²

A = (2a – 3b)² + 2(2a – 3b)(3a – 2b) + (3a – 2b)²

A = [(2a – 3b) + (3a – 2b)]²

A = (5a – 5b)²

A = 5²(a – b)²

A = 25 . 10²

A = 2500.

Câu 13: Chứng minh rằng với mọi n ∈ ℕ^* ta có 11ⁿ⁺¹ + 12^2n–1 chia hết cho 133.

Lời giải:

Đặt A_n ⁼ 11ⁿ⁺¹ + 12^2n–1

A₁ = 11² + 12 = 133 chia hết cho 133

Giả sử A_k = 11^k+1 + 12^2k–1 đã chia hết cho 133

Xét: A_k+1 = 11^k+2 + 12^2k+1

= 11 . 11^k+1 + 12² . 12^2k–1

= 11. 11^k+1 + 12^2k–1 (11 + 133)

= 11 . A_k + 133 . 12^2k–1

Vì A_k chia hết cho 133 và 133 . 12^2k–1 chia hết cho 133 nên A_k+1 chia hết cho 133.

Vậy điều giả sử là đúng.

Câu 14: Chứng minh rằng A = 7 + 7² + 7³ +.. + 7¹⁰⁰ chia hết cho 50.

Lời giải:

Ta có:

A = 7 + 7² + 7³ +.. + 7¹⁰⁰

A = (7 + 7² + 7³ + 7⁴) + (7⁵ + 7⁶ + 7⁷ + 7⁸) + (7⁹⁷ + 7⁹⁸ + 7⁹⁹ + 7¹⁰⁰)

A = (7 + 7² + 7³ + 7⁴) . (1 + 7⁴ + 7⁸ + … + 7⁹⁶)

Ta thấy 7 + 7² + 7³ + 7⁴ = 2800 = 50 . 56 chia hết cho 50

Vì vậy A chia hết cho 50.

Câu 15: Thu gọn tổng sau A = 2 + 2² + 2³ + … + 2¹⁰⁰.

Lời giải:

Ta có: 2A = 2² + 2³ + … + 2¹⁰¹

2A – A = (2² + 2³ + … + 2¹⁰¹) – (2 + 2² + 2³ + … + 2¹⁰⁰)

A = 2¹⁰¹ – 2

Câu 16: Cho p và 2p + 1 là các số nguyên tố ( p > 5 ). Hỏi 4p + 1 là số nguyên tố hay hợp số?

Lời giải:

Xét 3 số tự nhiên tiếp : 4p, 4p + 1, 4p + 2 .

Tích của ba số tự nhiên liên tiếp chia hết cho 3 nên trong 3 số này có một số chia hết cho 3 (1)

Ta xét : 

+ Vì p là số nguyên tố ( p > 5 ) nên p không chia hết cho 3 .

Do vậy 4p không chia hết cho 3 (2)

+ Vì 2p + 1 là số nguyên tố và p > 5 nên 2p + 1 > 3.

Suy ra 2p + 1 không chia hết cho 3 .

Mà 4p + 2 = 2(2p + 1) ⇒ 4p + 2 không chia hết cho 3 (3)              

Từ (1) , (2) , (3) ta suy ra được 4p + 1 chia hết cho 3 .

Mà p > 5 ⇒ 4p + 1 > 3 không thể là số nguyên tố .

Hay nói cách khác 4p + 1 là hợp số.

Câu 17: Rút gọn biểu thức: 3 (2² + 1) (2⁴ + 1) (2⁸ + 1) (2¹⁶ + 1).

Lời giải:

3 (2² + 1) (2⁴ + 1) (2⁸ + 1) (2¹⁶ + 1)

= (2² – 1) (2² + 1) (2⁴ + 1) (2⁸ + 1) (2¹⁶ + 1)

= (2⁴ – 1)( (2⁴ + 1) (2⁸ + 1) (2¹⁶ + 1)

= (2⁸ – 1)  (2⁸ + 1) (2¹⁶ + 1)

= (2¹⁶ – 1) (2¹⁶ + 1)

= 2³² – 1.

Câu 18: Số 2021 có thể viết thành tổng của hai số nguyên tố được không? Vì sao?

Lời giải:

Ta có: 2021 = 2 + 2019

Vì 2019 có tổng các chữ số là 2 + 0 + 1 + 9 = 12 ⁝ 3 nên 2019 ⁝ 3 vì thế 2019 không phải là số nguyên tố.

Ngoài số 2 là số chẵn nguyên tố duy nhất, các số nguyên tố khác hai đều là số lẻ.

Do vậy tổng của hai số nguyên tố khác 2 là một số chẵn.

Mà 2021 là số lẻ

Vậy 2021 không thể viết thành tổng của hai số nguyên tố được.

Câu 19: Một trường học bán trú chuẩn bị số gạo cho 80 học sinh ăn trong 20 ngày. Sau khi ăn hết một nửa số gạo đó trường học có thêm một số học sinh mới nên số gạo còn lại chỉ đủ cho ăn trong 5 ngày nữa. Hỏi trường đó thêm bao nhiêu học sinh nữa?

Lời giải:

Coi số gạo mỗi học sinh ăn trong một ngày là một suất gạo.

Số ngày còn lại là:

20 – 5 =15 (ngày)

Số học sinh ăn hết số gạo trong 5 ngày là:

(80 . 15) : 5 = 240 (học sinh)

Trường đó có thêm số học sinh là:

240 – 80 = 160 (học sinh).

Đáp số: 160 học sinh.

Câu 20: Một mảnh đất hình chữ nhật có nửa chu vi là 30m. Chiều dài hơn chiều rộng 16m. Tính diện tích hình chữ nhật đó.

Lời giải:

Chiều dài hình chữ nhật là:

(30 + 16) : 2 = 23 (m)

Chiều rộng của hình chữ nhật là:

30 – 23 = 7 (m)

Diện tích hình chữ nhật là:

7 . 23 = 161 (m²)

Đáp số: 161 m².

Câu 21: Một sân chơi có hình chữ nhật với chiều dài 12m và chiều rộng 8m.

a) Tính chu vi và diện tích sân chơi đó.

b) Người ta dùng các viên gạch hình vuông có chiều dài cạnh là 40cm để lát nền cho sân chơi. Hỏi cần dùng bao nhiêu viên gạch để lát kín nền sân chơi?

c) Biết mỗi viên gạch giá 25000 đồng và công lát nền là 15000 đồng/m². Tính tổng số tiền phải chi ra để lát nền cho sân chơi?

Lời giải:

a) Chu vi sân chơi đó là:

(12 + 8) . 2 = 40 (m).

Diện tích sân chơi đó là:

12 . 8 = 96 (m²).

b) Đổi 40 cm = 0,4 m

Diện tích một viên gạch là:

0,4 . 0,4 = 0,16 (m²).

Số viên gạch cần là:

96 : 0,16 = 600 (viên gạch ).

c) Số tiền để trả 600 viên gạch là:

600 . 25000 = 15000000 (đồng).

Công lát sân chơi đó:

96 . 15000 = 1440000 (đồng).

Tổng số tiền để chi cho việc lát nền là:

15000000 + 1440000 = 16440000 (đồng).

Câu 22: Một thửa ruộng hình chữ nhật có chu vi bằng 0,56 km chiều rộng bằng $\frac{1}{3}$ chiều dài

a) Tính diện tích thửa ruộng đó

b) Biết rằng trung bình cứ 100m² thu hoạch được 20 kg Hỏi trên cả thửa ruộng đó người ta thu hoạch được bao nhiêu kg ngô?

Lời giải:

a) Nửa chu vi của thửa ruộng là :

0,56 : 2 = 0,28 (km)

Chiều dài thửa ruộng là là :

(0,28 : 4) × 3 = 0,21 (km)

Chiều rộng thửa ruộng là :

0,28 – 0,21 = 0,07 (km)

Diện tích thửa ruộng là :

0,21 . 0,07 = 0,0147 (km²) = 14700 m².

b) Trên cả thửa ruộng đó người ta thu hoạch được số kg ngô là:

14700 : 100 . 20 = 2940 (kg).

Câu 23: Người ta cấy lúa trên một thửa ruộng hình chữ nhật có chiều dài 120 m, chiều rộng bằng $\frac{2}{3}$ chiều dài. Trung bình 150 m² thu hoạch dược 60 kg lúa. Hỏi thửa ruộng đó thu được bao nhiêu tạ lúa ?

Lời giải:

Chiều rộng thửa ruộng đó là: 

120 : 3  . 2 = 80 (m)

Diện tích của thửa ruộng là:

120 . 80 = 9600 (m²)

Thửa ruộng đó thu được số kg lúa là :

9600 : 150 . 60 = 3840 (kg)

Đổi 3840 kg = 38,4 tạ.

Đáp số: 38,4 tạ lúa.

Câu 24: Mảnh vườn hình chữ nhật có chiều rộng bằng 4 cm và diện tích bằng 160 cm².

a) Tính chu vi mảnh vườn hình chữ nhật?

b) Người ta dự định trồng cây xung quanh vườn sao cho mỗi góc vườn có một cây, khoảng cách giữa hai cây là 4cm . Tính số cây cần để trồng?

Lời giải:

a) Chiều dài mảnh vườn là:

160 : 4 = 40 (cm).

Chu vi mảnh vườn là:

(40 + 4) . 2 = 88 (cm).

b) Do khoảng cách giữa hai cây là 4 cm nên trên mỗi chiều rộng ta trồng được 2 cây và cây này nằm ở góc của mảnh vườn nên nó cũng nằm trên chiều dài của vườn.

Trên mỗi chiều dài ta trồng được số cây là:

40 : 4 = 10 (cây).

Tổng số cây trồng được là:

10 + 10 = 20 (cây).

Câu 25: Tìm tất cả số nguyên tố sao cho nó vừa là tổng vừa là hiệu của hai số nguyên tố.

Lời giải:

Trường hợp 1:  p chẵn 

Vì p là số nguyên tố chẵn nên nó chỉ có thể là 2, nhưng 2 không thể là tổng 2 số nguyên tố vì 2 là số nguyên tố nhỏ nhất . 

⇒ p không tồn tại

Trường hợp 2:  p lẻ

Giả sử p = m + n ( m,n là số nguyên tố ). Mà p lẻ ⇒  trong m và n có 1 lẻ, 1 chẵn

Nếu m là số lẻ, n là số chẵn ⇒  n = 2 ⇒ p = m + 2 ⇒ m = p – 2 (1)

Tương tự, p = q – r ( q, r là số nguyên tố ).

Vì p là số lẻ ⇒  trong q và r có 1 lẻ, 1 chẵn

Xét q chẵn ⇒ q = 2 ⇒  p = 2 – r < 0 ( loại ) 

Vậy  q là số lẻ , r là số chẵn ⇒  r = 2 ⇒  p = q – 2 ⇒  q = p + 2 (2)

Từ (1) , (2) ta thấy  p – 2 ; p ; p + 2 là 3 số nguyên tố lẻ (3) 

+ Nếu p < 5 ⇒ p – 2 < 3 ⇒  p – 2 không thể là số nguyên tố lẻ

+ Nếu p = 5 ⇒ (3) thỏa mãn ⇒  p = 5 .

+ Nếu p > 5 ⇒ p – 2 ; p ; p + 2 đều lớn hơn 3

+ Nếu p – 2 chia 3 dư 1 thì p chia hết cho 3 ⇒ p không phải số nguyên tố (loại) 

+ Nếu p–2 chia 3 dư 2 thì p + 2 chia hết cho 3 ⇒ p + 2 ko phải số nguyên tố (loại) 

⇒ p chỉ có thể là 5

Vậy p = 5. 

Câu 26: Tìm các số nguyên dương m, n biết: 2^m + 2ⁿ = 2^m+n.

Lời giải:

Ta có:

2^m + 2ⁿ = 2^m+n

⇔ 2^m + 2ⁿ = 2^m.2ⁿ

⇔ 2^m + 2ⁿ – 2^m.2ⁿ = 0

⇔ 2^m (2ⁿ – 1) – (2ⁿ –1) = 1

⇔ (2^m – 1)(2ⁿ – 1) = 1 = 1 . 1

Suy ra:

$\left\{\begin{array}{l}{2}^m-1=1\\ 2^n-1=1\end{array}\right.$ ⇒ $\left\{\begin{array}{l}m=1\\ n=1\end{array}\right.$

Vậy m = n = 1.

Câu 27: Tìm số tự nhiên nhỏ nhất khác 0 biết rằng a chia hết cho 15; a chia hết cho 18.

Lời giải:

Ta có: a ∈ BCNN (15; 18)

15 = 3 . 5

18 = 2 . 3²

Suy ra: BCNN (21; 35; 99) = 2 . 3² .  5 = 90

Vì a là số tự nhiên nhỏ nhất khác 0 nên a = 90.

Câu 28: Tìm số tự nhiên x biết 36 chia hết cho x + 5.

Lời giải:

Theo bài ra ta có:

36 ⋮ (x + 5)

Suy ra: x + 5 ∈ Ư(36)

Vì x là số tự nhiên nên x + 5 ∈ {1; 2; 3; 4; 6; 9; 12; 18; 36}

⇒ x ∈ {–4; –3; –2; –1; 1; 4; 7; 13; 21}  mà x thuộc ℕ.

Vậy x ∈{1; 4; 7; 13; 21}.

Câu 29: Tìm trung bình cộng của các số lẻ có 3 chữ số.

Lời giải:

Số lẻ lớn nhất có 3 chữ số là 999

Số lẻ nhỏ nhất có 3 chữ số là 101

Số các số hạng của dãy các số lẻ có 3 chữ số là:

(999 – 101) : 2 + 1 = 450

Tổng các số lẻ có 3 chữ số là:

(999 + 101) . 450 : 2 = 247500

Trung bình cộng của các số lẻ có 3 chữ số là:

247500 : 450 = 550.

Câu 30: Tổng hai số là 724. Tìm số lớn biết rằng khi xóa chữ số 7 ở hàng trăm của số lớn thì ta được số bé.

Lời giải:

Khi xoá đi chữ số 7 ở hàng trăm tức là số đó giảm đi 700 đơn vị.

Suy ra 700 là hiệu giữa số lớn và số bé.

Số lớn là:

(724 + 700) : 2 = 712.

Câu 31: Hỏi nếu bán kính 1 hình tròn giảm đi 20% thì diện tích hình tròn giảm đi bao nhiêu %?

Lời giải:

Khi giảm bán kính của hình tròn đi 20% thì bán kính của hình trong khi đó là:

100% – 20% = 80%

Diện tích hình tròn mới là:

80% . 80% = 64%

Diện tích hình tròn mới so với ban đầu giảm đi:

100% – 64% = 36%

Vậy nếu giảm bán kình 20% thì diện tích giảm 36%.

Câu 32: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB và D là điểm đối xứng của M qua I. Chứng minh rằng: AD // BM và tứ giác ADBM là hình thoi.

Lời giải:

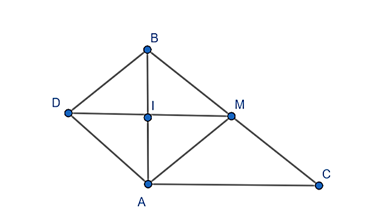
Ta có: ID = IM (D là điểm đối xứng của M qua I)

IA = IB (I là trung điểm AB)

Suy ra: tứ giác ADBM là hình bình hành (2 đường chéo đi qua trung điểm mỗi đường) (1)

Do đó: AD // BM.

Lại có:

IM là đường trung bình của tam giác ABC ⇒ IM // AC

Mà AB ⊥ AC

⇒ IM ⊥ AB hay DM ⊥ AB (2)

Từ (1) và (2) suy ra: ADBM là hình thoi.

Câu 33: Gọi S là tập hợp tất cả các số tự nhiên là ước của số A = 2² . 3³ . 5. Hỏi tập S có bao nhiêu phần tử?

Lời giải:

Số các ước của A là: 3 . 4 . 2 = 24

Vậy S có 24 phần tử.

Câu 34: Một thửa ruộng hình chữ nhật có chiều dài 140 m, chiều rộng bằng 0,75 lần chiều dài. Trên thửa ruộng người ta trồng lúa, trung bình cứ 100 m² thu hoạch được 50 kg thóc. Hỏi trên thửa ruộng đó người ta thu hoạch được bao nhiêu tấn thóc ?

Lời giải:

Chiều rộng thửa ruộng là:

140 . 0,75 = 105 (m)

Diện tích thửa ruộng là:

140 . 105 = 14700 (m²).

Trên thửa ruộng đó người ta thu hoạch được số tấn thóc là:

14700 : 100 . 50 = 7350 (kg)

Đổi 7350 kg = 7,35 tấn.

Vậy thu hoạch được 7,35 tấn thóc.

Câu 35: Một chiếc điện thoại sau khi hạ giá hai lần, mỗi lần giảm 10% giá đang bán thì có giá bán là 1215000 đồng. Tính giá tiền của chiếc điện thoại đó.

Lời giải:

Giá lần đầu tiên là 100%.

Giảm lần thứ nhất 10% thì còn 90%.

Giảm 10% lần 2 thì giảm: 90% : 10% = 9%

1215000 đồng ứng với:  

100% – 10% – 9% = 81% (giá lần đầu tiên)

Giá tiền của chiếc điện thoại đó là:

1215000 : 81 . 100 = 1500000 ( đồng )

Câu 36: Một người có số gạo nếp bằng 75% số gạo tẻ. Sau khi bán 6 kg gạo nếp thì số gạo nếp còn lại bằng 60% số gạo tẻ. Hỏi lúc đầu người đó có tất cả bao nhiêu kg gạo?

Lời giải:

6kg gạo nếp bằng:

75 – 60 = 15% (gạo tẻ)

Số gạo tẻ là:

6 : 15 . 100 = 40 (kg)

Số gạo nếp lúc đầu là:

40 : 100 . 75 = 30 (kg)

Lúc đầu có tất cả số kg gạo là:

40 + 30 = 70 (kg)

Câu 37: Viết số tự nhiên nhỏ nhất có bốn chữ số khác nhau và đều là số lẻ.

Lời giải:

Một số có bốn chữ số khác nhau và đều là số lẻ là số nhỏ nhất thì:

Chữ số lẻ đầu tiên của nó phải là số nhỏ nhất khác 0 là số 1

Chữ số lẻ kế tiếp phải là số nhỏ nhất khác 1 tức là số 3 

Chữ số lẻ kế tiếp phải là số nhỏ nhất khác 1 và 3 tức là số 5 

Chữ số lẻ hàng đơn vị phải nhỏ nhất khác 1,3,5 tức là số 7 

Vậy số tự nhiên nhỏ nhất có bốn chữ số khác nhau và đều là số lẻ: 1357.

Câu 38: Tìm số tự nhiên n sao cho 2ⁿ + 2023 là số chính phương.

Lời giải:

Với n = 0, 2ⁿ + 2023 = 2024 (loại vì không phải số chính phương)

Với n = 1, 2ⁿ + 2023 = 2025 = 45²

Với n ≥ 2 thì 2ⁿ chia hết cho 4

2ⁿ + 2023 = 2ⁿ + 4 . 505 + 3

Khi đó: 2ⁿ + 2023 chia 4 dư 3

Suy ra 2ⁿ + 2023 không phải số chính phương vì số chính phương chia hết cho 4 hoặc chia 4 dư 1)

Vậy n = 1.

Câu 39: Cho hình chữ nhật có chu vi 324 m. Nếu ta tăng chiều dài thêm 5 m và chiều rộng thêm 3 m thì chiều dài gấp 3 lần chiều rộng.Tính diện tích hình chữ nhật đó.

Lời giải:

Nửa chu vi hình chữ nhật là:

324 : 2 = 162 (m)

Nửa chu vi lúc sau là:

162 + (5 + 3) = 170 (m)

Chiều rộng là:

170 : (1 + 4)= 34 (m)

Chiều dài là:

170 – 34 = 136 (m)

Diện tích hình chữ nhật là:

136 . 34 = 4624 (m²)

Đáp số: 4624 m².

Câu 40: Bạn An và Khang đi mua 18 gói bánh và 12 gói kẹo để lớp liên hoan An đưa cho cô bán hàng bốn tờ 50 nghìn đồng và được cô trả lại 72 nghìn đồng. Khang nói: “cô tính sai rồi”. Bạn hãy cho biết Khang nói đúng hay sai ? Giải thích tại sao ?

Lời giải:

Do bạn An và bạn Khang đi mua tất cả là 30 gói bánh kẹo nên số tiền phải trả bắt buộc phải chia hết cho 3

Số tiền bạn An đưa cho cô bán hàng là: 4 . 50000 = 200000 (đồng)

Số tiền cô bán hàng nhận là: 200000 – 72000 = 128000(đồng)

Vì 128000 chia hết cho 3 nên bạn Khang nói đúng.

Câu 41: Các số chia hết cho 11 khi nào?

Lời giải:

Các số chia hết cho 11 khi tổng các chữ số hàng lẻ trừ tổng các chữ số hàng chẵn hoặc ngược lại chia hết cho 11.

Ví dụ: số 253 có (2 + 3) – 5 = 0 ⋮ 11 nên 253 ⋮ 11.

Câu 42: Nêu 3 ví dụ về các số chia hết cho 11

Lời giải:

3 số chia hết cho 11 là: 11; 121; 22; ….

Câu 43: Phân số $\frac{24056}{1000}$  được viết thành số thập phân là?

Lời giải:

$\frac{24056}{1000}$= 24,056.

Câu 44: Một người nuôi 85 con gà. Sau khi người đó mua thêm 20 con gà trống bằng $\frac{3}{4}$ số gà mái. Hỏi lúc đầu người đó mua bao nhiêu con gà trống, bao nhiêu con gà mái?

Lời giải:

Sau khi người đó mua thêm 20 con gà trống thì tổng số gà là:

85 + 20 = 105 (con)

Coi số gà trống là 3 phần bằng nhau thì số gà mái là 4 phần bằng nhau như thế

Số gà mái lúc đầu là:

105 : (3 + 4) . 4 = 60 (con)

Số gà trống lúc đầu là :

85 – 60 = 25 (con).

Câu 45: Cho phép tính :  30 + 31 + 32 + 33 + ..........+ 32008 + 32009. Lấy kết quả phép tính này chia cho 8 thì số dư là bao nhiêu ?

Lời giải:

Số số của dãy trên là:

(32009 – 30) : 1 + 1 = 31980 (số)

Số cặp số của dãy là:

31980 : 2 = 15990 (cặp)

Ta có:

30 + 31 + 32 +....+ 32008 + 32009

= (30 + 32009) + (31 + 32008) + ...

= 32039 . 15990

= 512303610

Vậy 512303610 : 8 = 64037951(dư 2).

Câu 46: Một ô tô trong 5 giờ đầu, mỗi giờ đi được 247 km. Trong 3 giờ sau mỗi giờ đi được 43km. Trung bình mỗi giờ đi được bao nhiêu km?

Lời giải:

Tổng số km ô tô đi được trong 8 giờ là:

5 . 247 + 3 . 43 = 1364

Trung bình mỗi giờ ô tô đi được số km là:

1364 : 8 = 170,5 (km).

Câu 47: Điền vào chỗ trống: 5 tấn 2 tạ = … tạ.

Lời giải:

Vì 1 tấn = 10 tạ

Nên: 5 tấn 2 tạ = 52 tạ.

Câu 48: Có 36 con vừa gà vừa chó. Tổng số chân của 36 con vừa gà vừa chó bằng 100. Hỏi có bao nhiêu con gà, bao nhiêu con chó?

Lời giải:

Gọi x là số con gà, y là số con chó chó (x, y > 0)

1 con gà có 2 chân, 1 con chó có 4 chân.

Theo bài ra ta có:

x + y = 36

2x + 4y = 100

Giải hệ phương trình : x = 22; y = 14

Vậy có 22 con gà và 14 con chó.

Câu 49: Hiện nay tuổi bố gấp 4 lần tuổi con biết rằng 5 năm nữa thì tổng số tuổi của hai bố con là 55 tuổi. Hỏi hiện nay bố bao nhiêu tuổi ? Con bao nhiêu tuổi?

Lời giải:

Tổng số tuổi của bố và con hiện nay là:

55 – (5 + 5) = 45 (tuổi)

Tổng số phần bằng nhau là:

1 + 4 = 5 (phần)

Tuổi bố hiện tại là :

45 : 5 . 4 = 36 (tuổi)

Tuổi con hiện tại là :

45 – 36 = 9 (tuổi)

Câu 50: Khi nhân một số thập phân với 16,3 do sơ xuất một bạn học sinh đã đặt các tích riêng thẳng cột như trong phép cộng nên được 12,6. Tìm kết quả đúng với phép nhân đó.

Lời giải:

Theo bài ra, 12,6 gấp thừa số thứ nhất số lần là:

(1 + 6 + 3) : 10 = 1 (lần)

Thừa số thứ nhất là:

12,6 : 1 = 12,6

Tích đúng là:

12,6 . 16,3 = 205,38.