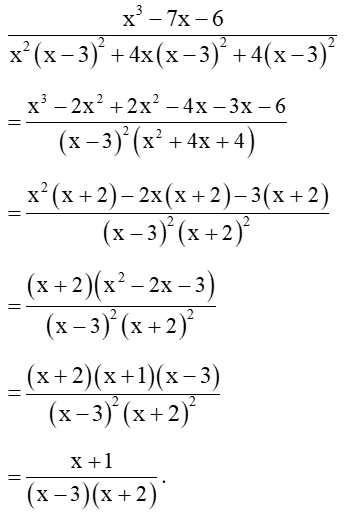Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 7)

Câu 1: Tính tổng 3 + 6 + 12 + 24 + … + 3072

Lời giải:

Đặt tổng A =  3 + 6 + 12 + 24 + … + 3072

Ta có: 2A = 6 + 24 + 47 + …. + 6144

⇒ 2A – A = 6144 – 3 = 6141.

Vậy A = 6141.

Câu 3: Giữa các số 7 và 35 hãy đặt thêm 6 số nữa để được một cấp số cộng

Lời giải:

Ta có: u₁ = 7 ; u₇ = 35

Do dãy số là cấp số cộng nên ta có: u₇ = u₁ + 6d ⇔ 35 = 7 + 6d ⇔ 6d = 28 ⇔ d = $\frac{14}{3}$

Vậy ta có các số cần tìm là: $u_2=\frac{35}{3};u_3=\frac{49}{3};u_4=21;u_5=\frac{77}{3};u_6^{}=\frac{91}{3}$

Câu 4: Cho 4 điểm A, B, C, D. Chứng minh: $\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}$ .

Lời giải:

Ta có:

$\begin{array}{l}VT=\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{BC}+\left(\overrightarrow{DC}+\overrightarrow{CD}\right)\\ =\overrightarrow{AD}+\overrightarrow{BC}=VP\end{array}$

Câu 8: Giải phương trình sau: 5sin x – 2 = 3(1 – sin x)tan² x.

Lời giải:

Điều kiện: cos x ≠ 0 (*)

Phương trình ⇔ 5sin x – 2 = 3(1 – sin x) . $\frac{{\sin }^{2}x}{{\cos }^{2}x}$

⇔ 5sin x – 2 = 3.(1 – sin x) . $\frac{{\sin }^{2}x}{1-{\sin }^{2}x}$

⇔ 5sin x – 2 = $\frac{3{\sin }^{2}x}{1+\sin x}$

⇒ 2sin² x + 3sin x – 2 = 0

⇔ $\left[\begin{array}{l}\sin x=\frac{1}{2}\left(TM\right)\\ \sin x=-2\left(L\right)\end{array}\right.$

Xét sin x = $\frac{1}{2}\iff \left[\begin{array}{l}x=\frac{\pi }{6}+k2\pi \\ x=\frac{5\pi }{6}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$ (thỏa mãn điều kiện (*)).

Vậy nghiệm của phương trình là $x=\frac{\pi }{6}+k2\pi$ và $x=\frac{5\pi }{6}+k2\pi ,k\in \mathbb{Z}$.

Câu 9: Chứng minh rằng x⁸ⁿ + x⁴ⁿ + 1 chia hết cho x²ⁿ + xⁿ + 1, với mọi số tự nhiên n.

Lời giải:

Ta có: x⁸ⁿ + x⁴ⁿ + 1 = x⁸ⁿ + 2x⁴ⁿ + 1 – x⁴ⁿ = (x⁴ⁿ + 1)² – (x²ⁿ)²

= (x⁴ⁿ + 1 – x²ⁿ)(x⁴ⁿ + 1 + x²ⁿ)

= (x⁴ⁿ + 1 – x²ⁿ)(x⁴ⁿ + 2x²ⁿ + 1 – x²ⁿ)

= (x⁴ⁿ + 1 – x²ⁿ)[(x²ⁿ + 1)² – (xⁿ)²]

= (x⁴ⁿ + 1 – x²ⁿ)(x²ⁿ – xⁿ + 1)(x²ⁿ + xⁿ + 1)

Vậy x⁸ⁿ + x⁴ⁿ + 1 chia hết cho x²ⁿ + xⁿ + 1, với mọi số tự nhiên n.

Câu 15: Cho hình bình hành ABCD. Dựng $\overrightarrow{AM}=\overrightarrow{BA},\overrightarrow{MN}=\overrightarrow{DA},\overrightarrow{NP}=\overrightarrow{DC},\overrightarrow{PQ}=\overrightarrow{BC}$ .

Chứng minh rằng: $\overrightarrow{AQ}=\overrightarrow{0}$ .

Lời giải:

Theo quy tắc ba điểm ta có: $\overrightarrow{AQ}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NP}+\overrightarrow{PQ}=\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{DC}+\overrightarrow{BC}$

Áp dụng quy tắc hình bình hành ta có: $\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BD},\overrightarrow{DA}+\overrightarrow{DC}=\overrightarrow{DB}$  (do ABCD là hình bình hành).

Do đó, $\overrightarrow{AQ}=\overrightarrow{BD}+\overrightarrow{DB}=\overrightarrow{0}$  (đpcm).

Câu 16: Cho tam giác ABC nhọn. Vẽ AH vuông góc với BC tại H. Chứng minh rằng:

AC² + BH² = AB² + CH².

Lời giải:

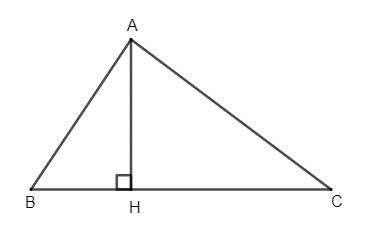
Vì tam giác ABH vuông tại H nên AB² = AH² + BH² (định lí Pythagore).

Suy ra BH² = AB² – AH².

Vì tam giác ACH vuông tại H nên AC² = AH² + HC² (định lí Pythagore).

Do đó ta có: AC² + BH² = (AH² + HC²) + (AB² – AH²) = AB² + HC² (đpcm).

Câu 23: Tìm m để đa thức A(x) = x³ – 3x² + 5x + m chia hết cho đa thức B(x) = x – 2.

Lời giải:

Ta có:

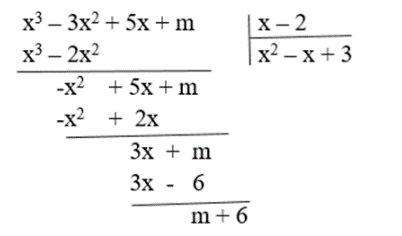
Do đó, A(x) chia hết cho B(x) khi m + 6 = 0, suy ra m = – 6.

Câu 25: Cho ba điểm A(– 4; 0), B(0; 3) và C(2; 1). Xác định tọa độ của vectơ $\overrightarrow{u}=2\overrightarrow{AB}-\overrightarrow{AC}$ .

Lời giải:

Ta có: $\overrightarrow{AB}=\left(4;3\right),\overrightarrow{AC}=\left(6;1\right)$ .

Do đó, $\overrightarrow{u}=2\overrightarrow{AB}-\overrightarrow{AC}$  = 2.(4; 3) – (6; 1) = (2 . 4 – 6; 2 . 3 – 1) = (2; 5).

Vậy $\overrightarrow{u}=\left(2;5\right)$ .

Câu 27: Nghiệm của phương trình cos x = 0 là

A. x = kπ, k ∈ ℤ.

B. x = k2π, k ∈ ℤ.

C. $x=\frac{\pi }{2}+k\pi$ , k ∈ ℤ.

D. $x=\frac{\pi }{2}+k2\pi$ , k ∈ ℤ.

Lời giải:

Đáp án đúng là: C

Ta có: cos x = 0 $x=\frac{\pi }{2}+k\pi$ , k ∈ ℤ.

Câu 28: Một cột đèn có bóng trên mặt đất dài 7,5 m. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 42°. Tính chiều cao của cột đèn (làm tròn đến chữ số thập phân thứ ba).

Lời giải:

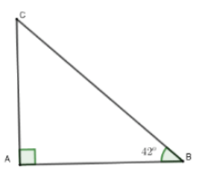
Gọi chiều cao cột đèn là AC, AB là bóng của cột đèn trên mặt đất, AB = 7,5 m.

Góc tạo bởi tia nắng mặt trời với mặt đất là $\widehat{ABC}=42°$ .

Xét tam giác ABC vuông tại A, ta có:

AC = AB . tanB = 7,5 . tan42° ≈ 6,753 (m).

Vậy cột đèn cao khoảng 6,753 m.

Câu 30: Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Lời giải:

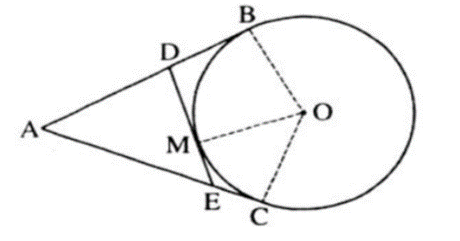
Vì AB, AC là hai tiếp tuyến của (O) lần lượt tại B và C. Theo tính chất của hai tiếp tuyến cắt nhau ta có: AB = AC.

Vì DB, DM là hai tiếp tuyến của (O) lần lượt tại B và M. Theo tính chất của hai tiếp tuyến cắt nhau ta có: DB = DM.

Vì EM, EC là hai tiếp tuyến của (O) lần lượt tại M và C. Theo tính chất của hai tiếp tuyến cắt nhau ta có: EM = EC.

Chu vi tam giác ADE là:

AD + DE + EA

= AD + (DM + ME) + EA

= (AD + DM) + (ME + EA)

= (AD + DB) + (EC + EA) (do DB = DM, EM = EC)

= AB + AC = 2AB (do AB = AC).

Câu 31: Cho ba điểm A (1; −1), B (2; 1), C (−3; 1). Chứng minh đường thẳng AB vuông góc với đường thẳng AC.

Lời giải:

Gọi pt đường thẳng AB có dạng  y = ax + b, do AB đi qua A và B nên:

$$\begin{gathered} \left\{\begin{array}{c}a+b=-1\\ 2a+b=1\end{array}\right. \\ \Rightarrow \left\{\begin{array}{c}a=2\\ b=-3\end{array}\right. \end{gathered}$$

⇒ y = 2x – 3

Gọi phương trình đường thẳng AC có dạng y = cx +d

$$\begin{gathered} \Rightarrow \left\{\begin{array}{c}a+b=-1\\ -3a+b=1\end{array}\right. \\ \Rightarrow \left\{\begin{array}{c}a=-\frac{1}{2}\\ b=-\frac{1}{2}\end{array}\right. \\ \Rightarrow y=-\frac{1}{2}x-\frac{1}{2} \end{gathered}$$

Do tích 2 hệ số góc $2.\left(-\frac{1}{2}\right)=-1$ .

Vậy AB và AC vuông góc.

Câu 32: Cho ba điểm A (1; 1); B (2; 0); C (3; 4). Viết phương trình đường thẳng đi qua A và cách đều hai điểm B, C.

A. 4x – y – 3 = 0; 2x – 3y + 1 = 0;

B. 4x – y – 3 = 0; 2x + 3y + 1 = 0

C. 4x + y – 3 = 0; 2x – 3y + 1 = 0;

D. x – y = 0; 2x – 3y + 1 = 0.

Lời giải:

Gọi (d) là đường thẳng đi qua A và cách đều B, C. Khi đó ta có các trường hợp sau:

TH1: d đi qua trung điểm của BC.

$I\left(\frac{5}{2};2\right)$ là trung điểm của BC.

$\overrightarrow{AI}=\left(\frac{3}{2};1\right)$ là vec tơ chỉ phương của đường thẳng d.

Khi đó (d): – 2(x – 1) + 3(y – 1) = 0 ⟺ 2x – 3y + 1 = 0.

TH2: d song song với BC, khi đó d nhận $\overrightarrow{BC}=\left(1;4\right)$ là vectơ chỉ phương.

Phương trình đường thẳng d là: – 4(x – 1) + y – 1 = 0 ⇔ 4x – y – 3 = 0.

Đáp án đúng là: A

Câu 33: Tìm tập xác định $\frac{\sqrt{x-1}}{x-3}$ .

Lời giải:

Hàm số xác định khi $\left\{\begin{array}{c}x-1\ge 0\\ x-3\ne 0\end{array}\right.\iff \left\{\begin{array}{c}x\ge 1\\ x\ne 3\end{array}\right.$ .

Vậy tập xác định của hàm số là $D=\left[-1;+\infty \right)/\left\{-3\right\}$ .

Câu 34: Tìm tập xác định D của hàm số $y=\sqrt{x+2}-\sqrt{x+3}$ .

Lời giải:

Hàm số xác định khi

$\left\{\begin{array}{c}x+2\ge 0\\ x+3\ge 0\end{array}\right.\iff \left\{\begin{array}{c}x\ge -2\\ x\ge -3\end{array}\right.\iff x\ge -2$

Vậy tập xác định của hàm số là $D=\left[-2;+\infty \right)$

Đáp án đúng là B.

Câu 35: Cho tam giác ABC có h_b + h_c = 2h_a. Chứng minh rằng: $\frac{1}{\sin B}+\frac{1}{\sin C}=\frac{2}{\sin A}.$

Lời giải:

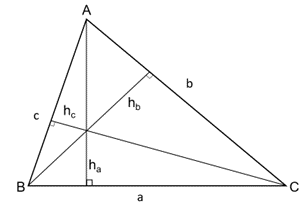
Ta có: h_b + h_c = 2h_a

$$\begin{gathered} \iff \frac{2S_{ABC}}{b}+\frac{2S_{ABC}}{c}=\frac{4S_{ABC}}{a} \\ \iff \frac{1}{b}+\frac{1}{c}=\frac{2}{a} \end{gathered}$$

Áp dụng định lý Sin trong tam giác ABC:

$\frac{1}{\sin B}+\frac{1}{\sin C}=\frac{2R}{b}+\frac{2R}{c}=2R\left(\frac{1}{b}+\frac{1}{c}\right)$; (R: bán kính đường tròn ngoại tiếp tam giác)

$\Rightarrow \frac{1}{\sin B}+\frac{1}{\sin C}=2R.\frac{2}{a}=\frac{4R}{a}=\frac{2}{\sin A}$.

Vậy $\frac{1}{\sin B}+\frac{1}{\sin C}=\frac{2}{\sin A}$ .

Câu 36: Định nghĩa hình chiếu là gì?

Lời giải:

Hình chiếu là hình biểu diễn một mặt nhìn thấy của vật thể đối với người quan sát đứng trước vật thể, phần khuất được thể hiện bằng nét đứt.

Câu 37: Số liền trước của số tròn chục lớn nhất có 6 chữ số khác nhau là?

Lời giải:

Số tròn chục lớn nhất có 6 chữ số khác nhau là số 987650.

Vậy số liền trước của số tròn chục lớn nhất có 6 chữ số khác nhau là số 987649.

Câu 38: Gọi d là đường thẳng đi qua A(1;0) và có hệ số góc m. Tìm tất cả giá trị thực của tham số m để d cắt đồ thị hàm số $y=\frac{x+2}{x-1}$  (C) tại hai điểm phân biệt thuộc hai nhánh của đồ thị?

Lời giải:

Đường thẳng d có dạng y = m(x – 1) = mx – m.

Phương trình hoành độ giao điểm:

$\frac{x+2}{x-1}=mx-m$ với (x ≠ 1)

⇔ x + 2 = (mx – m)(x – 1)

⇔ mx² – (2m + 1)x + m – 2 = 0 (1)

Để d cắt (C) tại hai điểm phân biệt thuộc hai nhánh của đồ thị ⇔ phương trình (1) có hai nghiệm phân biệt x₁ < x₂ thỏa mãn x₁ < 1 < x₂ hay (x₁ – 1)(x₂ – 1) < 0

$$\begin{gathered} \left\{\begin{array}{c}m\ne 0\\ \Delta >0\\ \left(x_1-1\right)\left(x_2-1\right)<0\end{array}\right. \\ \iff \left\{\begin{array}{c}m\ne 0\\ 12m+1>0\\ x_1{x}_2-\left(x_1+x_2\right)+1<0\end{array}\right. \\ \iff \left\{\begin{array}{c}m\ne 0\\ m>-\frac{1}{12}\\ \frac{m-2}{m}-\frac{2m+1}{m}+1=-\frac{3}{m}<0\end{array}\right. \\ \iff \left\{\begin{array}{c}m\ne 0\\ m>-\frac{1}{12}\\ m>0\end{array}\right. \end{gathered}$$

⇔ m > 0

Vậy m > 0.

Câu 39: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A (2; 4), B (5; 1), C(– 1; – 2). Phép tịnh tiến theo véc tơ $\overrightarrow{BC}$  biến tam giác ABC thành tam giác A'B'C'. Tìm tọa độ trọng tâm của tam giác A'B'C'.

Lời giải:

Tọa độ vectơ $\overrightarrow{BC}$ = (–1 – 5; – 2 – 1) = ( – 6; – 3);

Gọi G (x₁; y₁) là trọng tâm tam giác ABC.

$\left\{\begin{array}{c}{x}_1=\frac{2+5-1}{3}\\ y_1=\frac{4+1-2}{3}\end{array}\right.\iff \left\{\begin{array}{c}{x}_1=2\\ y_1=1\end{array}\right.$

⇒ Tọa độ trong tâm tam giác ABC là G (2; 1).

Gọi G^’ (x₂; y₂) là trọng tâm tam giác A'B'C'.

Phép tịnh tiến theo véc tơ $\overrightarrow{BC}$  biến tam giác ABC thành tam giác A'B'C' nên G(2; 1) cũng tịnh tiến theo véc tơ $\overrightarrow{BC}$  thành G’ (x₂; y₂).

Ta có:  $\overrightarrow{GG\text{'}}$ = $\overrightarrow{BC}$ = ( – 6; – 3)

$$\begin{gathered} \Rightarrow \left\{\begin{array}{c}{x}_2-2=-6\\ y_2-1=-3\end{array}\right. \\ \iff \left\{\begin{array}{c}{x}_2=-4\\ y_2=-2\end{array}\right. \end{gathered}$$

Vậy G’ (– 4; – 2).

Câu 40: Một lớp học có 25 học sinh nam và 15 học sinh nữ. Tính tỉ số phần trăm của học sinh nữ so với học sinh nam.

Lời giải:

Tỉ số phần trăm của học sinh nữ so với học sinh nam là :

15 : 25 × 100 = 60 %

Đáp số: 60%.

Câu 41: Một tổ có 25 học sinh nam, 15 học sinh nữ. Hỏi có bao nhiêu cách chọn 1 em làm lớp trưởng?

A. 15;

B. 40;

C. 39;

D. 25.

Lời giải:

Tổng số học sinh của tổ là: 25 + 15 = 40 (học sinh);

Vậy số cách để chọn ngẫu nhiên 1 em làm lớp trưởng là 40 cách.

Câu 42: Một căn phòng hình chữ nhật có chiều dài 12 m, chiều rộng bằng $\frac{1}{3}$  chiều dài. Để lát nền căn phòng đó, người ta dùng loại gạch men hình có có cạnh 8 dm. Hỏi căn phòng đó được lát bao nhiêu viên gạch men đó? (Phần diện tích mạch vữa không đáng kể).

Lời giải:

Chiều dài của căn phòng :

$12\times \frac{1}{3}=4$(m) = 40 (dm)

Ta có: 12 m = 120 dm

Diện tích của căn phòng :

120 × 40 = 4 800 (dm²)

Diện tích mỗi viên gạch men :

8 × 8 = 16 (dm²)

Số viên gạch men dùng để lát căn phòng là

4800 : 16 = 300 (viên gạch men)

Đáp số: 300 viên gạch men

Câu 43: Một căn phòng hình chữ nhật có chiều dài hơn chiều rộng 4 m chiều rộng bằng $\frac{3}{4}$  chiều dài. Người ta lát nền căn phòng bằng gạch men hình vuông có cạnh 2 dm. Hỏi cần bao nhiêu viên gạch men để lát kín phòng đó? (không tính mạch vữa)

Lời giải:

4 m = 40 dm

Chiều rộng căn phòng là :

40 : ( 4 − 3) × 3 = 120  (dm)

Chiều dài căn phòng là :

40 : ( 4 − 3 ) × 4 = 160 (dm)

Diện tích căn phòng là :

120 × 160 = 19200 (dm²)

Diện tích viên gạch là :

 2 × 2 = 4 (dm²)

Cần số gạch để lát căn phòng là :

 19200 : 4 = 4800 (viên gạch)

Đáp số: 4800 viên gạch.

Câu 44:  Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức $\sqrt{x-2}+\sqrt{4-x}$ .

Lời giải:

Điều kiện xác định của biểu thức: 2 ≤ x ≤ 4.

Ta có: $\sqrt{a}+\sqrt{b}\le \sqrt{2\left(a+b\right)}$  (với a, b ≥ 0).

Nên $\sqrt{x-2}+\sqrt{4-x}\le \sqrt{2\left(x-2+4-x\right)}$

$\Rightarrow \sqrt{x-2}+\sqrt{4-x}\le 2$

Do đó GTLN của biểu thức là 2.

Ta có: $\sqrt{a}+\sqrt{b}\ge \sqrt{a+b}$

Dấu “=” xảy ra khi a = 0 hoặc b = 0;

Áp dụng vào biểu thức:

 $$\begin{gathered} \sqrt{x-2}+\sqrt{4-x}\ge \sqrt{x-2+4-x} \\ \Rightarrow \sqrt{x+2}+\sqrt{4-x}\ge \sqrt{2} \end{gathered}$$

Đẳng thức xảy ra $\iff \left[\begin{array}{c}x=2\\ x=4\end{array}\right.$ .

GTNN của biểu thức là: $\sqrt{2}$  với x = 2 hoặc x = 4.

Câu 45: Tìm x biết: (x – 5)(x – 4) – (x + 1)(x – 2) = 7

Lời giải:

(x – 5)(x – 4) – (x + 1)(x – 2) = 7

⇔ x² – 4x – 5x + 20 – (x² – 2x + x – 2) = 7

⇔ x² – 4x – 5x + 20 – x² + 2x – x + 2 = 7

⇔ – 8x + 22 = 7

⇔ – 8x = 7 – 22

⇔ – 8x = – 15

$$\begin{gathered} \iff x=\frac{-15}{-8} \\ \iff x=\frac{15}{8} \end{gathered}$$

Vậy $x=\frac{15}{8}$ .

Câu 46: Chứng minh  A = n³ + (n + 1)³ + (n + 2)³ chia hết cho 9 với mọi n ∈ ℕ*.

Lời giải:

A = n³ + (n + 1)³ + (n + 2)³

= n³ + n³ + 3n² + 3n + 1 + n³ + 6n² + 12n + 8

= 3n³ + 9n² + 15n + 9

= 3n² (n + 1) + 6n ( n + 1) + 9 (n +1)

= 3 (n + 1)(n² + 2n + 3)

=3(n + 1)[n (n + 2) + 3]

= 3n (n + 1)(n + 2) + 9( n + 1)

Ta có: n; n + 1; n + 2 là 3 số tự nhiên liên tiếp

⇒ 3n(n + 1)(n + 2) ⋮ 9

Mặc khác: 9(n + 1) ⋮ 9

⇒ A = 3n (n + 1)(n + 2) + 9(n + 1) ⋮ 9.

Vậy A = n³ + (n + 1)³ + (n + 2)³ ⋮ 9.

Câu 47: Một chiếc thùng không cân nặng 8,7 kg, mỗi lít dầu cân nặng 0,95 kg. Hỏi thùng đó đựng 25 lít dầu cân nặng bao nhiêu kg?

Lời giải:

Số cân nặng của 25 lít dầu là:

25 × 0,95 = 23,75 (kg)

Tổng số cân nặng của thùng đựng 25 lít dầu là:

23,75 + 8,7 = 32,45 (kg).

Đáp số: 32,45 kg.

Câu 48: Thị trấn A cách thị trấn B là 20 km theo đường thẳng. Một người đi xe đạp rời thị trấn A và đi đến thị trấn B với tốc độ 20 km/h. Vào đúng thời điểm đó, người đi xe đạp thứ hai rời thị trấn B đi đến thị trấn A với tốc độ 15 km/h.

a) Hai người đi xe đạp sẽ gặp nhau ở đâu giữa hai thị trấn?

b) Khoảng thời gian từ lúc xuất phát đến khi họ gặp nhau (tính bằng phút)?

Lời giải:

a) Gọi s (km) là khoảng cách từ thị trấn A đến điểm gặp nhau.

Thời gian chuyển động của hai người là như nhau (do xuất phát cùng lúc) nên:

$$\begin{gathered} t_1=t_2\iff \frac{s_1}{v_1}=\frac{s_2}{v_2} \\ \Rightarrow \frac{s}{20}=\frac{20-s}{15}\iff s=\mathrm{11,4} \end{gathered}$$

Từ đây ta có s = 11,4 km.

Vậy hai người đi xe đạp sẽ gặp nhau ở vị trí cách thị trấn A là 11,4 km.

b) Thời gian từ lúc xuất phát đến lúc gặp nhau:

$t=\frac{s}{v}=\frac{\mathrm{11,4}}{20}=\mathrm{0,57}$ (giờ) = 34,2 (phút).

Câu 49: Tìm m để y = 2x³ − mx² + 2x đồng biến trên (−2; 0).

Lời giải:

Ta có:

$y\text{'}=f\text{'}\left(x\right)=6x^2-2mx+2$ (1)

Đề hàm số đồng biến trên (− 2; 0) $\iff f\left(x\right)\ge 0;\forall x\in (-2;0)$

$$\begin{gathered} \iff 6x^2+2\ge 2mx \\ \iff \frac{3x^2+1}{x}\le m \end{gathered}$$

$\iff m\ge \max \left(\frac{3x^2+1}{x}\right)$ với $x\in (-2;0)$

Xét $g\left(x\right)=\frac{3x^2+1}{x}\Rightarrow g\text{'}\left(x\right)=\frac{3x^2-1}{x^2}=0$

$$\begin{gathered} \Rightarrow x=-\frac{1}{\sqrt{3}} \\ \Rightarrow g\left(-\frac{1}{\sqrt{3}}\right)=-2\sqrt{3} \end{gathered}$$

Vậy $m\ge -2\sqrt{3}$ .

Câu 50: Rút gọn phân thức: $\frac{x^3-7x-6}{x^2{\left(x-3\right)}^2+4x{\left(x-3\right)}^2+4{\left(x-3\right)}^2}$ .

Lời giải:

ĐKXĐ: x ≠ 3; x ≠ − 2.