Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 76)

Câu 1: Biểu đồ ven là gì?

Lời giải:

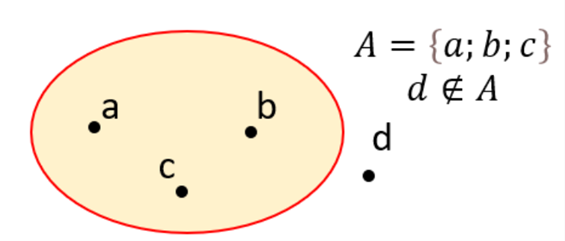
Biểu diễn tập hợp bằng một vòng tròn kín, mỗi phần tử của tập hợp được biểu bằng bởi một chấm trong vòng tròn kín, còn phần tử không thuộc tập hợp biểu diễn bởi một chấm bên ngoài vòng tròn kín (biểu diễn như hình dưới đây). Cách biễu diễn tập hợp như trên gọi là biểu đồ ven.

Câu 2: Phân tích thành nhân tử (bằng kĩ thuật bổ sung hằng đẳng thức): x² + x – 20.

Lời giải:

x² + x – 20

= x² – 4x + 5x – 20

= x(x – 4) + 5(x – 4)

= (x – 4)(x + 5).

Câu 3: Biểu diễn mỗi tập hợp số chẵn lẻ sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó:

a) A = {13; 15; 17; …; 29};

b) B = {22; 24; 26; …; 42};

c) C = {7; 11; 15; 19; 23; 27};

d) D = {4; 9; 16; 25; 36; 49}.

Lời giải:

a) Ta nhận thấy các phần tử của tập hợp A là các số tự nhiên lẻ lớn hơn 12 và nhỏ hơn 30.

Theo cách chỉ ra tính chất đặc trưng, ta viết:

A = {x | x là số tự nhiên lẻ, 12 < x < 30}.

b) Ta nhận thấy các phần tử của tập hợp B là các số tự nhiên chẵn lớn hơn hoặc bằng 22 và nhỏ hơn hoặc bằng 42.

Theo cách chỉ ra tính chất đặc trưng, ta viết:

B = {x|x là số tự nhiên chẵn, 22 ≤ x ≤ 42}.

c) Cách 1:

Ta có:

7 = 4.1 + 3; 11 = 4.2 + 3; 15 = 4.3 + 3; 19 = 4.4 + 3; 23 = 4.5 + 3; 27 = 4.6 + 3.

Ta nhận thấy các số trên đều có dạng 4.x + 3 với x ∈ {1,2,3,4,5,6} .

Theo cách chỉ ra tính chất đặc trưng, ta viết:

C = {4x + 3| x là số tự nhiên, 0 < x < 7}.

Cách 2:

Ta nhận thấy các phần tử trong tập hợp C là các số tự nhiên lẻ và cách nhau 4 đơn vị.

C = {xk| xk là số tự nhiên lẻ, xk+1 – xk = 4,k ∈ N }.

d) Ta thấy các phần tử của tập hợp D là các số chính phương lớn hơn 3 và nhỏ hơn 50.

Theo cách chỉ ra tính chất đặc trưng, ta viết:

D = {x| x là số chính phương, 3 < x < 50}.

Câu 4: Tính giá trị của các phép tính sau:

a) 19345 : 53

b) 2632 : 28

c) 3358 : 46

Lời giải:

a) 19345 : 53 = 365

b) 2632 : 28 = 94

c) 3358 : 46 = 73

Câu 5: a) Không tính tổng A, biết A = 2⁰ + 2¹ + 2² + 2³ + … + 2⁶⁰. Chứng tỏ A chia hết cho 7.

b) Tìm x biết 2x = a + 1 với a là số liền sau của số nhỏ nhất có 2 chữ số.

Lời giải:

a) A = 2⁰ + 2¹ + 2² + 2³ + … + 2⁶⁰

A = (1 + 2¹ + 2²) + (2³ + 2⁴ + 2⁵) + … + (2⁵⁸ + 2⁵⁹ + 2⁶⁰)

A = 7 + 2³ (1 + 2¹ + 2²) + … + 2⁵⁸ (1 + 2¹ + 2²)

A = 7 (1 + 2³ + … + 2⁵⁸)

Vì 7 ⋮ 7 nên 7 (1 + 2³ + … + 2⁵⁸) ⋮ 7

Vậy A ⋮ 7

b) Số nhỏ nhất có 2 chữ số là 10. Nên số liền sau nó là 11.

Khi đó: 2x = 11 + 1 = 12

⇔ x = 12 : 2

⇔ x = 6.

Vậy x = 6.

Câu 6: Cho a + b + c = 0 và a² + b² + c² = 14. Tính a⁴ + b⁴ + c⁴.

Lời giải:

a + b + c = 0

⇔ (a + b + c)² = 0

⇔ a² + b² + c² + 2(ab + bc + ca) = 0

⇔ ab + bc + ca = –7.

Bình phương 2 vế ta có:

(ab + bc + ca)² = 49

⇔ a²b² + b²c² + a²c² + 2abc (a + b + c) = 49

⇔ a²b² + b²c² + a²c² = 49.

Lại có:

a² + b² + c² = 14

⇔ (a² + b² + c²)² = 14² = 196

⇔ a⁴ + b⁴ + c⁴ + 2(a²b² + b²c² + a²c²) = 196

⇔ a⁴ + b⁴ + c⁴ + 2 . 49 = 196

⇔ a⁴ + b⁴ + c⁴ = 196 – 98

⇔ a⁴ + b⁴ + c⁴ = 98.

Vậy a⁴ + b⁴ + c⁴ = 98.

Câu 7: Mỗi khu đất hình chữ nhật có diện tích là 324 m² và chiều rộng là 12 m. Tính chu vi khu đất đó.

Lời giải:

Chiều dài khu đất là:

324 : 12 = 27 (m)

Chu vi khu đất là:

(27 + 12) . 2 = 78 (m).

Đáp số: 78 m.

Câu 8: Nhà bác Hà có 85 con gà và vịt. Sau khi bác bán đi 15 con gà và mua thêm 7 con vịt thì số vịt nhiều hơn số gà là 9 con. Hỏi lúc đầu mỗi loại có bao nhiêu con ?

Lời giải:

Tổng số gà và vịt sau khi bán và mua thêm là:

85 – 15 + 7 = 77 (con)

Lúc đầu, số con vịt là:

(77 + 9) : 2 – 7 = 36 (con)

Lúc đầu số con gà là:

85 – 36 = 49 (con).

Câu 9: Sau khi bớt ở số bị trừ đi 478 và thêm vào số trừ 235 thì hiệu hai số mới là 2084. Hỏi hiệu của hai số ban đầu là bao nhiêu?

Lời giải:

Sau khi bớt đi ở số bị trừ đi 478 và thêm vào số trừ 235 thì hiệu hai số mới là 2084.

Vậy hiệu của hai số ban đầu là:

2084 + 478 + 235 = 2797

Đáp số: 2797.

Câu 10: Trung bình cộng tuổi của bố mẹ và hoa là 30. Nếu không tính tuổi của bố thì trung bình cộng tuổi của mẹ và Hoa là 24. Hỏi tuổi của bố là bao nhiêu?

Lời giải:

Tổng số tuổi của bố, mẹ và Hoa cộng lại là:

30 . 3 = 90 (tuổi)

Tổng số tuổi của mẹ và Hoa cộng lại là:

24 . 2 = 48 (tuổi)

Tuổi bố hiện nay là:

90 – 48 = 42 (tuổi)

Đáp số: 42 tuổi

Câu 11: Tìm x biết x – 36 : 18 = 12.

Lời giải:

x – 36 : 18 = 12

x – 2 = 12

x = 12 + 2

x = 14.

Vậy x = 14.

Câu 12: Tìm số nguyên tố p để: 2p² + 1 cũng là số nguyên tố.

Lời giải:

Với p = 2, ta có: 2p² + 1 = 9 (loại vì không là số nguyên tố)

Với p = 3, ta có: 2p² + 1 = 19 (thỏa mãn)

Với p > 3, vì p là số nguyên tố nên p có dạng p = 3k + 1 hoặc p = 3k + 2.

+ Nếu p = 3k + 1 thì 2p² + 1 = 2(3k + 1)² + 1 = 18k² + 12k + 3 ⋮ 3

Suy ra: loại vì không là số nguyên tố

+ Nếu p = 3k + 2 thì 2p² + 1 = 2(3k + 2)² + 1 = 18k² + 24k + 9 ⋮ 3

Suy ra: loại vì không là số nguyên tố

Vậy p = 3.

Câu 13: Phân tích đa thức thành nhân tử: 40a³b³c³ + 12a³b⁴c² – 20a⁴b⁵c.

Lời giải:

40a³b³c³ + 12a³b⁴c² – 20a⁴b⁵c

= 4a³b³c (10c² + 3bc – 5ab²).

Câu 14: Tìm x biết: [(6x – 72) : 2 – 84] . 4 = 24⁵ : 24⁴.

Lời giải:

[(6x – 72) : 2 – 84] . 4 = 24⁵ : 24⁴

[(6x – 72) : 2 – 84] . 4 = 24

(6x – 72) : 2 – 84 = 24 : 4

(6x – 72) : 2 – 84 = 6

(6x – 72) : 2 = 90

6x – 72 = 180

6x = 252

x = 252 : 6

x = 42

Vậy x = 42.

Câu 15: Chia 10 cái bánh vào trong một số hộp sao cho mỗi hộp có số bánh bằng nhau và phải nhiều hơn 1, ít hơn 10. Hỏi cần ít nhất bao nhiêu hộp?

Lời giải:

Số hộp chia hết cho 10 là:

10 = 1 × 10 = 2 × 5

Vì mỗi hộp cần số bánh nhiều hơn 1 và ít hơn 10 nên số hộp cần là 2 hộp để mỗi hộp bánh có 5 cái bánh.

Vậy cần 2 hộp bánh.

Câu 16: Chứng minh với mọi số nguyên dương n thì n² + n + 1 không chia hết cho 9.

Lời giải:

Ta có: n² + n + 1 = (n – 1)(n + 2) + 3.

Giả sử n² + n + 1 chia hết cho 9

Khi đó (n – 1)(n + 2) + 3 chia hết cho 9 (1)

⇒ (n – 1)(n + 2) + 3 chia hết cho 3

Mà n + 2 – (n – 1) = 3 chia hết cho 3

n + 2 và n – 1 đều chia hết cho 3. Do đó: (n – 1)(n + 2) chia hết cho 9. (2)

Từ (1) và (2), suy ra 3 chia hết cho 9 (vô lý)

Vậy điều giả sử là sai.

Vậy với mọi số nguyên dương n thì n² + n + 1 không chia hết cho 9.

Câu 17: Có 5 người ăn trong 8 ngày hết 20kg rau. Hỏi 7 người ăn trong 5 ngày hết bao nhiêu kg rau?

Lời giải:

5 người trong 1 ngày ăn hết:

20 : 8 = 2,5 (kg rau)

1 người trong 1 ngày ăn hết:

2,5 : 5 = 0,5 (kg rau)

7 người trong 1 ngày ăn hết:

0,5 × 7 = 3,5 (kg rau)

7 người trong 5 ngày ăn hết:

3,5 × 5 = 17,5 (kg rau).

Câu 18: Có bao nhiêu cách sắp xếp các chữ cái của từ ACTIVE sao cho 2 chữ V, E luôn luôn đứng cạnh nhau?

Lời giải:

Ta thấy: VE là cụm từ 2 chữ cái. Mà từ ACTIVE có 6 chữ cái nên VE có đến 5 chỗ đứng.

(Ví dụ ACTIVE, VE có chỗ đứng ở cuối từ)

Trong mỗi lần VE chọn một chỗ đứng, 4 chữ cái còn lại sẽ thay phiên nhau mà chọn chỗ đứng.

Vì vậy, mỗi lần VE chọn một chỗ đứng, số cách để sắp xếp 4 chữ còn lại là:  

4 . 3 . 2 . 1 = 24 (cách)

Do VE có thể đứng ở 5 chỗ nên số cách xếp các chữ cái của ACTIVE là:    

24 . 5 = 120 (cách)

Đáp số: 120 cách.

Câu 19: Năm nay, tổng số tuổi của hai mẹ con là 44 tuổi, mẹ hơn con 28 tuổi. Tính tuổi hiện nay của mỗi người?

Lời giải:

Số tuổi hiện nay của mẹ là:

(44 + 28) : 2 = 36 ( tuổi )

Số tuổi hiện nay của con là

44 – 36 = 8 ( tuổi )

Đáp số: Mẹ: 36 tuổi; Con: 8 tuổi.

Câu 20: Có bao nhiêu số có 2 chữ số đều chia hết cho cả 2 và 3?

Lời giải:

Vì các số đó vừa chia hết cho 2 vừa chia hết cho 3

⇒ Khoảng cách giữa các số đó chính là BCNN(2; 3) = 6

Số lớn nhất có 2 chữ số chia hết cho 2 và 3 là 96

Số bé nhất có 2 chữ số chia hết cho 2 và 3 là 12

Khoảng cách giữa 2 số vừa chia hết cho 2 và 3 là: 6

Vậy số lượng số có 2 chữ số chia hết cho 2 và 3 là:

( 96 – 12 ) : 6 + 1 = 15 (số)

Đáp số: 15 số.

Câu 21: Có bao nhiêu số có 2 chữ số đều chia hết cho 3?

Lời giải:

Số có 2 chữ số nhỏ nhất chia hết cho 3 là: 12

Số có 2 chữ số lớn nhất chia hết cho 3 là: 99

Có số số có 2 chữ số chia hết cho 3 là:

 (99 – 12) : 3 + 1 = 30 (số)

Đáp số: 30 số.

Câu 22: Trong một trang trại có một số gà và thỏ. Số gà nhiều hơn số thỏ là 12 con. Chúng có tổng cộng 228 cái chân. Hỏi trang trại đó có bao nhiêu con gà?

Lời giải:

Gọi số gà là x (con) và số thỏ là y (con)

Số gà gấp đôi số thỏ nên x = 2y (1)

Tổng số chân gà và chân thỏ là 96 chân, trong đó gà 2 chân thỏ 4 chân nên ta có

2x + 4y = 96(2)

Ta thay (1) vào (2) được: 2 . 2y + 4y = 96 ⇒ y = 12

Vậy số thỏ là 12 con.

Vậy số gà là:

12 . 2 = 24 (con).

Câu 23: Tìm số tự nhiên n nhỏ nhất biết khi chia cho 11; 17; 29 thì số dư lần lượt là 6; 12; 24.

Lời giải:

n chia 11 dư 6, chia 17 dư 12, chia 29 dư 24

⇒ n chia 11; 17; 29 đều thiếu 5.

⇒ n + 5 chia hết cho 11; 17; 29

Vì n nhỏ nhất ⇒ n + 5 là BCNN(11; 17; 29)

Vì 11; 17; 29 nguyên tố cùng nhau

⇒ n + 5 = BCNN(11; 17; 29) = 11 . 17 . 29 = 5423

Vậy n = 5423 – 5 = 5418.

Câu 24: Tính tổng S = 1 – 2 + 3 – 4 +... + 99 – 100.

Lời giải:

S = 1 – 2 + 3 – 4 +... + 99 – 100

S = (–1) + (–1) + … +(–1)

Vì S có 100 số hạng nên sẽ chia thành 50 cặp

Vậy S = 50 . (–1) = –50.

Câu 25: Tổng hai số là 79. Nếu gấp thừa số 1 lên 4 lần , gấp thừa số 2 lên 7 lần thì được tổng mới là 475. Tìm hai số đó.

Lời giải:

Gọi 2 số cần tìm là a và b

Ta có:

a + b = 79 ⇒ a = 79 – b (1)

4a + 7b = 475(2)

Thế (1) vào (2), ta được:

4 . (79 – b) + 7b = 475

⇔ 316 – 4b + 7b = 475

⇔ 3b = 159

⇔ b = 53

⇒ a = 79 – 53 = 26

Vậy hai số cần tìm là 26 và 53.

Câu 26: Một tàu hỏa cần chở 620 hành khách. Biết rằng mỗi toa có 12 khoang, mỗi khoang có 8 chỗ ngồi. Số toa ít nhất để chở hết số hành khách trên là bao nhiêu?

Lời giải:

Mỗi toa có số chỗ ngồi là:

12 × 8 = 96 (chỗ)

Số toa ít nhất để chở hết số hành khách trên là:

620 : 96 ≈ 6,45 (toa)

Vậy cần ít nhất là 7 toa để chở hết 620 hành khách.

Câu 27: Một người rào xung quanh một mảnh đất hình chữ nhật có chiều dài 28 m, chiều rộng 15m hết 43 cái cọc. Hỏi người đó rào xung quanh khu đất hình vuông có cạnh 25 m hết bao nhiêu cái cọc?

Lời giải:

Chu vi mảnh đất là:

(28 + 15) × 2 = 86 (m)

Khoảng cách giữa những cái cọc là:

86 : 43 = 2 (m )

Chu vi mảnh đất hình vuông là:

25 × 4 = 100 (m)

Cần số cái cọc để đóng xung quanh khu đất là:

100 : 2 = 50 (cái)

Đáp số: 50 cái cọc.

Câu 28: Người ta xây dựng rào xung quanh một cái hồ hình chữ nhật có chiều dài 45m, chiều rộng kém chiều dài 23,5m, bức tường cao 1,6m. Cứ mỗi mét vuông tiêu tốn hết 40000 đồng. Hỏi xây bức tường rào đó hết tất cả bao nhiêu tiền?

Lời giải:

Chiều rộng cái hồ đó là:

45 − 23,5 = 21,5 (m).

Diện tích bức tường rào đó được xây lên là:   

(45 + 21,5) × 2 × 1,6 = 212,8 (m²)

Số tiền dùng để xây bức tường rào đó là: 

40000 × 212,8 = 8512000 (đồng)

Đáp số: 8512000 đồng.

Câu 29: Trung bình cộng của 5 số là 162. Số thứ năm gấp đôi số thứ tư, số thứ tư bằng trung bình cộng của 3 số đầu tiên. Tìm số thứ năm và số thứ tư.

Lời giải:

Tổng 5 số là: 

162 × 5 = 810

Số thứ 5 là:

810 : (1 + 2 + 3) × 2 = 270

Số thứ 4 là:  

810 : (1 + 2 + 3) × 1 = 135

Đáp số: Số thứ 5: 270; Số thứ tư: 135.

Câu 30: Tổng A = 10¹² + 1 có chia hết cho 3 hay không? Vì sao?

Lời giải:

A = 10¹² + 1 = 1000000000000 + 1 = 1000000000001.

Ta có tổng các chữ số là: 1 + 0 + 0 + 0 + … + 1 = 2.

Vì 2 không chia hết cho 3 nên 10¹² + 1 không chia hết cho 3.

Câu 31: Chứng minh n³ + 20n chia hết cho 48 với mọi số n là số tự nhiên chẵn.

Lời giải:

Giả sử n = 2k (k là số tự nhiên)

n³ + 20n = (2k)³ + 20 . 2k = 8k³ + 40k = 8k(k² + 5)

Ta thấy 8 ⋮ 8 nên 8k(k² + 5) ⋮ 8 (1)

+ Nếu k chẵn thì k ⋮ 2 ⇒ k(k² + 5) ⋮ 2

+ Nếu k lẻ thì k² lẻ ⇒ k² + 5 chẵn ⇒ k(k² + 5) ⋮ 2

Vậy k(k² + 5) ⋮ 2 (2)

+ Nếu k ⋮ 3 thì k(k² + 5) ⋮ 3

+ Nếu k chia 3 dư 1 thì k² + 5 = (3l + 1)² + 5 = 9l² + 6l + 6 ⋮ 3 (với l là số tự nhiên)

+ Nếu k chia 3 dư 2 thì k² + 5 = (3l + 2)² + 5 = 9l² + 12l + 9 ⋮ 3 (với l là số tự nhiên).

Vậy k(k² + 5) ⋮ 3 (3)

Từ (1), (2) và (3) suy ra: 8k(k² + 5) ⋮ 40.

Vậy n³ + 20n chia hết cho 48.

Câu 32: Tuổi con kém tuổi cha 30 tuổi, biết tuổi cha hiện nay là 33 tuổi. Hỏi sau bao lâu thì tuổi của cha là gấp đôi tuổi con?

Lời giải:

Hiệu số tuổi của cha và con là: 30 tuổi

Vì hiệu số tuổi không thay đổi theo thời gian nên khi tuổi cha gấp đôi tuổi con thì hiệu số tuổi giữa cha và con vẫn là 30 tuổi.

Tuổi cha lúc tuổi cha gấp đôi tuổi con là:

30 : (2 – 1) × 2 = 60 (tuổi)

Vậy sau số năm đến khi tuổi cha gấp đôi tuổi con là:

60 – 33 = 27 (năm).

Đáp số: 27 năm.

Câu 33: Bội chung nhỏ nhất của hai số là 45. Một trong hai số đó là 5. Hãy tìm số còn lại.

Lời giải:

Gọi số cần tìm là x

Ta có: BCNN(x, 5) = 45 

Mà 45 = 5 . 9 = 5 . 3² 

5 = 5¹ và 5 là số nguyên tố

Nên x và 5 phải là hai số nguyên tố cùng nhau, mà bội chung nhỏ nhất của hai số nguyên tố cùng nhau chính bằng tích của hai số đó. 

Do đó x = 3² = 9.  

Vậy số cần tìm là 9.

Câu 34: Có 10 người thợ dự định làm xong công việc trong 12 ngày. Nếu người ta muốn làm xong công việc đó trong 8 ngày thì phải cần bao nhiêu người?

Lời giải:

Nếu muốn làm công việc đó trong 1 ngày thì cần số người thợ là:

10 × 12 = 120 (người thợ).

Nếu muốn làm công việc đó trong 8 ngày thì cần số người thợ là:

120 : 8 = 15 (người thợ).

Đáp số: 15 người.

Câu 35: 75% của 15 bằng bao nhiêu?

Lời giải:

75% của 15 bằng:

75% . 15 = 11,25.

Vậy 75% của 15 bằng 11,25.

Câu 36: Cho 31 số nguyên trong đó tổng của 5 số bất kì là 1 số dương. Chứng minh rằng tổng của 31 số nguyên đó là 1 số dương.

Lời giải:

Trong các số đã cho ít nhất có 1 số dương vì nếu trái lại tất cả đều là số âm thì tổng của 5 số bất kỳ trong chúng sẽ là số âm trái với giả thiết.

Tách riêng số dương đó còn 30 số chia làm 6 nhóm. Theo đề bài tổng các số của mỗi nhóm đều là số dương nên tổng của 6 nhóm đều là số dương và do đó tổng của 31 số đã cho đều là số dương.

Câu 37: Chứng minh rằng 7n + 10 và 5n + 7 là hai số nguyên tố cùng nhau (n ∈ ℕ).

Lời giải:

ƯCLN(7n + 10; 5n + 7) = d

Ta có: 7n + 10 ⋮ d và 5n + 7 ⋮ d

Suy ra: 5 (7n + 10) – 7(5n + 7) ⋮ d

⇔ 1 ⋮ d hay d = 1

Vậy 7n +10 và 5n + 7 là hai số nguyên tố cùng nhau (n ∈ ℕ).

Câu 38: Chứng minh rằng 2n³ + 3n² + n chia hết cho 6 với mọi số nguyên n.

Lời giải:

2n³ + 3n² + n

= n (2n² + 3n + 1)

= n (2n² +2n + n + 1)

= n [2n (n + 1) + (n + 1)]

= n (n + 1) (2n + 1)

= n (n + 1) (2n – 2 + 3)

= n (n + 1) (2n – 2) + 3n (n + 1)

= 2n (n + 1) (n – 1) + 3n (n + 1)

Ta thấy: n – 1; n và n + 1 là 3 số nguyên liên tiếp nên tích của chúng chia hết cho 3.

Vì 2 ⋮ 2 nên 2n (n + 1) (n – 1) ⋮ 2

Vậy 2n (n + 1) (n – 1) ⋮ 6. (1)

Lại có: 3 ⋮ 3 nên 3n (n + 1) ⋮ 3

Mà n, n + 1 là 2 số nguyên liên tiếp nên n (n + 1) ⋮ 2

Vậy 3n (n + 1) ⋮ 6. (2)

Từ (1) và (2) suy ra: 2n (n + 1) (n – 1) + 3n (n + 1) ⋮ 6

Vậy 2n³ + 3n² + n ⋮ 6.

Câu 39: Một trường tổ chức cho khoảng từ 700 đến 800 học sinh đi tham quan bằng ô tô. Tính số học sinh đi tham quan, biết rằng nếu xếp 40 người hay 45 người lên một xe đều vừa vặn. Nếu xếp 40 người thì cần bao nhiêu xe?

Lời giải:

Gọi số học sinh của trường là x (học sinh) (x ∈ ℕ, 700 < x < 800).

Số học sinh có thể xếp 40 người hoặc 45 người lên 1 xe nên x là BC(40; 45).

Ta có: 40 = 2³ . 5

45 = 3² . 5

⇒ BCNN (40; 45) = 2³ . 3² . 5 = 360 ⇒ BC(40; 45) = {360; 720; 1080;.....}

Mà 700 < x < 800 ⇒ x = 720

Vậy để xếp 40 người 1 xe thì cần số xe là: 720 : 40 = 18 (xe).

Câu 40: Khu đất hình chữ nhật có chu vi 900m biết chiều dài bằng trung bình cộng của nửa chu vi và chiều rộng. Tìm diện tích khu đất?

Lời giải:

Nửa chu vi khu đất là:

900 : 2 = 450 (m).

Chiều rộng khu đất là:

450 : (2 + 1) = 150 (m)

Chiều dài khu đất là:

450 – 150 = 300 (m)

Diện tích khu đất là:

300 × 150 = 45000 (m²).

Đáp số: 45 000 m².

Câu 41: 1 công trường dự trữ lương thực đủ cho 1200 người ăn trong 35 ngày. Có một số người đến thêm nên số lương thực đó chỉ đủ ăn trong 25 ngày. Tính số người đến thêm?

Lời giải:

Tổng số lương thực đủ cho 1200 người ăn trong 35 ngày là:

1200 × 35 = 42000 (lương thực)

Số người ăn trong 25 ngày là:

42000 : 25 = 1680 (người)

Số người đến thêm là:

1680 – 1200 = 480 (người).

Đáp số: 480 người.

Câu 42: Năm nay cha 43 tuổi và con 12 tuổi. Sau bao nhiêu năm nữa cha gấp đôi tuổi con?

Lời giải:

Hiệu số tuổi của cha và con là :

43 – 12 = 31 (tuổi)

Vì hiệu số tuổi không thay đổi theo thời gian nên khi tuổi cha gấp đôi tuổi con thì hiệu số tuổi giữa cha và con vẫn là 31 tuổi.

Tuổi cha lúc tuổi cha gấp đôi tuổi con là :

31 : (2 – 1) × 2 = 62 (tuổi)

Vậy sau số năm đến khi tuổi cha gấp đôi tuổi con là :

62 – 43 = 19 (năm).

Đáp số: 19 năm.

Câu 43: Tìm 2 số lẻ có trung bình cộng bằng 63, biết rằng giữa chúng có 7 số lẻ nữa.

Lời giải:

Tổng 2 số là:

63 × 2 = 126

Hiệu 2 số là :

7 × 2 + 2 = 16

Số bé là :

(126 – 16) : 2 = 55

Số lớn là :

55 + 16 = 71 

Đáp số: 55 và 71.

Câu 44: Tìm hiệu hai số lẻ biết giữa chúng có 5 số lẻ khác nhau.

Lời giải:

Mỗi số lẻ cách nhau 2 đơn vị.

Mà giữa hai số lẻ này có 5 số lẻ khác nhau, do đó khoảng cách giữa 2 số lẻ này là 6 khoảng.

Vậy hiệu giữa 2 số lẻ đó là:

6 . 2 = 12.

Đáp số: 12.

Câu 45: Cho 10 số tự nhiên bất kỳ: a₁, a₂, ....., a₁₀. Chứng minh rằng thế nào cũng có một số hoặc tổng một số các số liên tiếp nhau trong dãy trên chia hết cho 10.

Lời giải:

Ta lập dãy số như sau:

Đặt B₁ = a₁

B₂ = a₁ + a₂

B_3­ = a₁ + a₂ + a₃

….

B₁₀ = a₁ + a₂ + a₃ + … + a₁₀

Nếu tồn tại B_i (i = 1, 2, 3, …, 10) nào đó chia hết cho 10 thì bài toán được chứng minh

Nếu không tồn tại B_i thì:

Ta đem B_i chia cho 10 sẽ được 10 số dư (các số dư từ 1 đến 9), Theo nguyên tắc Dirichlet, phải có ít nhất 2 số dư bằng nhau.

Các số B_m – B_n chia hết cho 10 (m > n)

Vậy thế nào cũng có một số hoặc tổng một số các số liên tiếp nhau trong dãy trên chia hết cho 10.

Câu 46: Cho dãy số 1, 2, 3, 4, ... x. Hãy tìm x để số chữ số của dãy gấp 2 lần số các số của dãy.

Lời giải:

Nếu dãy số chỉ gồm các chữ số có hai chữ số thì sẽ có số chữ số nhiều gấp đôi số các số. Song vì dãy số có 9 số chỉ có 1 chữ số (là 1, 2, 3, 4, 5, 6, 7, 8, 9) nên nó cũng phải có 9 chữ số có 3 chữ số để bù vào đó cho đủ mức trung bình mỗi số có hai chữ số.

9 số có 3 chữ số là : 100, 101, 102, 103, …., 108.

Vậy x = 108 (dãy số là 1, 2, 3, 4,…, 108)

Đáp số: x = 108.

Câu 47: Phân tích ra các thừa số nguyên tố của 148.

Lời giải:

148 = 4 . 37 = 2² . 37.

Câu 48: Giữa hai số chẵn có tất cả 8 số lẻ. Vậy hiệu của chúng bằng bao nhiêu?

Lời giải:

8 số lẻ cách nhau là:

7 . 2  = 14 (đơn vị)

Hiệu của hai số chẵn là:

14 + 1+ 1 = 16 (đơn vị).

Câu 49: Tính diện tích hình chữ nhật biết chiều dài gấp đôi chiều rộng. Nếu tăng chiều dài thêm 5m thì diện tích sẽ tăng thêm 130m.

Lời giải:

Gọi chiều rộng là a thì chiều dài là 2a (m)

Ta có:

(2a + 5) . a = 2a . a + 130

⇔ 2a² + 5a = 2a² + 130

⇔ 5a = 130

⇔ a = 130 : 5

⇔ a = 26.

Suy ra chiều rộng hình chữ nhật là 26 m.

Chiều dài hình chữ nhật là:

26 . 2 = 52 (m).

Diện tích hình chữ nhật là:

52 . 26 = 1352 (m²).

Câu 50: Đổi các đơn vị sau: 60g = ... kg; 2,5 tạ = ... g

Lời giải:

1kg = 1000 g hay 1g = 0,001 kg

Do đó, 60g = 0,06 kg.

1 tạ = 1000000 g.

Do đó, 2,5 tạ = 2500000 g.