Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 110)

Minh Nguyệt Ngày: 05-12-2024 Tổng hợp kiến thức

266

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 110)

263. Cho A = $2^{9} + 2^{99}$ . CMR A chia hết cho 100

Phương pháp giải:

Chứng minh A chia hết cho 4 và 25.

Kết luận.

Lời giải:

Một số có hai chữ số tận cùng bằng 25 $⋮$ 25. Một số $⋮$ 4 và 25 thì $⋮$ 100( 4 và 25 nguyên tố cùng nhau)

Mặt khác: $(2^{10}) + 1 ⋮ 25$ và $2^{9} + 2^{99} ⋮ 4$

Ta có:

$2^{9} - 2^{99} = (2^{9} + 2^{19}) - (2^{19} + 2^{29}) + (2^{29} + 2^{39}) - . . . + . . . - (2^{79} + 2^{89}) + (2^{89} + 2^{99})$

$= (1 + 2^{10}) \cdot (2^{9} - 2^{19} + 2^{29} - 2^{39} + . . . . + 2^{99})$
$\Rightarrow 2^{9} + 2^{99} ⋮ 25$

$\Rightarrow 2^{9} + 2^{99} ⋮ 100$

304. Tìm số có 2 chữ số. Nếu cùng viết thêm chữ số N vào bên trái và bên phải thì số đó tăng 21 lần. Tìm số đã cho.

Phương pháp giải:

Gọi số cần tìm là $ab$ (có hai chữ số) với $a \neq 0$ .

Viết thêm chữ số $N$ vào bên trái và bên phải của số $ab$ , ta sẽ được một số mới.

Thiết lập phương trình dựa trên điều kiện của bài toán và giải để tìm số $ab$ .

Lời giải:

Gọi số cần tìm là ab (a khác 0,a;b <10,a;b là chữ số)

Nếu viết thêm chữ số 1 vào đằng trước ta có số 1ab

Ta có: ab.21 = 1ab

ab.21 = 100+ab

ab.20=100

ab=100:20

ab=05

Vậy số cần tìm là 05

374. Cho tập hợp $A = {x \in R ∣ 1 : ∣ x - 3 ∣ > 3}$ ; $B = {x \in R ∣ ∣ x - 2 ∣ < 2}$ . Khi đó tập X = A giao B có bao nhiêu phần tử

Phương pháp giải:

Giải từng tập hợp: A và B và tìm khoảng cách của A và B.

Tìm giao giữa A và B và kết luận.

Lời giải:

$A = {x \in R ∣ 1 : ∣ x - 3 ∣ > 3}$

$1 : ∣ x - 3 ∣ > 3 \Leftrightarrow ∣ x - 3 ∣ > \frac{1}{3}$

$T H_{1} : x \geq 3 x - 3 > \frac{1}{3} \Leftrightarrow x > \frac{10}{3} (t m)$

$T H_{2} : x < 3 x - 3 > - \frac{1}{3} \Leftrightarrow x > \frac{8}{3} (t m)$

Vậy $A = {x \in R ∣ x > \frac{10}{3}}$ $\Rightarrow A = (- \infty; \frac{10}{3})$ (1)

$B = {x \in R ∣ ∣ x - 2 ∣ < 2}$

$∣ x - 2 ∣ < 2$

$T H_{1} : x \geq 2 x - 2 < 2 \Leftrightarrow x < 4 (t m) \Rightarrow 2 \leq x < 4$

$T H_{2} : x < 2 x - 2 < - 2 \Leftrightarrow x < 0 (t m) \Rightarrow x < 0$

Vậy $B = [2; 4)$ (2)

Từ (1),(2) $\Rightarrow X = A \cap B = [2; \frac{10}{3})$

Do cả 2 tập A và B đều có $x \in R$ nên số phần từ của tập X nằm trong khoảng từ 2 đến 10/3.

Lý thuyết Giao của hai tập hợp:

Tập hợp các phần tử thuộc cả hai tập hợp A và B được gọi là giao của hai tập hợp A và B, kí hiệu là A ∩ B.

Xác định hợp và giao của hai tập hợp (cách giải + bài tập)

Để xác định giao của hai tập hợp A và B, ta làm như sau:

Liệt kê các phần tử của hai tập hợp, những phần tử thuộc cả hai tập hợp là giao của hai tập hợp đó.

* Đối với các tập hợp được cho dưới dạng một đoạn, khoảng, nửa khoảng, ta có thể xác định giao của hai tập hợp như sau:

+ Bước 1. Biểu diễn A, Biểu diễn B trên cùng 1 trục số.

+ Bước 2. Lấy phần không bị gạch chéo.

+ Bước 3. Kiểm tra các điểm đặc biệt để tránh nhầm lẫn.

Nhận xét:

√ Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) – n(A ∩ B).

√ Nếu A và B không có phần tử chung, tức A ∩ B = ∅, thì n(A∪ B) = n(A) + n(B).

349. Tìm x biết $\frac{x - 1}{2011} + \frac{x - 2}{2010} - \frac{x - 3}{2009} = \frac{x - 4}{2008}$

Phương pháp giải:

Đưa các phân số về dạng có chung tử số

Kết hợp các phân số

Nhóm $x - 2012$ ra ngoài và xét điều kiện khi $x - 2012 = 0$

Lời giải:

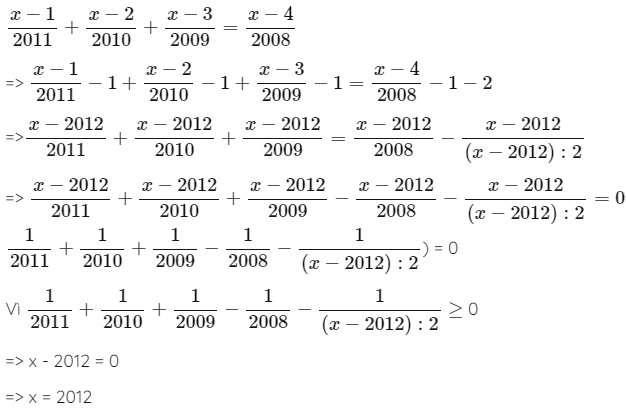
Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 107) (ảnh 1)

462. So sánh 2³⁰ và 3²⁰

Phương pháp giải:

Dạng này là dạng đưa về cùng số mũ để so sánh.

Lời giải:

Ta có : $2^{30} = {(2^{10})}^{20} = 102 4^{20}$

Vì : $1024 > 3$ nên $102 4^{20} > 3^{20}$

$\Rightarrow 2^{30} > 3^{20}$

472. Tìm x sao cho $\frac{- 3 \sqrt{x}}{2 \sqrt{x} + 4}$

Phương pháp giải:

Xác định điều kiện xác định của biểu thức.

Biến đổi bất phương trình.

Phân tích dấu biểu thức.

Kết hợp với điều kiện xác định.

Lời giải:

ĐKXĐ: $x \geq 0$

$\frac{- 3 \sqrt{x}}{2 \sqrt{x} + 4} < - 1 \Leftrightarrow \frac{- 3 \sqrt{x}}{2 \sqrt{x} + 4} + 1 < 0$

$\Leftrightarrow \frac{- 3 \sqrt{x} + 2 \sqrt{x} + 4}{2 \sqrt{x} + 4} < 0$

$\Leftrightarrow \frac{4 - \sqrt{x}}{2 \sqrt{x} + 4} < 0$

$\Rightarrow 4 - \sqrt{x} < 0$ (vì $2 \sqrt{x} + 4 > 0 \forall x \geq 0$ )

$\Leftrightarrow \sqrt{x} > 4$

$\Leftrightarrow x > 16$

Kết hợp với điều kiện xác định của $x$ , ta được: $x > 16$

473. Tính: $(1 - \frac{1}{2}) (1 - \frac{1}{3}) (1 - \frac{1}{4}) .. . (1 - \frac{1}{2024})$

Phương pháp giải:

Rút gọn từng thừa số.

Phân tích và rút gọn tích phân số.

Lời giải:

$(1 - \frac{1}{2}) (1 - \frac{1}{3}) (1 - \frac{1}{4}) . . . (1 - \frac{1}{2024})$

$= \frac{1}{2} \cdot \frac{2}{3} \cdot \frac{3}{4} \cdot \frac{4}{5} \cdot . . . \cdot \frac{2023}{2024}$

$= \frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot . . . \cdot 2023}{2 \cdot 3 \cdot 4 \cdot 5 \cdot . . . \cdot 2024}$

$= \frac{1}{2024}$

474. Tìm x, biết:

a) $(4 x^{4} + 3 x^{3}) : (- x^{3}) + (15 x^{2} + 6 x) : 3 x = 0$

b) $(x^{2} - \frac{1}{2} x) : (2 x) - (3 x - 1)^{2} : (3 x - 1) = 0$

Phương pháp giải:

Rút gọn từng biểu thức.

Giải phương trình.

Lời giải:

a. $(4 x^{4} + 3 x^{3}) : (- x^{3}) + (15 x^{2} + 6 x) : 3 x = 0$

$\Rightarrow - 4 x - 3 + (5 x + 2) = 0$

$\Rightarrow - 4 x - 3 + 5 x + 2 = 0$

$\Rightarrow x - 1 = 0$

$\Rightarrow x = 1$
b. $(x^{2} - \frac{1}{2} x) : (2 x) - (3 x - 1)^{2} : (3 x - 1) = 0$

$\Rightarrow \frac{x}{2} - \frac{1}{4} - (3 x - 1) = 0$

$\Rightarrow \frac{x}{2} - \frac{1}{4} - 3 x + 1 = 0$

$\Rightarrow \frac{- 5}{2} x + \frac{3}{4} = 0$

$\Rightarrow \frac{- 5}{2} x = \frac{- 3}{4}$

$\Rightarrow x = \frac{3}{10}$

475. Tìm ƯCLN rồi tìm ƯC của 36 và 120

Phương pháp giải:

Phân tích ra thừa số nguyên tố.

Tìm ƯCLN:

Lấy tích các thừa số chung với số mũ nhỏ nhất

Tìm ƯC

Lời giải:

$36 = 2^{2} \cdot 3^{2} 120 = 2^{3} \cdot 3 \cdot 5 Ư C L N (36, 120) = 2^{2} \cdot 3 = 12 Ư C (36, 120) = Ư (12) = {. . .}$

=> ƯC(36;120) = Ư(12) = { 1; 2; 3; 4; 6; 12}

476. Viết số thích hợp vào chỗ chấm :

420 giây = ................phút

Phương pháp giải:

Đổi: 1 giây = $\frac{1}{60}$ phút

1 phút = 60 giây

Lời giải:

Ta có: $\frac{420}{60} = 7$

nên: 420 giây = 7 phút

477. So sánh 2²⁷ và 3¹⁸

Phương pháp giải:

Viết lại biểu thức so sánh: Đưa về cùng số mũ để so sánh.

So sánh cơ số và kết luận.

Lời giải:

$2^{27}$ và $3^{18}$

$2^{27} = 2^{3.9} = {(2^{3})}^{9} = 8^{9}$

$3^{18} = 3^{2.9} = {(3^{2})}^{9} = 9^{9}$

Vì: $8^{9} < 9^{9} \Rightarrow 2^{27} < 3^{18}$

478. Tìm x biết:

a. 60 - 3 ( x - 2 ) = 51

b. 4x - 20 = 2⁵ : 2²

Phương pháp giải:

Với phương trình a):

Chuyển vế và thực hiện phép tính để tìm $3(x - 2)$ , sau đó rút gọn để tìm $x$ .

Với phương trình b):

Thực hiện phép chia , sau đó giải phương trình tuyến tính thông qua chuyển vế và rút $x$ .

Lời giải:

a) 60 - 3.(x - 2) = 51

3.(x - 2) = 60 - 51

3.(x - 2) = 9

x - 2 = 9 : 3

x - 2 = 3

x = 3 + 2

x = 5

b) 4x - 20 = 2⁵ : 2²

4x - 20 = 2³

4x - 20 = 8

4x = 8 + 20

4x = 28

x = 28 : 4

x = 7

479. Cho 3 đường thẳng AM, BN, CD đồng quy tại điểm O. Tìm các góc bằng nhau (không kể góc bẹt). Giải thích.

Phương pháp giải:

Định nghĩa góc giữa các đường thẳng:

Các góc được tạo bởi 3 đường thẳng đồng quy tại $O$ : $\angle AMO, \angle BNO, \angle CDO$ và các góc bù của chúng.

Sử dụng tính chất đồng quy:

Tổng các góc tại điểm $O$ là $360^\circ$ . Các cặp góc đối đỉnh tại $O$ bằng nhau.

Kết luận các góc bằng nhau:

Xác định các cặp góc đối đỉnh (không kể góc bẹt)

Lời giải:

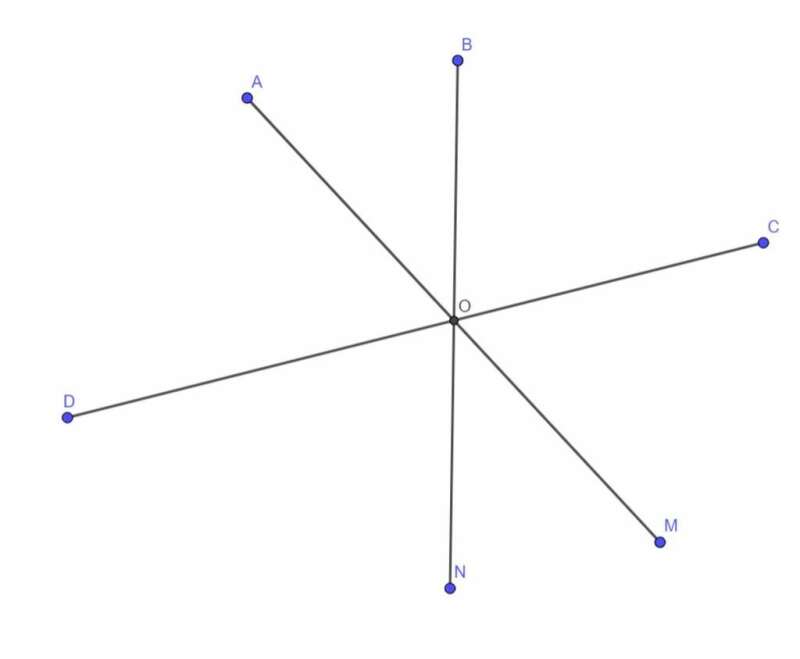
Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 110) (ảnh 1)

Các góc bằng nhau do đối đỉnh:

$\hat{A O B} - \hat{N O M} \hat{A O C} - \hat{M O D} \hat{A O N} - \hat{M O B} \hat{A O D} - \hat{M O C} \hat{B O C} - \hat{N O D} \hat{B O D} - \hat{N O C} .$

480. Tìm số nguyên x :

a) 46-x =-21+(-87)

b) x-96=(443-x)-15

c) (-x+281+534)= 499+(x-48)

d) -(754+x)=(x-12-741) -23

Phương pháp giải:

Bước 1: Rút gọn các biểu thức ở cả hai vế để đơn giản hóa phương trình.

Bước 2: Chuyển tất cả các hạng tử chứa $x$ về một vế, các hằng số về vế còn lại.

Bước 3: Giải phương trình để tìm giá trị của $x$ .

Lời giải:

a, 46 - x = (-21) + (-87)

46 - x = -108

x = 46 - (-108)

x = 154

Vậy x = 154

b, x - 96 = (443 - x) - 15

2x = 443 - 15 + 96

2x = 524

x = 524 : 2

x = 262

c, (-x + 281 + 534) = 499 + (x - 48)

-2x = 499 - 281 - 534 - 48

-2x = -364

x = 182

d, -(754 + x) = (x - 12 - 741) - 23

-2x = 754 - 12- 741 - 23

-2x = -22

x = 11

481. Chứng minh bđt Cô-si với 3 số ko âm a,b,c: $\frac{a + b + c}{3} \geq \sqrt[3]{a b c}$

Phương pháp giải:

Dựa vào BĐT giữa trung bình nhân và trung bình cộng

Chứng ming BDT $\frac{a + b + c + d}{4} \geq \sqrt[4]{a b c d}$

Áp dụng các BDT trên để chứng mình yêu cầu bài toán

Lời giải:

Ta có BĐT giữa trung bình nhân và trung bình cộng : $\frac{a + b}{2} \geq \sqrt{a b};$ $\frac{c + d}{2} \geq \sqrt{c d}$
Trước hết ta chứng minh BĐT $\frac{a + b + c + d}{4} \geq \sqrt[4]{a b c d}$

Áp dụng BĐT trên , ta được : $\frac{a + b + c + d}{2} = \frac{a + b}{2} + \frac{c + d}{2} \geq 2 \sqrt{\frac{(a + b)}{2} . \frac{(c + d)}{2}} \geq 2 \sqrt{\sqrt{a b} . \sqrt{c d}} = 2 \sqrt[4]{a b c d}$

$\Leftrightarrow \frac{a + b + c + d}{4} \geq \sqrt[4]{a b c d}$ (*)

Đặt $d = \frac{a + b + c}{3}$ thì $a + b + c = 3 d$ (**)

Từ (*) và (**) ta có : $\frac{3 d + d}{4} \geq \sqrt[4]{a b c d} \Leftrightarrow d \geq \sqrt[4]{a b c d} \Leftrightarrow d^{4} \geq a b c d \Leftrightarrow d^{3} \geq a b c \Leftrightarrow d \geq \sqrt[3]{a b c}$