Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 92)

Đề bài. Cho A = (m; m + 3) và B (2; 6m + 1). Tìm m để A ∩ B = ∅.

Lời giải:

Để A ∩ B = ∅ thì $\left[\begin{array}{l}2\ge m+3\\ 6m+1\le m\end{array}\right.$ ⇔ $\left[\begin{array}{l}m\ge -1\\ 5m+1\le 0\end{array}\right.$ ⇔ $\left[\begin{array}{l}m\ge -1\\ m\le -\frac{1}{5}\end{array}\right.$

⇔ $-1\le m\le -\frac{1}{5}$

Vậy $-1\le m\le -\frac{1}{5}$ thì A ∩ B = ∅.

Đề bài. Cho hai tập hợp khác rỗng A = [m – 1; 5) và B = [-3; 2m + 1]. Tìm m để A ⊂ B.

Lời giải:

Điều kiện tồn tại nửa đoạn và đoạn: thì $\left\{\begin{array}{l}m-1<5\\ -3\le 2m+1\end{array}\right.$ ⇔ $\left\{\begin{array}{l}m<6\\ m\ge -2\end{array}\right.$ ⇔ -2 ≤ m < 6.

Để A ⊂ B thì $\left\{\begin{array}{l}m-1>-3\\ 2m+1\ge 5\end{array}\right.$ ⇔ m > 2

Kết hợp điều kiện ta được: 2 < m < 6.

Đề bài. Cho tam giác ABC cân tại A, đường cao AD, K là trung điểm của AD. Gọi I là hình chiếu của điểm D trên CK. Chứng minh rằng $\widehat{AIB}=90°$.

Lời giải:

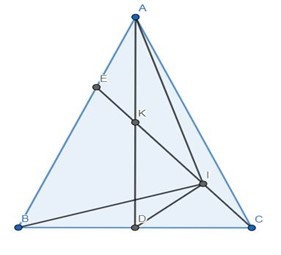
Gọi E là giao điểm của CK và AB.

Tam giác CDK vuông tại D có đường cao DI nên KD² = KI . KC

Mà KD = KA nên KA² = KI . KC

⇒ $\frac{KA}{KI}=\frac{KC}{DA}$

Xét ΔKAI và ΔKCA có:

$\frac{KA}{KI}=\frac{KC}{DA}$

$\widehat{K}$ chung

⇒ ΔKAI ∽ ΔKCA (c.g.c)

⇒ $\widehat{KIA}=\widehat{KAC}$

mà $\widehat{KAC}=\widehat{KAE}$(do AK là tia phân giác $\widehat{BAC}$) nên $\widehat{KIA}=\widehat{KAE}$

Từ đó suy ra: ΔEAK ∽ ΔEIA (g.g) ⇒ $\widehat{EKA}=\widehat{EAI}$

Hay $\widehat{DKC}=\widehat{BAI}$

Hơn nữa $\widehat{DKC}=\widehat{IDC}$(cùng phụ với $\widehat{DCK}$) nên $\widehat{DKC}=\widehat{BAI}$

⇒ Tứ giác IABD nội tiếp (góc ngoài bằng góc trong đối diện)

⇒$\widehat{AIB}=\widehat{ADB}$

Mà $\widehat{ADB}=90°$

Nên $\widehat{AIB}=90°$.

Đề bài. Cho tam giác ABC có 3 góc nhọn. Chứng minh sinA + cosA + sinC + cosC > 2.

Lời giải:

Xét (sinA + cosA)² = sin²A + cos²A + 2sinAcosA = 1 + 2sinAcosA > 1

(do tam giác ABC có 3 góc nhọn nên sinA, cosA > 0)

Suy ra: (sinA + cosA)² > 1

⇒ sinA + cosA > 1

Chứng minh tương tự: sinC + cos C > 1

Khi đó: sinA + cosA + sinC + cosC > 2.

Đề bài. Cho tam giác nhọn ABC. Chứng minh

$S_{ABC}=\frac{1}{2}.BC.BA.\sin \widehat{B}=\frac{1}{2}.AB.AC.\sin \widehat{A}=\frac{1}{2}.CA.CB.\sin \widehat{C}$.

Lời giải:

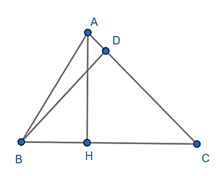
Kẻ đường cao AH, BD

$S_{ABC}=\frac{1}{2}.AH.BC$ (*)

Mà tam giác AHB vuông tại H nên: $\sin \widehat{B}=\frac{AH}{AB}\Rightarrow AH=AB.\sin \widehat{B}$

Khi đó: $S_{ABC}=\frac{1}{2}.AB.BC.\sin \widehat{B}$

Tương tự: Trong tam giác AHC vuông tại H có: $\sin \widehat{C}=\frac{AH}{AC}\Rightarrow AH=AC.\sin \widehat{C}$

Khi đó: $S_{ABC}=\frac{1}{2}.AC.BC.\sin \widehat{C}$

Ta có: $S_{ABC}=\frac{1}{2}.BD.AC$ (*)

Trong tam giác BAD vuông tại D có: $\sin A=\frac{BD}{AB}\Rightarrow BD=AB.\sin \widehat{A}$

Thay vào (*) có: $S_{ABC}=\frac{1}{2}.BD.AC=\frac{1}{2}.AB.AC.\sin \widehat{A}$.

Đề bài. Hình vẽ cho biết tam giác ABC vuông tại A, MN // BC, AB = 24cm, AM = 16cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC, BC.

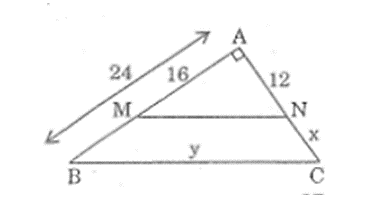
Lời giải:

Trong ΔABC, ta có: MN // BC (gt)

Suy ra: $\frac{AM}{AB}=\frac{AN}{AC}$

Suy ra: $AC=\frac{AB.AN}{AN}=\frac{24.12}{16}=18\left(cm\right)$

Vậy NC = AC – AN = 18 – 12 = 6(cm)

Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:

MN² = AM² + AN² = 16² + 12² = 400

MN = 20cm

Trong ΔABC, ta có: MN // BC (gt)

Suy ra: $\frac{AM}{AB}=\frac{MN}{BC}$(hệ quả định lý Ta-lét)

Vậy:$BC=\frac{MN.AB}{AM}=\frac{20.24}{16}=30\left(cm\right)$.

Đề bài. Cho hình thoi ABCD có $\widehat{A}=60°$. Trên AB, AC lấy điểm M, N sao cho BM = CN. Chứng minh rằng MDN là tam giác đều.

Lời giải:

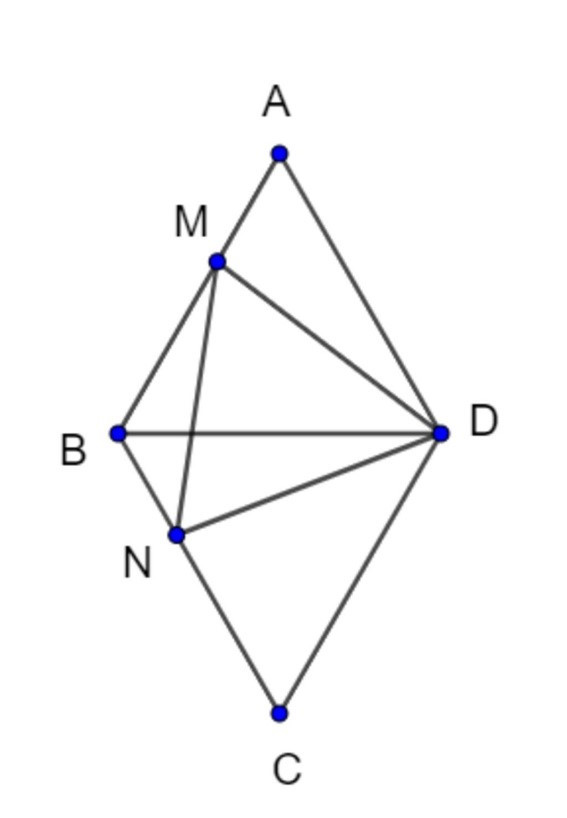
Ta có: MB + NB = AB = MB + AM

Suy ra: NB = AM

Tương tự: BM = NC

Ta có: $\widehat{A}=60°$⇒ $\widehat{D}=180°-60°=120°$

Vì ABCD là hình thoi nên $\widehat{D}=\widehat{B}=120°$

Xét tam giác BMD và tam giác CND có:

BM = NC

$\widehat{D}=\widehat{B}=120°$

Chung BD

⇒ ∆BMD = ∆CND (c.g.c)

⇒ MD = ND (1); $\widehat{BDM}=\widehat{CDN}$

Lại có: $\widehat{BDN}+\widehat{CDN}=60°$

⇒ $\widehat{BDN}+\widehat{BDM}=60°$ hay $\widehat{MDN}=60°$

Vậy tam giác MDN là tam giác đều.

Đề bài. Cho hình bình hành ABCD có $\widehat{A}=120°$. Tia phân giác của $\widehat{D}$ qua trung điểm I của AB. Kẻ AH vuông góc với DC. Chứng minh rằng:

a) AB = 2AD.

b) DI = 2AH.

c) AC vuông góc với AD.

Lời giải:

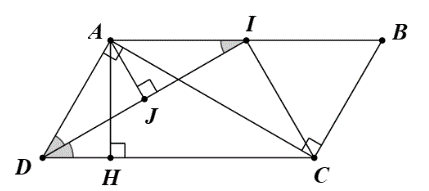
a) Hình bình hành ABCD có $\widehat{BAD},\widehat{ADC}$ ở vị trí trong cùng phía.

Suy ra $\widehat{ADC}=180°-\widehat{BAD}=60°$

Khi đó $\widehat{ADI}=\widehat{IDC}=\frac{\widehat{ADC}}{2}=30°$(do DI là tia phân giác của $\widehat{ADC}$).

Mà $\widehat{AID}=\widehat{IDC}$(cặp góc so le trong).

Vì vậy $\widehat{AID}=\widehat{ADI}$

Suy ra tam giác ADI cân tại A.

Do đó AD = AI.

Mà AB = 2AI (I là trung điểm của AB).

Vậy AB = 2AD (điều phải chứng minh).

b) Gọi J là trung điểm của DI.

Tam giác ADI có AJ là đường trung tuyến.

Suy ra AJ vừa là đường phân giác, vừa là đường cao của tam giác ADI.

Khi đó $\widehat{JAI}=\widehat{DAJ}=\frac{\widehat{DAI}}{2}=60°$

Xét ∆AJD và ∆DHA, có:

$\widehat{AJD}=\widehat{DHA}=90°$

AD là cạnh chung;

$\widehat{DAJ}=\widehat{ADH}=60°$

Do đó ∆AJD = ∆DHA (cạnh huyền – góc nhọn).

Suy ra DJ = AH (cặp cạnh tương ứng).

Mà DI = 2DJ (J là trung điểm của DI).

Vậy DI = 2AH (điều phải chứng minh).

c) Ta có BI = BC$\left(=\frac{1}{2}AB\right)$

Suy ra tam giác IBC cân tại B.

Mà $\widehat{IBC}=\widehat{ADC}=60°$

Do đó tam giác IBC đều.

Vì vậy IC = IB = IA.

Khi đó tam giác ABC vuông tại C hay $\widehat{ACB}=90°$

Suy ra $\widehat{DAC}=\widehat{ACB}=90°$

Vậy AD ⊥ AC (điều phải chứng minh).

Đề bài. Cho B = 1 + 5 + 5² + … + 5¹⁰⁰. Hỏi 4B + 1 có phải số chính phương không?

Lời giải:

B = 1 + 5 + 5² + … + 5¹⁰⁰

5B = 5 + 5² + 5³ + … + 5¹⁰¹

⇒ 5B – B = (5 + 5² + 5³ + … + 5¹⁰¹) – (1 + 5 + 5² + … + 5¹⁰⁰)

4B = 5¹⁰¹ – 1

4B + 1 = 5¹⁰¹

Mà 5¹⁰¹ không thể viết được dưới dạng số chính phương n²

Do đó 4B + 1 không phải số chính phương.

Đề bài. Cho 3 số dương x, y, z có tích bằng 144. Tìm GTNN của biểu thức

$P=\left(x+\frac{1}{4}y\right)\left(y+\frac{1}{9}z\right)\left(x+\frac{1}{36}z\right)$.

Lời giải:

Áp dụng bất đẳng thức Cauchy, ta có:

$P=\left(x+\frac{1}{4}y\right)\left(y+\frac{1}{9}z\right)\left(x+\frac{1}{36}z\right)$

$\ge 2\sqrt{x.\frac{1}{4}y}.2\sqrt{y.\frac{1}{9}z}.2\sqrt{x.\frac{1}{36}z}=8\sqrt{x^2{y}^2{z}^2.\frac{1}{4}.\frac{1}{9}.\frac{1}{36}}=32$

Vậy GTNN của P là 32 khi:

$\left\{\begin{array}{l}x=\frac{1}{4}y\\ y=\frac{1}{9}z\\ x=\frac{1}{36}z\\ xyz=144\end{array}\right.\iff \left\{\begin{array}{l}x=1\\ y=4\\ z=36\end{array}\right.$.

Đề bài. Cho 7 số tự nhiên khác nhau có tổng bằng 100. Chứng minh rằng trong 7 số luôn có 3 số mà tổng của chúng lớn hơn hoặc bằng 50.

Lời giải:

Gọi 7 số tự nhiên khác nhau là a, b, c, d, e, f, g

Giả sử các số theo thứ tự giảm dần a > b > c > d > e > f > g

Ta có: a + b + c + d + e + f + g = 100

Ta sẽ đi chứng minh a + b + c ≥ 50 (*)

Nếu c > 15 thì a + b + c ≥ (c + 2) + (c + 1) + c ≥ 51

Nếu c ≤ 15 thì d + e + f + g ≤ (c – 1) + (c – 2) + (c – 3) + (c – 4) ≤ 50.

Vậy trong trường hợp nào thì (*) cũng đúng vì tổng của 7 số là 100.

Đề bài. Cho biết $\cos \alpha =-\frac{2}{3}$. Tính giá trị của $P=\frac{\cot \alpha +3\tan \alpha }{2\cot \alpha +\tan \alpha }$.

Lời giải:

Ta có: sin²α + cos²α = 1

⇒ sin²α = 1 – cos²α = $1-\frac{4}{9}=\frac{5}{9}$

$P=\frac{\cot \alpha +3\tan \alpha }{2\cot \alpha +\tan \alpha }$

$=\frac{\frac{\cos \alpha }{\sin \alpha }+3\frac{\sin \alpha }{\cos \alpha }}{2\frac{\cos \alpha }{\sin \alpha }+\frac{\sin \alpha }{\cos \alpha }}$

$=\frac{{\cos }^2\alpha +3{\sin }^2\alpha }{2{\cos }^2\alpha +{\sin }^2\alpha }$

$=\frac{{\left(-\frac{2}{3}\right)}^2+3.\frac{5}{9}}{2.{\left(-\frac{2}{3}\right)}^2+\frac{5}{9}}=\frac{19}{13}$.

Đề bài. Với x > 0 cho biểu thức $A=\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1};B=\frac{\sqrt{x}}{x+\sqrt{x}};P=\frac{A}{B}$.

a) Rút gọn và tính giá trị P khi x = 4.

b) So sánh B với 1.

Lời giải:

$A=\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}=\frac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\frac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}=\frac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}$

$B=\frac{\sqrt{x}}{x+\sqrt{x}}=\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}$

$P=\frac{A}{B}=\frac{\frac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}}{\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}}=\frac{x+\sqrt{x}+1}{\sqrt{x}}$

Khi x = 4 thì $P=\frac{4+\sqrt{4}+1}{\sqrt{4}}=\frac{7}{2}$

b) $B=\frac{\sqrt{x}}{x+\sqrt{x}}=\frac{1}{\left(\sqrt{x}+1\right)}$

Ta có: $\sqrt{x}\ge 0\iff \sqrt{x}+1\ge 1\Rightarrow \frac{1}{\sqrt{x}+1}\le \frac{1}{1}=1$

Vậy B < 1.

Đề bài. Cho biểu thức: $A=\frac{1}{\sqrt{x}+1}+\frac{x}{\sqrt{x}-x}$ với x > 0, x khác 1.

a) Rút gọn A

b) Tìm x để A = 2017.

Lời giải:

a) $A=\frac{1}{\sqrt{x}+1}+\frac{x}{\sqrt{x}-x}=\frac{\sqrt{x}-x+x\sqrt{x}+x}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-x\right)}=\frac{\sqrt{x}\left(1+x\right)}{\sqrt{x}\left(1-x\right)}=\frac{1+x}{1-x}$

b) Để A = 2017 ta có: $\frac{1+x}{1-x}=2017$

⇒ 1 + x = 2017(1 – x)

⇔ 1 + x = 2017 – 2017x

⇔ 2018x = 2016

⇔ $x=\frac{2016}{2018}=\frac{1008}{1009}$.

Đề bài. Cho biểu thức $B=\frac{\sqrt{a}}{\sqrt{a}-3}-\frac{3}{\sqrt{a}+3}-\frac{a-2}{a-9}$ với a ≥ 0; a ≠ 9. Rút gọn B.

Lời giải:

Với a ≥ 0; a ≠ 9 ta có:

$B=\frac{\sqrt{a}\left(\sqrt{a}+3\right)}{\left(\sqrt{a}-3\right)\left(\sqrt{a}+3\right)}-\frac{3\left(\sqrt{a}-3\right)}{\left(\sqrt{a}+3\right)\left(\sqrt{a}-3\right)}-\frac{a-2}{\left(\sqrt{a}+3\right)\left(\sqrt{a}-3\right)}$

$B=\frac{a+3\sqrt{a}-3\sqrt{a}+9-a+2}{\left(\sqrt{a}-3\right)\left(\sqrt{a}+3\right)}$

$B=\frac{11}{\left(\sqrt{a}-3\right)\left(\sqrt{a}+3\right)}$

$B=\frac{11}{a-9}$.

Đề bài. Cho biểu thức $P=\frac{3x^2+3x}{\left(x+1\right)\left(2x-6\right)}$.

a) Tìm ĐK để phân thức xác định.

b) Tìm giá trị của x để P = 1.

Lời giải:

a) ĐKXĐ: $\left\{\begin{array}{l}x+1\ne 0\\ 2x-6\ne 0\end{array}\right.\iff \left\{\begin{array}{l}x\ne -1\\ x\ne 3\end{array}\right.$

b) $P=\frac{3x^2+3x}{\left(x+1\right)\left(2x-6\right)}=1$

⇔ $\frac{3x\left(x+1\right)}{\left(x+1\right)\left(2x-6\right)}=1$

⇔ $\frac{3x}{2x-6}=1$

⇔ 3x = 2x – 6

⇔ x = -6

Vậy x = -6 thì P = 1.

Đề bài. Cho biểu thức P = x³ + y³ – 3(x + y) + 1993. Tính giá trị biểu thức P với

$x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}};y=\sqrt[3]{3-2\sqrt{2}}+\sqrt[3]{3+2\sqrt{2}}$.

Lời giải:

$x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}$

⇒ $x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)$

⇒$x^3=18+3x\sqrt[3]{81-80}=18-3x$

$y=\sqrt[3]{3-2\sqrt{2}}+\sqrt[3]{3+2\sqrt{2}}$

⇒ $y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}.\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)$

⇒ $y^3=6+3y\sqrt[3]{9-8}=6+3y$

Suy ra: y³ – 3y = 6

Khi đó: P = x³ + y³ – 3(x + y) + 1993

⇔ P = x³ + y³ – 3x – 3y + 1993 = 18 + 6 + 1993 = 2017

Vậy P = 2017.

Đề bài. Cho biểu thức: $Q=\left(\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}}\right):\left(\frac{\sqrt{x}+1}{\sqrt{x}-2}-\frac{\sqrt{x}+2}{\sqrt{x}-1}\right)$.

a) Rút gọn biểu thức Q với x > 0; x khác 4 và x khác 1.

b) Tìm giá trị của x để Q dương.

Lời giải:

a) $Q=\left(\frac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\frac{x-1-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\right)$

$Q=\left(\frac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\frac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\right)$

$Q=\frac{\sqrt{x}-2}{3\sqrt{x}}$

b) Q > 0 ⇔ $\frac{\sqrt{x}-2}{3\sqrt{x}}>0$ ⇔ $\sqrt{x}-2>0$ ⇔ x > 4

Vậy Q dương khi x > 4.

Đề bài. Cho bốn số nguyên dương phân biệt sao cho tổng của mỗi hai số chia hết cho 2 và tổng của mỗi ba số chia hết cho 3. Tìm giá trị nhỏ nhất của tổng bốn số này?

Lời giải:

Gọi 4 số cần tìm là a, b, c, d (a, b, c,d ∈ ℕ^*; a < b < c < d)

Tổng của mỗi 2 số chia hết cho 2

⇒ a, b, c, d đồng dư với nhau theo môđun 2

Hay a ≡ b ≡ c ≡ d (mod 2)

Tổng của mỗi 3 số chia hết cho 3

⇒ a, b, c, d đồng dư với nhau theo mô đun 3

Hay a ≡ b ≡ c ≡ d(mod 3)

Ta có nếu hai số đồng dư với nhau theo nhiều môđun thì chúng đồng dư với nhau theo môđun là BCNN của các môđun ấy nên: a ≡ b ≡ c ≡ d (mod 6)

Vì cần tìm giá trị nhỏ nhất của 4 số thoả mãn nên ta chọn a là số nguyên dương nhỏ nhất hay a = 1

b = a + 6 = 7

c = b + 6 = 13

d = c + 6 = 19

Vậy 4 số nguyên dương phân biệt nhỏ nhất thoả mãn là 1; 7; 13; 19.

Đề bài. Cho x ∈ ℕ nhưng x ∉ ℕ^* số x là:

A.1

B. Bất kì số tự nhiên nào

C. 0

D. Không tồn tại số x

Lời giải:

Chọn C.

N = {0; 1; 2; 3; 4; ........} ⇒ Tập hợp ℕ bao gồm cả số 0.

ℕ^* = {1; 2; 3; 4; 5; ........} ⇒ Tập hợp ℕ^* không bao gồm số 0.

Đề bài. Cho C = 1 + 3¹ + 3² + … + 3¹¹. Chứng minh rằng C ⋮ 13.

Lời giải:

C = 1 + 3¹ + 3² + … + 3¹¹

C = (1 + 3¹ + 3²) + (3³ + 3⁴ + 3⁵) + … + (3⁹ + 3¹⁰ + 3¹¹)

C = (1 + 3¹ + 3²) + 3³(1 + 3¹ + 3²) + … + 3⁹(1 + 3¹ + 3²)

C = (1 + 3¹ + 3²)(1 + 3³ + … + 3⁹)

C = 13.(1 + 3³ + … + 3⁹) ⋮ 13.

Vậy C ⋮ 13.

Đề bài. Cho hai góc kề bù $\widehat{xOy}$ và $\widehat{yOz}$. Biết $\widehat{xOy}=50°$. Tính số đo góc $\widehat{xOt}$ để tia Ot là tia phân giác của góc $\widehat{yOz}$.

Lời giải:

Ta có: $\widehat{xOy}+\widehat{yOz}=180°$

Suy ra: $\widehat{yOz}=180°-50°=130°$

Để Ot là tia phân giác của góc $\widehat{yOz}$ thì $\widehat{zOt}=\frac{\widehat{yOz}}{2}=65°$

Khi đó theo tính chất cộng góc ta suy ra: $\widehat{xOt}=180°-65°=115°$.

Đề bài. Cho a, b, c là 3 số dương thỏa mãn ab + bc + ca = 3abc.

Chứng minh rằng: $\frac{a}{a^2+bc}+\frac{b}{b^2+ca}+\frac{c}{c^2+ab}\le \frac{3}{2}$.

Lời giải:

Từ điều kiện đề bài ta có: $\frac{ab+bc+ca}{abc}=3\iff \frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3$

Áp dụng hai lần bất đẳng thức Côsi cho hai số dương, ta có:

$a^2+bc\ge 2\sqrt{a^2.bc}=2a\sqrt{bc}$

⇒ $\frac{a}{a^2+bc}\le \frac{a}{2a\sqrt{bc}}=\frac{1}{2\sqrt{bc}}$

$\frac{1}{\sqrt{b}}.\frac{1}{\sqrt{c}}\le \frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}\right)$ ⇒ $\frac{a}{a^2+bc}\le \frac{1}{4}\left(\frac{1}{b}+\frac{1}{c}\right)$

Tương tự ta có: $\frac{b}{b^2+ac}\le \frac{1}{4}\left(\frac{1}{a}+\frac{1}{c}\right)$

$\frac{c}{c^2+ab}\le \frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}\right)$

Suy ra: $\frac{a}{a^2+bc}+\frac{b}{b^2+ca}+\frac{c}{c^2+ab}\le \frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=\frac{3}{2}$.

Đề bài. Cho các số nguyên a, b, c thỏa mãn điều kiện: (a – b)³ + (b – c)³ + (c – a)³ = 378. Tính giá trị của biểu thức .

Lời giải:

(a – b)³ + (b – c)³ + (c – a)³ = 378

⇔ a³ – 3a²b + 3ab² – b³ + b³ – 3b²c + 3bc² – c³ + c³ – 3c²a + 3ac² – c³ = 378

⇔ – 3a²b + 3ab² – 3b²c + 3bc² – 3c²a + 3ac² = 378

⇔ -3(a²b + ab² – b²c + bc² – c²a + ac²) = 378

⇔ -3[a²(b – c) + bc(b – c) – a(b² – c²)] = 378

⇔ -3[(b – c)(a² + bc – a(b + c)] = 378

⇔ (b – c)(a – b)(a – c) = 126

Suy ra: b – c = 3; a – b = 6; a – c = 7.

$A=\left|a-b\right|+\left|b-c\right|+\left|c-a\right|=3+6+7=16$.

Đề bài. Cho các số thực a, b, c thỏa mãn a + b + c = 0. Chứng minh rằng a⁵ + b⁵ + c⁵ chia hết cho 5.

Lời giải:

a⁵ – a = a(a⁴ – 1) = a(a² – 1)(a² + 1)

= a(a² – 1)(a² – 4 + 5)

= a(a² – 1)(a² – 4) + 5a(a² – 1)

= a(a + 1)(a – 1)(a + 2)(a – 2) + 5a(a² – 1) chia hết cho 5.

Vì a – 2, a – 1, a, a + 1, a + 2 là 5 số nguyên liên tiếp nên có một số chia hết cho 5

⇒ a(a + 1)(a – 1)(a + 2)(a – 2) chia hết cho 5

Mặt khác : 5a(a² – 1) chia hết cho 5

Tương tự có b⁵ – b chia hết cho 5, c⁵ – c chia hết cho 5.

Mà a + b + c = 0

Do đó a⁵ + b⁵ + c⁵ = (a⁵ – a) + (b⁵ – b) + (c⁵ – c) chia hết cho 5

Đề bài. Cho các số thực a, b, c thỏa mãn a² + b² + c² = 1.

Tìm GTLN của M = ab + bc + 2ac.

Lời giải:

Ta có: M = ab + bc + 2ac = (a + c)b + 2c

$\le \sqrt{2\left(a^2+c^2\right)b}+a^2+c^2=\sqrt{2\left(1-b^2\right)b}+1-b^2=f\left(b^2\right)$

Với hàm số f(t) = $\sqrt{2\left(1-t\right)t}+1-t,t\in \left[0;1\right]$

Ta có: $f\text{'}\left(t\right)=\frac{1-2t}{\sqrt{2\left(1-t\right)t}}-1=0$

⇔ $t=\frac{3-\sqrt{3}}{6}=t_0$

Từ đó f(t) đồng biến trên ( 0 , t0) và nghịch biến trên (t₀, 1)

Suy ra: $\max f\left(t\right)=f\left(\frac{3-\sqrt{3}}{6}\right)=\frac{\sqrt{3}+1}{2}$ tức là $\max P=\frac{\sqrt{3}+1}{2}$ chẳng hạn $b=\pm \sqrt{t_0}$

Và $a=c=\pm \frac{1}{\sqrt{2}}\sqrt{1-{t_0}^2}$.

Đề bài. Cho các số thực dương a, b, c thỏa mãn a + b + c = 3.

Chứng minh a² + b² + c² + ab + bc + ca ≥ 6.

Lời giải:

P = a² + b² + c² + ab + bc + ca $=\frac{1}{2}{\left(a+b+c\right)}^2+\frac{1}{2}\left(a^2+b^2+c^2\right)$

$P\ge \frac{1}{2}{\left(a+b+c\right)}^2+\frac{1}{6}{\left(a+b+c\right)}^2=6$

Vậy a² + b² + c² + ab + bc + ca ≥ 6

Dấu "=" xảy ra khi a = b = c = 1.

Đề bài. Cho các số thực x, y thỏa mãn 4x² + 2xy + y² = 3.

Tìm GTLN, GTNN của P = x² + 2xy – y².

Lời giải:

Ta có: $\frac{P}{3}=\frac{x^2+2xy-y^2}{4x^2+2xy+y^2}$ (*)

Xét y = 0 thì x² = $\frac{3}{4}\Rightarrow x=\pm \frac{\sqrt{3}}{2}$

Suy ra: $\left[\begin{array}{l}P={\left(\frac{\sqrt{3}}{2}\right)}^2+2.\frac{\sqrt{3}}{2}.0-0^2=\frac{3}{4}\\ P={\left(-\frac{\sqrt{3}}{2}\right)}^2+2.\left(-\frac{\sqrt{3}}{2}.\right)0-0^2=\frac{3}{4}\end{array}\right.$

Xét y khác 0, chia cả (*) cho y² ta được: $\frac{P}{3}=\frac{{\left(\frac{x}{y}\right)}^2+2\frac{x}{y}-1}{4{\left(\frac{x}{y}\right)}^2+2\frac{x}{y}+1}$

Đặt $\frac{x}{y}=a\Rightarrow \frac{P}{3}=\frac{a^2+2a-1}{4a^2+2a+1}$

* Xét $\frac{P}{3}-\left(-2\right)=\frac{a^2+2a-1}{4a^2+2a+1}+2=\frac{{\left(3a+1\right)}^2}{4a^2+2a+1}$

Vì (3a + 1)² ≥ 0 với mọi a nên $\frac{{\left(3a+1\right)}^2}{4a^2+2a+1}\ge 0$

Suy ra: $\frac{P}{3}-\left(-2\right)\ge 0\Rightarrow P\ge -6$

Vậy GTNN của P là -6 khi 3a + 1 = 0 hay a = $\frac{-1}{3}\iff \frac{x}{y}=\frac{-1}{3}\iff -3x=y$

Thay vào 4x² + 2xy + y² = 3, ta được: 7x² = 3

⇔ $\left[\begin{array}{l}x=\frac{\sqrt{21}}{7}\\ x=-\frac{\sqrt{21}}{7}\end{array}\right.\Rightarrow \left[\begin{array}{l}y=\frac{-3\sqrt{21}}{7}\\ y=\frac{3\sqrt{21}}{7}\end{array}\right.$

Vậy GTNN của P là -6 khi (x; y) = $\left(\frac{\sqrt{21}}{7};\frac{-3\sqrt{21}}{7}\right);\left(-\frac{\sqrt{21}}{7};\frac{3\sqrt{21}}{7}\right)$

* Xét $\frac{P}{3}-\frac{1}{3}=\frac{a^2+2a-1}{4a^2+2a+1}-\frac{1}{3}=\frac{-{\left(a-2\right)}^2}{4a^2+2a+1}$

Vì –(a – 2)² ≤ 0 với mọi a nên: $\frac{-{\left(a-2\right)}^2}{4a^2+2a+1}\le 0,\forall a$

Suy ra: $\frac{P}{3}-\frac{1}{3}\le 0\Rightarrow P\le 1$

Vậy GTLN của P là 1 khi a – 2 = 0 hay a = 2.

Khi đó x = 2y

Thay vào 4x² + 2xy + y² = 3, ta được: 21y² = 3

⇔ $\left[\begin{array}{l}y=\frac{1}{\sqrt{7}}\\ y=-\frac{1}{\sqrt{7}}\end{array}\right.\Rightarrow \left[\begin{array}{l}x=\frac{2}{\sqrt{7}}\\ x=-\frac{2}{\sqrt{7}}\end{array}\right.$

Vậy GTLN của P là 1 khi (x; y) = $\left(\frac{2}{\sqrt{7}};\frac{1}{\sqrt{7}}\right);\left(-\frac{2}{\sqrt{7}};-\frac{1}{\sqrt{7}}\right)$.

Đề bài. Cho các số thực x, y thỏa mãn x + y = 1, x³ + y³ = 2.

Tính giá trị của biểu thức M = xy, N = x⁵ + y⁵.

Lời giải:

x³ + y³ = (x + y)(x² – xy + y²) = x² – xy + y² = (x + y)² – 3xy = 1 – 3xy

⇔ 3xy = 1 – 2 = -1

⇔ $xy=-\frac{1}{3}$

Suy ra: $M=xy=-\frac{1}{3}$

Lại có: x² + y² = (x + y)² – 2xy = $1-2\left(-\frac{1}{3}\right)=1+\frac{2}{3}=\frac{5}{3}$

N(x + y) = (x⁵ + y⁵)(x + y) = x⁶ + x⁵y + xy⁵ + y⁶

= (x²)³ + (y²)³ + xy(x⁴ + y⁴)

= (x² + y²)[(x²)² – x²y² + (y²)²] + xy[(x²)² + 2x²y² + (y²)² - 2x²y²]

$=\frac{5}{3}\left[{\left(x^2+y^2\right)}^2-3{\left(xy\right)}^2\right]-\frac{1}{3}\left[{\left(\frac{5}{3}\right)}^2-2.{\left(-\frac{1}{3}\right)}^2\right]$

$=\frac{5}{3}\left[{\left(\frac{5}{3}\right)}^2-3.{\left(-\frac{1}{3}\right)}^2\right]-\frac{1}{3}.\frac{23}{9}$

$=\frac{5}{3}.\frac{22}{9}-\frac{23}{27}=\frac{29}{9}$

Suy ra: N = x⁵ + y⁵ = $\frac{29}{9}$.

Đề bài. cho các tập hợp A = (2; +∞) và B =[m² - 7; +∞) với m > 0. Tìm m để A\B là một khoảng có độ dài bằng 16.

Lời giải:

Để A\B là 1 khoảng có độ dài bằng 16

⇔ $\left\{\begin{array}{l}{m}^2-7>2\\ m^2-7-2=16\end{array}\right.$

⇔ $\left\{\begin{array}{l}{m}^2>9\\ m^2=25\end{array}\right.$

⇔ $\left\{\begin{array}{l}\left[\begin{array}{l}m>3\\ m<-3\end{array}\right.\\ \left[\begin{array}{l}m=5\\ m=-5\end{array}\right.\end{array}\right.$

Vậy m = 5 hoặc m = -5 thỏa mãn điều kiện đề bài.

Đề bài. Cho D = 9 + 9² + 9³ + … + 9²⁰²⁰. Chứng tỏ D là bội của 41.

Lời giải:

D = 9 + 9² + 9³ + … + 9²⁰²⁰

D = (9 + 9² + 9³ + 9⁴) + (9⁵ + 9⁶ + 9⁷ + 9⁸) + … + (9²⁰¹⁷ + 9²⁰¹⁸ + 9²⁰¹⁹ + 9²⁰²⁰)

D = 9.(1 + 9 + 9² + 9³) + 9⁵(1 + 9 + 9² + 9³) + … + 9²⁰¹⁷(1 + 9 + 9² + 9³)

D = (1 + 9 + 9² + 9³)(9 + 9⁵ + … + 9²⁰¹⁷)

D = 820(9 + 9⁵ + … + 9²⁰¹⁷)

D = 41.20.(9 + 9⁵ + … + 9²⁰¹⁷)

Vậy D là bội của 41.

Đề bài. Cho đa thức P(x) với các hệ số nguyên thỏa mãn P(2021).P(2022) = 2023. Chứng minh rằng đa thức P(x) - 2024 không có nghiệm nguyên.

Lời giải:

Giả sử P(x) − 2024 có nghiệm nguyên là a, khi đó: P(x)−2024 = Q(x)(x − a)với Q(x) là đa thức hệ số nguyên

⇒ P(x) = Q(x)(x − a) + 2024

Với x = 2021, thay vào biểu thức trên, ta được: P(2021) = Q(2021)(x − 2021) + 2024

Với x = 2022, thay vào biểu thức trên, ta được : P(2022) = Q(2022)(x − 2022) + 2024

Có P(2021).P(2022) = 2023

⇒ [Q(2021)(x−2021)+2024][Q(2022)(x−2022)+2024] = 2023

⇔Q(2021).Q(2022)(x − 2021)(x − 2022) + 2024Q(2021)(x − 2021) + 2024Q(2022)(x − 2022) + 2024.2024 = 2023

Xét x – 2021 và x – 2022 là 2 số nguyên liên tiếp nên (x – 2021)(x – 2022) chia hết cho 2

Suy ra: Q(2021).Q(2022)(x – 2021)(x – 2022) ⋮ 2

⇒ VT = Q(2021).Q(2022)(x − 2021)(x − 2022) + 2024Q(2021)(x − 2021) + 2024Q(2022)(x − 2022) + 2024.2024 ⋮ 2.

Mà VP = 2023 không chia hết cho 2⇒ Vô lý

⇒ Giả sử trên là vô lý ⇒ Đa thức P(x) − 2024 không có nghiệm nguyên (đpcm)

Vậy đa thức P(x) − 2024 không có nghiệm nguyên.

Đề bài. Cho dãy số: 2; 5; 8; 11; 14; … Tìm số thứ 100 của dãy số trên?

Lời giải:

Ta thấy khoảng cách giữa các số hạng là 3.

Số hạng thứ 100 là:

2 + 3.(100 – 1) = 299.

Đề bài. Cho dãy số: 2; 5; 8; 11; 14; … Tìm số thứ 2024 của dãy số trên?

Lời giải:

Ta thấy khoảng cách giữa các số hạng là 3.

Số hạng thứ 2024 là:

2 + 3.(2024 – 1) = 6071.

Đề bài. Cho cấp số cộng (u_n) và gọi S_n là tổng n số hạng đầu tiên của nó. Biết S₇ = 77, S₁₂ = 192. Tìm số hạng tổng quát u_n của cấp số cộng đó?

Lời giải:

$\left\{\begin{array}{l}{S}_7=77\\ S_{12}=192\end{array}\right.\iff \left\{\begin{array}{l}7u_1+\frac{7.6d}{2}=77\\ 12u_1+\frac{12.11d}{2}=192\end{array}\right.\iff \left\{\begin{array}{l}7u_1+21d=77\\ 12u_1+66d=192\end{array}\right.\iff \left\{\begin{array}{l}{u}_1=5\\ d=2\end{array}\right.$

Khi đó u_n = u₁ + (n – 1)d = 5 + 2(n – 1) = 3 + 2n.

Đề bài. Cho dãy số $u_n=\frac{1}{1.1!}+\frac{1}{2.2!}+\frac{1}{3.3!}+\mathrm{...}+\frac{1}{2013.2013!}$. Chứng minh rằng $u_n<\frac{3}{2}$.

Lời giải:

Ta thấy:$\frac{1}{1.1!}=1;\frac{1}{2.2!}=\frac{1}{4}$

Đặt $P=\frac{1}{3.3!}+\mathrm{...}+\frac{1}{2013.2013!}$

$P=\frac{1}{\mathrm{3.1.2.3}}+\mathrm{...}+\frac{1}{\mathrm{2013.1.2....2013}}$

$P<\frac{1}{\mathrm{1.2.3}}+\mathrm{...}+\frac{1}{\mathrm{2011.2012.2013}}$

$P<\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2.3}+\mathrm{...}+\frac{1}{2011.2012}-\frac{1}{2012.2013}\right)$

$P<\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2012.2013}\right)$

$P<\frac{1}{4}-\frac{1}{\mathrm{2.2012.2013}}<\frac{1}{4}$

Suy ra: $u_n<1+\frac{1}{4}+\frac{1}{4}=\frac{3}{2}$.

Đề bài. Cho dãy số thập phân: 1,1; 2,2; 3,3; ......; 97,9; 99,0.

a) Số hạng thứ 50 của dãy là số nào?

b) Dãy số này có bao nhiêu số hạng?

c) Tính tổng của dãy số trên?

Lời giải:

Khoảng cách giữa 2 số là 1,1.

a) Gọi số hạng thứ 50 là a, ta có:

(a - 1,1) : 1,1 + 1 = 50

(a - 1,1) : 1,1 = 49

a - 1,1 = 49 . 1,1

a = 53,9 + 1,1

a = 55

Vậy số cần tìm là 55.

b) Số số hạng của dãy số là:

(99 - 1,1) : 1,1 + 1 = 90 (số)

c) Tổng dãy số trên là:

(99 + 1,1) . 90 : 2 = 4504,5

Đề bài. Cho dãy số 1,1; 2,2; 3,3; …; 108,9; 110,0

a) Dãy số có bao nhiêu số hạng?

b) Số hạng thứ 30 của dãy là bao nhiêu?

Lời giải:

a) Khoảng cách giữa 2 số là 1,1.

Dãy có số số hạng là:

(110 − 1,1) : 1,1 + 1 = 100

b) Số hạng thứ 30 của dãy là:

(30 – 1).1,1 + 1,1 = 33

Đề bài. Cho điểm A và vectơ $\overrightarrow{a}$ khác 0. Tìm điểm M sao cho $\overrightarrow{AM}$ cùng phương với vectơ $\overrightarrow{a}$.

Lời giải:

Từ A kẻ AM // a, ta được $\overrightarrow{AM}$ cùng phương với $\overrightarrow{a}$

Để cùng hướng thì ngoài điều kiện cùng phương ra, $\overrightarrow{AM}$ phải chỉ cùng hướng với $\overrightarrow{a}$.

Đề bài. Cho đường thẳng (d) có phương trình y = mx + 2. Tính m để khoảng cách từ gốc tọa độ O đến d là $\sqrt{2}$.

Lời giải:

Do m = 0 không thỏa mãn nên ta tiếp tục xét m ≠ 0

Thay y = 0 vào phương trình đường thẳng (d), ta có:

mx + 2 = 0

⇔ mx = -2

⇔ $x=-\frac{2}{m}$

(d) cắt trục hoành tại $A\left(-\frac{2}{m};0\right)$

Thay x = 0 vào phương trình đường thẳng (d), ta có: y = 2

⇒ (d) cắt trục tung tại B(0;2)

Kẻ OH⊥(d) tại H

⇒ Độ dài OH chính là khoảng cách từ O đến đường thẳng d

Ta có: $OA=\left|x_A\right|=\left|\frac{-2}{m}\right|$; $OB=\left|y_B\right|=\left|2\right|=2$

Xét ΔAOB vuông tại O, có: $\frac{1}{O{A}^2}+\frac{1}{O{B}^2}=\frac{1}{O{H}^2}$

⇒ $\frac{m^2}{4}+\frac{1}{4}=\frac{1}{2}$

⇔ m² = 1

⇔ m = ±1 (thoả mãn)

Vậy m = 1 hoặc m = -1.

Đề bài. Cho đường thẳng d song song với mặt phẳng (P). Mệnh đề nào sau đây đúng?

A. Đường thẳng d không có điểm chung với mặt phẳng (P).

B. Đường thẳng d có một điểm chung với mặt phẳng (P).

C. Đường thẳng d có đúng hai điểm chung với mặt phẳng (P).

D. Đường thẳng d có vô số điểm chung với mặt phẳng (P).

Lời giải:

Đáp án A. đường thẳng d không có điểm chung với mặt phẳng (P) vì: d//(P).

Đề bài. Cho đường tròn (O) đường kính AB. Vẽ đường tròn (I) đường kính OA. Bán kính OC của đường tròn (I) cắt đường tròn (I) tại O. Vẽ CH ⊥ AB. Chứng minh tứ giác ACDH là hình thang cân.

Lời giải:

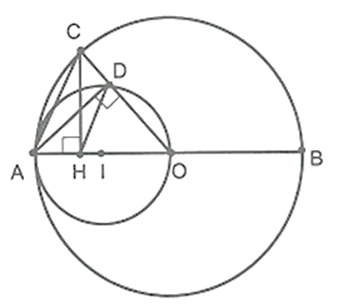
Xét ΔADO và ΔCHO có:

$\widehat{ADO}=\widehat{CHO}=90°$(giả thiết).

$\widehat{AOD}$chung.

OA = OC (bán kính đường tròn (O).

⇒ ΔADO = ΔCHO (cạnh huyền – góc nhọn)

⇒ OH = OD (hai cạnh tương ứng).

⇒ $\frac{OH}{OA}=\frac{OD}{OC}$

⇒ DH // AC (định lí Ta-lét đảo) ⇒ ACDH là hình thang. (1)

Mà $\widehat{OAC}=\widehat{OCA}$ (do ΔAOC cân tại O) (2)

Từ (1) và (2) suy ra ACDH là hình thang cân.

Đề bài. Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc. Gọi I là điểm trên cung AC sao cho khi vẽ tiếp tuyến qua I và cắt DC kéo dài tại M thì IC = CM. Độ dài OM tính theo bán kính là?

Lời giải:

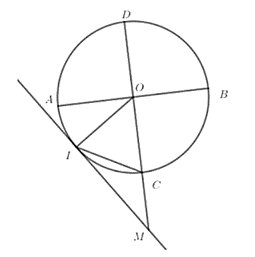
Ta có: $\widehat{CIM}=\frac{1}{2}\widehat{IOC}$ (góc tạo bởi tiếp tuyến và dây cung với góc ở tâm chắn cung IC)

⇒ $\widehat{IOC}=2\widehat{CIM}$

Lại có $\widehat{OCI}=\widehat{CIM}+\widehat{CMI}=2\widehat{CIM}$(do Δ∆CMI cân tại C)

Do đó Δ∆OIC đều (vì $\widehat{OIC}=\widehat{IOC}=\widehat{OCI}$)

⇒ $\widehat{IOM}=60°$

+) Xét Δ∆OIM vuông tại I có:

cos$\widehat{IOM}=\cos 60°=\frac{OI}{OM}=\frac{R}{OM}=\frac{1}{2}$

⇒ OM = 2R.

Đề bài. Cho ba điểm A, B, C trên đường tròn (O). Tiếp tuyến tại A cắt dây cung CB kéo dài tại điểm M. Chứng minh: $\widehat{MAC}=\widehat{ABC}-\widehat{ACB}$.

Lời giải:

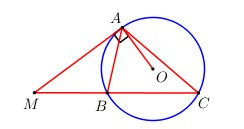
Xét tam giác ABM ta có $\widehat{ABC}=\widehat{MAC}+\widehat{MAB}$ (góc ngoài bằng tổng hai góc trong không kề với nó).

Mà $\widehat{MAB}=\widehat{ACB}$(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AB)

Suy ra: $\widehat{ABC}=\widehat{MAC}+\widehat{ACB}$ hay $\widehat{MAC}=\widehat{ABC}-\widehat{ACB}$.

Đề bài. Cho đường tròn tâm O. Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB, nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng:

a) Hai cung nhỏ CF và BD bằng nhau.

b) Hai cung nhỏ BF và DE bằng nhau.

c) DE = BF.

Lời giải:

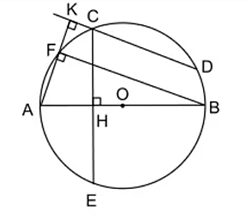
a) Tam giác AFB nội tiếp đường tròn (O) có AB là đường kính nên tam giác AFB vuông tại F

⇒ $\widehat{AFB}=90°$

⇒ BF ⊥ AK tại F

Mà AK vuông góc với CD (gt)

⇒ BF // CD

⇒ $\stackrel{⏜}{BD}=\stackrel{⏜}{CF}$(hai cung chắn giữa hai dây song song thì bằng nhau).

b) Đường kính AB vuông góc với CE tại H nên H là trung điểm của CE

Do đó, C đối xứng với E qua trục AB

⇒ BC = BE

⇒ $\stackrel{⏜}{BC}=\stackrel{⏜}{BE}$ (hai dây cung bằng nhau căng hai cung bằng nhau)

Mà $\stackrel{⏜}{BD}=\stackrel{⏜}{CF}$(cmt)

⇒ $\stackrel{⏜}{BC}+\stackrel{⏜}{CF}=\stackrel{⏜}{BE}+\stackrel{⏜}{BD}\iff \stackrel{⏜}{BF}=\stackrel{⏜}{DE}$

c) Có: $\stackrel{⏜}{BF}=\stackrel{⏜}{DE}$ (cmt)

Do đó, BF = DE (hai cung bằng nhau căng hai dây bằng nhau).

Đề bài. Cho $0<\alpha <\frac{\pi }{2}$. Khẳng định nào sau đây đúng?

A. sin(α – π) ≥ 0

B. sin(α – π) ≤ 0

C. sin(α – π) > 0

D. sin(α – π) < 0

Lời giải:

Chọn D

Ta có: $0<\alpha <\frac{\pi }{2}\Rightarrow -\pi <\alpha -\pi <-\frac{\pi }{2}$

Do đó; điểm cuối cung α – π thuộc góc phần tư thứ 3 nên sin(α – π) < 0.

Đề bài. Cho $\widehat{BAC}$ = 70°, $\widehat{ACB}$ = 55°, tia Ax là tia phân giác của $\widehat{yAC}$.

a) Tính số đo của $\widehat{yAC}$, $\widehat{yAx}$.

b) Chứng minh: Ax // BC.

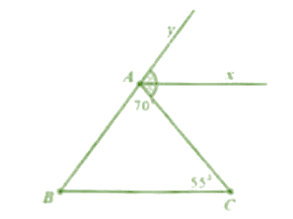
Lời giải:

a) Ta có: $\widehat{yAC}+\widehat{CAB}=180°$

⇒ $\widehat{yAC}+70°=180°$

⇒ $\widehat{yAC}=110°$

Mà Ax là tia phân giác của góc $\widehat{yAC}$ nên $\widehat{yAx}=\widehat{xAC}=\frac{1}{2}\widehat{yAC}=\frac{110°}{2}=55°$

b) Ta có: $\widehat{ACB}=\widehat{xAC}=55°$

Mà góc trên là 2 góc so le trong nên Ax // BC.

Đề bài. Cho góc nhọn xOy. Trên cạnh Ox lấy hai điểm A, B sao cho A nằm giữa O và B. Trên cạnh Oy lấy hai điểm C, D sao cho C nằm giữa O và D.

Chứng minh rằng: AB + CD < AD + BC.

Lời giải:

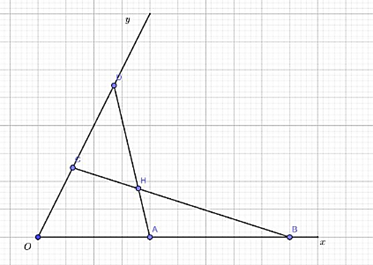
Giả sử: AB ∩ CD = {H}

Xét ΔCHD: CD < DH + CH (Bất đẳng thức Δ)

Xét ΔAHB: AB < AH + BH (Bất đẳng thức Δ)

⇒ AB + CD < (DH + CH) + (AH + BH)

⇒ AB + CD < DH + CH + AH + BH

⇒ AB + CD < (DH + AH) + (CH + BH)

⇒ AB + CD < AD + CB.

Đề bài. Cho góc $\widehat{xOy}=80°$Vẽ tia Oz là tia đối của tia Ox. Vẽ tia Om là tia phân giác của góc $\widehat{zOy}$.

a) Tính góc $\widehat{zOm}$?

b) Vẽ tia On là tia đối của tia Om. Tia Ox có là tia phân giác của góc $\widehat{yOn}$ không? Vì sao?

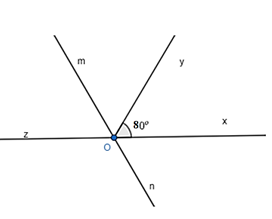
Lời giải:

Vì Oz và Ox là hai tia đối nhau nên $\widehat{zOx}=180°$

Do đó: $\widehat{zOy}$và $\widehat{xOy}$ là 2 góc kề bù

$\widehat{zOy}+\widehat{xOy}=180°$

Suy ra: $\widehat{zOy}=180°-\widehat{xOy}=180°-80°=100°$

Mà Om là tia phân giác $\widehat{zOy}$ nên ta có: $\widehat{zOm}=\widehat{mOy}=\frac{\widehat{zOy}}{2}=\frac{100°}{2}=50°$

Vậy $\widehat{zOm}=50°$

b) $\widehat{zOm}=\widehat{xOn}=50°$(2 góc đối đỉnh)

Ta thấy: $\widehat{xOn}=50°;\widehat{xOy}=80°$nên Ox không là tia phân giác của $\widehat{yOn}$.

Đề bài. cho hai đường thẳng a và b cắt đường thẳng c. Để có một cặp góc so le trong bằng nhau thì điều gì sau đây không thể xảy ra?

A. Các cặp góc đồng vị bằng nhau.

B. Các cặp góc so le ngoài bằng nhau.

C. Các cặp góc trong cùng phía bằng nhau.

D. Các cặp góc trong cùng phía bù nhau.

Lời giải:

Để có 1 cặp góc so le trong bằng nhau thì suy ra a song song với b

⇒ các cặp góc trong cùng phía bù nhau, đồng vị bằng nhau, so le ngoài bằng nhau

Nên đáp án C không thể xảy ra.

Đề bài. Cho hai đường tròn (O; R) và (O'; R') (R > R') tiếp xúc ngoài nhau tại A. Qua A kẻ hai cát tuyến BD và CE (B, C ∈ (O')); D, E ∈ (O)). Chứng minh: $\widehat{ABC}=\widehat{ADE}$.

Lời giải:

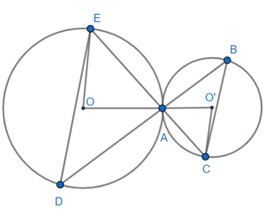
Xét tam giác O'AC có O'A = O'C = R' nên tam giác O'AC cân tại O'

Suy ra: $\widehat{CO\text{'}A}=180°-2\widehat{O\text{'}AC}$

Tương tự: tam giác OAE cân tại O nên: $\widehat{EOA}=180°-2\widehat{OAE}$

Mà $\widehat{O\text{'}AC},\widehat{OAE}$ là 2 góc đối đỉnh nên $\widehat{O\text{'}AC}=\widehat{OAE}$

Suy ra: $\widehat{CO\text{'}A}=\widehat{EOA}$

Xét tam giác O'CA và OAE có:

$\frac{OA\text{'}}{OA}=\frac{OC\text{'}}{OC}=\frac{R\text{'}}{R}$

$\widehat{CO\text{'}A}=\widehat{EOA}$

⇒ ∆O'AC ∽ ∆OAE (c.g.c)

Suy ra: $\widehat{AOE}=\widehat{AO\text{'}C}$

Mà: $\widehat{AOE}=2\widehat{ADE}$(vì $\widehat{AOE}$ là góc ở tâm, chắn cung $\stackrel{⏜}{AE}$, $\widehat{ADE}=\frac{1}{2}\stackrel{⏜}{AE}$)

Và $\widehat{AO\text{'}C}=2\widehat{ABC}$(vì $\widehat{AO\text{'}C}$ là góc ở tâm, chắn cung $\stackrel{⏜}{AC}$, $\widehat{ABC}=\frac{1}{2}\stackrel{⏜}{AC}$)

Suy ra: $\widehat{ABC}=\widehat{ADE}$.

Đề bài. Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB, AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC.

a) Chứng minh rằng tứ giác DBCE là hình thoi.

b) Gọi I là giao điểm của EC và đường tròn (O'). Chứng minh rằng ba điểm D, A, I thẳng hàng.

c) Chứng minh rằng KI là tiếp tuyến của đường tròn (O').

Lời giải:

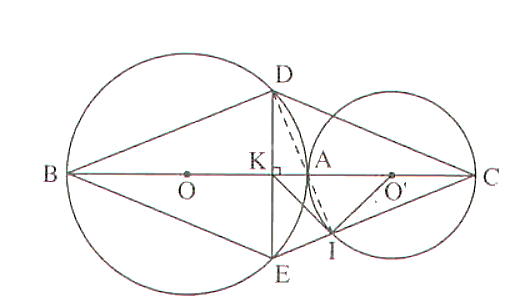
a) Tứ giác BDCE có: BK = KC, DK = KE nên BDCE là hình bình hành

Lại có BC vuông góc DE nên BDCE là hình thoi

b) Ta có: $\widehat{BDA}=90°$(góc nội tiếp chắn nửa đường tròn) nên AD ⊥ BD

$\widehat{AIC}=90°$(góc nội tiếp chắn nửa đường tròn) nên AI ⊥ IC (tức AI ⊥ EC)

Mặt khác BD // EC vì là các cạnh đối của hình thoi

Các đường thẳng AD, AI cùng đi qua A và vuông góc với 2 đường thẳng song song BD, EC nên A, D, I thẳng hàng

c) Tam giác DIE vuông có IK là đường trung tuyến ứng với cạnh huyền nên IK = KD = KE

Do đó: $\widehat{KIA}=\widehat{KDA}$

Tam giác O'IA cân tại O' nên $\widehat{O\text{'}IA}=\widehat{O\text{'}AI}=\widehat{DAK}$

Suy ra: $\widehat{KIA}+\widehat{O\text{'}IA}=\widehat{KDA}+\widehat{DAK}=90°$

Do đó: $\widehat{KIO\text{'}}=\widehat{KIA}+\widehat{O\text{'}IA}=90°$

Vậy KI là tiếp tuyến của (O').

Đề bài. Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’ và N’. Chứng minh

a) (ADF) // (BCE).

b) M′N′ // DF.

c) (DEF) // (MM′N′N) và MN // (DEF).

Lời giải:

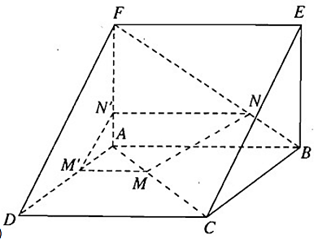
a) AD // BC; BC ⊂ (BCE) nên AD // (BCE)

AF // BE; BE ⊂ (BCE) nên AF // (BCE)

Mà AD, AF ⊂ (ADF)

Vậy (ADF) // (BCE)

b) Vì ABCD và ABEF là các hình vuông nên AC = BF. Ta có:

$MM\text{'}\parallel CD\Rightarrow \frac{AM\text{'}}{AD}=\frac{AM}{AC}\left(1\right)$

$NN\text{'}\parallel AB\Rightarrow \frac{AN\text{'}}{AF}=\frac{BN}{BF}\left(2\right)$

So sánh (1) và (2) ta được:

$\frac{AM\text{'}}{AD}=\frac{AN\text{'}}{AF}$ suy ra: M’N’ // DF

c) Từ chứng minh trên suy ra DF // (MM′N′N)

NN’ // AB nên NN’ // EF

Và NN’ ⊂ (MM’NN’) nên EF // (MM’NN’)

Mà DF, EF ⊂ (DEF) nên (DEF) // (MM′N′N)

Vì MN ⊂ (MM′N′N) và (MM′N′N) // (DEF) nên MN // (DEF).

Đề bài. Cho hai số thực a , b thỏa điều kiện ab = 1, a + b ≠ 0. Tính giá trị của biểu thức:

$P=\frac{1}{{\left(a+b\right)}^3}\left(\frac{1}{a^3}+\frac{1}{b^3}\right)+\frac{3}{{\left(a+b\right)}^4}\left(\frac{1}{a^2}+\frac{1}{b^2}\right)+\frac{6}{{\left(a+b\right)}^5}$.

Lời giải:

Với ab = 1, a + b ≠ 0 ta có:

$P=\frac{1}{{\left(a+b\right)}^3}\left(\frac{1}{a^3}+\frac{1}{b^3}\right)+\frac{3}{{\left(a+b\right)}^4}\left(\frac{1}{a^2}+\frac{1}{b^2}\right)+\frac{6}{{\left(a+b\right)}^5}$

$P=\frac{a^3+b^3}{{\left(a+b\right)}^3{\left(ab\right)}^3}+\frac{3\left(a^2+b^2\right)}{{\left(a+b\right)}^4{\left(ab\right)}^2}+\frac{6\left(a+b\right)}{{\left(a+b\right)}^5.ab}$

$P=\frac{a^3+b^3}{{\left(a+b\right)}^3}+\frac{3\left(a^2+b^2\right)}{{\left(a+b\right)}^4}+\frac{6\left(a+b\right)}{{\left(a+b\right)}^5}$

$P=\frac{a^2+b^2-1}{{\left(a+b\right)}^3}+\frac{3\left(a^2+b^2\right)}{{\left(a+b\right)}^4}+\frac{6}{{\left(a+b\right)}^4}$

$P=\frac{\left(a^2+b^2-1\right){\left(a+b\right)}^2+3\left(a^2+b^2\right)+6}{{\left(a+b\right)}^4}$

$P=\frac{{\left(a^2+b^2\right)}^2+4\left(a^2+b^2\right)+4}{{\left(a+b\right)}^4}$

$P=\frac{{\left(a^2+b^2+2\right)}^2}{{\left(a+b\right)}^4}$

$P=\frac{{\left(a^2+b^2+2ab\right)}^2}{{\left(a+b\right)}^4}$

$P=\frac{{\left[{\left(a+b\right)}^2\right]}^2}{{\left(a+b\right)}^4}=1$

Vậy P = 1.

Đề bài. Cho hai tập hợp E = (2;5] và F = [2m - 3; 2m + 2]. Tìm tất cả các giá trị của tham số m để E hợp F là một đoạn có độ dài bằng 5.

Lời giải:

Do (2m + 2) − (2m − 3) = 5 nên độ dài của tập F bằng 5.

Để C = E ∪ F là một đoạn có độ dài bằng 5 khi và chỉ khi C = F ⇔ E ⊂ F

⇔ $\left\{\begin{array}{l}2m-3\le 2\\ 2m+2\ge 5\end{array}\right.\iff \left\{\begin{array}{l}m\le \frac{5}{2}\\ m\ge \frac{3}{2}\end{array}\right.\iff \frac{3}{2}\le m\le \frac{5}{2}$

Vậy các giá trị của tham số m thỏa mãn yêu cầu bài toán là m ∈ $\left[\frac{3}{2};\frac{5}{2}\right]$.

Đề bài. Cho 2 tập hợp M = [2m − 1; 2m + 5] và N = [m + 1; m + 7] (với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.

Lời giải:

Nhận thấy M, N là 2 đoạn cùng có độ dài bằng 6, nên để M ∪ Nlà một đoạn có độ dài bằng 10 thì ta có các trường hợp sau:

+) 2m – 1 ≤ m + 1 ≤ 2m + 5 ⟺ m ∈ [−4; 2] (1)

Khi đó: M ∪ N = [2m − 1; m + 7] nên M ∪ N là 1 đoạn có độ dài bằng 10 khi:

(m + 7) − (2m − 1) = 10 ⇔ m = −2 (TM (1))

+) 2m – 1 ≤ m + 7 ≤ 2m + 5 ⟺ m ∈ [2; 8] (2)

Khi đó: M ∪ N = [m + 1; 2m + 5] nên M ∪ N là 1 đoạn có độ dài bằng 10 khi:

(2m + 5) − (m + 1) = 10 ⇔ m = 6 (TM(2))

Vậy tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10 là –2 + 6 = 4.

Đề bài. Cho hàm số y = x – 2 có đồ thị là đường thẳng (d).
a, Vẽ đồ thị hàm số đã cho.

b, Gọi A, B lần lượt là giao điểm của (d) với Ox, Oy. Tính diện tích tam giác OAB (đơn vị đo trên các trục tọa độ centimet).

c, Tìm giá trị của m để đường thẳng (d) và đường thẳng (d₁): y = -2x + m² - 3 cắt nhau tại một điểm trên trục tung.

Lời giải:

a, y = x - 2

Với x = 0 thì y = -2

y = 0 thì x = 2

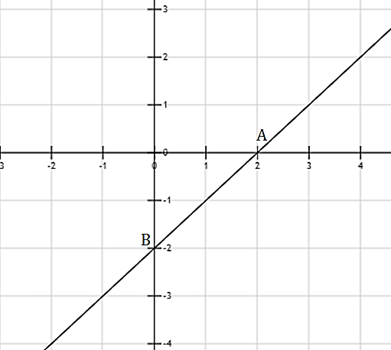
b, Theo a, ta có: A(2; 0)

⇒ OA = 2 cm

B(0; -2)

⇒ OB = 2 cm

Tam giác OAB vuông tại O nên diện tích tam giác OAB là:

S_OAB = $\frac{1}{2}$.OA.OB = $\frac{1}{2}$.2.2=2 (cm²)

vậy S = 2cm²

c, Ta có: (d) cắt Oy tại B(0; −2)

Để (d) cắt (d₁) tại điểm trên Oy

⇒ (d₁) qua B(0; −2)

⇒ −2.0 + m² – 3 = −2

⇒ m² = 1

⇔ m = ±1

Vậy m = ±1.

Đề bài. Cho hàm số f(x) hàm số y = f'(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Với giá trị nào của tham số m thì phương trình f(x) = 3x + m có nghiệm thuộc khoảng (-1;1).

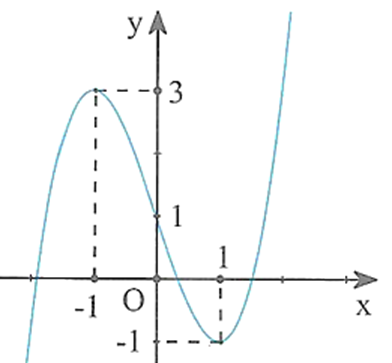
A. f(−1) + 3 < m < f(1) – 3.

B. f(−1) + 3 < m < f(1) + 3.

C. f(1) + 3 < m < f(-1) − 3.

D. f(0) – 1 < m < f(0) + 1.

Lời giải:

Chọn A.

Ta có f(x) = 3x + m ⇔ f(x) − 3x = m.

Để phương trình đã cho có nghiệm thuộc khoảng (-1;1) thì đường thẳng y=m phải cắt đồ thị hàm số g(x) = f(x) − 3x, x ∈ (−1;1).

Xét hàm số g(x) = f(x) − 3x, x ∈ (−1;1)

Có g'(x) = f'(x) − 3.

Nhìn đồ thị f'(x) ta thấy, với x ∈ (−1;1) thì −1 < f'(x) < 3

⇒ g'(x) = f'(x) – 3 < 0.

Do đó, ta có bảng biến thiên như hình bên

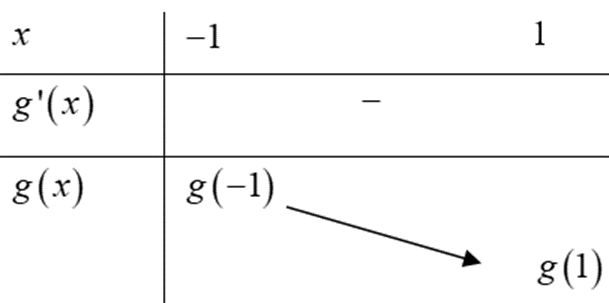
Từ bảng biến thiên, suy ra giá trị cần tìm là g(−1) < m < g(1)

⇔ f(−1) + 3 < m < f(1) − 3.

Đề bài. Cho hàm số f(x) = ln(4x - x²). Tính đạo hàm của hàm số tại x = 2.

Lời giải:

Điều kiện xác định:

4x – x² > 0 ⇔ x(4 – x) > 0

⇔ 0 < x < 4.

$f\text{'}\left(x\right)=\frac{4-2x}{4x-x^2}$

Do đó: $f\text{'}\left(2\right)=\frac{4-2.2}{4.2-2^2}=0$.

Đề bài. Xác định hàm số y = ax + b, biết đồ thị của hàm số đi qua hai điểm A(−2; 5) và B(1; −4).

Lời giải:

Đồ thị của hàm số đi qua hai điểm A(−2;5) và B(1;−4) nên ta có:

$\left\{\begin{array}{l}-2a+b=5\\ a+b=-4\end{array}\right.\iff \left\{\begin{array}{l}a=-3\\ b=-1\end{array}\right.$

Vậy hàm số cần tìm là y = –3x – 1.

Đề bài. Xác định các tham số a, b sao cho hàm số $y=\frac{ax+b}{x^2+1}$ đạt GTLN = 4 và GTNN = -1.

Lời giải:

Bài toán tương đương giải hệ: $\left\{\begin{array}{l}\frac{ax+b}{x^2+1}\ge -1\left(1\right)\\ \frac{ax+b}{x^2+1}\le 4\left(2\right)\end{array}\right.,\forall x$

(1) ⇔ $\frac{ax+b+x^2+1}{x^2+1}\ge 0\iff \frac{\left(b+1-\frac{a^2}{4}\right){\left(x-\frac{a}{2}\right)}^2}{x^2+1}\ge 0\iff b+1-\frac{a^2}{4}=0$

(2) ⇔ $\frac{ax+b-4\left(x^2+1\right)}{x^2+1}\le 0\iff \frac{\left(b-4+\frac{a^2}{16}\right){\left(4x-\frac{a}{4}\right)}^4}{x^2+1}\ge 0\iff b-4+\frac{a^2}{16}=0$

Suy ra ta có hệ: $\left\{\begin{array}{l}b+1-\frac{a^2}{4}=0\\ b-4+\frac{a^2}{16}=0\end{array}\right.\iff \left\{\begin{array}{l}4b+4-a^2=0\\ 16b-64+a^2=0\end{array}\right.\iff \left\{\begin{array}{l}b=3\\ a=\pm 4\end{array}\right.$

Hàm số cần tìm là $y=\frac{\pm 4x+3}{x^2+1}$.

Đề bài. Hàm số y = ∣x² − 2x − 3∣ đồng biến trên khoảng nào dưới đây?

A. (-∞;-1).

B. (-1;3).

C. (1;+∞).

D. (3;+∞).

Lời giải:

Chọn D.

Tập xác định D = ℝ .

Ta có: $y=\left|x^2-2x-3\right|=\sqrt{{\left(x^2-2x-3\right)}^2}\Rightarrow y\text{'}=\frac{\left(2x-2\right)\left(x^2-2x-3\right)}{\sqrt{{\left(x^2-2x-3\right)}^2}}$

Xét y’ = 0 ⇔ 2x – 2 = 0 ⇔ x = 1; y’ không xác định nếu x = -1; x = 3

Ta có bảng biến thiên:

Hàm số đồng biến trên khoảng (−1; 1) và (3; +∞).

Đề bài. Cho hàm số y = (m + 1)x + 3 (d) (m là tham số, m ≠ −1). Đường thẳng d cắt đường thẳng $y=-\frac{3}{2}x+3\left(d\text{'}\right)$ tại điểm M. Gọi N và P lần lượt là giao điểm của đường thẳng (d) và (d′) với trục hoành Ox. Tìm m để diện tích tam giác OMP bằng 2 lần diện tích tam giác OMN.

Lời giải:

Hai đường thẳng (d) và (d′) cắt nhau khi và chỉ khi $m+1\ne -\frac{3}{2}m\ne \frac{-5}{2}$

Hoành độ giao điểm M của (d) và (d′) là nghiệm của phương trình

$\left(m+1\right)x+3=\frac{-3}{2}x+3\iff x=0$

Mà $y=-\frac{3}{2}x+3\Rightarrow y=3$

d cắt d' tại điểm M(0; 3)

N là giao điểm của d' với trục Ox nên $N\left(\frac{-3}{m+1};0\right)$

P là giao điểm của d' với trục Ox nên P(2; 0)

Suy ra $ON=\frac{3}{\left|m+1\right|};OP=2$

Ta có: $S_{OMP}=2S_{OMN}\iff \frac{1}{2}.OM.OP=2.\frac{1}{2}.OM.ON$

⇔ OP = 2ON

⇔ $2=2.\frac{3}{\left|m+1\right|}\iff \left|m+1\right|=3\iff \left[\begin{array}{l}m+1=3\\ m+1=-3\end{array}\right.\iff \left[\begin{array}{l}m=2\\ m=-4\end{array}\right.$

Vậy m ∈ {2; -4}.

Đề bài. Cho hàm số y= 2x³ - 3(m + 1)x² + 6mx + m³ với m là tham số thực. Tìm tất cả các giá trị của m để đồ thị hàm số có hai điểm cực trị A; B thỏa mãn $AB=\sqrt{2}$.

Lời giải:

Ta có: y’ = 6x² – 6(m + 1)x + 6m

y’ = 0 ⇔ x² – (m+ 1)x + m = 0

⇔ $\left[\begin{array}{l}x=1\\ x=m\end{array}\right.$

Để hàm số có hai điểm cực trị khi m khác -1

Tọa độ các điểm cực trị là A( 1; m³+ 3m-1) và B( m; 3m²)

Suy ra: AB² = (m – 1)² + (m³ – 3m² + 3m – 1)² = (m – 1)² + (m – 1)⁶

Theo yêu cầu bài toán có: $AB=\sqrt{2}$

⇔ ${\left(m-1\right)}^6+{\left(m-1\right)}^2-2=0$

⇔ ${\left[{\left(m-1\right)}^2\right]}^3-1+\left[{\left(m-1\right)}^2-1\right]=0$

⇔ $\left[{\left(m-1\right)}^2-1\right]\left[{\left(m-1\right)}^4+{\left(m-1\right)}^2+2\right]=0$

⇔ (m – 1)² – 1 = 0

⇔ (m – 1)² = 1

⇔ $\left[\begin{array}{l}m-1=1\\ m-1=-1\end{array}\right.$

⇔ $\left[\begin{array}{l}m=0\\ m=-2\end{array}\right.$.

Đề bài. Cho hàm số f(x) = 4x² − 4mx + m² − 2m + 2 (m là tham số). Gọi S là tập hợp tất cả các giá trị của m sao cho $\underset{\left[0;2\right]}{Minf\left(x\right)}=3$. Khẳng định nào đúng?

A. S ⊂ (-4; 6).

B. S ⊂ (-3; 7).

C. S ⊂ [-2; 8].

D. S ⊂ [-1; 9].

Lời giải:

Chọn D.

Có hoành độ của đỉnh x_I = m²; a = 4 > 0

Xét 3 trường hợp sau:

TH1: $\frac{m}{2}<0\iff m<0$

Suy ra hàm số đồng biến trên đoạn [0;2]

Suy ra: $\underset{\left[0;2\right]}{Minf\left(x\right)}=f\left(0\right)=m^2-2m+2=3\Rightarrow m=1-\sqrt{2}$

TH2: $0\le \frac{m}{2}\le 2$ ⇔ 0 ≤ m ≤ 4
Suy ra: $\underset{\left[0;2\right]}{Minf\left(x\right)}=f\left(\frac{m}{2}\right)=-2m+2=3\Rightarrow m=\frac{-1}{2}$(loại)

TH3: $\frac{m}{2}>2\iff m>4$

Suy ra hàm số nghịch biến trên đoạn

⇒ $\underset{\left[0;2\right]}{Minf\left(x\right)}=f\left(2\right)=m^2-10m+18=3\Rightarrow m=5+\sqrt{10}$(thỏa mãn)

Vậy $S=\left\{1-\sqrt{2};5+\sqrt{10}\right\}$⊂ [−1; 9].

Đề bài. Cho hàm số bậc nhất y = (m – 2)x + 3. Tìm các giá trị của m để hàm số đồng biến.

Lời giải:

Hàm số y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0

Áp dụng vào bài toán:

y = (m – 2)x + 3 đồng biến khi m – 2 > 0 ⇔ m > 2

Vậy với m > 2 thì hàm số đồng biến.

Đề bài. Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới: Tìm tất cả các giá trị của tham số m để đồ thị hàm số $h\left(x\right)=\left|f^2\left(x\right)+f\left(x\right)+m\right|$ có đúng 3 điểm cực trị.

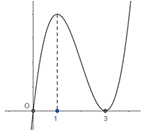
Lời giải:

Xét g(x) = f²(x) + f(x) + m, lập bảng biến thiên tìm số cực trị của y = g(x)

Tìm điều kiện để y = h(x) = $\left|g\left(x\right)\right|$ có đúng 3 điểm cực trị.

Xét g(x) = f²(x) + f(x) + m có g’(x) = 2f(x).f’(x) + f’(x) = f’(x)[2f(x) + 1]

g’(x) = 0 ⇔ $\left[\begin{array}{l}f\text{'}\left(x\right)=0\\ 2f\left(x\right)+1=0\end{array}\right.\iff \left[\begin{array}{l}x=1\\ x=3\\ x=a\left(a<0\right)\end{array}\right.\iff \left\{\begin{array}{l}g\left(1\right)=f^2\left(1\right)+f\left(1\right)+m\\ g\left(3\right)=m\\ g\left(a\right)=m-\frac{1}{4}\end{array}\right.$

Bảng biến thiên của hàm số y = g(x)

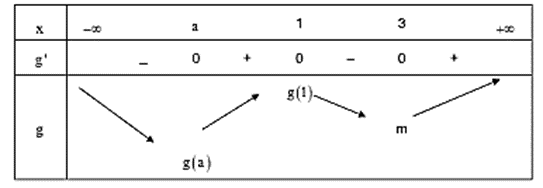
Dựa vào bảng biến thiên suy ra đồ thị hàm số y = g(x) có 3 điểm cực trị

Suy ra: $h\left(x\right)=\left|f^2\left(x\right)+f\left(x\right)+m\right|$ có 3 điểm cực trị khi và chỉ khi đồ thị hàm số y = g(x) nằm hoàn toàn phía trên trực Ox (kể cả tiếp xúc)

Do đó: g(a) ≥ 0 hay $m-\frac{1}{4}\ge 0\Rightarrow m\ge \frac{1}{4}$.

Đề bài. Cho hàm số y = f(x) có đồ thị như hình vẽ sau. So sánh f(3) và f(-2).

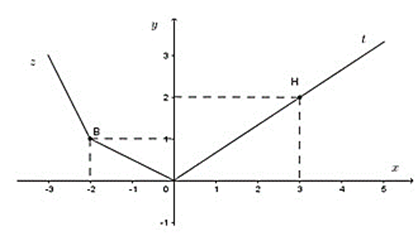
Lời giải:

Từ đồ thị hàm số y = f(x) đã cho, ta có f(−2) = 1; f(3) = 2.

Vậy f(3) > f(-2).

Đề bài. Cho hàm số: y = mx + 1 (1), trong đó m là tham số. Tìm m để đồ thị hàm số (1) đi qua điểm A(1; 4). Với giá trị m vừa tìm được, hàm số (1) đồng biến hay nghịch biến trên R?

Lời giải:

a) Ta có y = mx + 1 đi qua A(1;4) khi và chỉ khi 4 = m + 1 hay m = 3.

Khi đó ta có đường thẳng y = 3x + 1 đồng biến trên R.

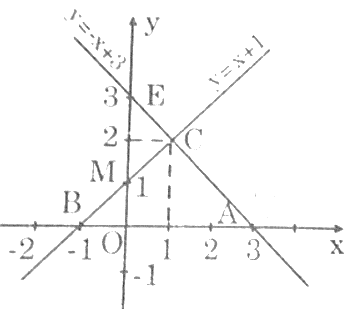
Đề bài. Vẽ đồ thị của các hàm số y = x + 1 và y = -x +3 trên cùng một mặt phẳng tọa độ.

Lời giải:

- Với hàm số y = x + 1:

Cho x = 0 ⇒ y = 1 ta được M(0; 1).

Cho y = 0 ⇒ x + 1 = 0 ⇒ x = -1 ta được B(-1; 0).

Nối MB ta được đồ thị hàm số y = x + 1.

- Với hàm số y = -x + 3:

Cho x = 0 ⇒ y = 3 ta được E(0; 3).

Cho y = 0 ⇒ -x + 3 = 0 ⇒ x = 3 ta được A(3; 0).

Nối EA ta được đồ thị hàm số y = -x + 3.

Đề bài. Cho hàm số $y=\frac{3-x}{x+1}$. Hỏi mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên mỗi khoảng (-∞; -1) và (-1; +∞).

B. Hàm số nghịch biến với mọi x khác 1.

C. Hàm số nghịch biển trên tập ℝ\{-1}.

D. Hàm số nghịch biến trên mỗi khoảng (-∞; -1) và (-1; +∞).

Lời giải:

Chọn D.

TXĐ: D = ℝ\ {-1}.

Chiều biến thiên:

$y\text{'}=\frac{-\left(x+1\right)-\left(-x+3\right)}{{\left(x+1\right)}^2}=\frac{-4}{{\left(x+1\right)}^2}$

y’ không xác định khi x = 1.

y’ luôn âm với mọi x ≠ 1.

Vậy hàm số nghịch biến trên các khoảng (-∞; -1) và (-1; +∞).

Đề bài. Cho phương trình x² – 5mx – 4m = 0 với m là tham số. Chứng minh rằng khi phương trình có 2 nghiệm phân biệt x₁, x₂ thì x₁² + 5mx₂ + m² + 14m + 1 > 0.

Lời giải:

Xét x² – 5mx – 4m = 0

Ta có: ∆ = 25m² + 16m

Để phương trình có 2 nghiệm phân biệt thì ∆ > 0

Suy ra: 25m² + 16m > 0 hay $\left[\begin{array}{l}m>0\\ m<\frac{-16}{25}\end{array}\right.$

Theo hệ thức Vi-ét ta có:

$\left\{\begin{array}{l}{x}_1+x_2=5m\\ x_1{x}_2=-4m\end{array}\right.$

Xét x₁² + 5mx₂ + m² + 14m + 1

= x₁² + (x₁ + x₂)x₂ + m² + 14m + 1

= x₁² + x₂² + x₁x₂ + m² + 14m + 1

= (x₁ + x₂)² - x₁x₂ + m² + 14m + 1

= 25m² + 4m + m² + 14m + 1

= 26m² + 18m + 1

= (m + 1)² + 25m² + 16m

Mà 25m² + 16m > 0 và (m + 1)² > 0 theo điều kiện của m

Vậy (m + 1)² + 25m² + 16m > 0 tức là x₁² + 5mx₂ + m² + 14m + 1 > 0.

Đề bài. Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x³ + 3x² – 4. Nêu nhận xét về đồ thị của hàm số này.

Lời giải:

TXĐ: D = ℝ.

Sự biến thiên: $\underset{x\to +\infty }{\lim }y=-\infty ;\underset{x\to -\infty }{\lim }y=+\infty$

Xét y' = -3x² + 6x.

Cho y' = 0 thì x = 0 hoặc x = 2

Bảng biến thiên:

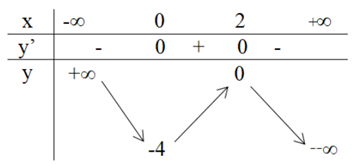
Hàm số đồng biến trên khoảng (0; 2)

Hàm số nghịch biến trên các khoảng (-∞; 0), (2; + ∞).

Hàm số đạt cực đại bằng 0 tại x = 2.

Hàm số đạt cực tiểu bằng -4 tại x = 0

* Đồ thị

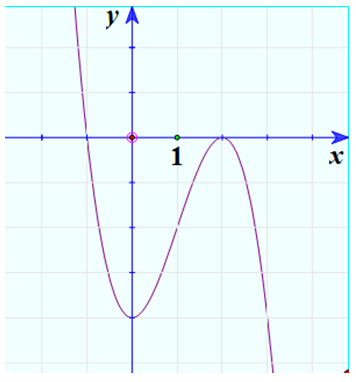
Đề bài. Cho hàm số y = x² – x – 2. Khảo sát sự biến thiên và vẽ đồ thị hàm số (P) của hàm số.

Lời giải:

Ta lần lượt tính: $\frac{-b}{2a}=\frac{1}{2};\frac{-\Delta }{4a}=-\frac{9}{4}$

Vậy đồ thị hàm số là một parabol có đỉnh $\left(\frac{1}{2};\frac{-9}{4}\right)$; nhận đường thẳng $x=\frac{1}{2}$ làm trục đối xứng và hướng bề lõm lên trên

Bảng biến thiên:

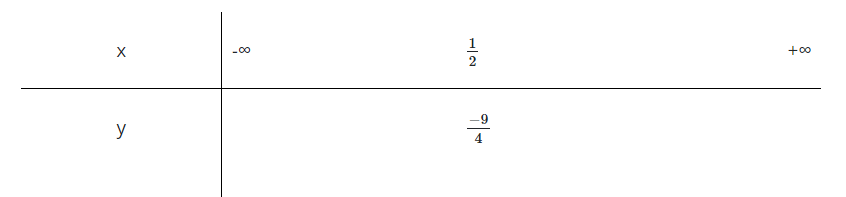
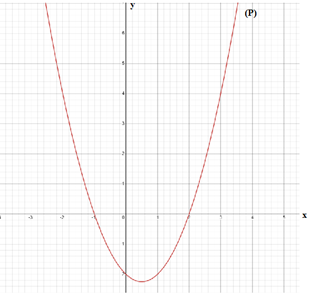
Ta lấy thêm điểm A(0; -2), B(1; -2)

Ta có đồ thị hàm số:

Đề bài. Cho hình bình hành ABCD với AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE, MF cắt BC tại N.

a) Tứ giác MNCD là hình gì?

b) Tam giác EMC là tam giác gì?

c) Chứng minh: $\widehat{BAD}=2\widehat{AEM}$.

Lời giải:

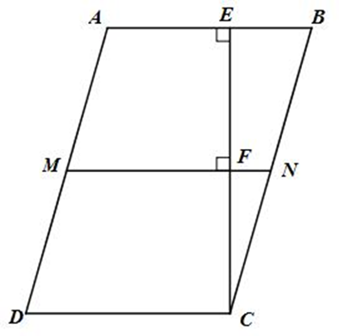
a) Ta có MN ⊥ CE (gt); AB ⊥ CE (gt)

Suy ra: MN // AB

Mà AB // CD (ABCD là hình bình hành) nên MN // CD

Tứ giác MNCD có MN // CD

Và MD // CN (AD // BC)

Do đó tứ giác MNCD là hình bình hành.

b) Gọi F là giao điểm của MN và EC

Hình thang AECD (EC // CD) có MF // AE // CD

Và M là trung điểm của AD (gt)

* F là trung điểm của EC.

ΔMEC có MF là đường trung tuyến (F là trung điểm của EC)

Và MF là đường cao

Suy ra: ΔMEC cân tại M.

c) Ta có AD = 2AB (gt)

AD = 2MD (M là trung điểm của AD)

Và AB = CD (ABCD là hình bình hành); MD = CD

Hình bình hành MNCD có MD = CD nên là hình thoi.

CM là đường phân giác nên: $\widehat{EMF}=\widehat{CMF}$

Mà $\widehat{EMF}=\widehat{AEM}$ (hai góc so le trong và AE // MF)

Và $\widehat{CMF}=\widehat{MCD}$ (hai góc so le trong và MF // CD)

Nên: $\widehat{MCD}=\widehat{AEM}$

Ta có: $\widehat{MCD}=\widehat{AEM};2\widehat{MCD}=\widehat{NCD}$(CM là phân giác $\widehat{NCD}$)

Và $\widehat{BAD}=\widehat{NCD}$(ABCD là hình bình hành)

Vậy $\widehat{BAD}=2\widehat{AEM}$.

Đề bài. Cho hình vẽ có MA // xy, NB // xy; $\widehat{MAN}=105°$.

a) Tính $\widehat{M_1}$.

b) Tính $\widehat{N_1}$.

Lời giải:

a) $\widehat{M_1}=\widehat{MHy}=65°$(vì MA // xy nên 2 góc ở vị trí đồng vị)

b) NB // xy nên: $\widehat{yHN}=\widehat{N_1}=105°-\widehat{MHy}=105°-65°=40°$

($\widehat{yHN};\widehat{N_1}$ là 2 góc so le trong).

Đề bài. Cho hình 20 biết a // AB, b // AB và $\widehat{MAN}=100°$. Tính $\widehat{N_1}$.

Lời giải:

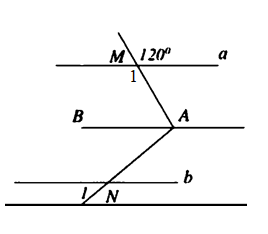
Ta có: a // AB và b // AB nên a // b

Vì a // AB nên $\widehat{MAB}+\widehat{M_1}=180°$

Mà $\widehat{M_1}=120°$(vì đối đỉnh)

Nên: $\widehat{MAB}=180°-\widehat{M_1}=180°-120°=60°$

Lại có: $\widehat{MAN}=\widehat{MAB}+\widehat{BAN}=100°$

Suy ra: $\widehat{BAN}=100°-60=40°$

Lại có: AB // b nên: $\widehat{BAN}=\widehat{ANb}=40°$

Mà $\widehat{ANb}=\widehat{N_1}$

Vậy $\widehat{N_1}=40°$.

Đề bài. Cho Hình 21. Biết x // z, y // z và góc $\widehat{CAD}=120°$.

a) Tính góc $\widehat{DAz}$.

b) Tính góc$\widehat{ C_1}$.

Lời giải:

a) Vì y // z nên $\widehat{DAz}=40°$(2 góc đồng vị)

b) Ta có: $\widehat{CAD}=\widehat{CAz}+\widehat{DAz}=120°$

Suy ra: $\widehat{CAz}=120°-\widehat{DAz}=120°-40°=80°$

Vì x // z nên: $\widehat{ C_1}+\widehat{CAz}=180°$

Suy ra: $\widehat{ C_1}=180°-\widehat{CAz}=180-80°=100°$.

Đề bài. Cho hình vẽ biết AB // CD< AD // BC, AC cắt BD tại O. Chứng minh

a) AB = CD; AD = BC.

b) OA = OC; OB = OD.

Lời giải:

a) Xét tam giác ABD và tam giác CBD có:

$\widehat{ABD}=\widehat{BDC}$ (vì AB // CD)

Chung BD
$\widehat{ADB}=\widehat{DBC}$ (vì AD // CB)

Suy ra: ΔABD = ΔCDB (g.c.g)

⇒ AB = CD, AD = CB

b) Xét tam giác AOD và tam giác CBO có:

$\widehat{OAD}=\widehat{OCB}$(vì AD // BC)

AD = BC

$\widehat{ODA}=\widehat{OBC}$ (vì AD // CB)

Suy ra: ΔOAD = ΔOCB (g.c.g)

⇒ OA = OC; OB = OD.

Đề bài. Cho ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Gọi K là giao điểm của AC và DM, L là trung điểm cuả BD và CM.

a. MNPQ là hình gì?

b. MDPB là hình gì?

Lời giải:

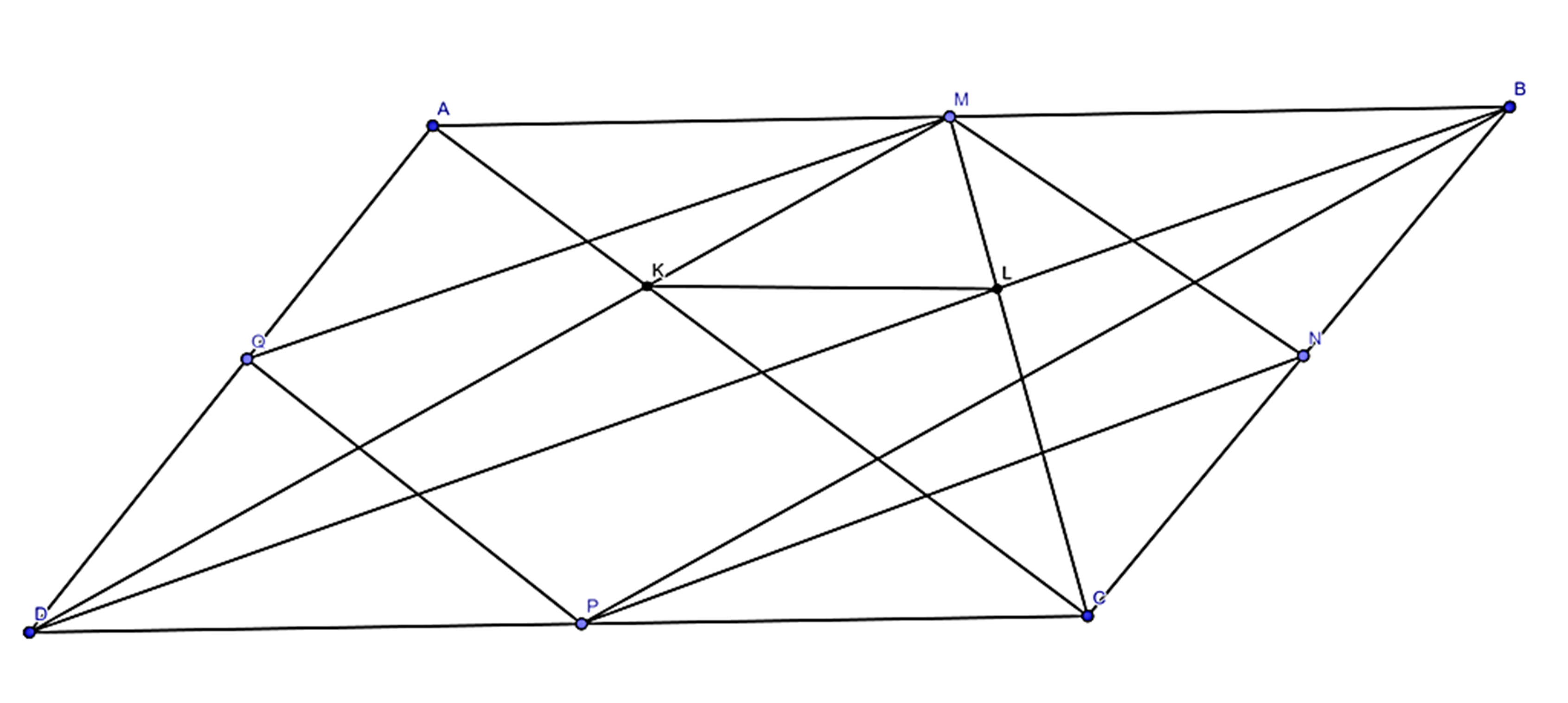
a, ΔABC có M là trung điểm của AB, N là trung điểm của BC

⇒ MN là đường trung bình của ΔABC

⇒ MN // AC và MN = $\frac{1}{2}$AC (1)

ΔADC có Q là trung điểm của AD, P là trung điểm của CD

⇒ PQ là đường trung bình của ΔADC

⇒ PQ // AC và PQ = $\frac{1}{2}$AC (2)

Từ (1) và (2) suy ra: MN // PQ và MN = PQ

⇒ Tứ giác MNPQ là hình bình hành

b, ABCD là hình bình hành ⇒ AB = CD và AB // CD

mà M là trung điểm của AB, P là trung điểm của CD

⇒ BM = DP và BM // DP

⇒ Tứ giác MDPB là hình bình hành.

Đề bài. Cho hình bình hành ABCD có $\widehat{A}=60°$, AB = 10cm, AD = 15cm. Tia phân giác của $\widehat{A}$ cắt BC tại E.

a) Chứng minh: tam giác ABE cân.

b) Tính EC.

c) Tính S_ABCD.

Lời giải:

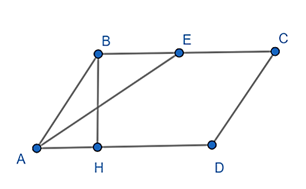
a) ABCD là hình bình hành nên BC // AD

Suy ra: $\widehat{BEA}=\widehat{EAD}$(2 góc so le trong)

Mà $\widehat{BAE}+\widehat{EAD}=60°$

Lại có: $\widehat{BAE}=\widehat{EAD}=30°$vì AE là phân giác

Nên $\widehat{BEA}=\widehat{BAE}$

Suy ra: tam giác ABE cân tại B

b) Vì tam giác ABE cân tại B nên AB = BE = 10

Mà BE + EC = BC = AD = 15

Suy ra: EC = 15 – 10 = 5 cm

c) Kẻ đường cao BH

Xét tam giác ABH vuông tại H có $\widehat{A}=60°$

$\sin \widehat{A}=\sin 60°=\frac{BH}{AB}=\frac{BH}{10}\Rightarrow BH=5\sqrt{3}$(cm)

S_ABCD = BH.AD = $5\sqrt{3}.15=75\sqrt{3}\left(c{m}^2\right)$.

Đề bài. Cho hình bình hành ABCD biết BD vuông góc với BC, AB = a, $\widehat{A}=\alpha$. Tính S hình bình hành theo a và α?

Lời giải:

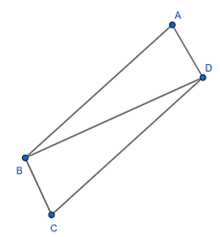
Ta có: BD = AB.sinA = a.sinα

AD = AB.cosA = a.cosα

⇒ S_ABCD = 2S_ABD =BD.AD = a².sinα.cosα.

Đề bài. Cho hình bình hành ABCD có $\widehat{BAD}=60°$; AD = 2AB. Gọi M là trung điểm của BC, N là trung điểm của AD.

a) MCND là hình thoi.

b) ABMD là hình thang cân.

Lời giải:

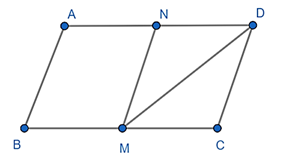
a) Ta có: BM = MC vì M là trung điểm BC

AN = ND vì N là trung điểm AD

Nên MN là đường trung bình ABCD

Suy ra: MN // AB // CD

Lại có: BC = AD, nên BM = AN

Xét ABMN có: BM // AN và BM = AN nên ABMN là hình bình hành

Suy ra: MN = AB

Mà AB = CD nên MN = CD

Lại có: AD = BC = 2AB nên ND = MC = AB = CD = MN

Vậy MNDC là hình thoi

b) Xét tứ giác BMDA có: BM // AD nên BMAD là hình thang

Vì MNDC là hình thoi nên MC = CD

Nên tam giác MCD cân tại C

Mà: $\widehat{MCD}=\widehat{BAD}=60°$

Nên tam giác MCD đều

Suy ra: MC = CD = MD

Mà CD = AB nên MD = Ba

Vậy BMDA là hình thang cân.

Đề bài. Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của AB và CD. Gọi M, N là giao điểm của AI, CK với BD. Chứng minh: ∆ADM = ∆CBN.

Lời giải:

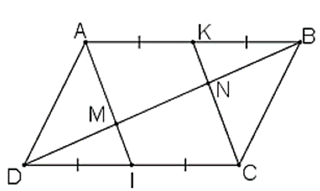
a) ABCD là hình bình hành

⇒ AB // CD ⇒ AB // IC

AB = CD

Mà K, I lần lượt là trung điểm của AB và CD.

⇒AK = IC

Mà AK // IC

⇒ AKIC là hình bình hành

Xét ΔADI và ΔBCKcó:

DI = BK

AI = CK

AD = BC

⇒ ΔADI = ΔBCK (c.c.c)

⇒ $\widehat{DAI}=\widehat{BCK}$

Xét ΔADM và ΔCBN có:

$\widehat{DAI}=\widehat{BCK}$

AD=BC

$\widehat{ADB}=\widehat{DBC}$(Do AD // BC)

⇒ ΔADM = ΔCBN (g.c.g).

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a,$\widehat{BAC}=60°$; SO⊥(ABCD) và $SO=\frac{3a}{4}$. Tính thể tích khối chóp S.ABCD.

Lời giải:

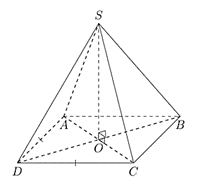
Ta có: $\widehat{BAC}=60°$ nên tam giác BAC là tam giác đều cạnh a

Suy ra: AC = a; BO = $\frac{a\sqrt{3}}{2}\Rightarrow BD=a\sqrt{3}$

Khi đó: $S_{ABCD}=\frac{1}{2}.AC.BD=\frac{a^2\sqrt{3}}{2}$

$V_{S.ABCD}=\frac{1}{3}.SO.S_{ABCD}=\frac{1}{3}.\frac{3}{4}a.\frac{a^2\sqrt{3}}{2}=\frac{\sqrt{3}{a}^3}{8}$.

Đề bài. Cho hình chóp S.ABCD . Gọi M, N lần lượt là trung điểm của SB và SD. Thiết diện của hình chóp S.ABCD và mặt phẳng (AMN) là hình gì?

A. Tam giác.

B. Ngũ giác.

C. Tam giác cân.

D. Tứ giác.

Lời giải:

Chọn D.

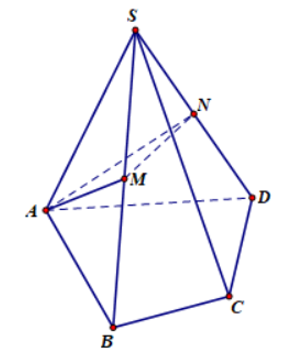
Gọi SC ∩ (AMN) = {P}

Khi đó thiết diện của hình chóp S.ABCD và mặt phẳng (AMN) là hình tứ giác AMPN.

Đề bài. Cho chóp S.ABCD. M, N lần lượt là trung điểm của SB, SD. Tìm giao điểm của (AMN) và SC.

Lời giải:

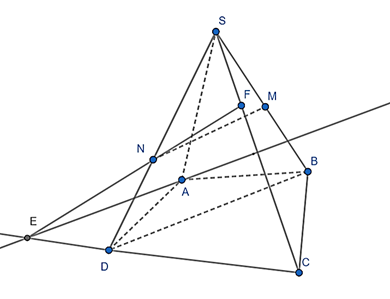
MN là đường trung bình tam giác SBD ⇒ MN // BD.

⇒ Giao tuyến của (AMN) và (ABCD) là 1 đường thẳng song song BD

Trong mp (ABCD), qua A kẻ đường thẳng d song song BD cắt CD kéo dài tại E

Trong mp (SCD), nối EN kéo dài cắt SC tại F

⇒ F = SC ∩ (AMN).

Đề bài. Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD.

Tìm giao tuyến của hai mặt phẳng

a) (SBM) và (SCD);

b) (ABM) và (SCD);

c) (ABM) và (SAC).

Lời giải:

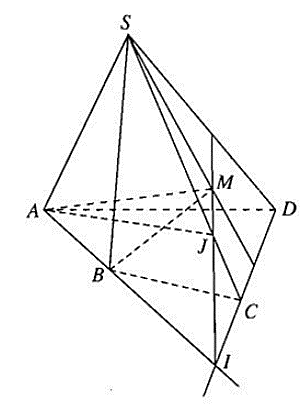
a) Ta có ngay S, M là hai điểm chung của (SBM) và (SCD) nên (SBM) ∩ (SCD) = SM

b) M là điểm chung thứ nhất của (AMB) và (SCD)

Gọi I = AB ∩ CD

Ta có: I ∈ AB ⇒ I ∈ (ABM)

Mặt khác: I ∈ CD ⇒ I ∈ (SCD)

Nên (AMB) ∩ (SCD) = IM.

c) Gọi J = IM ∩ SC.

Ta có: J ∈ SC ⇒ J ∈ (SAC) và J ∈ IM ⇒ J ∈ (ABM).

Hiển nhiên A ∈ (SAC) và A ∈ (ABM)

Vậy (SAC) ∩ (ABM) = AJ.

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn BC = 2a đáy bé AD = a , AB = b. Mặt bên SAD là tam giác đều. M là một điểm di động trên AB, Mặt phẳng (P) đi qua M và song song với SA, BC.1. Tìm thiết diện của hình chóp khi cắt bởi mp (P). Thiết diện là hình gì?

Lời giải:

+ Từ M kẻ đuờng thẳng song song với BC và SA lần luợt cắt DC tại N, SB tại Q.

+ Từ Q kẻ đuờng thẳng song song với BC cắt SC tại P.

Thiết diện hình thang cân MNPQ

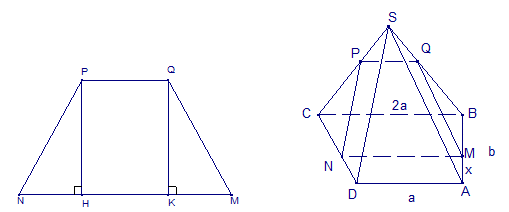
Đặt AM = x

Ta tính đuợc MQ = NP = $\frac{b-x}{b}a,PQ=\frac{2ax}{b},MN=\frac{ab+ax}{b}$
Từ đó: $QK=\frac{ab-ax}{b}.\frac{\sqrt{3}}{2}$

$S_{MNPQ}=\frac{1}{2}.\left(MN+PQ\right).QK=\frac{\sqrt{3}{a}^2}{4b^2}\left(b-x\right)\left(b+3x\right)$

$S_{MNPQ}=\frac{\sqrt{3}{a}^2}{4b^2}\left(b-x\right)\left(b+3x\right)\le \frac{\sqrt{3}{a}^2}{4b^2}.{\left(\frac{3b-3x+b+3x}{2}\right)}^2=\frac{\sqrt{3}{a}^2}{12}$

Dấu “=” xảy ra khi: $x=\frac{b}{3}$.

Đề bài. Cho hình chóp S.ABCD. M là một điểm trên cạnh SC.

a) Tìm giao điểm của AM và (SBD).

b) Gọi N là một điểm trên cạnh BC. Tìm giao điểm của SD và (AMN).

Lời giải:

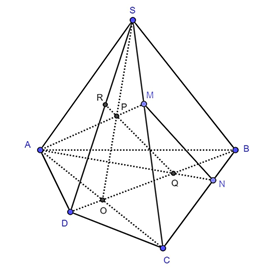
a) Gọi AC ∩ BD = O

Khi đó O∈(SAC) và O ∈ (SBD)

⇒ O ∈ (SAC) ∩ (SBD)

Lại có S ∈ (SAC) ∩ (SBD)

Do đó (SAC) ∩ (SBD) = SO

Gọi AM ∩ SO = P

Khi đó P ∈ AM và P ∈ SO, SO ⊂ (SBD)

Vậy AM ∩ (SBD) = P

b) Gọi AN ∩ BD = Q

Khi đó Q ∈ (AMN) và Q∈(SBD)

Lại có P ∈ (AMN) và P ∈ (SBD)

Vậy (AMN) ∩ (SBD) = PQ

Gọi PQ ∩ SD = R

Suy ra R ∈ (AMN) và R ∈ SD

Vậy SD ∩ (AMN) = R.

Đề bài. Cho hình chóp S.ABCD, AB và CD không song song và M là trung điểm của SC.

a, Tìm N = SD ∩ (MAB).

b, Gọi O = AC ∩ BD. Chứng minh SO, AM, BN đồng quy.

Lời giải:

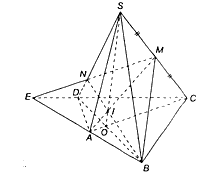
a) + Trong mp(ABCD), AB cắt CD tại E.

E ∈ AB ⊂ (MAB) ⇒ E ∈ (MAB) ⇒ ME ⊂ (MAB)

E ∈ CD ⊂ (SCD) ⇒ E ∈ (SCD)

Mà M ∈ SC ⊂ (SCD)

⇒ ME ⊂ (SCD).

+ Trong mp(SCD), EM cắt SD tại N.

Ta có:

N ∈ SD

N ∈ EM ⊂ mp(MAB)

Vậy N = SD ∩ mp(MAB)

b) Chứng minh SO, MA, BN đồng quy:

+ Trong mặt phẳng (SAC) : SO và AM cắt nhau.

+ Trong mp(MAB) : MA và BN cắt nhau

+ Trong mp(SBD) : SO và BN cắt nhau.

+ Qua AM và BN xác định được duy nhất (MAB), mà SO không nằm trong mặt phẳng (MAB) nên AM; BN; SO không đồng phẳng.

Vậy SO, MA, BN đồng quy.