Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 3)

Bài 1: Khối chóp tứ giác S. ABCD có đáy là hình bình hành. Có bao nhiêu mặt phẳng cách đều cả 5 điểm S, A, B, C, D?

Lời giải: Có 5 mặt phẳng cách đều 5 điểm S, A, B, C, D. Cụ thể như sau:

+ Mặt phẳng đi qua 4 trung điểm của 4 cạnh bên: có 1 mặt.

+ Mặt phẳng đi qua tâm O và song song với từng mặt bên: có 4 mặt như vậy.

Bài 2: Khối chóp tứ giác S. ABCD có đáy là hình bình hành. Mặt phẳng (SAC) chia khối chóp S. ABCD thành mấy khối tứ diện.

Lời giải: Mặt phẳng (SAC) chia khối chóp S.ABCD thành 2 khối tứ diện là S.ABC và S.ACD.

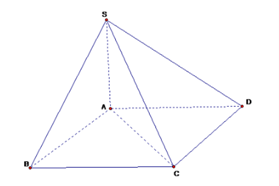
Bài 3: Tứ diện đều có bao nhiêu trục đối xứng?

Lời giải: Tứ diện đều có ba trục đối xứng đó là ba đường thẳng đi qua trung điểm của các cặp cạnh đối của nó.

Bài 4: Gọi $n_1,n_2,n_3$  lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối lập phương. Tính các giá trị của $n_1,n_2,n_3$

Lời giải: Khối tứ diện đều có 3 trục đối xứng (đi qua trung điểm của các cặp cạnh đối diện) nên $n_1=3.$

Khối chóp tứ giác đều có 1 trục đối xứng (đi qua đỉnh và tâm của mặt tứ giác) nên $n_2=1.$

Khối lập phương có 9 trục đối xứng (Loại 1: đi qua tâm của các mặt đối diện; Loại 2: đi qua trung điểm các cặp cạnh đối diện) nên $n_3=9.$

Bài 5: Trong hình học không gian:

A.   Điểm luôn luôn phải thuộc mặt phẳng.

B.   Điểm luôn luôn không phải thuộc mặt phẳng.

C.   Điểm vừa thuộc mặt phẳng đồng thời không thuộc mặt phẳng.

D.   Điểm có thể thuộc mặt phẳng, có thể không thuộc mặt phẳng.

Lời giải: Đáp án D.

Bài 6: Trong hình học không gian:

A.   Qua ba điểm xác định một và chỉ một mặt phẳng.

B.   Qua ba điểm phân biệt xác định một và chỉ một mặt phẳng.

C.   Qua ba điểm phân biệt không thẳng hàng xác định một mặt phẳng.

D.   Qua ba điểm phân biệt không thẳng hàng xác định một và chỉ một mặt phẳng.

Lời giải: Đáp án D.

Bài 7: Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 sao cho số đó chia hết cho 15?

Lời giải: Gọi số cần tìm có dạng $N=\overline{abcd}.$  Do N chia hết cho 15 nên N phải chia hết cho 3 và 5.

Vì vậy d có 1 cách chọn là bằng 5, và (a+b+c+d) chia hết cho 3.

Do vai trò của các chữ số a, b, c là như nhau, mỗi số a, b và c có 9 cách chọn nên ta xét các trường hợp sau

TH1: Nếu $a+b+d$  chia hết cho 3, khi đó c chia hết cho 3$\Rightarrow c\in \text{{}3;6;9\}\Rightarrow$ c có 3 cách chọn.

TH2: Nếu $a+b+d$  chia cho 3 dư 1, khi đó c chia 3 dư 2$\Rightarrow c\in \text{{2};5;8\}\Rightarrow$  c có 3 cách chọn.

TH3: Nếu $a+b+d$  chia cho 3 dư 2, khi đó c chia 3 dư 1 $\Rightarrow c\in \text{{1};4;7\}\Rightarrow$ c có 3 cách chọn.

Vậy trong mọi trường hợp thì c đều có 3 cách chọn nên ta có tất cả $\mathrm{9.9.3.1}=243$  số thỏa mãn.

Bài 8: Giải phương trình: $\sin \left(2x+\frac{3\text{π}}{4}\right)+\cos x\text{\hspace{0.17em}= 0}$

Lời giải: Ta có

$$\begin{gathered} \sin \left(2x+\frac{3\text{π}}{4}\right)+\cos x\text{\hspace{0.17em}= 0}\iff \cos x=\sin \left(-2x-\frac{3\text{π}}{4}\right) \\ \iff \cos x=\sin \left(\frac{\text{π}}{2}-\left(2x+\frac{\text{5π}}{4}\right)\right)\iff \cos x=\cos \left(2x+\frac{\text{5π}}{4}\right) \\ \iff \left[\begin{array}{l}x=2x+\frac{\text{5π}}{4}+k2\text{π}\\ x=-2x-\frac{\text{5π}}{4}+k2\text{π}\end{array}\right.\iff \left[\begin{array}{l}x=-\frac{\text{5π}}{4}-k2\text{π}\\ x=-\frac{\text{5π}}{12}+\frac{2}{3}k\text{π}\end{array}\right.(k\in {\rm Z}) \end{gathered}$$

Vậy phương trình đã cho có 2 họ nghiệm là: $x=-\frac{\text{5π}}{4}-k2\text{π}$  và  $x=-\frac{\text{5π}}{12}+\frac{2}{3}k\text{π.}$

Bài 9: Lớp 11A1 có 41 học sinh trong đó có 21 bạn nam và 20 bạn nữ. Thứ hai đầu tuần lớp phải xếp hàng chào cờ thành một hàng dọc. Hỏi có bao nhiêu cách sắp xếp để 21 bạn nam xen kẽ với 20 bạn nữ?

Lời giải: Vì số học sinh nam là lẻ nên bạn nam phải đứng đầu hàng.

Khi đó xếp 21 bạn nam vào 21 vị trí cố định có: $21!=P_{21}$  (cách).

Sau đó ta xếp 20 bạn nữ vào 20 vị trí trống xen kẽ với các bạn nam thì sẽ có: $20!=P_{20}$  (cách).

Vậy có tất cả số cách là: $20!.21!=P_{20}.P_{21}$ .

Bài 10: Đồ thị hàm số nào dưới đây nhận trục tung làm trục đối xứng?

A. y = sinx – cosx;

B. y = 2sinx;

C. y = 2sin(-x);

D. y = 0 – 2cosx.

Lời giải:

Đáp án đúng là: D

Bài 11: Một hình trục có chiều cao bằng 6cm nội tiếp trong hình cầu có bán kính bằng 5cm. Thể tích khối trụ này bằng bao nhiêu?

Lời giải: Ta có hình vẽ sau:

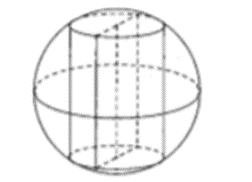
Bán kính đường tròn đáy của hình trụ là $r=\sqrt{R^2-d^2}=\sqrt{5^2-3^2}=4.$

Vậy thể tích của khối trụ cần tính là: $V=\text{π}{r}^2.h=\text{π}{.4}^2.6=96\text{π}.$

Bài 12: Cho hình bình hành ABCD có M là trung điểm của AB. Tính vecto DM.

Lời giải: Ta sẽ phân tích vecto DM theo hai vecto DC và BC.

Vì ABCD là hình bình hành nên ta có: $\overrightarrow{BD}=\overrightarrow{DA}+\overrightarrow{DC}.$

Mặt khác M là trung điểm của AB nên 

$2\overrightarrow{DM}=\overrightarrow{DA}+\overrightarrow{DB}\iff 2\overrightarrow{DM}=2\overrightarrow{DA}+\overrightarrow{DC}\iff 2\overrightarrow{DM}=-2\overrightarrow{BC}+\overrightarrow{DC}$

Suy ra $\overrightarrow{DM}=\frac{1}{2}\overrightarrow{DC}-\overrightarrow{BC}.$

Bài 13: Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số chẵn, mỗi số gồm 5 chữ số khác nhau trong đó có đúng 2 chữ số lẻ và 2 chữ số lẻ đó đứng cạnh nhau.

Lời giải: Gọi số cần tìm có dạng $\overline{abcde}$

+ TH1: 2 số lẻ liên tiếp ở vị trí ab. Khi đó: a có 3 cách chọn; b có 2 cách chọn; c có 4 cách chọn; d có 3 cách chọn và e có 2 cách chọn. Theo quy tắc nhân ta có: $\mathrm{3.2.4.3.2}=144$  (số).

+ TH2: 2 số lẻ liên tiếp ở vị trí bc. Khi đó: a có 3 cách chọn; b có 3 cách chọn; c có 2 cách chọn; d có 3 cách chọn và e có 2 cách chọn. Theo quy tắc nhân ta có: $\mathrm{3.3.2.3.2}=108$  (số).

+ TH3: 2 số lẻ liên tiếp ở vị trí cd (tượng tự TH2).

Vậy số cách chọn thỏa mãn yêu cầu đề bài là: $144+108.2=360$  (số).

Bài 14: Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.

a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).

b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.

c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α).

Lời giải:

 

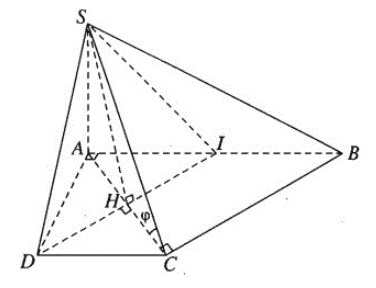
a) Ta có:

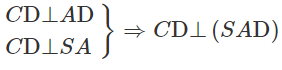
⇒ (SCD) ⊥ (SAD)

Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).

Vậy (SBC) ⊥ (SAC).

b) Ta có:

c) 

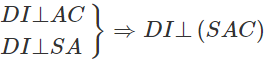
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và   .

Tam giác SDI có diện tích:

.

Bài 15: Cho hình chóp S.ABC có SA=SB=SC=3, AC=2; ABC là tam giác vuông cân tại B. Tính thể tích V của khối chóp S.ABC.

Lời giải:

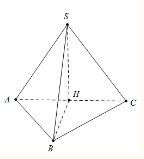
Ta có SA = SB = SC nên hình chiếu của đinh S xuống mặt phẳng (ABC) là tâm đường tròn ngoại tiếp tam giác ABC

Mà ABC là tam giác vuông cân tại B nên tâm đường tròn ngoại tiếp là trung điểm H của AC.

Ta có: Diện tích tam giác ABC là: $S_{ABC}=\frac{1}{2}AC.BH=\frac{1}{2}\mathrm{.2.1}=1$ .

Xét tam giác SAC, có: SH = $\sqrt{3^2-1^2}=2\sqrt{2}$ .

Vậy thể tích hình chóp là: $V_{SABC}=\frac{1}{3}\mathrm{.1.2}\sqrt{2}=\frac{2\sqrt{2}}{3}$ .

Bài 16: Xét phép thử gieo một con xúc xắc cân đối, đồng chất hai lần. Số phần tử của không gian mẫu là?

Lời giải: Số phần tử của không gian mẫu là: $\left|\Omega \right|=C_6^1.C_6^1=6.6=36.$

Bài 17: Xét phép thử T: “Gieo một con súc sắc cân đối và đồng chất” và biến cố A liên quan đến phép thử: “Mặt lẻ chấm xuất hiện”. Tính xác suất của biến cố A.

Lời giải: Khi đó ta có: $\left\{\begin{array}{l}n\left(\Omega \right)=6\\ n\left(A\right)=3\end{array}\right.\Rightarrow P\left(A\right)=\frac{3}{6}=\frac{1}{2}$

Bài 18: Tìm m để $m{x}^2-2(m+1)x+m+3=0$  là phương trình bậc hai nhận x = -2 là nghiệm.

Lời giải: Ta có phương trình $m{x}^2-2(m+1)x+m+3=0$  là phương trình bậc hai khi $m\ne 0.$

Thay $x=-\mathrm{2,}$  ta được: $m{(-2)}^2-2(m+1)(-2)-m+3=0$

$\iff 9m+7=0\iff m=-\frac{7}{9}$  (thỏa mãn)

Vậy $m=-\frac{7}{9}.$

Bài 19: Tìm m để hàm số $y=x^3-3m{x}^2+3(2m-1)x+1$  đồng biến trên R.

Lời giải: Ta có

$y=x^3-3m{x}^2+3(2m-1)x+1\Rightarrow y^{\text{'}}=3x^2-6mx+3(2m-1);\forall x\in \text{R}.$

Hàm số đồng biến trên R khi và chỉ khi

$y^{\text{'}}\ge 0;\forall x\in \text{R}\iff x^2-2mx+2m-1\ge 0;\forall x\in \text{R}.$

$\iff \left\{\begin{array}{l}a=1>0\\ {\Delta }^{\text{'}}=m^2-2m+1\le 0\end{array}\right.\iff {(m-1)}^2\le 0\iff m=1.$

Vậy m  = 1 là giá trị cần tìm thỏa mãn bài toán.

Bài 20: Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có $BC=\mathrm{3,}\widehat{BAC}={30}^0.$  Tính diện tích tam giác ABC.

Lời giải: Xét bài toán: Tam giác ABC, điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là:

$b^2+c^2=5a^2.$

Ta có: Gọi G là giao điểm của hai trung tuyến BM, CN. Áp dụng công thức trung tuyến ta có:

$G{B}^2=\frac{4}{9}B{M}^2=\frac{1}{9}(2a^2+2c^2-b^2);G{C}^2=\frac{4}{9}C{N}^2=\frac{1}{9}(2a^2+2b^2-c^2)$

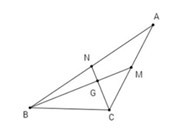
Áp dụng định lý Pythago cho tam giác vuông BGC, ta có: $B{G}^2+C{G}^2=B{C}^2$

Khi đó ta có:

$\frac{1}{9}(2a^2+2c^2-b^2)+\frac{1}{9}(2a^2+2b^2-c^2)=a^2\iff 4a^2+b^2+c^2=9a^2\iff b^2+c^2=5a^2.$

Quay trở lại bài toán trên, xét tam giác ABC ta có:

$a^2=b^2+c^2-2bc.\cos A=5a^2-2bc.\cos A\Rightarrow bc=\frac{2a^2}{\cos A}.$

Khi đó: $S=\frac{1}{2}bc.\sin A=\frac{1}{2}\frac{2a^2}{\cos A}.\sin A=a^2\tan A=3\sqrt{3}.$

Bài 21: Cho hàm số $y=x^3+m{x}^2+3x-2m+5$  (với m là tham số thực). Với giá trị nào của m thì hàm số đã cho đồng biến trên R.

Lời giải: Ta có: $y=x^3+m{x}^2+3x-2m+5$

$\Rightarrow y^{\text{'}}=3x^2+2mx+3.$

Khi đó xét: ${\Delta }^{\text{'}}=m^2-9.$

Để hàm số trên đồng biến trên R khi và chỉ khi $y^{\text{'}}\ge 0$  với mọi giá trị của m là tham số thực.

Tức là: ${\Delta }^{\text{'}}=m^2-9\ge \iff -3\le m\le 3.$

Vậy $m\in \text{[}-3;3].$

Bài 22: Gọi m là giá trị nhỏ nhất của hàm số $y=x+\frac{4}{x}$  trên khoảng $(0;+\infty ).$  Tìm m.

Lời giải: Hàm số $y=x+\frac{4}{x}$  liên tục trên $(0;+\infty ).$

Ta có: $y^{\text{'}}=1-\frac{4}{x^2}=0\iff \left[\begin{array}{l}x=-2\notin (0;+\infty )\\ x=2\notin (0;+\infty )\end{array}\right.$

Bảng biến thiên của hàm số $y=x+\frac{4}{x}$  trên $(0;+\infty )$  như sau:

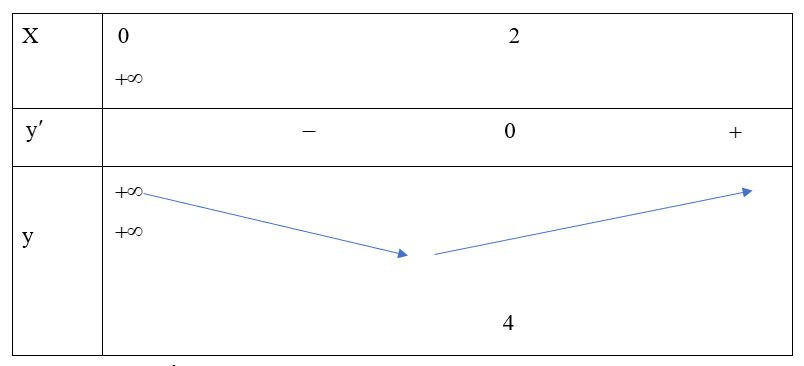
Dựa vào bảng biến thiên, suy ra ta có: $m=\underset{(0;+\infty )}{\min }y=y\left(2\right)=4.$

Nhắc lại: $\underset{x\to 0^{+}}{\lim }y=\underset{x\to 0^{+}}{\lim }\left(x+\frac{4}{x}\right)=+\infty ;\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\left(x+\frac{4}{x}\right)=+\infty .$

Bài 23: Với giá trị nào của m để phương trình $4^x-m{.2}^{x+1}+2m+3=0$ có hai nghiệm $x_1,x_2$ thỏa mãn $x_1+x_2=4.$

Lời giải: Xét phương trình đã cho tương đương với phương trình sau:

$2^{2x}-2m{.2}^x+2m+3=0\left(1\right).$

Đặt $2^x=t(t>0),$  khi đó phương trình (1) trở thành: $t^2-2m.t+2m+3=0\left(2\right).$

Phương trình (1) có hai nghiệm là $x_1,x_2$  khi và chỉ khi phương trình (2) có hai nghiệm $t_1,t_2$dương;

$\iff \left\{\begin{array}{l}{\Delta }^{\text{'}}\ge 0\\ S>0\\ P>0\end{array}\right.\iff \left\{\begin{array}{l}{m}^2-2m-3\ge 0\\ 2m>0\\ 2m+3>0\end{array}\right.\iff m\ge 3.$

Theo định lý Viet ta có: $\left\{\begin{array}{l}{t}_1+t_2=2m\\ t_1.t_2=2m+3\end{array}\right..$  Với $t=2^x$  khi đó ta có:

$t_1.t_2=2^{x_1}{.2}^{x_2}\iff 2m+3=2^{x_1+x_2}\iff 16=2m+3\iff m=\frac{13}{2}.$

Bài 24: Có hai giỏ đựng trứng là giỏ A và giỏ B, các quả trứng trong mỗi giỏ đều có hai loại là trứng lành và trứng hỏng. Tổng số trứng trong hai giỏ là 20 quả và số trứng giỏ A nhiều hơn số trứng giỏ B. Lấy ngẫu nhiên một quả trứng, biết xác suất để lấy được hai quả trứng lành là$\frac{55}{84}.$  Tính số trứng lành trong giỏ A.

Lời giải: Gọi a là số trứng lành, b là số trứng hỏng trong giỏ A.

Gọi x là số trứng lành, y là số trứng hỏng trong giỏ B.

Lấy ngẫu nhiên mỗi giỏ 1 quả trứng thì khi đó xác suất để lấy được 2 quả trứng lành là: $\frac{a}{a+b}.\frac{x}{x+y}=\frac{55}{84}.$

Do đó theo giả thiết bài toán ta có:

$\left\{\begin{array}{l}(a.x)⋮55\\ (a+b)(x+y)⋮84\\ a+b+x+y=20\\ (a+b)(x+y)\le {\left(\frac{a+b+x+y}{2}\right)}^2=100\end{array}\right.\Rightarrow \left\{\begin{array}{l}a+b=14\\ x+y=6\\ (a.x)⋮55\end{array}\right.\Rightarrow \left\{\begin{array}{l}a=11\\ x=5\end{array}\right..$

Vậy giỏ A có 11 quả trứng lành.

Bài 25: Cho tam giác ABC, gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Số vectơ bằng vectơ MN có điểm đầu và điểm cuối trùng với một trong các điểm A, B, C, M, N, P là bao nhiêu vectơ?

Lời giải: Do M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác ABC.

Suy ra $MN\text{//}AB;MN=\frac{1}{2}AB.\left(1\right)$

Lại có P là trung điểm của AB nên: $AP=BP=\frac{1}{2}AB.\left(2\right)$

Từ (1) và (2) suy ra:  $MN=AP=BP.$

Vậy khi đó số vecto bằng $\overrightarrow{MN}$  mà có điểm đầu và cuối trùng với các điểm trên là: $\overrightarrow{BP};\overrightarrow{PA}.$

Bài 26: Cho khối lăng trụ tam giác đều ABC.A'B'C'. Các mặt phẳng (ABC') và (A'B'C') chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu $H_1,H_2$  lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Tính giá trị của $\frac{V_{\left(H_1\right)}}{V_{\left(H_2\right)}}.$

Lời giải:

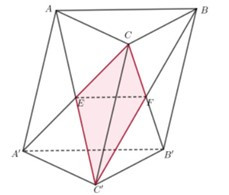
Gọi $E=A{C}^{\text{'}}\cap A^{\text{'}}C$  và $F=B{C}^{\text{'}}\cap B^{\text{'}}C.$  Khi đó (ABC') và (A'B'C') chia khối lăng trụ đều ABC.A'B'C' thành 4 khối đa

diện: $CEF{C}^{\text{'}};FE{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}};FEABC$ và $FEAB{B}^{\text{'}}{A}^{\text{'}}.$

Gọi V là thể tích của khối lăng trụ đều ABC.A'B'C'. Ta có:

$$\begin{gathered} V_{C.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=V_{C^{\text{'}\text{'}}.ABC}=\frac{1}{3}V;V_{FE{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=V_{C.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}-V_{CEF{C}^{\text{'}}}; \\ {V}_{FEABC}=V_{C.ABC}-V_{CEF{C}^{\text{'}}}\Rightarrow V_{FE{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=V_{FEABC}. \end{gathered}$$

Mặt khác: $\frac{V_{CEF{C}^{\text{'}}}}{V_{C.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}}=\frac{CE}{C{A}^{\text{'}}}\cdot \frac{CF}{C{B}^{\text{'}}}=\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}\Rightarrow V_{CEF{C}^{\text{'}}}=\frac{1}{4}{V}_{C.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=\frac{1}{4}\cdot \frac{1}{3}V=\frac{1}{12}V$

Suy ra 

$$\begin{gathered} V_{FE{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=V_{FEABC}=V_{C.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}-V_{CEF{C}^{\text{'}}}=\frac{1}{3}V-\frac{1}{12}V=\frac{1}{4}V \\ \Rightarrow V_{FEAB{B}^{\text{'}}{A}^{\text{'}}}=V-2.\frac{1}{4}V-\frac{1}{12}V=\frac{5}{12}V. \end{gathered}$$

Do đó $H_1$  là thể tích lớn nhất của khối đa diện $FEAB{B}^{\text{'}}{A}^{\text{'}};H_2$ là thể tích nhỏ nhất của khối đa diện $CEF{C}^{\text{'}}$

Khi đó: $\frac{V_{\left(H_1\right)}}{V_{\left(H_2\right)}}=5.$

Bài 27: Một hình chóp 16 cạnh thì có bao nhiêu mặt?

Lời giải: Hình chóp $S.A_1{A}_2\mathrm{...}{A}_n(n\ge 3)$ có n cạnh bên và n cạnh đáy nên sẽ có 2n cạnh.

Khi đó ta có: $2n=16\iff n=8.$

Vậy hình chóp 16 cạnh sẽ có 8 mặt bên và 1 mặt đáy nên tổng số là 9 mặt.

Bài 28: Với các số a, b > 0 thỏa mãn $a^2+b^2=6ab,$ tính biểu thức ${\log }_2(a+b).$

Lời giải: Ta có: $a^2+b^2=6ab\Rightarrow {(a+b)}^2=8ab\iff a+b=\sqrt{8ab}$

Suy ra ${\log }_2(a+b)={\log }_2\sqrt{8ab}\iff {\log }_2(a+b)=\frac{1}{2}{\log }_2\left(8ab\right)$

Do đó ${\log }_2(a+b)=\frac{1}{2}(3+{\log }_{2}a+{\log }_{2}b).$

Bài 29: Với các số a, b > 0 thỏa mãn $9a^2+b=10ab.$ Hãy chọn đẳng thức đúng sau:

Lời giải: Ta có: $9a^2+b=10ab\iff {\left(\frac{3a+b}{4}\right)}^2=ab.$

Lấy log của cả hai vế của đẳng thức trên thì ta có được:

$\log {\left(\frac{3a+b}{4}\right)}^2=\log \left(ab\right)\Rightarrow 2\log \left(\frac{3a+b}{4}\right)=\log \left(a\right)+\log \left(b\right)\Rightarrow \log \left(\frac{3a+b}{4}\right)=\frac{\log \left(a\right)+\log \left(b\right)}{2}.$

Chọn đáp án B.

Bài 30: Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương?

Lời giải: Ta chia hình lập phương thành 6 khối tứ diện bằng nhau như sau:

+ Chia khối lập phương $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ thành hai khối lăng trụ tam giác bằng nhau: ABC.A'B'C' và  BCD.B'C'D'

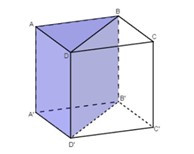
+ Tiếp theo, lần lượt chia khối lăng trụ $ABD.A^{\text{'}}{B}^{\text{'}}{D}^{\text{'}}$ và $BCD.B^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ thành ba tứ diện: $DAB{B}^{\text{'}};DA{A}^{\text{'}}B$ và  $DCB{B}^{\text{'}},DC{C}^{\text{'}}{B}^{\text{'}},D{D}^{\text{'}}{C}^{\text{'}}{B}^{\text{'}}.$

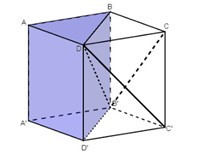
+ Ta chứng minh được các khối tứ diện này bằng nhau như sau:

Hai khối tứ diện DABB' và DAA'B' bằng nhau vì chúng đối xứng nhau qua mặt phẳng (DAB')         (1)

Hai khối tứ diện DAA'B' và DD'A'B' bằng nhau vì chúng đối xứng nhau qua mặt phẳng (B'A'D)         (2)

Từ (1) và (2) suy ra ba khối tứ diện $DAB{B}^{\text{'}},DA{A}^{\text{'}}{B}^{\text{'}}$ và $D{D}^{\text{'}}{A}^{\text{'}}{B}^{\text{'}}$ bằng nhau.

Tương tự, ba khối tứ diện $DCB{B}^{\text{'}},DC{C}^{\text{'}}{B}^{\text{'}},D{D}^{\text{'}}{C}^{\text{'}}{B}^{\text{'}}$ cũng bằng nhau.

Vậy khối lập phương $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ được chia thành sáu khối tứ diện bằng nhau.

Bài 31: Tìm ví dụ về khối đa diện lồi và khối đa diện không lồi trong thực tế.

Lời giải: Khối đa diện lồi trong thực tế: kim tự tháp Ai Cập, viên kim cương, rubic, …

Khối đa diện không lồi trong thực tế: cái bàn, cái ghế, …

Bài 32: Đếm số đỉnh, số cạnh của khối đa diện lồi đều như hình vẽ sau:

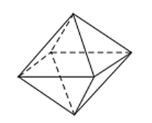
Lời giải: Khối bát diện đều trên có 6 đỉnh và 12 cạnh.

Bài 33: Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với đáy (ABCD). Gọi φ là góc giữa SD và mặt phẳng (ABCD). Tính cot φ?

Lời giải:

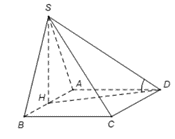
Gọi H là trung điểm của AB. Khi đó ta có $SH\perp AB\Rightarrow SH\perp \left(ABCD\right)$  nên hình chiếu của SD trên (ABCD) là HD.

Do đó $\widehat{SD,\left(ABCD\right)}=\widehat{SD,HD}=\widehat{SDH}.$

Mặt khác tam giác SAB đều cạnh a nên $SH=\frac{a\sqrt{3}}{2}.$

Suy ra $HD=\sqrt{A{H}^2+A{B}^2}=\frac{a\sqrt{5}}{2}.$

Khi đó xét tam giác vuông SHD, ta có: $\cot \widehat{SHD}=\frac{DH}{SH}=\frac{5}{\sqrt{15}}.$

Bài 34: By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất.

Lời giải:

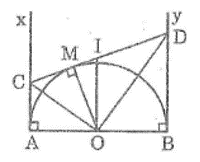
Theo tính chất hai tiếp tuyến cắt nhau ta có:

CA = CM

DB = DM

Suy ra: AC + BD = CM + DM = CD

Chu vi hình thang ABDC bằng: AB + BD + DC + CA = AB + 2CD

Vì đường kính AB của (O) không thay đổi nên chu vi hình thang nhỏ nhất khi CD nhỏ nhất

Ta có: CD   AB nên CD nhỏ nhât khi và chỉ khi CD = AB

Khi đó $\text{CD // AB}\iff \text{OM }\perp \text{AB}$

Vậy khi M là giao điểm của đường thẳng vuông góc với AB tại O với nửa đường tròn (O) thì hình thang ABDC có chu vi

nhỏ nhất.

Bài 35: Cho nửa đường tròn (O) có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn cùng thuộc một nửa mặt phẳng có bờ là AB ). Qua một điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt Ax và By theo thứ tự ở C và D. Gọi $N=AD\cap BC,H=MN\cap AB.$Chọn câu đúng nhất.

A. $MN\perp AB$

B. MN > NH

C. Cả A, B đều đúng      

D. Cả A, B đều sai.

Lời giải:

Theo tính chất hai tiếp tuyến cắt nhau ta có: AC = CM và BD = DM

AC // BD (vì cùng vuông góc vớiAB )

Theo hệ quả của định lý Ta – lét ta có:

$\frac{\text{CN}}{\text{BN}}\text{ = }\frac{\text{AC}}{\text{BD}}\Rightarrow \frac{\text{CN}}{\text{BN}}\text{ = }\frac{\text{CM}}{\text{DM}}$

Theo định lý Ta – Lét đảo ta đượcMN // BD.

Mà $\text{BD\hspace{0.33em}}\perp \text{AB}\Rightarrow \text{MN}\perp \text{AB}$

Theo hệ quả của định lý Ta – Lét ta có:

$\frac{\text{NH}}{\text{BD}}\text{=}\frac{\text{AH}}{\text{AB}}\text{ = }\frac{\text{CN}}{\text{CB}}\text{ = }\frac{\text{MN}}{\text{BD}}\Rightarrow \text{MN = NH}$

nên B sai.

Đáp án cần chọn là: A

Bài 36: Rút gọn phân thức: $\frac{{\text{x}}^{\text{3}}{\text{ + y}}^{\text{3}}{\text{ + z}}^{\text{3}}\text{ - 3xyz}}{{\left(\text{x - y}\right)}^{\text{2}}\text{ + }{\left(\text{y - z}\right)}^{\text{2}}\text{ + }{\left(\text{z - x}\right)}^{\text{2}}}$

Lời giải:

$\frac{{\text{x}}^{\text{3}}{\text{ + y}}^{\text{3}}{\text{ + z}}^{\text{3}}\text{ - 3xyz}}{{\left(\text{x - y}\right)}^{\text{2}}\text{ + }{\left(\text{y - z}\right)}^{\text{2}}\text{ + }{\left(\text{z - x}\right)}^{\text{2}}}$

$\begin{array}{l}\text{= }\frac{{\text{x}}^{\text{3}}{\text{ + y}}^{\text{3}}{\text{ + z}}^{\text{3}}\text{ - 3xyz}}{{\text{x}}^{\text{2}}{\text{ - 2xy + y}}^{\text{2}}{\text{ + y}}^{\text{2}}{\text{ - 2yz + z}}^{\text{2}}{\text{ + z}}^{\text{2}}{\text{ - 2xz + x}}^{\text{2}}}\\ \text{= }\frac{\left(\text{x + y + z}\right)\text{ . }\left({\text{x}}^{\text{2}}{\text{ + y}}^{\text{2}}{\text{ +z}}^{\text{2}}\text{ - xy - yz - zx}\right)}{\text{2 . }\left({\text{x}}^{\text{2}}{\text{ + y}}^{\text{2}}{\text{ + z}}^{\text{2}}\text{ - xy - yz - zx}\right)}\\ \text{= }\frac{\text{x + y + z}}{\text{2}}\end{array}$

Bài 37: Tìm các chữ số a, b, c, d sao cho tổng abc + dba chia hết cho aa và được thương là aa (abc, dba là các số có 3 chữ số theo thứ tự là a, b, c và d, b, a; aa là số có 2 chữ số đều bằng a).

Lời giải:

Ta có $\left(\overline{abc}+\overline{dba}\right):\overline{\text{aa}}=\overline{\text{aa}}$  nên $\left(\overline{abc}+\overline{dba}\right)=\overline{\text{aa}}.\overline{\text{aa}}=121a.a$

Vì $\overline{abc}+\overline{dba}<2000$  nên a.a.121 < 2000

Suy ra a.a < 17 nên a ∈ {1; 2; 3; 4}.

TH1. a = 1, ta có: $\overline{abc}+\overline{dba}=\mathrm{1.1.121}=121<2000$

Mà $\overline{abc}+\overline{dba}$  không thể nhỏ hơn 200 nên loại.

TH2. a = 2, ta có: $\overline{abc}+\overline{dba}=\mathrm{2.2.121}=484<2000$

Ở hàng đơn vị ta có c + 2 = 4 thì c = 2

Ở hàng chục ta có: b + b = 8 ⇔ b = 4 ⇒ d = 2 hoặc b + b = 18 ⇔ b = 9 ⇒ d = 1.

Vậy a = 2, b = 4, c = 2, d = 2 hoặc a = 2, b = 9, c = 2, d = 2.

TH3. a = 3, ta có: $\overline{abc}+\overline{dba}=\mathrm{3.3.121}=1089<2000$

Ở hàng đơn vị ta có c + 3 = 9 thì c = 6

Ở hàng chục ta có: b + b = 8 ⇔ b = 4 ⇒ d = 7 hoặc b + b = 18 ⇔ b = 9 ⇒ d = 6.

Vậy a = 3, b = 4, c = 6, d = 7 hoặc a = 3, b = 9, c = 6, d = 6.

TH4. a = 4, ta có: $\overline{abc}+\overline{dba}=\mathrm{4.4.121}=1936<2000$

Vì $\overline{abc}=\overline{4bc}<500$  và $\overline{dba}<1000$ . Do đó trường hợp này loại.

Bài 38: Giải phương trình : x⁴ - 8x² + x + 12 = 0

Lời giải:

Đặt t bằng x²

Đk $t\ge 0$

Ta có phương trình

t² - 8t + t +12 = 0

$\text{Δ = }{\left(\text{-8}\right)}^{\text{2}}\text{ - 1 . }\left(\text{t + 12}\right)$

= 64 – t - 12

= 52  -  t

Suy ra 52  -  t  > 0⇔ - t > - 52⇔ t < 52

${\text{t}}_{\text{1}}\text{ = - }\frac{\text{- 8 - }\sqrt{\text{52}}}{\text{2 . 1}}\text{ = 4 + }\sqrt{\text{3}}$ (nhận)

${\text{t}}_{\text{2}}\text{ = - }\frac{\text{- 8 + }\sqrt{\text{52}}}{\text{2 . 1}}\text{ = 4 - }\sqrt{\text{3}}$ (nhận )

Bài 39: Điểm thuộc đồ thị hàm số y = -2x là:

A. M(-2; -2)

B. N(1; 4)

C. P(-1; -2)

D. Q(-1; 2)

Lời giải:

Thay các điểm M, N, P vào hàm số đều không thỏa mãn, chỉ có điểm Q(-1; 2) thỏa mãn vì 2 = -2 . (-1)

Chọn đáp án D

Bài 40: Cho hình chữ nhật ABCD có chiều dài 6 cm, chiều rộng 4 cm (như hình vẽ). Diện tích hình tam giác MDC bên trong hình chữ nhật là bao nhiêu?

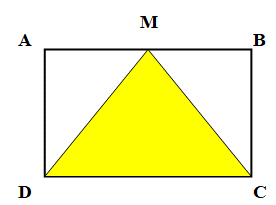
Lời giải:

Diện tích hình tam giác MDC là:

6 × 4 : 2 = 12(cm²)

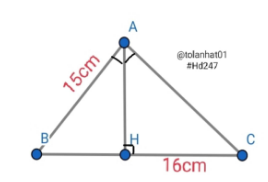
Bài 41: Cho $\Delta ABC$ vuông tại A có đường cao AH. Biết AC = 15cm; HB = 16cm. Tính BC; AB; AH; CH

Lời giải:

Ta có:  ${\text{AC}}^{\text{2}}\text{ = CH . BC}$

$$\begin{gathered} \iff {\text{CH}}^{\text{2}}\text{ + 16HC - 225 = 0} \\ \iff {\text{CH}}^{\text{2}}\text{ + 25HC - 9HC - 225 = 0} \\ \iff \text{CH = 9 (cm)} \end{gathered}$$

Áp dụng định lí Pytago vào $\Delta ACH$ vuông tại H, ta được:

$$\begin{gathered} {\text{AC}}^{\text{2}}{\text{ = AH}}^{\text{2}}{\text{ + HC}}^{\text{2}} \\ \iff {\text{AH}}^{\text{2}}{\text{ = 15}}^{\text{2}}{\text{ - 9}}^{\text{2}}\text{ = 144} \end{gathered}$$

hay AH = 12cm

Áp dụng định lí Pytago vào $\Delta ABH$ vuông tại H, ta được:

$$\begin{gathered} {\text{AB}}^{\text{2}}{\text{ = AH}}^{\text{2}}{\text{ + HB}}^{\text{2}} \\ \iff {\text{AB}}^{\text{2}}{\text{ = 12}}^{\text{2}}{\text{ + 16}}^{\text{2}}\text{ = 400} \end{gathered}$$

Ta có: BC = BH + HC

nên BC = 9 + 16 = 25cm

Bài 42: Cho $\text{ΔABC}$ vuông tại A đường cao AH. Biết AB = 15cm, HC = 16cm. Tính BC, AC, HC

Lời giải:

Áp dụng hệ thức lượng trong tam giác vuông ABC có:

$$\begin{gathered} {\text{AC}}^{\text{2}}\text{ = CH . BC = 16 . BC} \\ {\text{AB}}^{\text{2}}{\text{ + AC}}^{\text{2}}{\text{ = BC}}^{\text{2}} \\ \iff {\text{15}}^{\text{2}}{\text{ + 16 . BC = BC}}^{\text{2}} \\ \iff {\text{BC}}^{\text{2}}\text{ - 16 . BC - 225 = 0} \\ \iff {\text{BC}}^{\text{2}}\text{ - 25BC + 9BC - 225 = 0} \\ \iff \text{BC}\left(\text{BC - 25}\right)\text{ + 9}\left(\text{BC - 25}\right)\text{ = 0} \\ \iff \left(\text{BC - 25}\right)\left(\text{BC + 9}\right)\text{ = 0} \\ \iff \left[\begin{array}{c}BC=25\left(tm\right)\\ BC=-9\left(loai\right)\end{array}\right. \\ \Rightarrow {\text{AC}}^{\text{2}}\text{ = 16 . BC = 16 . 25 = 400} \\ \Rightarrow \text{AC = 20} \end{gathered}$$

+ Xét tam giác vuông ABC có: AH . BC = AB . AC ( hệ thức lượng )

Vậy BC = 25(cm); AC = 20(cm); HC = 16(cm).

Bài 43: Hai vòi nước cùng chảy vào một bể. Nếu chảy một mình thì vòi I chảy đầy bể trong 10 giờ, vòi II chảy đầy bể

trong 15 giờ. Còn vòi thứ ba được lắp sát đáy bể để tháo nước từ bể ra. Nếu bể đang đầy thì vòi thứ ba tháo hết

nước ra trong 30 giờ. Trong bể đã có 4 1 bể nước, người ta mở cho vòi I và vòi II chảy trong 3 giờ rồi mở tiếp vòi thứ

ba. Hỏi sau khi mở vòi thứ ba thì sau bao lâu bể nước đầy?

Lời giải:

Mỗi giờ vòi thứ nhất chảy được số phần bể là: 

$\text{1 ÷ 10 = }\frac{\text{1}}{\text{10}}\text{}$(bể) 

Mỗi giờ vòi thứ hai chảy được số phần bể là: 

$\text{1 ÷ 15 = }\frac{\text{1}}{\text{15}}$(bể) 

Mỗi giờ vòi thứ ba rút số phần bể là: 

$\text{1 ÷ 30 = }\frac{\text{1}}{\text{30}}$(bể) 

Khi mở vòi I và vòi II mỗi giờ chảy được số phần bể là: 

$\frac{1}{10}+\frac{1}{15}=\frac{1}{6}$(bể) 

Sau 3 giờ bể mở vòi I và vòi II bể chứa số nước là: 

$\frac{\text{1}}{\text{4}}\text{ + }\frac{\text{1}}{\text{6}}\text{ x 3 = }\frac{\text{3}}{\text{4}}$(bể) 

Khi mở cả ba vòi thì mỗi giờ chảy được số phần bể là: 

$\frac{\text{1}}{\text{6}}\text{ - }\frac{\text{1}}{\text{30}}\text{ = }\frac{\text{2}}{\text{15}}$(bể) 

Sau khi mở vòi thứ ba thì bể nước đầy sau số giờ là: 

$\left(\text{1 - }\frac{\text{3}}{\text{4}}\right)\text{ ÷ }\frac{\text{2}}{\text{15}}\text{ = }\frac{\text{15}}{\text{8}}$(giờ) 

Bài 44: Ba vòi nước 1, 2, 3 .Nếu chảy một mình vào một bể cạn thì chảy đầy bể theo thứ tự 4 giờ, 6 giờ, 9 giờ. Lúc đầu người ta mở hai vòi 1 và 2 trong 1 giờ 30 phút, sau đó đóng vòi 1 rồi mở tiếp vòi 3 cùng chảy với vòi 2 cho đến khi đầy bể. Hỏi vòi chảy trong bao lâu?

Lời giải:

Trong 1 giờ vòi I và II chảy được $\frac{1}{6}$ bể  

Trong 1 giờ vòi II và III chảy được $\frac{1}{8}$ bể

Trong 1 giờ vòi III và I chảy được $\frac{1}{12}$ bể              

Do đó trong 1 giờ cả 3 vòi chảy được 

$\left(\frac{\text{1}}{\text{6}}\text{ + }\frac{\text{1}}{\text{8}}\text{ + }\frac{\text{1}}{\text{12}}\right)\text{ : 2 = }\frac{\text{3}}{\text{16}}$ (bể)

Vậy thời gian để cả 3 vòi chảy đầy bể là 1:

 $\frac{3}{16}=\frac{16}{3}$  (giờ) = 320 (phút)       

b) Trong 1 giờ vòi III chảy được

$\frac{3}{16}-\frac{1}{6}=\frac{1}{48}$  (bể)

Bài 45: Cho một số có hai chữ số, khi ta viết thêm vào bên trái số đó một chữ số 1 thì tổng của số mới và số đã cho là 168 . Tìm số đã cho.

Lời giải:

Khi ta viết thêm vào bên trái số đó 1 thì tổng của số mới và số đã cho là:

(168 - 100) : 2 = 34

Đáp số: 34

Bài 46: Cho đa thức: f(x) = x⁴ + ax³ + bx² + cx + d ( với a, b, c, d là các số thực). Biết f(1) = 10; f(2) = 20; f(3) = 30. Tính giá trị của biểu thức: A = f(9) + f(-5)

Lời giải:

Đặt g(x) = f(x) – 10 (bậc 4)

$\iff \left\{\begin{array}{c}\text{g(1) = 0}\\ \text{g(2) = 0}\\ \text{g(3) = 0}\end{array}\right.\iff \text{g(x) = (x - 1)(x - 2)(x - 3)(x - m)}$ (m là hằng số)

$\begin{array}{l}\iff \text{f}\left(\text{x}\right)\text{ = }\left(\text{x - 1}\right)\left(\text{x - 2}\right)\left(\text{x - 3}\right)\left(\text{x - m}\right)\text{ - 10}\\ \iff \text{f}\left(\text{9}\right)\text{ = 8 . 7 . 6}\left(\text{9 - m}\right)\text{ - 10 = 336}\left(\text{9 - m}\right)\text{ - 10}\\ \text{f}\left(\text{-5}\right)\text{ = }\left(\text{- 6}\right)\left(\text{- 7}\right)\left(\text{- 8}\right)\left(\text{- 5 - m}\right)\text{ - 10 = 336}\left(\text{m + 5}\right)\text{ - 10}\end{array}$

Vậy A = 336(9 − m) + 336(m + 5) – 20 = 4684

Bài 47: Tìm 4 số lập thành một CSN biết tổng bốn số bằng 15 và tổng các bình phương của chúng bằng 85

Lời giải:

Giả sử 4 số cần tìm là ${\text{a; aq; aq}}^{\text{2}}{\text{; aq}}^{\text{3}}\text{, a}\ne \text{0}$

Theo Đề bài ta có: $\left\{\begin{array}{c}{\text{a + aq + aq}}^{\text{2}}{\text{ + aq}}^{\text{3}}\text{ = 15}\\ {\text{a}}^{\text{2}}{\text{ + a}}^{\text{2}}{\text{q}}^{\text{2}}{\text{ + a}}^{\text{2}}{\text{q}}^{\text{4}}{\text{ + a}}^{\text{2}}{\text{q}}^{\text{6}}\text{ = 85}\end{array}\right.$

$$\begin{gathered} \iff \left\{\begin{array}{c}{\text{a(1 + q + q}}^{\text{2}}{\text{ + q}}^{\text{3}}\text{) = 15}\\ {\text{a}}^{\text{2}}{\text{(1 + q}}^{\text{2}}{\text{ + q}}^{\text{4}}{\text{ + q}}^{\text{6}}\text{) = 85}\end{array}\right. \\ \left\{\begin{array}{c}{\text{a}}^2{{\text{(1 + q + q}}^{\text{2}}{\text{ + q}}^{\text{3}}\text{)}}^2{\text{ = 15}}^2\\ {\text{a}}^{\text{2}}{\text{(1 + q}}^{\text{2}}{\text{ + q}}^{\text{4}}{\text{ + q}}^{\text{6}}\text{) = 85}\end{array}\right. \\ \iff \frac{{{\text{(1 + q + q}}^{\text{2}}{\text{ + q}}^{\text{3}}\text{)}}^{\text{2}}}{{\text{(1 + q}}^{\text{2}}{\text{ + q}}^{\text{4}}{\text{ + q}}^{\text{6}}\text{)}}\text{ = }\frac{{\text{15}}^{\text{2}}}{\text{85}} \\ \iff {\text{85(1 + q + q}}^{\text{2}}{\text{ + q}}^{\text{3}}{\text{)}}^{\text{2}}{\text{ = 225(1 + q}}^{\text{2}}{\text{ + q}}^{\text{4}}{\text{ + q}}^{\text{6}}\text{)} \\ \iff {\text{14q}}^{\text{6}}{\text{ - 17q}}^{\text{5}}{\text{ - 3q}}^{\text{4}}{\text{ - 34q}}^{\text{3}}{\text{ - 3q}}^{\text{2}}\text{ - 17q + 14 = 0} \\ \iff {\text{(q - 2)(2q - 1)(7q}}^{\text{2}}{\text{ + q + 7)(q}}^{\text{2}}\text{ + 1) = 0} \\ \iff \left[\begin{array}{c}q=2\\ q=\frac{{\displaystyle 1}}{{\displaystyle 2}}\end{array}\right. \end{gathered}$$

Với  $\text{q = 2}\Rightarrow \text{a = }\frac{\text{15}}{{\text{1 + q + q}}^{\text{2}}{\text{ + q}}^{\text{3}}}\text{ = 1}$ ta có CSN: 1; 2; 4; 8

Với $\text{q = }\frac{\text{1}}{\text{2}}\Rightarrow \text{a = }\frac{\text{15}}{{\text{1 + q + q}}^{\text{2}}{\text{ + q}}^{\text{3}}}\text{ = 8}$ ta có CSN: 8; 4; 2; 1

Bài 48: Tính trung bình cộng hai đáy của một hình thang, biết rằng diện tích hình thang bằng 7m² và chiều cao bằng 2m.

A.3,5 m

B.7 m

C.14 m

D.9 m

Lời giải:

Trung bình cộng hai đáy của hình thang là: 7 : 2 = 3,5 (m)

Đáp án cần chọn là: A

Bài 49: Tính $\text{P = }\frac{\frac{\text{1}}{\text{2}}\text{ + }\frac{\text{1}}{\text{3}}\text{ + }\frac{\text{1}}{\text{4}}\text{ + }\mathrm{...}\text{ + }\frac{\text{1}}{\text{2012}}}{\frac{\text{2011}}{\text{1}}\text{ + }\frac{\text{2010}}{\text{2}}\text{ + }\frac{\text{2009}}{\text{3}}\text{ + }\mathrm{...}\text{ + }\frac{\text{1}}{\text{2011}}}$

Lời giải:

Đặt $B=\frac{\text{2011}}{\text{1}}\text{ + }\frac{\text{2010}}{\text{2}}\text{ + }\frac{\text{2009}}{\text{3}}\text{ + }\mathrm{...}\text{ + }\frac{\text{1}}{\text{2011}}$

Cộng 1 vào ta được

$B=\left(\frac{\text{2012}}{\text{1}}\text{ + }\frac{\text{2012}}{\text{2}}\text{ + }\frac{\text{2012}}{\text{3}}\text{ + }\mathrm{...}\text{ + }\frac{2012}{\text{2011}}+\frac{2012}{2012}\right)-2012$

$\Rightarrow \text{B = 2012}\left(\frac{\text{1}}{\text{2}}\text{ + }\frac{\text{1}}{\text{3}}\text{ + }\mathrm{...}\text{ + }\frac{\text{1}}{\text{2011}}\text{ + }\frac{\text{1}}{\text{2012}}\right)\text{ - 2012 + }\frac{\text{2012}}{\text{1}}$

Thay vào P ta được

$P=\frac{\frac{\text{1}}{\text{2}}\text{ + }\frac{\text{1}}{\text{3}}\text{ + }\mathrm{...}\text{ + }\frac{\text{1}}{\text{2012}}}{2012\left(\frac{\text{1}}{\text{2}}\text{ + }\frac{\text{1}}{\text{3}}\text{ + }\mathrm{...}\text{ + }\frac{\text{1}}{\text{2012}}\right)}$

$\Rightarrow P=\frac{1}{2012}$

Bài 50: Tìm x biết 135 - 5(x + 4) = 35

Lời giải:

135 - 5(x + 4) = 35

5(x + 4) = 135 - 35

5(x + 4) = 100

x + 4 = 100 : 5

x + 4 = 20

x = 20 - 4

x = 16

Bài 51: Có 4 đội bóng đá thi đấu vòng tròn( hai đội bất kì đều gặp nhau một trận)

a) Hỏi có bao nhiêu trận.

b) Câu hỏi với n đội bóng thi đấu vòng tròn thì có tất cả bao nhiêu trận

Lời giải:

a) Có 4 đội bóng thi đấu với nhau mà mỗi đội đều được đá với 3 đội còn lại nên số trận đấu là:

4 x 3 = 12 ( trận đấu )

Nhưng do mỗi trận đã bị tính hai lần nên số trận đấu là:

12 : 2 = 6 ( trận đấu )

b) Tương tự như câu a ta sẽ có công thức tổng quát cho n đội

n ( n - 1 ) : 2 ( trận đấu ) 

Bài 52: Trong 1 bảng đấu loại bóng đá có 4 đội thi đấu vòng tròn 1 lượt đội thắng được 3 điểm, đội hòa được 1 điểm, đội thua được 0 điểm. Tổng số điểm của 4 đội khi kết thúc bảng đấu là 16 điểm. Tính số trận hòa.

Lời giải:

Tổng số trận trong bảng đấu là: 4 . 3 : 2 = 6 ( trận)

Tổng số điểm trong trận thắng ( cũng như trận thua) là: 3 + 0 = 3 ( điểm)

Tổng số điểm trong trận hòa là: 1 + 1 = 2 ( điểm)

Nếu cả 6 trận đều thắng thì có tổng số điểm là: 6 . 3 = 18 ( điểm)

Số điểm còn thiếu là: 18 – 16 = 2 ( điểm)

Có số trận hòa là: 2 : 1 = 2 ( trận)

Vậy có 2 trận hòa

Bài 53: Cho tam giác ABC có AB = 2, AC = 3, $\widehat{\text{BAC}}\text{ = 60°}$ . Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn $\overrightarrow{\text{AD}}\text{ = }\frac{\text{7}}{\text{12}}\overrightarrow{\text{AC}}$

a) Tính $\overrightarrow{\text{AB}}\text{ . }\overrightarrow{\text{AC}}$

b) Biểu diễn $\overrightarrow{\text{AM}}\text{, }\overrightarrow{\text{BD}}$ theo $\overrightarrow{\text{AB}}\text{, }\overrightarrow{\text{AC}}$

c) Chứng minh $AM\perp BD$

Lời giải:

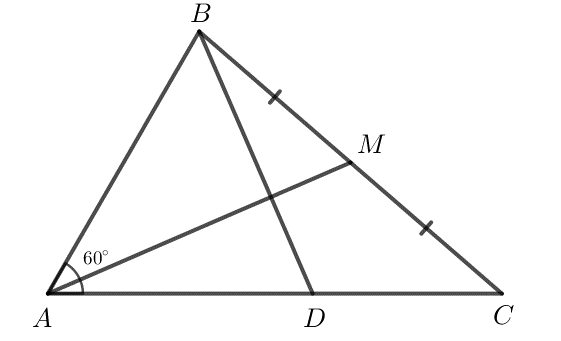
a) Ta có $\overrightarrow{\text{AB}}\text{ . }\overrightarrow{\text{AC}}\text{ = }\left|\overrightarrow{\text{AB}}\right|\text{ . }\left|\overrightarrow{\text{AC}}\right|\text{ . cos}\left(\overrightarrow{\text{AB}}\text{, }\overrightarrow{\text{AC}}\right){\text{ = 2 . 3 . cos 60}}^{\text{o}}\text{ = 3.}$

Vậy $\overrightarrow{\text{AB}}\text{ . }\overrightarrow{\text{AC}}=3$

b) Do M là trung điểm của BC nên $\overrightarrow{\text{AM}}\text{ = }\frac{\text{1}}{\text{2}}\overrightarrow{\text{AB}}\text{ + }\frac{\text{1}}{\text{2}}\overrightarrow{\text{AC}}$

Ta có $\overrightarrow{\text{BD}}\text{ = }\overrightarrow{\text{AD}}\text{ - }\overrightarrow{\text{AB}}\text{ = }\frac{\text{7}}{\text{12}}\overrightarrow{\text{AC}}\text{ - }\overrightarrow{\text{AB}}$

c) Ta có $\overrightarrow{\text{AM}}\text{ . }\overrightarrow{\text{BD}}\text{ = }\left(\frac{\text{1}}{\text{2}}\overrightarrow{\text{AB}}\text{ + }\frac{\text{1}}{\text{2}}\overrightarrow{\text{AC}}\right)\text{ . }\left(\frac{\text{7}}{\text{12}}\overrightarrow{\text{AC}}\text{ - }\overrightarrow{\text{AB}}\right)$

$$\begin{gathered} \text{= }\frac{\text{7}}{\text{24}}\overrightarrow{\text{AB}}\text{ . }\overrightarrow{\text{AC}}\text{ - }\frac{\text{1}}{\text{2}}{\overrightarrow{\text{AB}}}^{\text{2}}\text{ + }\frac{\text{7}}{\text{24}}{\overrightarrow{\text{AC}}}^{\text{2}}\text{ - }\frac{\text{1}}{\text{2}}\overrightarrow{\text{AC}}\text{ . }\overrightarrow{\text{AB}} \\ \text{= }\frac{\text{7}}{\text{24}}\text{ . 3 - }\frac{\text{1}}{\text{2}}{\text{ . 2}}^{\text{2}}\text{ + }\frac{\text{7}}{\text{24}}{\text{ . 3}}^{\text{2}}\text{ - }\frac{\text{1}}{\text{2}}\text{ . 3 = 0} \end{gathered}$$

Do đó $AM\perp BD$.

Bài 54: Khoanh vào chữ đặt trước câu trả lời đúng:

Có 20 viên bi, trong đó có 3 viên bi nâu, 4 viên bi xanh, 5 viên bi đỏ, 8 viên bi vàng. Như vậy, 1515 số viên bi có màu:

A. Nâu

B. Xanh

C. Đỏ

D. Vàng

Lời giải:

$\frac{3}{20}$ số viên bi có màu nâu.

$\frac{\text{4}}{\text{20}}\text{ = }\frac{\text{1}}{\text{5}}$ số viên bi có màu xanh

$\frac{\text{5}}{\text{20}}\text{ = }\frac{\text{1}}{\text{4}}$ số viên bi có màu đỏ.

$\frac{\text{8}}{\text{20}}\text{ = }\frac{\text{2}}{\text{5}}$ số viên bi có màu vàng.

Khoanh vào B.

Bài 55: Hoa có 48 viên bi đỏ, 30 viên bi xanh và 60 viên bi vàng. Hoa muốn chia đều số bi vào các túi, sao cho mỗi túi có đủ 3 loại bi. Hỏi Hoa có thể chia vào nhiều nhất bao nhiêu túi mà mỗi túi có số bi mỗi màu bằng nhau.

A.6                    

B.8                  

C.4            

D.12

Lời giải:

Ta có: 

Gọi số túi mà Hoa chia được là x  (túi) 

Vì số bi mỗi màu ở mỗi túi cũng bằng nhau nên $\text{48 }⋮\text{ x; 30 }⋮\text{x}$ và $\text{60 }⋮\text{ x}$

$\Rightarrow \text{x}\in$ ƯC(48; 30; 60)

Vì x  là lớn nhất nên x = ƯCLN(48; 30; 60)
Ta có: 48 = 2⁴ . 3; 30 = 2 . 3 . 5; 60 = 2² . 3 . 5

$\Rightarrow$x = ƯCLN(48; 30; 60) = 2 . 3 = 6 .

Vậy Hoa chia được nhiều nhất là 6 túi mà mỗi túi có số bi mỗi màu bằng nhau.

Đáp án cần chọn là: A

Bài 56: Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng

(d) : y = (m - 3)x + 1 $\left(\text{m }\ne \text{3}\right)$ bằng $\frac{1}{2}$

Lời giải:

Gọi A là giao điểm của d với Ox $\Rightarrow \text{A}\left(\text{-}\frac{\text{1}}{\text{m-3}}\text{; 0}\right)\Rightarrow \text{OA = }\frac{\text{1}}{\left|\text{m - 3}\right|}$

Gọi B là giao điểm của d với Oy $\Rightarrow \text{B}\left(\text{0; 1}\right)\Rightarrow \text{OB = 1}$

Từ O kẻ OH vuông góc AB $\Rightarrow \text{OH = }\frac{\text{1}}{\text{2}}$

Áp dụng hệ thức lượng trong tam giác vuông OAB:

$$\begin{gathered} \frac{\text{1}}{{\text{OH}}^{\text{2}}}\text{ = }\frac{\text{1}}{{\text{OA}}^{\text{2}}}\text{ + }\frac{\text{1}}{{\text{OB}}^{\text{2}}}\Rightarrow \text{4 = }{\left(\text{m - 3}\right)}^{\text{2}}\text{ + 1} \\ \Rightarrow {\left(m-3\right)}^2=3\Rightarrow \left[\begin{array}{c}m=3+\sqrt{3}\\ m=3-\sqrt{3}\end{array}\right. \end{gathered}$$

Bài 57: Tìm m để khoảng cách từ gốc tọa độ O đến đồ thị hàm số (1) bằng $\frac{2}{\sqrt{5}}$

Lời giải:

Điều kiện $m\ne 0$

Gọi A, B lần lượt là các giao điểm của đường thẳng (1) với các trục Ox, Oy.

Khi đó ta có: $\text{A}\left({\text{x}}_{\text{1}}\text{;\hspace{0.33em}0}\right)\text{,\hspace{0.33em}\hspace{0.33em}B}\left({\text{0;\hspace{0.33em}y}}_{\text{2}}\right)\text{.}$

$\Rightarrow \left\{\begin{array}{c}{\text{0 = mx}}_{\text{1}}\text{ + 1}\\ {\text{m . 0 + 1 = y}}_{\text{2}}\end{array}\iff \left\{\begin{array}{c}{\text{x}}_{\text{1}}\text{ = -}\frac{\text{1}}{\text{m}}\\ {\text{y}}_{\text{2}}\text{ = 1}\end{array}\right.\right.\iff \left\{\begin{array}{c}\text{A(-}\frac{\text{1}}{\text{m}}\text{; 0)}\\ \text{B(0; 1)}\end{array}\right.\iff \left\{\begin{array}{c}\text{OA = }\left|\text{-}\frac{\text{1}}{\text{m}}\right|\text{ = }\frac{\text{1}}{\left|\text{m}\right|}\\ \text{OB = |1| = 1}\end{array}\right.$

Gọi H là hình chiếu của O trên đường thẳng (1)  $\Rightarrow \text{OH = }\frac{\text{2}}{\sqrt{\text{5}}}\text{.}$

Khi đó ta có  vuông tại O và có đường cao OH.

Áp dụng hệ thức lượng cho  vuông tại O và có đường cao OH ta có:

$\begin{array}{l}\frac{\text{1}}{{\text{OH}}^{\text{2}}}\text{ = }\frac{\text{1}}{{\text{OA}}^{\text{2}}}\text{ + }\frac{\text{1}}{{\text{OB}}^{\text{2}}}\iff \frac{\text{1}}{{\left(\frac{\text{2}}{\sqrt{\text{5}}}\right)}^{\text{2}}}\text{ = }\frac{\text{1}}{{\left|{\text{x}}_{\text{1}}\right|}^{\text{2}}}\text{ + }\frac{\text{1}}{{\left|{\text{y}}_{\text{2}}\right|}^{\text{2}}}\\ \iff \frac{\text{5}}{\text{4}}\text{ = }\frac{\text{1}}{{\left(\text{-}\frac{\text{1}}{\text{m}}\right)}^{\text{2}}}\text{ + }\frac{\text{1}}{{\text{1}}^{\text{2}}}\iff \frac{\text{5}}{\text{4}}{\text{ = m}}^{\text{2}}\text{ + 1}\\ \iff {\text{5 = 4m}}^{\text{2}}\text{ + 4}\iff {\text{4m}}^{\text{2}}\text{ = 1}\iff {\text{m}}^{\text{2}}\text{ = }\frac{\text{1}}{\text{4}}\iff \text{m = ±}\frac{\text{1}}{\text{2}}\left(\text{tm}\right)\end{array}$

Vậy $\text{m = ±}\frac{\text{1}}{\text{2}}$ thỏa mãn điều kiện bài toán.

Chọn C.

Bài 58: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

Lời giải:

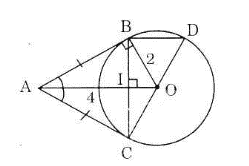
Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).

Xét $\Delta CBD$ có :

CI = IB

CO = OD (bán kính)

⇒ BD // HO (HO là đường trung bình của BCD) ⇒ BD // AO.

Bài 59: Cho $\text{ΔABC}$. Gọi I là điểm trên cạnh BC sao cho 2CI = 3BI và J là điểm trên BC kéo dài sao cho 5JB = 2JC. Gọi G là trọng tâm tam giác.

a) Biểu diễn AB, AC theo hai vectơ $\overrightarrow{\text{AI}}\text{, }\overrightarrow{\text{AJ}}$ và biểu diễn AJ qua AB, AC

b) Biểu diễn AG theo hai vectơ $\overrightarrow{\text{AI}}\text{, }\overrightarrow{\text{AJ}}$

Lời giải:

a) I là điểm trên cạnh BC mà: $\text{2CI = 3BI}\Rightarrow \frac{\text{BI}}{\text{CI}}\text{ = }\frac{\text{2}}{\text{3}}$

$$\begin{gathered} \Rightarrow \frac{\text{BI}}{\text{CI + BI}}\text{ = }\frac{\text{2}}{\text{3 + 2}}\Rightarrow \frac{\text{BI}}{\text{BC}}\text{ = }\frac{\text{2}}{\text{5}} \\ \Rightarrow \text{BI = }\frac{\text{2}}{\text{5}}\text{BC} \end{gathered}$$

Tương tự $\text{IC = }\frac{\text{3}}{\text{5}}\text{BC}$

J là điểm trên BC kéo dài:  $\text{5JB = 2JC}\Rightarrow \frac{\text{JB}}{\text{JC}}\text{ = }\frac{\text{2}}{\text{5}}$

Bài 60: Cho đường thẳng d và hai điểm A, B nằm cùng phía với d. Tìm điểm M trên d sao cho MA + MB đạt giá trị nhỏ nhất ?

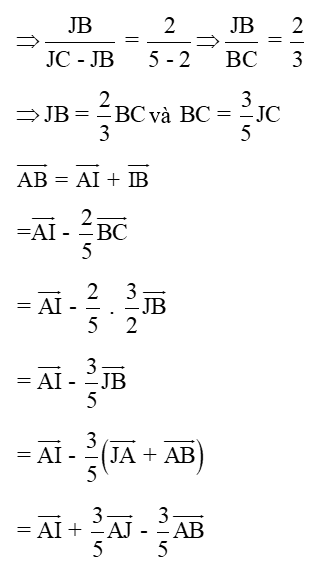
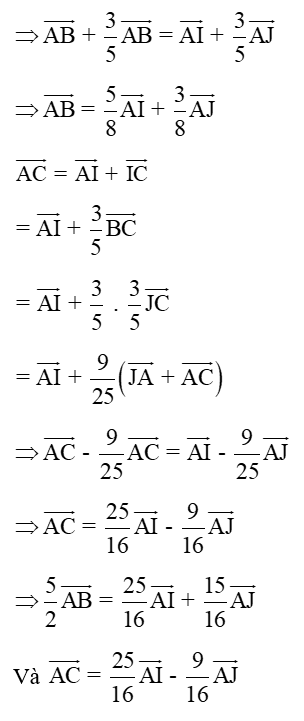
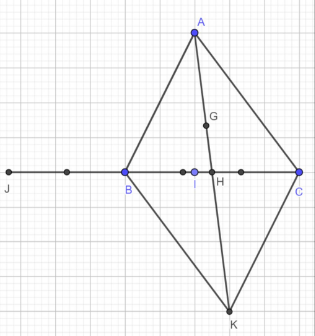
Lời giải:

- Tìm điểm A’ đối xứng với A qua d

- Nối A’B cắt d tại M. M chính là điểm cần tìm.

- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA = MA’.

Do đó : MA + MB = MA’ + MB = A’B .

- Giả sử tồn tại M’ khác M thuộc d thì : M’A + M’B = M’A’ + M’B lớn hơn hoặc bằng A'B. Dấu bằng chỉ xảy ra khi A’M’B thẳng hàng. Nghĩa là M trùng với M’